Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán thành phố Đà Nẵng năm 2020 chính thức. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi sắp tới.
Bộ đề thi này bao gồm đầy đủ các đề thi chính thức, kèm theo đáp án chi tiết và lời giải bài bản, giúp các em hiểu rõ phương pháp giải từng dạng bài.
Bài 1: a) Tính giá trị của biểu thức
Bài 1:
a) Tính giá trị của biểu thức \(A = \sqrt 3 + \sqrt {12} - \sqrt {27} - \sqrt {36} \)
b) Cho biểu thức \(B = \dfrac{2}{{\sqrt x - 1}} - \dfrac{1}{{\sqrt x }} + \dfrac{{3\sqrt x - 5}}{{\sqrt x \left( {\sqrt x - 1} \right)}}\) với \(x > 0\) và \(x \ne 1\). Rút gọn biểu thức \(B\) và tìm \(x\) để \(B = 2\)
Bài 2:
Cho hàm số \(y = \dfrac{1}{2}{x^2}\).
a) Vẽ đồ thị \(\left( P \right)\) của hàm số đã cho.
b) Đường thẳng \(y = 8\) cắt đồ thị \(\left( P \right)\) tại hai điểm phân biệt \(A\) và \(B\), trong đó điểm \(B\) có hoành độ dương. Gọi \(H\) là chân đường cao hạ từ \(A\) của tam giác \(OAB\), với \(O\) là gốc tọa độ. Tính diện tích tam giác \(AHB\) (đơn vị đo trên các trục tọa độ là xentimét).
Bài 3:
a) Giải phương trình \(3{x^2} - 7x + 2 = 0.\)
b) Biết phương trình \({x^2} - 19x + 7 = 0\) có hai nghiệm là \({x_1}\) và \({x_2},\) không giải phương trình, hãy tính giá trị biểu thức: \(P = {x_2}{\left( {2x_1^2 - 38{x_1} + {x_1}{x_2} - 3} \right)^2} + {x_1}{\left( {2x_2^2 - 38{x_2} + {x_1}{x_2} - 3} \right)^2} + 120.\)
Bài 4:
a) Một số tự nhiên nhỏ hơn bình phương của nó 20 đơn vị. Tìm số tự nhiên đó.
b) Quãng đường AB gồm một đoạn lên dốc và một đoạn xuống dốc. Một người đi xe đạp từ A đến B hết 16 phút và đi từ B về A hết 14 phút. Biết vận tốc lúc lên dốc là 10km/h, vận tốc lúc xuống dốc là 15km/h (vận tốc lên dốc, xuống dốc lúc đi và về như nhau). Tính quãng đường AB.
Bài 5:
Cho tam giác ABC nội tiếp đường tròn O đường kính AB. Trên cung nhỏ \(BC\) của đường tròn \(\left( O \right)\) lấy điểm \(D\) (không trùng với \(B\) và \(C\)). Gọi \(H\) là chân đường vuông góc kẻ từ \(C\) đến \(AB\,\,\left( {H \in AB} \right)\) và \(E\) là giao điểm của \(CH\) với \(AD\).
a) Chứng minh rằng tứ giác \(BDEH\) là tứ giác nội tiếp.
b) Chứng minh rằng \(A{B^2} = AE.AD + BH.BA\).
c) Đường thẳng qua \(E\) song song với \(AB\), cắt \(BC\) tại \(F\). Chứng minh rằng \(\angle CDF = {90^0}\) và đường tròn ngoại tiếp tam giác \(OBD\) đi qua trung điểm của đoạn \(CF\).
Bài 1:
a) Tính giá trị của biểu thức \(A = \sqrt 3 + \sqrt {12} - \sqrt {27} - \sqrt {36} \)
b) Cho biểu thức \(B = \dfrac{2}{{\sqrt x - 1}} - \dfrac{1}{{\sqrt x }} + \dfrac{{3\sqrt x - 5}}{{\sqrt x \left( {\sqrt x - 1} \right)}}\) với \(x > 0\) và \(x \ne 1\). Rút gọn biểu thức \(B\) và tìm \(x\) để \(B = 2\)
Bài 2:
Cho hàm số \(y = \dfrac{1}{2}{x^2}\).
a) Vẽ đồ thị \(\left( P \right)\) của hàm số đã cho.
b) Đường thẳng \(y = 8\) cắt đồ thị \(\left( P \right)\) tại hai điểm phân biệt \(A\) và \(B\), trong đó điểm \(B\) có hoành độ dương. Gọi \(H\) là chân đường cao hạ từ \(A\) của tam giác \(OAB\), với \(O\) là gốc tọa độ. Tính diện tích tam giác \(AHB\) (đơn vị đo trên các trục tọa độ là xentimét).
Bài 3:
a) Giải phương trình \(3{x^2} - 7x + 2 = 0.\)
b) Biết phương trình \({x^2} - 19x + 7 = 0\) có hai nghiệm là \({x_1}\) và \({x_2},\) không giải phương trình, hãy tính giá trị biểu thức: \(P = {x_2}{\left( {2x_1^2 - 38{x_1} + {x_1}{x_2} - 3} \right)^2} + {x_1}{\left( {2x_2^2 - 38{x_2} + {x_1}{x_2} - 3} \right)^2} + 120.\)
Bài 4:
a) Một số tự nhiên nhỏ hơn bình phương của nó 20 đơn vị. Tìm số tự nhiên đó.
b) Quãng đường AB gồm một đoạn lên dốc và một đoạn xuống dốc. Một người đi xe đạp từ A đến B hết 16 phút và đi từ B về A hết 14 phút. Biết vận tốc lúc lên dốc là 10km/h, vận tốc lúc xuống dốc là 15km/h (vận tốc lên dốc, xuống dốc lúc đi và về như nhau). Tính quãng đường AB.
Bài 5:
Cho tam giác ABC nội tiếp đường tròn O đường kính AB. Trên cung nhỏ \(BC\) của đường tròn \(\left( O \right)\) lấy điểm \(D\) (không trùng với \(B\) và \(C\)). Gọi \(H\) là chân đường vuông góc kẻ từ \(C\) đến \(AB\,\,\left( {H \in AB} \right)\) và \(E\) là giao điểm của \(CH\) với \(AD\).
a) Chứng minh rằng tứ giác \(BDEH\) là tứ giác nội tiếp.
b) Chứng minh rằng \(A{B^2} = AE.AD + BH.BA\).
c) Đường thẳng qua \(E\) song song với \(AB\), cắt \(BC\) tại \(F\). Chứng minh rằng \(\angle CDF = {90^0}\) và đường tròn ngoại tiếp tam giác \(OBD\) đi qua trung điểm của đoạn \(CF\).
Bài 1. (1,0 điểm)
Cách giải:
a) Tính giá trị của biểu thức \(A = \sqrt 3 + \sqrt {12} - \sqrt {27} - \sqrt {36} \)
\(\begin{array}{l}\,\,\,\,\,A = \sqrt 3 + \sqrt {12} - \sqrt {27} - \sqrt {36} \\ \Leftrightarrow A = \sqrt 3 + \sqrt {{2^2}.3} - \sqrt {{3^2}.3} - \sqrt {{6^2}} \\ \Leftrightarrow A = \sqrt 3 + 2\sqrt 3 - 3\sqrt 3 - 6\\ \Leftrightarrow A = \sqrt 3 .\left( {1 + 2 - 3} \right) - 6\\ \Leftrightarrow A = - 6\end{array}\)
Vậy \(A = - 6\).
b) Cho biểu thức \(B = \dfrac{2}{{\sqrt x - 1}} - \dfrac{1}{{\sqrt x }} + \dfrac{{3\sqrt x - 5}}{{\sqrt x \left( {\sqrt x - 1} \right)}}\) với \(x > 0\) và \(x \ne 1\). Rút gọn biểu thức \(B\) và tìm \(x\) để \(B = 2\)
Với \(x > 0\) và \(x \ne 1\) ta có:
\(\begin{array}{l}\,\,\,\,\,B = \dfrac{2}{{\sqrt x - 1}} - \dfrac{1}{{\sqrt x }} + \dfrac{{3\sqrt x - 5}}{{\sqrt x \left( {\sqrt x - 1} \right)}}\\ \Leftrightarrow B = \dfrac{{2\sqrt x - \left( {\sqrt x - 1} \right) + 3\sqrt x - 5}}{{\sqrt x \left( {\sqrt x - 1} \right)}}\\ \Leftrightarrow B = \dfrac{{2\sqrt x - \sqrt x + 1 + 3\sqrt x - 5}}{{\sqrt x \left( {\sqrt x - 1} \right)}}\\ \Leftrightarrow B = \dfrac{{4\sqrt x - 4}}{{\sqrt x \left( {\sqrt x - 1} \right)}}\\ \Leftrightarrow B = \dfrac{{4\left( {\sqrt x - 1} \right)}}{{\sqrt x \left( {\sqrt x - 1} \right)}} = \dfrac{4}{{\sqrt x }}\end{array}\)
Vậy với \(x > 0,\,\,x \ne 1\) thì \(B = \dfrac{4}{{\sqrt x }}\).
Để \(B = 2\) thì \(\dfrac{4}{{\sqrt x }} = 2 \Leftrightarrow \sqrt x = 2 \Leftrightarrow x = 4\,\,\left( {tm} \right)\).
Vậy để \(B = 2\) thì \(x = 4\).
Bài 2. (1,5 điểm)
Cách giải:
Cho hàm số \(y = \dfrac{1}{2}{x^2}\).
a) Vẽ đồ thị \(\left( P \right)\) của hàm số đã cho.
Ta có bảng giá trị:
\(x\) | \( - 4\) | \( - 2\) | \(0\) | \(2\) | \(4\) |
\(y = \dfrac{1}{2}{x^2}\) | \(8\) | \(2\) | \(0\) | \(2\) | \(8\) |
Vậy đồ thị hàm số \(\left( P \right):\,\,y = \dfrac{1}{2}{x^2}\) là đường cong nhận trục tung làm trục đối xứng và đi qua các điểm \(\left( { - 4;\,\,8} \right),\,\,\left( { - 2;\,\,2} \right),\,\,\left( {0;\,\,0} \right),\,\,\,\left( {2;\,\,2} \right),\,\,\,\left( {4;\,\,8} \right).\)
Đồ thị hàm số:
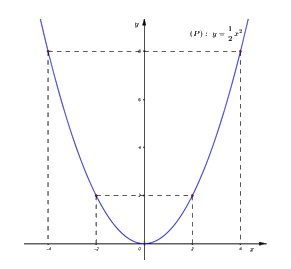
b) Đường thẳng \(y = 8\) cắt đồ thị \(\left( P \right)\) tại hai điểm phân biệt \(A\) và \(B\), trong đó điểm \(B\) có hoành độ dương. Gọi \(H\) là chân đường cao hạ từ \(A\) của tam giác \(OAB\), với \(O\) là gốc tọa độ. Tính diện tích tam giác \(AHB\) (đơn vị đo trên các trục tọa độ là xentimét).
Xét phương trình hoành độ giao điểm của đồ thị hàm số \(\left( P \right)\) và đường thẳng \(y = 8\) ta có:
\(\dfrac{1}{2}{x^2} = 8 \Leftrightarrow {x^2} = 16 \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = - 4\end{array} \right.\)
+) Với \(x = - 4 \Rightarrow A\left( { - 4;\,\,8} \right)\).
+) Với \(x = 4 \Rightarrow B\left( {4;\,\,8} \right)\) (Vì \(B\) là điểm có hoành độ dương).
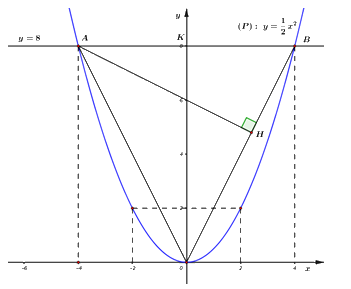
Gọi \(K\) là giao điểm của đường thẳng \(y = 8\) với trục tung \( \Rightarrow K\left( {0;\,\,8} \right).\)
Ta có: \(\Delta AOB\) cân tại \(O\), có \(OK \bot AB\), \(OK = 8\,\,\left( {cm} \right),\,\,AB = 8\,\,\left( {cm} \right)\).
\( \Rightarrow {S_{OAB}} = \dfrac{1}{2}OK.AB = \dfrac{1}{2}.8.8 = 32\,\,c{m^2}.\)
Áp dụng định lý Pi-ta-go cho \(\Delta OBK\) vuông tại \(K\) ta có:
\(OB = \sqrt {O{K^2} + K{B^2}} = \sqrt {{8^2} + {4^2}} = 4\sqrt 5 \,\,\left( {cm} \right)\)
Lại có: \({S_{OAB}} = \dfrac{1}{2}AH.OB\)\( \Leftrightarrow \dfrac{1}{2}AH.4\sqrt 5 = 32 \Leftrightarrow AH = \dfrac{{16\sqrt 5 }}{5}\,\,\left( {cm} \right).\)
Áp dụng định lý Pitago cho \(\Delta ABH\) vuông tại \(H\) ta có:
\(BH = \sqrt {A{B^2} - A{H^2}} = \sqrt {{8^2} - {{\left( {\dfrac{{16\sqrt 5 }}{5}} \right)}^2}} = \sqrt {\dfrac{{64}}{5}} = \dfrac{{8\sqrt 5 }}{5}.\)
\( \Rightarrow {S_{ABH}} = \dfrac{1}{2}AH.BH = \dfrac{1}{2}.\dfrac{{16\sqrt 5 }}{5}.\dfrac{{8\sqrt 5 }}{5} = \dfrac{{64}}{5}\, = 12,8\,\,c{m^2}.\)
Vậy diện tích tam giác \(ABH\) là \(12,8\,c{m^2}.\)
Bài 3. (1,5 điểm)
Cách giải:
a) Giải phương trình \(3{x^2} - 7x + 2 = 0.\)
Phương trình có: \(\Delta = {b^2} - 4ac = {7^2} - 4.3.2 = 25 > 0\)
\( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \(\left[ \begin{array}{l}{x_1} = \dfrac{{7 + \sqrt {25} }}{6} = 2\\{x_2} = \dfrac{{7 - \sqrt {25} }}{6} = \dfrac{1}{3}\end{array} \right..\)
Vậy phương trình đã cho tập nghiệm: \(S = \left\{ {\dfrac{1}{3};\,\,2} \right\}.\)
b) Biết phương trình \({x^2} - 19x + 7 = 0\) có hai nghiệm là \({x_1}\) và \({x_2},\) không giải phương trình, hãy tính giá trị biểu thức: \(P = {x_2}{\left( {2x_1^2 - 38{x_1} + {x_1}{x_2} - 3} \right)^2} + {x_1}{\left( {2x_2^2 - 38{x_2} + {x_1}{x_2} - 3} \right)^2} + 120.\)
Xét phương trình: \({x^2} - 19x + 7 = 0\) có \(\Delta = {19^2} - 4.7 = 333 > 0\) \( \Rightarrow \) Phương trình có hai nghiệm phân biệt\({x_1},\,\,{x_2}.\)
Áp dụng hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 19\\{x_1}{x_2} = 7\end{array} \right..\)
Ta có: \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình đã cho \( \Rightarrow \left\{ \begin{array}{l}x_1^2 - 19{x_1} + 7 = 0\\x_2^2 - 19{x_2} + 7 = 0\end{array} \right..\)
Theo đề bài ta có:
\(\begin{array}{l}P = {x_2}{\left( {2x_1^2 - 38{x_1} + {x_1}{x_2} - 3} \right)^2} + {x_1}{\left( {2x_2^2 - 38{x_2} + {x_1}{x_2} - 3} \right)^2} + 120\\\,\,\,\,\, = {x_2}{\left[ {2\left( {x_1^2 - 19{x_1} + 7} \right) - 14 + {x_1}{x_2} - 3} \right]^2} + {x_1}{\left[ {2\left( {x_2^2 - 19{x_2} + 7} \right) - 14 + {x_1}{x_2} - 3} \right]^2} + 120\\\,\,\,\,\, = {x_2}{\left( {{x_1}{x_2} - 17} \right)^2} + {x_1}{\left( {{x_1}{x_2} - 17} \right)^2} + 120\\\,\,\,\,\, = {\left( {{x_1}{x_2} - 17} \right)^2}\left( {{x_1} + {x_2}} \right) + 120\\\,\,\,\,\, = {\left( {7 - 17} \right)^2}.19 + 120\\\,\,\,\,\, = {19.10^2} + 120\\\,\,\,\, = 1900 + 120\\\,\,\,\, = 2020\end{array}\)
Bài 4. (2,0 điểm)
Cách giải:
a) Một số tự nhiên nhỏ hơn bình phương của nó 20 đơn vị. Tìm số tự nhiên đó.
Gọi số tự nhiên cần tìm là \(x\) (ĐK: \(x \in \mathbb{N}\)).
Bình phương của số tự nhiên \(x\) là \({x^2}\).
Vì số tự nhiên cần tìm nhỏ hơn bình phương của nó 20 đơn vị nên ta có phương trình:
\(\begin{array}{l}\,\,\,\,\,\,\,{x^2} - x = 20\\ \Leftrightarrow {x^2} - x - 20 = 0\\ \Leftrightarrow {x^2} - 5x + 4x - 20 = 0\\ \Leftrightarrow x\left( {x - 5} \right) + 4\left( {x - 5} \right) = 0\\ \Leftrightarrow \left( {x - 5} \right)\left( {x + 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 5 = 0\\x + 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 5\,\,\,\,\,\,\,\left( {tm} \right)\\x = - 4\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy số tự nhiên cần tìm là 5.
b) Quãng đường AB gồm một đoạn lên dốc và một đoạn xuống dốc. Một người đi xe đạp từ A đến B hết 16 phút và đi từ B về A hết 14 phút. Biết vận tốc lúc lên dốc là 10km/h, vận tốc lúc xuống dốc là 15km/h (vận tốc lên dốc, xuống dốc lúc đi và về như nhau). Tính quãng đường AB.
Gọi quãng đường lên dốc lúc đi là \(x\) (km), quãng đường xuống dốc lúc đi là \(y\) (km) (ĐK: \(x,y > 0\))
\( \Rightarrow \) Quãng đường lên dốc lúc về là \(y\) (km), quãng đường xuống dốc lúc về là \(x\) (km).
Thời gian lúc đi là 16 phút \( = \dfrac{{16}}{{60}} = \dfrac{4}{{15}}\)(h) nên ta có phương trình:
\(\dfrac{x}{{10}} + \dfrac{y}{{15}} = \dfrac{4}{{15}} \Leftrightarrow 3x + 2y = 8\,\,\left( 1 \right)\).
Thời gian lúc về là 14 phút \( = \dfrac{{14}}{{60}} = \dfrac{7}{{30}}\)(h) nên ta có phương trình:
\(\dfrac{y}{{10}} + \dfrac{x}{{15}} = \dfrac{7}{{30}} \Leftrightarrow 3x + 2x = 7\,\,\left( 2 \right)\).
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{l}3x + 2y = 8\\3y + 2x = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}9x + 6y = 24\\4x + 6y = 14\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x = 10\\3x + 2y = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\3.2 + 2y = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\2y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.\,\,\left( {tm} \right)\)
\( \Rightarrow \) Quãng đường lên dốc lúc đi là \(2\,\,km\), quãng đường xuống dốc lúc đi là \(1km\).
Vậy độ dài quãng đường AB là \(2 + 1 = 3\,\,\left( {km} \right)\).
Bài 5. (2,0 điểm)
Cách giải:
Cho tam giác ABC nội tiếp đường tròn O đường kính AB. Trên cung nhỏ \(BC\) của đường tròn \(\left( O \right)\) lấy điểm \(D\) (không trùng với \(B\) và \(C\)). Gọi \(H\) là chân đường vuông góc kẻ từ \(C\) đến \(AB\,\,\left( {H \in AB} \right)\) và \(E\) là giao điểm của \(CH\) với \(AD\).
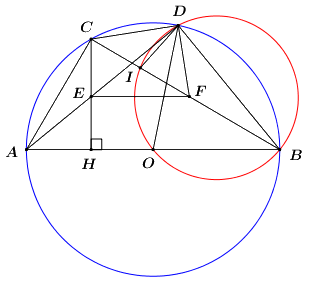
a) Chứng minh rằng tứ giác \(BDEH\) là tứ giác nội tiếp.
Vì \(\angle ADB\) là góc nội tiếp chắn nửa đường tròn \(\left( O \right)\) nên \(\angle ADB = {90^0}\) hay \(\angle EDB = {90^0}\).
Lại có \(CH \bot AB\) (gt) nên \(\angle CHB = {90^0} \Rightarrow \angle EHB = {90^0}\).
Xét tứ giác \(BDEH\) có: \(\angle EDB + \angle EHB = {90^0} + {90^0} = {180^0}\).
\( \Rightarrow BDEH\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng \({180^0}\)).
b) Chứng minh rằng \(A{B^2} = AE.AD + BH.BA\).
Vì \(ABDC\) là tứ giác nội tiếp đường tròn \(\left( O \right)\) nên \(\angle ADC = \angle ABC\) (1) (hai góc nội tiếp cùng chắn cung \(AC\)).
Ta lại có:
\(\angle ABC + \angle CAB = {90^0}\) (do tam giác \(ABC\) có \(\angle ACB = {90^0}\) - góc nội tiếp chắn nửa đường tròn).
\(\angle ACH + \angle CAB = {90^0}\) (do tam giác \(ACH\) vuông tại \(H\)).
\( \Rightarrow \angle ABC = \angle ACH\) (2) (cùng phụ với \(\angle CAB\)).
Từ (1) và (2) \( \Rightarrow \angle ADC = \angle ACH\) \(\left( { = \angle ABC} \right)\) hay \(\angle ADC = \angle ACE\).
Xét \(\Delta ACE\) và \(\Delta ADC\) có:
\(\angle CAD\) chung;
\(\angle ACE = \angle ADC\,\,\left( {cmt} \right)\).
\(\begin{array}{l} \Rightarrow \Delta ACE \sim \Delta ADC\,\,\left( {g.g} \right)\\ \Rightarrow \dfrac{{AC}}{{AD}} = \dfrac{{AE}}{{AC}} \Rightarrow A{C^2} = AE.AD\,\,\,\left( * \right)\end{array}\)
Xét tam giác \(ABC\) vuông tại \(C\), đường cao \(CH\) ta có:
\(B{C^2} = BH.BA\,\,\left( {2*} \right)\) (hệ thức lượng trong tam giác vuông).
Từ (*) và (2*) suy ra \(A{C^2} + B{C^2} = AE.AD + BH.BA\).
Lại có \(\Delta ABC\) vuông tại \(C\) nên \(A{C^2} + B{C^2} = A{B^2}\) (định lí Pytago).
Vậy \(A{B^2} = AE.AD + BH.BA\)(đpcm).
c) Đường thẳng qua \(E\) song song với \(AB\), cắt \(BC\) tại \(F\). Chứng minh rằng \(\angle CDF = {90^0}\) và đường tròn ngoại tiếp tam giác \(OBD\) đi qua trung điểm của đoạn \(CF\).
*) Vì \(EF//AB\,\,\,\left( {gt} \right)\) nên \(\angle CFE = \angle CBA\) (đồng vị).
Mà \(\angle CBA = \angle CDA\) (hai góc nội tiếp cùng chắn cung \(AC\)).
\( \Rightarrow \angle CFE = \angle CDA\).
\( \Rightarrow \) Tứ giác \(CDFE\) là tứ giác nội tiếp (Tứ giác có 2 đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau).
\(\angle CDF + \angle CEF = {180^0}\) (tổng hai góc đối của tứ giác nội tiếp).
Ta lại có:
\(\left\{ \begin{array}{l}CH \bot AB\,\,\left( {gt} \right)\\EF//AB\,\,\left( {gt} \right)\end{array} \right. \Rightarrow EF \bot CH\) (từ vuông góc đến song song) \( \Rightarrow \angle CEF = {90^0}\).
\( \Rightarrow \angle CDF = {180^0} - \angle CEF = {180^0} - {90^0} = {90^0}\,\,\left( {dpcm} \right)\).
*) Gọi \(I\) là giao điểm của \(CF\) và đường tròn ngoại tiếp tam giác \(OBD\).
Ta có:
\(\begin{array}{l}\angle ADB = \angle ADF + \angle FDB = {90^0}\\\angle CDF = \angle ADF + \angle CDA = {90^0}\end{array}\)
\( \Rightarrow \angle FBD = \angle CDA\) (cùng phụ với \(\angle ADF\)).
Mà \(\angle CDA = \angle CBA\) (hai góc nội tiếp cùng chắn cung \(AC\)).
\( \Rightarrow \angle FDB = \angle CBA\) \(\left( { = \angle CDA} \right)\).
Mà \(\angle CBA = \angle OBI = \angle ODI\) (hai góc nội tiếp cùng chắn cung \(OI\)).
\(\begin{array}{l} \Rightarrow \angle FDB = \angle ODI\\ \Rightarrow \angle FDB + \angle ODF = \angle ODI + \angle ODF\\ \Rightarrow \angle ODB = \angle IDF\,\,\left( 3 \right)\end{array}\)
Ta có: tứ giác \(CDFE\) nội tiếp (cmt) nên \(\angle IFD = \angle CFD = \angle CED = AEH\) (hai góc nội tiếp cùng chắn cung \(CD\)).
Ta lại có:
\(\begin{array}{l}\angle AEH + \angle EAH = {90^0}\\\angle ABD + \angle BAD = {90^0}\end{array}\)
Mà \(\angle EAH = \angle BAD\) nên \(\angle AEH = \angle ABD = \angle OBD\) \( \Rightarrow \angle IFD = \angle OBD\) (4)
Lại có: \(OD = OB\,\,\) (=bán kính) nên \(\Delta OBD\) cân tại \(O\), do đó \(\angle OBD = \angle ODB\) (5).
Từ (3), (4), (5) suy ra \(\angle IDF = \angle IFD\) \( \Rightarrow \Delta IDF\) cân tại \(I\) (định nghĩa) \( \Rightarrow ID = IF\) (3*) (tính chất tam giác cân).
Ta có:
\(\angle IDF + \angle IDC = \angle CDF = {90^0}\)
\(\angle IFD + \angle ICD = {90^0}\) (do tam giác \(CDF\) vuông tại \(D\)).
\( \Rightarrow \angle IDC = \angle ICD \Rightarrow \Delta ICD\) cân tại \(I\) (định nghĩa) \( \Rightarrow IC = ID\) (4*) (tính chất tam giác cân).
Từ (3*) và (4*) suy ra \(IC = IF\,\,\left( { = ID} \right)\).
Vậy \(I\) là trung điểm của \(CF\) (đpcm).
Bài 1. (1,0 điểm)
Cách giải:
a) Tính giá trị của biểu thức \(A = \sqrt 3 + \sqrt {12} - \sqrt {27} - \sqrt {36} \)
\(\begin{array}{l}\,\,\,\,\,A = \sqrt 3 + \sqrt {12} - \sqrt {27} - \sqrt {36} \\ \Leftrightarrow A = \sqrt 3 + \sqrt {{2^2}.3} - \sqrt {{3^2}.3} - \sqrt {{6^2}} \\ \Leftrightarrow A = \sqrt 3 + 2\sqrt 3 - 3\sqrt 3 - 6\\ \Leftrightarrow A = \sqrt 3 .\left( {1 + 2 - 3} \right) - 6\\ \Leftrightarrow A = - 6\end{array}\)
Vậy \(A = - 6\).
b) Cho biểu thức \(B = \dfrac{2}{{\sqrt x - 1}} - \dfrac{1}{{\sqrt x }} + \dfrac{{3\sqrt x - 5}}{{\sqrt x \left( {\sqrt x - 1} \right)}}\) với \(x > 0\) và \(x \ne 1\). Rút gọn biểu thức \(B\) và tìm \(x\) để \(B = 2\)
Với \(x > 0\) và \(x \ne 1\) ta có:
\(\begin{array}{l}\,\,\,\,\,B = \dfrac{2}{{\sqrt x - 1}} - \dfrac{1}{{\sqrt x }} + \dfrac{{3\sqrt x - 5}}{{\sqrt x \left( {\sqrt x - 1} \right)}}\\ \Leftrightarrow B = \dfrac{{2\sqrt x - \left( {\sqrt x - 1} \right) + 3\sqrt x - 5}}{{\sqrt x \left( {\sqrt x - 1} \right)}}\\ \Leftrightarrow B = \dfrac{{2\sqrt x - \sqrt x + 1 + 3\sqrt x - 5}}{{\sqrt x \left( {\sqrt x - 1} \right)}}\\ \Leftrightarrow B = \dfrac{{4\sqrt x - 4}}{{\sqrt x \left( {\sqrt x - 1} \right)}}\\ \Leftrightarrow B = \dfrac{{4\left( {\sqrt x - 1} \right)}}{{\sqrt x \left( {\sqrt x - 1} \right)}} = \dfrac{4}{{\sqrt x }}\end{array}\)
Vậy với \(x > 0,\,\,x \ne 1\) thì \(B = \dfrac{4}{{\sqrt x }}\).
Để \(B = 2\) thì \(\dfrac{4}{{\sqrt x }} = 2 \Leftrightarrow \sqrt x = 2 \Leftrightarrow x = 4\,\,\left( {tm} \right)\).
Vậy để \(B = 2\) thì \(x = 4\).
Bài 2. (1,5 điểm)
Cách giải:
Cho hàm số \(y = \dfrac{1}{2}{x^2}\).
a) Vẽ đồ thị \(\left( P \right)\) của hàm số đã cho.
Ta có bảng giá trị:
\(x\) | \( - 4\) | \( - 2\) | \(0\) | \(2\) | \(4\) |
\(y = \dfrac{1}{2}{x^2}\) | \(8\) | \(2\) | \(0\) | \(2\) | \(8\) |
Vậy đồ thị hàm số \(\left( P \right):\,\,y = \dfrac{1}{2}{x^2}\) là đường cong nhận trục tung làm trục đối xứng và đi qua các điểm \(\left( { - 4;\,\,8} \right),\,\,\left( { - 2;\,\,2} \right),\,\,\left( {0;\,\,0} \right),\,\,\,\left( {2;\,\,2} \right),\,\,\,\left( {4;\,\,8} \right).\)
Đồ thị hàm số:
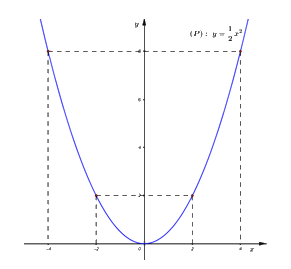
b) Đường thẳng \(y = 8\) cắt đồ thị \(\left( P \right)\) tại hai điểm phân biệt \(A\) và \(B\), trong đó điểm \(B\) có hoành độ dương. Gọi \(H\) là chân đường cao hạ từ \(A\) của tam giác \(OAB\), với \(O\) là gốc tọa độ. Tính diện tích tam giác \(AHB\) (đơn vị đo trên các trục tọa độ là xentimét).
Xét phương trình hoành độ giao điểm của đồ thị hàm số \(\left( P \right)\) và đường thẳng \(y = 8\) ta có:
\(\dfrac{1}{2}{x^2} = 8 \Leftrightarrow {x^2} = 16 \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = - 4\end{array} \right.\)
+) Với \(x = - 4 \Rightarrow A\left( { - 4;\,\,8} \right)\).
+) Với \(x = 4 \Rightarrow B\left( {4;\,\,8} \right)\) (Vì \(B\) là điểm có hoành độ dương).
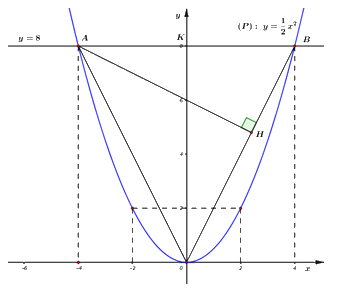
Gọi \(K\) là giao điểm của đường thẳng \(y = 8\) với trục tung \( \Rightarrow K\left( {0;\,\,8} \right).\)
Ta có: \(\Delta AOB\) cân tại \(O\), có \(OK \bot AB\), \(OK = 8\,\,\left( {cm} \right),\,\,AB = 8\,\,\left( {cm} \right)\).
\( \Rightarrow {S_{OAB}} = \dfrac{1}{2}OK.AB = \dfrac{1}{2}.8.8 = 32\,\,c{m^2}.\)
Áp dụng định lý Pi-ta-go cho \(\Delta OBK\) vuông tại \(K\) ta có:
\(OB = \sqrt {O{K^2} + K{B^2}} = \sqrt {{8^2} + {4^2}} = 4\sqrt 5 \,\,\left( {cm} \right)\)
Lại có: \({S_{OAB}} = \dfrac{1}{2}AH.OB\)\( \Leftrightarrow \dfrac{1}{2}AH.4\sqrt 5 = 32 \Leftrightarrow AH = \dfrac{{16\sqrt 5 }}{5}\,\,\left( {cm} \right).\)
Áp dụng định lý Pitago cho \(\Delta ABH\) vuông tại \(H\) ta có:
\(BH = \sqrt {A{B^2} - A{H^2}} = \sqrt {{8^2} - {{\left( {\dfrac{{16\sqrt 5 }}{5}} \right)}^2}} = \sqrt {\dfrac{{64}}{5}} = \dfrac{{8\sqrt 5 }}{5}.\)
\( \Rightarrow {S_{ABH}} = \dfrac{1}{2}AH.BH = \dfrac{1}{2}.\dfrac{{16\sqrt 5 }}{5}.\dfrac{{8\sqrt 5 }}{5} = \dfrac{{64}}{5}\, = 12,8\,\,c{m^2}.\)
Vậy diện tích tam giác \(ABH\) là \(12,8\,c{m^2}.\)
Bài 3. (1,5 điểm)
Cách giải:
a) Giải phương trình \(3{x^2} - 7x + 2 = 0.\)
Phương trình có: \(\Delta = {b^2} - 4ac = {7^2} - 4.3.2 = 25 > 0\)
\( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \(\left[ \begin{array}{l}{x_1} = \dfrac{{7 + \sqrt {25} }}{6} = 2\\{x_2} = \dfrac{{7 - \sqrt {25} }}{6} = \dfrac{1}{3}\end{array} \right..\)
Vậy phương trình đã cho tập nghiệm: \(S = \left\{ {\dfrac{1}{3};\,\,2} \right\}.\)
b) Biết phương trình \({x^2} - 19x + 7 = 0\) có hai nghiệm là \({x_1}\) và \({x_2},\) không giải phương trình, hãy tính giá trị biểu thức: \(P = {x_2}{\left( {2x_1^2 - 38{x_1} + {x_1}{x_2} - 3} \right)^2} + {x_1}{\left( {2x_2^2 - 38{x_2} + {x_1}{x_2} - 3} \right)^2} + 120.\)
Xét phương trình: \({x^2} - 19x + 7 = 0\) có \(\Delta = {19^2} - 4.7 = 333 > 0\) \( \Rightarrow \) Phương trình có hai nghiệm phân biệt\({x_1},\,\,{x_2}.\)
Áp dụng hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 19\\{x_1}{x_2} = 7\end{array} \right..\)
Ta có: \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình đã cho \( \Rightarrow \left\{ \begin{array}{l}x_1^2 - 19{x_1} + 7 = 0\\x_2^2 - 19{x_2} + 7 = 0\end{array} \right..\)
Theo đề bài ta có:
\(\begin{array}{l}P = {x_2}{\left( {2x_1^2 - 38{x_1} + {x_1}{x_2} - 3} \right)^2} + {x_1}{\left( {2x_2^2 - 38{x_2} + {x_1}{x_2} - 3} \right)^2} + 120\\\,\,\,\,\, = {x_2}{\left[ {2\left( {x_1^2 - 19{x_1} + 7} \right) - 14 + {x_1}{x_2} - 3} \right]^2} + {x_1}{\left[ {2\left( {x_2^2 - 19{x_2} + 7} \right) - 14 + {x_1}{x_2} - 3} \right]^2} + 120\\\,\,\,\,\, = {x_2}{\left( {{x_1}{x_2} - 17} \right)^2} + {x_1}{\left( {{x_1}{x_2} - 17} \right)^2} + 120\\\,\,\,\,\, = {\left( {{x_1}{x_2} - 17} \right)^2}\left( {{x_1} + {x_2}} \right) + 120\\\,\,\,\,\, = {\left( {7 - 17} \right)^2}.19 + 120\\\,\,\,\,\, = {19.10^2} + 120\\\,\,\,\, = 1900 + 120\\\,\,\,\, = 2020\end{array}\)
Bài 4. (2,0 điểm)
Cách giải:
a) Một số tự nhiên nhỏ hơn bình phương của nó 20 đơn vị. Tìm số tự nhiên đó.
Gọi số tự nhiên cần tìm là \(x\) (ĐK: \(x \in \mathbb{N}\)).
Bình phương của số tự nhiên \(x\) là \({x^2}\).
Vì số tự nhiên cần tìm nhỏ hơn bình phương của nó 20 đơn vị nên ta có phương trình:
\(\begin{array}{l}\,\,\,\,\,\,\,{x^2} - x = 20\\ \Leftrightarrow {x^2} - x - 20 = 0\\ \Leftrightarrow {x^2} - 5x + 4x - 20 = 0\\ \Leftrightarrow x\left( {x - 5} \right) + 4\left( {x - 5} \right) = 0\\ \Leftrightarrow \left( {x - 5} \right)\left( {x + 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 5 = 0\\x + 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 5\,\,\,\,\,\,\,\left( {tm} \right)\\x = - 4\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy số tự nhiên cần tìm là 5.
b) Quãng đường AB gồm một đoạn lên dốc và một đoạn xuống dốc. Một người đi xe đạp từ A đến B hết 16 phút và đi từ B về A hết 14 phút. Biết vận tốc lúc lên dốc là 10km/h, vận tốc lúc xuống dốc là 15km/h (vận tốc lên dốc, xuống dốc lúc đi và về như nhau). Tính quãng đường AB.
Gọi quãng đường lên dốc lúc đi là \(x\) (km), quãng đường xuống dốc lúc đi là \(y\) (km) (ĐK: \(x,y > 0\))
\( \Rightarrow \) Quãng đường lên dốc lúc về là \(y\) (km), quãng đường xuống dốc lúc về là \(x\) (km).
Thời gian lúc đi là 16 phút \( = \dfrac{{16}}{{60}} = \dfrac{4}{{15}}\)(h) nên ta có phương trình:
\(\dfrac{x}{{10}} + \dfrac{y}{{15}} = \dfrac{4}{{15}} \Leftrightarrow 3x + 2y = 8\,\,\left( 1 \right)\).
Thời gian lúc về là 14 phút \( = \dfrac{{14}}{{60}} = \dfrac{7}{{30}}\)(h) nên ta có phương trình:
\(\dfrac{y}{{10}} + \dfrac{x}{{15}} = \dfrac{7}{{30}} \Leftrightarrow 3x + 2x = 7\,\,\left( 2 \right)\).
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{l}3x + 2y = 8\\3y + 2x = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}9x + 6y = 24\\4x + 6y = 14\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x = 10\\3x + 2y = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\3.2 + 2y = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\2y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.\,\,\left( {tm} \right)\)
\( \Rightarrow \) Quãng đường lên dốc lúc đi là \(2\,\,km\), quãng đường xuống dốc lúc đi là \(1km\).
Vậy độ dài quãng đường AB là \(2 + 1 = 3\,\,\left( {km} \right)\).
Bài 5. (2,0 điểm)
Cách giải:
Cho tam giác ABC nội tiếp đường tròn O đường kính AB. Trên cung nhỏ \(BC\) của đường tròn \(\left( O \right)\) lấy điểm \(D\) (không trùng với \(B\) và \(C\)). Gọi \(H\) là chân đường vuông góc kẻ từ \(C\) đến \(AB\,\,\left( {H \in AB} \right)\) và \(E\) là giao điểm của \(CH\) với \(AD\).
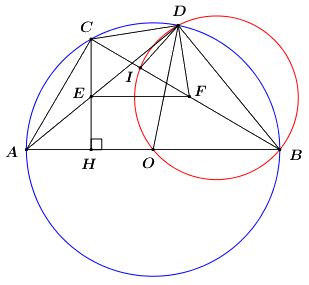
a) Chứng minh rằng tứ giác \(BDEH\) là tứ giác nội tiếp.
Vì \(\angle ADB\) là góc nội tiếp chắn nửa đường tròn \(\left( O \right)\) nên \(\angle ADB = {90^0}\) hay \(\angle EDB = {90^0}\).
Lại có \(CH \bot AB\) (gt) nên \(\angle CHB = {90^0} \Rightarrow \angle EHB = {90^0}\).
Xét tứ giác \(BDEH\) có: \(\angle EDB + \angle EHB = {90^0} + {90^0} = {180^0}\).
\( \Rightarrow BDEH\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng \({180^0}\)).
b) Chứng minh rằng \(A{B^2} = AE.AD + BH.BA\).
Vì \(ABDC\) là tứ giác nội tiếp đường tròn \(\left( O \right)\) nên \(\angle ADC = \angle ABC\) (1) (hai góc nội tiếp cùng chắn cung \(AC\)).
Ta lại có:
\(\angle ABC + \angle CAB = {90^0}\) (do tam giác \(ABC\) có \(\angle ACB = {90^0}\) - góc nội tiếp chắn nửa đường tròn).
\(\angle ACH + \angle CAB = {90^0}\) (do tam giác \(ACH\) vuông tại \(H\)).
\( \Rightarrow \angle ABC = \angle ACH\) (2) (cùng phụ với \(\angle CAB\)).
Từ (1) và (2) \( \Rightarrow \angle ADC = \angle ACH\) \(\left( { = \angle ABC} \right)\) hay \(\angle ADC = \angle ACE\).
Xét \(\Delta ACE\) và \(\Delta ADC\) có:
\(\angle CAD\) chung;
\(\angle ACE = \angle ADC\,\,\left( {cmt} \right)\).
\(\begin{array}{l} \Rightarrow \Delta ACE \sim \Delta ADC\,\,\left( {g.g} \right)\\ \Rightarrow \dfrac{{AC}}{{AD}} = \dfrac{{AE}}{{AC}} \Rightarrow A{C^2} = AE.AD\,\,\,\left( * \right)\end{array}\)
Xét tam giác \(ABC\) vuông tại \(C\), đường cao \(CH\) ta có:
\(B{C^2} = BH.BA\,\,\left( {2*} \right)\) (hệ thức lượng trong tam giác vuông).
Từ (*) và (2*) suy ra \(A{C^2} + B{C^2} = AE.AD + BH.BA\).
Lại có \(\Delta ABC\) vuông tại \(C\) nên \(A{C^2} + B{C^2} = A{B^2}\) (định lí Pytago).
Vậy \(A{B^2} = AE.AD + BH.BA\)(đpcm).
c) Đường thẳng qua \(E\) song song với \(AB\), cắt \(BC\) tại \(F\). Chứng minh rằng \(\angle CDF = {90^0}\) và đường tròn ngoại tiếp tam giác \(OBD\) đi qua trung điểm của đoạn \(CF\).
*) Vì \(EF//AB\,\,\,\left( {gt} \right)\) nên \(\angle CFE = \angle CBA\) (đồng vị).
Mà \(\angle CBA = \angle CDA\) (hai góc nội tiếp cùng chắn cung \(AC\)).
\( \Rightarrow \angle CFE = \angle CDA\).
\( \Rightarrow \) Tứ giác \(CDFE\) là tứ giác nội tiếp (Tứ giác có 2 đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau).
\(\angle CDF + \angle CEF = {180^0}\) (tổng hai góc đối của tứ giác nội tiếp).
Ta lại có:
\(\left\{ \begin{array}{l}CH \bot AB\,\,\left( {gt} \right)\\EF//AB\,\,\left( {gt} \right)\end{array} \right. \Rightarrow EF \bot CH\) (từ vuông góc đến song song) \( \Rightarrow \angle CEF = {90^0}\).
\( \Rightarrow \angle CDF = {180^0} - \angle CEF = {180^0} - {90^0} = {90^0}\,\,\left( {dpcm} \right)\).
*) Gọi \(I\) là giao điểm của \(CF\) và đường tròn ngoại tiếp tam giác \(OBD\).
Ta có:
\(\begin{array}{l}\angle ADB = \angle ADF + \angle FDB = {90^0}\\\angle CDF = \angle ADF + \angle CDA = {90^0}\end{array}\)
\( \Rightarrow \angle FBD = \angle CDA\) (cùng phụ với \(\angle ADF\)).
Mà \(\angle CDA = \angle CBA\) (hai góc nội tiếp cùng chắn cung \(AC\)).
\( \Rightarrow \angle FDB = \angle CBA\) \(\left( { = \angle CDA} \right)\).
Mà \(\angle CBA = \angle OBI = \angle ODI\) (hai góc nội tiếp cùng chắn cung \(OI\)).
\(\begin{array}{l} \Rightarrow \angle FDB = \angle ODI\\ \Rightarrow \angle FDB + \angle ODF = \angle ODI + \angle ODF\\ \Rightarrow \angle ODB = \angle IDF\,\,\left( 3 \right)\end{array}\)
Ta có: tứ giác \(CDFE\) nội tiếp (cmt) nên \(\angle IFD = \angle CFD = \angle CED = AEH\) (hai góc nội tiếp cùng chắn cung \(CD\)).
Ta lại có:
\(\begin{array}{l}\angle AEH + \angle EAH = {90^0}\\\angle ABD + \angle BAD = {90^0}\end{array}\)
Mà \(\angle EAH = \angle BAD\) nên \(\angle AEH = \angle ABD = \angle OBD\) \( \Rightarrow \angle IFD = \angle OBD\) (4)
Lại có: \(OD = OB\,\,\) (=bán kính) nên \(\Delta OBD\) cân tại \(O\), do đó \(\angle OBD = \angle ODB\) (5).
Từ (3), (4), (5) suy ra \(\angle IDF = \angle IFD\) \( \Rightarrow \Delta IDF\) cân tại \(I\) (định nghĩa) \( \Rightarrow ID = IF\) (3*) (tính chất tam giác cân).
Ta có:
\(\angle IDF + \angle IDC = \angle CDF = {90^0}\)
\(\angle IFD + \angle ICD = {90^0}\) (do tam giác \(CDF\) vuông tại \(D\)).
\( \Rightarrow \angle IDC = \angle ICD \Rightarrow \Delta ICD\) cân tại \(I\) (định nghĩa) \( \Rightarrow IC = ID\) (4*) (tính chất tam giác cân).
Từ (3*) và (4*) suy ra \(IC = IF\,\,\left( { = ID} \right)\).
Vậy \(I\) là trung điểm của \(CF\) (đpcm).
Kỳ thi tuyển sinh vào lớp 10 môn Toán tại Đà Nẵng năm 2020 là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Để chuẩn bị tốt nhất cho kỳ thi này, việc nắm vững cấu trúc đề thi, các dạng bài thường gặp và phương pháp giải quyết là vô cùng cần thiết. Bài viết này sẽ cung cấp một phân tích chi tiết về đề thi vào 10 môn Toán Đà Nẵng năm 2020, cùng với hướng dẫn giải các bài toán điển hình.
Đề thi vào 10 môn Toán Đà Nẵng năm 2020 thường bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Dưới đây là một số dạng bài thường gặp trong đề thi vào 10 môn Toán Đà Nẵng năm 2020:
Ví dụ 1: Giải phương trình 2x + 3 = 7
Lời giải:
2x + 3 = 7
2x = 7 - 3
2x = 4
x = 2
Ví dụ 2: Tính diện tích tam giác ABC vuông tại A, biết AB = 3cm, AC = 4cm.
Lời giải:
Diện tích tam giác ABC là: S = (1/2) * AB * AC = (1/2) * 3 * 4 = 6 cm2
Ngoài bộ đề thi vào 10 môn Toán Đà Nẵng năm 2020, các em học sinh có thể tham khảo thêm các tài liệu sau:
Đề thi vào 10 môn Toán Đà Nẵng năm 2020 là một kỳ thi quan trọng, đòi hỏi sự chuẩn bị kỹ lưỡng và nỗ lực không ngừng. Hy vọng với những phân tích và hướng dẫn giải trong bài viết này, các em học sinh sẽ có thêm kiến thức và tự tin hơn để đạt kết quả tốt nhất trong kỳ thi sắp tới. Chúc các em thành công!