Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Kiên Giang năm 2018. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi sắp tới.
Đề thi được biên soạn bám sát chương trình học lớp 9, bao gồm các dạng bài tập thường gặp như đại số, hình học, số học và giải bài toán thực tế.
Câu 1 (2 điểm): a) Tính
Câu 1 (2 điểm):
a) Tính \(E = 2\sqrt {48} + 3\sqrt {75} - 2\sqrt {108} .\)
b) Tìm điều kiện xác định và rút gọn biểu thức \(P\left( x \right) = \left( {\dfrac{1}{{{x^2} - x}} + \dfrac{1}{{x - 1}}} \right):\dfrac{{x + 1}}{{{x^2} - 2x + 1}}.\)
Câu 2 (2 điểm):
a) Vẽ đồ thị \(\left( P \right)\) của hàm số \(y = 2{x^2}\) trên hệ trục tọa độ \(Oxy.\)
b) Tìm các giá trị của tham số \(m\) để đường thẳng \(\left( {{d_m}} \right):\;\;y = \left( {{m^2} + m - 4} \right)x + m - 7\) song song với đường thẳng \(\left( d \right):\;\;y = 2x - 5.\)
Câu 3 (2 điểm):
a) Gọi \({x_1},\;{x_2}\) là hai nghiệm của phương trình \({x^2} - 2\left( {m - 1} \right)x - 2m - 7 = 0\) (\(m\) là tham số). Tìm các giá trị của \(m\) để biểu thức \(A = x_1^2 + x_2^2 + 6{x_1}{x_2}\) đạt giá trị nhỏ nhất.
b) Bạn Nam mua hai món hàng và phải trả tổng cộng 480000 đồng, trong đó đã tính cả 40000 đồng là thuế giá trị gia tăng (viết tắt là thuế VAT). Biết rằng thuế VAT đối với mặt hàng thứ nhất là 10%, thuế VAT đối với mặt hàng thứ hai là 8%. Hỏi nếu không kể thuế VAT thì bạn Nam phải trả mỗi món hàng là bao nhiêu tiền?
(Trong đó: Thuế VAT là thuế mà người mua hàng phải trả, người bán hàng thu và nộp cho Nhà nước. Giả sử thuế VAT đối với mặt hàng A được quy là 10%. Khi đó nếu giá bán của mặt hàng A là x đồng thì kể cả thuế VAT, người mua phải trả tổng cộng là \(x + 10\% x\) đồng).
Câu 4 (0,5 điểm):
Cho biểu thức \(Q\left( x \right) = \dfrac{{5{x^2} + 6x + 2018}}{{x + 1}}.\) Tìm các giá trị nguyên của \(x\) để \(Q\left( x \right)\) là số nguyên.
Câu 5 (3,5 điểm):
Cho đường tròn \(\left( O \right),\) từ điểm \(A\) ngoài đường tròn vẽ đường thẳng \(AO\) cắt đường tròn \(\left( O \right)\) tại \(B,\;\;C\;\left( {AB < AC} \right).\) Qua \(A\) vẽ đường thẳng không đi qua \(O\) cắt đường tròn \(\left( O \right)\) tại \(D,\;E\;\;\left( {AD < AE} \right).\) Đường thẳng vuông góc với \(AB\) tại \(A\) cắt đường thẳng \(CE\) tại \(F.\)
a) Chứng minh tứ giác \(ABEF\) nội tiếp.
b) Gọi \(M\) là giao điểm thứ hai của \(FB\) với đường tròn \(\left( O \right).\) Chứng minh \(DM \bot AC.\)
c) Chứng minh \(CE.CF + AD.AE = A{C^2}.\)
Câu 1:Phương pháp:
a) Sử dụng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \;\;khi\;\;A \ge 0\\ - A\sqrt B \;\;khi\;\;A < 0\end{array} \right..\)
b) Để phân thức: \(\dfrac{1}{{f\left( x \right)}}\) có nghĩa thì \(f\left( x \right) \ne 0.\)
+) Quy đồng mẫu các phân thức sau đó biến đổi và rút gọn biểu thức.
Cách giải: a) Tính \(E = 2\sqrt {48} + 3\sqrt {75} - 2\sqrt {108} .\)
\(\begin{array}{l}E = 2\sqrt {48} + 3\sqrt {75} - 2\sqrt {108} \\\;\;\; = 2\sqrt {{4^2}.3} + 3\sqrt {{5^2}.3} - 2\sqrt {{6^2}.3} \\\;\;\; = 2.4\sqrt 3 + 3.5\sqrt 3 - 2.6\sqrt 3 \\\;\;\; = 8\sqrt 3 + 15\sqrt 3 - 12\sqrt 3 \\\;\;\; = 11\sqrt 3 .\end{array}\)
Vậy \(E = 11\sqrt 3 .\)
b) Tìm điều kiện xác định và rút gọn biểu thức \(P\left( x \right) = \left( {\dfrac{1}{{{x^2} - x}} + \dfrac{1}{{x - 1}}} \right):\dfrac{{x + 1}}{{{x^2} - 2x + 1}}.\)
Ta có \(P\left( x \right)\) xác định \( \Leftrightarrow \left\{ \begin{array}{l}{x^2} - x \ne 0\\x - 1 \ne 0\\x + 1 \ne 0\\{x^2} - 2x + 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x\left( {x - 1} \right) \ne 0\\x \ne \pm 1\\{\left( {x - 1} \right)^2} \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\x \ne \pm 1\end{array} \right..\)
\(\begin{array}{l}P\left( x \right) = \left( {\dfrac{1}{{{x^2} - x}} + \dfrac{1}{{x - 1}}} \right):\dfrac{{x + 1}}{{{x^2} - 2x + 1}}\\\;\;\;\;\;\;\;\; = \left( {\dfrac{1}{{x\left( {x - 1} \right)}} + \dfrac{1}{{x - 1}}} \right):\dfrac{{x + 1}}{{{{\left( {x - 1} \right)}^2}}}\\\;\;\;\;\;\;\;\; = \dfrac{{x + 1}}{{x\left( {x - 1} \right)}}.\dfrac{{{{\left( {x - 1} \right)}^2}}}{{x + 1}}\\\;\;\;\;\;\;\;\; = \dfrac{{x - 1}}{x}.\end{array}\)
Câu 2:Phương pháp:
a) Lập bảng giá trị mà đồ thị hàm số đi qua sau đó vẽ đồ thị trên hệ trục tọa độ.
b) Hai đường thẳng \(\left\{ \begin{array}{l}{d_1}:\;\;y = {a_1}x + {b_1}\\{d_2}:\;y = {a_2}x + {b_2}\end{array} \right.\) song song \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right..\)
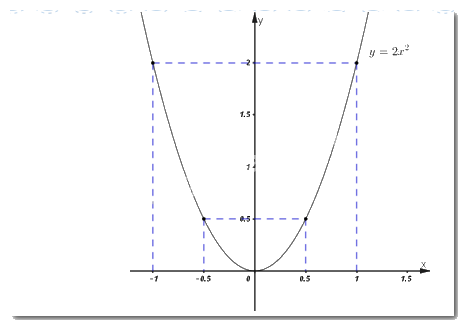
Cách giải: a) Vẽ đồ thị \(\left( P \right)\) của hàm số \(y = 2{x^2}\) trên hệ trục tọa độ \(Oxy.\)
+) Vẽ đồ thị hàm số \(\left( P \right):\)
\(x\) | \( - 1\) | \( - \dfrac{1}{2}\) | \(0\) | \(\dfrac{1}{2}\) | \(1\) |
\(y = 2{x^2}\) | \(2\) | \(\dfrac{1}{2}\) | \(0\) | \(\dfrac{1}{2}\) | \(2\) |
Đồ thị \(\left( P \right)\) là parabol đi qua các điểm \(\left( { - 1;\;2} \right),\;\;\left( { - \dfrac{1}{2};\;\dfrac{1}{2}} \right),\;\left( {0;\;0} \right),\;\left( {\dfrac{1}{2};\;\dfrac{1}{2}} \right),\;\;\left( {1;\;2} \right).\)
b) Tìm các giá trị của tham số \(m\) để đường thẳng \(\left( {{d_m}} \right):\;\;y = \left( {{m^2} + m - 4} \right)x + m - 7\) song song với đường thẳng \(\left( d \right):\;\;y = 2x - 5.\)
Đường thẳng \(\left( {{d_m}} \right)//d \Leftrightarrow \left\{ \begin{array}{l}{m^2} + m - 4 = 2\\m - 7 \ne - 5\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{m^2} + m - 6 = 0\\m \ne 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {m - 2} \right)\left( {m + 3} \right) = 0\\m \ne 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m - 2 = 0\\m + 3 = 0\end{array} \right.\\m \ne 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 2\\m = - 3\end{array} \right.\\m \ne 2\end{array} \right. \Leftrightarrow m = - 3.\end{array}\)
Vậy \(m = - 3\)
Câu 3:
Phương pháp:
a) Phương trình có hai nghiệm \( \Leftrightarrow \Delta ' \ge 0.\)
+) Áp dụng hệ thức Vi-ét \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\) để suy ra giá trị nhỏ nhất của biểu thức bài cho và từ đó tìm \(m.\)
b) Giải bài toàn bằng cách lập hệ phương trình:
+) Gọi ẩn và đặt điều kiện cho ẩn.
+) Biểu diễn các đại lượng chữa biết theo ẩn và đại lượng đã biết.
+) Dựa vào giả thiết của bài toán để lập hệ phương trình.
+) Giải hệ phương trình tìm ẩn và đối chiếu với điều kiện của ẩn rồi kết luận.
Cách giải:
a) Gọi \({x_1},\;{x_2}\) là hai nghiệm của phương trình \({x^2} - 2\left( {m - 1} \right)x - 2m - 7 = 0\) (\(m\) là tham số). Tìm các giá trị của \(m\) để biểu thức \(A = x_1^2 + x_2^2 + 6{x_1}{x_2}\) đạt giá trị nhỏ nhất.
Phương trình có hai nghiệm \({x_1},\;{x_2} \Leftrightarrow \Delta ' \ge 0\)
\(\begin{array}{l} \Leftrightarrow {\left( {m - 1} \right)^2} + 2m + 7 \ge 0\\ \Leftrightarrow {m^2} - 2m + 1 + 2m + 7 \ge 0\\ \Leftrightarrow {m^2} + 8 \ge 0\;\;\;\forall m.\end{array}\)
Hay phương trình luôn có hai nghiệm phân biệt \({x_1},\;{x_2}\) với mọi \(m.\)
Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m - 1} \right)\\{x_1}{x_2} = - 2m - 7\end{array} \right..\)
Theo đề bài ta có:
\(\begin{array}{l}A = x_1^2 + x_2^2 + 6{x_1}{x_2} = {\left( {{x_1} + {x_2}} \right)^2} + 4{x_1}{x_2}\\\;\;\; = 4{\left( {m - 1} \right)^2} - 4\left( {2m + 7} \right)\\\;\;\; = 4\left( {{m^2} - 2m + 1 - 2m - 7} \right)\\\;\;\; = 4\left( {{m^2} - 4m + 4 - 10} \right)\\\;\;\; = 4\left[ {{{\left( {m - 2} \right)}^2} - 10} \right]\\\;\;\; = 4{\left( {m - 2} \right)^2} - 40.\end{array}\)
Vì \({\left( {m - 2} \right)^2} \ge 0 \Rightarrow 4{\left( {m - 2} \right)^2} \ge 0 \Rightarrow 4{\left( {m - 2} \right)^2} - 40 \ge - 40.\)
\( \Rightarrow A \ge - 40\) hay \(Min\;A = - 40\)
Dấu “=” xảy ra \( \Leftrightarrow m - 2 = 0 \Leftrightarrow m = 2.\)
Vậy \(m = 2.\)
b) Bạn Nam mua hai món hàng và phải trả tổng cộng 480000 đồng, trong đó đã tính cả 40000 đồng là thuế giá trị gia tăng (viết tắt là thuế VAT). Biết rằng thuế VAT đối với mặt hàng thứ nhất là 10%, thuế VAT đối với mặt hàng thứ hai là 8%. Hỏi nếu không kể thuế VAT thì bạn Nam phải trả mỗi món hàng là bao nhiêu tiền?
Gọi số phải trả cho món hàng thứ nhất không kể thuế VAT là \(x\) đồng, \(\left( {0 < x < 480000} \right).\)
Gọi số phải trả cho món hàng thứ nhất không kể thuế VAT là \(y\) đồng, \(\left( {0 < y < 480000} \right).\)
Số tiền phải trả cho hai món hàng không mất thuế là: \(x + y = 480000 - 40000 = 440000.\;\;\;\;\left( 1 \right)\)
Số tiền thuế phải trả cho món hàng thứ nhất là: \(x.10\% = \dfrac{x}{{10}}\) (đồng)
Số tiền thuế phải trả cho món hàng thứ hai là: \(y.8\% = \dfrac{{2y}}{{25}}\) (đồng).
Số tiền thuế phải trả cho hai món hàng là: \(\dfrac{x}{{10}} + \dfrac{{2y}}{{25}} = 40000 \Leftrightarrow 5x + 4y = 2000000\;\;\;\;\;\left( 2 \right).\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{l}x + y = 440000\\5x + 4y = 2000000\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x + 4y = 1760000\\5x + 4y = 2000000\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 240000\;\;\;\left( {tm} \right)\\y = 200000\;\;\;\left( {tm} \right)\end{array} \right..\)
Vậy số tiền phải trả cho món hàng thứ nhất không phải thuế là 240 000 đồng, món hàng thứ hai là 200 000 đồng.
Câu 4:
Phương pháp:
+) Biến đổi biểu thức về dạng: \(Q\left( x \right) = ax + b + \dfrac{c}{{x + 1}}.\,\,\left( {c = const} \right)\)
+) Khi đó, để \(Q\left( x \right) \in Z\) thì \(\dfrac{c}{{x + 1}} \in Z \Leftrightarrow \left( {x + 1} \right) \in U\left( c \right).\)
+) Từ đó ta giải phương trình hoặc lập bảng để tìm \(x \in Z\) thỏa mãn điều kiện bài toán.
Cách giải:
Cho biểu thức \(Q\left( x \right) = \dfrac{{5{x^2} + 6x + 2018}}{{x + 1}}.\) Tìm các giá trị nguyên của \(x\) để \(Q\left( x \right)\) là số nguyên.
Điều kiện: \(x \ne - 1.\)
Ta có: \(Q\left( x \right) = \dfrac{{5{x^2} + 6x + 2018}}{{x + 1}} = \dfrac{{5{x^2} + 5x + x + 1 + 2017}}{{x + 1}}\)
\( = \dfrac{{5x\left( {x + 1} \right)}}{{x + 1}} + \dfrac{{x + 1}}{{x + 1}} + \dfrac{{2017}}{{x + 1}} = 5x + 1 + \dfrac{{2017}}{{x + 1}}.\) \(\begin{array}{l} \Rightarrow Q\left( x \right) \in Z \Leftrightarrow \left( {5x + 1 + \dfrac{{2017}}{{x + 1}}} \right) \in Z \Leftrightarrow \dfrac{{2017}}{{x + 1}} \in Z\;\;\left( {do\;\;x \in Z} \right)\\ \Leftrightarrow \left( {x + 1} \right) \in U\left( {2017} \right).\end{array}\)
Mà \(U\left( {2017} \right) = \left\{ { - 2017; - 1;\;1;\;2017} \right\}.\)
\( \Rightarrow \left[ \begin{array}{l}x + 1 = - 2017\\x + 1 = - 1\\x + 1 = 1\\x + 1 = 2017\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 2018\;\;\;\left( {tm} \right)\\x = - 2\;\;\;\left( {tm} \right)\\x = 0\;\;\;\;\left( {tm} \right)\\x = 2016\;\;\left( {tm} \right)\end{array} \right..\)
Vậy \(x \in \left\{ { - 2018;\; - 2;\;0;\;\;2016} \right\}.\)
Câu 5:
Cách giải:
Cho đường tròn \(\left( O \right),\) từ điểm \(A\) ngoài đường tròn vẽ đường thẳng \(AO\) cắt đường tròn \(\left( O \right)\) tại \(B,\;\;C\;\left( {AB < AC} \right).\) Qua \(A\) vẽ đường thẳng không đi qua \(O\) cắt đường tròn \(\left( O \right)\) tại \(D,\;E\;\;\left( {AD < AE} \right).\) Đường thẳng vuông góc với \(AB\) tại \(A\) cắt đường thẳng \(CE\) tại \(F.\)
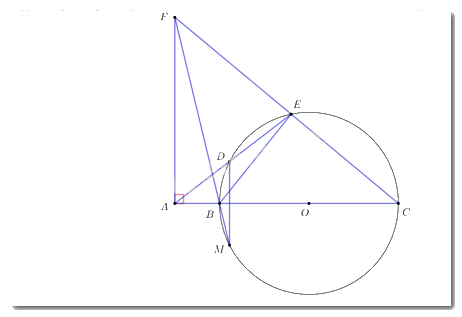
a) Chứng minh tứ giác \(ABEF\) nội tiếp.
Xét đường tròn \(\left( O \right)\) ta có: \(\widehat {BEC} = {90^0}\) (góc nội tiếp chắn nửa đường tròn).
Xét tứ giác \(ABEF\) ta có: \(\widehat {FAB} + \widehat {BEF} = {90^0} + {90^0} = {180^0}.\)
\( \Rightarrow ABEF\) là tứ giác nội tiếp. (tứ giác có tổng hai góc đối diện bằng \({180^0}\)).
b) Gọi \(M\) là giao điểm thứ hai của \(FB\) với đường tròn \(\left( O \right).\) Chứng minh \(DM \bot AC.\)
Vì tứ giác ABEF là tứ giác nội tiếp (cmt) \( \Rightarrow \widehat {AEB} = \widehat {AFB}\) (hai góc nội tiếp cùng chắn cung AB).
Lại có \(\widehat {AEB} = \widehat {BMD}\) (hai góc nội tiếp cùng chắn cung BD của đường tròn (O))
\( \Rightarrow \widehat {AFB} = \widehat {BMD}\). Mà hai góc này ở vị trí so le trong \( \Rightarrow AF//DM\).
Mà \(AF \bot AC \Rightarrow DM \bot AC\).
c) Chứng minh \(CE.CF + AD.AE = A{C^2}.\)
Xét tam giác ACD và tam giác ABE có
\(\widehat {CAE}\) chung;
\(\widehat {ACD} = \widehat {AEB}\) (hai góc nội tiếp cùng chắn cung BD)
\( \Rightarrow \Delta ACD \sim \Delta AEB\,\left( {g.g} \right) \Rightarrow \dfrac{{AC}}{{AE}} = \dfrac{{AD}}{{AB}} \Rightarrow AD.AE = AC.AB\,\,\left( 1 \right)\)
Xét tam giác CBE và tam giác CFA có:
\(\widehat {ACB}\) chung;
\(\widehat {CEB} = \widehat {CAF} = {90^0}\)
\( \Rightarrow \Delta CBE \sim \Delta CFA\,\,\left( {g.g} \right) \Rightarrow \dfrac{{CE}}{{CA}} = \dfrac{{CB}}{{CF}} \Rightarrow CE.CF = CA.CB\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow CE.CF + AD.AE = CA.CB + AC.AB = AC\left( {AB + BC} \right) = A{C^2}\,\,\left( {dpcm} \right)\)
Câu 1 (2 điểm):
a) Tính \(E = 2\sqrt {48} + 3\sqrt {75} - 2\sqrt {108} .\)
b) Tìm điều kiện xác định và rút gọn biểu thức \(P\left( x \right) = \left( {\dfrac{1}{{{x^2} - x}} + \dfrac{1}{{x - 1}}} \right):\dfrac{{x + 1}}{{{x^2} - 2x + 1}}.\)
Câu 2 (2 điểm):
a) Vẽ đồ thị \(\left( P \right)\) của hàm số \(y = 2{x^2}\) trên hệ trục tọa độ \(Oxy.\)
b) Tìm các giá trị của tham số \(m\) để đường thẳng \(\left( {{d_m}} \right):\;\;y = \left( {{m^2} + m - 4} \right)x + m - 7\) song song với đường thẳng \(\left( d \right):\;\;y = 2x - 5.\)
Câu 3 (2 điểm):
a) Gọi \({x_1},\;{x_2}\) là hai nghiệm của phương trình \({x^2} - 2\left( {m - 1} \right)x - 2m - 7 = 0\) (\(m\) là tham số). Tìm các giá trị của \(m\) để biểu thức \(A = x_1^2 + x_2^2 + 6{x_1}{x_2}\) đạt giá trị nhỏ nhất.
b) Bạn Nam mua hai món hàng và phải trả tổng cộng 480000 đồng, trong đó đã tính cả 40000 đồng là thuế giá trị gia tăng (viết tắt là thuế VAT). Biết rằng thuế VAT đối với mặt hàng thứ nhất là 10%, thuế VAT đối với mặt hàng thứ hai là 8%. Hỏi nếu không kể thuế VAT thì bạn Nam phải trả mỗi món hàng là bao nhiêu tiền?
(Trong đó: Thuế VAT là thuế mà người mua hàng phải trả, người bán hàng thu và nộp cho Nhà nước. Giả sử thuế VAT đối với mặt hàng A được quy là 10%. Khi đó nếu giá bán của mặt hàng A là x đồng thì kể cả thuế VAT, người mua phải trả tổng cộng là \(x + 10\% x\) đồng).
Câu 4 (0,5 điểm):
Cho biểu thức \(Q\left( x \right) = \dfrac{{5{x^2} + 6x + 2018}}{{x + 1}}.\) Tìm các giá trị nguyên của \(x\) để \(Q\left( x \right)\) là số nguyên.
Câu 5 (3,5 điểm):
Cho đường tròn \(\left( O \right),\) từ điểm \(A\) ngoài đường tròn vẽ đường thẳng \(AO\) cắt đường tròn \(\left( O \right)\) tại \(B,\;\;C\;\left( {AB < AC} \right).\) Qua \(A\) vẽ đường thẳng không đi qua \(O\) cắt đường tròn \(\left( O \right)\) tại \(D,\;E\;\;\left( {AD < AE} \right).\) Đường thẳng vuông góc với \(AB\) tại \(A\) cắt đường thẳng \(CE\) tại \(F.\)
a) Chứng minh tứ giác \(ABEF\) nội tiếp.
b) Gọi \(M\) là giao điểm thứ hai của \(FB\) với đường tròn \(\left( O \right).\) Chứng minh \(DM \bot AC.\)
c) Chứng minh \(CE.CF + AD.AE = A{C^2}.\)
Câu 1:Phương pháp:
a) Sử dụng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \;\;khi\;\;A \ge 0\\ - A\sqrt B \;\;khi\;\;A < 0\end{array} \right..\)
b) Để phân thức: \(\dfrac{1}{{f\left( x \right)}}\) có nghĩa thì \(f\left( x \right) \ne 0.\)
+) Quy đồng mẫu các phân thức sau đó biến đổi và rút gọn biểu thức.
Cách giải: a) Tính \(E = 2\sqrt {48} + 3\sqrt {75} - 2\sqrt {108} .\)
\(\begin{array}{l}E = 2\sqrt {48} + 3\sqrt {75} - 2\sqrt {108} \\\;\;\; = 2\sqrt {{4^2}.3} + 3\sqrt {{5^2}.3} - 2\sqrt {{6^2}.3} \\\;\;\; = 2.4\sqrt 3 + 3.5\sqrt 3 - 2.6\sqrt 3 \\\;\;\; = 8\sqrt 3 + 15\sqrt 3 - 12\sqrt 3 \\\;\;\; = 11\sqrt 3 .\end{array}\)
Vậy \(E = 11\sqrt 3 .\)
b) Tìm điều kiện xác định và rút gọn biểu thức \(P\left( x \right) = \left( {\dfrac{1}{{{x^2} - x}} + \dfrac{1}{{x - 1}}} \right):\dfrac{{x + 1}}{{{x^2} - 2x + 1}}.\)
Ta có \(P\left( x \right)\) xác định \( \Leftrightarrow \left\{ \begin{array}{l}{x^2} - x \ne 0\\x - 1 \ne 0\\x + 1 \ne 0\\{x^2} - 2x + 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x\left( {x - 1} \right) \ne 0\\x \ne \pm 1\\{\left( {x - 1} \right)^2} \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\x \ne \pm 1\end{array} \right..\)
\(\begin{array}{l}P\left( x \right) = \left( {\dfrac{1}{{{x^2} - x}} + \dfrac{1}{{x - 1}}} \right):\dfrac{{x + 1}}{{{x^2} - 2x + 1}}\\\;\;\;\;\;\;\;\; = \left( {\dfrac{1}{{x\left( {x - 1} \right)}} + \dfrac{1}{{x - 1}}} \right):\dfrac{{x + 1}}{{{{\left( {x - 1} \right)}^2}}}\\\;\;\;\;\;\;\;\; = \dfrac{{x + 1}}{{x\left( {x - 1} \right)}}.\dfrac{{{{\left( {x - 1} \right)}^2}}}{{x + 1}}\\\;\;\;\;\;\;\;\; = \dfrac{{x - 1}}{x}.\end{array}\)
Câu 2:Phương pháp:
a) Lập bảng giá trị mà đồ thị hàm số đi qua sau đó vẽ đồ thị trên hệ trục tọa độ.
b) Hai đường thẳng \(\left\{ \begin{array}{l}{d_1}:\;\;y = {a_1}x + {b_1}\\{d_2}:\;y = {a_2}x + {b_2}\end{array} \right.\) song song \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right..\)
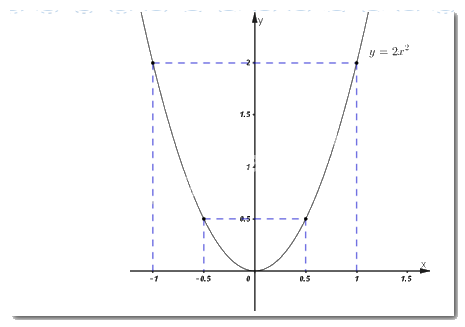
Cách giải: a) Vẽ đồ thị \(\left( P \right)\) của hàm số \(y = 2{x^2}\) trên hệ trục tọa độ \(Oxy.\)
+) Vẽ đồ thị hàm số \(\left( P \right):\)
\(x\) | \( - 1\) | \( - \dfrac{1}{2}\) | \(0\) | \(\dfrac{1}{2}\) | \(1\) |
\(y = 2{x^2}\) | \(2\) | \(\dfrac{1}{2}\) | \(0\) | \(\dfrac{1}{2}\) | \(2\) |
Đồ thị \(\left( P \right)\) là parabol đi qua các điểm \(\left( { - 1;\;2} \right),\;\;\left( { - \dfrac{1}{2};\;\dfrac{1}{2}} \right),\;\left( {0;\;0} \right),\;\left( {\dfrac{1}{2};\;\dfrac{1}{2}} \right),\;\;\left( {1;\;2} \right).\)
b) Tìm các giá trị của tham số \(m\) để đường thẳng \(\left( {{d_m}} \right):\;\;y = \left( {{m^2} + m - 4} \right)x + m - 7\) song song với đường thẳng \(\left( d \right):\;\;y = 2x - 5.\)
Đường thẳng \(\left( {{d_m}} \right)//d \Leftrightarrow \left\{ \begin{array}{l}{m^2} + m - 4 = 2\\m - 7 \ne - 5\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{m^2} + m - 6 = 0\\m \ne 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {m - 2} \right)\left( {m + 3} \right) = 0\\m \ne 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m - 2 = 0\\m + 3 = 0\end{array} \right.\\m \ne 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 2\\m = - 3\end{array} \right.\\m \ne 2\end{array} \right. \Leftrightarrow m = - 3.\end{array}\)
Vậy \(m = - 3\)
Câu 3:
Phương pháp:
a) Phương trình có hai nghiệm \( \Leftrightarrow \Delta ' \ge 0.\)
+) Áp dụng hệ thức Vi-ét \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\) để suy ra giá trị nhỏ nhất của biểu thức bài cho và từ đó tìm \(m.\)
b) Giải bài toàn bằng cách lập hệ phương trình:
+) Gọi ẩn và đặt điều kiện cho ẩn.
+) Biểu diễn các đại lượng chữa biết theo ẩn và đại lượng đã biết.
+) Dựa vào giả thiết của bài toán để lập hệ phương trình.
+) Giải hệ phương trình tìm ẩn và đối chiếu với điều kiện của ẩn rồi kết luận.
Cách giải:
a) Gọi \({x_1},\;{x_2}\) là hai nghiệm của phương trình \({x^2} - 2\left( {m - 1} \right)x - 2m - 7 = 0\) (\(m\) là tham số). Tìm các giá trị của \(m\) để biểu thức \(A = x_1^2 + x_2^2 + 6{x_1}{x_2}\) đạt giá trị nhỏ nhất.
Phương trình có hai nghiệm \({x_1},\;{x_2} \Leftrightarrow \Delta ' \ge 0\)
\(\begin{array}{l} \Leftrightarrow {\left( {m - 1} \right)^2} + 2m + 7 \ge 0\\ \Leftrightarrow {m^2} - 2m + 1 + 2m + 7 \ge 0\\ \Leftrightarrow {m^2} + 8 \ge 0\;\;\;\forall m.\end{array}\)
Hay phương trình luôn có hai nghiệm phân biệt \({x_1},\;{x_2}\) với mọi \(m.\)
Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m - 1} \right)\\{x_1}{x_2} = - 2m - 7\end{array} \right..\)
Theo đề bài ta có:
\(\begin{array}{l}A = x_1^2 + x_2^2 + 6{x_1}{x_2} = {\left( {{x_1} + {x_2}} \right)^2} + 4{x_1}{x_2}\\\;\;\; = 4{\left( {m - 1} \right)^2} - 4\left( {2m + 7} \right)\\\;\;\; = 4\left( {{m^2} - 2m + 1 - 2m - 7} \right)\\\;\;\; = 4\left( {{m^2} - 4m + 4 - 10} \right)\\\;\;\; = 4\left[ {{{\left( {m - 2} \right)}^2} - 10} \right]\\\;\;\; = 4{\left( {m - 2} \right)^2} - 40.\end{array}\)
Vì \({\left( {m - 2} \right)^2} \ge 0 \Rightarrow 4{\left( {m - 2} \right)^2} \ge 0 \Rightarrow 4{\left( {m - 2} \right)^2} - 40 \ge - 40.\)
\( \Rightarrow A \ge - 40\) hay \(Min\;A = - 40\)
Dấu “=” xảy ra \( \Leftrightarrow m - 2 = 0 \Leftrightarrow m = 2.\)
Vậy \(m = 2.\)
b) Bạn Nam mua hai món hàng và phải trả tổng cộng 480000 đồng, trong đó đã tính cả 40000 đồng là thuế giá trị gia tăng (viết tắt là thuế VAT). Biết rằng thuế VAT đối với mặt hàng thứ nhất là 10%, thuế VAT đối với mặt hàng thứ hai là 8%. Hỏi nếu không kể thuế VAT thì bạn Nam phải trả mỗi món hàng là bao nhiêu tiền?
Gọi số phải trả cho món hàng thứ nhất không kể thuế VAT là \(x\) đồng, \(\left( {0 < x < 480000} \right).\)
Gọi số phải trả cho món hàng thứ nhất không kể thuế VAT là \(y\) đồng, \(\left( {0 < y < 480000} \right).\)
Số tiền phải trả cho hai món hàng không mất thuế là: \(x + y = 480000 - 40000 = 440000.\;\;\;\;\left( 1 \right)\)
Số tiền thuế phải trả cho món hàng thứ nhất là: \(x.10\% = \dfrac{x}{{10}}\) (đồng)
Số tiền thuế phải trả cho món hàng thứ hai là: \(y.8\% = \dfrac{{2y}}{{25}}\) (đồng).
Số tiền thuế phải trả cho hai món hàng là: \(\dfrac{x}{{10}} + \dfrac{{2y}}{{25}} = 40000 \Leftrightarrow 5x + 4y = 2000000\;\;\;\;\;\left( 2 \right).\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{l}x + y = 440000\\5x + 4y = 2000000\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x + 4y = 1760000\\5x + 4y = 2000000\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 240000\;\;\;\left( {tm} \right)\\y = 200000\;\;\;\left( {tm} \right)\end{array} \right..\)
Vậy số tiền phải trả cho món hàng thứ nhất không phải thuế là 240 000 đồng, món hàng thứ hai là 200 000 đồng.
Câu 4:
Phương pháp:
+) Biến đổi biểu thức về dạng: \(Q\left( x \right) = ax + b + \dfrac{c}{{x + 1}}.\,\,\left( {c = const} \right)\)
+) Khi đó, để \(Q\left( x \right) \in Z\) thì \(\dfrac{c}{{x + 1}} \in Z \Leftrightarrow \left( {x + 1} \right) \in U\left( c \right).\)
+) Từ đó ta giải phương trình hoặc lập bảng để tìm \(x \in Z\) thỏa mãn điều kiện bài toán.
Cách giải:
Cho biểu thức \(Q\left( x \right) = \dfrac{{5{x^2} + 6x + 2018}}{{x + 1}}.\) Tìm các giá trị nguyên của \(x\) để \(Q\left( x \right)\) là số nguyên.
Điều kiện: \(x \ne - 1.\)
Ta có: \(Q\left( x \right) = \dfrac{{5{x^2} + 6x + 2018}}{{x + 1}} = \dfrac{{5{x^2} + 5x + x + 1 + 2017}}{{x + 1}}\)
\( = \dfrac{{5x\left( {x + 1} \right)}}{{x + 1}} + \dfrac{{x + 1}}{{x + 1}} + \dfrac{{2017}}{{x + 1}} = 5x + 1 + \dfrac{{2017}}{{x + 1}}.\) \(\begin{array}{l} \Rightarrow Q\left( x \right) \in Z \Leftrightarrow \left( {5x + 1 + \dfrac{{2017}}{{x + 1}}} \right) \in Z \Leftrightarrow \dfrac{{2017}}{{x + 1}} \in Z\;\;\left( {do\;\;x \in Z} \right)\\ \Leftrightarrow \left( {x + 1} \right) \in U\left( {2017} \right).\end{array}\)
Mà \(U\left( {2017} \right) = \left\{ { - 2017; - 1;\;1;\;2017} \right\}.\)
\( \Rightarrow \left[ \begin{array}{l}x + 1 = - 2017\\x + 1 = - 1\\x + 1 = 1\\x + 1 = 2017\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 2018\;\;\;\left( {tm} \right)\\x = - 2\;\;\;\left( {tm} \right)\\x = 0\;\;\;\;\left( {tm} \right)\\x = 2016\;\;\left( {tm} \right)\end{array} \right..\)
Vậy \(x \in \left\{ { - 2018;\; - 2;\;0;\;\;2016} \right\}.\)
Câu 5:
Cách giải:
Cho đường tròn \(\left( O \right),\) từ điểm \(A\) ngoài đường tròn vẽ đường thẳng \(AO\) cắt đường tròn \(\left( O \right)\) tại \(B,\;\;C\;\left( {AB < AC} \right).\) Qua \(A\) vẽ đường thẳng không đi qua \(O\) cắt đường tròn \(\left( O \right)\) tại \(D,\;E\;\;\left( {AD < AE} \right).\) Đường thẳng vuông góc với \(AB\) tại \(A\) cắt đường thẳng \(CE\) tại \(F.\)
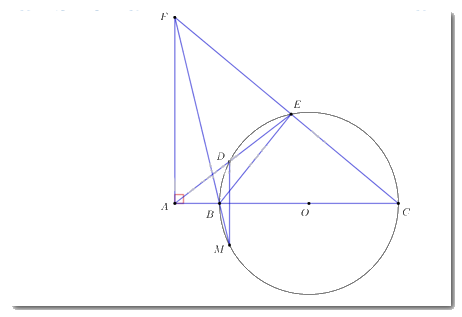
a) Chứng minh tứ giác \(ABEF\) nội tiếp.
Xét đường tròn \(\left( O \right)\) ta có: \(\widehat {BEC} = {90^0}\) (góc nội tiếp chắn nửa đường tròn).
Xét tứ giác \(ABEF\) ta có: \(\widehat {FAB} + \widehat {BEF} = {90^0} + {90^0} = {180^0}.\)
\( \Rightarrow ABEF\) là tứ giác nội tiếp. (tứ giác có tổng hai góc đối diện bằng \({180^0}\)).
b) Gọi \(M\) là giao điểm thứ hai của \(FB\) với đường tròn \(\left( O \right).\) Chứng minh \(DM \bot AC.\)
Vì tứ giác ABEF là tứ giác nội tiếp (cmt) \( \Rightarrow \widehat {AEB} = \widehat {AFB}\) (hai góc nội tiếp cùng chắn cung AB).
Lại có \(\widehat {AEB} = \widehat {BMD}\) (hai góc nội tiếp cùng chắn cung BD của đường tròn (O))
\( \Rightarrow \widehat {AFB} = \widehat {BMD}\). Mà hai góc này ở vị trí so le trong \( \Rightarrow AF//DM\).
Mà \(AF \bot AC \Rightarrow DM \bot AC\).
c) Chứng minh \(CE.CF + AD.AE = A{C^2}.\)
Xét tam giác ACD và tam giác ABE có
\(\widehat {CAE}\) chung;
\(\widehat {ACD} = \widehat {AEB}\) (hai góc nội tiếp cùng chắn cung BD)
\( \Rightarrow \Delta ACD \sim \Delta AEB\,\left( {g.g} \right) \Rightarrow \dfrac{{AC}}{{AE}} = \dfrac{{AD}}{{AB}} \Rightarrow AD.AE = AC.AB\,\,\left( 1 \right)\)
Xét tam giác CBE và tam giác CFA có:
\(\widehat {ACB}\) chung;
\(\widehat {CEB} = \widehat {CAF} = {90^0}\)
\( \Rightarrow \Delta CBE \sim \Delta CFA\,\,\left( {g.g} \right) \Rightarrow \dfrac{{CE}}{{CA}} = \dfrac{{CB}}{{CF}} \Rightarrow CE.CF = CA.CB\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow CE.CF + AD.AE = CA.CB + AC.AB = AC\left( {AB + BC} \right) = A{C^2}\,\,\left( {dpcm} \right)\)
Kỳ thi tuyển sinh vào lớp 10 là một bước ngoặt quan trọng trong quá trình học tập của mỗi học sinh. Để đạt kết quả tốt nhất, việc chuẩn bị kỹ lưỡng là điều cần thiết. Đề thi vào 10 môn Toán Kiên Giang năm 2018 là một nguồn tài liệu quý giá để các em học sinh ôn tập và rèn luyện kỹ năng.
Đề thi vào 10 môn Toán Kiên Giang năm 2018 thường có cấu trúc gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Để giúp các em học sinh hiểu rõ hơn về đề thi, chúng ta sẽ cùng phân tích một số câu hỏi điển hình:
Đây là một câu hỏi cơ bản về phương trình bậc nhất một ẩn. Để giải phương trình này, ta thực hiện các bước sau:
Vậy nghiệm của phương trình là x = 2.
Đây là một câu hỏi về định lý Pitago trong tam giác vuông. Ta có:
BC2 = AB2 + AC2 = 32 + 42 = 9 + 16 = 25
Suy ra BC = √25 = 5cm.
Để đạt kết quả tốt nhất trong kỳ thi vào 10 môn Toán, các em học sinh cần lưu ý những điều sau:
Giaitoan.edu.vn cung cấp đầy đủ các tài liệu ôn thi vào 10 môn Toán, bao gồm:
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi tuyển sinh vào lớp 10!
| Chủ đề | Mức độ quan trọng |
|---|---|
| Đại số | Cao |
| Hình học | Cao |
| Số học | Trung bình |
| Bài toán thực tế | Trung bình |