Giaitoan.edu.vn xin giới thiệu bộ đề thi vào 10 môn Toán Nghệ An năm 2023 chính thức và mới nhất. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin bước vào kỳ thi tuyển sinh sắp tới.
Chúng tôi cung cấp đầy đủ các đề thi, đáp án chi tiết và phương pháp giải bài tập hiệu quả.
Câu 1: a) Tính \(A = \sqrt 4 + \sqrt {49} + \sqrt {64} \). b) Rút gọn biểu thức \(P = \left( {\frac{{\sqrt x }}{2} - \frac{1}{{2\sqrt x }}} \right) \cdot \frac{{4x}}{{x - 1}}\), với \(x > 0\) và \(x \ne 1\). c) Tìm giá trị của \({\rm{b}}\) để đường thẳng \({\rm{y}} = 2{\rm{x}} + {\rm{b}} - 1\) cắt trục hoành tại điểm có hoành độ bằng 1 .
Câu 1:
a) Tính \(A = \sqrt 4 + \sqrt {49} + \sqrt {64} \).
b) Rút gọn biểu thức \(P = \left( {\frac{{\sqrt x }}{2} - \frac{1}{{2\sqrt x }}} \right) \cdot \frac{{4x}}{{x - 1}}\), với \(x > 0\) và \(x \ne 1\).
c) Tìm giá trị của \({\rm{b}}\) để đường thẳng \({\rm{y}} = 2{\rm{x}} + {\rm{b}} - 1\) cắt trục hoành tại điểm có hoành độ bằng 1 .
Câu 2:
a) Giải phương trình \({x^2} + 3x - 10 = 0\).
b) Cho biết phương trình \({x^2} - 5x + 3 = 0\) có hai nghiệm dương phân biệt \({x_1},{x_2}\).
Không giải phương trình, tính giá trị của biểu thức \({\rm{T}} = \frac{{\left( {{{\rm{x}}_1} + 1} \right)\left( {{{\rm{x}}_2} + 1} \right)}}{{{\rm{x}}_1^2 + 5{{\rm{x}}_2}}}\).
Câu 3:
a) Một cừa hàng kinh doanh xe đạp nhập về một lô hàng gồm hai loại: loại I có giá 2 triệu đồng/xe và loại II có giá 6 triệu dồng/xe. Biết rằng lô hàng nói trên có 50 xe với tổng số tiền mà cửa hàng phài thanh toán là 160 triệu đồng. Hòi cửa hàng đã nhập về bao nhiêu xe loại I và bao nhiêu xe loại II?
b) Bạn An bỏ một viên bi đặc không thấm nước vào một lọ thủy tinh chứa nước dạng hình trự có bán kinh đường tròn đáy bằng \(1,5{\rm{\;cm}}\). Biết rằng khi viên bi chìm hoàn toàn trong nước thì nước trong lọ dâng lên thêm \(0,5{\rm{\;cm}}\). Tính thể tích viên bi bạn An dã bỏ vào lọ thủy tinh (cho \(\pi = 3,14\); xem độ dày của lọ không dáng kể và nước trong lọ không thất thoát ra ngoài).
Câu 4: Cho tam giác nhọn \({\rm{ABC}}({\rm{AB}} < {\rm{AC}})\), các đường cao \({\rm{AD}},{\rm{BE}},{\rm{CF}}({\rm{D}} \in {\rm{BC}}\), \({\rm{E}} \in {\rm{AC}},{\rm{F}} \in {\rm{AB}})\) cắt nhau tại \({\rm{H}}\).
a) Chứng minh \({\rm{AEHF}}\) là tứ giác nội tiếp.
b) Gọi \({\rm{O}}\) là trung diểm của đoạn thẳng \({\rm{BC}},{\rm{M}}\) là giao điểm của tia \({\rm{EF}}\) và tia \({\rm{CB}}\). Chứng minh rằng \(\widehat {{\rm{FAD}}} = \widehat {{\rm{OFC}}}\) và \({\rm{O}}{{\rm{C}}^2} = {\rm{OD}} \cdot {\rm{OM}}\).
c) Chứng minh rằng hai đường thẳng \({\rm{MH}}\) và \({\rm{AO}}\) vuông góc với nhau.
Câu 5: Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{\left( {{x^2} + 1} \right)\left( {{y^2} + 1} \right) = 4\,\,\,}\\{x\sqrt {{y^2} + 1} + y\sqrt {{x^2} + 1} = {x^2}{y^2} - 1\,\,}\end{array}} \right.\) \((x,y \in \mathbb{R})\)
-----HẾT-----
Câu 1 (TH):
Phương pháp:
a) Khai căn và thực hiện phép tính.
b) Quy đồng và rút gọn.
c) Tìm giao điểm của đường thẳng và trục hoành từ đó thay vào đường thẳng để tìm giá trị b.
Cách giải:
a) Tính \(A = \sqrt 4 + \sqrt {49} + \sqrt {64} \)
\(\begin{array}{l}A = \sqrt 4 + \sqrt {49} + \sqrt {64} \\A = \sqrt {{2^2}} + \sqrt {{7^2}} + \sqrt {{8^2}} \\A = 2 + 7 + 8\\A = 17\end{array}\)
Vậy A = 17.
b) Rút gọn biểu thức \(P = \left( {\frac{{\sqrt x }}{2} - \frac{1}{{2\sqrt x }}} \right).\frac{{4x}}{{x - 1}}\) với \(x > 0\) và \(x \ne 1\).
Với \(x > 0,\,\,x \ne 1\) ta có:
\(\begin{array}{l}P = \left( {\frac{{\sqrt x }}{2} - \frac{1}{{2\sqrt x }}} \right).\frac{{4x}}{{x - 1}}\\P = \frac{{x - 1}}{{2\sqrt x }}.\frac{{4x}}{{x - 1}}\\P = \frac{{x - 1}}{{2\sqrt x }}.\frac{{2.2{{\left( {\sqrt x } \right)}^2}}}{{x - 1}}\\P = 2\sqrt x \end{array}\)
Vậy với \(x > 0,\,\,x \ne 1\) thì \(P = 2\sqrt x \).
c) Tìm giá trị của b để đường thẳng \(y = 2x + b - 1\) cắt trục hoành tại điểm có hoành độ bằng 1.
Đường thẳng d cắt trục hoành tại điểm có hoành độ bằng 1 => Đường thẳng d đi qua điểm A(1;0).
Thay x = 1 và y = 0 vào phương trình đường thẳng d ta có: \(0 = 2.1 + b - 1 \Leftrightarrow b + 1 = 0 \Leftrightarrow b = - 1.\)
Vậy b = -1.
Câu 2 (VD):
Phương pháp:
a) Tính \(\Delta \) và suy ra nghiệm của phương trình.
b) Áp dụng hệ thức vi-ét \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \frac{b}{a}\\{x_1}.{x_2} = \frac{c}{a}\end{array} \right.\)
Cách giải:
a) Giải phương trình \({x^2} + 3x - 10 = 0\)
Ta có: \(\Delta = {3^2} - 4.1.\left( { - 10} \right) = 49 > 0\)
Suy ra phương trình có hai nghiệm phân biệt là: \(\left[ \begin{array}{l}{x_1} = \frac{{ - 3 + \sqrt {49} }}{2} = \frac{{ - 3 + 7}}{2} = 2\\{x_2} = \frac{{ - 3 - \sqrt {49} }}{2} = \frac{{ - 3 - 7}}{2} = - 5\end{array} \right.\)
Vậy tập nghiệm của phương trình là: \(S = \left\{ {2; - 5} \right\}\).
b) Cho biết phương trình \({x^2} - 5x + 3 = 0\) có hai nghiệm dương phân biệt \({x_1},{x_2}\). Không giải phương trình, tính giá trị của biểu thức \(T = \frac{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}}{{x_1^2 + 5{x_2}}}\)
Vì \({x_1}\) là nghiệm của phương trình nên \(x_1^2 - 5{x_1} + 3 = 0 \Leftrightarrow x_1^2 = 5{x_1} - 3\).
Theo bài ra, ta có:
\(T = \frac{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}}{{x_1^2 + 5{x_2}}} = \frac{{{x_1}.{x_2} + {x_1} + {x_2} + 1}}{{5{x_1} + 5{x_2} - 3}} = \frac{{{x_1}.{x_2} + {x_1} + {x_2} + 1}}{{5\left( {{x_1} + {x_2}} \right) - 3}}\)
Theo hệ thức Vi-ét, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 5\\{x_1}.{x_2} = 3\end{array} \right.\)
Suy ra: \(T = \frac{{3 + 5 + 1}}{{5.5 - 3}} = \frac{9}{{22}}\).
Vậy \(T = \frac{9}{{22}}.\)
Câu 3 (VD):
Phương pháp:
a)
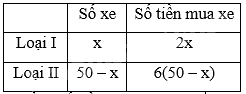
Vì tổng số tiền mà cửa hàng phài thanh toán là 160 triệu đồng nên ta tìm được phương trình.
b) Áp dụng công thức tính thể tích hình trụ: \(\pi {r^2}h\).
Cách giải:
a) Gọi số xe loại I cửa hàng nhập về là x (\(x \in {\mathbb{N}^*}\), xe) (x < 50).
Do lô hàng có tổng 50 xe nên số xe loại II là 50 – x (xe)
Tổng số tiền mua xe loại I là 2x (triệu đồng)
Tổng số tiền mua xe loại II là \(6\left( {50 - x} \right)\) (triệu đồng)
Do tổng số tiền mà cửa hàng phải thanh toán là 160 triệu đồng nên ta có phương trình:
\(\begin{array}{l}2x + 6\left( {50 - x} \right) = 160\\ \Leftrightarrow 2x + 300 - 6x = 160\\ \Leftrightarrow - 4x = - 140\\ \Leftrightarrow x = 35\left( {TM} \right)\end{array}\)
Vậy cửa hàng đã nhập về 35 xe loại I và 50 – 35 = 15 xe loại II
b) Thể tích của phần nước dâng lên trong bình hình trụ là thể tích của viên bi và bằng
\(\pi .{r^2}.h = 3,14.1,{5^2}.0,5 = 3,5325\,\,\left( {c{m^3}} \right)\)
Vậy thể tích viên bi là 3,5325 \(c{m^3}\).
Câu 4 (VD):
Phương pháp:
Cách giải:
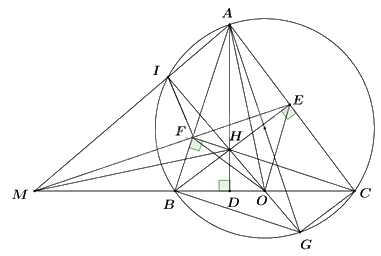
a) Chứng minh AEHF là tứ giác nội tiếp.
Xét tứ giác AEHF có \(\angle AFH = \angle AEH = {90^0}\) (do BE, CF là đường cao)
\( \Rightarrow \angle AFH + \angle AEH = {90^0} + {90^0} = {180^0}\)
Mà 2 góc này ở vị trí đối diện nên tứ giác AEHF nội tiếp (dhnb) (đpcm)
b) Gọi O là trung điểm của đoạn thẳng BC, M là giao điểm của tia EF và tia CB. Chứng minh rằng \(\angle FAD = \angle OFC\) và \(O{C^2} = OD.OM\).
+) Chứng minh \(\angle FAD = \angle OFC\)
Ta có \(\angle AFC = \angle ADC = {90^0}\) (do CE, AD là đường cao)
Mà F, D là 2 đỉnh kề nhau cùng nhìn AC dưới 2 góc bằng nhau nên AFDC nội tiếp (dhnb)
\( \Rightarrow \angle FAD = \angle FCD\) (hai góc nội tiếp cùng chắn cung FD)
Mà tam giác BFC vuông tại F, trung tuyến FO nên OB = OC = OF (tính chất đường trung tuyến)
\( \Rightarrow \Delta OCF\) cân tại O \( \Rightarrow \angle OFC = \angle OCF\) (tính chất tam giác cân)
\( \Rightarrow \angle OFC = \angle FAD\) (đpcm).
+) Chứng minh \(O{C^2} = OD.OM\)
Vì tứ giác AFDC là tứ giác nội tiếp (cmt) \( \Rightarrow \angle BAC = \angle BDF\) (góc ngoài và góc trong tại đối diện)
\(\begin{array}{l} \Rightarrow {180^0} - \angle BAC = {180^0} - \angle BDF\\ \Rightarrow \angle AFE + \angle AEF = \angle ODF\,\,\left( 1 \right)\end{array}\)
Xét tứ giác BFEC có: \(\angle BFC = \angle BEC = {90^0}\,\,\left( {gt} \right)\)
Mà hai đỉnh F, E kề nhau cùng nhìn BC dưới hai góc bằng nhau
=> BFEC là tứ giác nội tiếp.
\( \Rightarrow \angle AFE = \angle ACB\) (góc ngoài và góc trong tại đỉnh đối diện)
Mặt khác tam giác BEC vuông tại E có trung tuyến EO ứng với cạnh huyền BC \( \Rightarrow OB = OC = OE \Rightarrow \Delta OEC\) cân tại O \( \Rightarrow \angle ACB = \angle OCE = \angle OEC\).
\( \Rightarrow \angle AFE = \angle OEC\,\,\,\left( 2 \right)\)
Từ (1) và (2)
\(\begin{array}{l} \Rightarrow \angle OEC + \angle AEF = \angle ODF\\ \Rightarrow {180^0} - \angle OEF = \angle ODF\\ \Rightarrow \angle OEF + \angle ODF = {180^0}\end{array}\)
Ta có: \(OE = OF = \frac{1}{2}BC \Rightarrow \Delta OEF\) cân tại O \( \Rightarrow \angle OEF = \angle OFE\) (tính chất tam giác cân)
\( \Rightarrow \angle OFE + \angle ODF = {180^0}\)
Mà \(\angle OFE + \angle OFM = {180^0}\) (kề bù)
\( \Rightarrow \angle ODF = \angle OFM\). Xét \(\Delta ODF\) và \(\Delta OFM\) có:
$\begin{align} \angle FOM\,\,chung \\ \angle ODF=\angle OFM\,\,\left( cmt \right) \\ \Rightarrow \Delta ODF\backsim \Delta OFM\,\,\left( g.g \right) \\ \end{align}$
\( \Rightarrow \frac{{OD}}{{OF}} = \frac{{OF}}{{OM}}\) (cặp cạnh tương ứng tỉ lệ)
\( \Rightarrow O{F^2} = OD.OM = O{C^2}\) (đpcm).
c) Chứng minh rằng hai đường thẳng MH và AO vuông góc với nhau.
Vẽ đường tròn ngoại tiếp tam giác ABC, đường kính AG của đường tròn ngoại tiếp tam giác ABC.
Ta có: \(\angle ABG = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow AB \bot BG\).
Mà \(CH \bot AB\,\,\left( {gt} \right) \Rightarrow BG//CH\) (từ vuông góc đến song song).
Tương tự ta có: \(\angle ACG = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow AC \bot GC\).
Mà \(BH \bot AC\,\,\left( {gt} \right) \Rightarrow BH//GC\) (từ vuông góc đến song song).
\( \Rightarrow BHCG\) là hình bình hành (dhnb)
=> Hai đường chéo BC và HG cắt nhau tại trung điểm mỗi đường.
Mà O là trung điểm của BC (gt) => O cũng là trung điểm của HG.
=> H, O, G thẳng hàng.
Gọi \(AM\) cắt đường tròn ngoại tiếp tam giác ABC tại I.
Ta có \(MI.MA = MB.MC = ME.MF\) (do AIBC và BFEC là tứ giác nội tiếp)
\( \Rightarrow AIFE\) là tứ giác nội tiếp (dhnb)
\( \Rightarrow \angle AIH = \angle AFH = {90^0}\) (hai góc nội tiếp cùng chắn cung AH) \( \Rightarrow AI \bot IH\).
Mà \(\angle AIG = {90^0}\) (góc nội tiếp chắn nửa đường tròn ngoại tiếp tam giác ABC) \( \Rightarrow AI \bot IG\).
\( \Rightarrow I,\,\,H,\,\,G\) thẳng hàng.
\( \Rightarrow I,\,\,H,\,\,O,\,\,G\) thẳng hàng.
Mà \(AI \bot IG \Rightarrow OI \bot AM\).
Xét tam giác OAM có: \(\left\{ \begin{array}{l}OI \bot AM\,\,\left( {cmt} \right)\\AD \bot OM\,\,\left( {gt} \right)\\OI \cap AD = \left\{ H \right\}\end{array} \right. \Rightarrow H\) là trực tâm của tam giác OAM.
\( \Rightarrow MH\) là đường cao thứ ba ứng với cạnh AO.
Vậy \(MH \bot AO\,\,\left( {dpcm} \right)\).
Câu 5 (VD):
Phương pháp:
Cách giải:
\(\left\{ {\begin{array}{*{20}{l}}{\left( {{x^2} + 1} \right)\left( {{y^2} + 1} \right) = 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)}\\{x\sqrt {{y^2} + 1} + y\sqrt {{x^2} + 1} = {x^2}{y^2} - 1\,\,\,(2)}\end{array}} \right.\)
\(\begin{array}{l}\left( 1 \right) \Leftrightarrow 4 = {x^2} + {y^2} + 1 + {x^2}{y^2} \ge 2xy + {x^2}{y^2} + 1 = {(xy + 1)^2}\\ \Rightarrow - 2 \le xy + 1 \le 2 \Leftrightarrow - 3 \le xy \le 1\end{array}\).
Bình phương hai vế của phương trình (2) ta được:
\({x^2}\left( {{y^2} + 1} \right) + 2xy\sqrt {\left( {{x^2} + 1} \right)\left( {{y^2} + 1} \right)} + {y^2}\left( {{x^2} + 1} \right) = {x^4}{y^4} - 2{x^2}{y^2} + 1\)
\( \Leftrightarrow {x^2}{y^2} + {x^2} + {y^2} + {x^2}{y^2} + 2xy\sqrt {\left( {{x^2} + 1} \right)\left( {{y^2} + 1} \right)} = {x^4}{y^4} - 2{x^2}{y^2} + 1\)
\( \Leftrightarrow 3 + {x^2}{y^2} + 2xy.2 = {x^4}{y^4} - 2{x^2}{y^2} + 1\)
\( \Leftrightarrow {x^4}{y^4} - 3{x^2}{y^2} - 4xy - 2 = 0\) (3)
Đặt \(a = xy \Rightarrow - 3 \le a \le 1\). Khi đó phương trình (3) trở thành:
\(\begin{array}{l}{a^4} - 3{a^2} - 4a - 2 = 0\\ \Leftrightarrow {a^4} + {a^3} - {a^3} - {a^2} - 2{a^2} - 2a - 2a - 2 = 0\\ \Leftrightarrow {a^3}\left( {a + 1} \right) - {a^2}\left( {a + 1} \right) - 2a\left( {a + 1} \right) - 2\left( {a + 1} \right) = 0\\ \Leftrightarrow (a + 1)\left( {{a^3} - {a^2} - 2a - 2} \right) = 0\end{array}\)
\( \Leftrightarrow \left[ \begin{array}{l}a + 1 = 0\\{a^3} - {a^2} - 2a - 2 = 0\end{array} \right.\)
TH1: \(a + 1 = 0 \Leftrightarrow a = - 1\,\,\left( {tm} \right)\)
\( \Rightarrow xy = - 1 \Rightarrow y = - \frac{1}{x}\) (do \(x = 0\) không là nghiệm của phương trình)
Thay vào (1) ta được:
\(\begin{array}{l}\left( {{x^2} + 1} \right)\left( {\frac{1}{{{x^2}}} + 1} \right) = 4 \Leftrightarrow \frac{{{{\left( {{x^2} + 1} \right)}^2}}}{{{x^2}}} = 4\\ \Leftrightarrow {\left( {{x^2} + 1} \right)^2} = 4{x^2} \Leftrightarrow \left[ \begin{array}{l}{x^2} + 1 = 2x\\{x^2} + 1 = - 2x\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}{\left( {x - 1} \right)^2} = 0\\{\left( {x + 1} \right)^2} = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1 \Rightarrow y = - 1\\x = - 1 \Rightarrow y = 1\end{array} \right.\end{array}\)
TH2: \({a^3} - {a^2} - 2a - 2 = 0 \Leftrightarrow {a^3} - 1 = {a^2} + 2a + 1 \Leftrightarrow {a^3} - 1 = {\left( {a + 1} \right)^2}\)
Vì \(a \le 1\) nên \({a^3} \le 1 \Leftrightarrow {a^3} - 1 \le 0\) mà \({\left( {a + 1} \right)^2} \ge 0\) nên \({a^3} - 1 = {\left( {a + 1} \right)^2} \Leftrightarrow \left\{ \begin{array}{l}a - 1 = 0\\a + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 1\\a = 1\end{array} \right.\) (vô lý).
=> Phương trình vô nghiệm.
Vậy hệ phương trình có 2 nghiệm là \(\left( {x;y} \right) = \left( { - 1;1} \right)\) hoặc \(\left( {x;y} \right) = \left( {1; - 1} \right)\).
-----HẾT-----
Câu 1:
a) Tính \(A = \sqrt 4 + \sqrt {49} + \sqrt {64} \).
b) Rút gọn biểu thức \(P = \left( {\frac{{\sqrt x }}{2} - \frac{1}{{2\sqrt x }}} \right) \cdot \frac{{4x}}{{x - 1}}\), với \(x > 0\) và \(x \ne 1\).
c) Tìm giá trị của \({\rm{b}}\) để đường thẳng \({\rm{y}} = 2{\rm{x}} + {\rm{b}} - 1\) cắt trục hoành tại điểm có hoành độ bằng 1 .
Câu 2:
a) Giải phương trình \({x^2} + 3x - 10 = 0\).
b) Cho biết phương trình \({x^2} - 5x + 3 = 0\) có hai nghiệm dương phân biệt \({x_1},{x_2}\).
Không giải phương trình, tính giá trị của biểu thức \({\rm{T}} = \frac{{\left( {{{\rm{x}}_1} + 1} \right)\left( {{{\rm{x}}_2} + 1} \right)}}{{{\rm{x}}_1^2 + 5{{\rm{x}}_2}}}\).
Câu 3:
a) Một cừa hàng kinh doanh xe đạp nhập về một lô hàng gồm hai loại: loại I có giá 2 triệu đồng/xe và loại II có giá 6 triệu dồng/xe. Biết rằng lô hàng nói trên có 50 xe với tổng số tiền mà cửa hàng phài thanh toán là 160 triệu đồng. Hòi cửa hàng đã nhập về bao nhiêu xe loại I và bao nhiêu xe loại II?
b) Bạn An bỏ một viên bi đặc không thấm nước vào một lọ thủy tinh chứa nước dạng hình trự có bán kinh đường tròn đáy bằng \(1,5{\rm{\;cm}}\). Biết rằng khi viên bi chìm hoàn toàn trong nước thì nước trong lọ dâng lên thêm \(0,5{\rm{\;cm}}\). Tính thể tích viên bi bạn An dã bỏ vào lọ thủy tinh (cho \(\pi = 3,14\); xem độ dày của lọ không dáng kể và nước trong lọ không thất thoát ra ngoài).
Câu 4: Cho tam giác nhọn \({\rm{ABC}}({\rm{AB}} < {\rm{AC}})\), các đường cao \({\rm{AD}},{\rm{BE}},{\rm{CF}}({\rm{D}} \in {\rm{BC}}\), \({\rm{E}} \in {\rm{AC}},{\rm{F}} \in {\rm{AB}})\) cắt nhau tại \({\rm{H}}\).
a) Chứng minh \({\rm{AEHF}}\) là tứ giác nội tiếp.
b) Gọi \({\rm{O}}\) là trung diểm của đoạn thẳng \({\rm{BC}},{\rm{M}}\) là giao điểm của tia \({\rm{EF}}\) và tia \({\rm{CB}}\). Chứng minh rằng \(\widehat {{\rm{FAD}}} = \widehat {{\rm{OFC}}}\) và \({\rm{O}}{{\rm{C}}^2} = {\rm{OD}} \cdot {\rm{OM}}\).
c) Chứng minh rằng hai đường thẳng \({\rm{MH}}\) và \({\rm{AO}}\) vuông góc với nhau.
Câu 5: Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{\left( {{x^2} + 1} \right)\left( {{y^2} + 1} \right) = 4\,\,\,}\\{x\sqrt {{y^2} + 1} + y\sqrt {{x^2} + 1} = {x^2}{y^2} - 1\,\,}\end{array}} \right.\) \((x,y \in \mathbb{R})\)
-----HẾT-----
Câu 1 (TH):
Phương pháp:
a) Khai căn và thực hiện phép tính.
b) Quy đồng và rút gọn.
c) Tìm giao điểm của đường thẳng và trục hoành từ đó thay vào đường thẳng để tìm giá trị b.
Cách giải:
a) Tính \(A = \sqrt 4 + \sqrt {49} + \sqrt {64} \)
\(\begin{array}{l}A = \sqrt 4 + \sqrt {49} + \sqrt {64} \\A = \sqrt {{2^2}} + \sqrt {{7^2}} + \sqrt {{8^2}} \\A = 2 + 7 + 8\\A = 17\end{array}\)
Vậy A = 17.
b) Rút gọn biểu thức \(P = \left( {\frac{{\sqrt x }}{2} - \frac{1}{{2\sqrt x }}} \right).\frac{{4x}}{{x - 1}}\) với \(x > 0\) và \(x \ne 1\).
Với \(x > 0,\,\,x \ne 1\) ta có:
\(\begin{array}{l}P = \left( {\frac{{\sqrt x }}{2} - \frac{1}{{2\sqrt x }}} \right).\frac{{4x}}{{x - 1}}\\P = \frac{{x - 1}}{{2\sqrt x }}.\frac{{4x}}{{x - 1}}\\P = \frac{{x - 1}}{{2\sqrt x }}.\frac{{2.2{{\left( {\sqrt x } \right)}^2}}}{{x - 1}}\\P = 2\sqrt x \end{array}\)
Vậy với \(x > 0,\,\,x \ne 1\) thì \(P = 2\sqrt x \).
c) Tìm giá trị của b để đường thẳng \(y = 2x + b - 1\) cắt trục hoành tại điểm có hoành độ bằng 1.
Đường thẳng d cắt trục hoành tại điểm có hoành độ bằng 1 => Đường thẳng d đi qua điểm A(1;0).
Thay x = 1 và y = 0 vào phương trình đường thẳng d ta có: \(0 = 2.1 + b - 1 \Leftrightarrow b + 1 = 0 \Leftrightarrow b = - 1.\)
Vậy b = -1.
Câu 2 (VD):
Phương pháp:
a) Tính \(\Delta \) và suy ra nghiệm của phương trình.
b) Áp dụng hệ thức vi-ét \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \frac{b}{a}\\{x_1}.{x_2} = \frac{c}{a}\end{array} \right.\)
Cách giải:
a) Giải phương trình \({x^2} + 3x - 10 = 0\)
Ta có: \(\Delta = {3^2} - 4.1.\left( { - 10} \right) = 49 > 0\)
Suy ra phương trình có hai nghiệm phân biệt là: \(\left[ \begin{array}{l}{x_1} = \frac{{ - 3 + \sqrt {49} }}{2} = \frac{{ - 3 + 7}}{2} = 2\\{x_2} = \frac{{ - 3 - \sqrt {49} }}{2} = \frac{{ - 3 - 7}}{2} = - 5\end{array} \right.\)
Vậy tập nghiệm của phương trình là: \(S = \left\{ {2; - 5} \right\}\).
b) Cho biết phương trình \({x^2} - 5x + 3 = 0\) có hai nghiệm dương phân biệt \({x_1},{x_2}\). Không giải phương trình, tính giá trị của biểu thức \(T = \frac{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}}{{x_1^2 + 5{x_2}}}\)
Vì \({x_1}\) là nghiệm của phương trình nên \(x_1^2 - 5{x_1} + 3 = 0 \Leftrightarrow x_1^2 = 5{x_1} - 3\).
Theo bài ra, ta có:
\(T = \frac{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}}{{x_1^2 + 5{x_2}}} = \frac{{{x_1}.{x_2} + {x_1} + {x_2} + 1}}{{5{x_1} + 5{x_2} - 3}} = \frac{{{x_1}.{x_2} + {x_1} + {x_2} + 1}}{{5\left( {{x_1} + {x_2}} \right) - 3}}\)
Theo hệ thức Vi-ét, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 5\\{x_1}.{x_2} = 3\end{array} \right.\)
Suy ra: \(T = \frac{{3 + 5 + 1}}{{5.5 - 3}} = \frac{9}{{22}}\).
Vậy \(T = \frac{9}{{22}}.\)
Câu 3 (VD):
Phương pháp:
a)
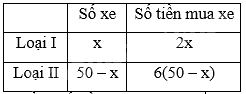
Vì tổng số tiền mà cửa hàng phài thanh toán là 160 triệu đồng nên ta tìm được phương trình.
b) Áp dụng công thức tính thể tích hình trụ: \(\pi {r^2}h\).
Cách giải:
a) Gọi số xe loại I cửa hàng nhập về là x (\(x \in {\mathbb{N}^*}\), xe) (x < 50).
Do lô hàng có tổng 50 xe nên số xe loại II là 50 – x (xe)
Tổng số tiền mua xe loại I là 2x (triệu đồng)
Tổng số tiền mua xe loại II là \(6\left( {50 - x} \right)\) (triệu đồng)
Do tổng số tiền mà cửa hàng phải thanh toán là 160 triệu đồng nên ta có phương trình:
\(\begin{array}{l}2x + 6\left( {50 - x} \right) = 160\\ \Leftrightarrow 2x + 300 - 6x = 160\\ \Leftrightarrow - 4x = - 140\\ \Leftrightarrow x = 35\left( {TM} \right)\end{array}\)
Vậy cửa hàng đã nhập về 35 xe loại I và 50 – 35 = 15 xe loại II
b) Thể tích của phần nước dâng lên trong bình hình trụ là thể tích của viên bi và bằng
\(\pi .{r^2}.h = 3,14.1,{5^2}.0,5 = 3,5325\,\,\left( {c{m^3}} \right)\)
Vậy thể tích viên bi là 3,5325 \(c{m^3}\).
Câu 4 (VD):
Phương pháp:
Cách giải:
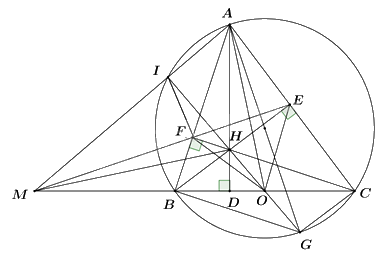
a) Chứng minh AEHF là tứ giác nội tiếp.
Xét tứ giác AEHF có \(\angle AFH = \angle AEH = {90^0}\) (do BE, CF là đường cao)
\( \Rightarrow \angle AFH + \angle AEH = {90^0} + {90^0} = {180^0}\)
Mà 2 góc này ở vị trí đối diện nên tứ giác AEHF nội tiếp (dhnb) (đpcm)
b) Gọi O là trung điểm của đoạn thẳng BC, M là giao điểm của tia EF và tia CB. Chứng minh rằng \(\angle FAD = \angle OFC\) và \(O{C^2} = OD.OM\).
+) Chứng minh \(\angle FAD = \angle OFC\)
Ta có \(\angle AFC = \angle ADC = {90^0}\) (do CE, AD là đường cao)
Mà F, D là 2 đỉnh kề nhau cùng nhìn AC dưới 2 góc bằng nhau nên AFDC nội tiếp (dhnb)
\( \Rightarrow \angle FAD = \angle FCD\) (hai góc nội tiếp cùng chắn cung FD)
Mà tam giác BFC vuông tại F, trung tuyến FO nên OB = OC = OF (tính chất đường trung tuyến)
\( \Rightarrow \Delta OCF\) cân tại O \( \Rightarrow \angle OFC = \angle OCF\) (tính chất tam giác cân)
\( \Rightarrow \angle OFC = \angle FAD\) (đpcm).
+) Chứng minh \(O{C^2} = OD.OM\)
Vì tứ giác AFDC là tứ giác nội tiếp (cmt) \( \Rightarrow \angle BAC = \angle BDF\) (góc ngoài và góc trong tại đối diện)
\(\begin{array}{l} \Rightarrow {180^0} - \angle BAC = {180^0} - \angle BDF\\ \Rightarrow \angle AFE + \angle AEF = \angle ODF\,\,\left( 1 \right)\end{array}\)
Xét tứ giác BFEC có: \(\angle BFC = \angle BEC = {90^0}\,\,\left( {gt} \right)\)
Mà hai đỉnh F, E kề nhau cùng nhìn BC dưới hai góc bằng nhau
=> BFEC là tứ giác nội tiếp.
\( \Rightarrow \angle AFE = \angle ACB\) (góc ngoài và góc trong tại đỉnh đối diện)
Mặt khác tam giác BEC vuông tại E có trung tuyến EO ứng với cạnh huyền BC \( \Rightarrow OB = OC = OE \Rightarrow \Delta OEC\) cân tại O \( \Rightarrow \angle ACB = \angle OCE = \angle OEC\).
\( \Rightarrow \angle AFE = \angle OEC\,\,\,\left( 2 \right)\)
Từ (1) và (2)
\(\begin{array}{l} \Rightarrow \angle OEC + \angle AEF = \angle ODF\\ \Rightarrow {180^0} - \angle OEF = \angle ODF\\ \Rightarrow \angle OEF + \angle ODF = {180^0}\end{array}\)
Ta có: \(OE = OF = \frac{1}{2}BC \Rightarrow \Delta OEF\) cân tại O \( \Rightarrow \angle OEF = \angle OFE\) (tính chất tam giác cân)
\( \Rightarrow \angle OFE + \angle ODF = {180^0}\)
Mà \(\angle OFE + \angle OFM = {180^0}\) (kề bù)
\( \Rightarrow \angle ODF = \angle OFM\). Xét \(\Delta ODF\) và \(\Delta OFM\) có:
$\begin{align} \angle FOM\,\,chung \\ \angle ODF=\angle OFM\,\,\left( cmt \right) \\ \Rightarrow \Delta ODF\backsim \Delta OFM\,\,\left( g.g \right) \\ \end{align}$
\( \Rightarrow \frac{{OD}}{{OF}} = \frac{{OF}}{{OM}}\) (cặp cạnh tương ứng tỉ lệ)
\( \Rightarrow O{F^2} = OD.OM = O{C^2}\) (đpcm).
c) Chứng minh rằng hai đường thẳng MH và AO vuông góc với nhau.
Vẽ đường tròn ngoại tiếp tam giác ABC, đường kính AG của đường tròn ngoại tiếp tam giác ABC.
Ta có: \(\angle ABG = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow AB \bot BG\).
Mà \(CH \bot AB\,\,\left( {gt} \right) \Rightarrow BG//CH\) (từ vuông góc đến song song).
Tương tự ta có: \(\angle ACG = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow AC \bot GC\).
Mà \(BH \bot AC\,\,\left( {gt} \right) \Rightarrow BH//GC\) (từ vuông góc đến song song).
\( \Rightarrow BHCG\) là hình bình hành (dhnb)
=> Hai đường chéo BC và HG cắt nhau tại trung điểm mỗi đường.
Mà O là trung điểm của BC (gt) => O cũng là trung điểm của HG.
=> H, O, G thẳng hàng.
Gọi \(AM\) cắt đường tròn ngoại tiếp tam giác ABC tại I.
Ta có \(MI.MA = MB.MC = ME.MF\) (do AIBC và BFEC là tứ giác nội tiếp)
\( \Rightarrow AIFE\) là tứ giác nội tiếp (dhnb)
\( \Rightarrow \angle AIH = \angle AFH = {90^0}\) (hai góc nội tiếp cùng chắn cung AH) \( \Rightarrow AI \bot IH\).
Mà \(\angle AIG = {90^0}\) (góc nội tiếp chắn nửa đường tròn ngoại tiếp tam giác ABC) \( \Rightarrow AI \bot IG\).
\( \Rightarrow I,\,\,H,\,\,G\) thẳng hàng.
\( \Rightarrow I,\,\,H,\,\,O,\,\,G\) thẳng hàng.
Mà \(AI \bot IG \Rightarrow OI \bot AM\).
Xét tam giác OAM có: \(\left\{ \begin{array}{l}OI \bot AM\,\,\left( {cmt} \right)\\AD \bot OM\,\,\left( {gt} \right)\\OI \cap AD = \left\{ H \right\}\end{array} \right. \Rightarrow H\) là trực tâm của tam giác OAM.
\( \Rightarrow MH\) là đường cao thứ ba ứng với cạnh AO.
Vậy \(MH \bot AO\,\,\left( {dpcm} \right)\).
Câu 5 (VD):
Phương pháp:
Cách giải:
\(\left\{ {\begin{array}{*{20}{l}}{\left( {{x^2} + 1} \right)\left( {{y^2} + 1} \right) = 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)}\\{x\sqrt {{y^2} + 1} + y\sqrt {{x^2} + 1} = {x^2}{y^2} - 1\,\,\,(2)}\end{array}} \right.\)
\(\begin{array}{l}\left( 1 \right) \Leftrightarrow 4 = {x^2} + {y^2} + 1 + {x^2}{y^2} \ge 2xy + {x^2}{y^2} + 1 = {(xy + 1)^2}\\ \Rightarrow - 2 \le xy + 1 \le 2 \Leftrightarrow - 3 \le xy \le 1\end{array}\).
Bình phương hai vế của phương trình (2) ta được:
\({x^2}\left( {{y^2} + 1} \right) + 2xy\sqrt {\left( {{x^2} + 1} \right)\left( {{y^2} + 1} \right)} + {y^2}\left( {{x^2} + 1} \right) = {x^4}{y^4} - 2{x^2}{y^2} + 1\)
\( \Leftrightarrow {x^2}{y^2} + {x^2} + {y^2} + {x^2}{y^2} + 2xy\sqrt {\left( {{x^2} + 1} \right)\left( {{y^2} + 1} \right)} = {x^4}{y^4} - 2{x^2}{y^2} + 1\)
\( \Leftrightarrow 3 + {x^2}{y^2} + 2xy.2 = {x^4}{y^4} - 2{x^2}{y^2} + 1\)
\( \Leftrightarrow {x^4}{y^4} - 3{x^2}{y^2} - 4xy - 2 = 0\) (3)
Đặt \(a = xy \Rightarrow - 3 \le a \le 1\). Khi đó phương trình (3) trở thành:
\(\begin{array}{l}{a^4} - 3{a^2} - 4a - 2 = 0\\ \Leftrightarrow {a^4} + {a^3} - {a^3} - {a^2} - 2{a^2} - 2a - 2a - 2 = 0\\ \Leftrightarrow {a^3}\left( {a + 1} \right) - {a^2}\left( {a + 1} \right) - 2a\left( {a + 1} \right) - 2\left( {a + 1} \right) = 0\\ \Leftrightarrow (a + 1)\left( {{a^3} - {a^2} - 2a - 2} \right) = 0\end{array}\)
\( \Leftrightarrow \left[ \begin{array}{l}a + 1 = 0\\{a^3} - {a^2} - 2a - 2 = 0\end{array} \right.\)
TH1: \(a + 1 = 0 \Leftrightarrow a = - 1\,\,\left( {tm} \right)\)
\( \Rightarrow xy = - 1 \Rightarrow y = - \frac{1}{x}\) (do \(x = 0\) không là nghiệm của phương trình)
Thay vào (1) ta được:
\(\begin{array}{l}\left( {{x^2} + 1} \right)\left( {\frac{1}{{{x^2}}} + 1} \right) = 4 \Leftrightarrow \frac{{{{\left( {{x^2} + 1} \right)}^2}}}{{{x^2}}} = 4\\ \Leftrightarrow {\left( {{x^2} + 1} \right)^2} = 4{x^2} \Leftrightarrow \left[ \begin{array}{l}{x^2} + 1 = 2x\\{x^2} + 1 = - 2x\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}{\left( {x - 1} \right)^2} = 0\\{\left( {x + 1} \right)^2} = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1 \Rightarrow y = - 1\\x = - 1 \Rightarrow y = 1\end{array} \right.\end{array}\)
TH2: \({a^3} - {a^2} - 2a - 2 = 0 \Leftrightarrow {a^3} - 1 = {a^2} + 2a + 1 \Leftrightarrow {a^3} - 1 = {\left( {a + 1} \right)^2}\)
Vì \(a \le 1\) nên \({a^3} \le 1 \Leftrightarrow {a^3} - 1 \le 0\) mà \({\left( {a + 1} \right)^2} \ge 0\) nên \({a^3} - 1 = {\left( {a + 1} \right)^2} \Leftrightarrow \left\{ \begin{array}{l}a - 1 = 0\\a + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 1\\a = 1\end{array} \right.\) (vô lý).
=> Phương trình vô nghiệm.
Vậy hệ phương trình có 2 nghiệm là \(\left( {x;y} \right) = \left( { - 1;1} \right)\) hoặc \(\left( {x;y} \right) = \left( {1; - 1} \right)\).
-----HẾT-----
Kỳ thi tuyển sinh vào lớp 10 tại Nghệ An là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Để đạt kết quả tốt nhất, việc chuẩn bị kỹ lưỡng và làm quen với cấu trúc đề thi là vô cùng cần thiết. Bài viết này sẽ cung cấp thông tin chi tiết về Đề thi vào 10 môn Toán Nghệ An năm 2023, bao gồm cấu trúc đề thi, các dạng bài tập thường gặp, và phương pháp giải bài tập hiệu quả.
Đề thi vào 10 môn Toán Nghệ An năm 2023 thường bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Dưới đây là một số dạng bài tập thường gặp trong Đề thi vào 10 môn Toán Nghệ An năm 2023:
Để giải bài tập Toán hiệu quả, các em học sinh cần:
Giaitoan.edu.vn cung cấp bộ đề thi vào 10 môn Toán Nghệ An năm 2023 chính thức và mới nhất, kèm theo đáp án chi tiết và phương pháp giải bài tập hiệu quả. Các em học sinh có thể luyện tập với các đề thi này để làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin bước vào kỳ thi tuyển sinh sắp tới.
Ngoài việc luyện tập với đề thi, các em học sinh cũng nên:
Dưới đây là một số tài liệu tham khảo hữu ích cho các em học sinh:
Đề thi vào 10 môn Toán Nghệ An năm 2023 là một kỳ thi quan trọng, đòi hỏi sự chuẩn bị kỹ lưỡng và nỗ lực không ngừng. Hy vọng với những thông tin và lời khuyên trên, các em học sinh sẽ đạt kết quả tốt nhất trong kỳ thi tuyển sinh sắp tới. Chúc các em thành công!