Chào mừng bạn đến với bài viết phân tích và giải chi tiết Đề số 26 - Đề thi vào lớp 10 môn Toán. Đây là một trong những đề thi thử quan trọng giúp học sinh lớp 9 làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Tại giaitoan.edu.vn, chúng tôi cung cấp không chỉ đáp án mà còn cả phương pháp giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong kỳ thi sắp tới.
Đề thi vào lớp 10 môn Toán - Đề số 26 có đáp án và lời giải chi tiết
Đề bài
Câu 1. (1,5 điểm)
1) Tìm \(x\) , biết \(2\sqrt x = 3.\)
2) Giải phương trình: \(43{x^2} - 2018x + 1975 = 0.\)
3) Cho hàm số \(y = \left( {a + 1} \right){x^2}.\) Tìm a để hàm số nghịch biến khi \(x < 0\) và đồng biến khi \(x > 0.\)
Câu 2. (2,0 điểm) Cho phương trình: \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 2 = 0\,\,\left( 1 \right),\) m là tham số
1) Tìm m để \(x = 2\) là nghiệm của phương trình (1).
2) Xác định m để phương trình (1) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn điều kiện: \(x_1^2 + x_2^2 = 10\)
Câu 3. (1,5 điểm):
1) Trong mặt phẳng tọa độ \(Oxy\) cho các đường thẳng có phương trình: \(\left( {{d_1}} \right):\;\;y = x + 2,\;\;\left( {{d_2}} \right):\;\;y = - 2\) và \(\;\left( {{d_3}} \right):\;\;y = \left( {k + 1} \right)x + k.\) Tìm \(k\) để các đường thẳng trên đồng quy.
2) Rút gọn và tìm giá trị lớn nhất của biểu thức:\(A = \left( {\dfrac{1}{{1 - \sqrt x }} + \dfrac{{x + 2}}{{x\sqrt x - 1}} + \dfrac{{\sqrt x }}{{x + \sqrt x + 1}}} \right):\dfrac{{\sqrt x - 1}}{3}\) (với \(x \ge 0,x \ne 1\)).
Câu 4. (3 điểm):
Cho tam giác \(ABC\) có ba góc nhọn và \(\widehat {A\;} = {45^0}.\) Gọi \(D,\;E\) lần lượt là hình chiếu vuông góc của \(B,\;C\) lên \(AC,\;AB;\;H\) là giao điểm của \(BD\) và \(CE.\)
1) Chứng minh tứ giác \(BEDC\) nội tiếp.
2) Chứng minh \(DE.AB = BC.AD\) và tính tỉ số \(\dfrac{{ED}}{{BC}}.\)
3) Chứng minh \(HE + HD = BE + CD.\)
4) Gọi \(I\) là tâm đường tròn ngoại tiếp tam giác \(ABC.\) Chứng minh \(AI \bot DE.\)
Câu 5. (1 điểm):
Cho \(n\) là số tự nhiên khác \(0.\) Tìm giá trị nhỏ nhất của:
\(Q = \sqrt {1 + \dfrac{1}{{{1^2}}} + \dfrac{1}{{{2^2}}}} + \sqrt {1 + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{3^2}}}} \)\(\,+ \sqrt {1 + \dfrac{1}{{{3^2}}} + \dfrac{1}{{{4^2}}}} + .....\)\(\, + \sqrt {1 + \dfrac{1}{{{n^2}}} + \dfrac{1}{{{{\left( {n + 1} \right)}^2}}}} + \dfrac{{101}}{{n + 1}}.\)
Lời giải chi tiết
Câu 1.
1) Tìm \(x\) , biết \(2\sqrt x = 3.\)
Điều kiện: \(x \ge 0\)
\(2\sqrt x = 3 \Leftrightarrow \sqrt x = \dfrac{3}{2} \Leftrightarrow x = \dfrac{9}{4}\left( {tm} \right)\)
Vậy \(x = \dfrac{9}{4}\) .
2) Giải phương trình: \(43{x^2} - 2018x + 1975 = 0.\)
Ta có: \(a + b + c = 43 - 2018 + 1975 = 0\) . Nên phương trình luôn có 1 nghiệm là\(x = 1\) và nghiệm còn lại là \(x = \dfrac{c}{a} = \dfrac{{1975}}{{43}}\)
Vậy tập nghiệm của phương trình là: \(S = \left\{ {1;\dfrac{{1975}}{{43}}} \right\}\)
3) Cho hàm số \(y = \left( {a + 1} \right){x^2}.\) Tìm a để hàm số nghịch biến khi \(x < 0\) và đồng biến khi \(x > 0.\)
+) Hàm số nghịch biến khi \(x < 0\) là: \(a + 1 > 0 \Leftrightarrow a > - 1\)
+) Hàm số đồng biến khi \(x > 0.\) là: \(a + 1 > 0 \Leftrightarrow a > - 1\)
Vậy với \(a > - 1\) thì hàm số nghịch biến khi \(x < 0\) và đồng biến khi \(x > 0.\)
Câu 2.
\({x^2} - 2\left( {m + 1} \right)x + {m^2} + 2 = 0\,\,\left( 1 \right),\)
1) Tìm m để \(x = 2\) là nghiệm của phương trình (1).
Thay \(x = 2\) vào phương trình (1) ta có: \({2^2} - 2\left( {m + 1} \right).2 + {m^2} + 2 = 0\,\, \)
\(\Leftrightarrow {m^2} - 4m + 2 = 0\)
\(\Leftrightarrow \left[ \begin{array}{l}m = 2 - \sqrt 2 \\m = 2 + \sqrt 2 \end{array} \right.\)
Vậy với \(x = 2\) thì \(m \in \left\{ {2 - \sqrt 2 ;2 + \sqrt 2 } \right\}\)
2) Xác định m để phương trình (1) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn điều kiện: \(x_1^2 + x_2^2 = 10\)
Phương trình có hai nghiệm phân biệt \({x_1},{x_2}\) khi và chỉ khi: \(\Delta ' > 0 \Leftrightarrow {\left( {m + 1} \right)^2} - {m^2} - 2 > 0\)
\(\Leftrightarrow {m^2} + 2m + 1 - {m^2} - 2 > 0\)
\(\Leftrightarrow m > \dfrac{1}{2}\)
Theo hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m + 1} \right)\\{x_1}{x_2} = {m^2} + 2\end{array} \right.\)
Theo đề bài ta có:
\(\begin{array}{l}\;\;\;\;x_1^2 + x_2^2 = 10 \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 10\\ \Leftrightarrow 4{\left( {m + 1} \right)^2} - 2\left( {{m^2} + 2} \right) = 10\\ \Leftrightarrow 2\left( {{m^2} + 2m + 1} \right) - {m^2} - 2 = 5\\ \Leftrightarrow 2{m^2} + 4m + 2 - {m^2} - 2 - 5 = 0\\ \Leftrightarrow {m^2} + 4m - 5 = 0\\ \Leftrightarrow {m^2} + 5m - m - 5 = 0\\ \Leftrightarrow \left( {m - 1} \right)\left( {m + 5} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}m = 1\left( {tm} \right)\\m = - 5\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy m = 1 thỏa mãn yêu cầu bài toán.
Câu 3:
1) Trong mặt phẳng tọa độ \(Oxy\) cho các đường thẳng có phương trình: \(\left( {{d_1}} \right):\;\;y = x + 2,\;\;\left( {{d_2}} \right):\;\;y = - 2\) và \(\;\left( {{d_3}} \right):\;\;y = \left( {k + 1} \right)x + k.\) Tìm \(k\) để các đường thẳng trên đồng quy.
Tọa độ giao điểm của đường thẳng \({d_1}\) và \({d_2}\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}y = x + 2\\y = - 2\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}x = - 4\\y = - 2\end{array} \right. \Rightarrow A\left( { - 4;\; - 2} \right).\)
\( \Rightarrow \) Ba đường thẳng đã cho đồng quy khi đường thẳng \({d_3}\) phải đi qua điểm \(A\left( { - 4; - 2} \right) \Rightarrow - 2 = \left( {k + 1} \right)\left( { - 4} \right) + k\)
\( \Leftrightarrow - 2 = - 4k - 4 + k \)
\(\Leftrightarrow 3k = - 2 \Leftrightarrow k = - \dfrac{2}{3}.\)
Vậy \(k = - \dfrac{2}{3}.\)
2) Rút gọn và tìm giá trị lớn nhất của biểu thức:\(A = \left( {\dfrac{1}{{1 - \sqrt x }} + \dfrac{{x + 2}}{{x\sqrt x - 1}} + \dfrac{{\sqrt x }}{{x + \sqrt x + 1}}} \right):\dfrac{{\sqrt x - 1}}{3}\) (với \(x \ge 0,\;\;x \ne 1\)).
\(\begin{array}{l}A = \left( {\dfrac{1}{{1 - \sqrt x }} + \dfrac{{x + 2}}{{x\sqrt x - 1}} + \dfrac{{\sqrt x }}{{x + \sqrt x + 1}}} \right):\dfrac{{\sqrt x - 1}}{3}\\\;\;\; = \left( {\dfrac{{ - 1}}{{\sqrt x - 1}} + \dfrac{{x + 2}}{{\left( {\sqrt x - 1} \right)\left( {x + \sqrt x + 1} \right)}} + \dfrac{{\sqrt x }}{{x + \sqrt x + 1}}} \right).\dfrac{3}{{\sqrt x - 1}}\\\;\;\; = \dfrac{{ - \left( {x + \sqrt x + 1} \right) + x + 2 + \sqrt x \left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {x + \sqrt x + 1} \right)}}.\dfrac{3}{{\sqrt x - 1}}\\\;\;\; = \dfrac{{ - x - \sqrt x - 1 + x + 2 + x - \sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {x + \sqrt x + 1} \right)}}.\dfrac{3}{{\sqrt x - 1}}\\\;\; = \dfrac{{x - 2\sqrt x + 1}}{{\left( {\sqrt x - 1} \right)\left( {x + \sqrt x + 1} \right)}}.\dfrac{3}{{\sqrt x - 1}}\\\;\; = \dfrac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\left( {\sqrt x - 1} \right)\left( {x + \sqrt x + 1} \right)}}.\dfrac{3}{{\sqrt x - 1}} \\\;\;= \dfrac{3}{{x + \sqrt x + 1}}.\end{array}\)
Ta có: \(A = \dfrac{3}{{x + \sqrt x + 1}}\)
Ta có: \(x \ge 0,x \ne 1 \Rightarrow \sqrt x \ge 0 \)
\(\Rightarrow x + \sqrt x + 1 \ge 1 \)
\(\Rightarrow \dfrac{3}{{x + \sqrt x + 1}} \le 3\)
Vậy giá trị lớn nhất của biểu thức A là 3. Dấu “=” xảy ra khi và chỉ khi: \(x = 0\)
Câu 4:
Cho tam giác \(ABC\) có ba góc nhọn và \(\widehat {A\;} = {45^0}.\) Gọi \(D,\;E\) lần lượt là hình chiếu vuông góc của \(B,\;C\) lên \(AC,\;AB;\;H\) là giao điểm của \(BD\) và \(CE.\)
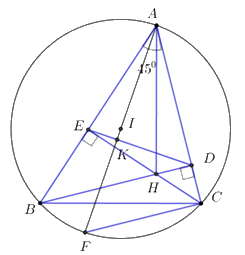
1) Chứng minh tứ giác \(BEDC\) nội tiếp.
Xét tứ giác \(BEDC\) ta có: \(\widehat {BDC} = \widehat {BEC} = {90^0}\left( {gt} \right)\)
Mà hai đỉnh kề nhau D và E cùng nhìn cạnh \(BC\) dưới hai góc bằng nhau.
\( \Rightarrow BEDC\) là tứ giác nội tiếp. (dấu hiện nhận biết tứ giác nội tiếp).
2) Chứng minh \(DE.AB = BC.AD\) và tính tỉ số \(\dfrac{{ED}}{{BC}}.\)
Vì \(BEDC\) là tứ giác nội tiếp (cmt) \( \Rightarrow \widehat {ADE} = \widehat {ABC}\) (góc trong tại một đỉnh bằng góc ngoài tại đỉnh đối diện).
Xét \(\Delta ADE\) và \(\Delta ABC\) ta có:
\(\begin{array}{l}\widehat {A\;}\;\;chung\\\widehat {ABC} = \widehat {ADE}\;\;\left( {cmt} \right)\\ \Rightarrow \Delta ADE \sim \Delta ABC\;\;\left( {g - g} \right).\\ \Rightarrow \dfrac{{AD}}{{AB}} = \dfrac{{ED}}{{BC}} \\\Rightarrow AD.BC = AB.DE\;\;\left( {dpcm} \right).\end{array}\)
Xét \(\Delta ADB\) vuông tại \(D\) có \(\widehat {BAD} = {45^0} \Rightarrow \Delta ADB\) vuông cân tại \(D \Rightarrow AD = BD \)
\(\Rightarrow AB = AD\sqrt 2 .\)
\( \Rightarrow \dfrac{{AD}}{{AB}} = \dfrac{{ED}}{{BC}} = \dfrac{{AD}}{{AD\sqrt 2 }} = \dfrac{1}{{\sqrt 2 }} = \dfrac{{\sqrt 2 }}{2}.\)
Vậy \(\dfrac{{ED}}{{BC}} = \dfrac{{\sqrt 2 }}{2}.\)
3) Chứng minh \(HE + HD = BE + CD.\)
Ta có \(\Delta ADB\) vuông cân tại \(D \Rightarrow \widehat {ABD} = \widehat {BAD} = {45^0}.\)
\( \Rightarrow \Delta BEH\) vuông cân tại \(E\;\;\left( {do\;\;\widehat {BEH} = {{90}^0},\;\;\widehat {EBH} = {{45}^0}} \right) \)
\(\Rightarrow EH = BE\) (tính chất tam giác cân).
\(\Delta AEC\) vuông cân tại \(E\;\;\left( {do\;\;\widehat {EAC} = {{45}^0}} \right)\)
\(\Rightarrow \widehat {ACD} = {45^0}.\)
\( \Rightarrow \Delta HDC\) vuông cân tại \(H\;\left( {do\;\;\widehat {HDC} = {{90}^0},\;\;\widehat {DCH} = {{45}^0}} \right)\)
\(\Rightarrow HD = DC.\) (tính chất tam giác cân).
\( \Rightarrow BE + CD = HE + HD\;\;\left( {dpcm} \right).\)
4) Gọi \(I\) là tâm đường tròn ngoại tiếp tam giác \(ABC.\) Chứng minh \(AI \bot DE.\)
Kéo dài \(AI\) cắt đường tròn tại điểm thứ hai là \(F.\)
Giả sử \(AI \cap DE = \left\{ K \right\}.\)
Khi đó ta có: \(\widehat {ACF}\) là góc nội tiếp chắn nửa đường tròn \( \Rightarrow \widehat {ACF} = {90^0}.\)
Ta có: \(\widehat {ABD} = \widehat {AFC}\) (hai góc nội tiếp cùng chắn cung \(AC\))
Mà \(\widehat {ABC} = \widehat {ADE}\;\;\left( {cmt} \right)\)
\(\Rightarrow \widehat {ADE} = \widehat {AFC}\;\;\left( { = \widehat {ADE}} \right).\)
Xét tứ giác \(DKFC\) ta có: \(\widehat {ADK} = \widehat {KFC}\;\;\left( {cmt} \right).\)
\( \Rightarrow DKFC\) là tứ giác nội tiếp (góc trong tại một đỉnh bằng góc ngoài tại đỉnh đối diện).
\( \Rightarrow \widehat {DCF} + \widehat {DKF} = {180^0}\)
\(\Leftrightarrow \widehat {DKF} = {180^0} - \widehat {DCF} = {90^0}\) (tổng hai góc đối diện trong tứ giác nội tiếp)
Hay \(AI \bot DE\;\;\left( {dpcm} \right).\)
Đề thi vào lớp 10 môn Toán là một bước ngoặt quan trọng trong quá trình học tập của học sinh. Việc làm quen với các dạng bài tập và rèn luyện kỹ năng giải quyết vấn đề là vô cùng cần thiết. Đề số 26 là một đề thi thử điển hình, bao gồm nhiều dạng bài tập khác nhau, từ đại số đến hình học, đòi hỏi học sinh phải có kiến thức vững chắc và khả năng vận dụng linh hoạt.
Đề thi Đề số 26 thường bao gồm các phần sau:
Phương trình bậc hai có dạng ax2 + bx + c = 0. Để giải phương trình này, ta có thể sử dụng công thức nghiệm hoặc phương pháp phân tích thành nhân tử. Ví dụ, với phương trình x2 - 5x + 6 = 0, ta có thể phân tích thành (x - 2)(x - 3) = 0, suy ra x = 2 hoặc x = 3.
Để chứng minh hai tam giác đồng dạng, ta có thể sử dụng các trường hợp đồng dạng sau:
Ví dụ, nếu tam giác ABC và tam giác A'B'C' có góc A bằng góc A', góc B bằng góc B', thì hai tam giác này đồng dạng.
Diện tích hình tròn được tính theo công thức S = πr2, trong đó r là bán kính của hình tròn. Ví dụ, nếu bán kính của hình tròn là 5cm, thì diện tích của hình tròn là S = π(52) = 25π cm2.
Giaitoan.edu.vn cung cấp đầy đủ các tài liệu ôn thi vào lớp 10 môn Toán, bao gồm:
Đề số 26 - Đề thi vào lớp 10 môn Toán là một đề thi thử hữu ích giúp học sinh chuẩn bị cho kỳ thi sắp tới. Bằng cách nắm vững kiến thức, luyện tập thường xuyên và áp dụng các lời khuyên trên, bạn có thể tự tin đạt kết quả tốt nhất trong kỳ thi vào lớp 10.