Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán của tỉnh Đồng Tháp năm 2018. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi sắp tới.
Đề thi này bao gồm các dạng bài tập đa dạng, từ cơ bản đến nâng cao, bao phủ đầy đủ các kiến thức trọng tâm của chương trình Toán lớp 9. Các em có thể sử dụng đề thi này để tự đánh giá năng lực của mình và tìm ra những điểm cần cải thiện.
Câu 1 (1 điểm): a) Tính
a
Câu 1 (1 điểm):
a) Tính \(H = \sqrt {81} - \sqrt {16} .\)
b) Tìm điều kiện của \(x\) để \(\sqrt {x + 2} \) có nghĩa.
Câu 2(1,0 điểm):
Giải hệ phương trình: \(\left\{ \begin{array}{l}x - 2y = 3\\3x + 2y = 1\end{array} \right..\)
Câu 3 (1,0 điểm):
Rút gọn biểu thức \(M = \left( {\dfrac{{x + \sqrt y + \sqrt {xy} - 1}}{{\sqrt x + 1}} + 1} \right).\left( {\sqrt x - \sqrt y } \right)\) (với \(x \ge 0,\;y \ge 0\)).
Câu 4 (1,0 điểm):
a) Giải phương trình \({x^2} - 2x - 8 = 0.\)
b) Cho phương trình \({x^2} + 6x + m = 0\) (với m là tham số). Tìm tất cả các giá trị của m để phương trình đã cho có hai nghiệm phân biệt.
Câu 5 (1,0 điểm):
Trong mặt phẳng tọa độ \(Oxy,\) cho đường thẳng \(\left( d \right):\;y = - 3x + b\) và parabol \(\left( P \right):\;\;y = 2{x^2}.\)
a) Xác định hệ số b để (d) đi qua điểm \(A\left( {0;\;1} \right).\)
b) Với \(b = - 1,\) tìm tọa độ giao điểm của (d) và (P) bằng phương pháp đại số.
Câu 6 (1,0 điểm):
Để chuẩn bị cho mùa giải sắp tới, một vận động viên đua xe ở Đồng Tháp đã luyện tập leo dốc và đổ dốc trên cầu Cao Lãnh. Biết rằng đoạn leo dốc và đổ dốc ở hai bên đầu cầu có độ dài cùng bằng \(1km.\) Trong một lần luyện tập, vận động viên khi đổ dốc nhanh hơn vận tốc khi leo dốc là \(9km/h\) và tổng thời gian hoàn thành là \(3\) phút. Tính vận tốc leo dốc của vận động viên trong lần luyện tập đó.
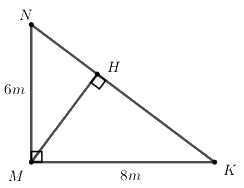
Câu 7 (1,0 điểm). Nhằm tiếp tục đẩy mạnh phong trào xây dựng trường học Xanh – Sạch – Đẹp, trường THCS A đã thiết kế một khuôn viên để trồng hoa có dạng hình tam giác vuông (như hình bên, biết rằng \(\Delta MNK\) vuông tại M, \(MN = 6m,\,\,MK = 8m,\,\,MH \bot NK\)). Nhà trường trồng hoa mười giờ dọc các đoạn NK, MH. a) Tính độ dài các đoạn NK, MH. b) Biết rằng chi phí trồng hoa mười giờ là 20000 đồng trên mỗi mét chiều dài. Tính tổng chi phí để trồng các luống hoa mười giờ đó. |
Câu 8 (3 điểm). Cho tam giác ABC vuông tại A \(\left( {AB < AC} \right)\), đường cao \(AH\,\,\left( {H \in BC} \right)\), trên cạnh BC lấy điểm D sao cho \(BD = BA\), vẽ CE vuông góc AD \(\left( {E \in AD} \right)\).
a) Chứng minh tứ giác AHEC là tứ giác nội tiếp.
b) Chứng minh \(DA.HE = DH.AC\)
c) Chứng minh tam giác \(EHC\) là tam giác cân.
Câu 1 (1 điểm):
a) Tính \(H = \sqrt {81} - \sqrt {16} .\)
b) Tìm điều kiện của \(x\) để \(\sqrt {x + 2} \) có nghĩa.
Câu 2(1,0 điểm):
Giải hệ phương trình: \(\left\{ \begin{array}{l}x - 2y = 3\\3x + 2y = 1\end{array} \right..\)
Câu 3 (1,0 điểm):
Rút gọn biểu thức \(M = \left( {\dfrac{{x + \sqrt y + \sqrt {xy} - 1}}{{\sqrt x + 1}} + 1} \right).\left( {\sqrt x - \sqrt y } \right)\) (với \(x \ge 0,\;y \ge 0\)).
Câu 4 (1,0 điểm):
a) Giải phương trình \({x^2} - 2x - 8 = 0.\)
b) Cho phương trình \({x^2} + 6x + m = 0\) (với m là tham số). Tìm tất cả các giá trị của m để phương trình đã cho có hai nghiệm phân biệt.
Câu 5 (1,0 điểm):
Trong mặt phẳng tọa độ \(Oxy,\) cho đường thẳng \(\left( d \right):\;y = - 3x + b\) và parabol \(\left( P \right):\;\;y = 2{x^2}.\)
a) Xác định hệ số b để (d) đi qua điểm \(A\left( {0;\;1} \right).\)
b) Với \(b = - 1,\) tìm tọa độ giao điểm của (d) và (P) bằng phương pháp đại số.
Câu 6 (1,0 điểm):
Để chuẩn bị cho mùa giải sắp tới, một vận động viên đua xe ở Đồng Tháp đã luyện tập leo dốc và đổ dốc trên cầu Cao Lãnh. Biết rằng đoạn leo dốc và đổ dốc ở hai bên đầu cầu có độ dài cùng bằng \(1km.\) Trong một lần luyện tập, vận động viên khi đổ dốc nhanh hơn vận tốc khi leo dốc là \(9km/h\) và tổng thời gian hoàn thành là \(3\) phút. Tính vận tốc leo dốc của vận động viên trong lần luyện tập đó.
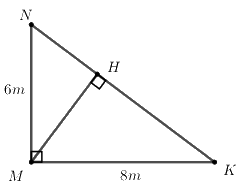
Câu 7 (1,0 điểm). Nhằm tiếp tục đẩy mạnh phong trào xây dựng trường học Xanh – Sạch – Đẹp, trường THCS A đã thiết kế một khuôn viên để trồng hoa có dạng hình tam giác vuông (như hình bên, biết rằng \(\Delta MNK\) vuông tại M, \(MN = 6m,\,\,MK = 8m,\,\,MH \bot NK\)). Nhà trường trồng hoa mười giờ dọc các đoạn NK, MH. a) Tính độ dài các đoạn NK, MH. b) Biết rằng chi phí trồng hoa mười giờ là 20000 đồng trên mỗi mét chiều dài. Tính tổng chi phí để trồng các luống hoa mười giờ đó. |
Câu 8 (3 điểm). Cho tam giác ABC vuông tại A \(\left( {AB < AC} \right)\), đường cao \(AH\,\,\left( {H \in BC} \right)\), trên cạnh BC lấy điểm D sao cho \(BD = BA\), vẽ CE vuông góc AD \(\left( {E \in AD} \right)\).
a) Chứng minh tứ giác AHEC là tứ giác nội tiếp.
b) Chứng minh \(DA.HE = DH.AC\)
c) Chứng minh tam giác \(EHC\) là tam giác cân.
a
Kỳ thi tuyển sinh vào lớp 10 là một bước ngoặt quan trọng trong sự nghiệp học tập của mỗi học sinh. Để đạt được kết quả tốt nhất, việc chuẩn bị kỹ lưỡng là vô cùng cần thiết. Đề thi vào 10 môn Toán Đồng Tháp năm 2018 là một nguồn tài liệu quý giá để các em học sinh ôn tập và rèn luyện kỹ năng giải toán.
Đề thi vào 10 môn Toán Đồng Tháp năm 2018 thường bao gồm các dạng bài tập sau:
Phương trình bậc hai là một trong những dạng bài tập cơ bản và thường xuyên xuất hiện trong các đề thi vào 10. Để giải phương trình bậc hai, các em có thể sử dụng công thức nghiệm hoặc phương pháp phân tích thành nhân tử.
Ví dụ: Giải phương trình 2x2 - 5x + 2 = 0
Sử dụng công thức nghiệm, ta có:
Δ = (-5)2 - 4 * 2 * 2 = 25 - 16 = 9
x1 = (5 + √9) / (2 * 2) = (5 + 3) / 4 = 2
x2 = (5 - √9) / (2 * 2) = (5 - 3) / 4 = 0.5
Vậy phương trình có hai nghiệm là x1 = 2 và x2 = 0.5
Các bài toán chứng minh tính chất hình học đòi hỏi các em phải nắm vững các định lý, tính chất cơ bản của hình học và biết cách áp dụng chúng vào giải quyết bài toán.
Ví dụ: Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh rằng AH2 = BH * CH.
Chứng minh:
Xét tam giác ABC vuông tại A, ta có: AH2 = BH * CH (theo hệ thức lượng trong tam giác vuông).
Ngoài đề thi vào 10 môn Toán Đồng Tháp năm 2018, các em có thể tham khảo thêm các tài liệu ôn thi sau:
Đề thi vào 10 môn Toán Đồng Tháp năm 2018 là một công cụ hữu ích giúp các em học sinh ôn tập và rèn luyện kỹ năng giải toán. Hy vọng rằng với những phân tích và hướng dẫn giải chi tiết trên đây, các em sẽ tự tin hơn trong kỳ thi sắp tới và đạt được kết quả tốt nhất.