Giaitoan.edu.vn xin giới thiệu bộ đề thi vào 10 môn Toán Hà Nội năm 2019 chính thức, được tổng hợp đầy đủ và cập nhật mới nhất. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi tuyển sinh sắp tới.
Chúng tôi cung cấp không chỉ đề thi mà còn cả đáp án chi tiết, lời giải bài bản, giúp các em hiểu rõ phương pháp giải và tự đánh giá năng lực của bản thân.
Bài I (2 điểm) Cho hai biểu thức:
Bài I (2 điểm)
Cho hai biểu thức: \(A = \dfrac{{4\left( {\sqrt x + 1} \right)}}{{25 - x}}\) và \(B = \left( {\dfrac{{15 - \sqrt x }}{{x - 25}} + \dfrac{2}{{\sqrt x + 5}}} \right):\dfrac{{\sqrt x + 1}}{{\sqrt x - 5}}\,\,\,\left( {x \ge 0,\,\,x \ne 25} \right)\)
1) Tính giá trị của biểu thức \(A\) khi \(x = 9.\)
2) Rút gọn biểu thức \(B.\)
3) Tìm tất cả các giá trị nguyên của \(x\) để biểu thức \(P = AB\) đạt giá trị nguyên lớn nhất.
Bài II (2,5 điểm)
1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Hai đội công nhân cùng làm chung một công việc thì sau 15 ngày làm xong. Nếu đội thứ nhất làm riêng trong 3 ngày rồi dừng lại và đội thứ hai làm tiếp công việc đó trong 5 ngày thì cả hai đội hoàn thành được 25% công việc. Hỏi nếu mỗi đội làm riêng thì trong bao nhiêu ngày mới xong công việc trên?
2) Một bồn nước inox có dạng một hình trụ có chiều cao \(1,75\,m\) và diện tích đáy là \(0,32\,{m^2}.\) Hỏi bồn nước này đựng đầy được bao nhiêu mét khối nước? (Bỏ qua bề đáy của bồn nước).
Bài III (2 điểm)
1) Giải phương trình \({x^4} - 7{x^2} - 18 = 0.\)
2) Trong mặt phẳng tọa độ \(Oxy,\) cho đường thẳng \(\left( d \right):\,\,y = 2mx - {m^2} + 1\) và parabol \(\left( P \right):\,\,y = {x^2}.\)
a) Chứng minh \(\left( d \right)\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt.
b) Tìm tất cả các giá trị của \(m\) để \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ \({x_1},\,\,{x_2}\) thỏa mãn \(\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} = \dfrac{{ - 2}}{{{x_1}{x_2}}} + 1.\)
Bài IV (3 điểm)
Cho tam giác \(ABC\) có ba góc nhọn \(\left( {AB < AC} \right)\) nội tiếp đường tròn \(\left( O \right)\). Hai đường cao \(BE\) và \(CF\) của tam giác \(ABC\) cắt nhau tại \(H\).
1) Chứng minh bốn điểm \(B,\,\,C,\,\,E,\,\,F\) cùng thuộc một đường tròn.
2) Chứng minh đường thẳng \(OA\) vuông góc với đường thẳng \(EF\).
3) Gọi \(K\) là trung điểm của đoạn thẳng \(BC\). Đường thẳng \(AO\) cắt đường thẳng \(BC\) tại điểm \(I\), đường thẳng \(EF\) cắt đường thẳng \(AH\) tại điểm \(P\) . Chứng minh tam giác \(APE\) đồng dạng với tam giác \(AIB\) và đường thẳng \(KH\) song song với đường thẳng \(IP\).
Bài V (0,5 điểm)
Cho biểu thức \(P = {a^4} + {b^4} - ab,\) với \(a,\,\,b\) là các số thực thỏa mãn \({a^2} + {b^2} + ab = 3.\) Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P.\)
Bài I (2 điểm) Cho hai biểu thức: \(A = \dfrac{{4\left( {\sqrt x + 1} \right)}}{{25 - x}}\) và \(B = \left( {\dfrac{{15 - \sqrt x }}{{x - 25}} + \dfrac{2}{{\sqrt x + 5}}} \right):\dfrac{{\sqrt x + 1}}{{\sqrt x - 5}}\,\,\,\left( {x \ge 0,\,\,x \ne 25} \right)\) 1) Tính giá trị của biểu thức \(A\) khi \(x = 9.\) 2) Rút gọn biểu thức \(B.\) 3) Tìm tất cả các giá trị nguyên của \(x\) để biểu thức \(P = AB\) đạt giá trị nguyên lớn nhất. |
Phương pháp:
1) Khi \(x = 9\,\,\left( {tm} \right)\) thay vào biểu thức để tính giá trị của biểu thức.
2) Quy đồng mẫu các phân thức rồi rút gọn biểu thức.
3) Tính biểu thức: \(P = AB.\) Biểu thức \(P \in \mathbb{Z} \Rightarrow \) tử số chia hết cho mẫu số.
Từ đó tìm các giá trị của \(x \in \mathbb{Z} \Rightarrow P \in \mathbb{Z}\) và tính được các giá trị của \(P\) và kết luận giá trị \(x \in \mathbb{Z}\) để \(P \in \mathbb{Z}\) và đạt giá trị lớn nhất.
Cách giải:
1) Tính giá trị của biểu thức \(A\) khi \(x = 9.\)
Khi \(x = 9\,\,\left( {tm} \right)\) thay vào biểu thức \(A = \dfrac{{4\left( {\sqrt x + 1} \right)}}{{25 - x}}\) ta được:
\(A = \dfrac{{4\left( {\sqrt 9 + 1} \right)}}{{25 - 9}} = \dfrac{{4\left( {3 + 1} \right)}}{{16}} = \dfrac{{16}}{{16}} = 1.\)
Vậy với \(x = 9\) thì \(A = 1.\)
2) Rút gọn biểu thức \(B.\)
Điều kiện: \(x \ge 0,\,\,x \ne 25.\)
\(\begin{array}{l}B = \left( {\dfrac{{15 - \sqrt x }}{{x - 25}} + \dfrac{2}{{\sqrt x + 5}}} \right):\dfrac{{\sqrt x + 1}}{{\sqrt x - 5}} = \left[ {\dfrac{{15 - \sqrt x }}{{\left( {\sqrt x - 5} \right)\left( {\sqrt x + 5} \right)}} + \dfrac{2}{{\sqrt x + 5}}} \right].\dfrac{{\sqrt x - 5}}{{\sqrt x + 1}}\\ = \dfrac{{15 - \sqrt x + 2\left( {\sqrt x - 5} \right)}}{{\left( {\sqrt x - 5} \right)\left( {\sqrt x + 5} \right)}}.\dfrac{{\sqrt x - 5}}{{\sqrt x + 1}} = \dfrac{{15 - \sqrt x + 2\sqrt x - 10}}{{\sqrt x + 5}}.\dfrac{1}{{\sqrt x + 1}}\\ = \dfrac{{\sqrt x + 5}}{{\sqrt x + 5}}.\dfrac{1}{{\sqrt x + 1}} = \dfrac{1}{{\sqrt x + 1}}.\end{array}\)
3) Tìm tất cả các giá trị nguyên của \(x\) để biểu thức \(P = AB\) đạt giá trị nguyên lớn nhất.
Điều kiện: \(x \ge 0,\,\,x \ne 25.\)
Ta có: \(P = A.B = \dfrac{{4\left( {\sqrt x + 1} \right)}}{{25 - x}}.\dfrac{1}{{\sqrt x + 1}} = \dfrac{4}{{25 - x}}.\)
\(x \in \mathbb{Z} \Rightarrow P \in \mathbb{Z} \Leftrightarrow \dfrac{4}{{25 - x}} \in \mathbb{Z} \Rightarrow 4\,\, \vdots \,\,\left( {25 - x} \right)\) hay \(\left( {25 - x} \right) \in U\left( 4 \right)\)
Mà \(U\left( 4 \right) = \left\{ { \pm 1;\,\, \pm 2;\,\, \pm 4} \right\} \Rightarrow \left( {25 - x} \right) \in \left\{ { \pm 1;\,\, \pm 2;\, \pm 4} \right\}.\)
Ta có bảng giá trị:
\(25 - x\) | \( - 4\) | \( - 2\) | \( - 1\) | \(1\) | \(2\) | \(4\) |
\(x\) | 29 (tm) | 27 (tm) | 26 (tm) | 24 (tm) | 23 (tm) | 1 (tm) |
\(P\) | \( - 1\) | \( - 2\) | \( - 4\) | \(4\) | \(2\) | \(1\) |
\( \Rightarrow \) với \(x \in \left\{ {23;\,\,24;\,\,26;\,\,27;\,\,29} \right\}\) thì \(P \in \mathbb{Z}.\)
Qua bảng giá trị ta thấy với \(x = 24\) thì \(P = 4\) là số nguyên lớn nhất.
Vậy \(x = 24\) thỏa mãn điều kiện bài toán.
Bài II (2,5 điểm) 1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình: Hai đội công nhân cùng làm chung một công việc thì sau 15 ngày làm xong. Nếu đội thứ nhất làm riêng trong 3 ngày rồi dừng lại và đội thứ hai làm tiếp công việc đó trong 5 ngày thì cả hai đội hoàn thành được 25% công việc. Hỏi nếu mỗi đội làm riêng thì trong bao nhiêu ngày mới xong công việc trên? 2) Một bồn nước inox có dạng một hình trụ có chiều cao \(1,75\,m\) và diện tích đáy là \(0,32\,{m^2}.\) Hỏi bồn nước này đựng đầy được bao nhiêu mét khối nước? (Bỏ qua bề đáy của bồn nước). |
Phương pháp:
1) Gọi số ngày làm một mình xong công việc của của đội 1 là \(x\)(ngày) \(\left( {x > 15} \right)\)
Số ngày làm một mình xong công việc của đội 2 là \(y\) (ngày) \(\left( {y > 15} \right)\)
Biểu diễn các đại lượng chưa biết theo ẩn đã gọi và lập hệ phương trình.
Giải hệ phương trình tìm các ẩn và đối chiều với điều kiện rồi kết luận.
2) Công thức tính thể tích khối trụ có diện tích đáy \(S\) và chiều cao \(h\) là: \(V = Sh.\)
Cách giải:
1) Gọi số ngày làm một mình xong công việc của của đội 1 là \(x\)(ngày) \(\left( {x > 15} \right)\)
Số ngày làm một mình xong công việc của đội 2 là \(y\) (ngày) \(\left( {y > 15} \right)\)
Trong một ngày đội 1 làm được số phần công việc là: \(\dfrac{1}{x}\) (công việc)
Trong một ngày đội 2 làm được số phần công việc là \(\dfrac{1}{y}\) (công việc)
Vì hai đội làm chung trong \(15\) ngày thì xong nên ta có phương trình: \(\dfrac{{15}}{x} + \dfrac{{15}}{y} = 1\) (1)
Trong \(3\) ngày đội 1 làm được \(\dfrac{3}{x}\) công việc, trong \(5\) ngày đội 2 làm được \(\dfrac{5}{y}\) công việc.
Đội 1 làm trong 3 ngày và đội 2 làm trong 5 ngày được \(25\% = \dfrac{1}{4}\) công việc nên ta có phương trình:
\(\dfrac{3}{x} + \dfrac{5}{y} = \dfrac{1}{4}\) (2)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có hệ phương trình: \(\left\{ \begin{array}{l}\dfrac{{15}}{x} + \dfrac{{15}}{y} = 1\\\dfrac{3}{x} + \dfrac{5}{y} = \dfrac{1}{4}\end{array} \right.\)
Đặt \(\left\{ \begin{array}{l}\dfrac{1}{x} = a\\\dfrac{1}{y} = b\end{array} \right.\) ta được: \(\left\{ \begin{array}{l}15a + 15b = 1\\3a + 5b = \dfrac{1}{4}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{1}{{24}}\\b = \dfrac{1}{{40}}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\dfrac{1}{x} = \dfrac{1}{{24}}\\\dfrac{1}{y} = \dfrac{1}{{40}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 24\,\,\,\left( {tm} \right)\\y = 40\,\,\,\,\left( {tm} \right)\end{array} \right.\)
Vậy đội 1 làm một mình trong \(24\) ngày thì xong công việc, đội 2 làm một mình trong \(40\) ngày thì xong công việc.
2) Thể tích bồn nước là: \(V = Sh = 0,32.1,75 = 0,56{m^3}\)
Vậy bồn nước đựng được \(0,56{m^3}\) nước.
Bài III (2 điểm) 1) Giải phương trình \({x^4} - 7{x^2} - 18 = 0.\) 2) Trong mặt phẳng tọa độ \(Oxy,\) cho đường thẳng \(\left( d \right):\,\,y = 2mx - {m^2} + 1\) và parabol \(\left( P \right):\,\,y = {x^2}.\) a) Chứng minh \(\left( d \right)\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt. b) Tìm tất cả các giá trị của \(m\) để \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ \({x_1},\,\,{x_2}\) thỏa mãn \(\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} = \dfrac{{ - 2}}{{{x_1}{x_2}}} + 1.\) |
Phương pháp:
1) Giải phương trình đã cho bằng cách đặt ẩn phụ \({x^2} = t\,\,\left( {t \ge 0} \right).\)
+) Giải phương trình tìm ẩn \(t,\) đối chiếu với điều kiện rồi tìm \(x.\)
2) Xét phương trình hoành độ giao điểm.
a) Hai đồ thị hàm số cắt nhau tại hai điểm phân biệt \( \Leftrightarrow \) phương trình hoành độ giao điểm có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0.\)
b) Sử dụng định lý Vi-et.
Cách giải:
1) Giải phương trình \({x^4} - 7{x^2} - 18 = 0\)
Đặt \({x^2} = t\,\left( {t \ge 0} \right)\) ta có phương trình \({t^2} - 7t - 18 = 0\)
\(\begin{array}{l} \Leftrightarrow {t^2} - 9t + 2t - 18 = 0\\ \Leftrightarrow t\left( {t - 9} \right) + 2\left( {t - 9} \right) = 0\\ \Leftrightarrow \left( {t + 2} \right)\left( {t - 9} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}t + 2 = 0\\t - 9 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = - 2\left( {ktm} \right)\\t = 9\left( {tm} \right)\end{array} \right.\end{array}\)
Với \(t = 9\) thì \({x^2} = 9 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = - 3\end{array} \right.\)
Vậy tập nghiệm của phương trình đã cho là: \(S = \left\{ { - 3;3} \right\}\)
2) Parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = 2mx - {m^2} + 1\)
Xét phương trình hoành độ giao điểm của đường thẳng \(\left( d \right)\) và parabol \(\left( P \right)\) ta có
\({x^2} = 2mx - {m^2} + 1 \Leftrightarrow {x^2} - 2mx + {m^2} - 1 = 0\,\,\left( * \right)\)
Số giao điểm của (d) và (P) cũng chính là số nghiệm của phương trình (*)
Phương trình \(\left( * \right)\) có \(\Delta ' = {m^2} - \left( {{m^2} - 1} \right) = 1 > 0\)
a) Vì \(\Delta ' > 0\) nên phương trình \(\left( * \right)\) luôn có hai nghiệm phân biệt với mọi \(m\) hay đường thẳng \(\left( d \right)\) luôn cắt parabol \(\left( P \right)\) tại hai điểm phân biệt.
b) Theo câu a) ta có đường thẳng \(\left( d \right)\) luôn cắt parabol \(\left( P \right)\) tại hai điểm phân biệt.
Gọi \({x_1};{x_2}\) là hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) thì \({x_1};{x_2}\) là hai nghiệm của phương trình \(\left( * \right)\)
Theo hệ thức Vi-et ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}{x_2} = {m^2} - 1\end{array} \right.\)
Xét \(\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} = \dfrac{{ - 2}}{{{x_1}{x_2}}} + 1\) ĐK: \({x_1}{x_2} \ne 0 \Leftrightarrow {m^2} - 1 \ne 0 \Leftrightarrow m \ne \pm 1\)
\( \Leftrightarrow \dfrac{{{x_1} + {x_2}}}{{{x_1}{x_2}}} = \dfrac{{ - 2}}{{{x_1}{x_2}}} + \dfrac{{{x_1}{x_2}}}{{{x_1}{x_2}}}\)
\(\begin{array}{l} \Rightarrow {x_1} + {x_2} = - 2 + {x_1}{x_2}\\ \Leftrightarrow 2m = - 2 + {m^2} - 1\\ \Leftrightarrow {m^2} - 2m - 3 = 0\\ \Leftrightarrow {m^2} - 3m + m - 3 = 0\\ \Leftrightarrow m\left( {m - 3} \right) + \left( {m - 3} \right) = 0\\ \Leftrightarrow \left( {m + 1} \right)\left( {m - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m + 1 = 0\\m - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - 1\,\,\,\,\,\left( {ktm} \right)\\m = 3\,\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy \(m = 3\) là giá trị thỏa mãn điều kiện đề bài.
Bài IV (3,0 điểm) Cho tam giác \(ABC\) có ba góc nhọn \(\left( {AB < AC} \right)\) nội tiếp đường tròn \(\left( O \right)\). Hai đường cao \(BE\) và \(CF\) của tam giác \(ABC\) cắt nhau tại \(H\). 1) Chứng minh bốn điểm \(B,\,\,C,\,\,E,\,\,F\) cùng thuộc một đường tròn. 2) Chứng minh đường thẳng \(OA\) vuông góc với đường thẳng \(EF\). 3) Gọi \(K\) là trung điểm của đoạn thẳng \(BC\). Đường thẳng \(AO\) cắt đường thẳng \(BC\) tại điểm \(I\), đường thẳng \(EF\) cắt đường thẳng \(AH\) tại điểm \(P\) . Chứng minh tam giác \(APE\) đồng dạng với tam giác \(AIB\) và đường thẳng \(KH\) song song với đường thẳng \(IP\). |
Phương pháp:
1) Chứng minh tứ giác nội tiếp bằng các dấu hiệu nhận biết.
2) Sử dụng định lý: Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung cùng chắn một cung thì bằng nhau.
3) Chứng minh các cặp tam giác tương ứng đồng dạng để suy ra các góc bằng nhau và chứng minh \(KH//IP.\)
Cách giải:
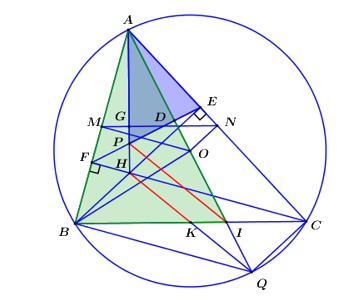
1) Chứng minh bốn điểm \(B,\,\,C,\,\,E,\,\,F\) cùng thuộc một đường tròn.
Ta có \(\angle BEC = \angle BFC = {90^0}\,\,\left( {gt} \right) \Rightarrow \) Tứ giác \(BFEC\) là tứ giác nội tiếp (Tứ giác có 2 đỉnh kề nhau cùng nhìn 1 cạnh dưới các góc bằng nhau).
Vậy bốn điểm \(B,\,\,C,\,\,E,\,\,F\) cùng thuộc một đường tròn.
2) Chứng minh đường thẳng \(OA\) vuông góc với đường thẳng \(EF\).
Cách 1:
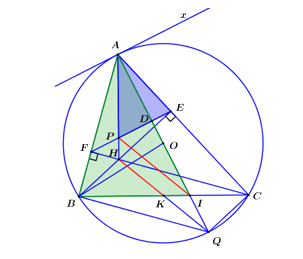
b) Kẻ tiếp tuyến Ax của đường tròn tại A, ta có \(Ax \bot OA\).
Ta có \(\angle xAE = \angle ABC\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AC).
Mà \(\angle ABC = \angle AEF\) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp).
\( \Rightarrow \angle xAE = \angle AEF\). Mà hai góc này ở vị trí so le trong \( \Rightarrow EF//Ax\).
\( \Rightarrow EF \bot OA\).
Cách 2:
Gọi \(D = OA \cap EF\).
Gọi \(M,\,\,N\) lần lượt là trung điểm của \(AB,\,\,AC\).
\( \Rightarrow OM \bot AB,\,\,ON \bot AC\) (quan hệ vuông góc giữa đường kính và dây cung).
Xét tứ giác \(AMON\) có \(\angle AMO + \angle ANO = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác \(AMON\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
Gọi \(G = MN \cap AH\).
Ta có: \(H\) là trực tâm tam giác \(ABC \Rightarrow AH \bot BC\).
Mà \(MN//BC\) (MN là đường trung bình của tam giác \(ABC\)) \( \Rightarrow MN \bot AH\) tại \(G\).
Xét tam giác \(AMG\) và tam giác \(AON\) có:
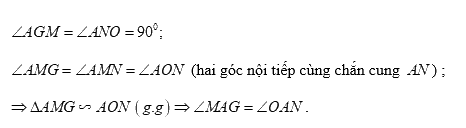
\(\begin{array}{l} \Rightarrow \angle MAG + \angle GAO = \angle OAN + \angle GAO\\ \Rightarrow \angle OAM = \angle GAN \Rightarrow \angle DAF = \angle GAN\,\,\left( 1 \right)\end{array}\)
Ta có : \(\angle AFE = \angle ACB\) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp) ;
Lại có \(\angle ACB = \angle ANM\) (đồng vị)
\( \Rightarrow \angle AFE = \angle ANM\) (2)
Từ (1) và (2) \( \Rightarrow \angle DAF + \angle AFE = \angle GAN + & \angle ANM = {90^0}\).
\( \Rightarrow \Delta ADF\) vuông tại \(D \Rightarrow AD \bot DF\) hay \(OA \bot EF\).
3) Gọi \(K\) là trung điểm của đoạn thẳng \(BC\). Đường thẳng \(AO\) cắt đường thẳng \(BC\) tại điểm \(I\), đường thẳng \(EF\) cắt đường thẳng \(AH\) tại điểm \(P\) . Chứng minh tam giác \(APE\) đồng dạng với tam giác \(AIB\) và đường thẳng \(KH\) song song với đường thẳng \(IP\).
Ta đã chứng minh được \(\angle DAF = \angle GAN\,\,\)hay \(\angle IAB = \angle PAE\).
Lại có \(\angle AEF = \angle ABC\) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp) ;
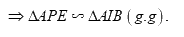
Kéo dài \(AI\) cắt \(\left( O \right)\) tại \(Q\) \( \Rightarrow AQ\) là đường kính của \(\left( O \right)\).
Nối \(BQ,\,\,CQ\) ta có \(\angle ABQ = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow AB \bot BQ\).
Mà \(CH \bot AB \Rightarrow CH//BQ\).
Hoàn toàn tương tự ta chứng minh được \(BH//CQ\).
Suy ra \(BHCQ\) là hình bình hành (Tứ giác có các cặp cạnh đối song song).
Mà \(K\) là trung điểm của \(BC\,\,\left( {gt} \right) \Rightarrow K\) cũng là trung điểm của \(HQ \Rightarrow H,\,\,K,\,\,Q\) thẳng hàng.
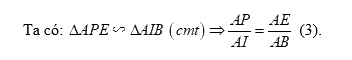
Xét tam giác \(AHE\) và tam giác \(AQB\) có:
\(\angle AEH = \angle ABQ = {90^0}\)
\(\angle QAB = \angle EAH\,\,\left( {cmt} \right)\) (do \(\angle DAF = \angle GAN\,\,\)).
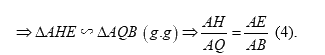
Từ (1) và (2) \( \Rightarrow \dfrac{{AP}}{{AI}} = \dfrac{{AH}}{{AQ}} \Rightarrow \dfrac{{AP}}{{AH}} = \dfrac{{AI}}{{AQ}} \Rightarrow PI//HQ\) (Định lí Ta-let đảo) (đpcm).
Bài V (VDC) (0,5 điểm)
Cách giải:
Ta có \({a^2} + {b^2} + ab = 3 \Leftrightarrow {a^2} + {b^2} = 3 - ab\)
Ta thấy \({\left( {a - b} \right)^2} \ge 0 \Leftrightarrow {a^2} + {b^2} \ge 2ab \Leftrightarrow 3 - ab \ge 2ab \Leftrightarrow ab \le 1\)
Lại có \({\left( {a + b} \right)^2} \ge 0 \Leftrightarrow {a^2} + {b^2} \ge - 2ab \Leftrightarrow 3 - ab \ge - 2ab \Leftrightarrow 3 \ge - ab \Leftrightarrow ab \ge - 3\)
\( \Rightarrow - 3 \le ab \le 1\).
Xét \({a^2} + {b^2} = 3 - ab\) với \( - 3 \le ab \le 1\)
\(\begin{array}{l} \Leftrightarrow {\left( {{a^2} + {b^2}} \right)^2} = {\left( {3 - ab} \right)^2}\\ \Leftrightarrow {a^4} + {b^4} + 2{a^2}{b^2} = 9 - 6ab + {a^2}{b^2}\\ \Leftrightarrow {a^4} + {b^4} = - {a^2}{b^2} - 6ab + 9\end{array}\)
Khi đó \(P = {a^4} + {b^4} - ab = - {a^2}{b^2} - 6ab + 9 - ab\) \( = - {\left( {ab} \right)^2} - 7ab + 9 = \dfrac{{85}}{4} - {\left( {ab + \dfrac{7}{2}} \right)^2}\)
Vì \( - 3 \le ab \le 1 \Rightarrow \dfrac{1}{2} \le ab + \dfrac{7}{2} \le \dfrac{9}{2} \Leftrightarrow {\left( {ab + \dfrac{7}{2}} \right)^2} \le \dfrac{{81}}{4}\).
Suy ra \(P = \dfrac{{85}}{4} - {\left( {ab + \dfrac{7}{2}} \right)^2} \ge \dfrac{{85}}{4} - \dfrac{{81}}{4} = 1 \Leftrightarrow P \ge 1\).
Dấu “=” xảy ra khi \(ab = 1\) và \({a^2} + {b^2} = 2 \Rightarrow \left[ \begin{array}{l}a = 1;\,\,b = 1\\a = - 1;\,\,b = - 1\end{array} \right.\)
Ta lại có \(P = - {\left( {ab} \right)^2} - 7ab + 9 = \left( {ab + 3} \right)\left( { - ab - 4} \right) + 21\)
Mà \( - 3 \le ab \le 1\) nên \(\left\{ \begin{array}{l}ab + 3 \ge 0\\ - ab - 4 < 0\end{array} \right.\) nên \(\left( {ab + 3} \right)\left( { - ab - 4} \right) \le 0 \Rightarrow P \le 21\).
Dấu “=” xảy ra khi \(\left\{ \begin{array}{l}ab = - 3\\{a^2} + {b^2} + ab = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}ab = - 3\\{\left( {a + b} \right)^2} = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a = \sqrt 3 \\b = - \sqrt 3 \end{array} \right.\\\left[ \begin{array}{l}a = - \sqrt 3 \\b = \sqrt 3 \end{array} \right.\end{array} \right.\)
Vậy giá trị lớn nhất của \(P\) là \(21\); giá trị nhỏ nhất của \(P\) là \(1.\)
Bài I (2 điểm)
Cho hai biểu thức: \(A = \dfrac{{4\left( {\sqrt x + 1} \right)}}{{25 - x}}\) và \(B = \left( {\dfrac{{15 - \sqrt x }}{{x - 25}} + \dfrac{2}{{\sqrt x + 5}}} \right):\dfrac{{\sqrt x + 1}}{{\sqrt x - 5}}\,\,\,\left( {x \ge 0,\,\,x \ne 25} \right)\)
1) Tính giá trị của biểu thức \(A\) khi \(x = 9.\)
2) Rút gọn biểu thức \(B.\)
3) Tìm tất cả các giá trị nguyên của \(x\) để biểu thức \(P = AB\) đạt giá trị nguyên lớn nhất.
Bài II (2,5 điểm)
1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Hai đội công nhân cùng làm chung một công việc thì sau 15 ngày làm xong. Nếu đội thứ nhất làm riêng trong 3 ngày rồi dừng lại và đội thứ hai làm tiếp công việc đó trong 5 ngày thì cả hai đội hoàn thành được 25% công việc. Hỏi nếu mỗi đội làm riêng thì trong bao nhiêu ngày mới xong công việc trên?
2) Một bồn nước inox có dạng một hình trụ có chiều cao \(1,75\,m\) và diện tích đáy là \(0,32\,{m^2}.\) Hỏi bồn nước này đựng đầy được bao nhiêu mét khối nước? (Bỏ qua bề đáy của bồn nước).
Bài III (2 điểm)
1) Giải phương trình \({x^4} - 7{x^2} - 18 = 0.\)
2) Trong mặt phẳng tọa độ \(Oxy,\) cho đường thẳng \(\left( d \right):\,\,y = 2mx - {m^2} + 1\) và parabol \(\left( P \right):\,\,y = {x^2}.\)
a) Chứng minh \(\left( d \right)\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt.
b) Tìm tất cả các giá trị của \(m\) để \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ \({x_1},\,\,{x_2}\) thỏa mãn \(\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} = \dfrac{{ - 2}}{{{x_1}{x_2}}} + 1.\)
Bài IV (3 điểm)
Cho tam giác \(ABC\) có ba góc nhọn \(\left( {AB < AC} \right)\) nội tiếp đường tròn \(\left( O \right)\). Hai đường cao \(BE\) và \(CF\) của tam giác \(ABC\) cắt nhau tại \(H\).
1) Chứng minh bốn điểm \(B,\,\,C,\,\,E,\,\,F\) cùng thuộc một đường tròn.
2) Chứng minh đường thẳng \(OA\) vuông góc với đường thẳng \(EF\).
3) Gọi \(K\) là trung điểm của đoạn thẳng \(BC\). Đường thẳng \(AO\) cắt đường thẳng \(BC\) tại điểm \(I\), đường thẳng \(EF\) cắt đường thẳng \(AH\) tại điểm \(P\) . Chứng minh tam giác \(APE\) đồng dạng với tam giác \(AIB\) và đường thẳng \(KH\) song song với đường thẳng \(IP\).
Bài V (0,5 điểm)
Cho biểu thức \(P = {a^4} + {b^4} - ab,\) với \(a,\,\,b\) là các số thực thỏa mãn \({a^2} + {b^2} + ab = 3.\) Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P.\)
Bài I (2 điểm) Cho hai biểu thức: \(A = \dfrac{{4\left( {\sqrt x + 1} \right)}}{{25 - x}}\) và \(B = \left( {\dfrac{{15 - \sqrt x }}{{x - 25}} + \dfrac{2}{{\sqrt x + 5}}} \right):\dfrac{{\sqrt x + 1}}{{\sqrt x - 5}}\,\,\,\left( {x \ge 0,\,\,x \ne 25} \right)\) 1) Tính giá trị của biểu thức \(A\) khi \(x = 9.\) 2) Rút gọn biểu thức \(B.\) 3) Tìm tất cả các giá trị nguyên của \(x\) để biểu thức \(P = AB\) đạt giá trị nguyên lớn nhất. |
Phương pháp:
1) Khi \(x = 9\,\,\left( {tm} \right)\) thay vào biểu thức để tính giá trị của biểu thức.
2) Quy đồng mẫu các phân thức rồi rút gọn biểu thức.
3) Tính biểu thức: \(P = AB.\) Biểu thức \(P \in \mathbb{Z} \Rightarrow \) tử số chia hết cho mẫu số.
Từ đó tìm các giá trị của \(x \in \mathbb{Z} \Rightarrow P \in \mathbb{Z}\) và tính được các giá trị của \(P\) và kết luận giá trị \(x \in \mathbb{Z}\) để \(P \in \mathbb{Z}\) và đạt giá trị lớn nhất.
Cách giải:
1) Tính giá trị của biểu thức \(A\) khi \(x = 9.\)
Khi \(x = 9\,\,\left( {tm} \right)\) thay vào biểu thức \(A = \dfrac{{4\left( {\sqrt x + 1} \right)}}{{25 - x}}\) ta được:
\(A = \dfrac{{4\left( {\sqrt 9 + 1} \right)}}{{25 - 9}} = \dfrac{{4\left( {3 + 1} \right)}}{{16}} = \dfrac{{16}}{{16}} = 1.\)
Vậy với \(x = 9\) thì \(A = 1.\)
2) Rút gọn biểu thức \(B.\)
Điều kiện: \(x \ge 0,\,\,x \ne 25.\)
\(\begin{array}{l}B = \left( {\dfrac{{15 - \sqrt x }}{{x - 25}} + \dfrac{2}{{\sqrt x + 5}}} \right):\dfrac{{\sqrt x + 1}}{{\sqrt x - 5}} = \left[ {\dfrac{{15 - \sqrt x }}{{\left( {\sqrt x - 5} \right)\left( {\sqrt x + 5} \right)}} + \dfrac{2}{{\sqrt x + 5}}} \right].\dfrac{{\sqrt x - 5}}{{\sqrt x + 1}}\\ = \dfrac{{15 - \sqrt x + 2\left( {\sqrt x - 5} \right)}}{{\left( {\sqrt x - 5} \right)\left( {\sqrt x + 5} \right)}}.\dfrac{{\sqrt x - 5}}{{\sqrt x + 1}} = \dfrac{{15 - \sqrt x + 2\sqrt x - 10}}{{\sqrt x + 5}}.\dfrac{1}{{\sqrt x + 1}}\\ = \dfrac{{\sqrt x + 5}}{{\sqrt x + 5}}.\dfrac{1}{{\sqrt x + 1}} = \dfrac{1}{{\sqrt x + 1}}.\end{array}\)
3) Tìm tất cả các giá trị nguyên của \(x\) để biểu thức \(P = AB\) đạt giá trị nguyên lớn nhất.
Điều kiện: \(x \ge 0,\,\,x \ne 25.\)
Ta có: \(P = A.B = \dfrac{{4\left( {\sqrt x + 1} \right)}}{{25 - x}}.\dfrac{1}{{\sqrt x + 1}} = \dfrac{4}{{25 - x}}.\)
\(x \in \mathbb{Z} \Rightarrow P \in \mathbb{Z} \Leftrightarrow \dfrac{4}{{25 - x}} \in \mathbb{Z} \Rightarrow 4\,\, \vdots \,\,\left( {25 - x} \right)\) hay \(\left( {25 - x} \right) \in U\left( 4 \right)\)
Mà \(U\left( 4 \right) = \left\{ { \pm 1;\,\, \pm 2;\,\, \pm 4} \right\} \Rightarrow \left( {25 - x} \right) \in \left\{ { \pm 1;\,\, \pm 2;\, \pm 4} \right\}.\)
Ta có bảng giá trị:
\(25 - x\) | \( - 4\) | \( - 2\) | \( - 1\) | \(1\) | \(2\) | \(4\) |
\(x\) | 29 (tm) | 27 (tm) | 26 (tm) | 24 (tm) | 23 (tm) | 1 (tm) |
\(P\) | \( - 1\) | \( - 2\) | \( - 4\) | \(4\) | \(2\) | \(1\) |
\( \Rightarrow \) với \(x \in \left\{ {23;\,\,24;\,\,26;\,\,27;\,\,29} \right\}\) thì \(P \in \mathbb{Z}.\)
Qua bảng giá trị ta thấy với \(x = 24\) thì \(P = 4\) là số nguyên lớn nhất.
Vậy \(x = 24\) thỏa mãn điều kiện bài toán.
Bài II (2,5 điểm) 1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình: Hai đội công nhân cùng làm chung một công việc thì sau 15 ngày làm xong. Nếu đội thứ nhất làm riêng trong 3 ngày rồi dừng lại và đội thứ hai làm tiếp công việc đó trong 5 ngày thì cả hai đội hoàn thành được 25% công việc. Hỏi nếu mỗi đội làm riêng thì trong bao nhiêu ngày mới xong công việc trên? 2) Một bồn nước inox có dạng một hình trụ có chiều cao \(1,75\,m\) và diện tích đáy là \(0,32\,{m^2}.\) Hỏi bồn nước này đựng đầy được bao nhiêu mét khối nước? (Bỏ qua bề đáy của bồn nước). |
Phương pháp:
1) Gọi số ngày làm một mình xong công việc của của đội 1 là \(x\)(ngày) \(\left( {x > 15} \right)\)
Số ngày làm một mình xong công việc của đội 2 là \(y\) (ngày) \(\left( {y > 15} \right)\)
Biểu diễn các đại lượng chưa biết theo ẩn đã gọi và lập hệ phương trình.
Giải hệ phương trình tìm các ẩn và đối chiều với điều kiện rồi kết luận.
2) Công thức tính thể tích khối trụ có diện tích đáy \(S\) và chiều cao \(h\) là: \(V = Sh.\)
Cách giải:
1) Gọi số ngày làm một mình xong công việc của của đội 1 là \(x\)(ngày) \(\left( {x > 15} \right)\)
Số ngày làm một mình xong công việc của đội 2 là \(y\) (ngày) \(\left( {y > 15} \right)\)
Trong một ngày đội 1 làm được số phần công việc là: \(\dfrac{1}{x}\) (công việc)
Trong một ngày đội 2 làm được số phần công việc là \(\dfrac{1}{y}\) (công việc)
Vì hai đội làm chung trong \(15\) ngày thì xong nên ta có phương trình: \(\dfrac{{15}}{x} + \dfrac{{15}}{y} = 1\) (1)
Trong \(3\) ngày đội 1 làm được \(\dfrac{3}{x}\) công việc, trong \(5\) ngày đội 2 làm được \(\dfrac{5}{y}\) công việc.
Đội 1 làm trong 3 ngày và đội 2 làm trong 5 ngày được \(25\% = \dfrac{1}{4}\) công việc nên ta có phương trình:
\(\dfrac{3}{x} + \dfrac{5}{y} = \dfrac{1}{4}\) (2)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có hệ phương trình: \(\left\{ \begin{array}{l}\dfrac{{15}}{x} + \dfrac{{15}}{y} = 1\\\dfrac{3}{x} + \dfrac{5}{y} = \dfrac{1}{4}\end{array} \right.\)
Đặt \(\left\{ \begin{array}{l}\dfrac{1}{x} = a\\\dfrac{1}{y} = b\end{array} \right.\) ta được: \(\left\{ \begin{array}{l}15a + 15b = 1\\3a + 5b = \dfrac{1}{4}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{1}{{24}}\\b = \dfrac{1}{{40}}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\dfrac{1}{x} = \dfrac{1}{{24}}\\\dfrac{1}{y} = \dfrac{1}{{40}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 24\,\,\,\left( {tm} \right)\\y = 40\,\,\,\,\left( {tm} \right)\end{array} \right.\)
Vậy đội 1 làm một mình trong \(24\) ngày thì xong công việc, đội 2 làm một mình trong \(40\) ngày thì xong công việc.
2) Thể tích bồn nước là: \(V = Sh = 0,32.1,75 = 0,56{m^3}\)
Vậy bồn nước đựng được \(0,56{m^3}\) nước.
Bài III (2 điểm) 1) Giải phương trình \({x^4} - 7{x^2} - 18 = 0.\) 2) Trong mặt phẳng tọa độ \(Oxy,\) cho đường thẳng \(\left( d \right):\,\,y = 2mx - {m^2} + 1\) và parabol \(\left( P \right):\,\,y = {x^2}.\) a) Chứng minh \(\left( d \right)\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt. b) Tìm tất cả các giá trị của \(m\) để \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ \({x_1},\,\,{x_2}\) thỏa mãn \(\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} = \dfrac{{ - 2}}{{{x_1}{x_2}}} + 1.\) |
Phương pháp:
1) Giải phương trình đã cho bằng cách đặt ẩn phụ \({x^2} = t\,\,\left( {t \ge 0} \right).\)
+) Giải phương trình tìm ẩn \(t,\) đối chiếu với điều kiện rồi tìm \(x.\)
2) Xét phương trình hoành độ giao điểm.
a) Hai đồ thị hàm số cắt nhau tại hai điểm phân biệt \( \Leftrightarrow \) phương trình hoành độ giao điểm có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0.\)
b) Sử dụng định lý Vi-et.
Cách giải:
1) Giải phương trình \({x^4} - 7{x^2} - 18 = 0\)
Đặt \({x^2} = t\,\left( {t \ge 0} \right)\) ta có phương trình \({t^2} - 7t - 18 = 0\)
\(\begin{array}{l} \Leftrightarrow {t^2} - 9t + 2t - 18 = 0\\ \Leftrightarrow t\left( {t - 9} \right) + 2\left( {t - 9} \right) = 0\\ \Leftrightarrow \left( {t + 2} \right)\left( {t - 9} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}t + 2 = 0\\t - 9 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = - 2\left( {ktm} \right)\\t = 9\left( {tm} \right)\end{array} \right.\end{array}\)
Với \(t = 9\) thì \({x^2} = 9 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = - 3\end{array} \right.\)
Vậy tập nghiệm của phương trình đã cho là: \(S = \left\{ { - 3;3} \right\}\)
2) Parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = 2mx - {m^2} + 1\)
Xét phương trình hoành độ giao điểm của đường thẳng \(\left( d \right)\) và parabol \(\left( P \right)\) ta có
\({x^2} = 2mx - {m^2} + 1 \Leftrightarrow {x^2} - 2mx + {m^2} - 1 = 0\,\,\left( * \right)\)
Số giao điểm của (d) và (P) cũng chính là số nghiệm của phương trình (*)
Phương trình \(\left( * \right)\) có \(\Delta ' = {m^2} - \left( {{m^2} - 1} \right) = 1 > 0\)
a) Vì \(\Delta ' > 0\) nên phương trình \(\left( * \right)\) luôn có hai nghiệm phân biệt với mọi \(m\) hay đường thẳng \(\left( d \right)\) luôn cắt parabol \(\left( P \right)\) tại hai điểm phân biệt.
b) Theo câu a) ta có đường thẳng \(\left( d \right)\) luôn cắt parabol \(\left( P \right)\) tại hai điểm phân biệt.
Gọi \({x_1};{x_2}\) là hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) thì \({x_1};{x_2}\) là hai nghiệm của phương trình \(\left( * \right)\)
Theo hệ thức Vi-et ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}{x_2} = {m^2} - 1\end{array} \right.\)
Xét \(\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} = \dfrac{{ - 2}}{{{x_1}{x_2}}} + 1\) ĐK: \({x_1}{x_2} \ne 0 \Leftrightarrow {m^2} - 1 \ne 0 \Leftrightarrow m \ne \pm 1\)
\( \Leftrightarrow \dfrac{{{x_1} + {x_2}}}{{{x_1}{x_2}}} = \dfrac{{ - 2}}{{{x_1}{x_2}}} + \dfrac{{{x_1}{x_2}}}{{{x_1}{x_2}}}\)
\(\begin{array}{l} \Rightarrow {x_1} + {x_2} = - 2 + {x_1}{x_2}\\ \Leftrightarrow 2m = - 2 + {m^2} - 1\\ \Leftrightarrow {m^2} - 2m - 3 = 0\\ \Leftrightarrow {m^2} - 3m + m - 3 = 0\\ \Leftrightarrow m\left( {m - 3} \right) + \left( {m - 3} \right) = 0\\ \Leftrightarrow \left( {m + 1} \right)\left( {m - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m + 1 = 0\\m - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - 1\,\,\,\,\,\left( {ktm} \right)\\m = 3\,\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy \(m = 3\) là giá trị thỏa mãn điều kiện đề bài.
Bài IV (3,0 điểm) Cho tam giác \(ABC\) có ba góc nhọn \(\left( {AB < AC} \right)\) nội tiếp đường tròn \(\left( O \right)\). Hai đường cao \(BE\) và \(CF\) của tam giác \(ABC\) cắt nhau tại \(H\). 1) Chứng minh bốn điểm \(B,\,\,C,\,\,E,\,\,F\) cùng thuộc một đường tròn. 2) Chứng minh đường thẳng \(OA\) vuông góc với đường thẳng \(EF\). 3) Gọi \(K\) là trung điểm của đoạn thẳng \(BC\). Đường thẳng \(AO\) cắt đường thẳng \(BC\) tại điểm \(I\), đường thẳng \(EF\) cắt đường thẳng \(AH\) tại điểm \(P\) . Chứng minh tam giác \(APE\) đồng dạng với tam giác \(AIB\) và đường thẳng \(KH\) song song với đường thẳng \(IP\). |
Phương pháp:
1) Chứng minh tứ giác nội tiếp bằng các dấu hiệu nhận biết.
2) Sử dụng định lý: Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung cùng chắn một cung thì bằng nhau.
3) Chứng minh các cặp tam giác tương ứng đồng dạng để suy ra các góc bằng nhau và chứng minh \(KH//IP.\)
Cách giải:
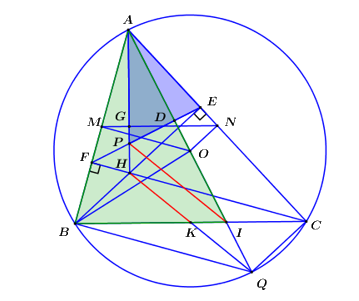
1) Chứng minh bốn điểm \(B,\,\,C,\,\,E,\,\,F\) cùng thuộc một đường tròn.
Ta có \(\angle BEC = \angle BFC = {90^0}\,\,\left( {gt} \right) \Rightarrow \) Tứ giác \(BFEC\) là tứ giác nội tiếp (Tứ giác có 2 đỉnh kề nhau cùng nhìn 1 cạnh dưới các góc bằng nhau).
Vậy bốn điểm \(B,\,\,C,\,\,E,\,\,F\) cùng thuộc một đường tròn.
2) Chứng minh đường thẳng \(OA\) vuông góc với đường thẳng \(EF\).
Cách 1:
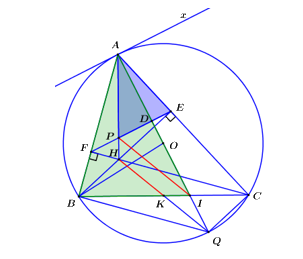
b) Kẻ tiếp tuyến Ax của đường tròn tại A, ta có \(Ax \bot OA\).
Ta có \(\angle xAE = \angle ABC\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AC).
Mà \(\angle ABC = \angle AEF\) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp).
\( \Rightarrow \angle xAE = \angle AEF\). Mà hai góc này ở vị trí so le trong \( \Rightarrow EF//Ax\).
\( \Rightarrow EF \bot OA\).
Cách 2:
Gọi \(D = OA \cap EF\).
Gọi \(M,\,\,N\) lần lượt là trung điểm của \(AB,\,\,AC\).
\( \Rightarrow OM \bot AB,\,\,ON \bot AC\) (quan hệ vuông góc giữa đường kính và dây cung).
Xét tứ giác \(AMON\) có \(\angle AMO + \angle ANO = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác \(AMON\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
Gọi \(G = MN \cap AH\).
Ta có: \(H\) là trực tâm tam giác \(ABC \Rightarrow AH \bot BC\).
Mà \(MN//BC\) (MN là đường trung bình của tam giác \(ABC\)) \( \Rightarrow MN \bot AH\) tại \(G\).
Xét tam giác \(AMG\) và tam giác \(AON\) có:
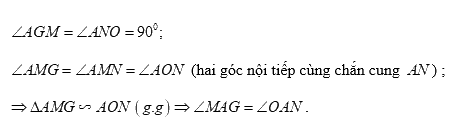
\(\begin{array}{l} \Rightarrow \angle MAG + \angle GAO = \angle OAN + \angle GAO\\ \Rightarrow \angle OAM = \angle GAN \Rightarrow \angle DAF = \angle GAN\,\,\left( 1 \right)\end{array}\)
Ta có : \(\angle AFE = \angle ACB\) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp) ;
Lại có \(\angle ACB = \angle ANM\) (đồng vị)
\( \Rightarrow \angle AFE = \angle ANM\) (2)
Từ (1) và (2) \( \Rightarrow \angle DAF + \angle AFE = \angle GAN + & \angle ANM = {90^0}\).
\( \Rightarrow \Delta ADF\) vuông tại \(D \Rightarrow AD \bot DF\) hay \(OA \bot EF\).
3) Gọi \(K\) là trung điểm của đoạn thẳng \(BC\). Đường thẳng \(AO\) cắt đường thẳng \(BC\) tại điểm \(I\), đường thẳng \(EF\) cắt đường thẳng \(AH\) tại điểm \(P\) . Chứng minh tam giác \(APE\) đồng dạng với tam giác \(AIB\) và đường thẳng \(KH\) song song với đường thẳng \(IP\).
Ta đã chứng minh được \(\angle DAF = \angle GAN\,\,\)hay \(\angle IAB = \angle PAE\).
Lại có \(\angle AEF = \angle ABC\) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp) ;
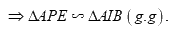
Kéo dài \(AI\) cắt \(\left( O \right)\) tại \(Q\) \( \Rightarrow AQ\) là đường kính của \(\left( O \right)\).
Nối \(BQ,\,\,CQ\) ta có \(\angle ABQ = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow AB \bot BQ\).
Mà \(CH \bot AB \Rightarrow CH//BQ\).
Hoàn toàn tương tự ta chứng minh được \(BH//CQ\).
Suy ra \(BHCQ\) là hình bình hành (Tứ giác có các cặp cạnh đối song song).
Mà \(K\) là trung điểm của \(BC\,\,\left( {gt} \right) \Rightarrow K\) cũng là trung điểm của \(HQ \Rightarrow H,\,\,K,\,\,Q\) thẳng hàng.
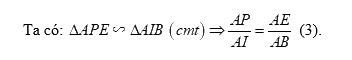
Xét tam giác \(AHE\) và tam giác \(AQB\) có:
\(\angle AEH = \angle ABQ = {90^0}\)
\(\angle QAB = \angle EAH\,\,\left( {cmt} \right)\) (do \(\angle DAF = \angle GAN\,\,\)).
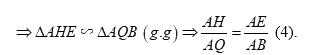
Từ (1) và (2) \( \Rightarrow \dfrac{{AP}}{{AI}} = \dfrac{{AH}}{{AQ}} \Rightarrow \dfrac{{AP}}{{AH}} = \dfrac{{AI}}{{AQ}} \Rightarrow PI//HQ\) (Định lí Ta-let đảo) (đpcm).
Bài V (VDC) (0,5 điểm)
Cách giải:
Ta có \({a^2} + {b^2} + ab = 3 \Leftrightarrow {a^2} + {b^2} = 3 - ab\)
Ta thấy \({\left( {a - b} \right)^2} \ge 0 \Leftrightarrow {a^2} + {b^2} \ge 2ab \Leftrightarrow 3 - ab \ge 2ab \Leftrightarrow ab \le 1\)
Lại có \({\left( {a + b} \right)^2} \ge 0 \Leftrightarrow {a^2} + {b^2} \ge - 2ab \Leftrightarrow 3 - ab \ge - 2ab \Leftrightarrow 3 \ge - ab \Leftrightarrow ab \ge - 3\)
\( \Rightarrow - 3 \le ab \le 1\).
Xét \({a^2} + {b^2} = 3 - ab\) với \( - 3 \le ab \le 1\)
\(\begin{array}{l} \Leftrightarrow {\left( {{a^2} + {b^2}} \right)^2} = {\left( {3 - ab} \right)^2}\\ \Leftrightarrow {a^4} + {b^4} + 2{a^2}{b^2} = 9 - 6ab + {a^2}{b^2}\\ \Leftrightarrow {a^4} + {b^4} = - {a^2}{b^2} - 6ab + 9\end{array}\)
Khi đó \(P = {a^4} + {b^4} - ab = - {a^2}{b^2} - 6ab + 9 - ab\) \( = - {\left( {ab} \right)^2} - 7ab + 9 = \dfrac{{85}}{4} - {\left( {ab + \dfrac{7}{2}} \right)^2}\)
Vì \( - 3 \le ab \le 1 \Rightarrow \dfrac{1}{2} \le ab + \dfrac{7}{2} \le \dfrac{9}{2} \Leftrightarrow {\left( {ab + \dfrac{7}{2}} \right)^2} \le \dfrac{{81}}{4}\).
Suy ra \(P = \dfrac{{85}}{4} - {\left( {ab + \dfrac{7}{2}} \right)^2} \ge \dfrac{{85}}{4} - \dfrac{{81}}{4} = 1 \Leftrightarrow P \ge 1\).
Dấu “=” xảy ra khi \(ab = 1\) và \({a^2} + {b^2} = 2 \Rightarrow \left[ \begin{array}{l}a = 1;\,\,b = 1\\a = - 1;\,\,b = - 1\end{array} \right.\)
Ta lại có \(P = - {\left( {ab} \right)^2} - 7ab + 9 = \left( {ab + 3} \right)\left( { - ab - 4} \right) + 21\)
Mà \( - 3 \le ab \le 1\) nên \(\left\{ \begin{array}{l}ab + 3 \ge 0\\ - ab - 4 < 0\end{array} \right.\) nên \(\left( {ab + 3} \right)\left( { - ab - 4} \right) \le 0 \Rightarrow P \le 21\).
Dấu “=” xảy ra khi \(\left\{ \begin{array}{l}ab = - 3\\{a^2} + {b^2} + ab = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}ab = - 3\\{\left( {a + b} \right)^2} = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a = \sqrt 3 \\b = - \sqrt 3 \end{array} \right.\\\left[ \begin{array}{l}a = - \sqrt 3 \\b = \sqrt 3 \end{array} \right.\end{array} \right.\)
Vậy giá trị lớn nhất của \(P\) là \(21\); giá trị nhỏ nhất của \(P\) là \(1.\)
Kỳ thi tuyển sinh vào lớp 10 tại Hà Nội luôn là một kỳ thi quan trọng, đánh dấu bước ngoặt trong sự nghiệp học tập của học sinh. Môn Toán, với vai trò then chốt, thường là môn thi có tính cạnh tranh cao. Đề thi vào 10 môn Toán Hà Nội năm 2019 không nằm ngoài xu hướng này, với độ khó và tính phân loại cao.
Đề thi vào 10 môn Toán Hà Nội năm 2019 thường bao gồm các dạng bài tập sau:
So với các năm trước, đề thi vào 10 môn Toán Hà Nội năm 2019 có xu hướng tăng độ khó và tính phân loại. Các bài toán đòi hỏi học sinh phải có kiến thức vững chắc, kỹ năng giải toán tốt, và khả năng tư duy logic cao. Bên cạnh đó, đề thi cũng chú trọng vào việc kiểm tra khả năng vận dụng kiến thức vào thực tế của học sinh.
Để giúp các em học sinh hiểu rõ hơn về đề thi vào 10 môn Toán Hà Nội năm 2019, chúng ta sẽ cùng phân tích chi tiết một số câu hỏi tiêu biểu:
Đây là một bài toán đại số cơ bản, đòi hỏi học sinh phải nắm vững các kiến thức về phương trình bậc hai và các phương pháp giải phương trình. Để giải bài toán này, học sinh có thể sử dụng công thức nghiệm của phương trình bậc hai hoặc phương pháp phân tích thành nhân tử.
Đây là một bài toán hình học phẳng, đòi hỏi học sinh phải nắm vững các kiến thức về tam giác vuông, đường cao, và các hệ thức lượng trong tam giác vuông. Để chứng minh bài toán này, học sinh có thể sử dụng các định lý về tam giác vuông và các hệ thức lượng.
Đây là một bài toán số học, đòi hỏi học sinh phải nắm vững các kiến thức về số nguyên tố, chia hết, và các tính chất của số nguyên tố. Để giải bài toán này, học sinh có thể sử dụng các định nghĩa và tính chất của số nguyên tố.
Để đạt kết quả tốt trong kỳ thi tuyển sinh vào lớp 10 môn Toán Hà Nội năm 2019, các em học sinh cần có một kế hoạch luyện thi khoa học và hiệu quả. Dưới đây là một số lời khuyên:
Giaitoan.edu.vn là một website học toán online uy tín, cung cấp đầy đủ các tài liệu và công cụ hỗ trợ học sinh luyện thi vào 10 môn Toán Hà Nội năm 2019. Chúng tôi cam kết mang đến cho các em một môi trường học tập chất lượng cao, hiệu quả, và thú vị.
| Tên tài liệu | Mô tả |
|---|---|
| Sách giáo khoa Toán lớp 9 | Nguồn kiến thức cơ bản quan trọng. |
| Sách bài tập Toán lớp 9 | Cung cấp nhiều bài tập luyện tập. |
| Đề thi thử vào 10 môn Toán Hà Nội các năm trước | Giúp làm quen với cấu trúc đề thi. |
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi tuyển sinh vào lớp 10 môn Toán Hà Nội năm 2019!