Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Quảng Ngãi năm 2023. Đây là tài liệu ôn tập vô cùng quan trọng dành cho các em học sinh đang chuẩn bị cho kỳ thi sắp tới.
Chúng tôi cung cấp đầy đủ các đề thi chính thức, đáp án chi tiết và phương pháp giải bài tập hiệu quả, giúp các em tự tin đối mặt với mọi dạng bài thi.
Câu 1: 1) Thực hiện phép tính \(3\sqrt {49} {\rm{ \;}} - \sqrt {121} \). 2) Vẽ đồ thị \((P)\) của hàm số \(y = \frac{1}{2}{x^2}\). 3) Cho hai đường thẳng \((d):y = 2x + 1\) và \(\left( {d'} \right):y = ax + b(a \ne 0)\).Tìm a, b biết \(\left( {d'} \right)\) song song với \((d)\) và đi qua điểm \(A(2;3)\).
Câu 1:
1) Thực hiện phép tính \(3\sqrt {49} {\rm{ \;}} - \sqrt {121} \).
2) Vẽ đồ thị \((P)\) của hàm số \(y = \frac{1}{2}{x^2}\).
3) Cho hai đường thẳng \((d):y = 2x + 1\) và \(\left( {d'} \right):y = ax + b(a \ne 0)\).Tìm a, b biết \(\left( {d'} \right)\) song song với \((d)\) và đi qua điểm \(A(2;3)\).
Câu 2:
1) Giải phương trình và hệ phương trình sau:
a) \({x^4} - 3{x^2} - 4 = 0\)
b) \(\left\{ {\begin{array}{*{20}{l}}{2x - y = 3}\\{3x + 2y = 1}\end{array}} \right.\)
2) Cho phương trình \({x^2} - 2(m - 1)x + {m^2} - 4 = 0\), với \(m\) là tham số.
a) Tìm \(m\) để phương trình có hai nghiệm phân biệt.
b) Khi phương trình có hai nghiệm \({x_1},{x_2}\), tìm tất cả các giá trị của \(m\) để biểu thức \(P = x_1^2 + x_2^2 + {x_1}{x_2} + {m^2}\) đạt giá trị nhỏ nhất.
Câu 3: Hai đội công nhân cùng thi công một đoạn đường nông thôn và dự định hoàn thành công việc đó trong 16 ngày. Khi làm được 12 ngày thì đội I được điều động đi làm việc ở nơi khác. Những ngày sau đó, đội II làm việc với năng suất gấp 1,5 lần năng suất ban đầu nên đã hoàn thành công việc đúng thời gian dự định. Hỏi theo năng suất ban đầu, nếu mỗi đội làm một mình thì phải bao nhiêu ngày mới hoàn thành công việc trên?
Câu 4:
1) Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 4cm, HC = 5cm (như hình vẽ). Tính độ dài AB và AH.
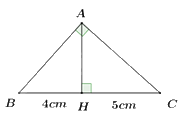
2) Cho tam giác ABC có ba góc nhọn (AB < AC) nội tiếp đường tròn (O;R). Hai đường cao AE và BF cắt nhau tại H.
a) Chứng minh tứ giác CEHF nội tiếp đường tròn. Xác định tâm của đường tròn đó.
b) Kẻ đường kính AD của đường tròn (O). Chứng minh tứ giác BHCD là hình bình hành. Biết \(BC = R\sqrt 3 \), tính AH theo R.
c) Gọi N là giao điểm của hai đường thẳng CH và AB, K là giao điểm của hai đường thẳng BC và FN. Chứng minh BK.CE = BE.CK.
Câu 5: Giải phương trình \(\frac{1}{{3{x^2}}} + \frac{1}{{{x^2} - 12x + 2024}} = \frac{1}{{{x^2} - 3x + 506}}\).
-----HẾT-----
Câu 1 (TH):
Phương pháp:
1) Tính toán với căn bậc hai \(\sqrt {{x^2}} {\rm{ \;}} = \left| x \right|\)
2) Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị tương ứng giữa \(x\) và \(y\).
Bước 3: Vẽ đồ thị và kết luận.
Chú ý: vì đồ thị hàm số \(y = a{x^2}(a \ne 0)\) luôn đi qua gốc tọa độ \(O\) và nhận trục Oy làm trục đối xứng nên khi vẽ đồ thị của hàm số này, ta chỉ cần tìn một số điểm bên phải trục Oy rồi lấy các điểm đối xứng với chúng qua Oy.
3) Hai đường thẳng \(d:y = ax + b;d':y = a'x + b'(a;a' \ne 0)\) song song khi \(\left\{ {\begin{array}{*{20}{l}}{a = a'}\\{b \ne b'}\end{array}} \right.\)
Thay giá trị của điểm đi qua vào đường thẳng.
Cách giải:
1) Ta có: \(3\sqrt {49} {\rm{ \;}} - \sqrt {121} {\rm{ \;}} = 3.\sqrt {{7^2}} {\rm{ \;}} - \sqrt {{{11}^2}} {\rm{ \;}} = 3.7 - 11 = 21 - 11 = 10\)
2) Xét hàm số \(y = \frac{1}{2}{x^2}\).
Ta có bảng giá trị sau:
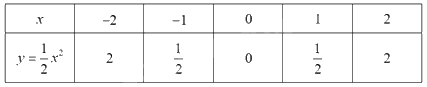
\( \Rightarrow \) Đồ thị hàm số là đường cong parabol đi qua các điểm
\(O{\mkern 1mu} \left( {0;0} \right);A\left( { - 2;2} \right);B\left( { - 1;\frac{1}{2}} \right);{\mkern 1mu} {\mkern 1mu} C\left( {1;\frac{1}{2}} \right);{\mkern 1mu} {\mkern 1mu} D\left( {2;2} \right)\)
Hệ số \(a = \frac{1}{2} > 0\)nên parabol có bề cong hướng lên.
Đồ thị hàm số nhận Oy làm trục đối xứng.
Ta vẽ được đồ thị hàm số \(y = \frac{1}{2}{x^2}\) như sau:
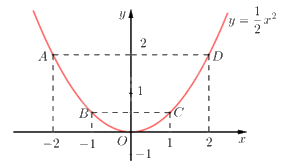
3) Vì \(\left( {d'} \right)\) song song với \((d)\) nên \(\left\{ {\begin{array}{*{20}{l}}{a = 2}\\{b \ne 1}\end{array}} \right.\) hay phương trình \(\left( {d'} \right)\) có dạng: \(y = 2x + b\) với \(b \ne 1\))
Vì \(\left( {d'} \right)\)đi qua điểm \(A(2;3)\) nên thay tọa độ điểm A vào phương trình đường thẳng \(\left( {d'} \right)\) ta được:
\(3 = 2.2 + b \Leftrightarrow 3 = 4 + b \Leftrightarrow b = {\rm{ \;}} - 1\) (thỏa mãn \(b \ne 1\))
Vậy \(a = 2\) và \(b = {\rm{ \;}} - 1.\)
Câu 2 (TH):
Phương pháp:
1)
a) Giải PT bằng cách đặt ẩn, đưa về PT bậc hai một ẩn.
Sử dụng phương pháp tính nhẩm \(a - b + c = 0\) thì PT có một nghiệm là \( - 1\); nghiệm còn lại là \(\frac{{ - c}}{a}\)
b) Giải hệ phương trình bằng phương pháp cộng đại số
2)
a) PT có hai nghiệm phân biệt khi \(\Delta ' > 0\)
Công thức \(\Delta ' = {\left( {\frac{b}{a}} \right)^2} - a.c\)
b) PT có hai nghiệm khi \(\Delta ' \ge 0\)
Hệ thức Vi-ét \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{{ - b}}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\)
Biến đổi biểu thức đề bài
Cách giải:
1) Giải phương trình và hệ phương trình sau:
a) \({x^4} - 3{x^2} - 4 = 0\) (1)
Đặt \(t = {x^2}\left( {t \ge 0} \right)\)
Khi đó \(\left( 1 \right) \Leftrightarrow {t^2} - 3t - 4 = 0\)
Do \(a - b + c = 1 - \left( { - 3} \right) - 4 = 0\) nên phương trình có 2 nghiệm phân biết \(\left[ {\begin{array}{*{20}{l}}{{t_1} = {\rm{ \;}} - 1\left( {KTM} \right)}\\{{t_2} = {\rm{ \;}} - \frac{{ - 4}}{1} = 4\left( {TM} \right)}\end{array}} \right.\)
Với \(t = 4 \Rightarrow {x^2} = 4 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 2}\\{x = {\rm{ \;}} - 2}\end{array}} \right.\) (thỏa mãn)
Vậy tập nghiệm của phương trình là \(S = \left\{ { - 2,2} \right\}\).
b) \(\left\{ {\begin{array}{*{20}{l}}{2x - y = 3}\\{3x + 2y = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4x - 2y = 6}\\{3x + 2y = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{7x = 7}\\{2x - y = 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1}\\{y = 2x - 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1}\\{y = 1}\end{array}} \right.\)
Vậy hệ phương trình có nghiệm \(\left( {x,y} \right) = \left( {1,1} \right)\).
2) Cho phương trình \({x^2} - 2(m - 1)x + {m^2} - 4 = 0\), với \(m\) là tham số.
a) Xét \(\Delta ' = {\left( {m - 1} \right)^2} - 1\left( {{m^2} - 4} \right) = {m^2} - 2m + 1 - {m^2} + 4 = 5 - 2m\)
Để phương trình có hai nghiệm phân biệt thì \(\Delta ' > 0 \Leftrightarrow 5 - 2m > 0 \Leftrightarrow m < \frac{5}{2}\)
Vậy \(m < \frac{5}{2}\) thì phương trình có hai nghiệm phân biệt
b) Để phương trình có 2 nghiệm \({x_1},{x_2}\) thì \(\Delta ' \ge 0 \Leftrightarrow 5 - 2m \ge 0 \Leftrightarrow m \le \frac{5}{2}\)
Khi đó áp dụng hệ thức Vi-et ta có \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 2\left( {m - 1} \right)}\\{{x_1}{x_2} = {m^2} - 4}\end{array}} \right.\)
Ta có \(P = x_1^2 + x_2^2 + {x_1}{x_2} + {m^2}\)
\(\begin{array}{*{20}{l}}{ = x_1^2 + 2{x_1}{x_2} + x_2^2 - {x_1}{x_2} + {m^2}}\\{ = {{\left( {{x_1} + {x_2}} \right)}^2} - {x_1}{x_2} + {m^2}}\\{ = {{\left( {2\left( {m - 1} \right)} \right)}^2} - \left( {{m^2} - 4} \right) + {m^2}}\\{ = 4{{\left( {m - 1} \right)}^2} - {m^2} + 4 + {m^2}}\\{ = 4{{\left( {m - 1} \right)}^2} + 4}\end{array}\)
Do \({\left( {m - 1} \right)^2} \ge 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \forall m \Rightarrow 4{\left( {m - 1} \right)^2} + 4 \ge 4 \Rightarrow P \ge 4\)
Dấu bằng xảy ra khi m = 1 (thỏa mãn \(m \le \frac{5}{2}\))
Vậy \({P_{\min }} = 4\) khi m = 1.
Câu 3 (TH):
Phương pháp:
Giải bài toán bằng cách lập hệ phương trình.
- Quy ước công việc cần hoàn thành là 1 đơn vị
- Tìm 1 trong 1 giờ (1 ngày, 1 phút, ...) mỗi người làm được bao nhiêu phần công việc
Cách giải:
Gọi thời gian đội I hoàn thành công việc một mình là x (\(x > 16\), ngày)
Gọi thời gian đội II hoàn thành công việc một mình là y (\(y > 16\), ngày)
Một ngày đội I làm một mình được \(\frac{1}{x}\) (công việc)
Một ngày đội II làm một mình được \(\frac{1}{y}\) (công việc)
Suy ra 1 ngày 2 đội làm được \(\frac{1}{x} + \frac{1}{y}\) (công việc)
Do 2 đội cùng thi công đoạn đường thì hoàn thành công việc trong 16 ngày nên ta có phương trình
\(\frac{1}{x} + \frac{1}{y} = \frac{1}{{16}}\) (1)
Ta có 2 đội làm cùng nhau trong 12 ngày được \(12\left( {\frac{1}{x} + \frac{1}{y}} \right) = \frac{{12}}{{16}} = \frac{3}{4}\) (công việc)
Đội II tăng năng suất lên 1,5 lần nên mỗi ngày đội 2 làm được \(\frac{{1,5}}{y} = \frac{3}{{2y}}\) (công việc)
Để hoàn thành công việc trong 16 ngày như dự định thì đội II phải hoàn thành nốt công việc trong 4 ngày
Khi đó ta có phương trình \(\frac{3}{4} + \frac{3}{{2y}}.4 = 1\) (2)
Từ (1) và (2) ta có hệ: \(\left\{ {\begin{array}{*{20}{l}}{\frac{1}{x} + \frac{1}{y} = \frac{1}{{16}}}\\{\frac{3}{4} + \frac{3}{{2y}}.4 = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\frac{6}{y} = \frac{1}{4}}\\{\frac{1}{x} = \frac{1}{{16}} - \frac{1}{y}}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = 24}\\{x = 1:\left( {\frac{1}{{16}} - \frac{1}{{24}}} \right)}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = 24}\\{x = 48}\end{array}} \right.(TM)\)
Vậy đội I hoàn thành công việc một mình trong 48 ngày, đội II hoàn thành công việc trong 24 ngày.
Câu 4 (VD):
Phương pháp:
1) Áp dụng hệ thức lượng trong tam giác vuông có đường cao.
2) a) Chứng minh tứ giác CEHF có tổng hai góc đối bằng \({180^\circ }\)
Gọi I là trung điểm của CH. Khi đó tứ giá CEHF nội tiếp đường tròn tâm I.
b) Chứng minh tứ giác BHCH có hai cặp cạnh đối song song với nhau.
Tính AH thông qua OM. Chứng minh OM là đường trung bình \(\Delta AHD\).
Áp dụng định lí Py-ta-go trong \(\Delta OBM\) vuông tại M tính OM.
c) Chứng minh NB là phân giác trong tại đỉnh N của tam giác NEK \( \Rightarrow \frac{{BE}}{{BK}} = \frac{{NE}}{{NK}}\)
Chứng minh NC là phân giác ngoài tại định N của tam giác NEK \( \Rightarrow \frac{{CE}}{{CK}} = \frac{{NE}}{{NK}}\)
Cách giải:
1)
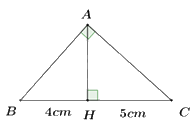
Ta có \(BC = BH + HC = 4 + 5 = 9{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)\).
Áp dụng hệ thức lượng trong tam giác ABC vuông tại A, đường cao AH ta có:
\(\begin{array}{*{20}{l}}{ + ){\mkern 1mu} {\mkern 1mu} A{B^2} = BH.BC}\\{ \Rightarrow A{B^2} = 4.9 = 36}\\{ \Rightarrow AB = \sqrt {36} {\rm{ \;}} = 6{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)}\\{ + ){\mkern 1mu} {\mkern 1mu} A{H^2} = BH.HC}\\{ \Rightarrow A{H^2} = 4.5 = 20}\\{ \Rightarrow AH = \sqrt {20} {\rm{ \;}} = 2\sqrt 5 {\mkern 1mu} {\mkern 1mu} \left( {cm} \right)}\end{array}\)
Vậy AB = 6 cm, AH = \(2\sqrt 5 \) cm.
2)
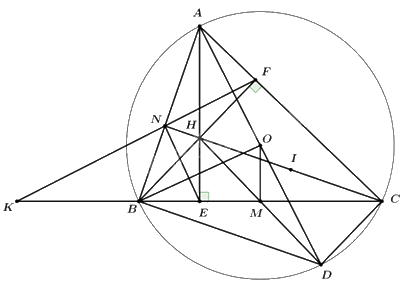
a) Ta có \(\left\{ {\begin{array}{*{20}{l}}{AE \bot BC \Rightarrow \angle HEC = {{90}^0}}\\{BF \bot AC \Rightarrow \angle HFC = {{90}^0}}\end{array}} \right.\)
Xét tứ giác CEHF có:
\(\angle HEC + \angle HFC = {90^0} + {90^0} = {180^0}\).
Mà E, F là hai đỉnh đối nhau của tứ giác CEHF.
Suy ra CEHF là tứ giác nội tiếp (dhnb).
Gọi I là trung điểm của CH.
Do tam giác HEC vuông tại E, có trung tuyến EI nên \(IE = \frac{1}{2}HC = IH = IC\).
Do tam giác HFC vuông tại F, có trung tuyến FI nên \(IF = \frac{1}{2}HC = IH = IC\).
\( \Rightarrow IE = IF = IH = IC\).
Vậy tứ giác CEHF nội tiếp đường tròn có tâm I là trung điểm của HC.
b) Ta có: \(\angle ABD = {90^0}\) (góc nội tiếp chắn nửa đường tròn (O)).
\( \Rightarrow BD \bot AB\).
Mà \(CH \bot AB\) (do H là trực tâm của tam giác ABC).
\( \Rightarrow \) BD // CH (từ vuông góc đến song song) (1)
Ta có: \(\angle ACD = {90^0}\) (góc nội tiếp chắn nửa đường tròn (O)).
\( \Rightarrow CD \bot AC\).
Mà \(BH \bot AC{\mkern 1mu} {\mkern 1mu} \left( {gt} \right)\)
\( \Rightarrow \) CD // BH (từ vuông góc đến song song) (2)
Từ (1), (2) => BHCD là hình bình hành (dhnb) (đpcm).
Gọi \(M = BC \cap HD \Rightarrow \) M là trung điểm của BC và HD (tính chất hình bình hành).
Ta có:
O là trung điểm của AD (gt)
M là trung điểm của HD (cmt)
=> OM là đường trung bình của tam giác AHD (định nghĩa).
\( \Rightarrow OM = \frac{1}{2}AH \Rightarrow AH = 2OM\) (tính chất đường trung bình của tam giác).
Vì M là trung điểm của BC (cmt) \( \Rightarrow OM \bot BC\) (quan hệ vuông góc giữa đường kính và dây cung)
\( \Rightarrow \Delta OBM\) vuông tại M, có OB = R, \(BM = \frac{1}{2}BC = \frac{{R\sqrt 3 }}{2}\).
Áp dụng định lí Pytago trong tam giác vuông OBM ta có:
\(\begin{array}{*{20}{l}}{O{M^2} + B{M^2} = O{B^2}}\\{ \Rightarrow O{M^2} = O{B^2} - B{M^2}}\\{ \Rightarrow O{M^2} = {R^2} - {{\left( {\frac{{R\sqrt 3 }}{2}} \right)}^2} = \frac{{{R^2}}}{4}}\\{ \Rightarrow OM = \frac{R}{2}}\end{array}\)
Vậy \(AH = 2OM = R.\)
c) Vì H là trực tâm của tam giác ABC nên \(CH \bot AB\) tại N hay \(CN \bot AB\).
Xét tứ giác ANHF có:
\(\begin{array}{*{20}{l}}{\angle ANH = {{90}^0}{\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} CN \bot AB} \right)}\\{\angle AFH = {{90}^0}{\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} BF \bot AC} \right)}\\{ \Rightarrow \angle ANH + \angle AFH = {{90}^0} + {{90}^0} = {{180}^0}}\end{array}\)
Mà hai đỉnh N, F là hai đỉnh đối diện của tứ giác ANHF.
=> ANHF là tứ giác nội tiếp (dhnb).
\( \Rightarrow \angle FNH = \angle FAH = \angle CAE\) (hai góc nội tiếp cùng chắn cung FH).
Chứng minh tương tự đối với tứ giác BEHN có:
\(\begin{array}{*{20}{l}}{\angle BNH = {{90}^0}{\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} CN \bot AB} \right)}\\{\angle BEH = {{90}^0}{\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} AE \bot BC} \right)}\\{ \Rightarrow \angle BNH + \angle BEH = {{90}^0} + {{90}^0} = {{180}^0}}\end{array}\)
Mà hai đỉnh N, E là hai đỉnh đối diện của tứ giác BEHN
=> BEHN là tứ giác nội tiếp (dhnb).
\( \Rightarrow \angle ENH = \angle EBH = \angle CBF\) (hai góc nội tiếp cùng chắn cung HE).
Mà \(\angle CEA = \angle CBF\) (cùng phụ với \(\angle ACB\)).
\( \Rightarrow \angle FNH = \angle ENH\).
\( \Rightarrow NH\) là phân giác của góc ENF.
Mà \(\angle ENK\) kề bù với \(\angle ENF\), \(NH \bot NB{\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} CN \bot AB} \right)\).
\( \Rightarrow NB\) là phân giác trong của \(\angle ENK\), NH là phân giác ngoài của \(\angle ENK\).
Áp dụng định lí đường phân giác ta có: \(\frac{{BE}}{{BK}} = \frac{{CE}}{{CK}} = \frac{{NE}}{{NK}}\).
Vậy BK.CE = BE.CK (đpcm).
Câu 5 (VDC):
Phương pháp:
Áp dụng bất đẳng thức Cô-si cho hai số \(a,b\) không âm ta (\(a + b \ge 2\sqrt {ab} \))
Để ta chứng minh \(\frac{1}{a} + \frac{1}{b} \ge \frac{4}{{a + b}}\)
Cách giải:
ĐKXĐ: \(x \ne 0\)
Ta chứng minh \(\frac{1}{a} + \frac{1}{b} \ge \frac{4}{{a + b}}\).
Thật vây, áp dụng bất đẳng thức Cô-si cho hai số a, b không âm ta được:
\(\begin{array}{*{20}{l}}{a + b \ge 2\sqrt {ab} }\\{\frac{1}{a} + \frac{1}{b} \ge 2\sqrt {\frac{1}{a}.\frac{1}{b}} }\end{array}\)
\(\begin{array}{*{20}{l}}{ \Rightarrow \left( {a + b} \right)\left( {\frac{1}{a} + \frac{1}{b}} \right) \ge 2\sqrt {ab} .2\sqrt {\frac{1}{a}.\frac{1}{b}} {\rm{ \;}} = 4}\\{ \Rightarrow \frac{1}{a} + \frac{1}{b} \ge \frac{4}{{a + b}}}\end{array}\)
Dấu “=” xảy ra khi và chỉ khi: \(a = b\)
Vì \(3{x^2} \ge 0\)với mọi \(x\) và \({x^2} - 12x + 2024 = {\left( {x - 6} \right)^2} + 1988 > 0\) với mọi \(x\) nên ta có:
\(\frac{1}{{3{x^2}}} + \frac{1}{{{x^2} - 12x + 2024}} \ge \frac{4}{{3{x^2} + {x^2} - 12x + 2024}} = \frac{4}{{4{x^2} - 12x + 2024}} = \frac{1}{{{x^2} - 3x + 506}}\)
Dấu “=” xảy ra khi và chỉ khi: \(3{x^2} = {x^2} - 12x + 2024\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow 2{x^2} + 12x - 2024 = 0}\\{ \Leftrightarrow {x^2} + 6x - 1012 = 0}\end{array}\)
Ta có: \(\Delta ' = {3^2} - 1.\left( { - 1012} \right) = 1021 > 0\)
Suy ra phương trình có hai nghiệm là: \({x_1} = {\rm{ \;}} - 3 + \sqrt {1021} \)và \({x_2} = {\rm{ \;}} - 3 - \sqrt {1021} \)
Vậy tập nghiệm phương trình đã cho là: \(S = \left\{ { - 3 + \sqrt {1021} ; - 3 - \sqrt {1021} } \right\}\).
Câu 1:
1) Thực hiện phép tính \(3\sqrt {49} {\rm{ \;}} - \sqrt {121} \).
2) Vẽ đồ thị \((P)\) của hàm số \(y = \frac{1}{2}{x^2}\).
3) Cho hai đường thẳng \((d):y = 2x + 1\) và \(\left( {d'} \right):y = ax + b(a \ne 0)\).Tìm a, b biết \(\left( {d'} \right)\) song song với \((d)\) và đi qua điểm \(A(2;3)\).
Câu 2:
1) Giải phương trình và hệ phương trình sau:
a) \({x^4} - 3{x^2} - 4 = 0\)
b) \(\left\{ {\begin{array}{*{20}{l}}{2x - y = 3}\\{3x + 2y = 1}\end{array}} \right.\)
2) Cho phương trình \({x^2} - 2(m - 1)x + {m^2} - 4 = 0\), với \(m\) là tham số.
a) Tìm \(m\) để phương trình có hai nghiệm phân biệt.
b) Khi phương trình có hai nghiệm \({x_1},{x_2}\), tìm tất cả các giá trị của \(m\) để biểu thức \(P = x_1^2 + x_2^2 + {x_1}{x_2} + {m^2}\) đạt giá trị nhỏ nhất.
Câu 3: Hai đội công nhân cùng thi công một đoạn đường nông thôn và dự định hoàn thành công việc đó trong 16 ngày. Khi làm được 12 ngày thì đội I được điều động đi làm việc ở nơi khác. Những ngày sau đó, đội II làm việc với năng suất gấp 1,5 lần năng suất ban đầu nên đã hoàn thành công việc đúng thời gian dự định. Hỏi theo năng suất ban đầu, nếu mỗi đội làm một mình thì phải bao nhiêu ngày mới hoàn thành công việc trên?
Câu 4:
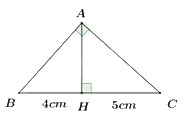
1) Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 4cm, HC = 5cm (như hình vẽ). Tính độ dài AB và AH.
2) Cho tam giác ABC có ba góc nhọn (AB < AC) nội tiếp đường tròn (O;R). Hai đường cao AE và BF cắt nhau tại H.
a) Chứng minh tứ giác CEHF nội tiếp đường tròn. Xác định tâm của đường tròn đó.
b) Kẻ đường kính AD của đường tròn (O). Chứng minh tứ giác BHCD là hình bình hành. Biết \(BC = R\sqrt 3 \), tính AH theo R.
c) Gọi N là giao điểm của hai đường thẳng CH và AB, K là giao điểm của hai đường thẳng BC và FN. Chứng minh BK.CE = BE.CK.
Câu 5: Giải phương trình \(\frac{1}{{3{x^2}}} + \frac{1}{{{x^2} - 12x + 2024}} = \frac{1}{{{x^2} - 3x + 506}}\).
-----HẾT-----
Câu 1 (TH):
Phương pháp:
1) Tính toán với căn bậc hai \(\sqrt {{x^2}} {\rm{ \;}} = \left| x \right|\)
2) Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị tương ứng giữa \(x\) và \(y\).
Bước 3: Vẽ đồ thị và kết luận.
Chú ý: vì đồ thị hàm số \(y = a{x^2}(a \ne 0)\) luôn đi qua gốc tọa độ \(O\) và nhận trục Oy làm trục đối xứng nên khi vẽ đồ thị của hàm số này, ta chỉ cần tìn một số điểm bên phải trục Oy rồi lấy các điểm đối xứng với chúng qua Oy.
3) Hai đường thẳng \(d:y = ax + b;d':y = a'x + b'(a;a' \ne 0)\) song song khi \(\left\{ {\begin{array}{*{20}{l}}{a = a'}\\{b \ne b'}\end{array}} \right.\)
Thay giá trị của điểm đi qua vào đường thẳng.
Cách giải:
1) Ta có: \(3\sqrt {49} {\rm{ \;}} - \sqrt {121} {\rm{ \;}} = 3.\sqrt {{7^2}} {\rm{ \;}} - \sqrt {{{11}^2}} {\rm{ \;}} = 3.7 - 11 = 21 - 11 = 10\)
2) Xét hàm số \(y = \frac{1}{2}{x^2}\).
Ta có bảng giá trị sau:
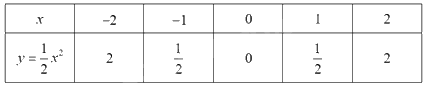
\( \Rightarrow \) Đồ thị hàm số là đường cong parabol đi qua các điểm
\(O{\mkern 1mu} \left( {0;0} \right);A\left( { - 2;2} \right);B\left( { - 1;\frac{1}{2}} \right);{\mkern 1mu} {\mkern 1mu} C\left( {1;\frac{1}{2}} \right);{\mkern 1mu} {\mkern 1mu} D\left( {2;2} \right)\)
Hệ số \(a = \frac{1}{2} > 0\)nên parabol có bề cong hướng lên.
Đồ thị hàm số nhận Oy làm trục đối xứng.
Ta vẽ được đồ thị hàm số \(y = \frac{1}{2}{x^2}\) như sau:
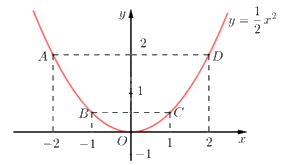
3) Vì \(\left( {d'} \right)\) song song với \((d)\) nên \(\left\{ {\begin{array}{*{20}{l}}{a = 2}\\{b \ne 1}\end{array}} \right.\) hay phương trình \(\left( {d'} \right)\) có dạng: \(y = 2x + b\) với \(b \ne 1\))
Vì \(\left( {d'} \right)\)đi qua điểm \(A(2;3)\) nên thay tọa độ điểm A vào phương trình đường thẳng \(\left( {d'} \right)\) ta được:
\(3 = 2.2 + b \Leftrightarrow 3 = 4 + b \Leftrightarrow b = {\rm{ \;}} - 1\) (thỏa mãn \(b \ne 1\))
Vậy \(a = 2\) và \(b = {\rm{ \;}} - 1.\)
Câu 2 (TH):
Phương pháp:
1)
a) Giải PT bằng cách đặt ẩn, đưa về PT bậc hai một ẩn.
Sử dụng phương pháp tính nhẩm \(a - b + c = 0\) thì PT có một nghiệm là \( - 1\); nghiệm còn lại là \(\frac{{ - c}}{a}\)
b) Giải hệ phương trình bằng phương pháp cộng đại số
2)
a) PT có hai nghiệm phân biệt khi \(\Delta ' > 0\)
Công thức \(\Delta ' = {\left( {\frac{b}{a}} \right)^2} - a.c\)
b) PT có hai nghiệm khi \(\Delta ' \ge 0\)
Hệ thức Vi-ét \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{{ - b}}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\)
Biến đổi biểu thức đề bài
Cách giải:
1) Giải phương trình và hệ phương trình sau:
a) \({x^4} - 3{x^2} - 4 = 0\) (1)
Đặt \(t = {x^2}\left( {t \ge 0} \right)\)
Khi đó \(\left( 1 \right) \Leftrightarrow {t^2} - 3t - 4 = 0\)
Do \(a - b + c = 1 - \left( { - 3} \right) - 4 = 0\) nên phương trình có 2 nghiệm phân biết \(\left[ {\begin{array}{*{20}{l}}{{t_1} = {\rm{ \;}} - 1\left( {KTM} \right)}\\{{t_2} = {\rm{ \;}} - \frac{{ - 4}}{1} = 4\left( {TM} \right)}\end{array}} \right.\)
Với \(t = 4 \Rightarrow {x^2} = 4 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 2}\\{x = {\rm{ \;}} - 2}\end{array}} \right.\) (thỏa mãn)
Vậy tập nghiệm của phương trình là \(S = \left\{ { - 2,2} \right\}\).
b) \(\left\{ {\begin{array}{*{20}{l}}{2x - y = 3}\\{3x + 2y = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4x - 2y = 6}\\{3x + 2y = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{7x = 7}\\{2x - y = 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1}\\{y = 2x - 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1}\\{y = 1}\end{array}} \right.\)
Vậy hệ phương trình có nghiệm \(\left( {x,y} \right) = \left( {1,1} \right)\).
2) Cho phương trình \({x^2} - 2(m - 1)x + {m^2} - 4 = 0\), với \(m\) là tham số.
a) Xét \(\Delta ' = {\left( {m - 1} \right)^2} - 1\left( {{m^2} - 4} \right) = {m^2} - 2m + 1 - {m^2} + 4 = 5 - 2m\)
Để phương trình có hai nghiệm phân biệt thì \(\Delta ' > 0 \Leftrightarrow 5 - 2m > 0 \Leftrightarrow m < \frac{5}{2}\)
Vậy \(m < \frac{5}{2}\) thì phương trình có hai nghiệm phân biệt
b) Để phương trình có 2 nghiệm \({x_1},{x_2}\) thì \(\Delta ' \ge 0 \Leftrightarrow 5 - 2m \ge 0 \Leftrightarrow m \le \frac{5}{2}\)
Khi đó áp dụng hệ thức Vi-et ta có \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 2\left( {m - 1} \right)}\\{{x_1}{x_2} = {m^2} - 4}\end{array}} \right.\)
Ta có \(P = x_1^2 + x_2^2 + {x_1}{x_2} + {m^2}\)
\(\begin{array}{*{20}{l}}{ = x_1^2 + 2{x_1}{x_2} + x_2^2 - {x_1}{x_2} + {m^2}}\\{ = {{\left( {{x_1} + {x_2}} \right)}^2} - {x_1}{x_2} + {m^2}}\\{ = {{\left( {2\left( {m - 1} \right)} \right)}^2} - \left( {{m^2} - 4} \right) + {m^2}}\\{ = 4{{\left( {m - 1} \right)}^2} - {m^2} + 4 + {m^2}}\\{ = 4{{\left( {m - 1} \right)}^2} + 4}\end{array}\)
Do \({\left( {m - 1} \right)^2} \ge 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \forall m \Rightarrow 4{\left( {m - 1} \right)^2} + 4 \ge 4 \Rightarrow P \ge 4\)
Dấu bằng xảy ra khi m = 1 (thỏa mãn \(m \le \frac{5}{2}\))
Vậy \({P_{\min }} = 4\) khi m = 1.
Câu 3 (TH):
Phương pháp:
Giải bài toán bằng cách lập hệ phương trình.
- Quy ước công việc cần hoàn thành là 1 đơn vị
- Tìm 1 trong 1 giờ (1 ngày, 1 phút, ...) mỗi người làm được bao nhiêu phần công việc
Cách giải:
Gọi thời gian đội I hoàn thành công việc một mình là x (\(x > 16\), ngày)
Gọi thời gian đội II hoàn thành công việc một mình là y (\(y > 16\), ngày)
Một ngày đội I làm một mình được \(\frac{1}{x}\) (công việc)
Một ngày đội II làm một mình được \(\frac{1}{y}\) (công việc)
Suy ra 1 ngày 2 đội làm được \(\frac{1}{x} + \frac{1}{y}\) (công việc)
Do 2 đội cùng thi công đoạn đường thì hoàn thành công việc trong 16 ngày nên ta có phương trình
\(\frac{1}{x} + \frac{1}{y} = \frac{1}{{16}}\) (1)
Ta có 2 đội làm cùng nhau trong 12 ngày được \(12\left( {\frac{1}{x} + \frac{1}{y}} \right) = \frac{{12}}{{16}} = \frac{3}{4}\) (công việc)
Đội II tăng năng suất lên 1,5 lần nên mỗi ngày đội 2 làm được \(\frac{{1,5}}{y} = \frac{3}{{2y}}\) (công việc)
Để hoàn thành công việc trong 16 ngày như dự định thì đội II phải hoàn thành nốt công việc trong 4 ngày
Khi đó ta có phương trình \(\frac{3}{4} + \frac{3}{{2y}}.4 = 1\) (2)
Từ (1) và (2) ta có hệ: \(\left\{ {\begin{array}{*{20}{l}}{\frac{1}{x} + \frac{1}{y} = \frac{1}{{16}}}\\{\frac{3}{4} + \frac{3}{{2y}}.4 = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\frac{6}{y} = \frac{1}{4}}\\{\frac{1}{x} = \frac{1}{{16}} - \frac{1}{y}}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = 24}\\{x = 1:\left( {\frac{1}{{16}} - \frac{1}{{24}}} \right)}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = 24}\\{x = 48}\end{array}} \right.(TM)\)
Vậy đội I hoàn thành công việc một mình trong 48 ngày, đội II hoàn thành công việc trong 24 ngày.
Câu 4 (VD):
Phương pháp:
1) Áp dụng hệ thức lượng trong tam giác vuông có đường cao.
2) a) Chứng minh tứ giác CEHF có tổng hai góc đối bằng \({180^\circ }\)
Gọi I là trung điểm của CH. Khi đó tứ giá CEHF nội tiếp đường tròn tâm I.
b) Chứng minh tứ giác BHCH có hai cặp cạnh đối song song với nhau.
Tính AH thông qua OM. Chứng minh OM là đường trung bình \(\Delta AHD\).
Áp dụng định lí Py-ta-go trong \(\Delta OBM\) vuông tại M tính OM.
c) Chứng minh NB là phân giác trong tại đỉnh N của tam giác NEK \( \Rightarrow \frac{{BE}}{{BK}} = \frac{{NE}}{{NK}}\)
Chứng minh NC là phân giác ngoài tại định N của tam giác NEK \( \Rightarrow \frac{{CE}}{{CK}} = \frac{{NE}}{{NK}}\)
Cách giải:
1)
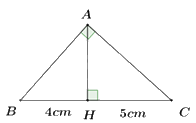
Ta có \(BC = BH + HC = 4 + 5 = 9{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)\).
Áp dụng hệ thức lượng trong tam giác ABC vuông tại A, đường cao AH ta có:
\(\begin{array}{*{20}{l}}{ + ){\mkern 1mu} {\mkern 1mu} A{B^2} = BH.BC}\\{ \Rightarrow A{B^2} = 4.9 = 36}\\{ \Rightarrow AB = \sqrt {36} {\rm{ \;}} = 6{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)}\\{ + ){\mkern 1mu} {\mkern 1mu} A{H^2} = BH.HC}\\{ \Rightarrow A{H^2} = 4.5 = 20}\\{ \Rightarrow AH = \sqrt {20} {\rm{ \;}} = 2\sqrt 5 {\mkern 1mu} {\mkern 1mu} \left( {cm} \right)}\end{array}\)
Vậy AB = 6 cm, AH = \(2\sqrt 5 \) cm.
2)
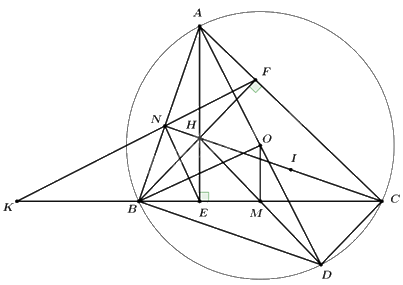
a) Ta có \(\left\{ {\begin{array}{*{20}{l}}{AE \bot BC \Rightarrow \angle HEC = {{90}^0}}\\{BF \bot AC \Rightarrow \angle HFC = {{90}^0}}\end{array}} \right.\)
Xét tứ giác CEHF có:
\(\angle HEC + \angle HFC = {90^0} + {90^0} = {180^0}\).
Mà E, F là hai đỉnh đối nhau của tứ giác CEHF.
Suy ra CEHF là tứ giác nội tiếp (dhnb).
Gọi I là trung điểm của CH.
Do tam giác HEC vuông tại E, có trung tuyến EI nên \(IE = \frac{1}{2}HC = IH = IC\).
Do tam giác HFC vuông tại F, có trung tuyến FI nên \(IF = \frac{1}{2}HC = IH = IC\).
\( \Rightarrow IE = IF = IH = IC\).
Vậy tứ giác CEHF nội tiếp đường tròn có tâm I là trung điểm của HC.
b) Ta có: \(\angle ABD = {90^0}\) (góc nội tiếp chắn nửa đường tròn (O)).
\( \Rightarrow BD \bot AB\).
Mà \(CH \bot AB\) (do H là trực tâm của tam giác ABC).
\( \Rightarrow \) BD // CH (từ vuông góc đến song song) (1)
Ta có: \(\angle ACD = {90^0}\) (góc nội tiếp chắn nửa đường tròn (O)).
\( \Rightarrow CD \bot AC\).
Mà \(BH \bot AC{\mkern 1mu} {\mkern 1mu} \left( {gt} \right)\)
\( \Rightarrow \) CD // BH (từ vuông góc đến song song) (2)
Từ (1), (2) => BHCD là hình bình hành (dhnb) (đpcm).
Gọi \(M = BC \cap HD \Rightarrow \) M là trung điểm của BC và HD (tính chất hình bình hành).
Ta có:
O là trung điểm của AD (gt)
M là trung điểm của HD (cmt)
=> OM là đường trung bình của tam giác AHD (định nghĩa).
\( \Rightarrow OM = \frac{1}{2}AH \Rightarrow AH = 2OM\) (tính chất đường trung bình của tam giác).
Vì M là trung điểm của BC (cmt) \( \Rightarrow OM \bot BC\) (quan hệ vuông góc giữa đường kính và dây cung)
\( \Rightarrow \Delta OBM\) vuông tại M, có OB = R, \(BM = \frac{1}{2}BC = \frac{{R\sqrt 3 }}{2}\).
Áp dụng định lí Pytago trong tam giác vuông OBM ta có:
\(\begin{array}{*{20}{l}}{O{M^2} + B{M^2} = O{B^2}}\\{ \Rightarrow O{M^2} = O{B^2} - B{M^2}}\\{ \Rightarrow O{M^2} = {R^2} - {{\left( {\frac{{R\sqrt 3 }}{2}} \right)}^2} = \frac{{{R^2}}}{4}}\\{ \Rightarrow OM = \frac{R}{2}}\end{array}\)
Vậy \(AH = 2OM = R.\)
c) Vì H là trực tâm của tam giác ABC nên \(CH \bot AB\) tại N hay \(CN \bot AB\).
Xét tứ giác ANHF có:
\(\begin{array}{*{20}{l}}{\angle ANH = {{90}^0}{\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} CN \bot AB} \right)}\\{\angle AFH = {{90}^0}{\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} BF \bot AC} \right)}\\{ \Rightarrow \angle ANH + \angle AFH = {{90}^0} + {{90}^0} = {{180}^0}}\end{array}\)
Mà hai đỉnh N, F là hai đỉnh đối diện của tứ giác ANHF.
=> ANHF là tứ giác nội tiếp (dhnb).
\( \Rightarrow \angle FNH = \angle FAH = \angle CAE\) (hai góc nội tiếp cùng chắn cung FH).
Chứng minh tương tự đối với tứ giác BEHN có:
\(\begin{array}{*{20}{l}}{\angle BNH = {{90}^0}{\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} CN \bot AB} \right)}\\{\angle BEH = {{90}^0}{\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} AE \bot BC} \right)}\\{ \Rightarrow \angle BNH + \angle BEH = {{90}^0} + {{90}^0} = {{180}^0}}\end{array}\)
Mà hai đỉnh N, E là hai đỉnh đối diện của tứ giác BEHN
=> BEHN là tứ giác nội tiếp (dhnb).
\( \Rightarrow \angle ENH = \angle EBH = \angle CBF\) (hai góc nội tiếp cùng chắn cung HE).
Mà \(\angle CEA = \angle CBF\) (cùng phụ với \(\angle ACB\)).
\( \Rightarrow \angle FNH = \angle ENH\).
\( \Rightarrow NH\) là phân giác của góc ENF.
Mà \(\angle ENK\) kề bù với \(\angle ENF\), \(NH \bot NB{\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} CN \bot AB} \right)\).
\( \Rightarrow NB\) là phân giác trong của \(\angle ENK\), NH là phân giác ngoài của \(\angle ENK\).
Áp dụng định lí đường phân giác ta có: \(\frac{{BE}}{{BK}} = \frac{{CE}}{{CK}} = \frac{{NE}}{{NK}}\).
Vậy BK.CE = BE.CK (đpcm).
Câu 5 (VDC):
Phương pháp:
Áp dụng bất đẳng thức Cô-si cho hai số \(a,b\) không âm ta (\(a + b \ge 2\sqrt {ab} \))
Để ta chứng minh \(\frac{1}{a} + \frac{1}{b} \ge \frac{4}{{a + b}}\)
Cách giải:
ĐKXĐ: \(x \ne 0\)
Ta chứng minh \(\frac{1}{a} + \frac{1}{b} \ge \frac{4}{{a + b}}\).
Thật vây, áp dụng bất đẳng thức Cô-si cho hai số a, b không âm ta được:
\(\begin{array}{*{20}{l}}{a + b \ge 2\sqrt {ab} }\\{\frac{1}{a} + \frac{1}{b} \ge 2\sqrt {\frac{1}{a}.\frac{1}{b}} }\end{array}\)
\(\begin{array}{*{20}{l}}{ \Rightarrow \left( {a + b} \right)\left( {\frac{1}{a} + \frac{1}{b}} \right) \ge 2\sqrt {ab} .2\sqrt {\frac{1}{a}.\frac{1}{b}} {\rm{ \;}} = 4}\\{ \Rightarrow \frac{1}{a} + \frac{1}{b} \ge \frac{4}{{a + b}}}\end{array}\)
Dấu “=” xảy ra khi và chỉ khi: \(a = b\)
Vì \(3{x^2} \ge 0\)với mọi \(x\) và \({x^2} - 12x + 2024 = {\left( {x - 6} \right)^2} + 1988 > 0\) với mọi \(x\) nên ta có:
\(\frac{1}{{3{x^2}}} + \frac{1}{{{x^2} - 12x + 2024}} \ge \frac{4}{{3{x^2} + {x^2} - 12x + 2024}} = \frac{4}{{4{x^2} - 12x + 2024}} = \frac{1}{{{x^2} - 3x + 506}}\)
Dấu “=” xảy ra khi và chỉ khi: \(3{x^2} = {x^2} - 12x + 2024\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow 2{x^2} + 12x - 2024 = 0}\\{ \Leftrightarrow {x^2} + 6x - 1012 = 0}\end{array}\)
Ta có: \(\Delta ' = {3^2} - 1.\left( { - 1012} \right) = 1021 > 0\)
Suy ra phương trình có hai nghiệm là: \({x_1} = {\rm{ \;}} - 3 + \sqrt {1021} \)và \({x_2} = {\rm{ \;}} - 3 - \sqrt {1021} \)
Vậy tập nghiệm phương trình đã cho là: \(S = \left\{ { - 3 + \sqrt {1021} ; - 3 - \sqrt {1021} } \right\}\).
Kỳ thi tuyển sinh vào lớp 10 môn Toán Quảng Ngãi năm 2023 là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Để đạt kết quả tốt nhất, việc nắm vững kiến thức, kỹ năng và làm quen với cấu trúc đề thi là vô cùng cần thiết. Bài viết này sẽ cung cấp thông tin chi tiết về kỳ thi, các dạng bài thường gặp, phương pháp giải và những lưu ý quan trọng để giúp các em chuẩn bị tốt nhất.
Đề thi vào 10 môn Toán Quảng Ngãi năm 2023 thường bao gồm các dạng bài sau:
Tỷ lệ phân bổ điểm giữa các phần thường khá cân bằng, tuy nhiên, có thể có sự thay đổi nhỏ tùy theo từng năm.
Dưới đây là một số dạng bài tập thường gặp trong đề thi vào 10 môn Toán Quảng Ngãi:
Để giải đề thi vào 10 môn Toán Quảng Ngãi năm 2023 hiệu quả, các em cần:
Dưới đây là một số lưu ý quan trọng dành cho các em học sinh:
Ngoài bộ đề thi mà giaitoan.edu.vn cung cấp, các em có thể tham khảo thêm các tài liệu ôn thi sau:
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi tuyển sinh vào lớp 10 môn Toán Quảng Ngãi năm 2023!