Giaitoan.edu.vn xin giới thiệu bộ đề thi vào 10 môn Toán Hải Phòng năm 2020 chính thức, được tổng hợp đầy đủ và cập nhật mới nhất. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin đạt kết quả cao trong kỳ thi tuyển sinh sắp tới.
Chúng tôi cung cấp không chỉ đề thi mà còn cả đáp án chi tiết, giúp các em tự đánh giá năng lực và tìm ra những điểm cần cải thiện.
Bài 1: Cho hai biểu thức:
Bài 1:
Cho hai biểu thức: \(A = 3\sqrt 7 - \sqrt {28} + \sqrt {175} - 3\) và \(B = \dfrac{{x - \sqrt x }}{{\sqrt x }} + \dfrac{{x + \sqrt x }}{{\sqrt x + 1}}\) với \(x > 0.\)
a) Rút gọn biểu thức \(A\) và biểu thức \(B.\)
b) Tìm các giá trị của \(x\) để giá trị của biểu thức \(A\) bằng ba lần giá trị của biểu thức \(B.\)
Bài 2:
a) Cho hàm số \(y = ax + b\) có đồ thị là đường thẳng \(\left( d \right)\). Xác định các giá trị của \(a\) và \(b\) biết \(\left( d \right)\) song song với đường thẳng \(y = - \dfrac{1}{2}x + 2020\) và \(\left( d \right)\) cắt trục hoành tại điểm có hoành độ bằng \( - 5\).
b) Giải hệ phương trình \(\left\{ \begin{array}{l}3\left( {x - 1} \right) + 2\left( {x - 2y} \right) = 10\\4\left( {x - 2} \right) - \left( {x - 2y} \right) = 2\end{array} \right.\).
Bài 3:
1. Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} - 1 = 0\,\,\,\,\,\left( 1 \right)\) (\(x\) là ẩn số, \(m\) là tham số).
a) Giải phương trình \(\left( 1 \right)\) với \(m = 7.\)
b) Xác định các giá trị của \(m\) để phương trình \(\left( 1 \right)\) có hai nghiệm \({x_1},\,\,{x_2}\) sao cho biểu thức \(M = x_1^2 + x_2^2 - {x_1}{x_2}\) đạt giá trị nhỏ nhất.
2. Bài toán có nội dung thực tế:
Một nhà máy theo kế hoạch phải sản xuất 2100 thùng nước sát khuẩn trong một thời gian quy định (số thùng nước sát khuẩn nhà máy phải sản xuất trong mỗi ngày là bằng nhau). Để đẩy nhanh tiến độ công việc trong giai đoạn tăng cường phòng chống đại dịch COVID-19, mỗi ngày nhà máy đã sản xuất nhiều hơn dự định 35 thùng nước sát khuẩn. Do đó, nhà máy đã hoàn thành công việc trước thời hạn 3 ngày. Hỏi theo kế hoạch, mỗi ngày nhà máy sản xuất bao nhiêu thùng nước sát khuẩn?
Bài 4:
1. Qua điểm \(A\) nằm ngoài đường tròn \(\left( O \right)\) vẽ hai tiếp tuyến \(AB\) và \(AC\) của đường tròn (\(B\) và \(C\) là các tiếp điểm). Gọi \(E\) là trung điểm của của đoạn thẳng \(AC\), \(F\) là giao điểm thứ hai của đường thẳng \(EB\) với đường tròn \(\left( O \right)\), \(K\) là giao điểm của đoạn thẳng \(AC\), \(F\) là giao điểm thứ hai của đường thẳng \(AF\) với đường tròn \(\left( O \right)\). Chứng minh:
a) Tứ giác \(ABOC\) là tứ giác nội tiếp và tam giác \(ABF\) đồng dạng với tam giác \(AKB\).
b) \(BF.CK = CF.BK\).
c) Tam giác \(FCE\) đồng dạng với tam giác \(CBE\) và \(EA\) là tiếp tuyến của đường tròn ngoại tiếp tam giác \(ABF\).
2. Một hình nón có bán kính đáy là \(5\,cm,\) diện tích xung quanh bằng \(65\pi \,\,c{m^2}.\) Tính chiều cao của hình nón đó.
Bài 5:
a) Cho \(x,y\) là hai số thực bất kì. Chứng minh \({x^2} - xy + {y^2} \ge \dfrac{1}{3}\left( {{x^2} + xy + {y^2}} \right)\)
b) Cho \(x,y,z\) là ba số thực dường thỏa mãn \(\sqrt x + \sqrt y + \sqrt z = 2\). Chứng minh
\(\dfrac{{x\sqrt x }}{{x + \sqrt {xy} + y}} + \dfrac{{y\sqrt y }}{{y + \sqrt {yz} + z}} + \dfrac{{z\sqrt z }}{{z + \sqrt {zx} + x}} \ge \dfrac{2}{3}\)
Bài 1 (1,5 điểm)
Cách giải:
Cho hai biểu thức: \(A = 3\sqrt 7 - \sqrt {28} + \sqrt {175} - 3\) và \(B = \dfrac{{x - \sqrt x }}{{\sqrt x }} + \dfrac{{x + \sqrt x }}{{\sqrt x + 1}}\) với \(x > 0.\)
a) Rút gọn biểu thức \(A\) và biểu thức \(B.\)
+) Rút gọn biểu thức \(A:\)
\(\begin{array}{l}A = 3\sqrt 7 - \sqrt {28} + \sqrt {175} - 3\\\,\,\,\,\, = 3\sqrt 7 - \sqrt {{2^2}.7} + \sqrt {{5^2}.7} - 3\\\,\,\,\,\, = 3\sqrt 7 - 2\sqrt 7 + 5\sqrt 7 - 3\\\,\,\,\,\, = 6\sqrt 7 - 3.\end{array}\)
+) Rút gọn biểu thức \(B:\)
Điều kiện: \(x > 0.\)
\(\begin{array}{l}B = \dfrac{{x - \sqrt x }}{{\sqrt x }} + \dfrac{{x + \sqrt x }}{{\sqrt x + 1}}\\\,\,\,\, = \dfrac{{\sqrt x \left( {\sqrt x - 1} \right)}}{{\sqrt x }} + \dfrac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\sqrt x + 1}}\\\,\,\,\, = \sqrt x - 1 + \sqrt x \\\,\,\,\, = 2\sqrt x - 1.\end{array}\)
Vậy với \(A = 6\sqrt 7 - 3\) và \(B = 2\sqrt x \) với \(x > 0.\)
b) Tìm các giá trị của \(x\) để giá trị của biểu thức \(A\) bằng ba lần giá trị của biểu thức \(B.\)
Điều kiện: \(x > 0.\)
Theo đề bài ta có:\(A = 3B\)
\(\begin{array}{l} \Leftrightarrow 6\sqrt 7 - 3 = 3.\left( {2\sqrt x - 1} \right)\\ \Leftrightarrow 6\sqrt 7 - 3 = 6\sqrt x - 3\\ \Leftrightarrow 6\sqrt x = 6\sqrt 7 \\ \Leftrightarrow \sqrt x = \sqrt 7 \\ \Leftrightarrow x = 7\,\,\,\left( {tm} \right)\end{array}\)
Vậy \(x = 7\) thì \(A = 3B.\)
Câu 2 (2,0 điểm)
Cách giải:
a) Cho hàm số \(y = ax + b\) có đồ thị là đường thẳng \(\left( d \right)\). Xác định các giá trị của \(a\) và \(b\) biết \(\left( d \right)\) song song với đường thẳng \(y = - \dfrac{1}{2}x + 2020\) và \(\left( d \right)\) cắt trục hoành tại điểm có hoành độ bằng \( - 5\).
Vì đường thẳng \(\left( d \right):\,\,y = ax + b\) song song với đường thẳng \(y = - \dfrac{1}{2}x + 2020\)nên: \(\left\{ \begin{array}{l}a = - \dfrac{1}{2}\\b \ne 2020\end{array} \right.\).
Khi đó phương trình đường thẳng \(\left( d \right)\) có dạng \(\left( d \right):\,\,y = - \dfrac{1}{2}x + b\), với \(b \ne 2020\).
Vì \(\left( d \right)\) cắt trục hoành tại điểm có hoành độ bằng \( - 5\) nên đường thẳng \(\left( d \right)\) đi qua điểm \(\left( { - 5;0} \right)\).
Thay tọa độ điểm \(\left( { - 5;0} \right)\) và phương trình đường thẳng \(\left( d \right)\) ta có:
\(0 = - \dfrac{1}{2}.\left( { - 5} \right) + b \Leftrightarrow 0 = \dfrac{5}{2} + b \Leftrightarrow b = - \dfrac{5}{2}\) (thỏa mãn).
Vậy \(a = - \dfrac{1}{2}\) và \(b = - \dfrac{5}{2}.\)
b) Giải hệ phương trình \(\left\{ \begin{array}{l}3\left( {x - 1} \right) + 2\left( {x - 2y} \right) = 10\\4\left( {x - 2} \right) - \left( {x - 2y} \right) = 2\end{array} \right.\).
Ta có:
\(\begin{array}{l}\,\,\,\,\,\left\{ \begin{array}{l}3\left( {x - 1} \right) + 2\left( {x - 2y} \right) = 10\\4\left( {x - 2} \right) - \left( {x - 2y} \right) = 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}3x - 3 + 2x - 4y = 10\\4x - 8 - x + 2y = 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}5x - 4y = 13\\3x + 2y = 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x - 4y = 13\\6x + 4y = 20\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}11x = 33\\3x + 2y = 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\3.3 + 2y = 10\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 3\\2y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = \dfrac{1}{2}\end{array} \right.\end{array}\)
Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( {3;\dfrac{1}{2}} \right)\).
Bài 3 (2,5 điểm)
Cách giải:
1. Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} - 1 = 0\,\,\,\,\,\left( 1 \right)\) (\(x\) là ẩn số, \(m\) là tham số).
a) Giải phương trình \(\left( 1 \right)\) với \(m = 7.\)
Với \(m = 7\) ta có phương trình:
\(\begin{array}{l}\,\,\,\,\,\,\,{x^2} - 2\left( {7 + 1} \right)x + {7^2} - 1 = 0\,\,\,\,\\ \Leftrightarrow {x^2} - 16x + 48 = 0\\ \Leftrightarrow {x^2} - 4x - 12x + 48 = 0\\ \Leftrightarrow x\left( {x - 4} \right) - 12\left( {x - 4} \right) = 0\\ \Leftrightarrow \left( {x - 12} \right)\left( {x - 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 12 = 0\\x - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 12\\x = 4\end{array} \right..\end{array}\)
Vậy với \(m = 7\) thì phương trình có tập nghiệm là \(S = \left\{ {4;\,\,12} \right\}.\)
b) Xác định các giá trị của \(m\) để phương trình \(\left( 1 \right)\) có hai nghiệm \({x_1},\,\,{x_2}\) sao cho biểu thức \(M = x_1^2 + x_2^2 - {x_1}{x_2}\) đạt giá trị nhỏ nhất.
Phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} - 1 = 0\,\,\,\,\,\left( 1 \right)\) có hai nghiệm \({x_1},\,\,{x_2}\)
\(\begin{array}{l} \Leftrightarrow \Delta ' \ge 0\\ \Leftrightarrow {\left( {m + 1} \right)^2} - {m^2} + 1 \ge 0\\ \Leftrightarrow {m^2} + 2m + 1 - {m^2} + 1 \ge 0\\ \Leftrightarrow 2m + 2 \ge 0\\ \Leftrightarrow m \ge - 1.\end{array}\)
Với \(m \ge - 1\) thì phương trình \(\left( 1 \right)\) có hai nghiệm \({x_1},\,\,{x_2}.\)
Áp dụng hệ thức Vi-et ta có:\(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m + 1} \right) = 2m + 2\\{x_1}{x_2} = {m^2} - 1\end{array} \right..\)
Theo đề bài ta có:
\(\begin{array}{l}M = x_1^2 + x_2^2 - {x_1}{x_2}\\\,\,\,\,\,\,\,\, = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} - {x_1}{x_2}\\\,\,\,\,\,\,\,\, = {\left( {{x_1} + {x_2}} \right)^2} - 3{x_1}{x_2}\\\,\,\,\,\,\,\,\, = {\left( {2m + 2} \right)^2} - 3\left( {{m^2} - 1} \right)\\\,\,\,\,\,\,\, = 4{m^2} + 8m + 4 - 3{m^2} + 3\\\,\,\,\,\,\,\, = {m^2} + 8m + 7\\\,\,\,\,\,\,\, = {m^2} + 8m + 16 - 9\\\,\,\,\,\,\,\, = {\left( {m + 4} \right)^2} - 9\end{array}\)
Với \(m \ge - 1\) \( \Rightarrow m + 4 \ge 3\) \( \Rightarrow {\left( {m + 4} \right)^2} \ge 9 \Rightarrow {\left( {m + 4} \right)^2} - 9 \ge 0\)
\( \Rightarrow Min\,\,M = 0\)
Dấu “=” xảy ra \( \Leftrightarrow m = - 1\,\,\,\left( {tm} \right).\)
Vậy \(m = - 1\) thỏa mãn điều kiện bài toán.
2. Bài toán có nội dung thực tế:
Một nhà máy theo kế hoạch phải sản xuất 2100 thùng nước sát khuẩn trong một thời gian quy định (số thùng nước sát khuẩn nhà máy phải sản xuất trong mỗi ngày là bằng nhau). Để đẩy nhanh tiến độ công việc trong giai đoạn tăng cường phòng chống đại dịch COVID-19, mỗi ngày nhà máy đã sản xuất nhiều hơn dự định 35 thùng nước sát khuẩn. Do đó, nhà máy đã hoàn thành công việc trước thời hạn 3 ngày. Hỏi theo kế hoạch, mỗi ngày nhà máy sản xuất bao nhiêu thùng nước sát khuẩn?
Gọi số thùng nước sát khuẩn mỗi ngày nhà máy sản xuất được theo kế hoạch là \(x\) (thùng), \(\left( {x < 2100,\,\,x \in {\mathbb{N}^*}} \right).\)
\( \Rightarrow \) Thời gian dự định nhà máy sản xuất xong 2100 thùng nước sát khuẩn là: \(\dfrac{{2100}}{x}\) (ngày).
Thực tế, mỗi ngày nhà máy sản xuất được số thùng nước sát khuẩn là: \(x + 35\) (thùng).
\( \Rightarrow \) Thời gian thực tế nhà máy sản xuất xong 2100 thùng nước sát khuẩn là: \(\dfrac{{2100}}{{x + 35}}\) (ngày).
Nhà máy đã hoàn thành xong công việc trước thời hạn 3 ngày nên ta có phương trình:
\(\begin{array}{l}\,\,\,\,\,\,\,\,\dfrac{{2100}}{x} - \dfrac{{2100}}{{x + 35}} = 3\\ \Leftrightarrow 2100\left( {x + 35} \right) - 2100x = 3x\left( {x + 35} \right)\\ \Leftrightarrow 2100x + 73500 - 2100x = 3{x^2} + 105x\\ \Leftrightarrow 3{x^2} + 105x - 73500 = 0\\ \Leftrightarrow {x^2} + 35x - 24500 = 0\\ \Leftrightarrow {x^2} + 175x - 140x - 24500 = 0\\ \Leftrightarrow x\left( {x + 175} \right) - 140\left( {x + 175} \right) = 0\\ \Leftrightarrow \left( {x + 175} \right)\left( {x - 140} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 175 = 0\\x - 140 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 175\,\,\,\left( {ktm} \right)\\x = 140\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy theo kế hoạch, mỗi ngày nhà máy sản xuất được 140 thùng nước sát khuẩn.
Bài 4 (3,5 điểm)
Cách giải:
1. Qua điểm \(A\) nằm ngoài đường tròn \(\left( O \right)\) vẽ hai tiếp tuyến \(AB\) và \(AC\) của đường tròn (\(B\) và \(C\) là các tiếp điểm). Gọi \(E\) là trung điểm của của đoạn thẳng \(AC\), \(F\) là giao điểm thứ hai của đường thẳng \(EB\) với đường tròn \(\left( O \right)\), \(K\) là giao điểm của đoạn thẳng \(AC\), \(F\) là giao điểm thứ hai của đường thẳng \(AF\) với đường tròn \(\left( O \right)\). Chứng minh:
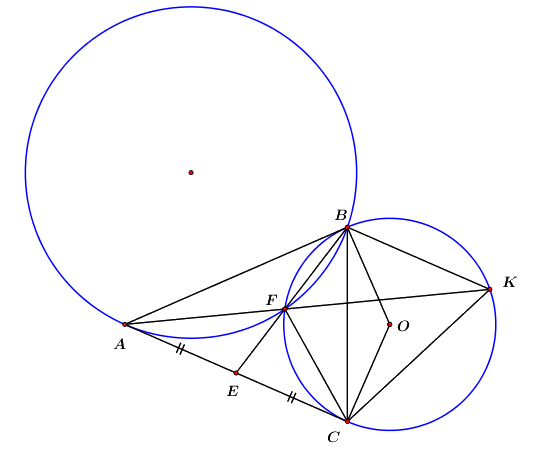
a) Tứ giác \(ABOC\) là tứ giác nội tiếp và tam giác \(ABF\) đồng dạng với tam giác \(AKB\).
Ta có: \(AB,\,\,AC\) là hai tiếp tuyến của \(\left( O \right)\) tại \(B,\,\,C\)
\( \Rightarrow \left\{ \begin{array}{l}OB \bot AB\\OB \bot AC\end{array} \right.\) \( \Rightarrow \angle ABO = \angle ACO = {90^0}\)
Xét tứ giác \(ABOC\) ta có:
\(\angle ABO + \angle ACO = {90^0} + {90^0} = {180^0}\)
Mà hai góc này là hai góc đối diện
\( \Rightarrow ABOC\) là tứ giác nội tiếp (dhnb). (đpcm)
Xét \(\Delta ABF\) và \(\Delta AKB\) ta có:
\(\angle A\) chung
\(\angle AKB = \angle ABF\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(BF\))
\( \Rightarrow \Delta ABF \sim \Delta AKB\,\,\,\left( {g - g} \right)\,\,\,\left( {dpcm} \right).\)
b) \(BF.CK = CF.BK\).
Ta có: \(\Delta ABF \sim \Delta AKB\,\,\,\left( {cmt} \right)\)
\( \Rightarrow \dfrac{{AB}}{{AK}} = \dfrac{{BF}}{{KB}} = \dfrac{{AF}}{{AB}}\) (các cặp cạnh tương ứng tỉ lệ).
Xét \(\Delta ACF\) và \(\Delta AKC\) ta có:
\(\angle A\) chung
\(\angle AKC = \angle ACF\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(CF\))
\( \Rightarrow \Delta ACF \sim \Delta AKC\,\,\,\left( {g - g} \right)\,\,\,\left( {dpcm} \right).\)
\( \Rightarrow \dfrac{{AC}}{{AK}} = \dfrac{{CF}}{{KC}} = \dfrac{{AF}}{{AC}}\) (các cặp cạnh tương ứng tỉ lệ).
Mà \(AB = AC\) (tính chất hai tiếp tuyến cắt nhau)
\(\begin{array}{l} \Rightarrow \dfrac{{AB}}{{AK}} = \dfrac{{AC}}{{AK}} = \dfrac{{BF}}{{KB}} = \dfrac{{CF}}{{KC}}\\ \Rightarrow BF.KC = KB.CF\,\,\,\,\left( {dpcm} \right).\end{array}\)
c) Tam giác \(FCE\) đồng dạng với tam giác \(CBE\) và \(EA\) là tiếp tuyến của đường tròn ngoại tiếp tam giác \(ABF\).
Ta có: \(\angle BKC = \angle BCE\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(BC\))
Lại có: \(BFCK\) là tứ giác nội tiếp đường tròn \(\left( O \right)\)
\( \Rightarrow \angle EFC = \angle BKC\) (góc ngoài tại 1 đỉnh bằng góc trong tại đỉnh đối diện)
\( \Rightarrow EFC = \angle BCE\,\,\left( { = \angle BKC} \right)\)
Xét \(\Delta FCE\) và \(\Delta CBE\) ta có:
\(\begin{array}{l}\angle E\,\,\,chung\\\angle EFC = \angle ECB\,\,\,\left( {cmt} \right)\\ \Rightarrow \Delta FCE \sim \Delta CBE\,\,\,\left( {g - g} \right)\,\,\,\left( {dpcm} \right).\end{array}\)
Vì \(\Delta FCE = \angle CBE\,\,\,\left( {cmt} \right)\)
\(\begin{array}{l} \Rightarrow \dfrac{{FE}}{{CE}} = \dfrac{{CE}}{{BE}} \Rightarrow C{E^2} = FE.BE = A{E^2}\\ \Rightarrow \dfrac{{EA}}{{EB}} = \dfrac{{EF}}{{EA}}\end{array}\)
Xét \(\Delta AEF\) và \(\Delta BEA\) ta có:
\(\begin{array}{l}\angle AEB\,\,\,chung\\\dfrac{{EA}}{{EB}} = \dfrac{{EF}}{{EA}}\,\,\left( {cmt} \right)\\ \Rightarrow \Delta AEF \sim \Delta BEA\,\,\,\left( {c - g - c} \right)\end{array}\)
\( \Rightarrow \angle FAE = \angle ABE\) (hai góc tương ứng)
Mà \(\angle ABE\) là góc nội tiếp chắn cung \(BF\) của đường tròn ngoại tiếp \(\Delta ABF\)
\(\angle FAE\) được tạo bởi dây cung \(AF\) và \(AE\)(\(E\) nằm ngoài đường tròn)
\( \Rightarrow AE\) là tiếp tuyến của đường tròn ngoại tiếp \(\Delta ABF.\) (đpcm)
2. Một hình nón có bán kính đáy là \(5\,cm,\) diện tích xung quanh bằng \(65\pi \,\,c{m^2}.\) Tính chiều cao của hình nón đó.
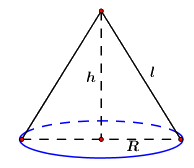
Ta có: \({S_{xq}} = \pi Rl\) \( \Leftrightarrow 5\pi l = 65\pi \)\( \Leftrightarrow l = \dfrac{{65\pi }}{{5\pi }} = 13\,\,cm.\)
Áp dụng định lý Pitago ta có chiều cao của hình nón là: \(h = \sqrt {{l^2} - {R^2}} = \sqrt {{{13}^2} - {5^2}} = 12\,\,cm.\)
Bài 5 (1,0 điểm)
Cách giải:
a) Cho \(x,y\) là hai số thực bất kì. Chứng minh \({x^2} - xy + {y^2} \ge \dfrac{1}{3}\left( {{x^2} + xy + {y^2}} \right)\)
Ta có:
\(\begin{array}{l}{x^2} - xy + {y^2} \ge \dfrac{1}{3}\left( {{x^2} + xy + {y^2}} \right)\\ \Leftrightarrow 3{x^2} - 3xy + 3{y^2} \ge {x^2} + xy + {y^2}\\ \Leftrightarrow 2{x^2} - 4xy + 2{y^2} \ge 0\\ \Leftrightarrow {x^2} - 2xy + {y^2} \ge 0\end{array}\)
\( \Leftrightarrow {\left( {x - y} \right)^2} \ge 0\) (luôn đúng)
Dấu “=” xảy ra khi \(x = y\).
Vậy ta có đpcm.
b) Cho \(x,y,z\) là ba số thực dường thỏa mãn \(\sqrt x + \sqrt y + \sqrt z = 2\). Chứng minh
\(\dfrac{{x\sqrt x }}{{x + \sqrt {xy} + y}} + \dfrac{{y\sqrt y }}{{y + \sqrt {yz} + z}} + \dfrac{{z\sqrt z }}{{z + \sqrt {zx} + x}} \ge \dfrac{2}{3}\)
Đặt \(\left\{ \begin{array}{l}a = \sqrt x > 0\\b = \sqrt y > 0\\c = \sqrt z > 0\end{array} \right. \Rightarrow a + b + c = 2\) ta được:
\(\begin{array}{l}VT = \dfrac{{{a^3}}}{{{a^2} + ab + {b^2}}} + \dfrac{{{b^3}}}{{{b^2} + bc + {c^2}}} + \dfrac{{{c^3}}}{{{c^2} + ca + {a^2}}}\\ = \dfrac{{{a^4}}}{{{a^3} + {a^2}b + a{b^2}}} + \dfrac{{{b^4}}}{{{b^3} + {b^2}c + b{c^2}}} + \dfrac{{{c^4}}}{{{c^3} + {c^2}a + c{a^2}}}\end{array}\)
Áp dụng BĐT \(\dfrac{{{a^2}}}{x} + \dfrac{{{b^2}}}{y} \ge \dfrac{{{{\left( {a + b} \right)}^2}}}{{x + y}}\) ta có:
\(\begin{array}{l}\dfrac{{{a^4}}}{{{a^3} + {a^2}b + a{b^2}}} + \dfrac{{{b^4}}}{{{b^3} + {b^2}c + b{c^2}}} \ge \dfrac{{{{\left( {{a^2} + {b^2}} \right)}^2}}}{{\left( {{a^3} + {a^2}b + a{b^2}} \right) + \left( {{b^3} + {b^2}c + b{c^2}} \right)}}\\ \Rightarrow \dfrac{{{a^4}}}{{{a^3} + {a^2}b + a{b^2}}} + \dfrac{{{b^4}}}{{{b^3} + {b^2}c + b{c^2}}} + \dfrac{{{c^4}}}{{{c^3} + {c^2}a + c{a^2}}}\\ \ge \dfrac{{{{\left( {{a^2} + {b^2}} \right)}^2}}}{{\left( {{a^3} + {a^2}b + a{b^2}} \right) + \left( {{b^3} + {b^2}c + b{c^2}} \right)}} + \dfrac{{{c^4}}}{{{c^3} + {c^2}a + c{a^2}}}\\ \ge \dfrac{{{{\left( {{a^2} + {b^2} + {c^2}} \right)}^2}}}{{\left( {{a^3} + {a^2}b + a{b^2}} \right) + \left( {{b^3} + {b^2}c + b{c^2}} \right) + \left( {{c^3} + {c^2}a + c{a^2}} \right)}}\\ = \dfrac{{{{\left( {{a^2} + {b^2} + {c^2}} \right)}^2}}}{{{a^3} + {a^2}b + {a^2}c + {b^3} + {b^2}a + {b^2}c + {c^3} + {c^2}a + {c^2}b}}\\ = \dfrac{{{{\left( {{a^2} + {b^2} + {c^2}} \right)}^2}}}{{{a^2}\left( {a + b + c} \right) + {b^2}\left( {a + b + c} \right) + {c^2}\left( {a + b + c} \right)}}\\ = \dfrac{{{{\left( {{a^2} + {b^2} + {c^2}} \right)}^2}}}{{\left( {{a^2} + {b^2} + {c^2}} \right)\left( {a + b + c} \right)}}\\ = \dfrac{{{a^2} + {b^2} + {c^2}}}{{a + b + c}}\\ = \dfrac{1}{2}\left( {\dfrac{{{a^2}}}{1} + \dfrac{{{b^2}}}{1} + \dfrac{{{c^2}}}{1}} \right)\\ \ge \dfrac{1}{2}.\dfrac{{{{\left( {a + b + c} \right)}^2}}}{{1 + 1 + 1}} = \dfrac{1}{2}.\dfrac{{{2^2}}}{3} = \dfrac{2}{3}\end{array}\)
\( \Rightarrow \dfrac{{{a^3}}}{{{a^2} + ab + {b^2}}} + \dfrac{{{b^3}}}{{{b^2} + bc + {c^2}}} + \dfrac{{{c^3}}}{{{c^2} + ca + {a^2}}} \ge \dfrac{2}{3}\) (đpcm)
Dấu “=” xảy ra khi \(a = b = c = \dfrac{2}{3}\).
Bài 1:
Cho hai biểu thức: \(A = 3\sqrt 7 - \sqrt {28} + \sqrt {175} - 3\) và \(B = \dfrac{{x - \sqrt x }}{{\sqrt x }} + \dfrac{{x + \sqrt x }}{{\sqrt x + 1}}\) với \(x > 0.\)
a) Rút gọn biểu thức \(A\) và biểu thức \(B.\)
b) Tìm các giá trị của \(x\) để giá trị của biểu thức \(A\) bằng ba lần giá trị của biểu thức \(B.\)
Bài 2:
a) Cho hàm số \(y = ax + b\) có đồ thị là đường thẳng \(\left( d \right)\). Xác định các giá trị của \(a\) và \(b\) biết \(\left( d \right)\) song song với đường thẳng \(y = - \dfrac{1}{2}x + 2020\) và \(\left( d \right)\) cắt trục hoành tại điểm có hoành độ bằng \( - 5\).
b) Giải hệ phương trình \(\left\{ \begin{array}{l}3\left( {x - 1} \right) + 2\left( {x - 2y} \right) = 10\\4\left( {x - 2} \right) - \left( {x - 2y} \right) = 2\end{array} \right.\).
Bài 3:
1. Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} - 1 = 0\,\,\,\,\,\left( 1 \right)\) (\(x\) là ẩn số, \(m\) là tham số).
a) Giải phương trình \(\left( 1 \right)\) với \(m = 7.\)
b) Xác định các giá trị của \(m\) để phương trình \(\left( 1 \right)\) có hai nghiệm \({x_1},\,\,{x_2}\) sao cho biểu thức \(M = x_1^2 + x_2^2 - {x_1}{x_2}\) đạt giá trị nhỏ nhất.
2. Bài toán có nội dung thực tế:
Một nhà máy theo kế hoạch phải sản xuất 2100 thùng nước sát khuẩn trong một thời gian quy định (số thùng nước sát khuẩn nhà máy phải sản xuất trong mỗi ngày là bằng nhau). Để đẩy nhanh tiến độ công việc trong giai đoạn tăng cường phòng chống đại dịch COVID-19, mỗi ngày nhà máy đã sản xuất nhiều hơn dự định 35 thùng nước sát khuẩn. Do đó, nhà máy đã hoàn thành công việc trước thời hạn 3 ngày. Hỏi theo kế hoạch, mỗi ngày nhà máy sản xuất bao nhiêu thùng nước sát khuẩn?
Bài 4:
1. Qua điểm \(A\) nằm ngoài đường tròn \(\left( O \right)\) vẽ hai tiếp tuyến \(AB\) và \(AC\) của đường tròn (\(B\) và \(C\) là các tiếp điểm). Gọi \(E\) là trung điểm của của đoạn thẳng \(AC\), \(F\) là giao điểm thứ hai của đường thẳng \(EB\) với đường tròn \(\left( O \right)\), \(K\) là giao điểm của đoạn thẳng \(AC\), \(F\) là giao điểm thứ hai của đường thẳng \(AF\) với đường tròn \(\left( O \right)\). Chứng minh:
a) Tứ giác \(ABOC\) là tứ giác nội tiếp và tam giác \(ABF\) đồng dạng với tam giác \(AKB\).
b) \(BF.CK = CF.BK\).
c) Tam giác \(FCE\) đồng dạng với tam giác \(CBE\) và \(EA\) là tiếp tuyến của đường tròn ngoại tiếp tam giác \(ABF\).
2. Một hình nón có bán kính đáy là \(5\,cm,\) diện tích xung quanh bằng \(65\pi \,\,c{m^2}.\) Tính chiều cao của hình nón đó.
Bài 5:
a) Cho \(x,y\) là hai số thực bất kì. Chứng minh \({x^2} - xy + {y^2} \ge \dfrac{1}{3}\left( {{x^2} + xy + {y^2}} \right)\)
b) Cho \(x,y,z\) là ba số thực dường thỏa mãn \(\sqrt x + \sqrt y + \sqrt z = 2\). Chứng minh
\(\dfrac{{x\sqrt x }}{{x + \sqrt {xy} + y}} + \dfrac{{y\sqrt y }}{{y + \sqrt {yz} + z}} + \dfrac{{z\sqrt z }}{{z + \sqrt {zx} + x}} \ge \dfrac{2}{3}\)
Bài 1 (1,5 điểm)
Cách giải:
Cho hai biểu thức: \(A = 3\sqrt 7 - \sqrt {28} + \sqrt {175} - 3\) và \(B = \dfrac{{x - \sqrt x }}{{\sqrt x }} + \dfrac{{x + \sqrt x }}{{\sqrt x + 1}}\) với \(x > 0.\)
a) Rút gọn biểu thức \(A\) và biểu thức \(B.\)
+) Rút gọn biểu thức \(A:\)
\(\begin{array}{l}A = 3\sqrt 7 - \sqrt {28} + \sqrt {175} - 3\\\,\,\,\,\, = 3\sqrt 7 - \sqrt {{2^2}.7} + \sqrt {{5^2}.7} - 3\\\,\,\,\,\, = 3\sqrt 7 - 2\sqrt 7 + 5\sqrt 7 - 3\\\,\,\,\,\, = 6\sqrt 7 - 3.\end{array}\)
+) Rút gọn biểu thức \(B:\)
Điều kiện: \(x > 0.\)
\(\begin{array}{l}B = \dfrac{{x - \sqrt x }}{{\sqrt x }} + \dfrac{{x + \sqrt x }}{{\sqrt x + 1}}\\\,\,\,\, = \dfrac{{\sqrt x \left( {\sqrt x - 1} \right)}}{{\sqrt x }} + \dfrac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\sqrt x + 1}}\\\,\,\,\, = \sqrt x - 1 + \sqrt x \\\,\,\,\, = 2\sqrt x - 1.\end{array}\)
Vậy với \(A = 6\sqrt 7 - 3\) và \(B = 2\sqrt x \) với \(x > 0.\)
b) Tìm các giá trị của \(x\) để giá trị của biểu thức \(A\) bằng ba lần giá trị của biểu thức \(B.\)
Điều kiện: \(x > 0.\)
Theo đề bài ta có:\(A = 3B\)
\(\begin{array}{l} \Leftrightarrow 6\sqrt 7 - 3 = 3.\left( {2\sqrt x - 1} \right)\\ \Leftrightarrow 6\sqrt 7 - 3 = 6\sqrt x - 3\\ \Leftrightarrow 6\sqrt x = 6\sqrt 7 \\ \Leftrightarrow \sqrt x = \sqrt 7 \\ \Leftrightarrow x = 7\,\,\,\left( {tm} \right)\end{array}\)
Vậy \(x = 7\) thì \(A = 3B.\)
Câu 2 (2,0 điểm)
Cách giải:
a) Cho hàm số \(y = ax + b\) có đồ thị là đường thẳng \(\left( d \right)\). Xác định các giá trị của \(a\) và \(b\) biết \(\left( d \right)\) song song với đường thẳng \(y = - \dfrac{1}{2}x + 2020\) và \(\left( d \right)\) cắt trục hoành tại điểm có hoành độ bằng \( - 5\).
Vì đường thẳng \(\left( d \right):\,\,y = ax + b\) song song với đường thẳng \(y = - \dfrac{1}{2}x + 2020\)nên: \(\left\{ \begin{array}{l}a = - \dfrac{1}{2}\\b \ne 2020\end{array} \right.\).
Khi đó phương trình đường thẳng \(\left( d \right)\) có dạng \(\left( d \right):\,\,y = - \dfrac{1}{2}x + b\), với \(b \ne 2020\).
Vì \(\left( d \right)\) cắt trục hoành tại điểm có hoành độ bằng \( - 5\) nên đường thẳng \(\left( d \right)\) đi qua điểm \(\left( { - 5;0} \right)\).
Thay tọa độ điểm \(\left( { - 5;0} \right)\) và phương trình đường thẳng \(\left( d \right)\) ta có:
\(0 = - \dfrac{1}{2}.\left( { - 5} \right) + b \Leftrightarrow 0 = \dfrac{5}{2} + b \Leftrightarrow b = - \dfrac{5}{2}\) (thỏa mãn).
Vậy \(a = - \dfrac{1}{2}\) và \(b = - \dfrac{5}{2}.\)
b) Giải hệ phương trình \(\left\{ \begin{array}{l}3\left( {x - 1} \right) + 2\left( {x - 2y} \right) = 10\\4\left( {x - 2} \right) - \left( {x - 2y} \right) = 2\end{array} \right.\).
Ta có:
\(\begin{array}{l}\,\,\,\,\,\left\{ \begin{array}{l}3\left( {x - 1} \right) + 2\left( {x - 2y} \right) = 10\\4\left( {x - 2} \right) - \left( {x - 2y} \right) = 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}3x - 3 + 2x - 4y = 10\\4x - 8 - x + 2y = 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}5x - 4y = 13\\3x + 2y = 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x - 4y = 13\\6x + 4y = 20\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}11x = 33\\3x + 2y = 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\3.3 + 2y = 10\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 3\\2y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = \dfrac{1}{2}\end{array} \right.\end{array}\)
Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( {3;\dfrac{1}{2}} \right)\).
Bài 3 (2,5 điểm)
Cách giải:
1. Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} - 1 = 0\,\,\,\,\,\left( 1 \right)\) (\(x\) là ẩn số, \(m\) là tham số).
a) Giải phương trình \(\left( 1 \right)\) với \(m = 7.\)
Với \(m = 7\) ta có phương trình:
\(\begin{array}{l}\,\,\,\,\,\,\,{x^2} - 2\left( {7 + 1} \right)x + {7^2} - 1 = 0\,\,\,\,\\ \Leftrightarrow {x^2} - 16x + 48 = 0\\ \Leftrightarrow {x^2} - 4x - 12x + 48 = 0\\ \Leftrightarrow x\left( {x - 4} \right) - 12\left( {x - 4} \right) = 0\\ \Leftrightarrow \left( {x - 12} \right)\left( {x - 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 12 = 0\\x - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 12\\x = 4\end{array} \right..\end{array}\)
Vậy với \(m = 7\) thì phương trình có tập nghiệm là \(S = \left\{ {4;\,\,12} \right\}.\)
b) Xác định các giá trị của \(m\) để phương trình \(\left( 1 \right)\) có hai nghiệm \({x_1},\,\,{x_2}\) sao cho biểu thức \(M = x_1^2 + x_2^2 - {x_1}{x_2}\) đạt giá trị nhỏ nhất.
Phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} - 1 = 0\,\,\,\,\,\left( 1 \right)\) có hai nghiệm \({x_1},\,\,{x_2}\)
\(\begin{array}{l} \Leftrightarrow \Delta ' \ge 0\\ \Leftrightarrow {\left( {m + 1} \right)^2} - {m^2} + 1 \ge 0\\ \Leftrightarrow {m^2} + 2m + 1 - {m^2} + 1 \ge 0\\ \Leftrightarrow 2m + 2 \ge 0\\ \Leftrightarrow m \ge - 1.\end{array}\)
Với \(m \ge - 1\) thì phương trình \(\left( 1 \right)\) có hai nghiệm \({x_1},\,\,{x_2}.\)
Áp dụng hệ thức Vi-et ta có:\(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m + 1} \right) = 2m + 2\\{x_1}{x_2} = {m^2} - 1\end{array} \right..\)
Theo đề bài ta có:
\(\begin{array}{l}M = x_1^2 + x_2^2 - {x_1}{x_2}\\\,\,\,\,\,\,\,\, = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} - {x_1}{x_2}\\\,\,\,\,\,\,\,\, = {\left( {{x_1} + {x_2}} \right)^2} - 3{x_1}{x_2}\\\,\,\,\,\,\,\,\, = {\left( {2m + 2} \right)^2} - 3\left( {{m^2} - 1} \right)\\\,\,\,\,\,\,\, = 4{m^2} + 8m + 4 - 3{m^2} + 3\\\,\,\,\,\,\,\, = {m^2} + 8m + 7\\\,\,\,\,\,\,\, = {m^2} + 8m + 16 - 9\\\,\,\,\,\,\,\, = {\left( {m + 4} \right)^2} - 9\end{array}\)
Với \(m \ge - 1\) \( \Rightarrow m + 4 \ge 3\) \( \Rightarrow {\left( {m + 4} \right)^2} \ge 9 \Rightarrow {\left( {m + 4} \right)^2} - 9 \ge 0\)
\( \Rightarrow Min\,\,M = 0\)
Dấu “=” xảy ra \( \Leftrightarrow m = - 1\,\,\,\left( {tm} \right).\)
Vậy \(m = - 1\) thỏa mãn điều kiện bài toán.
2. Bài toán có nội dung thực tế:
Một nhà máy theo kế hoạch phải sản xuất 2100 thùng nước sát khuẩn trong một thời gian quy định (số thùng nước sát khuẩn nhà máy phải sản xuất trong mỗi ngày là bằng nhau). Để đẩy nhanh tiến độ công việc trong giai đoạn tăng cường phòng chống đại dịch COVID-19, mỗi ngày nhà máy đã sản xuất nhiều hơn dự định 35 thùng nước sát khuẩn. Do đó, nhà máy đã hoàn thành công việc trước thời hạn 3 ngày. Hỏi theo kế hoạch, mỗi ngày nhà máy sản xuất bao nhiêu thùng nước sát khuẩn?
Gọi số thùng nước sát khuẩn mỗi ngày nhà máy sản xuất được theo kế hoạch là \(x\) (thùng), \(\left( {x < 2100,\,\,x \in {\mathbb{N}^*}} \right).\)
\( \Rightarrow \) Thời gian dự định nhà máy sản xuất xong 2100 thùng nước sát khuẩn là: \(\dfrac{{2100}}{x}\) (ngày).
Thực tế, mỗi ngày nhà máy sản xuất được số thùng nước sát khuẩn là: \(x + 35\) (thùng).
\( \Rightarrow \) Thời gian thực tế nhà máy sản xuất xong 2100 thùng nước sát khuẩn là: \(\dfrac{{2100}}{{x + 35}}\) (ngày).
Nhà máy đã hoàn thành xong công việc trước thời hạn 3 ngày nên ta có phương trình:
\(\begin{array}{l}\,\,\,\,\,\,\,\,\dfrac{{2100}}{x} - \dfrac{{2100}}{{x + 35}} = 3\\ \Leftrightarrow 2100\left( {x + 35} \right) - 2100x = 3x\left( {x + 35} \right)\\ \Leftrightarrow 2100x + 73500 - 2100x = 3{x^2} + 105x\\ \Leftrightarrow 3{x^2} + 105x - 73500 = 0\\ \Leftrightarrow {x^2} + 35x - 24500 = 0\\ \Leftrightarrow {x^2} + 175x - 140x - 24500 = 0\\ \Leftrightarrow x\left( {x + 175} \right) - 140\left( {x + 175} \right) = 0\\ \Leftrightarrow \left( {x + 175} \right)\left( {x - 140} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 175 = 0\\x - 140 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 175\,\,\,\left( {ktm} \right)\\x = 140\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy theo kế hoạch, mỗi ngày nhà máy sản xuất được 140 thùng nước sát khuẩn.
Bài 4 (3,5 điểm)
Cách giải:
1. Qua điểm \(A\) nằm ngoài đường tròn \(\left( O \right)\) vẽ hai tiếp tuyến \(AB\) và \(AC\) của đường tròn (\(B\) và \(C\) là các tiếp điểm). Gọi \(E\) là trung điểm của của đoạn thẳng \(AC\), \(F\) là giao điểm thứ hai của đường thẳng \(EB\) với đường tròn \(\left( O \right)\), \(K\) là giao điểm của đoạn thẳng \(AC\), \(F\) là giao điểm thứ hai của đường thẳng \(AF\) với đường tròn \(\left( O \right)\). Chứng minh:
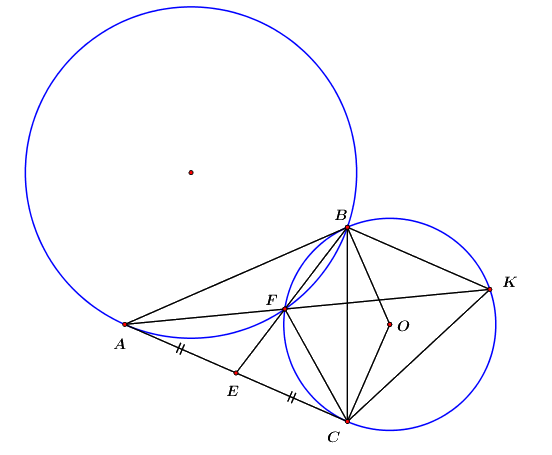
a) Tứ giác \(ABOC\) là tứ giác nội tiếp và tam giác \(ABF\) đồng dạng với tam giác \(AKB\).
Ta có: \(AB,\,\,AC\) là hai tiếp tuyến của \(\left( O \right)\) tại \(B,\,\,C\)
\( \Rightarrow \left\{ \begin{array}{l}OB \bot AB\\OB \bot AC\end{array} \right.\) \( \Rightarrow \angle ABO = \angle ACO = {90^0}\)
Xét tứ giác \(ABOC\) ta có:
\(\angle ABO + \angle ACO = {90^0} + {90^0} = {180^0}\)
Mà hai góc này là hai góc đối diện
\( \Rightarrow ABOC\) là tứ giác nội tiếp (dhnb). (đpcm)
Xét \(\Delta ABF\) và \(\Delta AKB\) ta có:
\(\angle A\) chung
\(\angle AKB = \angle ABF\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(BF\))
\( \Rightarrow \Delta ABF \sim \Delta AKB\,\,\,\left( {g - g} \right)\,\,\,\left( {dpcm} \right).\)
b) \(BF.CK = CF.BK\).
Ta có: \(\Delta ABF \sim \Delta AKB\,\,\,\left( {cmt} \right)\)
\( \Rightarrow \dfrac{{AB}}{{AK}} = \dfrac{{BF}}{{KB}} = \dfrac{{AF}}{{AB}}\) (các cặp cạnh tương ứng tỉ lệ).
Xét \(\Delta ACF\) và \(\Delta AKC\) ta có:
\(\angle A\) chung
\(\angle AKC = \angle ACF\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(CF\))
\( \Rightarrow \Delta ACF \sim \Delta AKC\,\,\,\left( {g - g} \right)\,\,\,\left( {dpcm} \right).\)
\( \Rightarrow \dfrac{{AC}}{{AK}} = \dfrac{{CF}}{{KC}} = \dfrac{{AF}}{{AC}}\) (các cặp cạnh tương ứng tỉ lệ).
Mà \(AB = AC\) (tính chất hai tiếp tuyến cắt nhau)
\(\begin{array}{l} \Rightarrow \dfrac{{AB}}{{AK}} = \dfrac{{AC}}{{AK}} = \dfrac{{BF}}{{KB}} = \dfrac{{CF}}{{KC}}\\ \Rightarrow BF.KC = KB.CF\,\,\,\,\left( {dpcm} \right).\end{array}\)
c) Tam giác \(FCE\) đồng dạng với tam giác \(CBE\) và \(EA\) là tiếp tuyến của đường tròn ngoại tiếp tam giác \(ABF\).
Ta có: \(\angle BKC = \angle BCE\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(BC\))
Lại có: \(BFCK\) là tứ giác nội tiếp đường tròn \(\left( O \right)\)
\( \Rightarrow \angle EFC = \angle BKC\) (góc ngoài tại 1 đỉnh bằng góc trong tại đỉnh đối diện)
\( \Rightarrow EFC = \angle BCE\,\,\left( { = \angle BKC} \right)\)
Xét \(\Delta FCE\) và \(\Delta CBE\) ta có:
\(\begin{array}{l}\angle E\,\,\,chung\\\angle EFC = \angle ECB\,\,\,\left( {cmt} \right)\\ \Rightarrow \Delta FCE \sim \Delta CBE\,\,\,\left( {g - g} \right)\,\,\,\left( {dpcm} \right).\end{array}\)
Vì \(\Delta FCE = \angle CBE\,\,\,\left( {cmt} \right)\)
\(\begin{array}{l} \Rightarrow \dfrac{{FE}}{{CE}} = \dfrac{{CE}}{{BE}} \Rightarrow C{E^2} = FE.BE = A{E^2}\\ \Rightarrow \dfrac{{EA}}{{EB}} = \dfrac{{EF}}{{EA}}\end{array}\)
Xét \(\Delta AEF\) và \(\Delta BEA\) ta có:
\(\begin{array}{l}\angle AEB\,\,\,chung\\\dfrac{{EA}}{{EB}} = \dfrac{{EF}}{{EA}}\,\,\left( {cmt} \right)\\ \Rightarrow \Delta AEF \sim \Delta BEA\,\,\,\left( {c - g - c} \right)\end{array}\)
\( \Rightarrow \angle FAE = \angle ABE\) (hai góc tương ứng)
Mà \(\angle ABE\) là góc nội tiếp chắn cung \(BF\) của đường tròn ngoại tiếp \(\Delta ABF\)
\(\angle FAE\) được tạo bởi dây cung \(AF\) và \(AE\)(\(E\) nằm ngoài đường tròn)
\( \Rightarrow AE\) là tiếp tuyến của đường tròn ngoại tiếp \(\Delta ABF.\) (đpcm)
2. Một hình nón có bán kính đáy là \(5\,cm,\) diện tích xung quanh bằng \(65\pi \,\,c{m^2}.\) Tính chiều cao của hình nón đó.
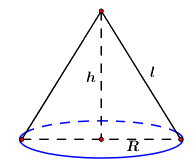
Ta có: \({S_{xq}} = \pi Rl\) \( \Leftrightarrow 5\pi l = 65\pi \)\( \Leftrightarrow l = \dfrac{{65\pi }}{{5\pi }} = 13\,\,cm.\)
Áp dụng định lý Pitago ta có chiều cao của hình nón là: \(h = \sqrt {{l^2} - {R^2}} = \sqrt {{{13}^2} - {5^2}} = 12\,\,cm.\)
Bài 5 (1,0 điểm)
Cách giải:
a) Cho \(x,y\) là hai số thực bất kì. Chứng minh \({x^2} - xy + {y^2} \ge \dfrac{1}{3}\left( {{x^2} + xy + {y^2}} \right)\)
Ta có:
\(\begin{array}{l}{x^2} - xy + {y^2} \ge \dfrac{1}{3}\left( {{x^2} + xy + {y^2}} \right)\\ \Leftrightarrow 3{x^2} - 3xy + 3{y^2} \ge {x^2} + xy + {y^2}\\ \Leftrightarrow 2{x^2} - 4xy + 2{y^2} \ge 0\\ \Leftrightarrow {x^2} - 2xy + {y^2} \ge 0\end{array}\)
\( \Leftrightarrow {\left( {x - y} \right)^2} \ge 0\) (luôn đúng)
Dấu “=” xảy ra khi \(x = y\).
Vậy ta có đpcm.
b) Cho \(x,y,z\) là ba số thực dường thỏa mãn \(\sqrt x + \sqrt y + \sqrt z = 2\). Chứng minh
\(\dfrac{{x\sqrt x }}{{x + \sqrt {xy} + y}} + \dfrac{{y\sqrt y }}{{y + \sqrt {yz} + z}} + \dfrac{{z\sqrt z }}{{z + \sqrt {zx} + x}} \ge \dfrac{2}{3}\)
Đặt \(\left\{ \begin{array}{l}a = \sqrt x > 0\\b = \sqrt y > 0\\c = \sqrt z > 0\end{array} \right. \Rightarrow a + b + c = 2\) ta được:
\(\begin{array}{l}VT = \dfrac{{{a^3}}}{{{a^2} + ab + {b^2}}} + \dfrac{{{b^3}}}{{{b^2} + bc + {c^2}}} + \dfrac{{{c^3}}}{{{c^2} + ca + {a^2}}}\\ = \dfrac{{{a^4}}}{{{a^3} + {a^2}b + a{b^2}}} + \dfrac{{{b^4}}}{{{b^3} + {b^2}c + b{c^2}}} + \dfrac{{{c^4}}}{{{c^3} + {c^2}a + c{a^2}}}\end{array}\)
Áp dụng BĐT \(\dfrac{{{a^2}}}{x} + \dfrac{{{b^2}}}{y} \ge \dfrac{{{{\left( {a + b} \right)}^2}}}{{x + y}}\) ta có:
\(\begin{array}{l}\dfrac{{{a^4}}}{{{a^3} + {a^2}b + a{b^2}}} + \dfrac{{{b^4}}}{{{b^3} + {b^2}c + b{c^2}}} \ge \dfrac{{{{\left( {{a^2} + {b^2}} \right)}^2}}}{{\left( {{a^3} + {a^2}b + a{b^2}} \right) + \left( {{b^3} + {b^2}c + b{c^2}} \right)}}\\ \Rightarrow \dfrac{{{a^4}}}{{{a^3} + {a^2}b + a{b^2}}} + \dfrac{{{b^4}}}{{{b^3} + {b^2}c + b{c^2}}} + \dfrac{{{c^4}}}{{{c^3} + {c^2}a + c{a^2}}}\\ \ge \dfrac{{{{\left( {{a^2} + {b^2}} \right)}^2}}}{{\left( {{a^3} + {a^2}b + a{b^2}} \right) + \left( {{b^3} + {b^2}c + b{c^2}} \right)}} + \dfrac{{{c^4}}}{{{c^3} + {c^2}a + c{a^2}}}\\ \ge \dfrac{{{{\left( {{a^2} + {b^2} + {c^2}} \right)}^2}}}{{\left( {{a^3} + {a^2}b + a{b^2}} \right) + \left( {{b^3} + {b^2}c + b{c^2}} \right) + \left( {{c^3} + {c^2}a + c{a^2}} \right)}}\\ = \dfrac{{{{\left( {{a^2} + {b^2} + {c^2}} \right)}^2}}}{{{a^3} + {a^2}b + {a^2}c + {b^3} + {b^2}a + {b^2}c + {c^3} + {c^2}a + {c^2}b}}\\ = \dfrac{{{{\left( {{a^2} + {b^2} + {c^2}} \right)}^2}}}{{{a^2}\left( {a + b + c} \right) + {b^2}\left( {a + b + c} \right) + {c^2}\left( {a + b + c} \right)}}\\ = \dfrac{{{{\left( {{a^2} + {b^2} + {c^2}} \right)}^2}}}{{\left( {{a^2} + {b^2} + {c^2}} \right)\left( {a + b + c} \right)}}\\ = \dfrac{{{a^2} + {b^2} + {c^2}}}{{a + b + c}}\\ = \dfrac{1}{2}\left( {\dfrac{{{a^2}}}{1} + \dfrac{{{b^2}}}{1} + \dfrac{{{c^2}}}{1}} \right)\\ \ge \dfrac{1}{2}.\dfrac{{{{\left( {a + b + c} \right)}^2}}}{{1 + 1 + 1}} = \dfrac{1}{2}.\dfrac{{{2^2}}}{3} = \dfrac{2}{3}\end{array}\)
\( \Rightarrow \dfrac{{{a^3}}}{{{a^2} + ab + {b^2}}} + \dfrac{{{b^3}}}{{{b^2} + bc + {c^2}}} + \dfrac{{{c^3}}}{{{c^2} + ca + {a^2}}} \ge \dfrac{2}{3}\) (đpcm)
Dấu “=” xảy ra khi \(a = b = c = \dfrac{2}{3}\).
Kỳ thi tuyển sinh vào lớp 10 tại Hải Phòng luôn là một kỳ thi quan trọng, đánh dấu bước ngoặt trong sự nghiệp học tập của các em học sinh. Môn Toán, với vai trò then chốt, đòi hỏi các em phải có sự chuẩn bị kỹ lưỡng về kiến thức và kỹ năng. Đề thi vào 10 môn Toán Hải Phòng năm 2020 là một nguồn tài liệu quý giá để các em có thể làm quen với dạng đề, mức độ khó và các chủ đề thường xuyên xuất hiện trong kỳ thi.
Đề thi vào 10 môn Toán Hải Phòng năm 2020 thường bao gồm các dạng bài tập sau:
Đây là một trong những dạng bài tập thường xuyên xuất hiện trong đề thi vào 10 môn Toán Hải Phòng. Các em cần nắm vững các phương pháp giải phương trình và hệ phương trình, như phương pháp thế, phương pháp cộng đại số, và phương pháp đặt ẩn phụ.
Các bài toán về hàm số đòi hỏi các em phải hiểu rõ các khái niệm về hàm số, như tập xác định, tập giá trị, đồ thị hàm số, và các tính chất của hàm số.
Các bài toán về hình học phẳng thường liên quan đến các tính chất của các hình hình học, như tam giác, tứ giác, đường tròn, và các định lý liên quan.
Để giải đề thi vào 10 môn Toán Hải Phòng năm 2020 hiệu quả, các em cần:
Ngoài việc giải đề thi vào 10 môn Toán Hải Phòng năm 2020, các em cũng nên luyện tập với các đề thi năm trước để làm quen với các dạng bài tập và rèn luyện kỹ năng giải toán. Giaitoan.edu.vn cung cấp một kho đề thi phong phú, đa dạng, giúp các em có thể luyện tập một cách hiệu quả.
Trong thời đại công nghệ 4.0, học toán online đang trở thành một xu hướng phổ biến. Học toán online mang lại nhiều lợi ích, như:
Giaitoan.edu.vn là một nền tảng học toán online uy tín, cung cấp các khóa học toán chất lượng cao, được thiết kế bởi các giáo viên giàu kinh nghiệm. Chúng tôi cam kết mang đến cho các em một môi trường học tập hiệu quả, giúp các em tự tin chinh phục môn Toán.
Đề thi vào 10 môn Toán Hải Phòng năm 2020 là một tài liệu quan trọng giúp các em chuẩn bị cho kỳ thi tuyển sinh sắp tới. Hãy tận dụng tối đa nguồn tài liệu này, kết hợp với việc luyện tập thường xuyên và học toán online trên Giaitoan.edu.vn để đạt kết quả tốt nhất.