Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Phú Thọ năm 2020 chính thức. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi sắp tới.
Chúng tôi cung cấp đầy đủ đề thi và đáp án chi tiết, được phân tích bởi đội ngũ giáo viên giàu kinh nghiệm.
PHẦN 1: TRẮC NGHIỆM KHÁCH QUAN (2,5 điểm) Câu 1. Điều kiện xác định của biểu thức
PHẦN I. TRẮC NGHIỆM (2,5 điểm)
1. A | 2. C | 3. D | 4. A | 5. B |
6. D | 7. D | 8. C | 9. C | 10. B |
Câu 1 Phương pháp:
Biểu thức \(\sqrt A \) xác định \( \Leftrightarrow A \ge 0\)
Cách giải:
Biểu thức đã cho xác định \( \Leftrightarrow 2020 - x \ge 0 \Leftrightarrow x \le 2020\)
Chọn A.
Câu 2
Phương pháp:
Hàm số bậc nhất \(y = ax + b\) đồng biến trên ℝ khi a > 0, nghịch biến khi a < 0
Cách giải:
Có 3 hàm số đồng biến trên ℝ là \(y = 17x + 2;y = 17x - 8;y = x + 10\)
Chọn C.
Câu 3
Phương pháp:
Xác định hệ số a, từ đó tìm ra m
Cách giải:
Hàm số đã cho \(y = ax + b\) đi qua gốc O nên b = 0, đi qua điểm (1;1) nên \(1 = a.1 \Rightarrow a = 1\)
⟹ m – 3 = 1 ⟹ m = 4
Chọn D.
Câu 4
Phương pháp:
Giải hệ phương trình bằng phương pháp thế, rồi tính \(x - y\)
Cách giải:
\(\begin{array}{l}\left\{ \begin{array}{l} - 5x + 3y = 1\\x + 5y = 11\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 11 - 5y\\ - 5\left( {11 - 5y} \right) + 3y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 11 - 5y\\28y - 55 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2\\x = 1\end{array} \right.\\ \Rightarrow x - y = - 1\end{array}\)
Chọn A.
Câu 5
Phương pháp:
Thay tọa độ các điểm vào hàm số
Cách giải:
Thay tọa độ điểm B(3;40) vào công thức hàm số, ta có 40 = 5.32 ⟺ 40 = 45 (không thỏa mãn)
Vậy điểm B không thuộc đồ thị
Chọn B.
Câu 6
Phương pháp:
Giải phương trình, tìm \({x_1},{x_2}\)
Cách giải:
Ta có \({x^2} - 16x + 55 = 0 \Leftrightarrow \left( {x - 11} \right)\left( {x - 5} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x_1} = 5\\{x_2} = 11\end{array} \right.\;\left( {do\;{x_1} < {x_2}} \right)\)
\( \Rightarrow {x_1} - 2{x_2} = 5 - 2.11 = - 17\)
Chọn D.
Câu 7
Phương pháp:
Viết phương trình hoành độ giao điểm, giải ra 2 nghiệm
Tìm giao điểm 2 đồ thị
Cách giải:
Xét phương trình hoành độ giao điểm của hai đồ thị hàm số
\({x^2} = - 2x + 3 \Leftrightarrow {x^2} + 2x - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 3\end{array} \right.\)
Với \(x = 1 \Rightarrow y = 1\)
Với \(x = - 3 \Rightarrow y = 9\)
Vậy \({y_1} + {y_2} = 1 + 9 = 10\)
Chọn D.
Câu 8
Phương pháp:
Tính cạnh góc vuông của tam giác, từ đó tính diện tích
Cách giải:
Vì ABC là tam giác vuông cân nên \(AB = AC = \dfrac{{BC}}{{\sqrt 2 }} = \dfrac{{\sqrt 6 }}{{\sqrt 2 }} = \sqrt 3 \)
\( \Rightarrow {S_{ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}A{B^2} = \dfrac{3}{2}\left( {c{m^2}} \right)\)
Chọn C.
Câu 9
Phương pháp:
Gọi H là giao điểm của AB và OO’
Tính OH và O’H
Cách giải:
Gọi H là giao điểm của AB và OO’. Vì \(OA = OB;O'A = O'B\)nên OO’ là trung trực của AB, suy ra \(AH = HB = \dfrac{{AB}}{2} = 4\left( {cm} \right)\)
Vì \(AB \bot O'O\) nên hai tam giác AHO và AHO’ vuông tại H
Áp dụng định lý Pitago ta có
\(\begin{array}{l}OH = \sqrt {O{A^2} - A{H^2}} = \sqrt {{6^2} - {4^2}} = \sqrt {20} = 2\sqrt 5 \left( {cm} \right)\\O'H = \sqrt {O'{A^2} - A{H^2}} = \sqrt {{5^2} - {4^2}} = \sqrt 9 = 3\left( {cm} \right)\\ \Rightarrow OO' = OH + O'H = 3 + 2\sqrt 5 \end{array}\)
Chọn C.
Câu 10
Phương pháp:
Chứng mình hai tam giác ABM và BCN bằng nhau
Chứng minh \(\angle EDF = \angle BDC\)
Cách giải:
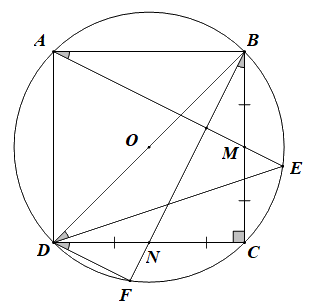
Xét hai tam giác vuông ABM và BCN có
\(\begin{array}{l}AB = BC\\\angle ABM = \angle BCN = {90^0}\\BM = CN\end{array}\)
\( \Rightarrow \Delta ABM = \Delta BCN\;\left( {c.g.c} \right)\)
\( \Rightarrow \angle BAM = \angle CBN\) (hai góc tương ứng)
Ta có các góc nội tiếp
\(\left\{ \begin{array}{l}\angle BAM = \angle BDE\\\angle CBN = \angle CDF\end{array} \right. \Rightarrow \angle BDE = \angle CDF\)
\( \Rightarrow \angle EDF = \angle CDE + \angle CDF\)\( = \angle CDE + \angle BDE = \angle BDC = {45^0}\)
(do tam giác BDC vuông cân tại C).
Chọn B.
PHẦN II. TỰ LUẬN (7,5 điểm)
Câu 1 (1,5 điểm)
Cách giải::
a) Tính giá trị biểu thức \(P = \sqrt {45} + \sqrt {9 - 4\sqrt 5 } \)
Ta có:
\(\begin{array}{l}P = \sqrt {45} + \sqrt {9 - 4\sqrt 5 } \\\,\,\,\,\, = \sqrt {{3^2}.5} + \sqrt {5 - 2.2\sqrt 5 + 4} \\\,\,\,\,\, = 3\sqrt 5 + \sqrt {{{\left( {\sqrt 5 - 2} \right)}^2}} \\\,\,\,\,\, = 3\sqrt 5 + \left| {\sqrt 5 - 2} \right|\\\,\,\,\,\, = 3\sqrt 5 + \sqrt 5 - 2\\\,\,\,\,\, = 4\sqrt 5 - 2\end{array}\)
Vậy \(P = 4\sqrt 5 - 2\)
b) Giải hệ phương trình \(\left\{ \begin{array}{l}2x + 5y = 9\\ - 2x + 7y = 3\end{array} \right.\)
\(\begin{array}{l}\left\{ \begin{array}{l}2x + 5y = 9\\ - 2x + 7y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}12y = 12\\2x + 5y = 9\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = 1\\2x + 5.1 = 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\2x = 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = 1\\x = 2\end{array} \right.\end{array}\)
Vậy hệ có nghiệm \(\left( {x;y} \right)\) là \(\left( {2;1} \right)\).
Câu 2 (2,5 điểm)
Cách giải::
Cho phương trình \({x^2} - 2mx + m - 1 = 0\) (\(m\) là tham số).
a) Giải phương trình khi \(m = 2\).
Khi \(m = 2\), phương trình trở thành \({x^2} - 4x + 1 = 0\).
Ta có: \(\Delta ' = {\left( { - 2} \right)^2} - 1.1 = 3 > 0\), do đó phương trình có 2 nghiệm phân biệt \({x_1} = 2 + \sqrt 3 \), \({x_2} = 2 - \sqrt 3 \).
Vậy khi \(m = 2\) tập nghiệm của phương trình là \(S = \left\{ {2 \pm \sqrt 3 } \right\}\).
b) Chứng minh rằng phương trình luôn có hai nghiệm phân biệt với mọi giá trị của \(m\).
Xét phương trình \({x^2} - 2mx + m - 1 = 0\) (*) ta có:
\(\begin{array}{l}\Delta ' = {m^2} - 1.\left( {m - 1} \right)\\\,\,\,\,\,\, = {m^2} - m + 1\\\,\,\,\,\,\, = {m^2} - 2.m.\dfrac{1}{2} + \dfrac{1}{4} + \dfrac{3}{4}\\\,\,\,\,\,\, = {\left( {m - \dfrac{1}{2}} \right)^2} + \dfrac{3}{4}\end{array}\)
Do \({\left( {m - \dfrac{1}{2}} \right)^2} \ge 0\,\,\forall m \Rightarrow {\left( {m - \dfrac{1}{2}} \right)^2} + \dfrac{3}{4} \ge \dfrac{3}{4} > 0\,\,\forall m\).
Vậy phương trình đã cho luôn có hai nghiệm phân biệt với mọi giá trị của \(m\).
c) Gọi \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình. Tìm \(m\) để \(x_1^2{x_2} + m{x_2} - {x_2} = 4\).
Theo ý b) phương trình luôn có hai nghiệm phân biệt với mọi \(m\).
Giả sử \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình, áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}{x_2} = m - 1\end{array} \right.\).
Theo bài ra ta có:
\(\begin{array}{l}\,\,\,\,\,\,x_1^2{x_2} + m{x_2} - {x_2} = 4\\ \Leftrightarrow x_1^2{x_2} + {x_2}\left( {m - 1} \right) = 4\\ \Leftrightarrow x_1^2{x_2} + {x_2}.{x_1}{x_2} = 4\\ \Leftrightarrow {x_1}{x_2}\left( {{x_1} + {x_2}} \right) = 4\\ \Leftrightarrow \left( {m - 1} \right).2m = 4\\ \Leftrightarrow m\left( {m - 1} \right) = 2\\ \Leftrightarrow {m^2} - m - 2 = 0\\ \Leftrightarrow {m^2} + m - 2m - 2 = 0\\ \Leftrightarrow m\left( {m + 1} \right) - 2\left( {m + 1} \right) = 0\\ \Leftrightarrow \left( {m + 1} \right)\left( {m - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m + 1 = 0\\m - 2 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}m = - 1\\m = 2\end{array} \right.\end{array}\)
Vậy \(m = - 1,\,\,m = 2\) thỏa mãn yêu cầu bài toán.
Câu 3 (3 điểm)
Cách giải:
Cho \(\Delta ABC\) có ba góc nhọn nội tiếp đường tròn \(\left( O \right).\) Tia phân giác \(\angle BAC\) cắt cạnh \(BC\) tại \(D\) và cắt đường tròn \(\left( O \right)\) tại \(M.\) Gọi \(K\) là hình chiếu của \(M\) trên \(AB,\)\(T\) là hình chiếu của \(M\) trên \(AC.\) Chứng minh rằng:
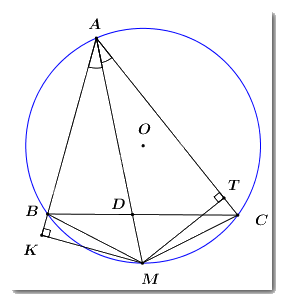
a) \(AKMT\) là tứ giác nội tiếp.
Ta có: \(\left\{ \begin{array}{l}MK \bot AB = \left\{ K \right\}\\MT \bot AC = \left\{ T \right\}\end{array} \right.\,\,\left( {gt} \right)\) \( \Rightarrow \angle AKM = \angle ATM = {90^0}\)
Xét tứ giác \(AKMT\) ta có: \(\angle AKM + \angle ATM = {90^0} + {90^0} = {180^0}\)
Mà hai góc này là hai góc đối diện
\( \Rightarrow AKMT\) là tứ giác nội tiếp (dhnb) (đpcm).
b) \(M{B^2} = M{C^2} = MD.MA.\)
Xét \(\left( O \right)\) ta có:
\(\angle MAB\) là góc nội tiếp chắn cung \(BM\)
\(\angle MAC\) là góc nội tiếp chắn cung \(CM\)
Lại có: \(MA\) là tia phân giác của \(\angle BAC\,\,\,\left( {gt} \right)\) \( \Rightarrow \angle MAB = \angle MAC.\)
\( \Rightarrow \) Số đo cung \(BM = \) Số đo cung \(CM\) (hai góc nội tiếp bằng nhau chắn hai cung bằng nhau).
Ta có:
\(\angle MBC\) là góc nội tiếp chắn cung \(MC\)
\(\angle BAM\) là góc nội tiếp chắn cung \(BM\)
\( \Rightarrow \angle MAB = \angle MBC = \angle MBD\) (hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau).
Xét \(\Delta MAB\) và \(\Delta MBD\) ta có:
\(\begin{array}{l}\angle AMB\,\,\,chung\\\angle MAB = \angle MBD\,\,\,\left( {cmt} \right)\\ \Rightarrow \Delta MAB \sim \Delta MBD\,\,\,\left( {g - g} \right)\\ \Rightarrow \dfrac{{MA}}{{MB}} = \dfrac{{MB}}{{MD}} \Rightarrow M{B^2} = MD.MA.\end{array}\)
Lại có: Số đo cung \(BM = \) Số đo cung \(CM\) (cmt) nên \(MB = MC\) (hai cung bằng nhau căng hai dây bằng nhau).
Vậy \(M{B^2} = M{C^2} = MD.MA\,\,\,\left( {dpcm} \right)\).
c) Khi đường tròn \(\left( O \right)\) và \(B,\,\,C\) cố định, điểm \(A\) thay đổi trên cung lớn \(BC\) thì tổng \(\dfrac{{AB}}{{MK}} + \dfrac{{AC}}{{MT}}\) có giá trị không đổi.
Đặt \(\angle BAM = \angle CAM = \alpha \).
Xét \(\Delta AKM\) và \(\Delta ATM\) có:
\(\begin{array}{l}AM\,\,chung\\\angle KAM = \angle TAM\,\,\left( {gt} \right)\end{array}\)
\( \Rightarrow \Delta AKM = \Delta ATM\) (cạnh huyền – góc nhọn)
\( \Rightarrow MK = MT\) (hai 2 tương ứng).
Giả sử \(AB \le AC\), khi đó ta có:
\(\begin{array}{l}\,\,\,\,\dfrac{{AB}}{{MK}} + \dfrac{{AC}}{{MT}}\\ = \dfrac{{AK - BK}}{{MK}} + \dfrac{{AT + TC}}{{MK}}\\ = \dfrac{{AK + AT - BK + TC}}{{MK}}\end{array}\)
Xét \(\Delta BMK\) và \(\Delta CMT\) có:
\(\begin{array}{l}MB = MC\,\,\left( {cmt} \right)\\MK = MT\,\,\left( {cmt} \right)\end{array}\)
\( \Rightarrow \Delta BMK = \Delta CMT\) (cạnh huyền – cạnh góc vuông)
\( \Rightarrow BK = TC\) (2 cạnh tương ứng).
\( \Rightarrow \dfrac{{AB}}{{MK}} + \dfrac{{AC}}{{MT}} = \dfrac{{AK + AT}}{{MK}}\).
Xét tam giác \(AKM\) vuông tại \(K\) có: \(AK = AM.\cos \alpha \), \(MK = AM.\sin \alpha \).
Xét tam giác \(AMT\) vuông tại \(T\) có: \(AT = AM.\cos \alpha \).
\( \Rightarrow \dfrac{{AB}}{{MK}} + \dfrac{{AC}}{{MT}} = \dfrac{{AM.\cos \alpha + AM.\cos \alpha }}{{AM.\sin \alpha }} = \dfrac{{2AM.\cos \alpha }}{{AM.\sin \alpha }} = 2\cot \alpha \).
Vì đường tròn \(\left( O \right)\) và \(BC\) cố định nên số đo cung \(BC\) không đổi.
\( \Rightarrow \angle BAC = 2\alpha = \dfrac{1}{2}\) số đo cung BC không đổi (góc nội tiếp bằng nửa số đo cung bị chắn).
\( \Rightarrow \alpha \) không đổi \( \Rightarrow 2\cot \alpha \) không đổi.
Vậy \(\dfrac{{AB}}{{MK}} + \dfrac{{AC}}{{MT}} = 2\cot \alpha \) không đổi, với \(\alpha = \dfrac{1}{4}\) số đo cung BC không đổi.
Câu 4 (1,0 điểm)
Cách giải::
Giải phương trình \(\sqrt {{x^2} + 3x} + \sqrt {9x + 18} = 3x + \sqrt {x + \dfrac{6}{x} + 5} \)
ĐK: \(\left\{ \begin{array}{l}{x^2} + 3x \ge 0\\9x + 18 \ge 0\\x + \dfrac{6}{x} + 5 \ge 0\\x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0,x \le - 3\\x \ge - 2\\\dfrac{{{x^2} + 5x + 6}}{x} \ge 0\\x \ne 0\end{array} \right. \Leftrightarrow x > 0\)
Khi đó
\(\begin{array}{l}PT \Leftrightarrow \sqrt {x\left( {x + 3} \right)} + 3\sqrt {x + 2} = 3x + \sqrt {\dfrac{{{x^2} + 5x + 6}}{x}} \\\,\,\,\,\,\,\, \Leftrightarrow \sqrt x \sqrt {x\left( {x + 3} \right)} + 3\sqrt x \sqrt {x + 2} = 3x\sqrt x + \sqrt {{x^2} + 5x + 6} \\\,\,\,\,\,\,\, \Leftrightarrow x\sqrt {x + 3} + 3\sqrt x \sqrt {x + 2} = 3x\sqrt x + \sqrt {\left( {x + 2} \right)\left( {x + 3} \right)} \\\,\,\,\,\,\,\, \Leftrightarrow x\sqrt {x + 3} - \sqrt {\left( {x + 2} \right)\left( {x + 3} \right)} + 3\sqrt x \sqrt {x + 2} - 3x\sqrt x = 0\\\,\,\,\,\,\,\, \Leftrightarrow \sqrt {x + 3} \left( {x - \sqrt {x + 2} } \right) - 3\sqrt x \left( {x - \sqrt {x + 2} } \right) = 0\\\,\,\,\,\,\,\, \Leftrightarrow \left( {x - \sqrt {x + 2} } \right)\left( {\sqrt {x + 3} - 3\sqrt x } \right) = 0\\\,\,\,\,\,\,\, \Leftrightarrow \left[ \begin{array}{l}x - \sqrt {x + 2} = 0\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\\sqrt {x + 3} - 3\sqrt x = 0\,\,\,\,\left( 2 \right)\end{array} \right.\end{array}\)
Ta có:
\(\begin{array}{l}\left( 1 \right) \Leftrightarrow x = \sqrt {x + 2} \Leftrightarrow {x^2} = x + 2\,\,\left( {Do\,\,x > 0} \right)\\\,\,\,\,\,\, \Leftrightarrow {x^2} - x - 2 = 0 \Leftrightarrow {x^2} + x - 2x - 2 = 0\\\,\,\,\,\,\, \Leftrightarrow x\left( {x + 1} \right) - 2\left( {x + 1} \right) = 0 \Leftrightarrow \left( {x + 1} \right)\left( {x - 2} \right) = 0\\\,\,\,\,\,\, \Leftrightarrow \left[ \begin{array}{l}x + 1 = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\,\,\,\left( {KTM} \right)\\x = 2\,\,\,\,\,\,\left( {TM} \right)\end{array} \right.\end{array}\)
\(\begin{array}{l}\left( 2 \right) \Leftrightarrow \sqrt {x + 3} = 3\sqrt x \\\,\,\,\,\,\,\, \Leftrightarrow x + 3 = 9x \Leftrightarrow 3 = 8x \Leftrightarrow x = \dfrac{3}{8}\,\,\,\,\left( {TM} \right)\end{array}\)
Vậy phương trình có tập nghiệm \(S = \left\{ {2;\dfrac{3}{8}} \right\}\).
PHẦN 1: TRẮC NGHIỆM KHÁCH QUAN (2,5 điểm)
Câu 1. Điều kiện xác định của biểu thức \(\sqrt {2020 - x} \) là
A.\(x \le 2020\)B. \(x \ge 2020\) C.\(x < 2020\) D. \(x > 2020\)
Câu 2. Có bao nhiêu hàm số đồng biến trên ℝ trong các hàm số sau \(y = 17x + 2;y = 17x - 8;y = 11 - 5x;y = x + 10;y = - x + 2020?\)
A. 5 B. 4 C. 3 D. 2
Câu 3. Cho hàm số \(y = \left( {m - 3} \right)x\) có đồ thị như hình vẽ dưới đây.
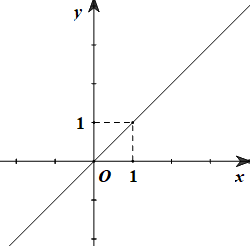
Khẳng định nào sau đây đúng?
A. m = –4
B. m = –3
C. m = 3
D. m = 4
Câu 4. Hệ phương trình \(\left\{ \begin{array}{l} - 5x + 3y = 1\\x + 5y = 11\end{array} \right.\) có nghiệm là\(\left( {x;y} \right)\). Khi đó \(x - y\) bằng
A. –1 B. 1 C. 3 D. 4
Câu 5. Điểm nào sau đây không thuộc đồ thị hàm số\(y = 5{x^2}\)?
A. A(1;5) B.B(3;40) C.C(2;20) D.D(–1;5)
Câu 6. Giả sử phương trình \({x^2} - 16x + 55 = 0\) có hai nghiệm \({x_1},{x_2}\left( {{x_1} < {x_2}} \right)\). Tính \({x_1} - 2{x_2}\)
A. 1 B. 24 C. 13 D. –17
Câu 7. Cho parabol \(y = {x^2}\) và đường thẳng \(y = - 2x + 3\) cắt nhau tại hai điểm\(A\left( {{x_1};{y_1}} \right);B\left( {{x_2};{y_2}} \right)\). Khi đó \({y_1} + {y_2}\) bằng:
A. 1 B. –2 C. 8 D. 10
Câu 8. Cho tam giác ABC vuông cân tại A, cạnh \(BC = \sqrt 6 \left( {cm} \right)\). Diện tích tam giác ABC bằng:
A. \(\sqrt 3 \left( {c{m^2}} \right)\) B. \(3\left( {c{m^2}} \right)\) C. \(\dfrac{3}{2}\left( {c{m^2}} \right)\) D. \(6\left( {c{m^2}} \right)\)
Câu 9. Cho hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) cắt nhau tại A và B. Biết\(OA = 6\left( {cm} \right);AO' = 5\left( {cm} \right);AB = 8\left( {cm} \right)\). (như hình vẽ bên).
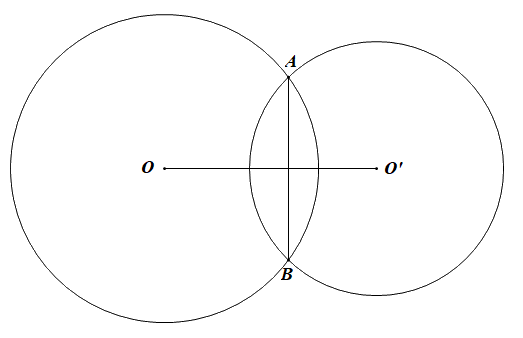
Độ dài GO’ bằng
A.5 (cm)
B. \(5\sqrt 5 \left( {cm} \right)\)
C. \(3 + 2\sqrt 5 \left( {cm} \right)\)
D. \(3 + 5\sqrt 2 \left( {cm} \right)\)
Câu 10. Cho hình vuông ABCD nội tiếp đường tròn tâm O. Gọi M, N lần lượt là trung điểm BC, CD. Đường thẳng AM, BN cắt đường tròn lần lượt tại E, F (như hình vẽ bên).
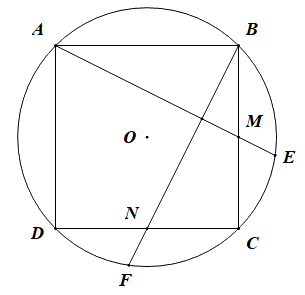
Số đo góc EDF bằng
A. \({30^0}\) B. \({45^0}\)
C. \({60^0}\) D.\({75^0}\)
PHẦN II. TỰ LUẬN (7,5 điểm)
Câu 1 (1,5 điểm):
a) Tính giá trị của biểu thức: \(P = \sqrt {45} + \sqrt {9 - 4\sqrt 5 } \)
b) Giải hệ phương trình: \(\left\{ \begin{array}{l}2x + 5y = 9\\ - 2x + 7y = 3\end{array} \right.\)
Câu 2 (2,0 điểm): Cho phương trình \({x^2} - 2mx + m - 1 = 0\)(m là tham số)
a) Giải phương trình khi m = 2
b) Chứng minh phương trình luôn có hai nghiệm phân biệt với mọi giá trị của m
c) Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình . Tìm m để \(x_1^2{x_2} + m{x_1} - {x_2} = 4\)
Câu 3 (3,0 điểm): Cho ∆ABC có 3 góc nhọn nội tiếp đường tròn (O). Tia phân giác góc \(\angle BAC\) cắt cạnh BC tại D và cắt đường tròn (O) tại M. Gọi K là hình chiếu của M trên AB.I là hình chiếu của M trên AC. Chứng minh rằng
a) AKMT là tứ giác nội tiếp
b) \(M{B^2} = M{C^2} = MD.MA\)
c) Khi đường tròn (O) và B;C cố định, điểm A thay đổi trên cung lớn BC thì tổng \(\dfrac{{AB}}{{MK}} + \dfrac{{AC}}{{MT}}\) có giá trị không đổi.
Câu 4. (1,0 điểm): Giải phương trình \(\sqrt {{x^2} + 3x} + \sqrt {9x + 18} = 3x + \sqrt {x + \dfrac{6}{x} + 5} \).
PHẦN 1: TRẮC NGHIỆM KHÁCH QUAN (2,5 điểm)
Câu 1. Điều kiện xác định của biểu thức \(\sqrt {2020 - x} \) là
A.\(x \le 2020\)B. \(x \ge 2020\) C.\(x < 2020\) D. \(x > 2020\)
Câu 2. Có bao nhiêu hàm số đồng biến trên ℝ trong các hàm số sau \(y = 17x + 2;y = 17x - 8;y = 11 - 5x;y = x + 10;y = - x + 2020?\)
A. 5 B. 4 C. 3 D. 2
Câu 3. Cho hàm số \(y = \left( {m - 3} \right)x\) có đồ thị như hình vẽ dưới đây.
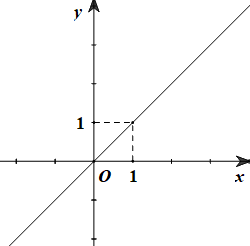
Khẳng định nào sau đây đúng?
A. m = –4
B. m = –3
C. m = 3
D. m = 4
Câu 4. Hệ phương trình \(\left\{ \begin{array}{l} - 5x + 3y = 1\\x + 5y = 11\end{array} \right.\) có nghiệm là\(\left( {x;y} \right)\). Khi đó \(x - y\) bằng
A. –1 B. 1 C. 3 D. 4
Câu 5. Điểm nào sau đây không thuộc đồ thị hàm số\(y = 5{x^2}\)?
A. A(1;5) B.B(3;40) C.C(2;20) D.D(–1;5)
Câu 6. Giả sử phương trình \({x^2} - 16x + 55 = 0\) có hai nghiệm \({x_1},{x_2}\left( {{x_1} < {x_2}} \right)\). Tính \({x_1} - 2{x_2}\)
A. 1 B. 24 C. 13 D. –17
Câu 7. Cho parabol \(y = {x^2}\) và đường thẳng \(y = - 2x + 3\) cắt nhau tại hai điểm\(A\left( {{x_1};{y_1}} \right);B\left( {{x_2};{y_2}} \right)\). Khi đó \({y_1} + {y_2}\) bằng:
A. 1 B. –2 C. 8 D. 10
Câu 8. Cho tam giác ABC vuông cân tại A, cạnh \(BC = \sqrt 6 \left( {cm} \right)\). Diện tích tam giác ABC bằng:
A. \(\sqrt 3 \left( {c{m^2}} \right)\) B. \(3\left( {c{m^2}} \right)\) C. \(\dfrac{3}{2}\left( {c{m^2}} \right)\) D. \(6\left( {c{m^2}} \right)\)
Câu 9. Cho hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) cắt nhau tại A và B. Biết\(OA = 6\left( {cm} \right);AO' = 5\left( {cm} \right);AB = 8\left( {cm} \right)\). (như hình vẽ bên).
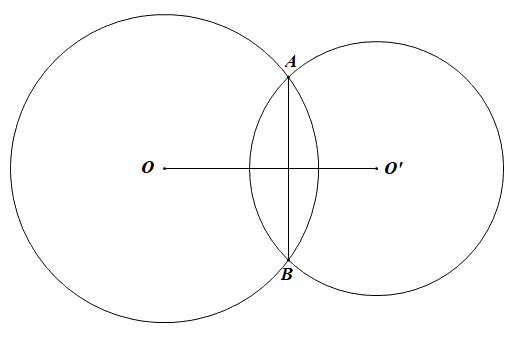
Độ dài GO’ bằng
A.5 (cm)
B. \(5\sqrt 5 \left( {cm} \right)\)
C. \(3 + 2\sqrt 5 \left( {cm} \right)\)
D. \(3 + 5\sqrt 2 \left( {cm} \right)\)
Câu 10. Cho hình vuông ABCD nội tiếp đường tròn tâm O. Gọi M, N lần lượt là trung điểm BC, CD. Đường thẳng AM, BN cắt đường tròn lần lượt tại E, F (như hình vẽ bên).
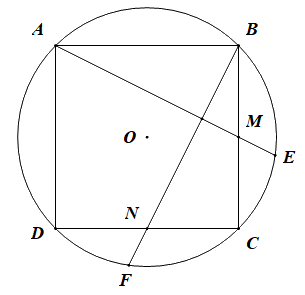
Số đo góc EDF bằng
A. \({30^0}\) B. \({45^0}\)
C. \({60^0}\) D.\({75^0}\)
PHẦN II. TỰ LUẬN (7,5 điểm)
Câu 1 (1,5 điểm):
a) Tính giá trị của biểu thức: \(P = \sqrt {45} + \sqrt {9 - 4\sqrt 5 } \)
b) Giải hệ phương trình: \(\left\{ \begin{array}{l}2x + 5y = 9\\ - 2x + 7y = 3\end{array} \right.\)
Câu 2 (2,0 điểm): Cho phương trình \({x^2} - 2mx + m - 1 = 0\)(m là tham số)
a) Giải phương trình khi m = 2
b) Chứng minh phương trình luôn có hai nghiệm phân biệt với mọi giá trị của m
c) Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình . Tìm m để \(x_1^2{x_2} + m{x_1} - {x_2} = 4\)
Câu 3 (3,0 điểm): Cho ∆ABC có 3 góc nhọn nội tiếp đường tròn (O). Tia phân giác góc \(\angle BAC\) cắt cạnh BC tại D và cắt đường tròn (O) tại M. Gọi K là hình chiếu của M trên AB.I là hình chiếu của M trên AC. Chứng minh rằng
a) AKMT là tứ giác nội tiếp
b) \(M{B^2} = M{C^2} = MD.MA\)
c) Khi đường tròn (O) và B;C cố định, điểm A thay đổi trên cung lớn BC thì tổng \(\dfrac{{AB}}{{MK}} + \dfrac{{AC}}{{MT}}\) có giá trị không đổi.
Câu 4. (1,0 điểm): Giải phương trình \(\sqrt {{x^2} + 3x} + \sqrt {9x + 18} = 3x + \sqrt {x + \dfrac{6}{x} + 5} \).
PHẦN I. TRẮC NGHIỆM (2,5 điểm)
1. A | 2. C | 3. D | 4. A | 5. B |
6. D | 7. D | 8. C | 9. C | 10. B |
Câu 1 Phương pháp:
Biểu thức \(\sqrt A \) xác định \( \Leftrightarrow A \ge 0\)
Cách giải:
Biểu thức đã cho xác định \( \Leftrightarrow 2020 - x \ge 0 \Leftrightarrow x \le 2020\)
Chọn A.
Câu 2
Phương pháp:
Hàm số bậc nhất \(y = ax + b\) đồng biến trên ℝ khi a > 0, nghịch biến khi a < 0
Cách giải:
Có 3 hàm số đồng biến trên ℝ là \(y = 17x + 2;y = 17x - 8;y = x + 10\)
Chọn C.
Câu 3
Phương pháp:
Xác định hệ số a, từ đó tìm ra m
Cách giải:
Hàm số đã cho \(y = ax + b\) đi qua gốc O nên b = 0, đi qua điểm (1;1) nên \(1 = a.1 \Rightarrow a = 1\)
⟹ m – 3 = 1 ⟹ m = 4
Chọn D.
Câu 4
Phương pháp:
Giải hệ phương trình bằng phương pháp thế, rồi tính \(x - y\)
Cách giải:
\(\begin{array}{l}\left\{ \begin{array}{l} - 5x + 3y = 1\\x + 5y = 11\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 11 - 5y\\ - 5\left( {11 - 5y} \right) + 3y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 11 - 5y\\28y - 55 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2\\x = 1\end{array} \right.\\ \Rightarrow x - y = - 1\end{array}\)
Chọn A.
Câu 5
Phương pháp:
Thay tọa độ các điểm vào hàm số
Cách giải:
Thay tọa độ điểm B(3;40) vào công thức hàm số, ta có 40 = 5.32 ⟺ 40 = 45 (không thỏa mãn)
Vậy điểm B không thuộc đồ thị
Chọn B.
Câu 6
Phương pháp:
Giải phương trình, tìm \({x_1},{x_2}\)
Cách giải:
Ta có \({x^2} - 16x + 55 = 0 \Leftrightarrow \left( {x - 11} \right)\left( {x - 5} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x_1} = 5\\{x_2} = 11\end{array} \right.\;\left( {do\;{x_1} < {x_2}} \right)\)
\( \Rightarrow {x_1} - 2{x_2} = 5 - 2.11 = - 17\)
Chọn D.
Câu 7
Phương pháp:
Viết phương trình hoành độ giao điểm, giải ra 2 nghiệm
Tìm giao điểm 2 đồ thị
Cách giải:
Xét phương trình hoành độ giao điểm của hai đồ thị hàm số
\({x^2} = - 2x + 3 \Leftrightarrow {x^2} + 2x - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 3\end{array} \right.\)
Với \(x = 1 \Rightarrow y = 1\)
Với \(x = - 3 \Rightarrow y = 9\)
Vậy \({y_1} + {y_2} = 1 + 9 = 10\)
Chọn D.
Câu 8
Phương pháp:
Tính cạnh góc vuông của tam giác, từ đó tính diện tích
Cách giải:
Vì ABC là tam giác vuông cân nên \(AB = AC = \dfrac{{BC}}{{\sqrt 2 }} = \dfrac{{\sqrt 6 }}{{\sqrt 2 }} = \sqrt 3 \)
\( \Rightarrow {S_{ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}A{B^2} = \dfrac{3}{2}\left( {c{m^2}} \right)\)
Chọn C.
Câu 9
Phương pháp:
Gọi H là giao điểm của AB và OO’
Tính OH và O’H
Cách giải:
Gọi H là giao điểm của AB và OO’. Vì \(OA = OB;O'A = O'B\)nên OO’ là trung trực của AB, suy ra \(AH = HB = \dfrac{{AB}}{2} = 4\left( {cm} \right)\)
Vì \(AB \bot O'O\) nên hai tam giác AHO và AHO’ vuông tại H
Áp dụng định lý Pitago ta có
\(\begin{array}{l}OH = \sqrt {O{A^2} - A{H^2}} = \sqrt {{6^2} - {4^2}} = \sqrt {20} = 2\sqrt 5 \left( {cm} \right)\\O'H = \sqrt {O'{A^2} - A{H^2}} = \sqrt {{5^2} - {4^2}} = \sqrt 9 = 3\left( {cm} \right)\\ \Rightarrow OO' = OH + O'H = 3 + 2\sqrt 5 \end{array}\)
Chọn C.
Câu 10
Phương pháp:
Chứng mình hai tam giác ABM và BCN bằng nhau
Chứng minh \(\angle EDF = \angle BDC\)
Cách giải:
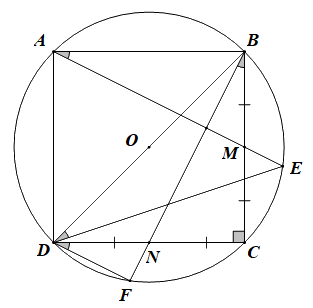
Xét hai tam giác vuông ABM và BCN có
\(\begin{array}{l}AB = BC\\\angle ABM = \angle BCN = {90^0}\\BM = CN\end{array}\)
\( \Rightarrow \Delta ABM = \Delta BCN\;\left( {c.g.c} \right)\)
\( \Rightarrow \angle BAM = \angle CBN\) (hai góc tương ứng)
Ta có các góc nội tiếp
\(\left\{ \begin{array}{l}\angle BAM = \angle BDE\\\angle CBN = \angle CDF\end{array} \right. \Rightarrow \angle BDE = \angle CDF\)
\( \Rightarrow \angle EDF = \angle CDE + \angle CDF\)\( = \angle CDE + \angle BDE = \angle BDC = {45^0}\)
(do tam giác BDC vuông cân tại C).
Chọn B.
PHẦN II. TỰ LUẬN (7,5 điểm)
Câu 1 (1,5 điểm)
Cách giải::
a) Tính giá trị biểu thức \(P = \sqrt {45} + \sqrt {9 - 4\sqrt 5 } \)
Ta có:
\(\begin{array}{l}P = \sqrt {45} + \sqrt {9 - 4\sqrt 5 } \\\,\,\,\,\, = \sqrt {{3^2}.5} + \sqrt {5 - 2.2\sqrt 5 + 4} \\\,\,\,\,\, = 3\sqrt 5 + \sqrt {{{\left( {\sqrt 5 - 2} \right)}^2}} \\\,\,\,\,\, = 3\sqrt 5 + \left| {\sqrt 5 - 2} \right|\\\,\,\,\,\, = 3\sqrt 5 + \sqrt 5 - 2\\\,\,\,\,\, = 4\sqrt 5 - 2\end{array}\)
Vậy \(P = 4\sqrt 5 - 2\)
b) Giải hệ phương trình \(\left\{ \begin{array}{l}2x + 5y = 9\\ - 2x + 7y = 3\end{array} \right.\)
\(\begin{array}{l}\left\{ \begin{array}{l}2x + 5y = 9\\ - 2x + 7y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}12y = 12\\2x + 5y = 9\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = 1\\2x + 5.1 = 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\2x = 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = 1\\x = 2\end{array} \right.\end{array}\)
Vậy hệ có nghiệm \(\left( {x;y} \right)\) là \(\left( {2;1} \right)\).
Câu 2 (2,5 điểm)
Cách giải::
Cho phương trình \({x^2} - 2mx + m - 1 = 0\) (\(m\) là tham số).
a) Giải phương trình khi \(m = 2\).
Khi \(m = 2\), phương trình trở thành \({x^2} - 4x + 1 = 0\).
Ta có: \(\Delta ' = {\left( { - 2} \right)^2} - 1.1 = 3 > 0\), do đó phương trình có 2 nghiệm phân biệt \({x_1} = 2 + \sqrt 3 \), \({x_2} = 2 - \sqrt 3 \).
Vậy khi \(m = 2\) tập nghiệm của phương trình là \(S = \left\{ {2 \pm \sqrt 3 } \right\}\).
b) Chứng minh rằng phương trình luôn có hai nghiệm phân biệt với mọi giá trị của \(m\).
Xét phương trình \({x^2} - 2mx + m - 1 = 0\) (*) ta có:
\(\begin{array}{l}\Delta ' = {m^2} - 1.\left( {m - 1} \right)\\\,\,\,\,\,\, = {m^2} - m + 1\\\,\,\,\,\,\, = {m^2} - 2.m.\dfrac{1}{2} + \dfrac{1}{4} + \dfrac{3}{4}\\\,\,\,\,\,\, = {\left( {m - \dfrac{1}{2}} \right)^2} + \dfrac{3}{4}\end{array}\)
Do \({\left( {m - \dfrac{1}{2}} \right)^2} \ge 0\,\,\forall m \Rightarrow {\left( {m - \dfrac{1}{2}} \right)^2} + \dfrac{3}{4} \ge \dfrac{3}{4} > 0\,\,\forall m\).
Vậy phương trình đã cho luôn có hai nghiệm phân biệt với mọi giá trị của \(m\).
c) Gọi \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình. Tìm \(m\) để \(x_1^2{x_2} + m{x_2} - {x_2} = 4\).
Theo ý b) phương trình luôn có hai nghiệm phân biệt với mọi \(m\).
Giả sử \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình, áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}{x_2} = m - 1\end{array} \right.\).
Theo bài ra ta có:
\(\begin{array}{l}\,\,\,\,\,\,x_1^2{x_2} + m{x_2} - {x_2} = 4\\ \Leftrightarrow x_1^2{x_2} + {x_2}\left( {m - 1} \right) = 4\\ \Leftrightarrow x_1^2{x_2} + {x_2}.{x_1}{x_2} = 4\\ \Leftrightarrow {x_1}{x_2}\left( {{x_1} + {x_2}} \right) = 4\\ \Leftrightarrow \left( {m - 1} \right).2m = 4\\ \Leftrightarrow m\left( {m - 1} \right) = 2\\ \Leftrightarrow {m^2} - m - 2 = 0\\ \Leftrightarrow {m^2} + m - 2m - 2 = 0\\ \Leftrightarrow m\left( {m + 1} \right) - 2\left( {m + 1} \right) = 0\\ \Leftrightarrow \left( {m + 1} \right)\left( {m - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m + 1 = 0\\m - 2 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}m = - 1\\m = 2\end{array} \right.\end{array}\)
Vậy \(m = - 1,\,\,m = 2\) thỏa mãn yêu cầu bài toán.
Câu 3 (3 điểm)
Cách giải:
Cho \(\Delta ABC\) có ba góc nhọn nội tiếp đường tròn \(\left( O \right).\) Tia phân giác \(\angle BAC\) cắt cạnh \(BC\) tại \(D\) và cắt đường tròn \(\left( O \right)\) tại \(M.\) Gọi \(K\) là hình chiếu của \(M\) trên \(AB,\)\(T\) là hình chiếu của \(M\) trên \(AC.\) Chứng minh rằng:
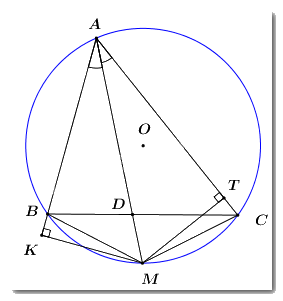
a) \(AKMT\) là tứ giác nội tiếp.
Ta có: \(\left\{ \begin{array}{l}MK \bot AB = \left\{ K \right\}\\MT \bot AC = \left\{ T \right\}\end{array} \right.\,\,\left( {gt} \right)\) \( \Rightarrow \angle AKM = \angle ATM = {90^0}\)
Xét tứ giác \(AKMT\) ta có: \(\angle AKM + \angle ATM = {90^0} + {90^0} = {180^0}\)
Mà hai góc này là hai góc đối diện
\( \Rightarrow AKMT\) là tứ giác nội tiếp (dhnb) (đpcm).
b) \(M{B^2} = M{C^2} = MD.MA.\)
Xét \(\left( O \right)\) ta có:
\(\angle MAB\) là góc nội tiếp chắn cung \(BM\)
\(\angle MAC\) là góc nội tiếp chắn cung \(CM\)
Lại có: \(MA\) là tia phân giác của \(\angle BAC\,\,\,\left( {gt} \right)\) \( \Rightarrow \angle MAB = \angle MAC.\)
\( \Rightarrow \) Số đo cung \(BM = \) Số đo cung \(CM\) (hai góc nội tiếp bằng nhau chắn hai cung bằng nhau).
Ta có:
\(\angle MBC\) là góc nội tiếp chắn cung \(MC\)
\(\angle BAM\) là góc nội tiếp chắn cung \(BM\)
\( \Rightarrow \angle MAB = \angle MBC = \angle MBD\) (hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau).
Xét \(\Delta MAB\) và \(\Delta MBD\) ta có:
\(\begin{array}{l}\angle AMB\,\,\,chung\\\angle MAB = \angle MBD\,\,\,\left( {cmt} \right)\\ \Rightarrow \Delta MAB \sim \Delta MBD\,\,\,\left( {g - g} \right)\\ \Rightarrow \dfrac{{MA}}{{MB}} = \dfrac{{MB}}{{MD}} \Rightarrow M{B^2} = MD.MA.\end{array}\)
Lại có: Số đo cung \(BM = \) Số đo cung \(CM\) (cmt) nên \(MB = MC\) (hai cung bằng nhau căng hai dây bằng nhau).
Vậy \(M{B^2} = M{C^2} = MD.MA\,\,\,\left( {dpcm} \right)\).
c) Khi đường tròn \(\left( O \right)\) và \(B,\,\,C\) cố định, điểm \(A\) thay đổi trên cung lớn \(BC\) thì tổng \(\dfrac{{AB}}{{MK}} + \dfrac{{AC}}{{MT}}\) có giá trị không đổi.
Đặt \(\angle BAM = \angle CAM = \alpha \).
Xét \(\Delta AKM\) và \(\Delta ATM\) có:
\(\begin{array}{l}AM\,\,chung\\\angle KAM = \angle TAM\,\,\left( {gt} \right)\end{array}\)
\( \Rightarrow \Delta AKM = \Delta ATM\) (cạnh huyền – góc nhọn)
\( \Rightarrow MK = MT\) (hai 2 tương ứng).
Giả sử \(AB \le AC\), khi đó ta có:
\(\begin{array}{l}\,\,\,\,\dfrac{{AB}}{{MK}} + \dfrac{{AC}}{{MT}}\\ = \dfrac{{AK - BK}}{{MK}} + \dfrac{{AT + TC}}{{MK}}\\ = \dfrac{{AK + AT - BK + TC}}{{MK}}\end{array}\)
Xét \(\Delta BMK\) và \(\Delta CMT\) có:
\(\begin{array}{l}MB = MC\,\,\left( {cmt} \right)\\MK = MT\,\,\left( {cmt} \right)\end{array}\)
\( \Rightarrow \Delta BMK = \Delta CMT\) (cạnh huyền – cạnh góc vuông)
\( \Rightarrow BK = TC\) (2 cạnh tương ứng).
\( \Rightarrow \dfrac{{AB}}{{MK}} + \dfrac{{AC}}{{MT}} = \dfrac{{AK + AT}}{{MK}}\).
Xét tam giác \(AKM\) vuông tại \(K\) có: \(AK = AM.\cos \alpha \), \(MK = AM.\sin \alpha \).
Xét tam giác \(AMT\) vuông tại \(T\) có: \(AT = AM.\cos \alpha \).
\( \Rightarrow \dfrac{{AB}}{{MK}} + \dfrac{{AC}}{{MT}} = \dfrac{{AM.\cos \alpha + AM.\cos \alpha }}{{AM.\sin \alpha }} = \dfrac{{2AM.\cos \alpha }}{{AM.\sin \alpha }} = 2\cot \alpha \).
Vì đường tròn \(\left( O \right)\) và \(BC\) cố định nên số đo cung \(BC\) không đổi.
\( \Rightarrow \angle BAC = 2\alpha = \dfrac{1}{2}\) số đo cung BC không đổi (góc nội tiếp bằng nửa số đo cung bị chắn).
\( \Rightarrow \alpha \) không đổi \( \Rightarrow 2\cot \alpha \) không đổi.
Vậy \(\dfrac{{AB}}{{MK}} + \dfrac{{AC}}{{MT}} = 2\cot \alpha \) không đổi, với \(\alpha = \dfrac{1}{4}\) số đo cung BC không đổi.
Câu 4 (1,0 điểm)
Cách giải::
Giải phương trình \(\sqrt {{x^2} + 3x} + \sqrt {9x + 18} = 3x + \sqrt {x + \dfrac{6}{x} + 5} \)
ĐK: \(\left\{ \begin{array}{l}{x^2} + 3x \ge 0\\9x + 18 \ge 0\\x + \dfrac{6}{x} + 5 \ge 0\\x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0,x \le - 3\\x \ge - 2\\\dfrac{{{x^2} + 5x + 6}}{x} \ge 0\\x \ne 0\end{array} \right. \Leftrightarrow x > 0\)
Khi đó
\(\begin{array}{l}PT \Leftrightarrow \sqrt {x\left( {x + 3} \right)} + 3\sqrt {x + 2} = 3x + \sqrt {\dfrac{{{x^2} + 5x + 6}}{x}} \\\,\,\,\,\,\,\, \Leftrightarrow \sqrt x \sqrt {x\left( {x + 3} \right)} + 3\sqrt x \sqrt {x + 2} = 3x\sqrt x + \sqrt {{x^2} + 5x + 6} \\\,\,\,\,\,\,\, \Leftrightarrow x\sqrt {x + 3} + 3\sqrt x \sqrt {x + 2} = 3x\sqrt x + \sqrt {\left( {x + 2} \right)\left( {x + 3} \right)} \\\,\,\,\,\,\,\, \Leftrightarrow x\sqrt {x + 3} - \sqrt {\left( {x + 2} \right)\left( {x + 3} \right)} + 3\sqrt x \sqrt {x + 2} - 3x\sqrt x = 0\\\,\,\,\,\,\,\, \Leftrightarrow \sqrt {x + 3} \left( {x - \sqrt {x + 2} } \right) - 3\sqrt x \left( {x - \sqrt {x + 2} } \right) = 0\\\,\,\,\,\,\,\, \Leftrightarrow \left( {x - \sqrt {x + 2} } \right)\left( {\sqrt {x + 3} - 3\sqrt x } \right) = 0\\\,\,\,\,\,\,\, \Leftrightarrow \left[ \begin{array}{l}x - \sqrt {x + 2} = 0\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\\sqrt {x + 3} - 3\sqrt x = 0\,\,\,\,\left( 2 \right)\end{array} \right.\end{array}\)
Ta có:
\(\begin{array}{l}\left( 1 \right) \Leftrightarrow x = \sqrt {x + 2} \Leftrightarrow {x^2} = x + 2\,\,\left( {Do\,\,x > 0} \right)\\\,\,\,\,\,\, \Leftrightarrow {x^2} - x - 2 = 0 \Leftrightarrow {x^2} + x - 2x - 2 = 0\\\,\,\,\,\,\, \Leftrightarrow x\left( {x + 1} \right) - 2\left( {x + 1} \right) = 0 \Leftrightarrow \left( {x + 1} \right)\left( {x - 2} \right) = 0\\\,\,\,\,\,\, \Leftrightarrow \left[ \begin{array}{l}x + 1 = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\,\,\,\left( {KTM} \right)\\x = 2\,\,\,\,\,\,\left( {TM} \right)\end{array} \right.\end{array}\)
\(\begin{array}{l}\left( 2 \right) \Leftrightarrow \sqrt {x + 3} = 3\sqrt x \\\,\,\,\,\,\,\, \Leftrightarrow x + 3 = 9x \Leftrightarrow 3 = 8x \Leftrightarrow x = \dfrac{3}{8}\,\,\,\,\left( {TM} \right)\end{array}\)
Vậy phương trình có tập nghiệm \(S = \left\{ {2;\dfrac{3}{8}} \right\}\).
Kỳ thi tuyển sinh vào lớp 10 là một bước ngoặt quan trọng trong quá trình học tập của mỗi học sinh. Để chuẩn bị tốt nhất cho kỳ thi này, việc nắm vững kiến thức và làm quen với các dạng đề thi là vô cùng cần thiết. Bài viết này sẽ cung cấp cho bạn đọc phân tích chi tiết về đề thi vào 10 môn Toán Phú Thọ năm 2020, cùng với hướng dẫn giải các bài toán khó, giúp bạn tự tin hơn khi bước vào phòng thi.
Đề thi vào 10 môn Toán Phú Thọ năm 2020 thường có cấu trúc gồm các phần sau:
Các kiến thức trọng tâm thường xuất hiện trong đề thi vào 10 môn Toán Phú Thọ năm 2020 bao gồm:
Dưới đây là phân tích một số câu hỏi khó thường gặp trong đề thi vào 10 môn Toán Phú Thọ năm 2020:
Một bài toán điển hình về phương trình bậc hai có thể yêu cầu học sinh tìm điều kiện để phương trình có nghiệm, tính tổng và tích các nghiệm, hoặc giải phương trình với các tham số. Để giải quyết bài toán này, học sinh cần nắm vững các công thức nghiệm của phương trình bậc hai và biết cách sử dụng các điều kiện để phương trình có nghiệm.
Các bài toán về hình học không gian thường yêu cầu học sinh tính diện tích bề mặt, thể tích của các hình khối, hoặc chứng minh các mối quan hệ giữa các yếu tố hình học. Để giải quyết bài toán này, học sinh cần nắm vững các công thức tính diện tích, thể tích và biết cách sử dụng các định lý hình học.
Các bài toán về bất đẳng thức thường yêu cầu học sinh chứng minh một bất đẳng thức, hoặc tìm giá trị lớn nhất, giá trị nhỏ nhất của một biểu thức. Để giải quyết bài toán này, học sinh cần nắm vững các bất đẳng thức cơ bản và biết cách sử dụng các phương pháp chứng minh bất đẳng thức.
Để ôn thi hiệu quả cho kỳ thi vào 10 môn Toán Phú Thọ năm 2020, bạn nên:
Dưới đây là một số tài liệu tham khảo hữu ích cho việc ôn thi vào 10 môn Toán:
Đề thi vào 10 môn Toán Phú Thọ năm 2020 là một kỳ thi quan trọng, đòi hỏi sự chuẩn bị kỹ lưỡng và nỗ lực không ngừng. Hy vọng rằng với những phân tích và hướng dẫn trong bài viết này, bạn sẽ có thêm kiến thức và tự tin hơn để đạt kết quả tốt nhất trong kỳ thi sắp tới. Chúc bạn thành công!