Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh An Giang năm 2020. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi sắp tới.
Bộ đề thi này được tổng hợp từ các nguồn chính thức, đảm bảo tính chính xác và độ tin cậy cao. Các em có thể sử dụng để tự học, luyện tập hoặc tham khảo cùng với thầy cô giáo.
Câu 1: Giải các phương trình và hệ phương trình sau đây:
Câu 1: Giải các phương trình và hệ phương trình sau đây:
a.\(\sqrt 3 x - \sqrt 3 = \sqrt 3 \) b. \(\left\{ \begin{array}{l}x + y = 7\\ - x + 2y = 2\end{array} \right.\) c. \({x^4} - 3{x^2} - 4 = 0\)
Câu 2: Cho hàm số \(y = {x^2}\) có đồ thị là parabol \(\left( P \right).\)
a. Vẽ đồ thị \(\left( P \right)\) trên hệ trục tọa độ
b. Viết phương trình đường thẳng \(\left( d \right)\) có hệ số góc bằng \( - 1\) và cắt parabol \(\left( P \right)\) tại điểm có hoành độ bằng \(1.\)
c. Với \(\left( d \right)\) vừa tìm được, tìm tọa độ giao điểm còn lại của \(\left( d \right)\) và \(\left( P \right)\)
Câu 3:
Cho phương trình bậc hai \({x^2} - 2x + m - 1 = 0\) (*), với \(m\) là tham số
a. Tìm tất cả các giá trị của \(m\) để phương trình (*) có nghiệm
b. Tính theo \(m\) giá trị của biểu thức \(A = x_1^3 + x_2^3\) với \({x_1},{x_2}\) là hai nghiệm của phương trình (*). Tìm giá trị nhỏ nhất của \(A.\)
Câu 4: Cho tam giác ABC có ba góc đều nhọn và nội tiếp trong đường tròn (O). Vẽ các đường cao AA’, BB’, CC’ cắt nhau tại H.
a) Chứng minh rằng tứ giác AB’HC’ là tứ giác nội tiếp.
b) Kéo dài AA’ cắt đường tròn (O) tại điểm D. Chứng minh rằng tam giác CDH cân.
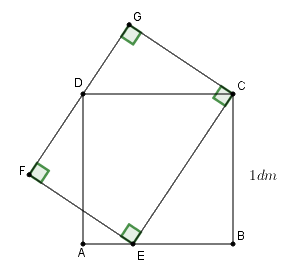
Câu 5: Cho \(ABCD\) là hình vuông có cạnh \(1dm.\) Trên cạnh \(AB\) lấy một điểm \(E.\) Dựng hình chữ nhật \(CEFG\) sao cho điểm \(D\) nằm trên cạnh \(FG.\) Tính diện tích hình chữ nhật \(CEFG\) (hình vẽ bên).
Câu 1 (3,0 điểm)
Cách giải:
Giải các phương trình và hệ phương trình sau đây:
a.\(\sqrt 3 x - \sqrt 3 = \sqrt 3 \)
Ta có: \(\sqrt 3 x - \sqrt 3 = \sqrt 3 \)
\(\begin{array}{l} \Leftrightarrow \sqrt 3 x = \sqrt 3 + \sqrt 3 \\ \Leftrightarrow \sqrt 3 x = 2\sqrt 3 \\ \Leftrightarrow x = 2\sqrt 3 :\sqrt 3 \\ \Leftrightarrow x = 2\end{array}\)
Vậy phương trình có nghiệm \(x = 2.\)
b. \(\left\{ \begin{array}{l}x + y = 7\\ - x + 2y = 2\end{array} \right.\)
Ta có:
\(\left\{ \begin{array}{l}x + y = 7\\ - x + 2y = 2\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}3y = 9\\x + y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 3\\x + 3 = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 3\\x = 4\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {4;3} \right)\)
c. \({x^4} - 3{x^2} - 4 = 0\)
Ta có:
\(\begin{array}{l}{x^4} - 3{x^2} - 4 = 0\\ \Leftrightarrow {x^4} - 4{x^2} + {x^2} - 4 = 0\\ \Leftrightarrow {x^2}\left( {{x^2} - 4} \right) + \left( {{x^2} - 4} \right) = 0\\ \Leftrightarrow \left( {{x^2} + 1} \right)\left( {{x^2} - 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}{x^2} + 1 = 0\\{x^2} - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^2} = - 1\left( {VN} \right)\\{x^2} = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 2\end{array} \right.\end{array}\)
Vậy phương trình có nghiệm \(x = - 2;x = 2.\)
Câu 2 (2 điểm)
Cách giải:
Cho hàm số \(y = {x^2}\) có đồ thị là parabol \(\left( P \right).\)
a. Vẽ đồ thị \(\left( P \right)\) trên hệ trục tọa độ
Bảng giá trị:
\(x\) | \( - 2\) | \( - 1\) | \(0\) | \(1\) | \(2\) |
\(y = {x^2}\) | \(4\) | \(1\) | \(0\) | \(1\) | \(4\) |
Đồ thị hàm số \(y = {x^2}\) là parabol \(\left( P \right)\) đi qua các điểm \(\left( { - 2;4} \right),\left( { - 1;1} \right),\left( {0;0} \right),\left( {1;1} \right),\left( {2;4} \right)\)
Hình vẽ:
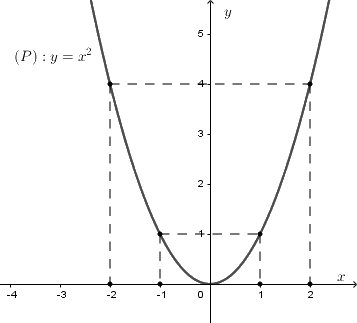
b. Viết phương trình đường thẳng \(\left( d \right)\) có hệ số góc bằng \( - 1\) và cắt parabol \(\left( P \right)\) tại điểm có hoành độ bằng \(1.\)
Gọi phương trình đường thẳng \(\left( d \right):y = ax + b\)
Vì đường thẳng \(\left( d \right)\) có hệ số góc bằng \( - 1\) nên \(a = - 1\)
Suy ra \(\left( d \right):y = - x + b\)
Gọi giao điểm của \(\left( d \right)\) và parabol \(\left( P \right)\) là \(M\left( {1;y} \right)\)
Vì \(M\left( {1;y} \right) \in \left( P \right)\) nên \(y = {x^2} = {1^2} = 1\), suy ra \(M\left( {1;1} \right)\)
Lại có \(M\left( {1;1} \right) \in \left( d \right)\) nên \(1 = - 1 + b \Leftrightarrow b = 2\)
Vậy phương trình đường thẳng \(\left( d \right):y = - x + 2\).
c. Với \(\left( d \right)\) vừa tìm được, tìm tọa độ giao điểm còn lại của \(\left( d \right)\) và \(\left( P \right)\)
Theo câu b) ta có: \(\left( d \right):y = - x + 2\)
Xét phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\), ta được:
\(\begin{array}{l}{x^2} = - x + 2\\ \Leftrightarrow {x^2} + x - 2 = 0\\ \Leftrightarrow {x^2} - x + 2x - 2 = 0\\ \Leftrightarrow x\left( {x - 1} \right) + 2\left( {x - 1} \right) = 0\\ \Leftrightarrow \left( {x + 2} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 2 = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 1\end{array} \right.\end{array}\)
Với \(x = 1 \Rightarrow y = {1^2} = 1\)
Với \(x = - 2 \Rightarrow y = {\left( { - 2} \right)^2} = 4\)
Vậy tọa độ giao điểm còn lại của \(\left( d \right)\) và \(\left( P \right)\) là: \(\left( { - 2;4} \right)\)
Câu 3 (2 điểm)
Cách giải:
Cho phương trình bậc hai \({x^2} - 2x + m - 1 = 0\) (*), với \(m\) là tham số
a. Tìm tất cả các giá trị của \(m\) để phương trình (*) có nghiệm
Xét phương trình \({x^2} - 2x + m - 1 = 0\) (*) có:
\(\Delta ' = {\left( { - 1} \right)^2} - 1.\left( {m - 1} \right) = 2 - m\)
Để phương trình (*) có nghiệm thì \(\left\{ \begin{array}{l}a \ne 0\\\Delta ' \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 \ne 0\left( {ld} \right)\\2 - m \ge 0\end{array} \right. \Leftrightarrow m \le 2\)
Vậy với \(m \le 2\) thì phương trình (*) có nghiệm
b. Tính theo \(m\) giá trị của biểu thức \(A = x_1^3 + x_2^3\) với \({x_1},{x_2}\) là hai nghiệm của phương trình (*). Tìm giá trị nhỏ nhất của \(A.\)
Theo câu a) với \(m \le 2\) thì phương trình (*) có nghiệm \({x_1},{x_2}\)
Theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}{x_2} = m - 1\end{array} \right.\)
Xét \(A = x_1^3 + x_2^3\)
\(\begin{array}{l} = x_1^3 + 3x_1^2{x_2} + 3{x_1}x_2^2 + x_2^3 - \left( {3x_1^2{x_2} + 3{x_1}x_2^2} \right)\\ = {\left( {{x_1} + {x_2}} \right)^3} - 3{x_1}{x_2}\left( {{x_1} + {x_2}} \right)\\ = {2^3} - 3\left( {m - 1} \right).2\\ = 8 - 6\left( {m - 1} \right)\\ = 8 - 6m + 6\\ = 14 - 6m\end{array}\)
Vậy \(A = 14 - 6m\)
Vì \(m \le 2\) nên ta có: \(6m \le 12 \Leftrightarrow 14 - 6m \ge 14 - 12 \Leftrightarrow 14 - 6m \ge 2\)
Dấu “=” xảy ra khi \(m = 2\)
Vậy giá trị nhỏ nhất của A là \(2 \Leftrightarrow m = 2\).
Câu 4 (2,0 điểm)
Cách giải:
Cho tam giác ABC có ba góc đều nhọn và nội tiếp trong đường tròn (O). Vẽ các đường cao AA’, BB’, CC’ cắt nhau tại H.
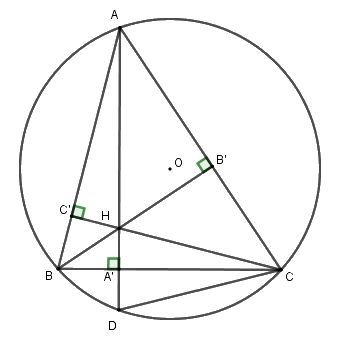
a) Chứng minh rằng tứ giác AB’HC’ là tứ giác nội tiếp.
Ta có:
\(\begin{array}{l}BB' \bot AC \Rightarrow \angle AB'H = {90^0}\\CC' \bot AB \Rightarrow \angle AC'H = {90^0}\end{array}\)
Tứ giác AB’HC’ có:
\(\angle AB'H + \angle AC'H = {90^0} + {90^0} = {180^0}\) nên là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\)) (đpcm)
b) Kéo dài AA’ cắt đường tròn (O) tại điểm D. Chứng minh rằng tam giác CDH cân.
Ta có:
\(\begin{array}{l}\angle BAA' + \angle ABA' = {90^0}\\\angle BCC' + \angle ABA' = {90^0}\\ \Rightarrow \angle BAA' = \angle BCC'\end{array}\)
Lại có \(\angle BAA' = \angle BCD\) (cùng chắn cung \(BD\) )
\( \Rightarrow \angle BCC' = \angle BCD\left( { = \angle BAA'} \right)\)
Xét tam giác CDH có \(CA'\) vừa là đường cao vừa là đường phân giác nên là tam giác cân (đpcm).
Câu 5 (1,0 điểm)
Cách giải:
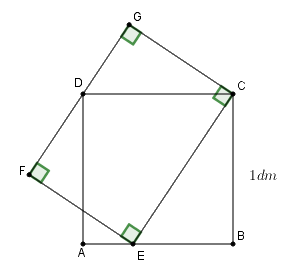
Cho \(ABCD\) là hình vuông có cạnh \(1dm.\) Trên cạnh \(AB\) lấy một điểm \(E.\) Dựng hình chữ nhật \(CEFG\) sao cho điểm \(D\) nằm trên cạnh \(FG.\) Tính diện tích hình chữ nhật \(CEFG\) (hình vẽ bên).
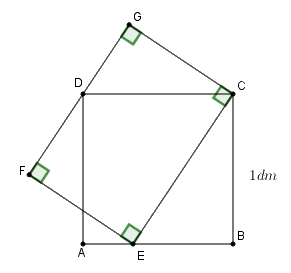
Ta có: \(\angle DCG = \angle BEC\) (cùng phụ với \(\angle DCE\))
Xét \(\Delta DCG\) và \(\Delta ECB\) có:
\(\angle G = \angle B = {90^0}\)
\(\angle DCG = \angle BEC\) (cmt)
Suy ra \(\Delta DCG \sim \Delta ECB\left( {g - g} \right)\)
\(\begin{array}{l} \Rightarrow \dfrac{{DC}}{{EC}} = \dfrac{{CG}}{{BC}}\\ \Rightarrow EC.CG = DC.BC = 1.1 = 1\end{array}\)
Suy ra \({S_{EFGC}} = EC.CG = 1d{m^2}\)
Câu 1: Giải các phương trình và hệ phương trình sau đây:
a.\(\sqrt 3 x - \sqrt 3 = \sqrt 3 \) b. \(\left\{ \begin{array}{l}x + y = 7\\ - x + 2y = 2\end{array} \right.\) c. \({x^4} - 3{x^2} - 4 = 0\)
Câu 2: Cho hàm số \(y = {x^2}\) có đồ thị là parabol \(\left( P \right).\)
a. Vẽ đồ thị \(\left( P \right)\) trên hệ trục tọa độ
b. Viết phương trình đường thẳng \(\left( d \right)\) có hệ số góc bằng \( - 1\) và cắt parabol \(\left( P \right)\) tại điểm có hoành độ bằng \(1.\)
c. Với \(\left( d \right)\) vừa tìm được, tìm tọa độ giao điểm còn lại của \(\left( d \right)\) và \(\left( P \right)\)
Câu 3:
Cho phương trình bậc hai \({x^2} - 2x + m - 1 = 0\) (*), với \(m\) là tham số
a. Tìm tất cả các giá trị của \(m\) để phương trình (*) có nghiệm
b. Tính theo \(m\) giá trị của biểu thức \(A = x_1^3 + x_2^3\) với \({x_1},{x_2}\) là hai nghiệm của phương trình (*). Tìm giá trị nhỏ nhất của \(A.\)
Câu 4: Cho tam giác ABC có ba góc đều nhọn và nội tiếp trong đường tròn (O). Vẽ các đường cao AA’, BB’, CC’ cắt nhau tại H.
a) Chứng minh rằng tứ giác AB’HC’ là tứ giác nội tiếp.
b) Kéo dài AA’ cắt đường tròn (O) tại điểm D. Chứng minh rằng tam giác CDH cân.
Câu 5: Cho \(ABCD\) là hình vuông có cạnh \(1dm.\) Trên cạnh \(AB\) lấy một điểm \(E.\) Dựng hình chữ nhật \(CEFG\) sao cho điểm \(D\) nằm trên cạnh \(FG.\) Tính diện tích hình chữ nhật \(CEFG\) (hình vẽ bên).
Câu 1 (3,0 điểm)
Cách giải:
Giải các phương trình và hệ phương trình sau đây:
a.\(\sqrt 3 x - \sqrt 3 = \sqrt 3 \)
Ta có: \(\sqrt 3 x - \sqrt 3 = \sqrt 3 \)
\(\begin{array}{l} \Leftrightarrow \sqrt 3 x = \sqrt 3 + \sqrt 3 \\ \Leftrightarrow \sqrt 3 x = 2\sqrt 3 \\ \Leftrightarrow x = 2\sqrt 3 :\sqrt 3 \\ \Leftrightarrow x = 2\end{array}\)
Vậy phương trình có nghiệm \(x = 2.\)
b. \(\left\{ \begin{array}{l}x + y = 7\\ - x + 2y = 2\end{array} \right.\)
Ta có:
\(\left\{ \begin{array}{l}x + y = 7\\ - x + 2y = 2\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}3y = 9\\x + y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 3\\x + 3 = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 3\\x = 4\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {4;3} \right)\)
c. \({x^4} - 3{x^2} - 4 = 0\)
Ta có:
\(\begin{array}{l}{x^4} - 3{x^2} - 4 = 0\\ \Leftrightarrow {x^4} - 4{x^2} + {x^2} - 4 = 0\\ \Leftrightarrow {x^2}\left( {{x^2} - 4} \right) + \left( {{x^2} - 4} \right) = 0\\ \Leftrightarrow \left( {{x^2} + 1} \right)\left( {{x^2} - 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}{x^2} + 1 = 0\\{x^2} - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^2} = - 1\left( {VN} \right)\\{x^2} = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 2\end{array} \right.\end{array}\)
Vậy phương trình có nghiệm \(x = - 2;x = 2.\)
Câu 2 (2 điểm)
Cách giải:
Cho hàm số \(y = {x^2}\) có đồ thị là parabol \(\left( P \right).\)
a. Vẽ đồ thị \(\left( P \right)\) trên hệ trục tọa độ
Bảng giá trị:
\(x\) | \( - 2\) | \( - 1\) | \(0\) | \(1\) | \(2\) |
\(y = {x^2}\) | \(4\) | \(1\) | \(0\) | \(1\) | \(4\) |
Đồ thị hàm số \(y = {x^2}\) là parabol \(\left( P \right)\) đi qua các điểm \(\left( { - 2;4} \right),\left( { - 1;1} \right),\left( {0;0} \right),\left( {1;1} \right),\left( {2;4} \right)\)
Hình vẽ:
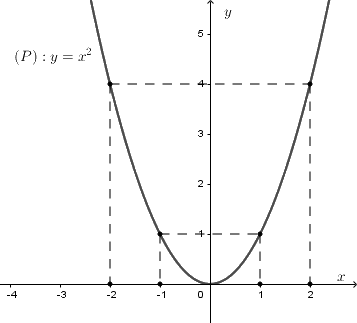
b. Viết phương trình đường thẳng \(\left( d \right)\) có hệ số góc bằng \( - 1\) và cắt parabol \(\left( P \right)\) tại điểm có hoành độ bằng \(1.\)
Gọi phương trình đường thẳng \(\left( d \right):y = ax + b\)
Vì đường thẳng \(\left( d \right)\) có hệ số góc bằng \( - 1\) nên \(a = - 1\)
Suy ra \(\left( d \right):y = - x + b\)
Gọi giao điểm của \(\left( d \right)\) và parabol \(\left( P \right)\) là \(M\left( {1;y} \right)\)
Vì \(M\left( {1;y} \right) \in \left( P \right)\) nên \(y = {x^2} = {1^2} = 1\), suy ra \(M\left( {1;1} \right)\)
Lại có \(M\left( {1;1} \right) \in \left( d \right)\) nên \(1 = - 1 + b \Leftrightarrow b = 2\)
Vậy phương trình đường thẳng \(\left( d \right):y = - x + 2\).
c. Với \(\left( d \right)\) vừa tìm được, tìm tọa độ giao điểm còn lại của \(\left( d \right)\) và \(\left( P \right)\)
Theo câu b) ta có: \(\left( d \right):y = - x + 2\)
Xét phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\), ta được:
\(\begin{array}{l}{x^2} = - x + 2\\ \Leftrightarrow {x^2} + x - 2 = 0\\ \Leftrightarrow {x^2} - x + 2x - 2 = 0\\ \Leftrightarrow x\left( {x - 1} \right) + 2\left( {x - 1} \right) = 0\\ \Leftrightarrow \left( {x + 2} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 2 = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 1\end{array} \right.\end{array}\)
Với \(x = 1 \Rightarrow y = {1^2} = 1\)
Với \(x = - 2 \Rightarrow y = {\left( { - 2} \right)^2} = 4\)
Vậy tọa độ giao điểm còn lại của \(\left( d \right)\) và \(\left( P \right)\) là: \(\left( { - 2;4} \right)\)
Câu 3 (2 điểm)
Cách giải:
Cho phương trình bậc hai \({x^2} - 2x + m - 1 = 0\) (*), với \(m\) là tham số
a. Tìm tất cả các giá trị của \(m\) để phương trình (*) có nghiệm
Xét phương trình \({x^2} - 2x + m - 1 = 0\) (*) có:
\(\Delta ' = {\left( { - 1} \right)^2} - 1.\left( {m - 1} \right) = 2 - m\)
Để phương trình (*) có nghiệm thì \(\left\{ \begin{array}{l}a \ne 0\\\Delta ' \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 \ne 0\left( {ld} \right)\\2 - m \ge 0\end{array} \right. \Leftrightarrow m \le 2\)
Vậy với \(m \le 2\) thì phương trình (*) có nghiệm
b. Tính theo \(m\) giá trị của biểu thức \(A = x_1^3 + x_2^3\) với \({x_1},{x_2}\) là hai nghiệm của phương trình (*). Tìm giá trị nhỏ nhất của \(A.\)
Theo câu a) với \(m \le 2\) thì phương trình (*) có nghiệm \({x_1},{x_2}\)
Theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}{x_2} = m - 1\end{array} \right.\)
Xét \(A = x_1^3 + x_2^3\)
\(\begin{array}{l} = x_1^3 + 3x_1^2{x_2} + 3{x_1}x_2^2 + x_2^3 - \left( {3x_1^2{x_2} + 3{x_1}x_2^2} \right)\\ = {\left( {{x_1} + {x_2}} \right)^3} - 3{x_1}{x_2}\left( {{x_1} + {x_2}} \right)\\ = {2^3} - 3\left( {m - 1} \right).2\\ = 8 - 6\left( {m - 1} \right)\\ = 8 - 6m + 6\\ = 14 - 6m\end{array}\)
Vậy \(A = 14 - 6m\)
Vì \(m \le 2\) nên ta có: \(6m \le 12 \Leftrightarrow 14 - 6m \ge 14 - 12 \Leftrightarrow 14 - 6m \ge 2\)
Dấu “=” xảy ra khi \(m = 2\)
Vậy giá trị nhỏ nhất của A là \(2 \Leftrightarrow m = 2\).
Câu 4 (2,0 điểm)
Cách giải:
Cho tam giác ABC có ba góc đều nhọn và nội tiếp trong đường tròn (O). Vẽ các đường cao AA’, BB’, CC’ cắt nhau tại H.
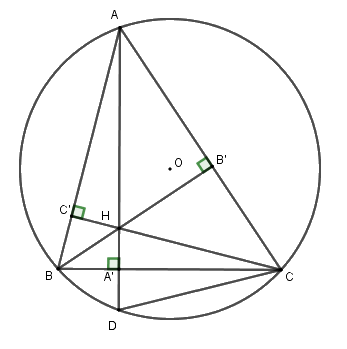
a) Chứng minh rằng tứ giác AB’HC’ là tứ giác nội tiếp.
Ta có:
\(\begin{array}{l}BB' \bot AC \Rightarrow \angle AB'H = {90^0}\\CC' \bot AB \Rightarrow \angle AC'H = {90^0}\end{array}\)
Tứ giác AB’HC’ có:
\(\angle AB'H + \angle AC'H = {90^0} + {90^0} = {180^0}\) nên là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\)) (đpcm)
b) Kéo dài AA’ cắt đường tròn (O) tại điểm D. Chứng minh rằng tam giác CDH cân.
Ta có:
\(\begin{array}{l}\angle BAA' + \angle ABA' = {90^0}\\\angle BCC' + \angle ABA' = {90^0}\\ \Rightarrow \angle BAA' = \angle BCC'\end{array}\)
Lại có \(\angle BAA' = \angle BCD\) (cùng chắn cung \(BD\) )
\( \Rightarrow \angle BCC' = \angle BCD\left( { = \angle BAA'} \right)\)
Xét tam giác CDH có \(CA'\) vừa là đường cao vừa là đường phân giác nên là tam giác cân (đpcm).
Câu 5 (1,0 điểm)
Cách giải:
Cho \(ABCD\) là hình vuông có cạnh \(1dm.\) Trên cạnh \(AB\) lấy một điểm \(E.\) Dựng hình chữ nhật \(CEFG\) sao cho điểm \(D\) nằm trên cạnh \(FG.\) Tính diện tích hình chữ nhật \(CEFG\) (hình vẽ bên).
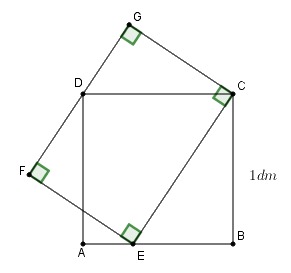
Ta có: \(\angle DCG = \angle BEC\) (cùng phụ với \(\angle DCE\))
Xét \(\Delta DCG\) và \(\Delta ECB\) có:
\(\angle G = \angle B = {90^0}\)
\(\angle DCG = \angle BEC\) (cmt)
Suy ra \(\Delta DCG \sim \Delta ECB\left( {g - g} \right)\)
\(\begin{array}{l} \Rightarrow \dfrac{{DC}}{{EC}} = \dfrac{{CG}}{{BC}}\\ \Rightarrow EC.CG = DC.BC = 1.1 = 1\end{array}\)
Suy ra \({S_{EFGC}} = EC.CG = 1d{m^2}\)
Kỳ thi tuyển sinh vào lớp 10 là một bước ngoặt quan trọng trong quá trình học tập của mỗi học sinh. Để đạt kết quả tốt nhất, việc chuẩn bị kỹ lưỡng là điều cần thiết. Đề thi vào 10 môn Toán An Giang năm 2020 là một nguồn tài liệu quý giá để các em học sinh có thể làm quen với dạng đề và rèn luyện kỹ năng giải toán.
Đề thi vào 10 môn Toán An Giang năm 2020 thường bao gồm các dạng bài tập sau:
Phương trình bậc hai là một trong những dạng bài tập cơ bản và thường xuyên xuất hiện trong đề thi vào 10. Để giải phương trình bậc hai, các em có thể sử dụng công thức nghiệm hoặc phương pháp phân tích thành nhân tử.
Ví dụ: Giải phương trình 2x2 - 5x + 2 = 0
Sử dụng công thức nghiệm, ta có:
x = (-b ± √(b2 - 4ac)) / 2a
Trong đó: a = 2, b = -5, c = 2
Thay vào công thức, ta được:
x = (5 ± √((-5)2 - 4 * 2 * 2)) / (2 * 2)
x = (5 ± √9) / 4
x = (5 ± 3) / 4
Vậy, phương trình có hai nghiệm: x1 = 2 và x2 = 1/2
Các bài toán chứng minh đẳng thức hình học đòi hỏi các em phải nắm vững các định lý và tính chất hình học. Để chứng minh đẳng thức hình học, các em có thể sử dụng các phương pháp như chứng minh tam giác bằng nhau, chứng minh tứ giác nội tiếp, hoặc sử dụng các hệ thức lượng trong tam giác vuông.
Ngoài đề thi vào 10 môn Toán An Giang năm 2020, các em có thể tham khảo thêm các tài liệu ôn thi sau:
Đề thi vào 10 môn Toán An Giang năm 2020 là một tài liệu quan trọng giúp các em học sinh chuẩn bị tốt nhất cho kỳ thi sắp tới. Hy vọng rằng với những phân tích và hướng dẫn giải chi tiết trên đây, các em sẽ tự tin hơn và đạt kết quả tốt nhất trong kỳ thi tuyển sinh vào lớp 10.