Giaitoan.edu.vn xin giới thiệu bộ đề thi vào 10 môn Toán Hải Phòng năm 2019 chính thức, được cập nhật mới nhất. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi sắp tới.
Đề thi bao gồm các dạng bài tập đa dạng, từ cơ bản đến nâng cao, bám sát chương trình học lớp 9 và kiến thức trọng tâm của môn Toán. Các em có thể tải đề thi về giải trực tiếp hoặc luyện thi online trên nền tảng của chúng tôi.
Bài 1: (1,5 điểm) Cho hai biểu thức:
\(A = \left( {\sqrt {20} - \sqrt {45} + 3\sqrt 5 } \right):\sqrt 5 ;\) \(B = \dfrac{{x + 2\sqrt x }}{{\sqrt x }} + \dfrac{{x - 9}}{{\sqrt x + 3}}\) (với \(x > 0\)).
a) Rút gọn các biểu thức \(A,\,\,B\).
b) Tìm các giá trị của \(x\) sao cho giá trị biểu thức \(B\)bằng giá trị biểu thức \(A\).
Bài 2:(1,5 điểm)
a) Tìm các giá trị của tham số \(m\) để đồ thị hai hàm số \(y = \left( {m + 4} \right)x + 11\) và \(y = x + {m^2} + 2\) cắt nhau tại một điểm trên trục tung.
b) Giải hệ phương trình \(\left\{ \begin{array}{l}3x - \dfrac{2}{{y + 1}} = - \dfrac{1}{2}\\2x + \dfrac{1}{{y + 1}} = 2\end{array} \right..\)
Bài 3:(2,5 điểm)
1. Cho phương trình \({x^2} - 2mx + 4m - 4 = 0\,\,(1)\) (\(x\) là ẩn số, \(m\) là tham số).
a) Giải phương trình (1) khi \(m = 1.\)
b) Xác định các giá trị của \(m\) để phương trình (1) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn điều kiện \(x_1^2 + ({x_1} + {x_2}){x_2} = 12\).
2. Bài toán có nội dung thực tế
Cho một thửa ruộng hình chữ nhật, biết rằng nếu chiều rộng tăng thêm \(2m\), chiều dài giảm đi \(2m\) thì diện tích thửa ruộng đó tăng thêm \(30{m^2}\); và nếu chiều rộng giảm đi \(2m\), chiều dài tăng thêm \(5m\) thì diện tích thửa ruộng giảm đi \(20{m^2}\). Tính diện tích thửa ruộng trên.
Bài 4:(3,5 điểm)
1. Từ điểm \(A\) nằm bên ngoài đường tròn \((O)\) vẽ hai tiếp tuyến \(AD,\,AE\) (\(D,\,E\)là các tiếp điểm). Vẽ cát tuyến \(ABC\) của đường tròn \((O)\)sao cho điểm \(B\) nằm giữa hai điểm \(A,\,C;\) tia \(AC\)nằm giữa hai tia \(AD\)và \(AO\). Từ điểm \(O\) kẻ \(OI \bot AC\) tại \(I.\)
a) Chứng minh năm điểm \(A,\,D,\,I,\,O,\,E\) cùng nằm trên một đường tròn.
b) Chứng minh \(IA\) là tia phân giác của \(\angle DIE\) và \(AB.AC = A{D^2}\).
c) Gọi \(K\) và \(F\) lần lượt là giao điểm của \(ED\) với \(AC\) và \(OI\).Qua điểm \(D\) vẽ đường thẳng song song với \(IE\) cắt \(OF\) và \(AC\) lần lượt tại \(H\) và \(P\). Chứng minh \(D\) là trung điểm của \(HP.\)
2.Một hình trụ có diện tích xung quanh \(140\pi \,\,\left( {c{m^2}} \right)\) và chiều cao là \(h = 7\,\,\left( {cm} \right).\) Tính thể tích của hình trụ đó.
Bài 5: (1,0 điểm)
a) Cho \(x,\,y,\,z\) là ba số dương. Chúng minh \(\left( {x + y + z} \right)\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right) \ge 9.\)
b) Cho \(a,\,b,\,c\) là ba số dương thỏa mãn \(a + b + c = 6.\) Tìm giá trị lớn nhất của biểu thức
\(A =\dfrac{{ab}}{{a + 3b + 2c}} + \dfrac{{bc}}{{b + 3c + 2a}} + \dfrac{{ca}}{{c + 3a + 2b}}.\)
Bài 1
Phương pháp:
a) Rút gọn biểu thức
b) Đưa bài toán về tìm \(x\) để \(A = B\)(chú ý đối chiếu điều kiện xác định).
Cách giải:
Cho hai biểu thức:
\(A = \left( {\sqrt {20} - \sqrt {45} + 3\sqrt 5 } \right):\sqrt 5 ;\)\(B = \dfrac{{x + 2\sqrt x }}{{\sqrt x }} + \dfrac{{x - 9}}{{\sqrt x + 3}}\) (với \(x > 0\)).
a) Rút gọn các biểu thức \(A,\,\,B\).
\(\begin{array}{l}A = \left( {\sqrt {20} - \sqrt {45} + 3\sqrt 5 } \right):\sqrt 5 \\\,\,\,\,\, = \left( {2\sqrt 5 - 3\sqrt 5 + 3\sqrt 5 } \right):\sqrt 5 \\\,\,\,\,\, = 2\sqrt 5 :\sqrt 5 \\\,\,\,\,\, = 2\end{array}\)
Điều kiện: \(x > 0.\)
\(\begin{array}{l}B = \dfrac{{x + 2\sqrt x }}{{\sqrt x }} + \dfrac{{x - 9}}{{\sqrt x + 3}}\\\,\,\,\,\, = \dfrac{{\sqrt x \left( {\sqrt x + 2} \right)}}{{\sqrt x }} + \dfrac{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}{{\sqrt x + 3}}\\\,\,\,\,\, = \sqrt x + 2 + \sqrt x - 3\\\,\,\,\,\, = 2\sqrt x - 1.\end{array}\)
b) Tìm các giá trị của \(x\) sao cho giá trị biểu thức \(B\)bằng giá trị biểu thức \(A\).
Điều kiện: \(x > 0.\)
Để \(A = B\) thì \(2\sqrt x - 1 = 2\, \Leftrightarrow \sqrt x = \dfrac{3}{2} \Leftrightarrow x = \dfrac{9}{4}\,\,\,\left( {tm} \right)\)
Vậy \(x = \dfrac{9}{4}\) thì \(A = B\).
Bài 2
Phương pháp:
a) Xét phương trình hoành độ giao điểm. Để 2 đồ thị hàm số cắt nhau tại một điểm trên trục tung thì tìm điều kiện để phương trình hoành độ giao điểm có nghiệm duy nhất \(x = 0\)
b) Đặt \(t = \dfrac{1}{{y + 1}}\) và giải hệ phương trình bằng phương pháp cộng đại số ra \(x,\,t\). Từ đó tìm được \(x,\,y\).
Cách giải:
a) Tìm các giá trị của tham số \(m\)để đồ thị hai hàm số \(y = \left( {m + 4} \right)x + 11\) và \(y = x + {m^2} + 2\) cắt nhau tại một điểm trên trục tung.
Xét phương trình hoành độ giao điểm của hai hàm số ta có:
\(\left( {m + 4} \right)x + 11 = x + {m^2} + 2 \Leftrightarrow \left( {m + 3} \right)x = {m^2} - 9\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
Để 2 đồ thị hàm số cắt nhau tại một điểm trên trục tung thì phương trình (1) có nghiệm duy nhất \(x = 0\)
\( \Leftrightarrow \left\{ \begin{array}{l}m + 3 \ne 0\\x = \dfrac{{{m^2} - 9}}{{m + 3}} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne - 3\\m - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne - 3\\m = 3\end{array} \right. \Rightarrow m = 3\)
Vậy \(m = 3.\)
b) Giải hệ phương trình \(\left\{ \begin{array}{l}3x - \dfrac{2}{{y + 1}} = - \dfrac{1}{2}\\2x + \dfrac{1}{{y + 1}} = 2\end{array} \right..\)
Điều kiện: \(y \ne - 1\)
Đặt \(t = \dfrac{1}{{y + 1}}\)
Hệ phương trình \( \Leftrightarrow \left\{ \begin{array}{l}3x - 2t = - \dfrac{1}{2}\\2x + t = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x - 2t = - \dfrac{1}{2}\\4x + 2t = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}7x = \dfrac{7}{2}\\2x + t = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{1}{2}\\t = 1\end{array} \right..\)
Với \(t = 1\) thì \(\dfrac{1}{{y + 1}} = 1 \Rightarrow y + 1 = 1 \Leftrightarrow y = 0\,\,\,\,\left( {tm} \right)\)
Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {\dfrac{1}{2};0} \right)\)
Bài 3
Phương pháp:
1a) Thay \(m = 1\) vào phương trình, giải phương trình bằng phương pháp đưa về phương trình tích.
1b) Tìm điều kiện \(\Delta ' > 0\) để phương trình có 2 nghiệm phân biệt rồi biến đổi điều kiện bài toán về tổng và tích 2 nghiệm và áp dụng hệ thức Vi-et và hệ thức bài cho để tìm \(m.\)
Đối chiếu với điều kiện của \(m\) rồi kết luận.
2) Gọi chiều rộng hình chữ nhật là \(x\,\,\left( m \right)\,\,\,\left( {x > 2} \right)\)
chiều dài hình chữ nhật là \(y\,\,\left( m \right)\,\,\,\left( {y > x > 2} \right).\)
Dựa vào các giả thiết của bài toán để lập hệ phương trình.
Giải hệ phương trình rồi đối chiếu với điều kiện sau đó kết luận.
Cách giải:
1. Cho phương trình \({x^2} - 2mx + 4m - 4 = 0\,\,(1)\) (\(x\) là ẩn số, \(m\) là tham số).
a) Giải phương trình (1) khi \(m = 1.\)
Với \(m = 1\) ta có phương trình \(\left( 1 \right) \Leftrightarrow {x^2} - 2x = 0 \Leftrightarrow x\left( {x - 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right..\)
Vậy với \(m = 1\) thì phương trình có tập nghiệm \(S = \left\{ {0;\,\,2} \right\}.\)
b) Xác định các giá trị của \(m\) để phương trình (1) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn điều kiện \(x_1^2 + ({x_1} + {x_2}){x_2} = 12\)
\({x^2} - 2mx + 4m - 4 = 0\,\,\,\,\,\,\left( 1 \right)\)
Có: \(\Delta ' = {m^2} - \left( {4m - 4} \right) = {m^2} - 4m + 4 = {\left( {m - 2} \right)^2} \ge 0\,\,\,\,\,\,\,\forall m\)
Để phương trình (1) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thì \(\Delta ' > 0 \Leftrightarrow m \ne 2\)
Với \(m \ne 2\), theo hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}.{x_2} = 4m - 4\end{array} \right.\,\,(*)\)
Theo đề bài ta có: \(x_1^2 + \left( {{x_1} + {x_2}} \right){x_2} = 12\)
\(\begin{array}{l} \Leftrightarrow x_1^2 + {x_2}^2 + {x_1}{x_2} = 12\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} + {x_1}{x_2} = 12\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - {x_1}{x_2} = 12\\ \Leftrightarrow {\left( {2m} \right)^2} - \left( {4m - 4} \right) = 12\\ \Leftrightarrow 4{m^2} - 4m - 8 = 0\\ \Leftrightarrow 4\left( {{m^2} - m - 2} \right) = 0\\ \Leftrightarrow 4\left( {m - 2} \right)\left( {m + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m - 2 = 0\\m + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 2\,\,\,\,\left( {ktm} \right)\\m = - 1\,\,\,\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy \(m = - 1\) là giá trị cần tìm.
2. Bài toán có nội dung thực tế
Cho một thửa ruộng hình chữ nhật, biết rằng nếu chiều rộng tăng thêm \(2m\), chiều dài giảm đi \(2m\) thì diện tích thửa ruộng đó tăng thêm \(30{m^2}\); và nếu chiều rộng giảm đi \(2m\), chiều dài tăng thêm \(5m\) thì diện tích thửa ruộng giảm đi \(20{m^2}\). Tính diện tích thửa ruộng trên.
Gọi chiều rộng hình chữ nhật là \(x\,\,\left( m \right)\,\,\,\left( {x > 2} \right)\)
chiều dài hình chữ nhật là \(y\,\,\left( m \right)\,\,\,\left( {y > x > 2} \right).\)
Diện tích thửa ruộng ban đầu là \(xy\,\,\,\,\left( {{m^2}} \right).\)
Khi chiều rộng tăng thêm \(2m\), chiều dài giảm đi \(2m\) thì diện tích thửa ruộng tăng thêm \(30{m^2}\) nên ta có:
\(\left( {x + 2} \right)\left( {y - 2} \right) = xy + 30 \Leftrightarrow - 2x + 2y = 34\,\,\,\,\,\,\left( 1 \right)\)
Khi chiều rộng giảm đi \(2m\), chiều dài tăng thêm \(5m\) thì diện tích thửa ruộng giảm đi \(20{m^2}\) nên ta có \(\left( {x - 2} \right)\left( {y + 5} \right) = xy - 20 \Leftrightarrow 5x - 2y = - 10\,\,\,\,\,\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{l} - 2x + 2y = 34\\5x - 2y = - 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - x + y = 17\\3x = 24\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 25\,\,\,\,\left( {tm} \right)\\x = 8\,\,\,\,\,\,\,\,\left( {tm} \right)\end{array} \right.\)
Diện tích thửa ruộng ban đầu là \(25.8 = 200\,\,{m^2}.\)
Bài 4
Phương pháp:
1a) Các góc cùng nhìn 1 cạnh dưới 1 góc vuông.
1b) Chứng minh \(\angle DIA = \angle EIA\) bằng cách sử dụng câu a) 5 điểm cùng thuộc một đường tròn.
1c) Chứng minh tam giác \(DIH\)và \(DIP\) cân tại \(D\). Khi đó \(DH = DP( = DI)\)
2) Dựa vào công thức \({S_{xq}} = 2\pi .r.h\) khi biết chiều cao \(h\) và diện tích xung quanh hình trụ để tính bán kính đáy trụ \(r.\) Sau đó dùng công thức \(V = \pi .{r^2}.h\) để tính thể tích hình trụ.
Cách giải:
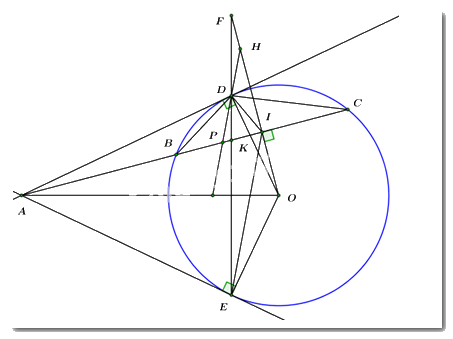
1a) Chứng minh năm điểm \(A,\,D,\,I,\,O,\,E\) cùng nằm trên một đường tròn.
\(AD,\,\,AE\) là các tiếp tuyến của \(\left( O \right) \Rightarrow \left\{ \begin{array}{l}OD \bot AD = \left\{ D \right\}\\OE \bot AE = \left\{ E \right\}\end{array} \right. \Rightarrow \angle ODA = \angle OEA = {90^0}\)
\(OI \bot AC = \left\{ I \right\} \Rightarrow \angle OIA = {90^0}\)
Ta có: \(\angle ODA,\,\,\,\angle OEA\) cùng nhìn \(OA\) dưới một góc vuông (cmt) và \(\angle OIA\) cũng nhìn \(OA\) dưới một góc vuông (cmt)
Nên \(D,\,\,\,E,\,\,\,O,\,\,\,A,\,\,\,I\) cùng thuộc một đường tròn đường kính \(OA\). (đpcm).
b) Chứng minh \(IA\) là tia phân giác của \(\angle DIE\) và \(AB.AC = A{D^2}\).
Do \(AD,\,AE\)là tiếp tuyến \(\left( O \right) \Rightarrow AO\) là phân giác của \(\angle DOE \Rightarrow \angle DOA = \angle AOE\,\,\,\,\left( 1 \right)\) (tính chất hai tiếp tuyến cắt nhau).
Ta có tứ giác \(ADOE\)nội tiếp đường tròn đường kính \(AO\,\,\,\left( {cmt} \right) \Rightarrow \angle DIA = \angle DOA\,\,\,\,\left( 2 \right)\) (hai góc nội tiếp cùng chắn cung \(DA\))
Ta có tứ giác \(AIOE\)nội tiếp đường tròn đường kính \(AO\,\,\,\left( {cmt} \right) \Rightarrow \angle EIA = \angle EOA\,\,\,\,\,\,\left( 3 \right)\) (hai góc nội tiếp cùng chắn cung \(EA\))
\( \Rightarrow \angle DIA = \angle EIA \Rightarrow IA\) là phân giác của góc \(\angle DIE.\) (đpcm)
Xét \(\Delta ABD\) và \(\Delta ADC\)ta có:
\(\angle A\,\,\,\,chung\)
\(\angle BDA = \angle DCA\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(BD\))
c) Gọi \(K\) và \(F\) lần lượt là giao điểm của \(ED\) với \(AC\) và \(OI\). Qua điểm \(D\) vẽ đường thẳng song song với \(IE\) cắt \(OF\) và \(AC\) lần lượt tại \(H\) và \(P\). Chứng minh \(D\) là trung điểm của \(HP.\)
Ta có: \(DP//IE\,\,\left( {gt} \right) \Rightarrow \angle DPI = \angle EIP\) (hai góc so le trong)
mà \(\angle DIP = \angle PIE\,\,\,\,\left( {cmt\,\,\,\,\angle DIA = \angle AIE} \right)\)
\( \Rightarrow \angle DIP = \angle DPI \Rightarrow \Delta DIP\) cân tại \(D\)
\( \Rightarrow DI = DP\,\,\,\,\,\left( 1 \right)\)
Ta có: \(DH//IE \Rightarrow \angle DHI = \angle EIO\) (hai góc đồng vị)
Ta có \(\angle HID + \angle PID = \angle PIE + \angle EIO = {90^0}\) mà \(\angle PID = \angle PIE \Rightarrow \angle HID = \angle EIO\,\)
\( \Rightarrow \angle DHI = \angle HID \Rightarrow \Delta HID\) cân tại \(D\)\( \Rightarrow DI = DH\,\,\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow D\) là trung điểm \(HP.\)
2. Một hình trụ có diện tích xung quanh \(140\pi \,\,\left( {c{m^2}} \right)\) và chiều cao là \(h = 7\,\,\left( {cm} \right).\) Tính thể tích của hình trụ đó.
Diện tích xung quanh của hình trụ là \({S_{xq}} = 2\pi .r.h = 2\pi .r.7 = 140\pi \)
\( \Rightarrow \) bán kính của đáy trụ là \(r = \dfrac{{140\pi }}{{2\pi .7}} = 10\,\,\left( {cm} \right)\)
Thể tích hình trụ là \(V = \pi .{r^2}.h = \pi {.10^2}.7 = 700\pi \,\,c{m^3}.\)
Bài 5
Phương pháp:
Sử dụng bất đẳng thức Cô-si cho 2 bộ 3 số dương \(x;y;z\) và \(\dfrac{1}{x};\dfrac{1}{y};\dfrac{1}{z}.\)
Cách giải:
a) Cho \(x,\,y,\,z\) là ba số dương. Chứng minh \(\left( {x + y + z} \right)\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right) \ge 9.\)
Áp dụng bất đẳng thức Cô-si cho bộ 3 số dương \(x;y;z\) ta có: \(\left( {x + y + z} \right) \ge 3\sqrt[3]{{xyz}}\)
Áp dụng bất đẳng thức Cô-si cho bộ 3 số dương \(\dfrac{1}{x};\dfrac{1}{y};\dfrac{1}{z}:\) \(\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right) \ge 3\sqrt[3]{{\dfrac{1}{{xyz}}}}.\)
\( \Rightarrow \left( {x + y + z} \right)\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right) \ge 9\sqrt[3]{{xyz.\dfrac{1}{{xyz}}}} = 9\) (đpcm)
Dấu “=” xảy ra \( \Leftrightarrow x = y = z.\)
b) Cho \(a,\,b,\,c\) là ba số dương thỏa mãn \(a + b + c = 6.\) Tìm giá trị lớn nhất của biểu thức
\(A = \dfrac{{ab}}{{a + 3b + 2c}} + \dfrac{{bc}}{{b + 3c + 2a}} + \dfrac{{ca}}{{c + 3a + 2b}}.\)
Ta có: \(\dfrac{{ab}}{{a + 3b + 2c}} = \dfrac{{ab}}{{a + c + b + c + 2b}}\)
Áp dụng câu a) \(9 \le \left( {x + y + z} \right)\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right) \Rightarrow \dfrac{1}{{x + y + z}} \le \dfrac{1}{9}\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right).\)
\( \Rightarrow \dfrac{{ab}}{{a + 3b + 2c}} \le ab.\dfrac{1}{9}\left( {\dfrac{1}{{a + c}} + \dfrac{1}{{b + c}} + \dfrac{1}{{2b}}} \right) = \dfrac{1}{9}\left( {\dfrac{{ab}}{{a + c}} + \dfrac{{ab}}{{b + c}} + \dfrac{a}{2}} \right)\)
Tương tự ta có: \(\left\{ \begin{array}{l}\dfrac{{bc}}{{b + 3c + 2a}} \le bc.\dfrac{1}{9}\left( {\dfrac{1}{{b + a}} + \dfrac{1}{{a + c}} + \dfrac{1}{{2c}}} \right) = \dfrac{1}{9}\left( {\dfrac{{bc}}{{b + a}} + \dfrac{{bc}}{{a + c}} + \dfrac{b}{2}} \right)\\\dfrac{{ca}}{{c + 3a + 2b}} \le ca.\dfrac{1}{9}\left( {\dfrac{1}{{c + b}} + \dfrac{1}{{b + a}} + \dfrac{1}{{2a}}} \right) = \dfrac{1}{9}\left( {\dfrac{{ca}}{{c + b}} + \dfrac{{ca}}{{a + b}} + \dfrac{c}{2}} \right)\end{array} \right.\)
\( \Rightarrow A \le \dfrac{1}{9}\left( {\dfrac{{ab + bc}}{{a + c}} + \dfrac{{ab + ca}}{{b + c}} + \dfrac{{bc + ca}}{{a + b}} + \dfrac{{a + b + c}}{2}} \right)\)
\( \Leftrightarrow A \le \dfrac{1}{9}\left( {b + a + c + \dfrac{{a + b + c}}{2}} \right) = \dfrac{1}{9}\left( {6 + \dfrac{6}{2}} \right) = 1\) với \(a + b + c = 6\)
Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}a = b = c\\a + b + c = 6\end{array} \right. \Leftrightarrow a = b = c = 2.\)
Vậy \(Max\,\,A = 1\) khi \(a = b = c = 2.\)
\(A = \left( {\sqrt {20} - \sqrt {45} + 3\sqrt 5 } \right):\sqrt 5 ;\) \(B = \dfrac{{x + 2\sqrt x }}{{\sqrt x }} + \dfrac{{x - 9}}{{\sqrt x + 3}}\) (với \(x > 0\)).
a) Rút gọn các biểu thức \(A,\,\,B\).
b) Tìm các giá trị của \(x\) sao cho giá trị biểu thức \(B\)bằng giá trị biểu thức \(A\).
Bài 2:(1,5 điểm)
a) Tìm các giá trị của tham số \(m\) để đồ thị hai hàm số \(y = \left( {m + 4} \right)x + 11\) và \(y = x + {m^2} + 2\) cắt nhau tại một điểm trên trục tung.
b) Giải hệ phương trình \(\left\{ \begin{array}{l}3x - \dfrac{2}{{y + 1}} = - \dfrac{1}{2}\\2x + \dfrac{1}{{y + 1}} = 2\end{array} \right..\)
Bài 3:(2,5 điểm)
1. Cho phương trình \({x^2} - 2mx + 4m - 4 = 0\,\,(1)\) (\(x\) là ẩn số, \(m\) là tham số).
a) Giải phương trình (1) khi \(m = 1.\)
b) Xác định các giá trị của \(m\) để phương trình (1) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn điều kiện \(x_1^2 + ({x_1} + {x_2}){x_2} = 12\).
2. Bài toán có nội dung thực tế
Cho một thửa ruộng hình chữ nhật, biết rằng nếu chiều rộng tăng thêm \(2m\), chiều dài giảm đi \(2m\) thì diện tích thửa ruộng đó tăng thêm \(30{m^2}\); và nếu chiều rộng giảm đi \(2m\), chiều dài tăng thêm \(5m\) thì diện tích thửa ruộng giảm đi \(20{m^2}\). Tính diện tích thửa ruộng trên.
Bài 4:(3,5 điểm)
1. Từ điểm \(A\) nằm bên ngoài đường tròn \((O)\) vẽ hai tiếp tuyến \(AD,\,AE\) (\(D,\,E\)là các tiếp điểm). Vẽ cát tuyến \(ABC\) của đường tròn \((O)\)sao cho điểm \(B\) nằm giữa hai điểm \(A,\,C;\) tia \(AC\)nằm giữa hai tia \(AD\)và \(AO\). Từ điểm \(O\) kẻ \(OI \bot AC\) tại \(I.\)
a) Chứng minh năm điểm \(A,\,D,\,I,\,O,\,E\) cùng nằm trên một đường tròn.
b) Chứng minh \(IA\) là tia phân giác của \(\angle DIE\) và \(AB.AC = A{D^2}\).
c) Gọi \(K\) và \(F\) lần lượt là giao điểm của \(ED\) với \(AC\) và \(OI\).Qua điểm \(D\) vẽ đường thẳng song song với \(IE\) cắt \(OF\) và \(AC\) lần lượt tại \(H\) và \(P\). Chứng minh \(D\) là trung điểm của \(HP.\)
2.Một hình trụ có diện tích xung quanh \(140\pi \,\,\left( {c{m^2}} \right)\) và chiều cao là \(h = 7\,\,\left( {cm} \right).\) Tính thể tích của hình trụ đó.
Bài 5: (1,0 điểm)
a) Cho \(x,\,y,\,z\) là ba số dương. Chúng minh \(\left( {x + y + z} \right)\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right) \ge 9.\)
b) Cho \(a,\,b,\,c\) là ba số dương thỏa mãn \(a + b + c = 6.\) Tìm giá trị lớn nhất của biểu thức
\(A =\dfrac{{ab}}{{a + 3b + 2c}} + \dfrac{{bc}}{{b + 3c + 2a}} + \dfrac{{ca}}{{c + 3a + 2b}}.\)
Bài 1
Phương pháp:
a) Rút gọn biểu thức
b) Đưa bài toán về tìm \(x\) để \(A = B\)(chú ý đối chiếu điều kiện xác định).
Cách giải:
Cho hai biểu thức:
\(A = \left( {\sqrt {20} - \sqrt {45} + 3\sqrt 5 } \right):\sqrt 5 ;\)\(B = \dfrac{{x + 2\sqrt x }}{{\sqrt x }} + \dfrac{{x - 9}}{{\sqrt x + 3}}\) (với \(x > 0\)).
a) Rút gọn các biểu thức \(A,\,\,B\).
\(\begin{array}{l}A = \left( {\sqrt {20} - \sqrt {45} + 3\sqrt 5 } \right):\sqrt 5 \\\,\,\,\,\, = \left( {2\sqrt 5 - 3\sqrt 5 + 3\sqrt 5 } \right):\sqrt 5 \\\,\,\,\,\, = 2\sqrt 5 :\sqrt 5 \\\,\,\,\,\, = 2\end{array}\)
Điều kiện: \(x > 0.\)
\(\begin{array}{l}B = \dfrac{{x + 2\sqrt x }}{{\sqrt x }} + \dfrac{{x - 9}}{{\sqrt x + 3}}\\\,\,\,\,\, = \dfrac{{\sqrt x \left( {\sqrt x + 2} \right)}}{{\sqrt x }} + \dfrac{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}{{\sqrt x + 3}}\\\,\,\,\,\, = \sqrt x + 2 + \sqrt x - 3\\\,\,\,\,\, = 2\sqrt x - 1.\end{array}\)
b) Tìm các giá trị của \(x\) sao cho giá trị biểu thức \(B\)bằng giá trị biểu thức \(A\).
Điều kiện: \(x > 0.\)
Để \(A = B\) thì \(2\sqrt x - 1 = 2\, \Leftrightarrow \sqrt x = \dfrac{3}{2} \Leftrightarrow x = \dfrac{9}{4}\,\,\,\left( {tm} \right)\)
Vậy \(x = \dfrac{9}{4}\) thì \(A = B\).
Bài 2
Phương pháp:
a) Xét phương trình hoành độ giao điểm. Để 2 đồ thị hàm số cắt nhau tại một điểm trên trục tung thì tìm điều kiện để phương trình hoành độ giao điểm có nghiệm duy nhất \(x = 0\)
b) Đặt \(t = \dfrac{1}{{y + 1}}\) và giải hệ phương trình bằng phương pháp cộng đại số ra \(x,\,t\). Từ đó tìm được \(x,\,y\).
Cách giải:
a) Tìm các giá trị của tham số \(m\)để đồ thị hai hàm số \(y = \left( {m + 4} \right)x + 11\) và \(y = x + {m^2} + 2\) cắt nhau tại một điểm trên trục tung.
Xét phương trình hoành độ giao điểm của hai hàm số ta có:
\(\left( {m + 4} \right)x + 11 = x + {m^2} + 2 \Leftrightarrow \left( {m + 3} \right)x = {m^2} - 9\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
Để 2 đồ thị hàm số cắt nhau tại một điểm trên trục tung thì phương trình (1) có nghiệm duy nhất \(x = 0\)
\( \Leftrightarrow \left\{ \begin{array}{l}m + 3 \ne 0\\x = \dfrac{{{m^2} - 9}}{{m + 3}} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne - 3\\m - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne - 3\\m = 3\end{array} \right. \Rightarrow m = 3\)
Vậy \(m = 3.\)
b) Giải hệ phương trình \(\left\{ \begin{array}{l}3x - \dfrac{2}{{y + 1}} = - \dfrac{1}{2}\\2x + \dfrac{1}{{y + 1}} = 2\end{array} \right..\)
Điều kiện: \(y \ne - 1\)
Đặt \(t = \dfrac{1}{{y + 1}}\)
Hệ phương trình \( \Leftrightarrow \left\{ \begin{array}{l}3x - 2t = - \dfrac{1}{2}\\2x + t = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x - 2t = - \dfrac{1}{2}\\4x + 2t = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}7x = \dfrac{7}{2}\\2x + t = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{1}{2}\\t = 1\end{array} \right..\)
Với \(t = 1\) thì \(\dfrac{1}{{y + 1}} = 1 \Rightarrow y + 1 = 1 \Leftrightarrow y = 0\,\,\,\,\left( {tm} \right)\)
Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {\dfrac{1}{2};0} \right)\)
Bài 3
Phương pháp:
1a) Thay \(m = 1\) vào phương trình, giải phương trình bằng phương pháp đưa về phương trình tích.
1b) Tìm điều kiện \(\Delta ' > 0\) để phương trình có 2 nghiệm phân biệt rồi biến đổi điều kiện bài toán về tổng và tích 2 nghiệm và áp dụng hệ thức Vi-et và hệ thức bài cho để tìm \(m.\)
Đối chiếu với điều kiện của \(m\) rồi kết luận.
2) Gọi chiều rộng hình chữ nhật là \(x\,\,\left( m \right)\,\,\,\left( {x > 2} \right)\)
chiều dài hình chữ nhật là \(y\,\,\left( m \right)\,\,\,\left( {y > x > 2} \right).\)
Dựa vào các giả thiết của bài toán để lập hệ phương trình.
Giải hệ phương trình rồi đối chiếu với điều kiện sau đó kết luận.
Cách giải:
1. Cho phương trình \({x^2} - 2mx + 4m - 4 = 0\,\,(1)\) (\(x\) là ẩn số, \(m\) là tham số).
a) Giải phương trình (1) khi \(m = 1.\)
Với \(m = 1\) ta có phương trình \(\left( 1 \right) \Leftrightarrow {x^2} - 2x = 0 \Leftrightarrow x\left( {x - 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right..\)
Vậy với \(m = 1\) thì phương trình có tập nghiệm \(S = \left\{ {0;\,\,2} \right\}.\)
b) Xác định các giá trị của \(m\) để phương trình (1) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn điều kiện \(x_1^2 + ({x_1} + {x_2}){x_2} = 12\)
\({x^2} - 2mx + 4m - 4 = 0\,\,\,\,\,\,\left( 1 \right)\)
Có: \(\Delta ' = {m^2} - \left( {4m - 4} \right) = {m^2} - 4m + 4 = {\left( {m - 2} \right)^2} \ge 0\,\,\,\,\,\,\,\forall m\)
Để phương trình (1) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thì \(\Delta ' > 0 \Leftrightarrow m \ne 2\)
Với \(m \ne 2\), theo hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}.{x_2} = 4m - 4\end{array} \right.\,\,(*)\)
Theo đề bài ta có: \(x_1^2 + \left( {{x_1} + {x_2}} \right){x_2} = 12\)
\(\begin{array}{l} \Leftrightarrow x_1^2 + {x_2}^2 + {x_1}{x_2} = 12\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} + {x_1}{x_2} = 12\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - {x_1}{x_2} = 12\\ \Leftrightarrow {\left( {2m} \right)^2} - \left( {4m - 4} \right) = 12\\ \Leftrightarrow 4{m^2} - 4m - 8 = 0\\ \Leftrightarrow 4\left( {{m^2} - m - 2} \right) = 0\\ \Leftrightarrow 4\left( {m - 2} \right)\left( {m + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m - 2 = 0\\m + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 2\,\,\,\,\left( {ktm} \right)\\m = - 1\,\,\,\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy \(m = - 1\) là giá trị cần tìm.
2. Bài toán có nội dung thực tế
Cho một thửa ruộng hình chữ nhật, biết rằng nếu chiều rộng tăng thêm \(2m\), chiều dài giảm đi \(2m\) thì diện tích thửa ruộng đó tăng thêm \(30{m^2}\); và nếu chiều rộng giảm đi \(2m\), chiều dài tăng thêm \(5m\) thì diện tích thửa ruộng giảm đi \(20{m^2}\). Tính diện tích thửa ruộng trên.
Gọi chiều rộng hình chữ nhật là \(x\,\,\left( m \right)\,\,\,\left( {x > 2} \right)\)
chiều dài hình chữ nhật là \(y\,\,\left( m \right)\,\,\,\left( {y > x > 2} \right).\)
Diện tích thửa ruộng ban đầu là \(xy\,\,\,\,\left( {{m^2}} \right).\)
Khi chiều rộng tăng thêm \(2m\), chiều dài giảm đi \(2m\) thì diện tích thửa ruộng tăng thêm \(30{m^2}\) nên ta có:
\(\left( {x + 2} \right)\left( {y - 2} \right) = xy + 30 \Leftrightarrow - 2x + 2y = 34\,\,\,\,\,\,\left( 1 \right)\)
Khi chiều rộng giảm đi \(2m\), chiều dài tăng thêm \(5m\) thì diện tích thửa ruộng giảm đi \(20{m^2}\) nên ta có \(\left( {x - 2} \right)\left( {y + 5} \right) = xy - 20 \Leftrightarrow 5x - 2y = - 10\,\,\,\,\,\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{l} - 2x + 2y = 34\\5x - 2y = - 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - x + y = 17\\3x = 24\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 25\,\,\,\,\left( {tm} \right)\\x = 8\,\,\,\,\,\,\,\,\left( {tm} \right)\end{array} \right.\)
Diện tích thửa ruộng ban đầu là \(25.8 = 200\,\,{m^2}.\)
Bài 4
Phương pháp:
1a) Các góc cùng nhìn 1 cạnh dưới 1 góc vuông.
1b) Chứng minh \(\angle DIA = \angle EIA\) bằng cách sử dụng câu a) 5 điểm cùng thuộc một đường tròn.
1c) Chứng minh tam giác \(DIH\)và \(DIP\) cân tại \(D\). Khi đó \(DH = DP( = DI)\)
2) Dựa vào công thức \({S_{xq}} = 2\pi .r.h\) khi biết chiều cao \(h\) và diện tích xung quanh hình trụ để tính bán kính đáy trụ \(r.\) Sau đó dùng công thức \(V = \pi .{r^2}.h\) để tính thể tích hình trụ.
Cách giải:
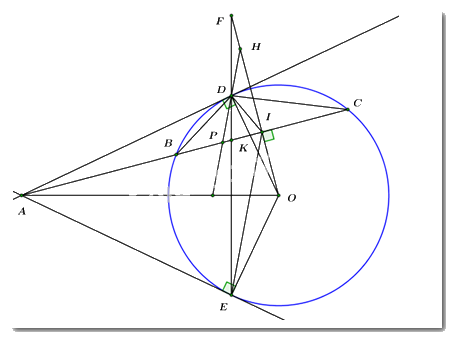
1a) Chứng minh năm điểm \(A,\,D,\,I,\,O,\,E\) cùng nằm trên một đường tròn.
\(AD,\,\,AE\) là các tiếp tuyến của \(\left( O \right) \Rightarrow \left\{ \begin{array}{l}OD \bot AD = \left\{ D \right\}\\OE \bot AE = \left\{ E \right\}\end{array} \right. \Rightarrow \angle ODA = \angle OEA = {90^0}\)
\(OI \bot AC = \left\{ I \right\} \Rightarrow \angle OIA = {90^0}\)
Ta có: \(\angle ODA,\,\,\,\angle OEA\) cùng nhìn \(OA\) dưới một góc vuông (cmt) và \(\angle OIA\) cũng nhìn \(OA\) dưới một góc vuông (cmt)
Nên \(D,\,\,\,E,\,\,\,O,\,\,\,A,\,\,\,I\) cùng thuộc một đường tròn đường kính \(OA\). (đpcm).
b) Chứng minh \(IA\) là tia phân giác của \(\angle DIE\) và \(AB.AC = A{D^2}\).
Do \(AD,\,AE\)là tiếp tuyến \(\left( O \right) \Rightarrow AO\) là phân giác của \(\angle DOE \Rightarrow \angle DOA = \angle AOE\,\,\,\,\left( 1 \right)\) (tính chất hai tiếp tuyến cắt nhau).
Ta có tứ giác \(ADOE\)nội tiếp đường tròn đường kính \(AO\,\,\,\left( {cmt} \right) \Rightarrow \angle DIA = \angle DOA\,\,\,\,\left( 2 \right)\) (hai góc nội tiếp cùng chắn cung \(DA\))
Ta có tứ giác \(AIOE\)nội tiếp đường tròn đường kính \(AO\,\,\,\left( {cmt} \right) \Rightarrow \angle EIA = \angle EOA\,\,\,\,\,\,\left( 3 \right)\) (hai góc nội tiếp cùng chắn cung \(EA\))
\( \Rightarrow \angle DIA = \angle EIA \Rightarrow IA\) là phân giác của góc \(\angle DIE.\) (đpcm)
Xét \(\Delta ABD\) và \(\Delta ADC\)ta có:
\(\angle A\,\,\,\,chung\)
\(\angle BDA = \angle DCA\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(BD\))
c) Gọi \(K\) và \(F\) lần lượt là giao điểm của \(ED\) với \(AC\) và \(OI\). Qua điểm \(D\) vẽ đường thẳng song song với \(IE\) cắt \(OF\) và \(AC\) lần lượt tại \(H\) và \(P\). Chứng minh \(D\) là trung điểm của \(HP.\)
Ta có: \(DP//IE\,\,\left( {gt} \right) \Rightarrow \angle DPI = \angle EIP\) (hai góc so le trong)
mà \(\angle DIP = \angle PIE\,\,\,\,\left( {cmt\,\,\,\,\angle DIA = \angle AIE} \right)\)
\( \Rightarrow \angle DIP = \angle DPI \Rightarrow \Delta DIP\) cân tại \(D\)
\( \Rightarrow DI = DP\,\,\,\,\,\left( 1 \right)\)
Ta có: \(DH//IE \Rightarrow \angle DHI = \angle EIO\) (hai góc đồng vị)
Ta có \(\angle HID + \angle PID = \angle PIE + \angle EIO = {90^0}\) mà \(\angle PID = \angle PIE \Rightarrow \angle HID = \angle EIO\,\)
\( \Rightarrow \angle DHI = \angle HID \Rightarrow \Delta HID\) cân tại \(D\)\( \Rightarrow DI = DH\,\,\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow D\) là trung điểm \(HP.\)
2. Một hình trụ có diện tích xung quanh \(140\pi \,\,\left( {c{m^2}} \right)\) và chiều cao là \(h = 7\,\,\left( {cm} \right).\) Tính thể tích của hình trụ đó.
Diện tích xung quanh của hình trụ là \({S_{xq}} = 2\pi .r.h = 2\pi .r.7 = 140\pi \)
\( \Rightarrow \) bán kính của đáy trụ là \(r = \dfrac{{140\pi }}{{2\pi .7}} = 10\,\,\left( {cm} \right)\)
Thể tích hình trụ là \(V = \pi .{r^2}.h = \pi {.10^2}.7 = 700\pi \,\,c{m^3}.\)
Bài 5
Phương pháp:
Sử dụng bất đẳng thức Cô-si cho 2 bộ 3 số dương \(x;y;z\) và \(\dfrac{1}{x};\dfrac{1}{y};\dfrac{1}{z}.\)
Cách giải:
a) Cho \(x,\,y,\,z\) là ba số dương. Chứng minh \(\left( {x + y + z} \right)\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right) \ge 9.\)
Áp dụng bất đẳng thức Cô-si cho bộ 3 số dương \(x;y;z\) ta có: \(\left( {x + y + z} \right) \ge 3\sqrt[3]{{xyz}}\)
Áp dụng bất đẳng thức Cô-si cho bộ 3 số dương \(\dfrac{1}{x};\dfrac{1}{y};\dfrac{1}{z}:\) \(\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right) \ge 3\sqrt[3]{{\dfrac{1}{{xyz}}}}.\)
\( \Rightarrow \left( {x + y + z} \right)\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right) \ge 9\sqrt[3]{{xyz.\dfrac{1}{{xyz}}}} = 9\) (đpcm)
Dấu “=” xảy ra \( \Leftrightarrow x = y = z.\)
b) Cho \(a,\,b,\,c\) là ba số dương thỏa mãn \(a + b + c = 6.\) Tìm giá trị lớn nhất của biểu thức
\(A = \dfrac{{ab}}{{a + 3b + 2c}} + \dfrac{{bc}}{{b + 3c + 2a}} + \dfrac{{ca}}{{c + 3a + 2b}}.\)
Ta có: \(\dfrac{{ab}}{{a + 3b + 2c}} = \dfrac{{ab}}{{a + c + b + c + 2b}}\)
Áp dụng câu a) \(9 \le \left( {x + y + z} \right)\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right) \Rightarrow \dfrac{1}{{x + y + z}} \le \dfrac{1}{9}\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right).\)
\( \Rightarrow \dfrac{{ab}}{{a + 3b + 2c}} \le ab.\dfrac{1}{9}\left( {\dfrac{1}{{a + c}} + \dfrac{1}{{b + c}} + \dfrac{1}{{2b}}} \right) = \dfrac{1}{9}\left( {\dfrac{{ab}}{{a + c}} + \dfrac{{ab}}{{b + c}} + \dfrac{a}{2}} \right)\)
Tương tự ta có: \(\left\{ \begin{array}{l}\dfrac{{bc}}{{b + 3c + 2a}} \le bc.\dfrac{1}{9}\left( {\dfrac{1}{{b + a}} + \dfrac{1}{{a + c}} + \dfrac{1}{{2c}}} \right) = \dfrac{1}{9}\left( {\dfrac{{bc}}{{b + a}} + \dfrac{{bc}}{{a + c}} + \dfrac{b}{2}} \right)\\\dfrac{{ca}}{{c + 3a + 2b}} \le ca.\dfrac{1}{9}\left( {\dfrac{1}{{c + b}} + \dfrac{1}{{b + a}} + \dfrac{1}{{2a}}} \right) = \dfrac{1}{9}\left( {\dfrac{{ca}}{{c + b}} + \dfrac{{ca}}{{a + b}} + \dfrac{c}{2}} \right)\end{array} \right.\)
\( \Rightarrow A \le \dfrac{1}{9}\left( {\dfrac{{ab + bc}}{{a + c}} + \dfrac{{ab + ca}}{{b + c}} + \dfrac{{bc + ca}}{{a + b}} + \dfrac{{a + b + c}}{2}} \right)\)
\( \Leftrightarrow A \le \dfrac{1}{9}\left( {b + a + c + \dfrac{{a + b + c}}{2}} \right) = \dfrac{1}{9}\left( {6 + \dfrac{6}{2}} \right) = 1\) với \(a + b + c = 6\)
Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}a = b = c\\a + b + c = 6\end{array} \right. \Leftrightarrow a = b = c = 2.\)
Vậy \(Max\,\,A = 1\) khi \(a = b = c = 2.\)
Kỳ thi tuyển sinh vào lớp 10 tại Hải Phòng luôn là một cột mốc quan trọng đối với học sinh lớp 9. Để chuẩn bị tốt nhất cho kỳ thi này, việc nắm vững cấu trúc đề thi và luyện tập với các đề thi thử, đề thi chính thức các năm trước là vô cùng cần thiết. Bài viết này sẽ cung cấp phân tích chi tiết về Đề thi vào 10 môn Toán Hải Phòng năm 2019, kèm theo hướng dẫn giải các bài toán khó, giúp các em học sinh tự tin hơn khi bước vào phòng thi.
Đề thi vào 10 môn Toán Hải Phòng năm 2019 thường có cấu trúc gồm các phần sau:
Độ khó của đề thi thường ở mức trung bình, đòi hỏi học sinh phải nắm vững kiến thức cơ bản và có kỹ năng giải toán tốt.
Phần đại số thường xuất hiện các dạng bài tập sau:
Phần hình học thường xuất hiện các dạng bài tập sau:
Các bài toán thực tế thường được đưa ra dưới dạng các tình huống quen thuộc trong cuộc sống, đòi hỏi học sinh phải vận dụng kiến thức toán học để giải quyết.
Dưới đây là hướng dẫn giải một số bài toán khó thường gặp trong Đề thi vào 10 môn Toán Hải Phòng năm 2019:
Bài toán 1: (Ví dụ về một bài toán đại số khó)
Giải phương trình: √(x+1) + √(x+6) = 5
Hướng dẫn giải: Bình phương hai vế, chú ý điều kiện xác định của phương trình.
Bài toán 2: (Ví dụ về một bài toán hình học khó)
Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh rằng: AH2 = BH.CH
Hướng dẫn giải: Sử dụng hệ thức lượng trong tam giác vuông.
Giaitoan.edu.vn cung cấp đầy đủ các tài liệu ôn thi và luyện thi vào 10 môn Toán, bao gồm:
Hãy truy cập giaitoan.edu.vn ngay hôm nay để bắt đầu hành trình chinh phục kỳ thi vào 10 môn Toán!
Đề thi vào 10 môn Toán Hải Phòng năm 2019 là một tài liệu quan trọng giúp các em học sinh chuẩn bị tốt nhất cho kỳ thi sắp tới. Hy vọng với những phân tích chi tiết và hướng dẫn giải bài tập trong bài viết này, các em sẽ tự tin hơn và đạt kết quả tốt nhất trong kỳ thi.