Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Đắk Lắk năm 2019. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi sắp tới.
Bộ đề thi này bao gồm đề thi chính thức và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm. Các em có thể sử dụng để tự học, luyện tập hoặc tham khảo ý tưởng giải bài.
Câu 1 (2 điểm): 1) Rút gọn biểu thức:
Câu 1 (2 điểm):
1) Rút gọn biểu thức: \(A = \sqrt {32} - \sqrt 6 .\sqrt 3 + \dfrac{{\sqrt {22} }}{{\sqrt {11} }}.\)
2) Giải phương trình: \({x^2} - 2x = 0.\)
3) Xác định hệ số \(a\) của hàm số \(y = a{x^2},\) biết đồ thị của hàm số đó đi qua điểm \(A\left( { - 3;\,\,1} \right).\)
Câu 2 (2 điểm): Cho phương trình \({x^2} - \left( {2m - n} \right)x + \left( {2m + 3n - 1} \right) = 0\,\,\,\,\left( 1 \right)\) (\(m,\,\,n\) là tham số)
1) Với \(n = 0,\) chứng minh rằng phương trình \(\left( 1 \right)\) luôn có nghiệm với mọi giá trị của \(m.\)
2) Tìm \(m,\,\,n\) để phương trình \(\left( 1 \right)\) luôn có hai nghiệm \({x_1},\,\,{x_2}\) thỏa mãn \({x_1} + {x_2} = - 1\) và \(x_1^2 + x_2^2 = 13.\)
Câu 3 (2 điểm):
1) Trong mặt phẳng tọa độ \(Oxy\) cho đường thẳng \(d\) có phương trình \(y = - x + \dfrac{{\sqrt 2 }}{2}.\) Gọi \(A,\,\,B\) lần lượt là giao điểm của \(d\) với trục hoành và trục tung; \(H\) là trung điểm của đoạn thẳng \(AB.\) Tính độ dài đoạn thẳng \(OH\) (đơn vị đo trên các trục tọa độ là xentimet).
2) Một cốc nước dạng hình trụ có chiều cao là 12 cm, bán kính đáy là \(2\)cm, lượng nước trong cốc cao 8 cm. Người ta thả vào cốc nước 6 viên bi hình cầu có cùng bán kính 1 cm và ngập hoàn toàn trong nước làm nước trong cốc dâng lên. Hỏi sau khi thả 6 viên bi vào thì mực nước trong cốc cách miệng côc bao nhiêu xentimet? (giả sử độ dày của cốc là không đáng kể).
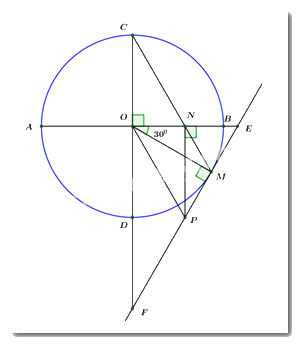
Câu 4 (3 điểm): Cho đường tròn \(\left( O \right)\) có hai đường kính \(AB\) và \(CD\) vuông góc với nhau. Điểm \(M\) thuộc cung nhỏ \(BD\) sao cho \(\angle BOM = {30^0}.\) Gọi \(N\) là giao điểm của \(CM\) và \(OB.\) Tiếp tuyến tại \(M\) của đường tròn \(\left( O \right)\) cắt \(OB,\,\,OD\) kéo dài lần lượt tại \(E\) và \(F.\) Đường thẳng qua \(N\) và vuông góc với \(AB\) cắt \(EF\) tại \(P.\)
1) Chứng minh tứ giác \(ONMP\) là tứ giác nội tiếp.
2) Chứng minh \(\Delta EMN\) là tam giác đều.
3) Chứng minh \(CN = OP.\)
4) Gọi \(H\) là trực tâm \(\Delta AEF.\) Hỏi ba điểm \(A,\,\,H,\,\,P\) có thẳng hàng không? Vì sao?
Câu 5 (1 điểm): Cho ba số thực dương \(x,\,\,y,\,\,z\) thỏa mãn \(x + 2y + 3z = 2.\)
Tìm giá trị lớn nhất của biểu thức: \(S = \sqrt {\dfrac{{xy}}{{xy + 3z}}} + \sqrt {\dfrac{{3yz}}{{3yz + x}}} + \sqrt {\dfrac{{3xz}}{{3xz + 4y}}} .\)
Câu 1
Phương pháp:
1) Sử dụng công thức: \(\sqrt A .\sqrt B = \sqrt {AB} ;\,\,\,\dfrac{{\sqrt A }}{{\sqrt B }} = \sqrt {\dfrac{A}{B}} ;\,\,\,\,\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,\,A < 0\end{array} \right..\)
2) Đưa phương trình về dạng phương trình tích để giải phương trình.
3) Thay tọa độ điểm \(A\left( { - 3;\,1} \right)\) vào công thức hàm số \(y = a{x^2}\) để tìm \(a.\)
Cách giải:
1) Rút gọn biểu thức: \(A = \sqrt {32} - \sqrt 6 .\sqrt 3 + \dfrac{{\sqrt {22} }}{{\sqrt {11} }}.\)
\(\begin{array}{l}A = \sqrt {32} - \sqrt 6 .\sqrt 3 + \dfrac{{\sqrt {22} }}{{\sqrt {11} }} = \sqrt {{4^2}.2} - \sqrt {6.3} + \sqrt {\dfrac{{22}}{{11}}} \\ = 4\sqrt 2 - \sqrt {{3^2}.2} + \sqrt 2 = 5\sqrt 2 - 3\sqrt 2 = 2\sqrt 2 .\end{array}\)
Vậy \(A = 2\sqrt 2 .\)
2) Giải phương trình: \({x^2} - 2x = 0.\)
\({x^2} - 2x = 0 \Leftrightarrow x\left( {x - 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right..\)
Vậy phương trình đã cho có tập nghiệm \(S = \left\{ {0;\,\,2} \right\}.\)
3) Xác định hệ số \(a\) của hàm số \(y = a{x^2},\) biết đồ thị của hàm số đó đi qua điểm \(A\left( { - 3;\,\,1} \right).\)
Đồ thị hàm số \(y = a{x^2}\) đi qua điểm \(A\left( { - 3;\,\,1} \right)\) nên thay tọa độ điểm \(A\) vào công thức hàm số ta được:
\(1 = a.{\left( { - 3} \right)^2} \Leftrightarrow a = \dfrac{1}{9}.\)
Vậy \(a = \dfrac{1}{9}.\)
Câu 2
Phương pháp:
1) Thay \(n = 0\) vào phương trình \(\left( 1 \right),\) chứng minh \(\Delta \ge 0\,\,\,\left( {\Delta ' \ge 0} \right)\) với mọi \(m.\)
2) Tìm điều kiện của \(m,\,\,n\) để phương trình \(\left( 1 \right)\) có nghiệm: \(\Delta \ge 0.\)
+) Áp dụng định lý Vi-et và các biểu thức bài cho để tìm \(m,\,\,n.\) Đối chiếu với điều kiện rồi kết luận.
Cách giải:
Cho phương trình \({x^2} - \left( {2m - n} \right)x + \left( {2m + 3n - 1} \right) = 0\,\,\,\,\left( 1 \right)\) (\(m,\,\,n\) là tham số)
1) Với \(n = 0,\) chứng minh rằng phương trình \(\left( 1 \right)\) luôn có nghiệm với mọi giá trị của \(m.\)
Với \(n = 0\) ta có phương trình \(\left( 1 \right) \Leftrightarrow {x^2} - 2mx + 2m - 1 = 0\)
Phương trình có \(\Delta ' = {m^2} - 2m + 1 = {\left( {m - 1} \right)^2} \ge 0\,\,\,\forall m\)
Vậy với \(n = 0\) thì phương trình \(\left( 1 \right)\) luôn có nghiệm với mọi \(m.\)
2) Tìm \(m,\,\,n\) để phương trình \(\left( 1 \right)\) luôn có hai nghiệm \({x_1},\,\,{x_2}\) thỏa mãn \({x_1} + {x_2} = - 1\)và \(x_1^2 + x_2^2 = 13.\)
Ta có: \(\Delta = {\left( {2m - n} \right)^2} - 4\left( {2m + 3n - 1} \right) = 4{m^2} - 4mn + {n^2} - 8m - 12n + 4.\)
Phương trình \(\left( 1 \right)\) có hai nghiệm\({x_1},\,\,{x_2} \Leftrightarrow \Delta \ge 0\)
\( \Leftrightarrow 4{m^2} - 4mn + {n^2} - 8m - 12n + 4 \ge 0.\,\,\,\,\left( * \right)\)
Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m - n\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\\{x_1}{x_2} = 2m + 3n - 1\,\,\,\,\,\,\,\left( 3 \right)\end{array} \right..\)
Theo đề bài ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 1\\x_1^2 + x_2^2 = 13\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_1} + {x_2} = - 1\,\,\,\,\,\,\,\left( 4 \right)\\{\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 13\,\,\,\,\,\left( 5 \right)\end{array} \right.\,\,\)
Thế (3) và (4) vào (5) ta được:
\(\begin{array}{l}\left( 5 \right) \Leftrightarrow {\left( { - 1} \right)^2} - 2\left( {2m + 3n - 1} \right) = 13\\ \Leftrightarrow 1 - 4m - 6n + 2 = 13\\ \Leftrightarrow 4m + 6n = - 10\\ \Leftrightarrow 2m + 3n = - 5\,\,\,\,\left( 6 \right)\end{array}\)
Từ (2) và (4) ta có: \(2m - n = - 1 \Leftrightarrow n = 2m + 1\,\,\,\left( 7 \right)\)
Thế \(\left( 7 \right)\) vào \(\left( 6 \right)\) ta được: \(2m + 3\left( {2m + 1} \right) = - 5 \Leftrightarrow 2m + 6m + 3 = - 5 \Leftrightarrow 8m = - 8 \Leftrightarrow m = - 1\)
\( \Rightarrow n = 2m + 1 = 2.\left( { - 1} \right) + 1 = - 1.\)
Thay \(m = - 1,\,\,n = - 1\) vào điều kiện \(\left( * \right)\) ta có:
\(4.{\left( { - 1} \right)^2} - 4.\left( { - 1} \right)\left( { - 1} \right) + {\left( { - 1} \right)^2} - 8.\left( { - 1} \right) - 12.\left( { - 1} \right) + 4 = 25 > 0\)
\( \Rightarrow \left\{ \begin{array}{l}m = - 1\\n = - 1\end{array} \right.\) thỏa mãn.
Vậy \(m = - 1,\,\,n = - 1\) là các giá trị cần tìm.
Câu 3
Phương pháp:
1) Tìm tọa độ các điểm \(A,\,\,B.\) Sử dụng hệ thức lượng trong \(\Delta AOB\) vuông tại \(O\) có đường cao \(OH\) để làm bài toán.
2) Thể tích của khối trụ có chiều cao \(h\) và bán kính đáy \(R\) là: \(V = \pi {R^2}h.\)
Thể tích khối cầu bán kính \(R\) là: \(V = \dfrac{4}{3}\pi {R^3}.\)
Cách giải:
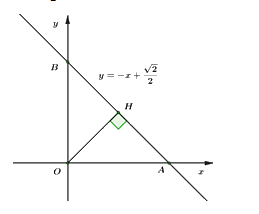
1) Cho \(d:\,\,\,y = - x + \dfrac{{\sqrt 2 }}{2}.\)
Ta có: \(d \cap Ox = \left\{ A \right\} \Rightarrow A\left( {{x_A};\,\,0} \right) \Rightarrow - {x_A} + \dfrac{{\sqrt 2 }}{2} = 0 \Leftrightarrow {x_A} = \dfrac{{\sqrt 2 }}{2} \Rightarrow A\left( {\dfrac{{\sqrt 2 }}{2};\,\,0} \right) \Rightarrow OA = \dfrac{{\sqrt 2 }}{2}.\)
\(d \cap Oy = \left\{ B \right\} \Rightarrow B\left( {0;\,\,{y_B}} \right) \Rightarrow 0 + \dfrac{{\sqrt 2 }}{2} = {y_B} \Leftrightarrow {y_B} = \dfrac{{\sqrt 2 }}{2} \Rightarrow B\left( {0;\,\,\dfrac{{\sqrt 2 }}{2}} \right) \Rightarrow OB = \dfrac{{\sqrt 2 }}{2}.\)
Vì tam giác \(OAB\) vuông cân tại \(O\) \(\left( {do\,OA = OB = \dfrac{{\sqrt 2 }}{2}} \right)\) mà \(OH\) là đường trung tuyến nên \(OH\) cũng là đường cao.
Sử dụng hệ thức lượng trong \(\Delta AOB\) vuông tại \(O\) có đường cao \(OH\) ta có: \(\begin{array}{l}\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} = \dfrac{1}{{{{\left( {\dfrac{{\sqrt 2 }}{2}} \right)}^2}}} + \dfrac{1}{{{{\left( {\dfrac{{\sqrt 2 }}{2}} \right)}^2}}} = 2 + 2 = 4.\\ \Rightarrow O{H^2} = \dfrac{1}{4} \Leftrightarrow OH = \dfrac{1}{2} = 0,5\,\,cm.\end{array}\) Vậy \(OH = 0,5\,\,cm.\) |
2) Thể tích nước dâng lên = thể tích 6 viên bi được thả vào cốc.
Thể tích nước có trong cốc ban đầu là: \({V_1} = \pi {.2^2}.8 = 32\pi \,\,\left( {c{m^3}} \right).\)
Ta có thể tích của 6 viên bi được thả vào cốc là: \({V_2} = 6.\dfrac{4}{3}\pi {.1^3} = 8\pi \,\,\,\left( {c{m^3}} \right).\)
Thể tích sau khi được thả thêm 6 viên bi là: \(V = {V_1} + {V_2} = 32\pi + 8\pi = 40\pi \,\,\left( {c{m^3}} \right).\)
\( \Rightarrow \) Chiều cao mực nước trong cốc lúc này là: \(h = \dfrac{V}{{\pi {R^2}}} = \dfrac{{40\pi }}{{\pi {{.2}^2}}} = 10\,\,\left( {cm} \right).\)
Vậy sau khi thả 6 viên bi vào cốc thì mực nước cách cốc là \(12 - 10 = 2\,\,cm.\)
Câu 4
Phương pháp:
1) Chứng minh tứ giác nội tiếp dựa vào các dấu hiệu nhận biết của tứ giác.
2) Chứng minh tam giác có hai góc có số đo bằng \({60^0}\) là tam giác đều.
3) Chứng minh tứ giác \(OCNP\) là hình bình hành.
Cách giải:
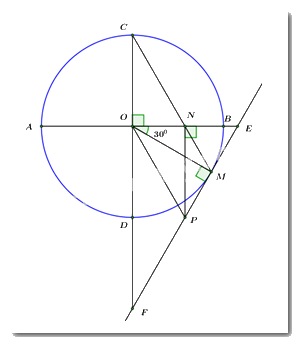
1) Chứng minh tứ giác \(ONMP\) là tứ giác nội tiếp.
Xét tứ giác \(ONMP\) ta có:
\(\angle ONP = {90^0}\,\,\,\left( {NP \bot AB} \right)\)
\(\angle OMP = {90^0}\) (\(EF\) là tiếp tuyến của \(\left( O \right)\))
\( \Rightarrow \angle ONP = \angle OMP = {90^0}\)
Mà hai đỉnh \(N,\,\,P\) là hai đỉnh kề nhau cùng nhìn cạnh \(OP.\)
\( \Rightarrow ONMP\) là tứ giác nội tiếp. (dhnb) (đpcm).
2) Chứng minh \(\Delta EMN\) là tam giác đều.
Xét \(\left( O \right)\) ta có:
\(\angle COM\) là góc ở tâm chắn cung \(CM\)
\(\angle CME\) là góc tạo bởi tia tiếp tuyến và dây cung chắn cung \(CM\)
\( \Rightarrow \angle CME = \dfrac{1}{2}\angle COM = \dfrac{1}{2}\left( {\angle COB + \angle BOM} \right) = \dfrac{1}{2}\left( {{{90}^0} + {{30}^0}} \right) = {60^0}.\) (tính chất góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn một cung).
Hay \(\angle NME = {60^0}.\)
Xét \(\Delta OME\) vuông tại \(M\) ta có:
\(\angle OEM = {90^0} - \angle EOM = {90^0} - {30^0} = {60^0}.\)
Xét \(\Delta MNE\) ta có:\(\angle NEM = \angle NME = {60^0}\,\,\left( {cmt} \right)\)
\( \Rightarrow \Delta NME\) là tam giác đều. (định nghĩa) (đpcm).
3) Chứng minh \(CN = OP.\)
Ta có: \(\Delta MNE\) là tam giác đều (cmt)
\( \Rightarrow \angle ENM = {60^0} = \angle ONC\) (hai góc đối đỉnh)
\( \Rightarrow \angle OCN = {90^0} - \angle ONC = {90^0} - {60^0} = {30^0}\)
Ta có: \(\angle OMN = {90^0} - \angle NME = {90^0} - {60^0} = {30^0}.\)
Vì \(ONMP\) là tứ giác nội tiếp (cmt) \( \Rightarrow \angle OPN = \angle OMN = {30^0}\) (hai góc nội tiếp cùng chắn cung \(ON\))
Ta có: \(\left\{ \begin{array}{l}OC \bot AB = \left\{ O \right\}\\NP \bot AB = \left\{ N \right\}\end{array} \right. \Rightarrow OC//NP \Rightarrow OCPN\) là hình thang.
Mà \(\angle OCN = \angle OPN = {30^0}\,\,\,\left( {cmt} \right).\)
Lại có hai góc này là hai góc đối nhau
\( \Rightarrow OCNP\) là hình bình hành.
\( \Rightarrow OC = NP\,\,\,\left( {dpcm} \right).\)
4) Gọi \(H\) là trực tâm \(\Delta AEF.\) Hỏi ba điểm \(A,\,\,H,\,\,P\) có thẳng hàng không? Vì sao?
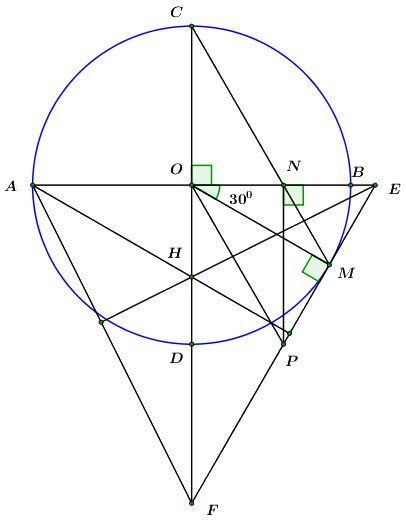
Gọi \(I\) là chân đường cao kẻ từ \(A\) đến \(EF\) thì \(H \in AI\).
Giả sử phản chứng \(A,H,P\) thẳng hàng thì \(P \equiv I\) hay \(AP \bot EF\).
Có \(\angle EOP = \angle NOP = {90^0} - \angle ONP = {60^0}\) và \(\angle OEP = {60^0}\left( {cmt} \right)\) nên \(\Delta OEP\) là tam giác cân có một góc bằng \({60^0}\) nên là tam giác đều \( \Rightarrow OP = PE\,\,\left( 1 \right)\).
Lại có \(\angle POF = {90^0} - \angle EOP = {90^0} - {60^0} = {30^0}\) và \(\angle PFO = {90^0} - \angle OEP = {90^0} - {60^0} = {30^0}\) nên tam giác \(OPF\) cân tại \(P\) hay \(OP = PF\,\,\left( 2 \right)\).
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(PE = PF\left( { = OP} \right)\).
Xét tam giác \(AEF\) có \(AP \bot EF\) (giả thiết) và \(PE = PF\) nên \(AP\) vừa là đường cao vừa là đường trung tuyến.
\( \Rightarrow \Delta AEF\) cân tại \(A\). Mà \(\angle AEF = {60^0}\) nên tam giác \(AEF\) đều.
\( \Rightarrow FO\) vừa là đường cao vừa là đường trung tuyến \( \Rightarrow OA = OE\) (vô lý vì \(OA < OE\)).
Vậy ba điểm \(A,H,P\) không thẳng hàng.
Câu 5
Phương pháp:
- Biến đổi các mẫu về dạng tích.
- Áp dụng bất đẳng thức Cô-si cho hai số dương \(\sqrt {ab} \le \dfrac{{a + b}}{2}\).
Cách giải:
Do \(x + 2y + 3z = 2\) nên \(\left\{ \begin{array}{l}x = 2 - 2y - 3z\\2y = 2 - x - 3z\\3z = 2 - x - 2y\end{array} \right.\). Khi đó,
\(\begin{array}{l}xy + 3z = xy + \left( {2 - x - 2y} \right) = \left( {xy - x} \right) - \left( {2y - 2} \right) = x\left( {y - 1} \right) - 2\left( {y - 1} \right) = \left( {x - 2} \right)\left( {y - 1} \right)\\3yz + x = 3yz + \left( {2 - 2y - 3z} \right) = \left( {3yz - 3z} \right) - \left( {2y - 2} \right) = \left( {y - 1} \right)\left( {3z - 2} \right)\\3xz + 4y = 3xz + 2\left( {2 - x - 3z} \right) = \left( {3xz - 6z} \right) - \left( {2x - 4} \right) = 3z\left( {x - 2} \right) - 2\left( {x - 2} \right) = \left( {x - 2} \right)\left( {3z - 2} \right)\end{array}\)
Suy ra:
\(\begin{array}{l}S = \sqrt {\dfrac{{xy}}{{\left( {x - 2} \right)\left( {y - 1} \right)}}} + \sqrt {\dfrac{{3yz}}{{\left( {y - 1} \right)\left( {3z - 2} \right)}}} + \sqrt {\dfrac{{3xz}}{{\left( {x - 2} \right)\left( {3z - 2} \right)}}} \\ = \sqrt {\dfrac{x}{{2\left( {1 - y} \right)}}} .\sqrt {\dfrac{{2y}}{{2 - x}}} + \sqrt {\dfrac{{2y}}{{2 - 3z}}} .\sqrt {\dfrac{{3z}}{{2\left( {1 - y} \right)}}} + \sqrt {\dfrac{x}{{2 - 3z}}} .\sqrt {\dfrac{{3z}}{{2 - x}}} \\ \le \dfrac{1}{2}\left( {\dfrac{x}{{2\left( {1 - y} \right)}} + \dfrac{{2y}}{{2 - x}}} \right) + \dfrac{1}{2}\left( {\dfrac{{2y}}{{2 - 3z}} + \dfrac{{3z}}{{2\left( {1 - y} \right)}}} \right) + \dfrac{1}{2}\left( {\dfrac{x}{{2 - 3z}} + \dfrac{{3z}}{{2 - x}}} \right)\\ = \dfrac{1}{2}\left( {\dfrac{x}{{2\left( {1 - y} \right)}} + \dfrac{{2y}}{{2 - x}} + \dfrac{{2y}}{{2 - 3z}} + \dfrac{{3z}}{{2\left( {1 - y} \right)}} + \dfrac{x}{{2 - 3z}} + \dfrac{{3z}}{{2 - x}}} \right)\\ = \dfrac{1}{2}\left( {\dfrac{{x + 3z}}{{2\left( {1 - y} \right)}} + \dfrac{{2y + 3z}}{{2 - x}} + \dfrac{{2y + x}}{{2 - 3z}}} \right)\\ = \dfrac{1}{2}\left( {\dfrac{{2 - 2y}}{{2\left( {1 - y} \right)}} + \dfrac{{2 - x}}{{2 - x}} + \dfrac{{2 - 3z}}{{2 - 3z}}} \right) = \dfrac{1}{2}.\left( {1 + 1 + 1} \right) = \dfrac{3}{2}\end{array}\)
Hay \(S \le \dfrac{3}{2}\) \( \Rightarrow \max S = \dfrac{3}{2}\)
Dấu “=” xảy ra khi \(\left\{ \begin{array}{l}\dfrac{x}{{2\left( {1 - y} \right)}} = \dfrac{{2y}}{{2 - x}}\\\dfrac{{2y}}{{2 - 3z}} = \dfrac{{3z}}{{2\left( {1 - y} \right)}}\\\dfrac{x}{{2 - 3z}} = \dfrac{{3z}}{{2 - x}}\end{array} \right. \Rightarrow 2x - {x^2} = 4y - 4{y^2} = 6z - 9{z^2}\) và \(x + 2y + 3z = 2\).
Câu 1 (2 điểm):
1) Rút gọn biểu thức: \(A = \sqrt {32} - \sqrt 6 .\sqrt 3 + \dfrac{{\sqrt {22} }}{{\sqrt {11} }}.\)
2) Giải phương trình: \({x^2} - 2x = 0.\)
3) Xác định hệ số \(a\) của hàm số \(y = a{x^2},\) biết đồ thị của hàm số đó đi qua điểm \(A\left( { - 3;\,\,1} \right).\)
Câu 2 (2 điểm): Cho phương trình \({x^2} - \left( {2m - n} \right)x + \left( {2m + 3n - 1} \right) = 0\,\,\,\,\left( 1 \right)\) (\(m,\,\,n\) là tham số)
1) Với \(n = 0,\) chứng minh rằng phương trình \(\left( 1 \right)\) luôn có nghiệm với mọi giá trị của \(m.\)
2) Tìm \(m,\,\,n\) để phương trình \(\left( 1 \right)\) luôn có hai nghiệm \({x_1},\,\,{x_2}\) thỏa mãn \({x_1} + {x_2} = - 1\) và \(x_1^2 + x_2^2 = 13.\)
Câu 3 (2 điểm):
1) Trong mặt phẳng tọa độ \(Oxy\) cho đường thẳng \(d\) có phương trình \(y = - x + \dfrac{{\sqrt 2 }}{2}.\) Gọi \(A,\,\,B\) lần lượt là giao điểm của \(d\) với trục hoành và trục tung; \(H\) là trung điểm của đoạn thẳng \(AB.\) Tính độ dài đoạn thẳng \(OH\) (đơn vị đo trên các trục tọa độ là xentimet).
2) Một cốc nước dạng hình trụ có chiều cao là 12 cm, bán kính đáy là \(2\)cm, lượng nước trong cốc cao 8 cm. Người ta thả vào cốc nước 6 viên bi hình cầu có cùng bán kính 1 cm và ngập hoàn toàn trong nước làm nước trong cốc dâng lên. Hỏi sau khi thả 6 viên bi vào thì mực nước trong cốc cách miệng côc bao nhiêu xentimet? (giả sử độ dày của cốc là không đáng kể).
Câu 4 (3 điểm): Cho đường tròn \(\left( O \right)\) có hai đường kính \(AB\) và \(CD\) vuông góc với nhau. Điểm \(M\) thuộc cung nhỏ \(BD\) sao cho \(\angle BOM = {30^0}.\) Gọi \(N\) là giao điểm của \(CM\) và \(OB.\) Tiếp tuyến tại \(M\) của đường tròn \(\left( O \right)\) cắt \(OB,\,\,OD\) kéo dài lần lượt tại \(E\) và \(F.\) Đường thẳng qua \(N\) và vuông góc với \(AB\) cắt \(EF\) tại \(P.\)
1) Chứng minh tứ giác \(ONMP\) là tứ giác nội tiếp.
2) Chứng minh \(\Delta EMN\) là tam giác đều.
3) Chứng minh \(CN = OP.\)
4) Gọi \(H\) là trực tâm \(\Delta AEF.\) Hỏi ba điểm \(A,\,\,H,\,\,P\) có thẳng hàng không? Vì sao?
Câu 5 (1 điểm): Cho ba số thực dương \(x,\,\,y,\,\,z\) thỏa mãn \(x + 2y + 3z = 2.\)
Tìm giá trị lớn nhất của biểu thức: \(S = \sqrt {\dfrac{{xy}}{{xy + 3z}}} + \sqrt {\dfrac{{3yz}}{{3yz + x}}} + \sqrt {\dfrac{{3xz}}{{3xz + 4y}}} .\)
Câu 1
Phương pháp:
1) Sử dụng công thức: \(\sqrt A .\sqrt B = \sqrt {AB} ;\,\,\,\dfrac{{\sqrt A }}{{\sqrt B }} = \sqrt {\dfrac{A}{B}} ;\,\,\,\,\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,\,A < 0\end{array} \right..\)
2) Đưa phương trình về dạng phương trình tích để giải phương trình.
3) Thay tọa độ điểm \(A\left( { - 3;\,1} \right)\) vào công thức hàm số \(y = a{x^2}\) để tìm \(a.\)
Cách giải:
1) Rút gọn biểu thức: \(A = \sqrt {32} - \sqrt 6 .\sqrt 3 + \dfrac{{\sqrt {22} }}{{\sqrt {11} }}.\)
\(\begin{array}{l}A = \sqrt {32} - \sqrt 6 .\sqrt 3 + \dfrac{{\sqrt {22} }}{{\sqrt {11} }} = \sqrt {{4^2}.2} - \sqrt {6.3} + \sqrt {\dfrac{{22}}{{11}}} \\ = 4\sqrt 2 - \sqrt {{3^2}.2} + \sqrt 2 = 5\sqrt 2 - 3\sqrt 2 = 2\sqrt 2 .\end{array}\)
Vậy \(A = 2\sqrt 2 .\)
2) Giải phương trình: \({x^2} - 2x = 0.\)
\({x^2} - 2x = 0 \Leftrightarrow x\left( {x - 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right..\)
Vậy phương trình đã cho có tập nghiệm \(S = \left\{ {0;\,\,2} \right\}.\)
3) Xác định hệ số \(a\) của hàm số \(y = a{x^2},\) biết đồ thị của hàm số đó đi qua điểm \(A\left( { - 3;\,\,1} \right).\)
Đồ thị hàm số \(y = a{x^2}\) đi qua điểm \(A\left( { - 3;\,\,1} \right)\) nên thay tọa độ điểm \(A\) vào công thức hàm số ta được:
\(1 = a.{\left( { - 3} \right)^2} \Leftrightarrow a = \dfrac{1}{9}.\)
Vậy \(a = \dfrac{1}{9}.\)
Câu 2
Phương pháp:
1) Thay \(n = 0\) vào phương trình \(\left( 1 \right),\) chứng minh \(\Delta \ge 0\,\,\,\left( {\Delta ' \ge 0} \right)\) với mọi \(m.\)
2) Tìm điều kiện của \(m,\,\,n\) để phương trình \(\left( 1 \right)\) có nghiệm: \(\Delta \ge 0.\)
+) Áp dụng định lý Vi-et và các biểu thức bài cho để tìm \(m,\,\,n.\) Đối chiếu với điều kiện rồi kết luận.
Cách giải:
Cho phương trình \({x^2} - \left( {2m - n} \right)x + \left( {2m + 3n - 1} \right) = 0\,\,\,\,\left( 1 \right)\) (\(m,\,\,n\) là tham số)
1) Với \(n = 0,\) chứng minh rằng phương trình \(\left( 1 \right)\) luôn có nghiệm với mọi giá trị của \(m.\)
Với \(n = 0\) ta có phương trình \(\left( 1 \right) \Leftrightarrow {x^2} - 2mx + 2m - 1 = 0\)
Phương trình có \(\Delta ' = {m^2} - 2m + 1 = {\left( {m - 1} \right)^2} \ge 0\,\,\,\forall m\)
Vậy với \(n = 0\) thì phương trình \(\left( 1 \right)\) luôn có nghiệm với mọi \(m.\)
2) Tìm \(m,\,\,n\) để phương trình \(\left( 1 \right)\) luôn có hai nghiệm \({x_1},\,\,{x_2}\) thỏa mãn \({x_1} + {x_2} = - 1\)và \(x_1^2 + x_2^2 = 13.\)
Ta có: \(\Delta = {\left( {2m - n} \right)^2} - 4\left( {2m + 3n - 1} \right) = 4{m^2} - 4mn + {n^2} - 8m - 12n + 4.\)
Phương trình \(\left( 1 \right)\) có hai nghiệm\({x_1},\,\,{x_2} \Leftrightarrow \Delta \ge 0\)
\( \Leftrightarrow 4{m^2} - 4mn + {n^2} - 8m - 12n + 4 \ge 0.\,\,\,\,\left( * \right)\)
Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m - n\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\\{x_1}{x_2} = 2m + 3n - 1\,\,\,\,\,\,\,\left( 3 \right)\end{array} \right..\)
Theo đề bài ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 1\\x_1^2 + x_2^2 = 13\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_1} + {x_2} = - 1\,\,\,\,\,\,\,\left( 4 \right)\\{\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 13\,\,\,\,\,\left( 5 \right)\end{array} \right.\,\,\)
Thế (3) và (4) vào (5) ta được:
\(\begin{array}{l}\left( 5 \right) \Leftrightarrow {\left( { - 1} \right)^2} - 2\left( {2m + 3n - 1} \right) = 13\\ \Leftrightarrow 1 - 4m - 6n + 2 = 13\\ \Leftrightarrow 4m + 6n = - 10\\ \Leftrightarrow 2m + 3n = - 5\,\,\,\,\left( 6 \right)\end{array}\)
Từ (2) và (4) ta có: \(2m - n = - 1 \Leftrightarrow n = 2m + 1\,\,\,\left( 7 \right)\)
Thế \(\left( 7 \right)\) vào \(\left( 6 \right)\) ta được: \(2m + 3\left( {2m + 1} \right) = - 5 \Leftrightarrow 2m + 6m + 3 = - 5 \Leftrightarrow 8m = - 8 \Leftrightarrow m = - 1\)
\( \Rightarrow n = 2m + 1 = 2.\left( { - 1} \right) + 1 = - 1.\)
Thay \(m = - 1,\,\,n = - 1\) vào điều kiện \(\left( * \right)\) ta có:
\(4.{\left( { - 1} \right)^2} - 4.\left( { - 1} \right)\left( { - 1} \right) + {\left( { - 1} \right)^2} - 8.\left( { - 1} \right) - 12.\left( { - 1} \right) + 4 = 25 > 0\)
\( \Rightarrow \left\{ \begin{array}{l}m = - 1\\n = - 1\end{array} \right.\) thỏa mãn.
Vậy \(m = - 1,\,\,n = - 1\) là các giá trị cần tìm.
Câu 3
Phương pháp:
1) Tìm tọa độ các điểm \(A,\,\,B.\) Sử dụng hệ thức lượng trong \(\Delta AOB\) vuông tại \(O\) có đường cao \(OH\) để làm bài toán.
2) Thể tích của khối trụ có chiều cao \(h\) và bán kính đáy \(R\) là: \(V = \pi {R^2}h.\)
Thể tích khối cầu bán kính \(R\) là: \(V = \dfrac{4}{3}\pi {R^3}.\)
Cách giải:
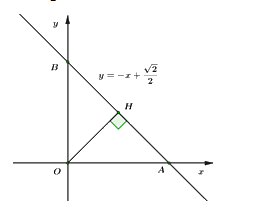
1) Cho \(d:\,\,\,y = - x + \dfrac{{\sqrt 2 }}{2}.\)
Ta có: \(d \cap Ox = \left\{ A \right\} \Rightarrow A\left( {{x_A};\,\,0} \right) \Rightarrow - {x_A} + \dfrac{{\sqrt 2 }}{2} = 0 \Leftrightarrow {x_A} = \dfrac{{\sqrt 2 }}{2} \Rightarrow A\left( {\dfrac{{\sqrt 2 }}{2};\,\,0} \right) \Rightarrow OA = \dfrac{{\sqrt 2 }}{2}.\)
\(d \cap Oy = \left\{ B \right\} \Rightarrow B\left( {0;\,\,{y_B}} \right) \Rightarrow 0 + \dfrac{{\sqrt 2 }}{2} = {y_B} \Leftrightarrow {y_B} = \dfrac{{\sqrt 2 }}{2} \Rightarrow B\left( {0;\,\,\dfrac{{\sqrt 2 }}{2}} \right) \Rightarrow OB = \dfrac{{\sqrt 2 }}{2}.\)
Vì tam giác \(OAB\) vuông cân tại \(O\) \(\left( {do\,OA = OB = \dfrac{{\sqrt 2 }}{2}} \right)\) mà \(OH\) là đường trung tuyến nên \(OH\) cũng là đường cao.
Sử dụng hệ thức lượng trong \(\Delta AOB\) vuông tại \(O\) có đường cao \(OH\) ta có: \(\begin{array}{l}\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} = \dfrac{1}{{{{\left( {\dfrac{{\sqrt 2 }}{2}} \right)}^2}}} + \dfrac{1}{{{{\left( {\dfrac{{\sqrt 2 }}{2}} \right)}^2}}} = 2 + 2 = 4.\\ \Rightarrow O{H^2} = \dfrac{1}{4} \Leftrightarrow OH = \dfrac{1}{2} = 0,5\,\,cm.\end{array}\) Vậy \(OH = 0,5\,\,cm.\) |
2) Thể tích nước dâng lên = thể tích 6 viên bi được thả vào cốc.
Thể tích nước có trong cốc ban đầu là: \({V_1} = \pi {.2^2}.8 = 32\pi \,\,\left( {c{m^3}} \right).\)
Ta có thể tích của 6 viên bi được thả vào cốc là: \({V_2} = 6.\dfrac{4}{3}\pi {.1^3} = 8\pi \,\,\,\left( {c{m^3}} \right).\)
Thể tích sau khi được thả thêm 6 viên bi là: \(V = {V_1} + {V_2} = 32\pi + 8\pi = 40\pi \,\,\left( {c{m^3}} \right).\)
\( \Rightarrow \) Chiều cao mực nước trong cốc lúc này là: \(h = \dfrac{V}{{\pi {R^2}}} = \dfrac{{40\pi }}{{\pi {{.2}^2}}} = 10\,\,\left( {cm} \right).\)
Vậy sau khi thả 6 viên bi vào cốc thì mực nước cách cốc là \(12 - 10 = 2\,\,cm.\)
Câu 4
Phương pháp:
1) Chứng minh tứ giác nội tiếp dựa vào các dấu hiệu nhận biết của tứ giác.
2) Chứng minh tam giác có hai góc có số đo bằng \({60^0}\) là tam giác đều.
3) Chứng minh tứ giác \(OCNP\) là hình bình hành.
Cách giải:
1) Chứng minh tứ giác \(ONMP\) là tứ giác nội tiếp.
Xét tứ giác \(ONMP\) ta có:
\(\angle ONP = {90^0}\,\,\,\left( {NP \bot AB} \right)\)
\(\angle OMP = {90^0}\) (\(EF\) là tiếp tuyến của \(\left( O \right)\))
\( \Rightarrow \angle ONP = \angle OMP = {90^0}\)
Mà hai đỉnh \(N,\,\,P\) là hai đỉnh kề nhau cùng nhìn cạnh \(OP.\)
\( \Rightarrow ONMP\) là tứ giác nội tiếp. (dhnb) (đpcm).
2) Chứng minh \(\Delta EMN\) là tam giác đều.
Xét \(\left( O \right)\) ta có:
\(\angle COM\) là góc ở tâm chắn cung \(CM\)
\(\angle CME\) là góc tạo bởi tia tiếp tuyến và dây cung chắn cung \(CM\)
\( \Rightarrow \angle CME = \dfrac{1}{2}\angle COM = \dfrac{1}{2}\left( {\angle COB + \angle BOM} \right) = \dfrac{1}{2}\left( {{{90}^0} + {{30}^0}} \right) = {60^0}.\) (tính chất góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn một cung).
Hay \(\angle NME = {60^0}.\)
Xét \(\Delta OME\) vuông tại \(M\) ta có:
\(\angle OEM = {90^0} - \angle EOM = {90^0} - {30^0} = {60^0}.\)
Xét \(\Delta MNE\) ta có:\(\angle NEM = \angle NME = {60^0}\,\,\left( {cmt} \right)\)
\( \Rightarrow \Delta NME\) là tam giác đều. (định nghĩa) (đpcm).
3) Chứng minh \(CN = OP.\)
Ta có: \(\Delta MNE\) là tam giác đều (cmt)
\( \Rightarrow \angle ENM = {60^0} = \angle ONC\) (hai góc đối đỉnh)
\( \Rightarrow \angle OCN = {90^0} - \angle ONC = {90^0} - {60^0} = {30^0}\)
Ta có: \(\angle OMN = {90^0} - \angle NME = {90^0} - {60^0} = {30^0}.\)
Vì \(ONMP\) là tứ giác nội tiếp (cmt) \( \Rightarrow \angle OPN = \angle OMN = {30^0}\) (hai góc nội tiếp cùng chắn cung \(ON\))
Ta có: \(\left\{ \begin{array}{l}OC \bot AB = \left\{ O \right\}\\NP \bot AB = \left\{ N \right\}\end{array} \right. \Rightarrow OC//NP \Rightarrow OCPN\) là hình thang.
Mà \(\angle OCN = \angle OPN = {30^0}\,\,\,\left( {cmt} \right).\)
Lại có hai góc này là hai góc đối nhau
\( \Rightarrow OCNP\) là hình bình hành.
\( \Rightarrow OC = NP\,\,\,\left( {dpcm} \right).\)
4) Gọi \(H\) là trực tâm \(\Delta AEF.\) Hỏi ba điểm \(A,\,\,H,\,\,P\) có thẳng hàng không? Vì sao?
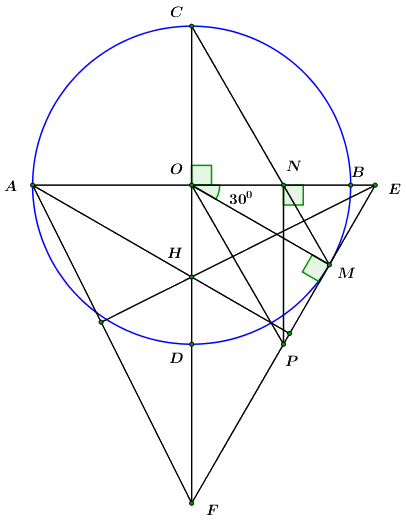
Gọi \(I\) là chân đường cao kẻ từ \(A\) đến \(EF\) thì \(H \in AI\).
Giả sử phản chứng \(A,H,P\) thẳng hàng thì \(P \equiv I\) hay \(AP \bot EF\).
Có \(\angle EOP = \angle NOP = {90^0} - \angle ONP = {60^0}\) và \(\angle OEP = {60^0}\left( {cmt} \right)\) nên \(\Delta OEP\) là tam giác cân có một góc bằng \({60^0}\) nên là tam giác đều \( \Rightarrow OP = PE\,\,\left( 1 \right)\).
Lại có \(\angle POF = {90^0} - \angle EOP = {90^0} - {60^0} = {30^0}\) và \(\angle PFO = {90^0} - \angle OEP = {90^0} - {60^0} = {30^0}\) nên tam giác \(OPF\) cân tại \(P\) hay \(OP = PF\,\,\left( 2 \right)\).
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(PE = PF\left( { = OP} \right)\).
Xét tam giác \(AEF\) có \(AP \bot EF\) (giả thiết) và \(PE = PF\) nên \(AP\) vừa là đường cao vừa là đường trung tuyến.
\( \Rightarrow \Delta AEF\) cân tại \(A\). Mà \(\angle AEF = {60^0}\) nên tam giác \(AEF\) đều.
\( \Rightarrow FO\) vừa là đường cao vừa là đường trung tuyến \( \Rightarrow OA = OE\) (vô lý vì \(OA < OE\)).
Vậy ba điểm \(A,H,P\) không thẳng hàng.
Câu 5
Phương pháp:
- Biến đổi các mẫu về dạng tích.
- Áp dụng bất đẳng thức Cô-si cho hai số dương \(\sqrt {ab} \le \dfrac{{a + b}}{2}\).
Cách giải:
Do \(x + 2y + 3z = 2\) nên \(\left\{ \begin{array}{l}x = 2 - 2y - 3z\\2y = 2 - x - 3z\\3z = 2 - x - 2y\end{array} \right.\). Khi đó,
\(\begin{array}{l}xy + 3z = xy + \left( {2 - x - 2y} \right) = \left( {xy - x} \right) - \left( {2y - 2} \right) = x\left( {y - 1} \right) - 2\left( {y - 1} \right) = \left( {x - 2} \right)\left( {y - 1} \right)\\3yz + x = 3yz + \left( {2 - 2y - 3z} \right) = \left( {3yz - 3z} \right) - \left( {2y - 2} \right) = \left( {y - 1} \right)\left( {3z - 2} \right)\\3xz + 4y = 3xz + 2\left( {2 - x - 3z} \right) = \left( {3xz - 6z} \right) - \left( {2x - 4} \right) = 3z\left( {x - 2} \right) - 2\left( {x - 2} \right) = \left( {x - 2} \right)\left( {3z - 2} \right)\end{array}\)
Suy ra:
\(\begin{array}{l}S = \sqrt {\dfrac{{xy}}{{\left( {x - 2} \right)\left( {y - 1} \right)}}} + \sqrt {\dfrac{{3yz}}{{\left( {y - 1} \right)\left( {3z - 2} \right)}}} + \sqrt {\dfrac{{3xz}}{{\left( {x - 2} \right)\left( {3z - 2} \right)}}} \\ = \sqrt {\dfrac{x}{{2\left( {1 - y} \right)}}} .\sqrt {\dfrac{{2y}}{{2 - x}}} + \sqrt {\dfrac{{2y}}{{2 - 3z}}} .\sqrt {\dfrac{{3z}}{{2\left( {1 - y} \right)}}} + \sqrt {\dfrac{x}{{2 - 3z}}} .\sqrt {\dfrac{{3z}}{{2 - x}}} \\ \le \dfrac{1}{2}\left( {\dfrac{x}{{2\left( {1 - y} \right)}} + \dfrac{{2y}}{{2 - x}}} \right) + \dfrac{1}{2}\left( {\dfrac{{2y}}{{2 - 3z}} + \dfrac{{3z}}{{2\left( {1 - y} \right)}}} \right) + \dfrac{1}{2}\left( {\dfrac{x}{{2 - 3z}} + \dfrac{{3z}}{{2 - x}}} \right)\\ = \dfrac{1}{2}\left( {\dfrac{x}{{2\left( {1 - y} \right)}} + \dfrac{{2y}}{{2 - x}} + \dfrac{{2y}}{{2 - 3z}} + \dfrac{{3z}}{{2\left( {1 - y} \right)}} + \dfrac{x}{{2 - 3z}} + \dfrac{{3z}}{{2 - x}}} \right)\\ = \dfrac{1}{2}\left( {\dfrac{{x + 3z}}{{2\left( {1 - y} \right)}} + \dfrac{{2y + 3z}}{{2 - x}} + \dfrac{{2y + x}}{{2 - 3z}}} \right)\\ = \dfrac{1}{2}\left( {\dfrac{{2 - 2y}}{{2\left( {1 - y} \right)}} + \dfrac{{2 - x}}{{2 - x}} + \dfrac{{2 - 3z}}{{2 - 3z}}} \right) = \dfrac{1}{2}.\left( {1 + 1 + 1} \right) = \dfrac{3}{2}\end{array}\)
Hay \(S \le \dfrac{3}{2}\) \( \Rightarrow \max S = \dfrac{3}{2}\)
Dấu “=” xảy ra khi \(\left\{ \begin{array}{l}\dfrac{x}{{2\left( {1 - y} \right)}} = \dfrac{{2y}}{{2 - x}}\\\dfrac{{2y}}{{2 - 3z}} = \dfrac{{3z}}{{2\left( {1 - y} \right)}}\\\dfrac{x}{{2 - 3z}} = \dfrac{{3z}}{{2 - x}}\end{array} \right. \Rightarrow 2x - {x^2} = 4y - 4{y^2} = 6z - 9{z^2}\) và \(x + 2y + 3z = 2\).
Kỳ thi tuyển sinh vào lớp 10 môn Toán tại tỉnh Đắk Lắk năm 2019 là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Để giúp các em chuẩn bị tốt nhất, giaitoan.edu.vn xin cung cấp phân tích chi tiết về cấu trúc đề thi, các dạng bài tập thường gặp và hướng dẫn giải chi tiết.
Đề thi vào 10 môn Toán Đắk Lắk năm 2019 thường bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Dưới đây là một số dạng bài tập thường gặp trong đề thi vào 10 môn Toán Đắk Lắk năm 2019:
Bài 1: Giải phương trình 2x + 3 = 7
Lời giải:
2x + 3 = 7
2x = 7 - 3
2x = 4
x = 2
Bài 2: Cho tam giác ABC vuông tại A, AB = 3cm, AC = 4cm. Tính độ dài cạnh BC.
Lời giải:
Áp dụng định lý Pitago vào tam giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2
BC2 = 32 + 42
BC2 = 9 + 16
BC2 = 25
BC = 5cm
Để chuẩn bị tốt hơn cho kỳ thi vào 10 môn Toán, các em có thể tham khảo thêm các tài liệu sau:
Đề thi vào 10 môn Toán Đắk Lắk năm 2019 là một kỳ thi quan trọng, đòi hỏi các em học sinh phải có sự chuẩn bị kỹ lưỡng. Hy vọng với những phân tích và hướng dẫn trên, các em sẽ tự tin hơn và đạt kết quả tốt nhất trong kỳ thi sắp tới. Chúc các em thành công!