Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Bến Tre năm 2022 chính thức và mới nhất. Đây là tài liệu ôn tập vô cùng quan trọng dành cho các em học sinh đang chuẩn bị cho kỳ thi sắp tới.
Chúng tôi cung cấp đầy đủ các đề thi, đáp án và lời giải chi tiết, giúp các em làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi.
A. PHẦN TRẮC NGHIỆM (4,0 điểm, từ câu 1 đến câu 20, mỗi câu 0,2 điểm): Câu 1: Giá trị của biểu thức
A. PHẦN TRẮC NGHIỆM
1. A | 2. D | 3. B | 4. D | 5. B | 6. B | 7. A | 8. A | 9. A | 10. C |
11. D | 12. C | 13. D | 14. A | 15. C | 16. C | 17. A | 18. D | 19. C | 20. B |
Câu 1 (NB):
Phương pháp:
Vận dụng hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,\,A \ge 0\\ - A\,\,\,\,khi\,\,\,\,A < 0\end{array} \right.\)
Cách giải:
\(\dfrac{{\sqrt {99} }}{{\sqrt {11} }} = \dfrac{{\sqrt {9.11} }}{{\sqrt {11} }} = \dfrac{{\sqrt {{3^2}} .\sqrt {11} }}{{\sqrt {11} }} = \left| 3 \right| = 3\) (vì 3 > 0)
Chọn A.
Câu 2 (NB):
Phương pháp:
Vận dụng hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,\,A \ge 0\\ - A\,\,\,\,khi\,\,\,\,A < 0\end{array} \right.\)
Cách giải:
Khẳng định đúng là: \(\sqrt {{a^2}} = \left| a \right|\)
Chọn D.
Câu 3 (TH):
Phương pháp:
Giải phương trình: \(\sqrt A = B \Leftrightarrow \left\{ \begin{array}{l}B \ge 0\\A = {B^2}\end{array} \right.\)
Cách giải:
Điều kiện: \(x \ge 0\)
\(\sqrt {9x} = 27\)
\(\begin{array}{l} \Leftrightarrow 9x = {27^2}\\ \Leftrightarrow x = 729:9\\ \Leftrightarrow x = 81\,\,\left( {tmdk} \right)\end{array}\)
Vậy \(x = 81\)
Chọn B.
Câu 4 (NB):
Phương pháp:
Hàm số \(y = ax + b\) đồng biến trên \(\mathbb{R} \Leftrightarrow a > 0\)
Cách giải:
Hàm số \(y = \left( {m - 6} \right)x + 2022\) đồng biến trên \(\mathbb{R}\)\( \Leftrightarrow m - 6 > 0 \Leftrightarrow m > 6\)
Chọn B.
Câu 5 (NB):
Phương pháp:
Hai đường thẳng \(y = ax + b\) và \(y = a'x + b\) \(\left( {a \ne 0;a' \ne 0} \right)\)\( \Leftrightarrow \left\{ \begin{array}{l}a \ne a'\\b \ne b'\end{array} \right.\)
Cách giải:
Điều kiện để hai đường thẳng \(y = ax + b\) và \(y = a'x + b\) \(\left( {a \ne 0;a' \ne 0} \right)\) là \(a \ne a'\)và \(b \ne b'\).
Chọn D.
Câu 6 (NB):
Phương pháp:
Đường thẳng \(y = ax + b\) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) khi \({y_0} = a{x_0} + b\)
Cách giải:
Đường thẳng y = ax + 7 đi qua điểm A(2; 3) nên ta có: \(a.2 + 7 = 3 \Leftrightarrow a = - 2\)
Vậy hệ số góc của đường thẳng là -2.
Chọn B.
Câu 7 (TH):
Phương pháp:
Nhận xét đồ thị từ đó xác định được hàm số cần tìm.
Cách giải:
+ Gọi hàm số cần tìm là \(y = ax + b\left( {a \ne 0} \right)\)
+ Đồ thị hàm số đi qua điểm (0; -1) và (2; 0) nên ta có hệ phương trình: \(\left\{ \begin{array}{l}a.0 + b = - 1\\2.a + b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 1\\2a - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 1\\a = \dfrac{1}{2}\end{array} \right.\)
Hàm số cần tìm là: \(y = \dfrac{1}{2}x - 1\)
Chọn A.
Câu 8 (NB):
Phương pháp:
Hệ phương trình bậc nhất hai ẩn x, y có dạng: \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\)
Cách giải:
Hệ phương trình bậc nhất hai ẩn x, y là: \(\left\{ \begin{array}{l}x + 3y = 1\\x - y = 7\end{array} \right.\)
Chọn A.
Câu 9 (NB):
Phương pháp:
Nhận xét hệ số a của hàm số bậc hai một ẩn để xác định khẳng định đúng.
Cách giải:
Hàm số \(y = 2022{x^2}\) có a = 2022 > 0 nên hàm số hàm số đồng biến khi x > 0 và nghịch biến khi x < 0.
Chọn A.
Câu 10 (NB):
Phương pháp:
Đồ thị hàm số \(y = a{x^2}\)\(\left( {a \ne 0} \right)\) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) khi và chỉ khi \({y_0} = a{x_0}\).
Cách giải:
Đồ thị hàm số \(y = \left( {m - 6} \right){x^2}\) đi qua điểm E(1; 2) nên ta có: \(\left( {m - 6} \right){.1^2} = 2 \Leftrightarrow m = 8\)
Vậy \(m = 8\)
Chọn A.
Câu 11 (NB):
Phương pháp:
Phương trình bậc hai \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có biệt thức \(\Delta = {b^2} - 4ac\)
Cách giải:
Ta có: \(\Delta = {6^2} - 4.\left( { - 6} \right) = 60\)
Chọn D.
Câu 12 (NB):
Phương pháp:
Phương trình bậc hai \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt \({x_1},{x_2}\) khi đó theo hệ thức Vi – ét, ta có: \({x_1} + {x_2} = \dfrac{{ - b}}{a}\)
Cách giải:
Phương trình có có hai nghiệm phân biệt \({x_1},{x_2}\), khi đó theo hệ thức Vi – ét, ta có: \({x_1} + {x_2} = \dfrac{{ - 6}}{7}\)
Chọn C.
Câu 13 (NB):
Phương pháp:
Phương trình trùng phương là phương trình có dạng: \(a{x^4} + b{x^2} + c = 0\) với a, b, c là các số thực và \(a \ne 0\)
Cách giải:
Phương trình trùng phương là phương trình có dạng: \(a{x^4} + b{x^2} + c = 0\) với a, b, c là các số thực và \(a \ne 0\)
Chọn D.
Câu 14 (NB):
Phương pháp:
Áp dụng định lý Py – ta – go
Cách giải:
Tam giác ABC vuông cân tại A, nên AB = AC = 8cm
Tam giác ABC vuông tại A, theo định lý Py – ta – go, ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2}\\ \Leftrightarrow B{C^2} = {8^2} + {8^2} = 128\\ \Rightarrow BC = 8\sqrt 2 cm\end{array}\)
Chọn A.
Câu 15 (TH):
Phương pháp:
Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông.
Cách giải:
Khẳng định không đúng là \(\cos \alpha > 1\)
Chọn C.
Câu 16 (TH):
Phương pháp:
Vận dụng kiến thức vị trí tương đối của hai đường tròn.
Cách giải:
Đường tròn tâm O bán kính OA và đường tròn đường kính OA tiếp xúc trong với nhau.
Chọn C.
Câu 17 (NB):
Phương pháp:
Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì có số đo bằng nhau.
Cách giải:
Xét (O) có: \(\angle BDC = \angle BAC = {70^0}\) (hai góc nội tiếp cùng chắn cung BC)
Chọn A.
Câu 18 (NB):
Phương pháp:
Góc nội tiếp chắn nửa đường tròn có số đo bằng \({90^0}\).
Cách giải:
Góc nội tiếp chắn nửa đường tròn có số đo bằng \({90^0}\).
Chọn D.
Câu 19 (NB):
Phương pháp:
Thể tích hình lăng trụ có bán kình đáy là r, chiều cao h là \(V = \pi {r^2}h\)
Cách giải:
Thể tích hình trụ đó là: \(V = \pi {.3^2}.5 = 45\pi \,\left( {c{m^3}} \right)\)
Chọn C.
Câu 20 (NB):
Phương pháp:
Thể tích của hình cầu có bán kính R là: \(V = \dfrac{4}{3}\pi {R^3}\)
Cách giải:
Thể tích của hình cầu là: \(V = \dfrac{4}{3}\pi {.7^3} = \dfrac{{1372}}{3}\pi \left( {c{m^3}} \right)\)
Chọn B.
B. PHẦN TỰ LUẬN
Câu 21 (NB):
Phương pháp:
Áp dụng công thức nghiệm của phương trình bậc hai một ẩn số.
Cách giải:
Giải phương trình \(2{x^2} + 4x - 5 = 0\)
Ta có: \(\Delta ' = {2^2} - 2.\left( { - 5} \right) = 14 > 0\) nên phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}x = \dfrac{{ - 2 + \sqrt {14} }}{2}\\x = \dfrac{{ - 2 - \sqrt {14} }}{2}\end{array} \right.\).
Vậy tập nghiệm của phương trình là: \(S = \left\{ {\dfrac{{ - 2 \pm \sqrt {14} }}{2}} \right\}\).
Câu 22 (TH):
Phương pháp:
Sử dụng phương pháp cộng đại số, tìm được nghiệm \(x\)
Sử dụng phương pháp thế, tìm được nghiệm \(y\)
Kết luận nghiệm \(\left( {x;y} \right)\) của hệ phương trình.
Cách giải:
Giải hệ phương trình \(\left\{ \begin{array}{l}x - 2y = 5\\7x + y = 6\end{array} \right.\)
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}x - 2y = 5\\7x + y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 2y = 5\\14x + 2y = 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}15x = 17\\7x + y = 6\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{17}}{{15}}\\7.\dfrac{{17}}{5} + y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{17}}{{15}}\\y = \dfrac{{ - 29}}{{15}}\end{array} \right.\end{array}\)
Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {\dfrac{{17}}{{15}}; - \dfrac{{29}}{{15}}} \right)\).
Câu 23 (TH):
Phương pháp:
Vẽ đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
+ Nhận xét về hệ số \(a\) và sự biến thiên của hàm số
+ Lập bảng giá trị tương ứng của \(x\) và \(y\)
+ Xác định được các điểm mà đồ thị đi qua, vẽ đồ thị.
Cách giải:
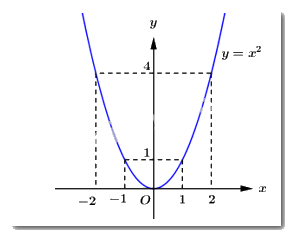
Vẽ đồ thị hàm số \(y = {x^2}\)
Hệ số \(a = 1 > 0\) nên hàm số đồng biến khi \(x > 0\), nghịch biến khi \(x < 0\) và có bề lõm hướng lên trên.
Bảng giá trị:
\(x\) | \( - 2\) | \( - 1\) | 0 | 1 | 2 |
\(y = {x^2}\) | 4 | 1 | 0 | 1 | 4 |
\( \Rightarrow \) Parabol \(y = {x^2}\)là đường cong đi qua các điểm \(\left( { - 2;4} \right),\,\,\left( { - 1;1} \right),\,\,\left( {0;0} \right),\,\,\left( {1;1} \right),\,\,\left( {2;4} \right)\).
Câu 24 (TH):
Phương pháp:
Vận dụng hằng đẳng thức \(a - b = \left( {\sqrt a - \sqrt b } \right)\left( {\sqrt a + \sqrt b } \right)\) xác định mẫu thức chung của biểu thức
Quy đồng các phân thức, thực hiện các phép toán từ đó rút gọn được biểu thức.
Cách giải:
Rút gọn biểu thức \(A = \dfrac{1}{{\sqrt a }}.\left( {\dfrac{1}{{\sqrt a + \sqrt b }} + \dfrac{1}{{\sqrt a - \sqrt b }}} \right)\) với\(a,\,\,b > 0\) và \(a \ne b\).
Với\(a,\,\,b > 0\) và \(a \ne b\) ta có:
\(\begin{array}{l}A = \dfrac{1}{{\sqrt a }}.\left( {\dfrac{1}{{\sqrt a + \sqrt b }} + \dfrac{1}{{\sqrt a - \sqrt b }}} \right)\\A = \dfrac{1}{{\sqrt a }}.\dfrac{{\sqrt a - \sqrt b + \sqrt a + \sqrt b }}{{\left( {\sqrt a + \sqrt b } \right)\left( {\sqrt a - \sqrt b } \right)}}\\A = \dfrac{1}{{\sqrt a }}.\dfrac{{2\sqrt a }}{{a - b}}\\A = \dfrac{2}{{a - b}}\end{array}\)
Vậy với\(a,\,\,b > 0\) và \(a \ne b\) thì \(A = \dfrac{2}{{a - b}}\).
Câu 25 (VD):
Phương pháp:
a) Vận dụng dấu hiệu nhận biết: Tứ giác có tổng hai góc đối bằng 180 độ là tứ giác nội tiếp.
b) Áp dụng hệ thức lượng trong tam giác vuông.
Cách giải:
Trên đường tròn (O) đường kính AB, lấy điểm E (khác A và B). Vẽ tiếp tuyến của (O) tại A. Đường thẳng BE cắt tiếp tuyến đó tại M. Từ điểm M kẻ tiếp tuyến với đường tròn (O) tại điểm C (C là tiếp điểm, \(C \ne A\)). Chứng minh rằng:
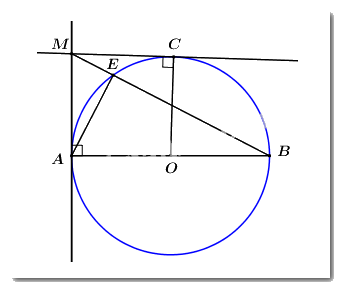
a) Tứ giác AOCM là tứ giác nội tiếp.
Vì MA là tiếp tuyến của (O) tại A nên \(\angle OAM = {90^0}\)
Vì MC là tiếp tuyến của (O) tại C nên \(\angle OCM = {90^0}\)
Xét tứ giác AOCM có: \(\angle OAM + \angle OCM = {90^0} + {90^0} = {180^0}\), mà 2 góc này là 2 góc đối nhau của tứ giác AOCM.
\( \Rightarrow AOCM\) là tứ giác nội tiếp (dhnb).
b) \(E{A^2} = EM.EB\).
Ta có \(\angle AEB = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow AE \bot EB\) hay \(AE \bot BM\).
Áp dụng hệ thức lượng trong tam giác vuông ABM, đường cao AE ta có: \(A{E^2} = EM.EB\) (đpcm).
Câu 26 (VD):
Phương pháp:
Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) \( \Leftrightarrow \Delta ' > 0\)
Áp dụng hệ thức Vi – ét, ta có: \({x_1} + {x_2} = \dfrac{{ - b}}{a};{x_1}.{x_2} = \dfrac{c}{a}\)
Biến đổi \(x_1^3 + x_2^3 = {\left( {{x_1} + {x_2}} \right)^2} - 3{x_1}{x_2}\left( {{x_1} + {x_2}} \right)\)
Cách giải:
Cho phương trình bậc hai \({x^2} + 2mx + {m^2} + 2m + 3 = 0\), với m là tham số. Tìm các giá trị của m để phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa \(x_1^3 + x_2^3 = 108.\)
Ta có: \(\Delta ' = {m^2} - \left( {{m^2} + 2m + 3} \right) = - 2m - 3\).
Để phương trình có 2 nghiệm phân biệt \({x_1},\,\,{x_2}\) thì \(\Delta ' > 0 \Leftrightarrow - 2m - 3 > 0 \Leftrightarrow 2m < - 3 \Leftrightarrow m < - \dfrac{3}{2}\).
Khi đó áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 2m\\{x_1}{x_2} = {m^2} + 2m + 3\end{array} \right.\)
Theo giả thiết ta có:
\(\begin{array}{l}\,\,\,\,\,\,x_1^3 + x_2^3 = 108\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^3} - 3{x_1}{x_2}\left( {{x_1} + {x_2}} \right) = 108\\ \Leftrightarrow {\left( { - 2m} \right)^3} - 3.\left( {{m^2} + 2m + 3} \right).\left( { - 2m} \right) = 108\\ \Leftrightarrow - 8{m^3} + 6m\left( {{m^2} + 2m + 3} \right) = 108\\ \Leftrightarrow - 8{m^3} + 6{m^3} + 12{m^2} + 18m - 108 = 0\\ \Leftrightarrow - 2{m^3} + 12{m^2} + 18m - 108 = 0\\ \Leftrightarrow \left( { - 2{m^3} + 18m} \right) + \left( {12{m^2} - 108} \right) = 0\\ \Leftrightarrow - 2m\left( {{m^2} - 9} \right) + 12\left( {{m^2} - 9} \right) = 0\end{array}\)
\(\begin{array}{l} \Leftrightarrow - 2\left( {{m^2} - 9} \right)\left( {m - 6} \right) = 0\\ \Leftrightarrow - 2\left( {m - 3} \right)\left( {m + 3} \right)\left( {m - 6} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m - 3 = 0\\m + 3 = 0\\m - 6 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 3\,\,\,\,\,\,\,\left( {ktm} \right)\\m = - 3\,\,\,\,\left( {tm} \right)\\m = 6\,\,\,\,\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy \(m = - 3\).
Câu 27 (VD):
Phương pháp:
Gọi số tiền phải trả cho loại hàng thứ nhất (chưa kể thuế VAT) là \(x\) (triệu đồng) (ĐK: \(x > 0\))
Gọi số tiền phải trả cho loại hàng thứ hai (chưa kể thuế VAT) là \(y\) (triệu đồng) (ĐK: \(y > 0\))
Lập hệ phương trình bậc nhất hai ẩn của x và y.
Giải hệ phương trình, đối chiếu điều kiện và kết luận.
Cách giải:
Một người mua hai loại hàng và phải trả tổng cộng 4,35 triệu đồng, kể cả thuế giá trị gia tăng (VAT) với mức 10% đối với loại hàng thứ nhất và 8% đối với loại hàng thứ hai. Nếu thuế VAT là 9% đối với cả hai loại hàng thì người đó phải trả tổng cộng 4,36 triệu đồng. Nếu chưa kể thuế VAT thì người đó phải trả bao nhiêu tiền cho mỗi loại hàng?
Gọi số tiền phải trả cho loại hàng thứ nhất (chưa kể thuế VAT) là \(x\) (triệu đồng) (ĐK: \(x > 0\))
Gọi số tiền phải trả cho loại hàng thứ hai (chưa kể thuế VAT) là \(y\) (triệu đồng) (ĐK: \(y > 0\))
Vì một người mua hai loại hàng và phải trả tổng cộng 4,35 triệu đồng, kể cả thuế giá trị gia tăng (VAT) với mức 10% đối với loại hàng thứ nhất và 8% đối với loại hàng thứ hai nên ta có phương trình:
\(1,1x + 1,08y = 4,35\) (1).
Vì nếu thuế VAT là 9% đối với cả hai loại hàng thì người đó phải trả tổng cộng 4,36 triệu đồng nên ta có phương trình
\(1,09x + 1,09y = 4,36\) (2)
Từ (1) và (2) ta có hệ phương trình \(\left\{ \begin{array}{l}1,1x + 1,08y = 4,35\\1,09x + 1,09y = 4,36\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1,1x + 1,08y = 4,35\\x + y = 4\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}1,1x + 1,08\left( {4 - x} \right) = 4,35\\y = 4 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1,1x + 4,32 - 1,08x = 4,35\\y = 4 - x\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}0,02x = 0,03\\y = 4 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1,5\,\,\left( {tm} \right)\\y = 4 - 1,5 = 2,5\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy số tiền phải trả cho loại hàng thứ nhất (chưa kể thuế VAT) là 1,5 triệu đồng và số tiền phải trả cho loại hàng thứ hai (chưa kể thuế VAT) là 2,5 triệu đồng.
A. PHẦN TRẮC NGHIỆM (4,0 điểm, từ câu 1 đến câu 20, mỗi câu 0,2 điểm):
Câu 1: Giá trị của biểu thức \(\dfrac{{\sqrt {99} }}{{\sqrt {11} }}\) bằng:
A. 3 B. 6 C. 9 D. \(\sqrt 3 \)
Câu 2: Cho số thực a. Khẳng định nào dưới đây là đúng?
A. \(\sqrt {{a^2}} = {a^4}\) B. \(\sqrt {{a^2}} = a\) C. \(\sqrt {{a^2}} = - {a^4}\) D. \(\sqrt {{a^2}} = \left| a \right|\)
Câu 3: Nghiệm của phương trình \(\sqrt {9x} = 27\) là:
A. \(x = 3\) B. \(x = 81\) C. \(x = 27\) D. \(x = 9\)
Câu 4: Tìm tất cả các giá trị của tham số m để hàm số bậc nhất \(y = \left( {m - 6} \right)x + 2022\) đồng biến trên \(\mathbb{R}\) là:
A. \(m \ge 6\) B. \(m < 6\) C. \(m \le 6\) D. \(m > 6\)
Câu 5: Điều kiện để hai đường thẳng \(y = ax + b\) và \(y = a'x + b\) \(\left( {a \ne 0;a' \ne 0} \right)\)
A. \(a = a'\)và \(b = b'\) B. \(a = a'\)và \(b \ne b'\) C. \(a \ne a'\)và \(b = b'\) D. \(a \ne a'\)và \(b \ne b'\)
Câu 6: Đường thẳng y = ax + 7 đi qua điểm A(2; 3) có hệ số góc a bằng:
A. 3 B. -2 C. 5 D. -3
Câu 7: Hàm số nào sau đây có đồ thị như hình vẽ bên?
A. \(y = \dfrac{1}{2}x - 1\) B. \(y = \dfrac{1}{2}x\) C. \(y = x - 1\) D. \(y = x + 2\)
Câu 8: Hệ phương trình sau đây là hệ phương trình bậc nhất hai ẩn x, y?
A. \(\left\{ \begin{array}{l}x + 3y = 1\\x - y = 7\end{array} \right.\) B. \(\left\{ \begin{array}{l}x + y = 1\\{x^2} + y = 3\end{array} \right.\) C. \(\left\{ \begin{array}{l}x + y = 1\\x + {y^2} = 3\end{array} \right.\) D. \(\left\{ \begin{array}{l}x + 2y = 0\\x + \dfrac{2}{y} = 3y\end{array} \right.\)
Câu 9: Cho hàm số \(y = 2022{x^2}\). Khẳng định nào sau đây đúng?
A. Hàm số đồng biến khi x > 0 và nghịch biến khi x < 0
B. Hàm số luôn đồng biến trên \(\mathbb{R}\)
C. Hàm số luôn nghịch biến trên \(\mathbb{R}\)
D. Hàm số đồng biến khi x < 0 và nghịch biến khi x > 0
Câu 10: Với giá trị nào của tham số m thì đồ thị hàm số \(y = \left( {m - 6} \right){x^2}\) đi qua điểm E(1; 2)?
A. m = 6 B. m = 4 C. m = 8 D. m = -8
Câu 11: Tính biệt thức \(\Delta \) của phương trình bậc hai \({x^2} + 6x - 6 = 0\).
A. \(\Delta = 42\) B. \(\Delta = 36\) C. \(\Delta = 15\) D. \(\Delta = 60\)
Câu 12: Phương trình bậc hai \(7{x^2} + 6x - 22 = 0\) có hai nghiệm phân biệt \({x_1},{x_2}\). Khi đó \({x_1} + {x_2}\) bằng:
A. \(\dfrac{{22}}{7}\) B. \( - \dfrac{{22}}{7}\) C. \( - \dfrac{6}{7}\) D. \(\dfrac{6}{7}\)
Câu 13: Phương trình trùng phương là phương trình có dạng:
A. \(a{x^2} + bx + c = 0\)với a, b, c là các số thực B. \(ax + b = 0\) với a, b là các số thực
C. \(a{x^4} + b{x^2} + c = 0\)với a, b, c là các số thực D. \(a{x^4} + b{x^2} + c = 0\)với a, b, c là các số thực và \(a \ne 0\)
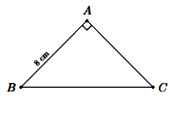
Câu 14: Cho tam giác ABC vuông cân tại A, AB = 8cm. Độ dài đoạn thẳng BC bằng:
A. \(8\sqrt 2 cm\) B. \(4cm\)
C. \(16\sqrt 2 cm\) D. \(128cm\)
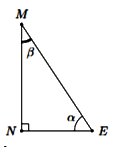
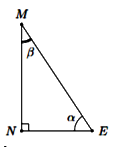
Câu 15: Trong hình vẽ bên, biết \(\angle NEM = \alpha \) và \(\angle NME = \beta \). Khẳng định nào sau đây là không đúng?
A. \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) B. \(\sin \alpha = \cos \beta \)
C. \(\cos \alpha > 1\) D. \(\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }}\)
Câu 16: Cho đường tròn tâm O bán kính OA và đường tròn đường kính OA. Vị trí tương đói của hai đường tròn này là:
A. nằm ngoài nhau B. cắt nhau C. tiếp xúc trong D. tiếp xúc ngoài
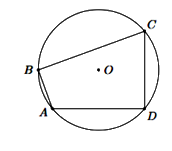
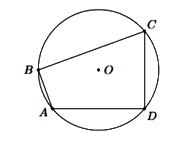
Câu 17: Cho tứ giác ABCD nội tiếp đường tròn như hình vẽ bên và \(\angle BDC = {70^0}\). Số đo \(\angle BAC\) bằng:
A. \({70^0}\) B. \({120^0}\)
C. \({110^0}\) D. \({90^0}\)
Câu 18: Góc nội tiếp chắn nửa đường tròn có số đo bằng:
A. \({180^0}\) B. \({120^0}\) C. \({360^0}\) D. \({90^0}\)
Câu 19: Một hình trụ có bán kính đường tròn đáy r = 3 cm, chiều cao h = 5 cm. Thể tích hình trụ đó bằng:
A. \(45c{m^3}\) B. \(15\pi c{m^3}\) C. \(45\pi c{m^3}\) D. \(75\pi c{m^3}\)
Câu 20: Thể tích của một hình cầu có bán kính R = 7cm bằng:
A. \(\dfrac{{343}}{3}\pi c{m^3}\) B. \(\dfrac{{1372}}{3}\pi c{m^3}\) C. \(45\pi c{m^3}\) D. \(75\pi c{m^3}\)
B. PHẦN TỰ LUẬN (6,0 điểm, từ câu 21 đến câu 27):
Câu 21 (1,0 điểm): Giải phương trình \(2{x^2} + 4x - 5 = 0\)
Câu 22 (1,0 điểm): Giải hệ phương trình \(\left\{ \begin{array}{l}x - 2y = 5\\7x + y = 6\end{array} \right.\)
Câu 23 (0,5 điểm): Vẽ đồ thị hàm số \(y = {x^2}\)
Câu 24 (0,5 điểm): Rút gọn biểu thức \(A = \dfrac{1}{{\sqrt a }}.\left( {\dfrac{1}{{\sqrt a + \sqrt b }} + \dfrac{1}{{\sqrt a - \sqrt b }}} \right)\) với\(a,\,\,b > 0\) và \(a \ne b\).
Câu 25 (0,5 điểm): Trên đường tròn (O) đường kính AB, lấy điểm E (khác A và B). Vẽ tiếp tuyến của (O) tại A. Đường thẳng BE cắt tiếp tuyến đó tại M. Từ điểm M kẻ tiếp tuyến với đường tròn (O) tại điểm C (C là tiếp điểm, \(C \ne A\)). Chứng minh rằng:
a) Tứ giác AOCM là tứ giác nội tiếp.
b) \(E{A^2} = EM.EB\).
Câu 26 (0,5 điểm): Cho phương trình bậc hai \({x^2} + 2mx + {m^2} + 2m + 3 = 0\), với m là tham số. Tìm các giá trị của m để phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa \(x_1^3 + x_2^3 = 108.\)
Câu 27 (0,5 điểm): Một người mua hai loại hàng và phải trả tổng cộng 4,35 triệu đồng, kể cả thuế giá trị gia tăng (VAT) với mức 10% đối với loại hàng thứ nhất và 8% đối với loại hàng thứ hai. Nếu thuế VAT là 9% đối với cả hai loại hàng thì người đó phải trả tổng cộng 4,36 triệu đồng. Nếu chưa kể thuế VAT thì người đó phải trả bao nhiêu tiền cho mỗi loại hàng?
A. PHẦN TRẮC NGHIỆM (4,0 điểm, từ câu 1 đến câu 20, mỗi câu 0,2 điểm):
Câu 1: Giá trị của biểu thức \(\dfrac{{\sqrt {99} }}{{\sqrt {11} }}\) bằng:
A. 3 B. 6 C. 9 D. \(\sqrt 3 \)
Câu 2: Cho số thực a. Khẳng định nào dưới đây là đúng?
A. \(\sqrt {{a^2}} = {a^4}\) B. \(\sqrt {{a^2}} = a\) C. \(\sqrt {{a^2}} = - {a^4}\) D. \(\sqrt {{a^2}} = \left| a \right|\)
Câu 3: Nghiệm của phương trình \(\sqrt {9x} = 27\) là:
A. \(x = 3\) B. \(x = 81\) C. \(x = 27\) D. \(x = 9\)
Câu 4: Tìm tất cả các giá trị của tham số m để hàm số bậc nhất \(y = \left( {m - 6} \right)x + 2022\) đồng biến trên \(\mathbb{R}\) là:
A. \(m \ge 6\) B. \(m < 6\) C. \(m \le 6\) D. \(m > 6\)
Câu 5: Điều kiện để hai đường thẳng \(y = ax + b\) và \(y = a'x + b\) \(\left( {a \ne 0;a' \ne 0} \right)\)
A. \(a = a'\)và \(b = b'\) B. \(a = a'\)và \(b \ne b'\) C. \(a \ne a'\)và \(b = b'\) D. \(a \ne a'\)và \(b \ne b'\)
Câu 6: Đường thẳng y = ax + 7 đi qua điểm A(2; 3) có hệ số góc a bằng:
A. 3 B. -2 C. 5 D. -3
Câu 7: Hàm số nào sau đây có đồ thị như hình vẽ bên?
A. \(y = \dfrac{1}{2}x - 1\) B. \(y = \dfrac{1}{2}x\) C. \(y = x - 1\) D. \(y = x + 2\)
Câu 8: Hệ phương trình sau đây là hệ phương trình bậc nhất hai ẩn x, y?
A. \(\left\{ \begin{array}{l}x + 3y = 1\\x - y = 7\end{array} \right.\) B. \(\left\{ \begin{array}{l}x + y = 1\\{x^2} + y = 3\end{array} \right.\) C. \(\left\{ \begin{array}{l}x + y = 1\\x + {y^2} = 3\end{array} \right.\) D. \(\left\{ \begin{array}{l}x + 2y = 0\\x + \dfrac{2}{y} = 3y\end{array} \right.\)
Câu 9: Cho hàm số \(y = 2022{x^2}\). Khẳng định nào sau đây đúng?
A. Hàm số đồng biến khi x > 0 và nghịch biến khi x < 0
B. Hàm số luôn đồng biến trên \(\mathbb{R}\)
C. Hàm số luôn nghịch biến trên \(\mathbb{R}\)
D. Hàm số đồng biến khi x < 0 và nghịch biến khi x > 0
Câu 10: Với giá trị nào của tham số m thì đồ thị hàm số \(y = \left( {m - 6} \right){x^2}\) đi qua điểm E(1; 2)?
A. m = 6 B. m = 4 C. m = 8 D. m = -8
Câu 11: Tính biệt thức \(\Delta \) của phương trình bậc hai \({x^2} + 6x - 6 = 0\).
A. \(\Delta = 42\) B. \(\Delta = 36\) C. \(\Delta = 15\) D. \(\Delta = 60\)
Câu 12: Phương trình bậc hai \(7{x^2} + 6x - 22 = 0\) có hai nghiệm phân biệt \({x_1},{x_2}\). Khi đó \({x_1} + {x_2}\) bằng:
A. \(\dfrac{{22}}{7}\) B. \( - \dfrac{{22}}{7}\) C. \( - \dfrac{6}{7}\) D. \(\dfrac{6}{7}\)
Câu 13: Phương trình trùng phương là phương trình có dạng:
A. \(a{x^2} + bx + c = 0\)với a, b, c là các số thực B. \(ax + b = 0\) với a, b là các số thực
C. \(a{x^4} + b{x^2} + c = 0\)với a, b, c là các số thực D. \(a{x^4} + b{x^2} + c = 0\)với a, b, c là các số thực và \(a \ne 0\)
Câu 14: Cho tam giác ABC vuông cân tại A, AB = 8cm. Độ dài đoạn thẳng BC bằng:
A. \(8\sqrt 2 cm\) B. \(4cm\)
C. \(16\sqrt 2 cm\) D. \(128cm\)
Câu 15: Trong hình vẽ bên, biết \(\angle NEM = \alpha \) và \(\angle NME = \beta \). Khẳng định nào sau đây là không đúng?
A. \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) B. \(\sin \alpha = \cos \beta \)
C. \(\cos \alpha > 1\) D. \(\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }}\)
Câu 16: Cho đường tròn tâm O bán kính OA và đường tròn đường kính OA. Vị trí tương đói của hai đường tròn này là:
A. nằm ngoài nhau B. cắt nhau C. tiếp xúc trong D. tiếp xúc ngoài
Câu 17: Cho tứ giác ABCD nội tiếp đường tròn như hình vẽ bên và \(\angle BDC = {70^0}\). Số đo \(\angle BAC\) bằng:
A. \({70^0}\) B. \({120^0}\)
C. \({110^0}\) D. \({90^0}\)
Câu 18: Góc nội tiếp chắn nửa đường tròn có số đo bằng:
A. \({180^0}\) B. \({120^0}\) C. \({360^0}\) D. \({90^0}\)
Câu 19: Một hình trụ có bán kính đường tròn đáy r = 3 cm, chiều cao h = 5 cm. Thể tích hình trụ đó bằng:
A. \(45c{m^3}\) B. \(15\pi c{m^3}\) C. \(45\pi c{m^3}\) D. \(75\pi c{m^3}\)
Câu 20: Thể tích của một hình cầu có bán kính R = 7cm bằng:
A. \(\dfrac{{343}}{3}\pi c{m^3}\) B. \(\dfrac{{1372}}{3}\pi c{m^3}\) C. \(45\pi c{m^3}\) D. \(75\pi c{m^3}\)
B. PHẦN TỰ LUẬN (6,0 điểm, từ câu 21 đến câu 27):
Câu 21 (1,0 điểm): Giải phương trình \(2{x^2} + 4x - 5 = 0\)
Câu 22 (1,0 điểm): Giải hệ phương trình \(\left\{ \begin{array}{l}x - 2y = 5\\7x + y = 6\end{array} \right.\)
Câu 23 (0,5 điểm): Vẽ đồ thị hàm số \(y = {x^2}\)
Câu 24 (0,5 điểm): Rút gọn biểu thức \(A = \dfrac{1}{{\sqrt a }}.\left( {\dfrac{1}{{\sqrt a + \sqrt b }} + \dfrac{1}{{\sqrt a - \sqrt b }}} \right)\) với\(a,\,\,b > 0\) và \(a \ne b\).
Câu 25 (0,5 điểm): Trên đường tròn (O) đường kính AB, lấy điểm E (khác A và B). Vẽ tiếp tuyến của (O) tại A. Đường thẳng BE cắt tiếp tuyến đó tại M. Từ điểm M kẻ tiếp tuyến với đường tròn (O) tại điểm C (C là tiếp điểm, \(C \ne A\)). Chứng minh rằng:
a) Tứ giác AOCM là tứ giác nội tiếp.
b) \(E{A^2} = EM.EB\).
Câu 26 (0,5 điểm): Cho phương trình bậc hai \({x^2} + 2mx + {m^2} + 2m + 3 = 0\), với m là tham số. Tìm các giá trị của m để phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa \(x_1^3 + x_2^3 = 108.\)
Câu 27 (0,5 điểm): Một người mua hai loại hàng và phải trả tổng cộng 4,35 triệu đồng, kể cả thuế giá trị gia tăng (VAT) với mức 10% đối với loại hàng thứ nhất và 8% đối với loại hàng thứ hai. Nếu thuế VAT là 9% đối với cả hai loại hàng thì người đó phải trả tổng cộng 4,36 triệu đồng. Nếu chưa kể thuế VAT thì người đó phải trả bao nhiêu tiền cho mỗi loại hàng?
A. PHẦN TRẮC NGHIỆM
1. A | 2. D | 3. B | 4. D | 5. B | 6. B | 7. A | 8. A | 9. A | 10. C |
11. D | 12. C | 13. D | 14. A | 15. C | 16. C | 17. A | 18. D | 19. C | 20. B |
Câu 1 (NB):
Phương pháp:
Vận dụng hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,\,A \ge 0\\ - A\,\,\,\,khi\,\,\,\,A < 0\end{array} \right.\)
Cách giải:
\(\dfrac{{\sqrt {99} }}{{\sqrt {11} }} = \dfrac{{\sqrt {9.11} }}{{\sqrt {11} }} = \dfrac{{\sqrt {{3^2}} .\sqrt {11} }}{{\sqrt {11} }} = \left| 3 \right| = 3\) (vì 3 > 0)
Chọn A.
Câu 2 (NB):
Phương pháp:
Vận dụng hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,\,A \ge 0\\ - A\,\,\,\,khi\,\,\,\,A < 0\end{array} \right.\)
Cách giải:
Khẳng định đúng là: \(\sqrt {{a^2}} = \left| a \right|\)
Chọn D.
Câu 3 (TH):
Phương pháp:
Giải phương trình: \(\sqrt A = B \Leftrightarrow \left\{ \begin{array}{l}B \ge 0\\A = {B^2}\end{array} \right.\)
Cách giải:
Điều kiện: \(x \ge 0\)
\(\sqrt {9x} = 27\)
\(\begin{array}{l} \Leftrightarrow 9x = {27^2}\\ \Leftrightarrow x = 729:9\\ \Leftrightarrow x = 81\,\,\left( {tmdk} \right)\end{array}\)
Vậy \(x = 81\)
Chọn B.
Câu 4 (NB):
Phương pháp:
Hàm số \(y = ax + b\) đồng biến trên \(\mathbb{R} \Leftrightarrow a > 0\)
Cách giải:
Hàm số \(y = \left( {m - 6} \right)x + 2022\) đồng biến trên \(\mathbb{R}\)\( \Leftrightarrow m - 6 > 0 \Leftrightarrow m > 6\)
Chọn B.
Câu 5 (NB):
Phương pháp:
Hai đường thẳng \(y = ax + b\) và \(y = a'x + b\) \(\left( {a \ne 0;a' \ne 0} \right)\)\( \Leftrightarrow \left\{ \begin{array}{l}a \ne a'\\b \ne b'\end{array} \right.\)
Cách giải:
Điều kiện để hai đường thẳng \(y = ax + b\) và \(y = a'x + b\) \(\left( {a \ne 0;a' \ne 0} \right)\) là \(a \ne a'\)và \(b \ne b'\).
Chọn D.
Câu 6 (NB):
Phương pháp:
Đường thẳng \(y = ax + b\) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) khi \({y_0} = a{x_0} + b\)
Cách giải:
Đường thẳng y = ax + 7 đi qua điểm A(2; 3) nên ta có: \(a.2 + 7 = 3 \Leftrightarrow a = - 2\)
Vậy hệ số góc của đường thẳng là -2.
Chọn B.
Câu 7 (TH):
Phương pháp:
Nhận xét đồ thị từ đó xác định được hàm số cần tìm.
Cách giải:
+ Gọi hàm số cần tìm là \(y = ax + b\left( {a \ne 0} \right)\)
+ Đồ thị hàm số đi qua điểm (0; -1) và (2; 0) nên ta có hệ phương trình: \(\left\{ \begin{array}{l}a.0 + b = - 1\\2.a + b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 1\\2a - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 1\\a = \dfrac{1}{2}\end{array} \right.\)
Hàm số cần tìm là: \(y = \dfrac{1}{2}x - 1\)
Chọn A.
Câu 8 (NB):
Phương pháp:
Hệ phương trình bậc nhất hai ẩn x, y có dạng: \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\)
Cách giải:
Hệ phương trình bậc nhất hai ẩn x, y là: \(\left\{ \begin{array}{l}x + 3y = 1\\x - y = 7\end{array} \right.\)
Chọn A.
Câu 9 (NB):
Phương pháp:
Nhận xét hệ số a của hàm số bậc hai một ẩn để xác định khẳng định đúng.
Cách giải:
Hàm số \(y = 2022{x^2}\) có a = 2022 > 0 nên hàm số hàm số đồng biến khi x > 0 và nghịch biến khi x < 0.
Chọn A.
Câu 10 (NB):
Phương pháp:
Đồ thị hàm số \(y = a{x^2}\)\(\left( {a \ne 0} \right)\) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) khi và chỉ khi \({y_0} = a{x_0}\).
Cách giải:
Đồ thị hàm số \(y = \left( {m - 6} \right){x^2}\) đi qua điểm E(1; 2) nên ta có: \(\left( {m - 6} \right){.1^2} = 2 \Leftrightarrow m = 8\)
Vậy \(m = 8\)
Chọn A.
Câu 11 (NB):
Phương pháp:
Phương trình bậc hai \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có biệt thức \(\Delta = {b^2} - 4ac\)
Cách giải:
Ta có: \(\Delta = {6^2} - 4.\left( { - 6} \right) = 60\)
Chọn D.
Câu 12 (NB):
Phương pháp:
Phương trình bậc hai \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt \({x_1},{x_2}\) khi đó theo hệ thức Vi – ét, ta có: \({x_1} + {x_2} = \dfrac{{ - b}}{a}\)
Cách giải:
Phương trình có có hai nghiệm phân biệt \({x_1},{x_2}\), khi đó theo hệ thức Vi – ét, ta có: \({x_1} + {x_2} = \dfrac{{ - 6}}{7}\)
Chọn C.
Câu 13 (NB):
Phương pháp:
Phương trình trùng phương là phương trình có dạng: \(a{x^4} + b{x^2} + c = 0\) với a, b, c là các số thực và \(a \ne 0\)
Cách giải:
Phương trình trùng phương là phương trình có dạng: \(a{x^4} + b{x^2} + c = 0\) với a, b, c là các số thực và \(a \ne 0\)
Chọn D.
Câu 14 (NB):
Phương pháp:
Áp dụng định lý Py – ta – go
Cách giải:
Tam giác ABC vuông cân tại A, nên AB = AC = 8cm
Tam giác ABC vuông tại A, theo định lý Py – ta – go, ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2}\\ \Leftrightarrow B{C^2} = {8^2} + {8^2} = 128\\ \Rightarrow BC = 8\sqrt 2 cm\end{array}\)
Chọn A.
Câu 15 (TH):
Phương pháp:
Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông.
Cách giải:
Khẳng định không đúng là \(\cos \alpha > 1\)
Chọn C.
Câu 16 (TH):
Phương pháp:
Vận dụng kiến thức vị trí tương đối của hai đường tròn.
Cách giải:
Đường tròn tâm O bán kính OA và đường tròn đường kính OA tiếp xúc trong với nhau.
Chọn C.
Câu 17 (NB):
Phương pháp:
Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì có số đo bằng nhau.
Cách giải:
Xét (O) có: \(\angle BDC = \angle BAC = {70^0}\) (hai góc nội tiếp cùng chắn cung BC)
Chọn A.
Câu 18 (NB):
Phương pháp:
Góc nội tiếp chắn nửa đường tròn có số đo bằng \({90^0}\).
Cách giải:
Góc nội tiếp chắn nửa đường tròn có số đo bằng \({90^0}\).
Chọn D.
Câu 19 (NB):
Phương pháp:
Thể tích hình lăng trụ có bán kình đáy là r, chiều cao h là \(V = \pi {r^2}h\)
Cách giải:
Thể tích hình trụ đó là: \(V = \pi {.3^2}.5 = 45\pi \,\left( {c{m^3}} \right)\)
Chọn C.
Câu 20 (NB):
Phương pháp:
Thể tích của hình cầu có bán kính R là: \(V = \dfrac{4}{3}\pi {R^3}\)
Cách giải:
Thể tích của hình cầu là: \(V = \dfrac{4}{3}\pi {.7^3} = \dfrac{{1372}}{3}\pi \left( {c{m^3}} \right)\)
Chọn B.
B. PHẦN TỰ LUẬN
Câu 21 (NB):
Phương pháp:
Áp dụng công thức nghiệm của phương trình bậc hai một ẩn số.
Cách giải:
Giải phương trình \(2{x^2} + 4x - 5 = 0\)
Ta có: \(\Delta ' = {2^2} - 2.\left( { - 5} \right) = 14 > 0\) nên phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}x = \dfrac{{ - 2 + \sqrt {14} }}{2}\\x = \dfrac{{ - 2 - \sqrt {14} }}{2}\end{array} \right.\).
Vậy tập nghiệm của phương trình là: \(S = \left\{ {\dfrac{{ - 2 \pm \sqrt {14} }}{2}} \right\}\).
Câu 22 (TH):
Phương pháp:
Sử dụng phương pháp cộng đại số, tìm được nghiệm \(x\)
Sử dụng phương pháp thế, tìm được nghiệm \(y\)
Kết luận nghiệm \(\left( {x;y} \right)\) của hệ phương trình.
Cách giải:
Giải hệ phương trình \(\left\{ \begin{array}{l}x - 2y = 5\\7x + y = 6\end{array} \right.\)
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}x - 2y = 5\\7x + y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 2y = 5\\14x + 2y = 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}15x = 17\\7x + y = 6\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{17}}{{15}}\\7.\dfrac{{17}}{5} + y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{17}}{{15}}\\y = \dfrac{{ - 29}}{{15}}\end{array} \right.\end{array}\)
Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {\dfrac{{17}}{{15}}; - \dfrac{{29}}{{15}}} \right)\).
Câu 23 (TH):
Phương pháp:
Vẽ đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
+ Nhận xét về hệ số \(a\) và sự biến thiên của hàm số
+ Lập bảng giá trị tương ứng của \(x\) và \(y\)
+ Xác định được các điểm mà đồ thị đi qua, vẽ đồ thị.
Cách giải:
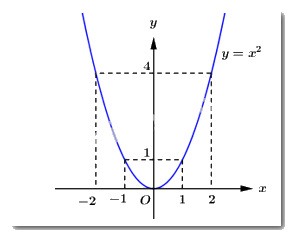
Vẽ đồ thị hàm số \(y = {x^2}\)
Hệ số \(a = 1 > 0\) nên hàm số đồng biến khi \(x > 0\), nghịch biến khi \(x < 0\) và có bề lõm hướng lên trên.
Bảng giá trị:
\(x\) | \( - 2\) | \( - 1\) | 0 | 1 | 2 |
\(y = {x^2}\) | 4 | 1 | 0 | 1 | 4 |
\( \Rightarrow \) Parabol \(y = {x^2}\)là đường cong đi qua các điểm \(\left( { - 2;4} \right),\,\,\left( { - 1;1} \right),\,\,\left( {0;0} \right),\,\,\left( {1;1} \right),\,\,\left( {2;4} \right)\).
Câu 24 (TH):
Phương pháp:
Vận dụng hằng đẳng thức \(a - b = \left( {\sqrt a - \sqrt b } \right)\left( {\sqrt a + \sqrt b } \right)\) xác định mẫu thức chung của biểu thức
Quy đồng các phân thức, thực hiện các phép toán từ đó rút gọn được biểu thức.
Cách giải:
Rút gọn biểu thức \(A = \dfrac{1}{{\sqrt a }}.\left( {\dfrac{1}{{\sqrt a + \sqrt b }} + \dfrac{1}{{\sqrt a - \sqrt b }}} \right)\) với\(a,\,\,b > 0\) và \(a \ne b\).
Với\(a,\,\,b > 0\) và \(a \ne b\) ta có:
\(\begin{array}{l}A = \dfrac{1}{{\sqrt a }}.\left( {\dfrac{1}{{\sqrt a + \sqrt b }} + \dfrac{1}{{\sqrt a - \sqrt b }}} \right)\\A = \dfrac{1}{{\sqrt a }}.\dfrac{{\sqrt a - \sqrt b + \sqrt a + \sqrt b }}{{\left( {\sqrt a + \sqrt b } \right)\left( {\sqrt a - \sqrt b } \right)}}\\A = \dfrac{1}{{\sqrt a }}.\dfrac{{2\sqrt a }}{{a - b}}\\A = \dfrac{2}{{a - b}}\end{array}\)
Vậy với\(a,\,\,b > 0\) và \(a \ne b\) thì \(A = \dfrac{2}{{a - b}}\).
Câu 25 (VD):
Phương pháp:
a) Vận dụng dấu hiệu nhận biết: Tứ giác có tổng hai góc đối bằng 180 độ là tứ giác nội tiếp.
b) Áp dụng hệ thức lượng trong tam giác vuông.
Cách giải:
Trên đường tròn (O) đường kính AB, lấy điểm E (khác A và B). Vẽ tiếp tuyến của (O) tại A. Đường thẳng BE cắt tiếp tuyến đó tại M. Từ điểm M kẻ tiếp tuyến với đường tròn (O) tại điểm C (C là tiếp điểm, \(C \ne A\)). Chứng minh rằng:
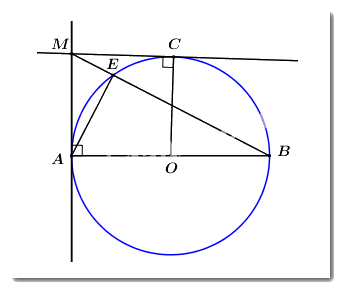
a) Tứ giác AOCM là tứ giác nội tiếp.
Vì MA là tiếp tuyến của (O) tại A nên \(\angle OAM = {90^0}\)
Vì MC là tiếp tuyến của (O) tại C nên \(\angle OCM = {90^0}\)
Xét tứ giác AOCM có: \(\angle OAM + \angle OCM = {90^0} + {90^0} = {180^0}\), mà 2 góc này là 2 góc đối nhau của tứ giác AOCM.
\( \Rightarrow AOCM\) là tứ giác nội tiếp (dhnb).
b) \(E{A^2} = EM.EB\).
Ta có \(\angle AEB = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow AE \bot EB\) hay \(AE \bot BM\).
Áp dụng hệ thức lượng trong tam giác vuông ABM, đường cao AE ta có: \(A{E^2} = EM.EB\) (đpcm).
Câu 26 (VD):
Phương pháp:
Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) \( \Leftrightarrow \Delta ' > 0\)
Áp dụng hệ thức Vi – ét, ta có: \({x_1} + {x_2} = \dfrac{{ - b}}{a};{x_1}.{x_2} = \dfrac{c}{a}\)
Biến đổi \(x_1^3 + x_2^3 = {\left( {{x_1} + {x_2}} \right)^2} - 3{x_1}{x_2}\left( {{x_1} + {x_2}} \right)\)
Cách giải:
Cho phương trình bậc hai \({x^2} + 2mx + {m^2} + 2m + 3 = 0\), với m là tham số. Tìm các giá trị của m để phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa \(x_1^3 + x_2^3 = 108.\)
Ta có: \(\Delta ' = {m^2} - \left( {{m^2} + 2m + 3} \right) = - 2m - 3\).
Để phương trình có 2 nghiệm phân biệt \({x_1},\,\,{x_2}\) thì \(\Delta ' > 0 \Leftrightarrow - 2m - 3 > 0 \Leftrightarrow 2m < - 3 \Leftrightarrow m < - \dfrac{3}{2}\).
Khi đó áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 2m\\{x_1}{x_2} = {m^2} + 2m + 3\end{array} \right.\)
Theo giả thiết ta có:
\(\begin{array}{l}\,\,\,\,\,\,x_1^3 + x_2^3 = 108\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^3} - 3{x_1}{x_2}\left( {{x_1} + {x_2}} \right) = 108\\ \Leftrightarrow {\left( { - 2m} \right)^3} - 3.\left( {{m^2} + 2m + 3} \right).\left( { - 2m} \right) = 108\\ \Leftrightarrow - 8{m^3} + 6m\left( {{m^2} + 2m + 3} \right) = 108\\ \Leftrightarrow - 8{m^3} + 6{m^3} + 12{m^2} + 18m - 108 = 0\\ \Leftrightarrow - 2{m^3} + 12{m^2} + 18m - 108 = 0\\ \Leftrightarrow \left( { - 2{m^3} + 18m} \right) + \left( {12{m^2} - 108} \right) = 0\\ \Leftrightarrow - 2m\left( {{m^2} - 9} \right) + 12\left( {{m^2} - 9} \right) = 0\end{array}\)
\(\begin{array}{l} \Leftrightarrow - 2\left( {{m^2} - 9} \right)\left( {m - 6} \right) = 0\\ \Leftrightarrow - 2\left( {m - 3} \right)\left( {m + 3} \right)\left( {m - 6} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m - 3 = 0\\m + 3 = 0\\m - 6 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 3\,\,\,\,\,\,\,\left( {ktm} \right)\\m = - 3\,\,\,\,\left( {tm} \right)\\m = 6\,\,\,\,\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy \(m = - 3\).
Câu 27 (VD):
Phương pháp:
Gọi số tiền phải trả cho loại hàng thứ nhất (chưa kể thuế VAT) là \(x\) (triệu đồng) (ĐK: \(x > 0\))
Gọi số tiền phải trả cho loại hàng thứ hai (chưa kể thuế VAT) là \(y\) (triệu đồng) (ĐK: \(y > 0\))
Lập hệ phương trình bậc nhất hai ẩn của x và y.
Giải hệ phương trình, đối chiếu điều kiện và kết luận.
Cách giải:
Một người mua hai loại hàng và phải trả tổng cộng 4,35 triệu đồng, kể cả thuế giá trị gia tăng (VAT) với mức 10% đối với loại hàng thứ nhất và 8% đối với loại hàng thứ hai. Nếu thuế VAT là 9% đối với cả hai loại hàng thì người đó phải trả tổng cộng 4,36 triệu đồng. Nếu chưa kể thuế VAT thì người đó phải trả bao nhiêu tiền cho mỗi loại hàng?
Gọi số tiền phải trả cho loại hàng thứ nhất (chưa kể thuế VAT) là \(x\) (triệu đồng) (ĐK: \(x > 0\))
Gọi số tiền phải trả cho loại hàng thứ hai (chưa kể thuế VAT) là \(y\) (triệu đồng) (ĐK: \(y > 0\))
Vì một người mua hai loại hàng và phải trả tổng cộng 4,35 triệu đồng, kể cả thuế giá trị gia tăng (VAT) với mức 10% đối với loại hàng thứ nhất và 8% đối với loại hàng thứ hai nên ta có phương trình:
\(1,1x + 1,08y = 4,35\) (1).
Vì nếu thuế VAT là 9% đối với cả hai loại hàng thì người đó phải trả tổng cộng 4,36 triệu đồng nên ta có phương trình
\(1,09x + 1,09y = 4,36\) (2)
Từ (1) và (2) ta có hệ phương trình \(\left\{ \begin{array}{l}1,1x + 1,08y = 4,35\\1,09x + 1,09y = 4,36\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1,1x + 1,08y = 4,35\\x + y = 4\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}1,1x + 1,08\left( {4 - x} \right) = 4,35\\y = 4 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1,1x + 4,32 - 1,08x = 4,35\\y = 4 - x\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}0,02x = 0,03\\y = 4 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1,5\,\,\left( {tm} \right)\\y = 4 - 1,5 = 2,5\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy số tiền phải trả cho loại hàng thứ nhất (chưa kể thuế VAT) là 1,5 triệu đồng và số tiền phải trả cho loại hàng thứ hai (chưa kể thuế VAT) là 2,5 triệu đồng.
Kỳ thi tuyển sinh vào lớp 10 môn Toán tỉnh Bến Tre năm 2022 là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Đề thi thường bao gồm các dạng bài tập thuộc nhiều chủ đề khác nhau, đòi hỏi học sinh phải có kiến thức vững chắc và kỹ năng giải quyết vấn đề tốt. Việc nắm vững cấu trúc đề thi, các dạng bài tập thường gặp và phương pháp giải quyết hiệu quả là chìa khóa để đạt kết quả cao trong kỳ thi này.
Thông thường, đề thi vào 10 môn Toán Bến Tre năm 2022 có cấu trúc gồm hai phần chính:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Dưới đây là một số dạng bài tập thường gặp trong đề thi vào 10 môn Toán Bến Tre năm 2022:
Để giải đề thi vào 10 môn Toán Bến Tre năm 2022 hiệu quả, các em học sinh cần:
Ngoài bộ đề thi vào 10 môn Toán Bến Tre năm 2022 mà Giaitoan.edu.vn cung cấp, các em học sinh có thể tham khảo thêm các tài liệu ôn thi hữu ích khác như:
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi tuyển sinh vào lớp 10 môn Toán tỉnh Bến Tre năm 2022!