Chào mừng các em học sinh đến với đề tham khảo thi vào 10 môn Toán Hà Nội năm 2025 - Đề số 9 của giaitoan.edu.vn. Đề thi này được biên soạn dựa trên cấu trúc đề thi tuyển sinh vào 10 của các trường THPT chuyên và không chuyên tại Hà Nội.
Mục đích của đề thi là giúp các em làm quen với dạng đề, rèn luyện kỹ năng giải toán và đánh giá năng lực bản thân trước kỳ thi quan trọng. Đề thi đi kèm với đáp án chi tiết và lời giải dễ hiểu, giúp các em tự học hiệu quả.
Câu 1: (1,5 điểm) 1) Khảo sát thời gian tập thể dục của một số học sinh lớp 9 thu được mẫu số liệu ghép nhóm sau:
Câu 1:(1,5 điểm)
1) Khảo sát thời gian tập thể dục của một số học sinh lớp 9 thu được mẫu số liệu ghép nhóm sau:

Tính tần số tương đối của nhóm [40;60) (làm tròn đến hàng phần mười).
2) Hình dưới đây mô tả một đĩa tròn, cân đối bằng bìa cứng được chia làm tám phần bằng nhau và ghi các số 1; 2; 3; 4; 5; 6; 7; 8. Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Quay đĩa tròn một lần. Tính xác suất của biến cố sau: “Mũi tên chỉ vào hình quạt ghi số là ước của 8”.
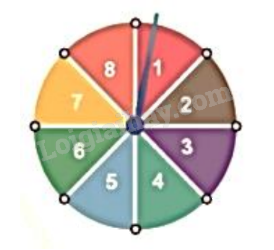
Câu 2:(1,5 điểm) Cho biểu thức \(M = \frac{{\sqrt x - 1}}{{\sqrt x }}\); \(P = \frac{{\sqrt x - 2}}{{\sqrt x + 1}} + \frac{{2 + 8\sqrt x }}{{x - 1}} - \frac{2}{{1 - \sqrt x }}\) với x > 0; \(x \ne 1\).
1) Tính M khi x = 0,49.
2) Chứng minh \(P = \frac{{\sqrt x + 6}}{{\sqrt x - 1}}\).
3) Đặt \(Q = M.P + \frac{{x - 5}}{{\sqrt x }}\). So sánh Q với 3.
Câu 3:(2,5 điểm)
1) Hai vòi nước cùng chảy vào một cái bể không có nước thì trong 5 giờ sẽ đầy bể. Nếu vòi thứ nhất chảy trong 3 giờ và vòi thứ hai chảy trong 4 giờ thì được \(\frac{2}{3}\) bể nước. Hỏi nếu mỗi vòi nước chảy một mình thì sau bao nhiêu giờ mới đầy bể?
2) Một người đi ô tô từ A đến B cách nhau 100 km với vận tốc xác định. Khi từ B trở về A, người đó đi theo đường khác dài hơn đường cũ 20 km nhưng với vận tốc lớn hơn vận tốc lúc đi mỗi giờ 20 km. Vì vậy thời gian về ít hơn thời gian đi 30 phút. Tính vận tốc lúc đi.
3) Biết phương trình bậc hai \({x^2} + 5x + a = 0\) có một nghiệm là \(x = \frac{{ - 5 + \sqrt {13} }}{2}\). Tìm tổng các lập phương hai nghiệm của phương trình trên.
Câu 4:(4 điểm)
1) Một téc nước hình trụ tròn có bán kính 60 cm, chiều cao 220 cm.
a) Diện tích inox cần làm ra cái téc nước (có nắp) là bao nhiêu mét vuông (giả sử phần nắp cong không đáng kể)?
b) Téc nước hình trụ có thể chứa tối đa bao nhiêu lít nước?
Các kết quả làm tròn tới hàng phần trăm.
2) Cho (O) đường kính AB. Kẻ đường kính CD vuông góc với AB. Lấy M thuộc cung nhỏ BC, AM cắt CD tại E. Qua D kẻ tiếp tuyến với (O) cắt đường thẳng BM tại N. Gọi P là hình chiếu vuông góc của B lên DN.
a) Chứng minh các điểm M, N, D, E cùng thuộc một đường tròn.
b) Chứng minh EN // CB.
c) Chứng minh \(AB.BN = 2{R^2}\) và tìm vị trí điểm M trên cung nhỏ BC để diện tích tam giác BNC đạt giá trị lớn nhất.
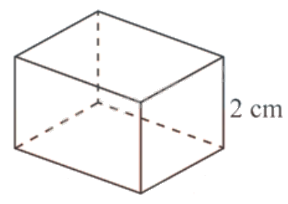
Câu 5:(0,5 điểm) Người ta muốn chế tạo một chiếc hộp hình chữ nhật có thể tích 500 \(c{m^3}\), chiều cao của hộp là 2 cm. Tìm kích thước đáy của hộp sao cho sử dụng ít vật liệu nhất.
Câu 1:(1,5 điểm)
1) Khảo sát thời gian tập thể dục của một số học sinh lớp 9 thu được mẫu số liệu ghép nhóm sau:

Tính tần số tương đối của nhóm [40;60) (làm tròn đến hàng phần mười).
2) Hình dưới đây mô tả một đĩa tròn, cân đối bằng bìa cứng được chia làm tám phần bằng nhau và ghi các số 1; 2; 3; 4; 5; 6; 7; 8. Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Quay đĩa tròn một lần. Tính xác suất của biến cố sau: “Mũi tên chỉ vào hình quạt ghi số là ước của 8”.
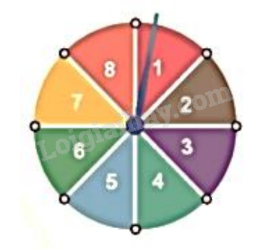
Phương pháp
1) Tính tổng số học sinh.
Tần số tương đối của nhóm bằng: tần số của nhóm : tổng . 100%.
2) Xác định không gian mẫu của phép thử, tính số phần tử của không gian mẫu.
Tính số kết quả thuận lợi của biến cố.
Xác suất của biến cố = số kết quả thuận lợi của biến cố : số phần tử của không gian mẫu.
Lời giải
1) Tổng số học sinh là: 8 + 9 + 11 + 8 = 36.
Tần số tương đối của nhóm [40;60) là \(\frac{{11}}{{36}}.100\% \approx 30,6\% \).
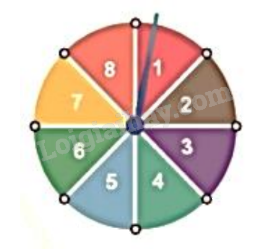
2) Số phần tử của không gian mẫu là \(n\left( \Omega \right) = 8\).
Gọi A là biến cố “Mũi tên chỉ vào hình quạt ghi số là ước của 8”.
Các kết quả thuận lợi cho A là 1; 2; 4; 8. Suy ra n(A) = 4.
Xác suất của biến cố A là \(P(A) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{4}{8} = \frac{1}{2}\).
Câu 2:(1,5 điểm) Cho biểu thức \(M = \frac{{\sqrt x - 1}}{{\sqrt x }}\); \(P = \frac{{\sqrt x - 2}}{{\sqrt x + 1}} + \frac{{2 + 8\sqrt x }}{{x - 1}} - \frac{2}{{1 - \sqrt x }}\) với x > 0; \(x \ne 1\).
1) Tính M khi x = 0,49.
2) Chứng minh \(P = \frac{{\sqrt x + 6}}{{\sqrt x - 1}}\).
3) Đặt \(Q = M.P + \frac{{x - 5}}{{\sqrt x }}\). So sánh Q với 3.
Phương pháp
1) Kiểm tra điều kiện của x. Nếu thỏa mãn, thay x = 0,49 vào M.
2) Kết hợp các tính chất của căn thức bậc hai để rút gọn biểu thức.
3) Rút gọn \(Q = M.P + \frac{{x - 5}}{{\sqrt x }}\) rồi xét hiệu Q – 3.
Lời giải
1) Thay x = 0,49 (thỏa mãn điều kiện) vào M, ta được:
\(M = \frac{{\sqrt {0,49} - 1}}{{\sqrt {0,49} }} = - \frac{3}{7}\).
Vậy khi x = 0,49 thì \(M = - \frac{3}{7}\).
2) \(P = \frac{{\sqrt x - 2}}{{\sqrt x + 1}} + \frac{{2 + 8\sqrt x }}{{x - 1}} - \frac{2}{{1 - \sqrt x }}\) (với x > 0; \(x \ne 1\)).
\( = \frac{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} + \frac{{2 + 8\sqrt x }}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} + \frac{{2\left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\)
\( = \frac{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 1} \right) + 2 + 8\sqrt x + 2\left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\)
\( = \frac{{x - 3\sqrt x + 2 + 2 + 8\sqrt x + 2\sqrt x + 2}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\)
\( = \frac{{x + 7\sqrt x + 6}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\)
\( = \frac{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 6} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\)
\( = \frac{{\sqrt x + 6}}{{\sqrt x - 1}}\) (đpcm).
3) \(Q = \frac{{\sqrt x - 1}}{{\sqrt x }}.\frac{{\sqrt x + 6}}{{\sqrt x - 1}} + \frac{{x - 5}}{{\sqrt x }} = \frac{{\sqrt x + 6}}{{\sqrt x }} + \frac{{x - 5}}{{\sqrt x }} = \frac{{x + \sqrt x + 1}}{{\sqrt x }}\).
Xét hiệu \(Q - 3 = \frac{{x + \sqrt x + 1}}{{\sqrt x }} - 3 = \frac{{x - 2\sqrt x + 1}}{{\sqrt x }} = \frac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\sqrt x }}\).
Với x > 0; \(x \ne 1\) thì \(\frac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\sqrt x }} > 0\) hay Q > 3.
Câu 3:(2,5 điểm)
1) Hai vòi nước cùng chảy vào một cái bể không có nước thì trong 5 giờ sẽ đầy bể. Nếu vòi thứ nhất chảy trong 3 giờ và vòi thứ hai chảy trong 4 giờ thì được \(\frac{2}{3}\) bể nước. Hỏi nếu mỗi vòi nước chảy một mình thì sau bao nhiêu giờ mới đầy bể?
2) Một người đi ô tô từ A đến B cách nhau 100 km với vận tốc xác định. Khi từ B trở về A, người đó đi theo đường khác dài hơn đường cũ 20 km nhưng với vận tốc lớn hơn vận tốc lúc đi mỗi giờ 20 km. Vì vậy thời gian về ít hơn thời gian đi 30 phút. Tính vận tốc lúc đi.
3) Biết phương trình bậc hai \({x^2} + 5x + a = 0\) có một nghiệm là \(x = \frac{{ - 5 + \sqrt {13} }}{2}\). Tìm tổng các lập phương hai nghiệm của phương trình trên.
Phương pháp
1) Gọi thời gian vòi I và vòi II chảy một mình đẩy bể lần lượt là x và y (giờ; x, y > 5).
Biểu diễn lượng nước mỗi vòi chảy được theo thời gian đề bài cho và lập hệ phương trình ẩn x, y.
Giải hệ phương trình tìm x, y và kết luận.
2) Gọi vận tốc lúc đi là x (km; x > 0).
Biểu diễn thời gian lúc đi và lúc về theo x.
Vì thời gian về ít hơn thời gian đi 30 phút nên ta lập được phương trình ẩn x.
Giải phương trình và kết luận.
3) Thay nghiệm vào phương trình, tính a.
Tổng lập phương các nghiệm là \({x_1}^3 + {x_2}^3\).
Biến đổi biểu thức và áp dụng định lí Viète: \(S = {x_1} + {x_2} = - \frac{b}{a}\); \(P = {x_1}.{x_2} = \frac{c}{a}\).
Lời giải
1) Gọi thời gian vòi I và vòi II chảy một mình đẩy bể lần lượt là x và y (giờ; x, y > 5).
Trong 1 giờ, vòi I chảy được \(\frac{1}{x}\) bể, vòi II chảy được \(\frac{1}{y}\) bể.
Hai vòi cùng chảy sau 5 giờ thì đầy bể, suy ra trong 1 giờ, hai vòi cùng chảy được \(\frac{1}{5}\) bể.
Ta có phương trình \(\frac{1}{x} + \frac{1}{y} = \frac{1}{5}\) (1)
Trong 3 giờ, vòi I chảy được \(\frac{3}{x}\) bể. Trong 4 giờ, vòi II chảy được \(\frac{4}{y}\) bể.
Vì vòi I chảy trong 3 giờ và vòi II chảy trong 4 giờ được \(\frac{2}{3}\) bể nên ta có phương trình \(\frac{3}{x} + \frac{4}{y} = \frac{2}{3}\) (2)
Ta có hệ \(\left\{ \begin{array}{l}\frac{1}{x} + \frac{1}{y} = \frac{1}{5}\\\frac{3}{x} + \frac{4}{y} = \frac{2}{3}\end{array} \right.\)
Giải hệ phương trình được \(\frac{1}{x} = \frac{2}{{15}}\), \(\frac{1}{y} = \frac{1}{{15}}\), suy ra x = 7,5 và y = 15 (thỏa mãn).
Vậy vòi I chảy một mình mất 7,5 giờ để đầy bể, vòi II chảy một mình mất 15 giờ để đầy bể.
2) Gọi vận tốc lúc đi là x (km; x > 0).
Thời gian lúc đi là \(\frac{{100}}{x}\) (giờ).
Quãng đường lúc về là 100 + 20 = 120 (km).
Vận tốc lúc về là x + 20 (km/h).
Thời gian lúc về là \(\frac{{120}}{{x + 20}}\) (giờ).
Vì thời gian về ít hơn thời gian đi 30 phút = \(\frac{1}{2}\) giờ nên ta có:
\(\frac{{100}}{x} - \frac{{120}}{{x + 20}} = \frac{1}{2}\)
\(\frac{{2.100\left( {x + 20} \right)}}{{2x\left( {x + 20} \right)}} - \frac{{2.120x}}{{2x\left( {x + 20} \right)}} = \frac{{x\left( {x + 20} \right)}}{{2x\left( {x + 20} \right)}}\)
\(200\left( {x + 20} \right) - 240x = x\left( {x + 20} \right)\)
\(200x + 4000 - 240x = {x^2} + 20x\)
\({x^2} + 60x - 4000 = 0\)
Giải phương trình trên, ta được x = 40 (thỏa mãn) và x = -100 (loại).
Vậy vận tốc lúc đi là 40 km/h.
3) Vì \(x = \frac{{ - 5 + \sqrt {13} }}{2}\) là một nghiệm của phương trình \({x^2} + 5x + a = 0\) nên thay nghiệm đó vào phương trình, ta được \({\left( {\frac{{ - 5 + \sqrt {13} }}{2}} \right)^2} + 5.\frac{{ - 5 + \sqrt {13} }}{2} + a = 0\), suy ra a = 3.
Vậy phương trình là \({x^2} + 5x + 3 = 0\).
Gọi \({x_1}\), \({x_2}\) là hai nghiệm của phương trình.
Áp dụng hệ thức Viète: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \frac{b}{a} = - \frac{5}{1} = - 5\\{x_1}{x_2} = \frac{c}{a} = \frac{3}{1} = 3\end{array} \right.\)
Ta có \({x_1}^3 + {x_2}^3\)
\( = \left( {{x_1} + {x_2}} \right)\left( {{x_1}^2 - {x_1}{x_2} + {x_2}^2} \right)\)
\( = \left( {{x_1} + {x_2}} \right)\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 3{x_1}{x_2}} \right]\)
\( = - 5\left[ {{{\left( { - 5} \right)}^2} - 3.3} \right] = - 80\).
Vậy tổng lập phương các nghiệm là -80.
Câu 4:(4 điểm)
1) Một téc nước hình trụ tròn có bán kính 60 cm, chiều cao 220 cm.
a) Diện tích inox cần làm ra cái téc nước (có nắp) là bao nhiêu mét vuông (giả sử phần nắp cong không đáng kể)?
b) Téc nước hình trụ có thể chứa tối đa bao nhiêu lít nước?
Các kết quả làm tròn tới hàng phần trăm.
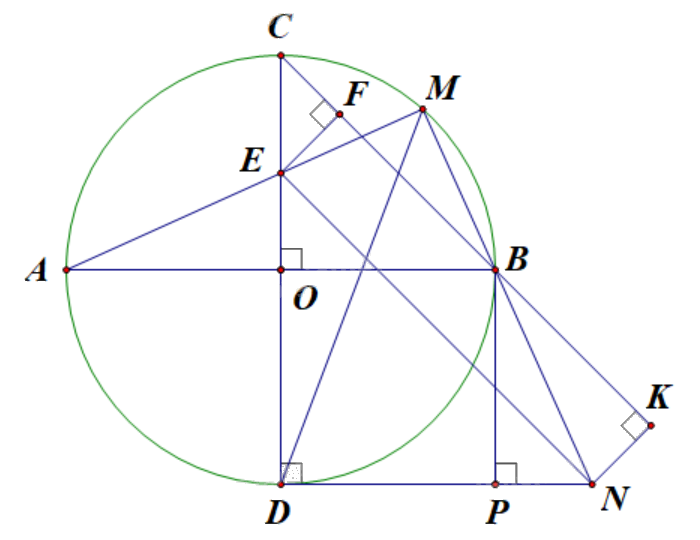
2) Cho (O) đường kính AB. Kẻ đường kính CD vuông góc với AB. Lấy M thuộc cung nhỏ BC, AM cắt CD tại E. Qua D kẻ tiếp tuyến với (O) cắt đường thẳng BM tại N. Gọi P là hình chiếu vuông góc của B lên DN.
a) Chứng minh các điểm M, N, D, E cùng thuộc một đường tròn.
b) Chứng minh EN // CB.
c) Chứng minh \(AB.BN = 2{R^2}\) và tìm vị trí điểm M trên cung nhỏ BC để diện tích tam giác BNC đạt giá trị lớn nhất.
Phương pháp
1)
a) Áp dụng công thức tính diện tích toàn phần hình trụ: \(S = 2\pi {r^2} + 2\pi rh\).
b) Áp dụng công thức tính thể tích hình trụ: \(V = \pi {r^2}h\).
2)
a) Chứng minh \(\widehat {AMB} = \widehat {EMN} = {90^o}\).
b) Chứng minh \(\widehat {DEN} = \widehat {DCB}\).
c)
- Để chứng minh \(AB.BN = 2{R^2}\):
+ Chứng minh \(\widehat {MBA} = \widehat {PNB}\), suy ra $\Delta MBA\backsim \Delta PNB$, từ đó được \(\frac{{AM}}{{BP}} = \frac{{AB}}{{BN}}\)
+ Chứng minh OBPD là hình vuông, suy ra BP = OB = R.
+ Biến đổi các đẳng thức trên và kết luận.
- Để tìm M trên cung nhỏ BC sao cho diện tích tam giác BNC đạt giá trị lớn nhất:
+ Kẻ \(EF \bot BC\), \(NK \bot BC\) (F, K thuộc đường thẳng BC). Chứng minh EF = NK.
+ \({S_{NBC}} = \frac{1}{2}BC.NK\) max khi EF = NK max.
+ Kết luận vị trí điểm M.
Lời giải
1)
a) Diện tích inox cần làm ra cái téc nước (có nắp) là diện tích toàn phần của hình trụ.
\(S = 2\pi {r^2} + 2\pi rh = 2\pi {.60^2} + 2\pi 60.220 = 33600\pi \)\(c{m^2}\) \( \approx 10,56\) \(\left( {{m^2}} \right)\).
b) Thể tích téc nước là \(V = \pi {r^2}h = \pi {.60^2}.220 = 792000\pi \) \(c{m^3}\)\( \approx 2488,14\) (lít).
2)
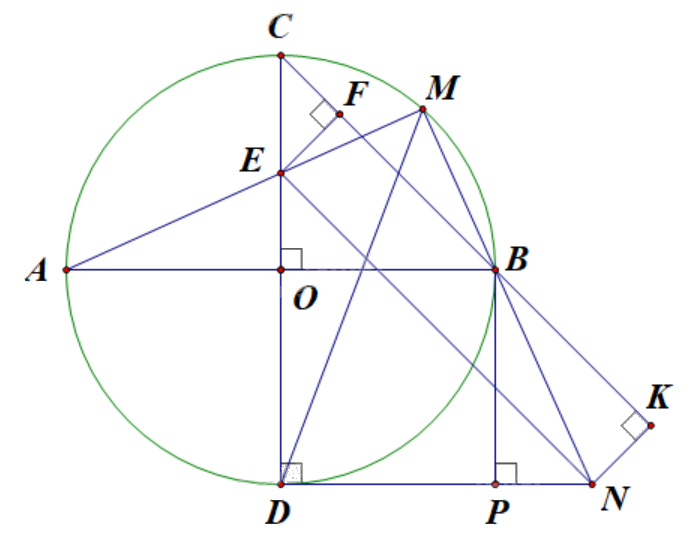
a) Vì M thuộc đường tròn (O) đường kính AB nên \(\widehat {AMB} = \widehat {EMN} = {90^o}\).
Mặt khác, DN là tiếp tuyến của (O) tại D nên đường kính \(CD \bot DN\), do đó \(\widehat {EDN} = {90^o}\).
Có \(\widehat {EMN} = \widehat {EDN} = {90^o}\) nên D, M cùng thuộc đường tròn đường kính EN.
Vậy M, N, E, D cùng thuộc một đường tròn.
b) Vì tứ giác MNDE nội tiếp (chứng minh trên) nên \(\widehat {DEN} = \widehat {DMN}\) (góc nội tiếp cùng chắn cung DN).
Mặt khác, xét (O) có \(\widehat {DMB} = \widehat {DCB}\).
Do đó \(\widehat {DEN} = \widehat {DCB}\), mà hai góc trên ở vị trí đồng vị nên EN // BC.
c) Xét tứ giác OBPD có OB // DP (cùng vuông góc với CD), OD // BP (cùng vuông góc với DN) suy ra OBPD là hình bình hành.
Mặt khác, \(\widehat {BOD} = {90^o}\) và OB = OD nên OBPD là hình vuông, suy ra BP = OB = R.
Ta có AB // DN (cùng vuông góc với CD) nên \(\widehat {MBA} = \widehat {PNB}\) (góc đồng vị).
Xét \(\Delta MBA\) và \(\Delta PNB\):
+ \(\widehat {MBA} = \widehat {PNB}\) (chứng minh trên);
+ \(\widehat {AMB} = \widehat {BPN} = {90^o}\).
Do đó $\Delta MBA\backsim \Delta PNB$ (g.g), suy ra \(\frac{{AM}}{{BP}} = \frac{{AB}}{{BN}}\)
\(AM.BN = AB.BP\)
\(AM.BN = 2R.R\)
\(AM.BN = 2{R^2}\) (đpcm).
Kẻ \(EF \bot BC\), \(NK \bot BC\) (F, K thuộc đường thẳng BC).
Xét từ giác EFKN có EN // FK, EF // NK (cùng vuông góc với BC), do đó EFKN là hình bình hành.
Mặt khác, \(\widehat {EFK} = {90^o}\) nên EFKN là hình chữ nhật, suy ra EF = NK.
Diện tích tam giác NBC là \({S_{NBC}} = \frac{1}{2}BC.NK\).
Do BC không đổi nên \({S_{NBC}}\) max khi và chỉ khi NK = EF max. Khi đó, E trùng O và M trùng B.
Vậy, để diện tích tam giác NBC lớn nhất thì M trùng B.
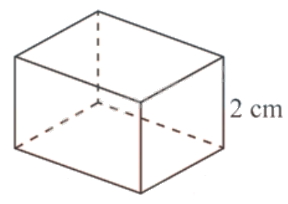
Câu 5:(0,5 điểm) Người ta muốn chế tạo một chiếc hộp hình chữ nhật có thể tích 500 \(c{m^3}\), chiều cao của hộp là 2 cm. Tìm kích thước đáy của hộp sao cho sử dụng ít vật liệu nhất.
Phương pháp
Gọi chiều rộng của đáy hộp là x (x > 0, cm).
Lập công thức tính diện tích toàn phần hình hộp theo x.
Áp dụng bất đẳng thức Cauchy để tìm x sao cho diện tích toàn phần hộp nhỏ nhất.
Lời giải
Gọi chiều rộng của đáy hộp là x (x > 0, cm). Khi đó, chiều dài đáy hộp là \(\frac{{500}}{{2x}}\) (cm).
Diện tích toàn phần của hộp là:
\(S = 2.\left( {x.\frac{{500}}{{2x}} + 2x + 2.\frac{{500}}{{2x}}} \right) = 500 + 4x + \frac{{1000}}{x}\) \(\left( {c{m^2}} \right)\).
Áp dụng bất đẳng thức Cauchy cho hai số thực dương \(4x\) và \(\frac{{1000}}{x}\):
\(4x + \frac{{1000}}{x} \ge 2\sqrt {4x.\frac{{1000}}{x}} \)
\(4x + \frac{{1000}}{x} \ge 40\sqrt {10} \)
\(S \ge 40\sqrt {10} + 500\).
Dấu “=” xảy ra khi \(4x = \frac{{1000}}{x}\), suy ra \(x = 5\sqrt {10} \).
Vậy để sử dụng ít vật liệu nhất thì chiều rộng và chiều dài đáy hộp là \(5\sqrt {10} \) cm.
Tải về
Câu 1:(1,5 điểm)
1) Khảo sát thời gian tập thể dục của một số học sinh lớp 9 thu được mẫu số liệu ghép nhóm sau:

Tính tần số tương đối của nhóm [40;60) (làm tròn đến hàng phần mười).
2) Hình dưới đây mô tả một đĩa tròn, cân đối bằng bìa cứng được chia làm tám phần bằng nhau và ghi các số 1; 2; 3; 4; 5; 6; 7; 8. Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Quay đĩa tròn một lần. Tính xác suất của biến cố sau: “Mũi tên chỉ vào hình quạt ghi số là ước của 8”.
Câu 2:(1,5 điểm) Cho biểu thức \(M = \frac{{\sqrt x - 1}}{{\sqrt x }}\); \(P = \frac{{\sqrt x - 2}}{{\sqrt x + 1}} + \frac{{2 + 8\sqrt x }}{{x - 1}} - \frac{2}{{1 - \sqrt x }}\) với x > 0; \(x \ne 1\).
1) Tính M khi x = 0,49.
2) Chứng minh \(P = \frac{{\sqrt x + 6}}{{\sqrt x - 1}}\).
3) Đặt \(Q = M.P + \frac{{x - 5}}{{\sqrt x }}\). So sánh Q với 3.
Câu 3:(2,5 điểm)
1) Hai vòi nước cùng chảy vào một cái bể không có nước thì trong 5 giờ sẽ đầy bể. Nếu vòi thứ nhất chảy trong 3 giờ và vòi thứ hai chảy trong 4 giờ thì được \(\frac{2}{3}\) bể nước. Hỏi nếu mỗi vòi nước chảy một mình thì sau bao nhiêu giờ mới đầy bể?
2) Một người đi ô tô từ A đến B cách nhau 100 km với vận tốc xác định. Khi từ B trở về A, người đó đi theo đường khác dài hơn đường cũ 20 km nhưng với vận tốc lớn hơn vận tốc lúc đi mỗi giờ 20 km. Vì vậy thời gian về ít hơn thời gian đi 30 phút. Tính vận tốc lúc đi.
3) Biết phương trình bậc hai \({x^2} + 5x + a = 0\) có một nghiệm là \(x = \frac{{ - 5 + \sqrt {13} }}{2}\). Tìm tổng các lập phương hai nghiệm của phương trình trên.
Câu 4:(4 điểm)
1) Một téc nước hình trụ tròn có bán kính 60 cm, chiều cao 220 cm.
a) Diện tích inox cần làm ra cái téc nước (có nắp) là bao nhiêu mét vuông (giả sử phần nắp cong không đáng kể)?
b) Téc nước hình trụ có thể chứa tối đa bao nhiêu lít nước?
Các kết quả làm tròn tới hàng phần trăm.
2) Cho (O) đường kính AB. Kẻ đường kính CD vuông góc với AB. Lấy M thuộc cung nhỏ BC, AM cắt CD tại E. Qua D kẻ tiếp tuyến với (O) cắt đường thẳng BM tại N. Gọi P là hình chiếu vuông góc của B lên DN.
a) Chứng minh các điểm M, N, D, E cùng thuộc một đường tròn.
b) Chứng minh EN // CB.
c) Chứng minh \(AB.BN = 2{R^2}\) và tìm vị trí điểm M trên cung nhỏ BC để diện tích tam giác BNC đạt giá trị lớn nhất.
Câu 5:(0,5 điểm) Người ta muốn chế tạo một chiếc hộp hình chữ nhật có thể tích 500 \(c{m^3}\), chiều cao của hộp là 2 cm. Tìm kích thước đáy của hộp sao cho sử dụng ít vật liệu nhất.
Câu 1:(1,5 điểm)
1) Khảo sát thời gian tập thể dục của một số học sinh lớp 9 thu được mẫu số liệu ghép nhóm sau:

Tính tần số tương đối của nhóm [40;60) (làm tròn đến hàng phần mười).
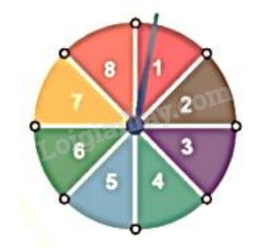
2) Hình dưới đây mô tả một đĩa tròn, cân đối bằng bìa cứng được chia làm tám phần bằng nhau và ghi các số 1; 2; 3; 4; 5; 6; 7; 8. Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Quay đĩa tròn một lần. Tính xác suất của biến cố sau: “Mũi tên chỉ vào hình quạt ghi số là ước của 8”.
Phương pháp
1) Tính tổng số học sinh.
Tần số tương đối của nhóm bằng: tần số của nhóm : tổng . 100%.
2) Xác định không gian mẫu của phép thử, tính số phần tử của không gian mẫu.
Tính số kết quả thuận lợi của biến cố.
Xác suất của biến cố = số kết quả thuận lợi của biến cố : số phần tử của không gian mẫu.
Lời giải
1) Tổng số học sinh là: 8 + 9 + 11 + 8 = 36.
Tần số tương đối của nhóm [40;60) là \(\frac{{11}}{{36}}.100\% \approx 30,6\% \).
2) Số phần tử của không gian mẫu là \(n\left( \Omega \right) = 8\).
Gọi A là biến cố “Mũi tên chỉ vào hình quạt ghi số là ước của 8”.
Các kết quả thuận lợi cho A là 1; 2; 4; 8. Suy ra n(A) = 4.
Xác suất của biến cố A là \(P(A) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{4}{8} = \frac{1}{2}\).
Câu 2:(1,5 điểm) Cho biểu thức \(M = \frac{{\sqrt x - 1}}{{\sqrt x }}\); \(P = \frac{{\sqrt x - 2}}{{\sqrt x + 1}} + \frac{{2 + 8\sqrt x }}{{x - 1}} - \frac{2}{{1 - \sqrt x }}\) với x > 0; \(x \ne 1\).
1) Tính M khi x = 0,49.
2) Chứng minh \(P = \frac{{\sqrt x + 6}}{{\sqrt x - 1}}\).
3) Đặt \(Q = M.P + \frac{{x - 5}}{{\sqrt x }}\). So sánh Q với 3.
Phương pháp
1) Kiểm tra điều kiện của x. Nếu thỏa mãn, thay x = 0,49 vào M.
2) Kết hợp các tính chất của căn thức bậc hai để rút gọn biểu thức.
3) Rút gọn \(Q = M.P + \frac{{x - 5}}{{\sqrt x }}\) rồi xét hiệu Q – 3.
Lời giải
1) Thay x = 0,49 (thỏa mãn điều kiện) vào M, ta được:
\(M = \frac{{\sqrt {0,49} - 1}}{{\sqrt {0,49} }} = - \frac{3}{7}\).
Vậy khi x = 0,49 thì \(M = - \frac{3}{7}\).
2) \(P = \frac{{\sqrt x - 2}}{{\sqrt x + 1}} + \frac{{2 + 8\sqrt x }}{{x - 1}} - \frac{2}{{1 - \sqrt x }}\) (với x > 0; \(x \ne 1\)).
\( = \frac{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} + \frac{{2 + 8\sqrt x }}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} + \frac{{2\left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\)
\( = \frac{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 1} \right) + 2 + 8\sqrt x + 2\left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\)
\( = \frac{{x - 3\sqrt x + 2 + 2 + 8\sqrt x + 2\sqrt x + 2}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\)
\( = \frac{{x + 7\sqrt x + 6}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\)
\( = \frac{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 6} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\)
\( = \frac{{\sqrt x + 6}}{{\sqrt x - 1}}\) (đpcm).
3) \(Q = \frac{{\sqrt x - 1}}{{\sqrt x }}.\frac{{\sqrt x + 6}}{{\sqrt x - 1}} + \frac{{x - 5}}{{\sqrt x }} = \frac{{\sqrt x + 6}}{{\sqrt x }} + \frac{{x - 5}}{{\sqrt x }} = \frac{{x + \sqrt x + 1}}{{\sqrt x }}\).
Xét hiệu \(Q - 3 = \frac{{x + \sqrt x + 1}}{{\sqrt x }} - 3 = \frac{{x - 2\sqrt x + 1}}{{\sqrt x }} = \frac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\sqrt x }}\).
Với x > 0; \(x \ne 1\) thì \(\frac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\sqrt x }} > 0\) hay Q > 3.
Câu 3:(2,5 điểm)
1) Hai vòi nước cùng chảy vào một cái bể không có nước thì trong 5 giờ sẽ đầy bể. Nếu vòi thứ nhất chảy trong 3 giờ và vòi thứ hai chảy trong 4 giờ thì được \(\frac{2}{3}\) bể nước. Hỏi nếu mỗi vòi nước chảy một mình thì sau bao nhiêu giờ mới đầy bể?
2) Một người đi ô tô từ A đến B cách nhau 100 km với vận tốc xác định. Khi từ B trở về A, người đó đi theo đường khác dài hơn đường cũ 20 km nhưng với vận tốc lớn hơn vận tốc lúc đi mỗi giờ 20 km. Vì vậy thời gian về ít hơn thời gian đi 30 phút. Tính vận tốc lúc đi.
3) Biết phương trình bậc hai \({x^2} + 5x + a = 0\) có một nghiệm là \(x = \frac{{ - 5 + \sqrt {13} }}{2}\). Tìm tổng các lập phương hai nghiệm của phương trình trên.
Phương pháp
1) Gọi thời gian vòi I và vòi II chảy một mình đẩy bể lần lượt là x và y (giờ; x, y > 5).
Biểu diễn lượng nước mỗi vòi chảy được theo thời gian đề bài cho và lập hệ phương trình ẩn x, y.
Giải hệ phương trình tìm x, y và kết luận.
2) Gọi vận tốc lúc đi là x (km; x > 0).
Biểu diễn thời gian lúc đi và lúc về theo x.
Vì thời gian về ít hơn thời gian đi 30 phút nên ta lập được phương trình ẩn x.
Giải phương trình và kết luận.
3) Thay nghiệm vào phương trình, tính a.
Tổng lập phương các nghiệm là \({x_1}^3 + {x_2}^3\).
Biến đổi biểu thức và áp dụng định lí Viète: \(S = {x_1} + {x_2} = - \frac{b}{a}\); \(P = {x_1}.{x_2} = \frac{c}{a}\).
Lời giải
1) Gọi thời gian vòi I và vòi II chảy một mình đẩy bể lần lượt là x và y (giờ; x, y > 5).
Trong 1 giờ, vòi I chảy được \(\frac{1}{x}\) bể, vòi II chảy được \(\frac{1}{y}\) bể.
Hai vòi cùng chảy sau 5 giờ thì đầy bể, suy ra trong 1 giờ, hai vòi cùng chảy được \(\frac{1}{5}\) bể.
Ta có phương trình \(\frac{1}{x} + \frac{1}{y} = \frac{1}{5}\) (1)
Trong 3 giờ, vòi I chảy được \(\frac{3}{x}\) bể. Trong 4 giờ, vòi II chảy được \(\frac{4}{y}\) bể.
Vì vòi I chảy trong 3 giờ và vòi II chảy trong 4 giờ được \(\frac{2}{3}\) bể nên ta có phương trình \(\frac{3}{x} + \frac{4}{y} = \frac{2}{3}\) (2)
Ta có hệ \(\left\{ \begin{array}{l}\frac{1}{x} + \frac{1}{y} = \frac{1}{5}\\\frac{3}{x} + \frac{4}{y} = \frac{2}{3}\end{array} \right.\)
Giải hệ phương trình được \(\frac{1}{x} = \frac{2}{{15}}\), \(\frac{1}{y} = \frac{1}{{15}}\), suy ra x = 7,5 và y = 15 (thỏa mãn).
Vậy vòi I chảy một mình mất 7,5 giờ để đầy bể, vòi II chảy một mình mất 15 giờ để đầy bể.
2) Gọi vận tốc lúc đi là x (km; x > 0).
Thời gian lúc đi là \(\frac{{100}}{x}\) (giờ).
Quãng đường lúc về là 100 + 20 = 120 (km).
Vận tốc lúc về là x + 20 (km/h).
Thời gian lúc về là \(\frac{{120}}{{x + 20}}\) (giờ).
Vì thời gian về ít hơn thời gian đi 30 phút = \(\frac{1}{2}\) giờ nên ta có:
\(\frac{{100}}{x} - \frac{{120}}{{x + 20}} = \frac{1}{2}\)
\(\frac{{2.100\left( {x + 20} \right)}}{{2x\left( {x + 20} \right)}} - \frac{{2.120x}}{{2x\left( {x + 20} \right)}} = \frac{{x\left( {x + 20} \right)}}{{2x\left( {x + 20} \right)}}\)
\(200\left( {x + 20} \right) - 240x = x\left( {x + 20} \right)\)
\(200x + 4000 - 240x = {x^2} + 20x\)
\({x^2} + 60x - 4000 = 0\)
Giải phương trình trên, ta được x = 40 (thỏa mãn) và x = -100 (loại).
Vậy vận tốc lúc đi là 40 km/h.
3) Vì \(x = \frac{{ - 5 + \sqrt {13} }}{2}\) là một nghiệm của phương trình \({x^2} + 5x + a = 0\) nên thay nghiệm đó vào phương trình, ta được \({\left( {\frac{{ - 5 + \sqrt {13} }}{2}} \right)^2} + 5.\frac{{ - 5 + \sqrt {13} }}{2} + a = 0\), suy ra a = 3.
Vậy phương trình là \({x^2} + 5x + 3 = 0\).
Gọi \({x_1}\), \({x_2}\) là hai nghiệm của phương trình.
Áp dụng hệ thức Viète: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \frac{b}{a} = - \frac{5}{1} = - 5\\{x_1}{x_2} = \frac{c}{a} = \frac{3}{1} = 3\end{array} \right.\)
Ta có \({x_1}^3 + {x_2}^3\)
\( = \left( {{x_1} + {x_2}} \right)\left( {{x_1}^2 - {x_1}{x_2} + {x_2}^2} \right)\)
\( = \left( {{x_1} + {x_2}} \right)\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 3{x_1}{x_2}} \right]\)
\( = - 5\left[ {{{\left( { - 5} \right)}^2} - 3.3} \right] = - 80\).
Vậy tổng lập phương các nghiệm là -80.
Câu 4:(4 điểm)
1) Một téc nước hình trụ tròn có bán kính 60 cm, chiều cao 220 cm.
a) Diện tích inox cần làm ra cái téc nước (có nắp) là bao nhiêu mét vuông (giả sử phần nắp cong không đáng kể)?
b) Téc nước hình trụ có thể chứa tối đa bao nhiêu lít nước?
Các kết quả làm tròn tới hàng phần trăm.
2) Cho (O) đường kính AB. Kẻ đường kính CD vuông góc với AB. Lấy M thuộc cung nhỏ BC, AM cắt CD tại E. Qua D kẻ tiếp tuyến với (O) cắt đường thẳng BM tại N. Gọi P là hình chiếu vuông góc của B lên DN.
a) Chứng minh các điểm M, N, D, E cùng thuộc một đường tròn.
b) Chứng minh EN // CB.
c) Chứng minh \(AB.BN = 2{R^2}\) và tìm vị trí điểm M trên cung nhỏ BC để diện tích tam giác BNC đạt giá trị lớn nhất.
Phương pháp
1)
a) Áp dụng công thức tính diện tích toàn phần hình trụ: \(S = 2\pi {r^2} + 2\pi rh\).
b) Áp dụng công thức tính thể tích hình trụ: \(V = \pi {r^2}h\).
2)
a) Chứng minh \(\widehat {AMB} = \widehat {EMN} = {90^o}\).
b) Chứng minh \(\widehat {DEN} = \widehat {DCB}\).
c)
- Để chứng minh \(AB.BN = 2{R^2}\):
+ Chứng minh \(\widehat {MBA} = \widehat {PNB}\), suy ra $\Delta MBA\backsim \Delta PNB$, từ đó được \(\frac{{AM}}{{BP}} = \frac{{AB}}{{BN}}\)
+ Chứng minh OBPD là hình vuông, suy ra BP = OB = R.
+ Biến đổi các đẳng thức trên và kết luận.
- Để tìm M trên cung nhỏ BC sao cho diện tích tam giác BNC đạt giá trị lớn nhất:
+ Kẻ \(EF \bot BC\), \(NK \bot BC\) (F, K thuộc đường thẳng BC). Chứng minh EF = NK.
+ \({S_{NBC}} = \frac{1}{2}BC.NK\) max khi EF = NK max.
+ Kết luận vị trí điểm M.
Lời giải
1)
a) Diện tích inox cần làm ra cái téc nước (có nắp) là diện tích toàn phần của hình trụ.
\(S = 2\pi {r^2} + 2\pi rh = 2\pi {.60^2} + 2\pi 60.220 = 33600\pi \)\(c{m^2}\) \( \approx 10,56\) \(\left( {{m^2}} \right)\).
b) Thể tích téc nước là \(V = \pi {r^2}h = \pi {.60^2}.220 = 792000\pi \) \(c{m^3}\)\( \approx 2488,14\) (lít).
2)
a) Vì M thuộc đường tròn (O) đường kính AB nên \(\widehat {AMB} = \widehat {EMN} = {90^o}\).
Mặt khác, DN là tiếp tuyến của (O) tại D nên đường kính \(CD \bot DN\), do đó \(\widehat {EDN} = {90^o}\).
Có \(\widehat {EMN} = \widehat {EDN} = {90^o}\) nên D, M cùng thuộc đường tròn đường kính EN.
Vậy M, N, E, D cùng thuộc một đường tròn.
b) Vì tứ giác MNDE nội tiếp (chứng minh trên) nên \(\widehat {DEN} = \widehat {DMN}\) (góc nội tiếp cùng chắn cung DN).
Mặt khác, xét (O) có \(\widehat {DMB} = \widehat {DCB}\).
Do đó \(\widehat {DEN} = \widehat {DCB}\), mà hai góc trên ở vị trí đồng vị nên EN // BC.
c) Xét tứ giác OBPD có OB // DP (cùng vuông góc với CD), OD // BP (cùng vuông góc với DN) suy ra OBPD là hình bình hành.
Mặt khác, \(\widehat {BOD} = {90^o}\) và OB = OD nên OBPD là hình vuông, suy ra BP = OB = R.
Ta có AB // DN (cùng vuông góc với CD) nên \(\widehat {MBA} = \widehat {PNB}\) (góc đồng vị).
Xét \(\Delta MBA\) và \(\Delta PNB\):
+ \(\widehat {MBA} = \widehat {PNB}\) (chứng minh trên);
+ \(\widehat {AMB} = \widehat {BPN} = {90^o}\).
Do đó $\Delta MBA\backsim \Delta PNB$ (g.g), suy ra \(\frac{{AM}}{{BP}} = \frac{{AB}}{{BN}}\)
\(AM.BN = AB.BP\)
\(AM.BN = 2R.R\)
\(AM.BN = 2{R^2}\) (đpcm).
Kẻ \(EF \bot BC\), \(NK \bot BC\) (F, K thuộc đường thẳng BC).
Xét từ giác EFKN có EN // FK, EF // NK (cùng vuông góc với BC), do đó EFKN là hình bình hành.
Mặt khác, \(\widehat {EFK} = {90^o}\) nên EFKN là hình chữ nhật, suy ra EF = NK.
Diện tích tam giác NBC là \({S_{NBC}} = \frac{1}{2}BC.NK\).
Do BC không đổi nên \({S_{NBC}}\) max khi và chỉ khi NK = EF max. Khi đó, E trùng O và M trùng B.
Vậy, để diện tích tam giác NBC lớn nhất thì M trùng B.
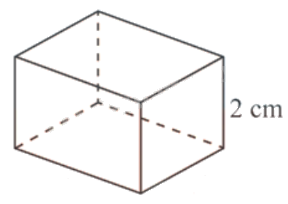
Câu 5:(0,5 điểm) Người ta muốn chế tạo một chiếc hộp hình chữ nhật có thể tích 500 \(c{m^3}\), chiều cao của hộp là 2 cm. Tìm kích thước đáy của hộp sao cho sử dụng ít vật liệu nhất.
Phương pháp
Gọi chiều rộng của đáy hộp là x (x > 0, cm).
Lập công thức tính diện tích toàn phần hình hộp theo x.
Áp dụng bất đẳng thức Cauchy để tìm x sao cho diện tích toàn phần hộp nhỏ nhất.
Lời giải
Gọi chiều rộng của đáy hộp là x (x > 0, cm). Khi đó, chiều dài đáy hộp là \(\frac{{500}}{{2x}}\) (cm).
Diện tích toàn phần của hộp là:
\(S = 2.\left( {x.\frac{{500}}{{2x}} + 2x + 2.\frac{{500}}{{2x}}} \right) = 500 + 4x + \frac{{1000}}{x}\) \(\left( {c{m^2}} \right)\).
Áp dụng bất đẳng thức Cauchy cho hai số thực dương \(4x\) và \(\frac{{1000}}{x}\):
\(4x + \frac{{1000}}{x} \ge 2\sqrt {4x.\frac{{1000}}{x}} \)
\(4x + \frac{{1000}}{x} \ge 40\sqrt {10} \)
\(S \ge 40\sqrt {10} + 500\).
Dấu “=” xảy ra khi \(4x = \frac{{1000}}{x}\), suy ra \(x = 5\sqrt {10} \).
Vậy để sử dụng ít vật liệu nhất thì chiều rộng và chiều dài đáy hộp là \(5\sqrt {10} \) cm.
Kỳ thi tuyển sinh vào lớp 10 tại Hà Nội là một bước ngoặt quan trọng trong sự nghiệp học tập của mỗi học sinh. Để đạt kết quả tốt nhất, việc luyện tập với các đề tham khảo là vô cùng cần thiết. Đề tham khảo thi vào 10 môn Toán Hà Nội năm 2025 - Đề số 9 của giaitoan.edu.vn được thiết kế để đáp ứng nhu cầu này.
Đề thi bao gồm các dạng bài tập thường gặp trong các kỳ thi tuyển sinh vào 10 tại Hà Nội, bao gồm:
Câu 1: Giải phương trình x2 - 5x + 6 = 0. Đây là một bài toán cơ bản về phương trình bậc hai. Học sinh cần nắm vững các phương pháp giải phương trình bậc hai như phân tích thành nhân tử, sử dụng công thức nghiệm, hoặc hoàn thành bình phương.
Câu 2: Cho tam giác ABC vuông tại A, có AB = 3cm, AC = 4cm. Tính độ dài cạnh BC và diện tích tam giác ABC. Đây là một bài toán ứng dụng định lý Pitago và công thức tính diện tích tam giác vuông. Học sinh cần nhớ rõ các định lý và công thức này để giải quyết bài toán một cách nhanh chóng và chính xác.
Câu 3: Tìm tất cả các số nguyên tố p sao cho p + 2 cũng là số nguyên tố. Đây là một bài toán về số nguyên tố. Học sinh cần hiểu rõ định nghĩa của số nguyên tố và sử dụng các tính chất của số nguyên tố để giải quyết bài toán.
Đáp án và lời giải chi tiết của từng câu hỏi trong đề thi sẽ được cung cấp sau khi học sinh hoàn thành bài làm. Lời giải được trình bày một cách dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải toán.
Ngoài đề tham khảo số 9, giaitoan.edu.vn còn cung cấp nhiều đề tham khảo khác cho kỳ thi tuyển sinh vào 10 môn Toán Hà Nội năm 2025. Các em có thể truy cập website để xem và tải về các đề thi này.
Đề tham khảo thi vào 10 môn Toán Hà Nội năm 2025 - Đề số 9 là một công cụ hữu ích giúp các em học sinh ôn tập và chuẩn bị tốt nhất cho kỳ thi quan trọng này. Chúc các em đạt kết quả cao trong kỳ thi tuyển sinh vào lớp 10!