Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Quảng Ninh năm 2020 chính thức, kèm đáp án chi tiết. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi sắp tới.
Chúng tôi cung cấp đầy đủ các đề thi, đáp án và lời giải chi tiết, giúp các em hiểu rõ từng bước giải và áp dụng vào các bài toán tương tự. Hãy cùng giaitoan.edu.vn chinh phục kỳ thi vào 10 môn Toán Quảng Ninh năm 2020!
Câu 1: 1. Thực hiện phép tính
Câu 1:
1. Thực hiện phép tính \(2 + \sqrt 9 .\)
2. Rút gọn biểu thức \(B = \left( {\dfrac{1}{{\sqrt x + 2}} - \dfrac{1}{{\sqrt x + 7}}} \right):\dfrac{5}{{\sqrt x + 7}}\) với \(x \ge 0.\)
3. Giải hệ phương trình \(\left\{ \begin{array}{l}x + 2y = 4\\x - 2y = 0\end{array} \right..\)
Câu 2:
Cho phương trình \({x^2} + 4x + 3m - 2 = 0\), với \(m\) là tham số.
1. Giải phương trình với \(m = - 1\).
2. Tìm giá trị của \(m\) để phương trình đã cho có một nghiệm \(x = 2\).
3. Tìm giá trị của \(m\) để phương trình đã cho có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) sao cho \({x_1} + 2{x_2} = 1\).
Câu 3:
Khoảng cách giữa hai bến sông A và B là 32 km. Một canô xuôi dòng từ bến A đến bến B rồi lập tức quay về bến A. Kể từ lúc khởi hành đến lúc về tới bến A hết tất cả 6 giờ. Tính vận tốc của canô khi nước yên lặng biết vận tốc của dòng nước là 4 km/h.
Câu 4:
Cho đường tròn \(\left( {O;R} \right)\) và \(A\) là một điểm nằm bên ngoài đường tròn. Từ điểm A kẻ hai tiếp tuyến \(AB\) và \(AC\) với đường tròn \(\left( O \right)\) ( B và C là hai tiếp điểm). Gọi \(H\) là giao điểm của \(AO\) và \(BC\). Kẻ đường kính \(BD\) của đường tròn \(\left( O \right)\), \(AD\) cắt đường tròn tại điểm thứ hai là \(E\).
a. Chứng minh \(ABOC\) là tứ giác nội tiếp
b. Tính độ dài \(AH\) biết \(R = 3cm,AB = 4cm.\)
c. Chứng minh \(AE.AD = AH.AO\)
d. Tia \(CE\) cắt \(AH\) tại \(F\). Chứng tỏ \(F\) là trung điểm của \(AH.\)
Câu 5:
Cho \(x,\,\,y\) là các số thực dương thỏa mãn \(x + y \le 3\). Tìm giá trị nhỏ nhất của biểu thức
\(Q = {x^2} + {y^2} - 9x - 12y + \dfrac{{16}}{{2x + y}} + 25\)
Câu 1:
1. Thực hiện phép tính \(2 + \sqrt 9 .\)
2. Rút gọn biểu thức \(B = \left( {\dfrac{1}{{\sqrt x + 2}} - \dfrac{1}{{\sqrt x + 7}}} \right):\dfrac{5}{{\sqrt x + 7}}\) với \(x \ge 0.\)
3. Giải hệ phương trình \(\left\{ \begin{array}{l}x + 2y = 4\\x - 2y = 0\end{array} \right..\)
Câu 2:
Cho phương trình \({x^2} + 4x + 3m - 2 = 0\), với \(m\) là tham số.
1. Giải phương trình với \(m = - 1\).
2. Tìm giá trị của \(m\) để phương trình đã cho có một nghiệm \(x = 2\).
3. Tìm giá trị của \(m\) để phương trình đã cho có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) sao cho \({x_1} + 2{x_2} = 1\).
Câu 3:
Khoảng cách giữa hai bến sông A và B là 32 km. Một canô xuôi dòng từ bến A đến bến B rồi lập tức quay về bến A. Kể từ lúc khởi hành đến lúc về tới bến A hết tất cả 6 giờ. Tính vận tốc của canô khi nước yên lặng biết vận tốc của dòng nước là 4 km/h.
Câu 4:
Cho đường tròn \(\left( {O;R} \right)\) và \(A\) là một điểm nằm bên ngoài đường tròn. Từ điểm A kẻ hai tiếp tuyến \(AB\) và \(AC\) với đường tròn \(\left( O \right)\) ( B và C là hai tiếp điểm). Gọi \(H\) là giao điểm của \(AO\) và \(BC\). Kẻ đường kính \(BD\) của đường tròn \(\left( O \right)\), \(AD\) cắt đường tròn tại điểm thứ hai là \(E\).
a. Chứng minh \(ABOC\) là tứ giác nội tiếp
b. Tính độ dài \(AH\) biết \(R = 3cm,AB = 4cm.\)
c. Chứng minh \(AE.AD = AH.AO\)
d. Tia \(CE\) cắt \(AH\) tại \(F\). Chứng tỏ \(F\) là trung điểm của \(AH.\)
Câu 5:
Cho \(x,\,\,y\) là các số thực dương thỏa mãn \(x + y \le 3\). Tìm giá trị nhỏ nhất của biểu thức
\(Q = {x^2} + {y^2} - 9x - 12y + \dfrac{{16}}{{2x + y}} + 25\)
Câu 1 (2 điểm)
Cách giải:
1. Thực hiện phép tính \(2 + \sqrt 9 .\)
Ta có: \(2 + \sqrt 9 = 2 + 3 = 5.\)
2. Rút gọn biểu thức \(B = \left( {\dfrac{1}{{\sqrt x + 2}} - \dfrac{1}{{\sqrt x + 7}}} \right):\dfrac{5}{{\sqrt x + 7}}\) với \(x \ge 0.\)
Điều kiện: \(x \ge 0\)
\(\begin{array}{l}B = \left( {\dfrac{1}{{\sqrt x + 2}} - \dfrac{1}{{\sqrt x + 7}}} \right):\dfrac{5}{{\sqrt x + 7}}\\\,\,\,\, = \dfrac{{\sqrt x + 7 - \sqrt x - 2}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x + 7} \right)}}.\dfrac{{\sqrt x + 7}}{5}\\\,\,\,\, = \dfrac{5}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x + 7} \right)}}.\dfrac{{\sqrt x + 7}}{5}\\\,\,\, = \dfrac{1}{{\sqrt x + 2}}.\end{array}\)
Vậy \(B = \dfrac{1}{{\sqrt x + 2}}\) với \(x \ge 2.\)
3. Giải hệ phương trình \(\left\{ \begin{array}{l}x + 2y = 4\\x - 2y = 0\end{array} \right..\)
\(\left\{ \begin{array}{l}x + 2y = 4\\x - 2y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x = 4\\x = 2y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right..\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;\,\,y} \right) = \left( {2;\,\,1} \right).\)
Câu 2 (2,0 điểm)
Cách giải:
Cho phương trình \({x^2} + 4x + 3m - 2 = 0\), với \(m\) là tham số.
1. Giải phương trình với \(m = - 1\).
Thay \(m = - 1\) vào phương trình đã cho ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,{x^2} + 4x - 5 = 0\\ \Leftrightarrow {x^2} - x + 5x - 5 = 0\\ \Leftrightarrow x\left( {x - 1} \right) + 5\left( {x - 1} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x + 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x + 5 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 5\end{array} \right.\end{array}\)
Vậy khi \(m = - 1\) thì tập nghiệm của phương trình là \(S = \left\{ {1; - 5} \right\}\).
2. Tìm giá trị của \(m\) để phương trình đã cho có một nghiệm \(x = 2\).
Vì \(x = 2\) là một nghiệm của phương trình nên thay \(x = 2\) vào phương trình ta có:
\(\begin{array}{l}\,\,\,\,\,\,{2^2} + 4.2 + 3m - 2 = 0\\ \Leftrightarrow 3m + 10 = 0\\ \Leftrightarrow m = - \dfrac{{10}}{3}\end{array}\)
Vậy khi \(m = - \dfrac{{10}}{3}\) thì phương trình đã cho có một nghiệm \(x = 2\).
3. Tìm giá trị của \(m\) để phương trình đã cho có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) sao cho \({x_1} + 2{x_2} = 1\).
Ta có: \(\Delta ' = {\left( { - 2} \right)^2} - \left( {3m - 2} \right) = 4 - 3m + 2 = 6 - 3m\).
Để phương trình đã cho có 2 nghiệm phân biệt \({x_1},\,\,{x_2}\) thì \(\Delta ' > 0 \Leftrightarrow 6 - 3m > 0 \Leftrightarrow m < 2\).
Khi đó áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 4\\{x_1}{x_2} = 3m - 2\end{array} \right.\,\,\left( * \right)\).
Theo bài ra ta có: \({x_1} + 2{x_2} = 1 \Leftrightarrow {x_1} = 1 - 2{x_2}\).
Thế vào hệ (*) ta có:
\(\begin{array}{l}\,\,\,\,\,\,\left\{ \begin{array}{l}1 - 2{x_2} + {x_2} = - 4\\\left( {1 - 2{x_2}} \right).{x_2} = 3m - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_2} = 5\\\left( {1 - 2.5} \right).5 = 3m - 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x_2} = 5\\3m - 2 = - 45\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_2} = 5\\m = - \dfrac{{43}}{3}\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy \(m = - \dfrac{{43}}{3}\).
Câu 3 (2 điểm)
Cách giải:
Khoảng cách giữa hai bến sông A và B là 32 km. Một canô xuôi dòng từ bến A đến bến B rồi lập tức quay về bến A. Kể từ lúc khởi hành đến lúc về tới bến A hết tất cả 6 giờ. Tính vận tốc của canô khi nước yên lặng biết vận tốc của dòng nước là 4 km/h.
Gọi vận tốc của canô khi nước yên lặng là \(x\) (km/h) \(\left( {x > 4} \right)\)
Vận tốc canô khi xuôi dòng là \(x + 4\) (km/h)
Vận tốc canô khi ngược dòng là \(x - 4\) (km/h)
Thời gian canô xuôi dòng từ bến A đến bến B là \(\dfrac{{32}}{{x + 4}}\) giờ
Thời gian canô ngược dòng từ bến B về bến A là \(\dfrac{{32}}{{x - 4}}\) giờ
Vì từ lúc khởi hành đến lúc về tới bến A hết tất cả 6 giờ nên ta có phương trình:
\(\begin{array}{l}\dfrac{{32}}{{x + 4}} + \dfrac{{32}}{{x - 4}} = 6\\ \Leftrightarrow \dfrac{{32\left( {x - 4} \right) + 32\left( {x + 4} \right)}}{{\left( {x - 4} \right)\left( {x + 4} \right)}} = 6\\ \Leftrightarrow \dfrac{{32x - 128 + 32x + 128}}{{\left( {x - 4} \right)\left( {x + 4} \right)}} = 6\\ \Leftrightarrow \dfrac{{64x}}{{{x^2} - 16}} = 6\\ \Rightarrow 6{x^2} - 96 = 64x\\ \Leftrightarrow 6{x^2} - 64x - 96 = 0\\ \Leftrightarrow 3{x^2} - 32x - 48 = 0\\ \Leftrightarrow 3{x^2} - 36x + 4x - 48 = 0\\ \Leftrightarrow 3x\left( {x - 12} \right) + 4\left( {x - 12} \right) = 0\\ \Leftrightarrow \left( {3x + 4} \right)\left( {x - 12} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}3x + 4 = 0\\x - 12 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{4}{3}\,\,\left( {ktm} \right)\\x = 12\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy vận tốc của canô khi nước yên lặng là 12 km/h.
Câu 4 (3,5 điểm)
Cách giải:
Cho đường tròn \(\left( {O;R} \right)\) và \(A\) là một điểm nằm bên ngoài đường tròn. Từ điểm A kẻ hai tiếp tuyến \(AB\) và \(AC\) với đường tròn \(\left( O \right)\) ( B và C là hai tiếp điểm). Gọi \(H\) là giao điểm của \(AO\) và \(BC\). Kẻ đường kính \(BD\) của đường tròn \(\left( O \right)\), \(AD\) cắt đường tròn tại điểm thứ hai là \(E\).
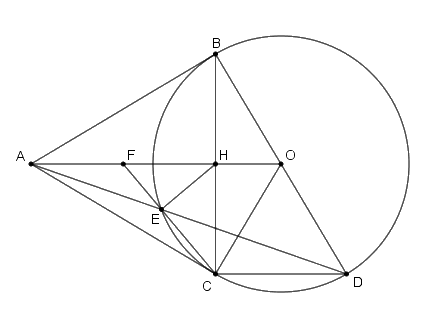
a. Chứng minh \(ABOC\) là tứ giác nội tiếp
Xét đường tròn \(\left( O \right)\) có \(AB\) và \(AC\) là các tiếp tuyến, \(B,C\) là các tiếp điểm tương ứng nên \(\angle ABO = {90^0};\angle ACO = {90^0}\)
Xét tứ giác \(ABOC\) có \(\angle ABO + \angle ACO = {90^0} + {90^0} = {180^0}\) mà hai góc \(\angle ABO;\angle ACO\) đối nhau nên tứ giác \(ABOC\) là tứ giác nội tiếp (dhnb)
b. Tính độ dài \(AH\) biết \(R = 3cm,AB = 4cm.\)
Xét đường tròn \(\left( O \right)\) có \(AB\) và \(AC\) là hai tiếp tuyến cắt nhau tại \(A.\)
Suy ra \(AB = AC\) (tính chất), mà \(OB = OC = R\) nên \(AO\) là đường trung trực của đoạn \(BC\)
Do đó \(OA \bot BC\) tại \(H.\)
Xét tam giác \(ABO\) vuông tại \(B\), theo định lý Pytago ta có: \(A{O^2} = A{B^2} + O{B^2} = {4^2} + {3^2} = 25\) \( \Rightarrow OA = 5cm\)
Xét tam giác \(ABO\) vuông tại \(B\) có \(BH\) là đường cao, theo hệ thức lượng trong tam giác vuông ta có: \(A{B^2} = AH.AO\)\( \Leftrightarrow AH = \dfrac{{A{B^2}}}{{AO}} = \dfrac{{{4^2}}}{5} = 3,2cm\)
Vậy \(AH = 3,2cm\).
c. Chứng minh \(AE.AD = AH.AO\)
Xét tam giác \(ABO\) vuông tại \(B\) có \(BH\) là đường cao, theo hệ thức lượng trong tam giác vuông ta có: \(A{B^2} = AH.AO\) (1)
Xét tam giác \(AEB\) và tam giác \(ABD\) có:
\(\angle BAE\) chung
\(\angle ABE = \angle BDE\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \(BE\) trong đường tròn \(\left( O \right)\))
Suy ra \(\Delta AEB \sim \Delta ABD\left( {g - g} \right)\)
\( \Rightarrow \dfrac{{AE}}{{AB}} = \dfrac{{AB}}{{AD}} \Rightarrow AE.AD = A{B^2}\) (2)
Từ (1) và (2) suy ra \(AE.AD = AH.AO\).
d. Tia \(CE\) cắt \(AH\) tại \(F\). Chứng tỏ \(F\) là trung điểm của \(AH.\)
Xét đường tròn \(\left( O \right)\) có \(\angle BCD = {90^0}\) (góc nội tiếp chắn nửa đường tròn), suy ra \(BC \bot CD\)
Lại có \(AO \bot BC\) nên \(CD//AO\)
Suy ra \(\angle ADC = \angle OAD\) (so le trong)
Xét \(\left( O \right)\) có \(\angle ACE = \angle EDC\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \(EC\))
Suy ra \(\angle ACE = \angle FAE\) \(\left( { = \angle CDE} \right)\)
Xét \(\Delta AFE\) và \(\Delta CFA\) có:
\(\angle AFE\) chung
\(\angle ACE = \angle FAE\) (cmt)
Suy ra \(\Delta AFE \sim \Delta CFA\left( {g - g} \right)\)
\(\begin{array}{l} \Rightarrow \dfrac{{AF}}{{CF}} = \dfrac{{FE}}{{FA}}\\ \Rightarrow F{A^2} = FC.FE\left( * \right)\end{array}\)
Theo câu b ta có \(AE.AD = AH.AO\)\( \Rightarrow \dfrac{{AE}}{{AH}} = \dfrac{{AO}}{{AD}}\)
Suy ra \(\Delta AEH \sim \Delta AOD\left( {c - g - c} \right)\) \( \Rightarrow \angle AHE = \angle ADO\)
Suy ra tứ giác \(EHOD\) là tứ giác nội tiếp (góc ngoài tại 1 đỉnh bằng góc trong tại đỉnh đối với đỉnh đó)
Suy ra \(\angle HED = \angle BOA\) (cùng phụ với \(\angle AOD\))
Xét đường tròn \(\left( O \right)\) có \(\angle CED = \angle CBD\) (2 góc nội tiếp cùng chắn cung \(CD\))
Lại có \(\angle BOH + \angle HBO = {90^0}\) (do \(\Delta BHO\) vuông tại \(H\))
Nên \(\angle EHD + \angle CED = {90^0} \Rightarrow \angle HEC = {90^0}\) hay \(EH \bot FC\)
Xét tam giác \(HFC\) vuông tại H có \(HE\) là đường cao, theo hệ thức lượng trong tam giác vuông ta có:
\(F{H^2} = FE.FC\) (**)
Từ (*) và (**) suy ra \(F{A^2} = F{H^2}\) \( \Leftrightarrow FA = FH \Rightarrow F\) là trung điểm \(AH\).
Câu 5 (0,5 điểm)
Cách giải:
Cho \(x,y\) là các số thực dương thỏa mãn \(x + y \le 3\). Tìm giá trị nhỏ nhất của biểu thức
\(Q = {x^2} + {y^2} - 9x - 12y + \dfrac{{16}}{{2x + y}} + 25\)
Ta có:
\(\begin{array}{l}Q = {x^2} + {y^2} - 9x - 12y + \dfrac{{16}}{{2x + y}} + 25\\ = \left( {{x^2} - 2x + 1} \right) + \left( {{y^2} - 4y + 4} \right) + \left( {2x + y} \right) + \dfrac{{16}}{{2x + y}} - 9\left( {x + y} \right) + 20\\ = {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + \left( {2x + y} \right) + \dfrac{{16}}{{2x + y}} - 9\left( {x + y} \right) + 20\end{array}\)
\(\begin{array}{l}{\left( {x - 1} \right)^2} \ge 0\\{\left( {y - 2} \right)^2} \ge 0\\2x + y + \dfrac{{16}}{{2x + y}} \ge 2\sqrt {\left( {2x + y} \right).\dfrac{{16}}{{2x + y}}} = 8\\ - 9\left( {x + y} \right) \ge - 9.3 = - 27\\ \Rightarrow Q \ge 0 + 0 + 8 - 27 + 20 = 1\\ \Rightarrow Q \ge 1\end{array}\)
Dấu “=” xảy ra khi \(x = 1,y = 2\).
Vậy \({Q_{\min }} = 1\) khi \(x = 1,y = 2\).
Câu 1 (2 điểm)
Cách giải:
1. Thực hiện phép tính \(2 + \sqrt 9 .\)
Ta có: \(2 + \sqrt 9 = 2 + 3 = 5.\)
2. Rút gọn biểu thức \(B = \left( {\dfrac{1}{{\sqrt x + 2}} - \dfrac{1}{{\sqrt x + 7}}} \right):\dfrac{5}{{\sqrt x + 7}}\) với \(x \ge 0.\)
Điều kiện: \(x \ge 0\)
\(\begin{array}{l}B = \left( {\dfrac{1}{{\sqrt x + 2}} - \dfrac{1}{{\sqrt x + 7}}} \right):\dfrac{5}{{\sqrt x + 7}}\\\,\,\,\, = \dfrac{{\sqrt x + 7 - \sqrt x - 2}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x + 7} \right)}}.\dfrac{{\sqrt x + 7}}{5}\\\,\,\,\, = \dfrac{5}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x + 7} \right)}}.\dfrac{{\sqrt x + 7}}{5}\\\,\,\, = \dfrac{1}{{\sqrt x + 2}}.\end{array}\)
Vậy \(B = \dfrac{1}{{\sqrt x + 2}}\) với \(x \ge 2.\)
3. Giải hệ phương trình \(\left\{ \begin{array}{l}x + 2y = 4\\x - 2y = 0\end{array} \right..\)
\(\left\{ \begin{array}{l}x + 2y = 4\\x - 2y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x = 4\\x = 2y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right..\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;\,\,y} \right) = \left( {2;\,\,1} \right).\)
Câu 2 (2,0 điểm)
Cách giải:
Cho phương trình \({x^2} + 4x + 3m - 2 = 0\), với \(m\) là tham số.
1. Giải phương trình với \(m = - 1\).
Thay \(m = - 1\) vào phương trình đã cho ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,{x^2} + 4x - 5 = 0\\ \Leftrightarrow {x^2} - x + 5x - 5 = 0\\ \Leftrightarrow x\left( {x - 1} \right) + 5\left( {x - 1} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x + 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x + 5 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 5\end{array} \right.\end{array}\)
Vậy khi \(m = - 1\) thì tập nghiệm của phương trình là \(S = \left\{ {1; - 5} \right\}\).
2. Tìm giá trị của \(m\) để phương trình đã cho có một nghiệm \(x = 2\).
Vì \(x = 2\) là một nghiệm của phương trình nên thay \(x = 2\) vào phương trình ta có:
\(\begin{array}{l}\,\,\,\,\,\,{2^2} + 4.2 + 3m - 2 = 0\\ \Leftrightarrow 3m + 10 = 0\\ \Leftrightarrow m = - \dfrac{{10}}{3}\end{array}\)
Vậy khi \(m = - \dfrac{{10}}{3}\) thì phương trình đã cho có một nghiệm \(x = 2\).
3. Tìm giá trị của \(m\) để phương trình đã cho có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) sao cho \({x_1} + 2{x_2} = 1\).
Ta có: \(\Delta ' = {\left( { - 2} \right)^2} - \left( {3m - 2} \right) = 4 - 3m + 2 = 6 - 3m\).
Để phương trình đã cho có 2 nghiệm phân biệt \({x_1},\,\,{x_2}\) thì \(\Delta ' > 0 \Leftrightarrow 6 - 3m > 0 \Leftrightarrow m < 2\).
Khi đó áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 4\\{x_1}{x_2} = 3m - 2\end{array} \right.\,\,\left( * \right)\).
Theo bài ra ta có: \({x_1} + 2{x_2} = 1 \Leftrightarrow {x_1} = 1 - 2{x_2}\).
Thế vào hệ (*) ta có:
\(\begin{array}{l}\,\,\,\,\,\,\left\{ \begin{array}{l}1 - 2{x_2} + {x_2} = - 4\\\left( {1 - 2{x_2}} \right).{x_2} = 3m - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_2} = 5\\\left( {1 - 2.5} \right).5 = 3m - 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x_2} = 5\\3m - 2 = - 45\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_2} = 5\\m = - \dfrac{{43}}{3}\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy \(m = - \dfrac{{43}}{3}\).
Câu 3 (2 điểm)
Cách giải:
Khoảng cách giữa hai bến sông A và B là 32 km. Một canô xuôi dòng từ bến A đến bến B rồi lập tức quay về bến A. Kể từ lúc khởi hành đến lúc về tới bến A hết tất cả 6 giờ. Tính vận tốc của canô khi nước yên lặng biết vận tốc của dòng nước là 4 km/h.
Gọi vận tốc của canô khi nước yên lặng là \(x\) (km/h) \(\left( {x > 4} \right)\)
Vận tốc canô khi xuôi dòng là \(x + 4\) (km/h)
Vận tốc canô khi ngược dòng là \(x - 4\) (km/h)
Thời gian canô xuôi dòng từ bến A đến bến B là \(\dfrac{{32}}{{x + 4}}\) giờ
Thời gian canô ngược dòng từ bến B về bến A là \(\dfrac{{32}}{{x - 4}}\) giờ
Vì từ lúc khởi hành đến lúc về tới bến A hết tất cả 6 giờ nên ta có phương trình:
\(\begin{array}{l}\dfrac{{32}}{{x + 4}} + \dfrac{{32}}{{x - 4}} = 6\\ \Leftrightarrow \dfrac{{32\left( {x - 4} \right) + 32\left( {x + 4} \right)}}{{\left( {x - 4} \right)\left( {x + 4} \right)}} = 6\\ \Leftrightarrow \dfrac{{32x - 128 + 32x + 128}}{{\left( {x - 4} \right)\left( {x + 4} \right)}} = 6\\ \Leftrightarrow \dfrac{{64x}}{{{x^2} - 16}} = 6\\ \Rightarrow 6{x^2} - 96 = 64x\\ \Leftrightarrow 6{x^2} - 64x - 96 = 0\\ \Leftrightarrow 3{x^2} - 32x - 48 = 0\\ \Leftrightarrow 3{x^2} - 36x + 4x - 48 = 0\\ \Leftrightarrow 3x\left( {x - 12} \right) + 4\left( {x - 12} \right) = 0\\ \Leftrightarrow \left( {3x + 4} \right)\left( {x - 12} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}3x + 4 = 0\\x - 12 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{4}{3}\,\,\left( {ktm} \right)\\x = 12\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy vận tốc của canô khi nước yên lặng là 12 km/h.
Câu 4 (3,5 điểm)
Cách giải:
Cho đường tròn \(\left( {O;R} \right)\) và \(A\) là một điểm nằm bên ngoài đường tròn. Từ điểm A kẻ hai tiếp tuyến \(AB\) và \(AC\) với đường tròn \(\left( O \right)\) ( B và C là hai tiếp điểm). Gọi \(H\) là giao điểm của \(AO\) và \(BC\). Kẻ đường kính \(BD\) của đường tròn \(\left( O \right)\), \(AD\) cắt đường tròn tại điểm thứ hai là \(E\).
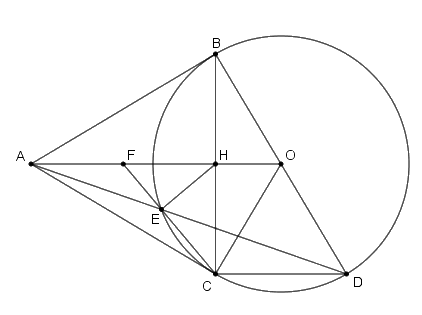
a. Chứng minh \(ABOC\) là tứ giác nội tiếp
Xét đường tròn \(\left( O \right)\) có \(AB\) và \(AC\) là các tiếp tuyến, \(B,C\) là các tiếp điểm tương ứng nên \(\angle ABO = {90^0};\angle ACO = {90^0}\)
Xét tứ giác \(ABOC\) có \(\angle ABO + \angle ACO = {90^0} + {90^0} = {180^0}\) mà hai góc \(\angle ABO;\angle ACO\) đối nhau nên tứ giác \(ABOC\) là tứ giác nội tiếp (dhnb)
b. Tính độ dài \(AH\) biết \(R = 3cm,AB = 4cm.\)
Xét đường tròn \(\left( O \right)\) có \(AB\) và \(AC\) là hai tiếp tuyến cắt nhau tại \(A.\)
Suy ra \(AB = AC\) (tính chất), mà \(OB = OC = R\) nên \(AO\) là đường trung trực của đoạn \(BC\)
Do đó \(OA \bot BC\) tại \(H.\)
Xét tam giác \(ABO\) vuông tại \(B\), theo định lý Pytago ta có: \(A{O^2} = A{B^2} + O{B^2} = {4^2} + {3^2} = 25\) \( \Rightarrow OA = 5cm\)
Xét tam giác \(ABO\) vuông tại \(B\) có \(BH\) là đường cao, theo hệ thức lượng trong tam giác vuông ta có: \(A{B^2} = AH.AO\)\( \Leftrightarrow AH = \dfrac{{A{B^2}}}{{AO}} = \dfrac{{{4^2}}}{5} = 3,2cm\)
Vậy \(AH = 3,2cm\).
c. Chứng minh \(AE.AD = AH.AO\)
Xét tam giác \(ABO\) vuông tại \(B\) có \(BH\) là đường cao, theo hệ thức lượng trong tam giác vuông ta có: \(A{B^2} = AH.AO\) (1)
Xét tam giác \(AEB\) và tam giác \(ABD\) có:
\(\angle BAE\) chung
\(\angle ABE = \angle BDE\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \(BE\) trong đường tròn \(\left( O \right)\))
Suy ra \(\Delta AEB \sim \Delta ABD\left( {g - g} \right)\)
\( \Rightarrow \dfrac{{AE}}{{AB}} = \dfrac{{AB}}{{AD}} \Rightarrow AE.AD = A{B^2}\) (2)
Từ (1) và (2) suy ra \(AE.AD = AH.AO\).
d. Tia \(CE\) cắt \(AH\) tại \(F\). Chứng tỏ \(F\) là trung điểm của \(AH.\)
Xét đường tròn \(\left( O \right)\) có \(\angle BCD = {90^0}\) (góc nội tiếp chắn nửa đường tròn), suy ra \(BC \bot CD\)
Lại có \(AO \bot BC\) nên \(CD//AO\)
Suy ra \(\angle ADC = \angle OAD\) (so le trong)
Xét \(\left( O \right)\) có \(\angle ACE = \angle EDC\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \(EC\))
Suy ra \(\angle ACE = \angle FAE\) \(\left( { = \angle CDE} \right)\)
Xét \(\Delta AFE\) và \(\Delta CFA\) có:
\(\angle AFE\) chung
\(\angle ACE = \angle FAE\) (cmt)
Suy ra \(\Delta AFE \sim \Delta CFA\left( {g - g} \right)\)
\(\begin{array}{l} \Rightarrow \dfrac{{AF}}{{CF}} = \dfrac{{FE}}{{FA}}\\ \Rightarrow F{A^2} = FC.FE\left( * \right)\end{array}\)
Theo câu b ta có \(AE.AD = AH.AO\)\( \Rightarrow \dfrac{{AE}}{{AH}} = \dfrac{{AO}}{{AD}}\)
Suy ra \(\Delta AEH \sim \Delta AOD\left( {c - g - c} \right)\) \( \Rightarrow \angle AHE = \angle ADO\)
Suy ra tứ giác \(EHOD\) là tứ giác nội tiếp (góc ngoài tại 1 đỉnh bằng góc trong tại đỉnh đối với đỉnh đó)
Suy ra \(\angle HED = \angle BOA\) (cùng phụ với \(\angle AOD\))
Xét đường tròn \(\left( O \right)\) có \(\angle CED = \angle CBD\) (2 góc nội tiếp cùng chắn cung \(CD\))
Lại có \(\angle BOH + \angle HBO = {90^0}\) (do \(\Delta BHO\) vuông tại \(H\))
Nên \(\angle EHD + \angle CED = {90^0} \Rightarrow \angle HEC = {90^0}\) hay \(EH \bot FC\)
Xét tam giác \(HFC\) vuông tại H có \(HE\) là đường cao, theo hệ thức lượng trong tam giác vuông ta có:
\(F{H^2} = FE.FC\) (**)
Từ (*) và (**) suy ra \(F{A^2} = F{H^2}\) \( \Leftrightarrow FA = FH \Rightarrow F\) là trung điểm \(AH\).
Câu 5 (0,5 điểm)
Cách giải:
Cho \(x,y\) là các số thực dương thỏa mãn \(x + y \le 3\). Tìm giá trị nhỏ nhất của biểu thức
\(Q = {x^2} + {y^2} - 9x - 12y + \dfrac{{16}}{{2x + y}} + 25\)
Ta có:
\(\begin{array}{l}Q = {x^2} + {y^2} - 9x - 12y + \dfrac{{16}}{{2x + y}} + 25\\ = \left( {{x^2} - 2x + 1} \right) + \left( {{y^2} - 4y + 4} \right) + \left( {2x + y} \right) + \dfrac{{16}}{{2x + y}} - 9\left( {x + y} \right) + 20\\ = {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + \left( {2x + y} \right) + \dfrac{{16}}{{2x + y}} - 9\left( {x + y} \right) + 20\end{array}\)
\(\begin{array}{l}{\left( {x - 1} \right)^2} \ge 0\\{\left( {y - 2} \right)^2} \ge 0\\2x + y + \dfrac{{16}}{{2x + y}} \ge 2\sqrt {\left( {2x + y} \right).\dfrac{{16}}{{2x + y}}} = 8\\ - 9\left( {x + y} \right) \ge - 9.3 = - 27\\ \Rightarrow Q \ge 0 + 0 + 8 - 27 + 20 = 1\\ \Rightarrow Q \ge 1\end{array}\)
Dấu “=” xảy ra khi \(x = 1,y = 2\).
Vậy \({Q_{\min }} = 1\) khi \(x = 1,y = 2\).
Kỳ thi tuyển sinh vào lớp 10 tại tỉnh Quảng Ninh luôn là một kỳ thi quan trọng, đánh dấu bước chuyển mình của học sinh từ bậc trung học cơ sở lên trung học phổ thông. Môn Toán, với vai trò then chốt, đòi hỏi học sinh phải có sự chuẩn bị kỹ lưỡng về kiến thức và kỹ năng. Đề thi vào 10 môn Toán Quảng Ninh năm 2020 không nằm ngoài xu hướng này, với cấu trúc đề thi và nội dung kiến thức được đánh giá là có độ khó vừa phải, tập trung vào các chủ đề trọng tâm của chương trình Toán lớp 9.
Đề thi vào 10 môn Toán Quảng Ninh năm 2020 thường bao gồm các dạng bài tập sau:
Để giúp học sinh có sự chuẩn bị tốt nhất, chúng tôi sẽ phân tích chi tiết từng đề thi vào 10 môn Toán Quảng Ninh năm 2020, bao gồm:
Giaitoan.edu.vn cung cấp một loạt các công cụ và tài liệu hỗ trợ học sinh luyện thi vào 10 môn Toán Quảng Ninh năm 2020 hiệu quả:
Để đạt kết quả tốt nhất trong kỳ thi vào 10 môn Toán Quảng Ninh năm 2020, học sinh cần lưu ý những điều sau:
Ngoài các đề thi và tài liệu luyện thi do giaitoan.edu.vn cung cấp, học sinh có thể tham khảo thêm các tài liệu sau:
Đề thi vào 10 môn Toán Quảng Ninh năm 2020 là một kỳ thi quan trọng, đòi hỏi học sinh phải có sự chuẩn bị kỹ lưỡng. Hy vọng với những thông tin và tài liệu mà giaitoan.edu.vn cung cấp, các em học sinh sẽ có một kỳ thi thành công và đạt được kết quả tốt nhất.