Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Long An năm 2023. Đây là tài liệu ôn tập vô cùng quan trọng dành cho các em học sinh đang chuẩn bị cho kỳ thi sắp tới.
Chúng tôi đã tổng hợp đầy đủ các đề thi chính thức, đáp án chi tiết và hướng dẫn giải bài tập để giúp các em nắm vững kiến thức và tự tin làm bài.
Câu 1: a. Tính giá trị biểu thức \(A = \sqrt {50} {\rm{ \;}} + \sqrt {32} {\rm{ \;}} - 3\sqrt {18} \). b. Rút gọn biểu thức \(B = \left( {\frac{{x + 2\sqrt x }}{{\sqrt x }} + \sqrt x {\rm{ \;}} - 2} \right):\sqrt x \) với \(x > 0\).
Câu 1:
a. Tính giá trị biểu thức \(A = \sqrt {50} {\rm{ \;}} + \sqrt {32} {\rm{ \;}} - 3\sqrt {18} \).
b. Rút gọn biểu thức \(B = \left( {\frac{{x + 2\sqrt x }}{{\sqrt x }} + \sqrt x {\rm{ \;}} - 2} \right):\sqrt x \) với \(x > 0\).
c. Giải phương trình \(\sqrt {{x^2} - 2x + 1} {\rm{ \;}} = 3\).
Câu 2:
a. Giải phương trình \(3{x^2} - 7x + 4 = 0\).
b. Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{3x + y = 9}\\{2x - y = 1}\end{array}} \right.\).
c. Cho phương trình \({x^2} - 2x + m + 3 = 0\) ( \(x\) là ẩn số, \(m\) là tham số). Với giá trị nào của \(m\) thì phương trình có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \(x_1^2 \cdot {x_2} + {x_1} \cdot x_2^2 = {\rm{ \;}} - 4\).
Câu 3: Trong mặt phẳng toạ độ Oxy cho parabol \((P):y = 2{x^2}\) và đường thả̉ng \((d):y = {\rm{ \;}} - 2x + 4\).
a. Vẽ parabol \((P)\) và đường thẳng \((d)\) trên cùng mặt phẳng tọa độ.
b. Tìm tọa độ giao điểm của \((P)\) và \((d)\) bằng phép tính.
Câu 4:
a. Cho tam giác ABC vuông tại A, đường cao AH. Biết AH = 3cm, HC = 4cm. Tính độ dài đoạn thẳng HB, AC và số đo góc C (kết quả làm tròn đến độ).
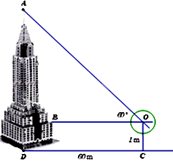
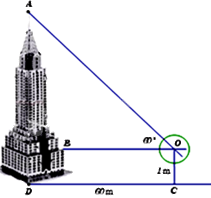
b. Để xác định chiều cao của một tòa tháp cao tầng (hình vẽ bên), một người đứng tại điểm C cách chân tháp một khoảng CD = 60m, sử dụng giác kế nhìn thấy đỉnh tòa tháp với góc AOB = 60. Hãy tính chiều cao của tòa tháp. Biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế là OC = 1m, (kết quả làm tròn đến hàng đơn vị).
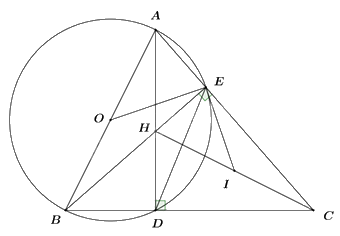
Câu 5: Cho tam giác ABC có ba góc nhọn. Hai đường cao của tam giác ABC và AD, BE cắt nhau tại H.
a) Chứng minh tứ giác CDHE nội tiếp đường tròn.
b) Chứng minh HA.HD = HB.HE.
c) Gọi điểm I là tâm đường tròn ngoại tiếp tứ giác CDHE. Chứng minh IE là tiếp tuyến của đường tròn đường kính AB.
Câu 6: Cho các số thực x, y thoả mãn \(x + y + 2 = 0\). Tìm giá trị lớn nhất của biểu thức
\(A = 3\left( {{x^2} + {y^2}} \right) + 10xy\)
----- HẾT -----
Câu 1 (VD):
Phương pháp:
a) Sử dụng tính chất căn bậc hai.
b) Quy đồng và rút gọn.
c) Sử dụng tính chất căn bậc hai.
Cách giải:
a. Tính giá trị biểu thức \(A = \sqrt {50} + \sqrt {32} - 3\sqrt {18} \).
Ta có \(A = \sqrt {50} + \sqrt {32} - 3\sqrt {18} \)
\(\begin{array}{l} = \sqrt {25.2} + \sqrt {16.2} - 3\sqrt {9.2} \\ = 5\sqrt 2 + 4\sqrt 2 - 9\sqrt 2 \\ = 0\end{array}\)
Vậy A = 0
b. Rút gọn biểu thức \(B = \left( {\frac{{x + 2\sqrt x }}{{\sqrt x }} + \sqrt x - 2} \right):\sqrt x \) với \(x > 0\).
Ta có \(B = \left( {\frac{{x + 2\sqrt x }}{{\sqrt x }} + \sqrt x - 2} \right):\sqrt x \)
\(\begin{array}{l} = \left( {\frac{{\sqrt x \left( {\sqrt x + 2} \right)}}{{\sqrt x }} + \sqrt x - 2} \right):\sqrt x \\ = \left( {\sqrt x + 2 + \sqrt x - 2} \right).\frac{1}{{\sqrt x }}\\ = 2\sqrt x .\frac{1}{{\sqrt x }} = 2\end{array}\)
Vậy B = 2 với \(x > 0\)
c. Giải phương trình \(\sqrt {{x^2} - 2x + 1} = 3\).
ĐKXĐ: Với mọi giá trị của x
Phương trình \(\sqrt {{x^2} - 2x + 1} = 3\)
\(\begin{array}{l} \Leftrightarrow \sqrt {{{\left( {x - 1} \right)}^2}} = 3\\ \Leftrightarrow \left| {x - 1} \right| = 3\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 3\\x - 1 = - 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = - 2\end{array} \right.\left( {TM} \right)\end{array}\)
Vậy tập nghiệm của phương trình là \(S = \left\{ { - 2,4} \right\}\)
Câu 2 (VD):
Phương pháp:
a) \(\Delta = {b^2} - 4.a.c\)
- \(\Delta = 0\) thì phương trình có nghiệm kép \({x_1} = {x_2} = \frac{{ - b}}{{2a}}\)
- \(\Delta < 0\) thì phương trình vô nghiệm
- \(\Delta > 0\)thì phương trình có hai nghiệm phân biệt:
\({x_1} = \frac{{ - b + \sqrt \Delta }}{{2.a}}\)
\({x_2} = \frac{{ - b - \sqrt \Delta }}{{2.a}}\)
b) Sử dụng phương pháp thế hoặc trừ vế.
c) Sử dụng định lí Vi-ét.
Cách giải:
a. Giải phương trình \(3{x^2} - 7x + 4 = 0\).
Xét Phương trình \(3{x^2} - 7x + 4 = 0\) có \(a + b + c = 3 - 7 + 4 = 0\)nên phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = 1\\{x_2} = 4\end{array} \right.\).
Vậy phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = 1\\{x_2} = 4\end{array} \right.\).
b. Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{3x + y = 9}\\{2x - y = 1}\end{array}} \right.\).
Cộng vế với vế, ta có
\(\left\{ {\begin{array}{*{20}{l}}{3x + y = 9}\\{2x - y = 1}\end{array}} \right. \Leftrightarrow \left\{ \begin{array}{l}5x = 10\\y = 2x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 2.2 - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3\end{array} \right.\).
Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {2;3} \right)\).
c. Cho phương trình \({x^2} - 2x + m + 3 = 0\) ( \(x\) là ẩn số, \(m\) là tham số). Với giá trị nào của \(m\) thì phương trình có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \(x_1^2 \cdot {x_2} + {x_1} \cdot x_2^2 = - 4\).
Xét phương trình \({x^2} - 2x + m + 3 = 0\) có \(\Delta ' = {\left( { - 1} \right)^2} - 1.\left( {m + 3} \right) = 1 - m - 3 = - m - 2\)
Để phương trình có hai nghiệm phân biệt thì \(\Delta ' > 0 \Leftrightarrow - m - 2 > 0 \Leftrightarrow m < - 2\).
Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình, áp dụng định lí Vi – ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a} = 2\\{x_1}.{x_2} = \frac{c}{a} = m + 3\end{array} \right.\) (1)
Khi đó để \(x_1^2 \cdot {x_2} + {x_1} \cdot x_2^2 = - 4 \Leftrightarrow {x_1}.{x_2}\left( {{x_1} + {x_2}} \right) = - 4\) (2)
Thay (1) vào (2) ta có:
\(\begin{array}{l}\left( 2 \right) \Leftrightarrow \left( {m + 3} \right)2 = - 4\\ \Leftrightarrow m + 3 = - 2\\ \Leftrightarrow m = - 5\left( {tm} \right).\end{array}\)
Vậy với \(m = - 5\) thì phương trình có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \(x_1^2 \cdot {x_2} + {x_1} \cdot x_2^2 = - 4\).
Câu 3 (VD):
Phương pháp:
a) Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị (thường từ 5 đến 7 giá trị) tương ứng giữa \(x\) và \(y\).
Bước 3: Vẽ đồ thị và kết luận.
b) Cho hai vế của đồ thị bằng nhau rồi giải phương trình tìm giao điểm.
Cách giải:
Trong mặt phẳng toạ độ Oxy cho parabol \((P):y = 2{x^2}\) và đường thả̉ng \((d):y = - 2x + 4\).
a. Vẽ parabol \((P)\) và đường thẳng \((d)\) trên cùng mặt phẳng tọa độ.
* Vẽ đường thẳng \((d)\)
Với \(x = 0 \Rightarrow y = - 2.0 + 4 = 4\)
Với \(y = 0 \Rightarrow 0 = - 2x + 4 \Leftrightarrow 2x = 4 \Leftrightarrow x = 2\)
\( \Rightarrow \) Đồ thị \((d):y = - 2x + 4\)là đường thẳng đi qua 2 điểm \(M\left( {2;0} \right)\) và \(N\left( {0;4} \right)\)
* Vẽ parabol \((P)\)
Ta có bảng giá trị sau:

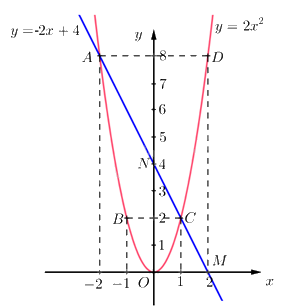
\( \Rightarrow \) Đồ thị hàm số là đường cong parabol đi qua các điểm \(O\,\left( {0;0} \right);A\left( { - 2;8} \right);\,\,B\left( { - 1;2} \right);C\left( {1;2} \right);\,\,D\left( {2;8} \right)\)
Hệ số \(a = 2 > 0\) nên parabol có bề cong hướng lên. Đồ thị hàm số nhận Oy làm trục đối xứng.
Ta vẽ được đồ thị hàm số \(y = 2{x^2}\) như sau:
b. Tìm tọa độ giao điểm của \((P)\) và \((d)\) bằng phép tính.
Xét phương trình hoành độ giao điểm của \((P)\) và \((d)\) ta được:
\(\begin{array}{l}2{x^2} = - 2x + 4\\ \Leftrightarrow {x^2} = - x + 2\\ \Leftrightarrow {x^2} + x - 2 = 0\\ \Leftrightarrow {x^2} + 2x - x - 2 = 0\\ \Leftrightarrow x\left( {x + 2} \right) - \left( {x + 2} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 2\end{array} \right.\end{array}\)
Với \(x = 1 \Rightarrow y = {2.1^2} = 2\)
Với \(x = - 2 \Rightarrow y = 2.{\left( { - 2} \right)^2} = 8\)
Vậy \((P)\) và \((d)\)cắt nhau tại 2 giao điểm là: \(A\left( { - 2;8} \right)\)và \(C\left( {1;2} \right)\).
Câu 4 (VD):
Phương pháp:
Sử dụng hệ thức lượng trong tam giác vuông.
Cách giải:
a. Cho tam giác ABC vuông tại A, đường cao AH. Biết AH = 3cm, HC = 4cm. Tính độ dài đoạn thẳng HB, AC và số đo góc C (kết quả làm tròn đến độ).
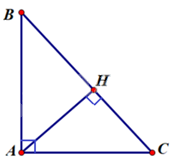
Do tam giác ABC vuông tại A, đường cao AH nên áp dụng hệ thức lượng trong tam giác vuông có:
\(A{H^2} = HB.HC \Rightarrow HB = \frac{{A{H^2}}}{{HC}} = \frac{{{3^2}}}{4} = \frac{9}{4}\) cm
Suy ra \(BC = HB + HC = \frac{9}{4} + 4 = \frac{{25}}{4}\) cm
\( \Rightarrow A{C^2} = HC.BC = 4.\frac{{25}}{4} = 25 \Rightarrow AC = 5\)cm
\( \Rightarrow \sin C = \frac{{AH}}{{AC}} = \frac{3}{5} \Rightarrow \angle C \approx 36,{87^0}\)
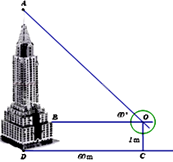
b. Để xác định chiều cao của một tòa tháp cao tầng (hình vẽ bên), một người đứng tại điểm C cách chân tháp một khoảng CD = 60m, sử dụng giác kế nhìn thấy đỉnh tòa tháp với góc AOB = 60. Hãy tính chiều cao của tòa tháp. Biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế là OC = 1m, (kết quả làm tròn đến hàng đơn vị).
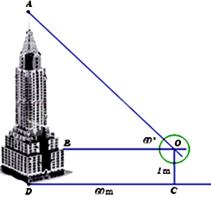
Do tam giác ABO vuông tại B, góc AOB = \({60^0}\) nên
\(AB = OB.\tan \angle O = CD.\tan {60^0} = 60.\tan {60^0} = 60\sqrt 3 \) m
Lại có BD = CO = 1m
\( \Rightarrow AD = AB + BD = 60\sqrt 3 + 1 \approx 105\) m
Vậy tòa nhà cao khoảng 105 m
Câu 5 (VD):
Cách giải:
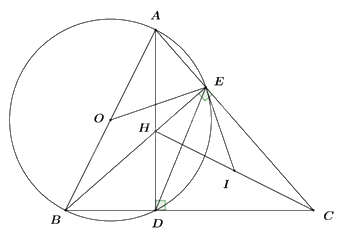
Cho tam giác ABC có ba góc nhọn. Hai đường cao của tam giác ABC và AD, BE cắt nhau tại H.
a) Chứng minh tứ giác CDHE nội tiếp đường tròn.
Ta có:
\(\begin{array}{l}\angle HDC = {90^0}\,\,\left( {do\,\,AD \bot BC} \right)\\\angle HEC = {90^0}\,\,\left( {do\,\,BE \bot AC} \right)\\ \Rightarrow \angle HDC + \angle HEC = {90^0} + {90^0} = {180^0}\end{array}\)
Mà 2 góc này ở vị trí đối nhau của tứ giác CDHE.
=> CDHE là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng \({180^0}\)). (đpcm)
b) Chứng minh HA.HD = HB.HE.
Xét \(\Delta AHE\) và \(\Delta BHD\) có:
\(\angle AEH = \angle BDH = {90^0}\,\,\left( {do\,\,BE \bot AC,\,\,AD \bot BC} \right)\)
\(\angle AHE = \angle BHD\) (đối đỉnh)
$\Rightarrow \Delta AHE\backsim \Delta BHD\,\,\left( g.g \right)$
\( \Rightarrow \frac{{HA}}{{HB}} = \frac{{HE}}{{HD}}\) (cặp cạnh tương ứng tỉ lệ) \( \Rightarrow HA.HD = HB.HE\,\,\left( {dpcm} \right)\).
c) Gọi điểm I là tâm đường tròn ngoại tiếp tứ giác CDHE. Chứng minh IE là tiếp tuyến của đường tròn đường kính AB.
Xét tứ giác nội tiếp CDHE có: \(\angle HEC = {90^0}\,\,\left( {gt} \right)\) nên \(\angle HEC\) là góc nội tiếp chắn nửa đường tròn.
\( \Rightarrow HC\) là đường kính của đường tròn ngoại tiếp tứ giác CDHE.
\( \Rightarrow I\) là trung điểm của HC.
Gọi O là trung điểm của AB => O là tâm đường tròn đường kính AB.
Ta cần chứng minh \(OE \bot IE\) tại E.
Vì tam giác AEB vuông tại E có EO là trung tuyến ứng với cạnh huyền AB nên \(OE = \frac{1}{2}AB = OA = OB \Rightarrow E \in \left( O \right)\).
Vì tam giác ADB vuông tại D có DO là trung tuyến ứng với cạnh huyền AB nên \(OD = \frac{1}{2}AB = OA = OB \Rightarrow D \in \left( O \right)\)
Vì CDHE là tứ giác nội tiếp (cmt) nên \(\angle ECH = \angle EDH \Rightarrow \angle ECI = \angle EDA\) (hai góc nội tiếp cùng chắn cung HE).
Mà \(\angle EDA = \angle EBA = \angle EBO\) (hai góc nội tiếp cùng chắn cung EA của (O)).
\( \Rightarrow \angle ECI = \angle EBO\). (1)
Vì tứ giác CDHE nội tiếp đường tròn tâm I đường kính HC nên IE = IC
\( \Rightarrow \Delta IEC\) cân tại I (định nghĩa)
\( \Rightarrow \angle ECI = \angle CEI\) (tính chất tam giác cân). (2)
Vì E thuộc (O) nên OB = OE
\( \Rightarrow \Delta OBE\) cân tại O (định nghĩa)
\( \Rightarrow \angle EBO = \angle BEO\) (tính chất tam giác cân). (3)
Từ (1), (2), (3)
\(\begin{array}{l} \Rightarrow \angle CEI = \angle BEO\\ \Rightarrow \angle CEI + \angle IEH = \angle BEO + \angle IEH\\ \Rightarrow \angle CEH = \angle IEO\\ \Rightarrow {90^0} = \angle IEO\end{array}\)
Vậy \(OE \bot IE\) tại E hay IE là tiếp tuyến của đường tròn (O) đường kính AB (đpcm).
Câu 6 (VD):
Cách giải:
Theo bài ra ta có: \(x + y + 2 = 0 \Leftrightarrow x + y = - 2\).
Ta có:
\(\begin{array}{l}A = 3\left( {{x^2} + {y^2}} \right) + 10xy\\A = 3\left( {{x^2} + {y^2} + 2xy} \right) + 4xy\\A = 3{\left( {x + y} \right)^2} + 4xy\\A = 3.{\left( { - 2} \right)^2} + 4xy\\A = 12 + 4xy\end{array}\)
Ta có: \(xy \le {\left( {\frac{{x + y}}{2}} \right)^2} = {\left( {\frac{{ - 2}}{2}} \right)^2} = 1\).
\( \Rightarrow A \le 12 + 4 = 16\).
Vậy \({A_{\max }} = 16 \Leftrightarrow \left\{ \begin{array}{l}x = y\\x + y + 2 = 0\end{array} \right. \Leftrightarrow x = y = - 1\).
Câu 1:
a. Tính giá trị biểu thức \(A = \sqrt {50} {\rm{ \;}} + \sqrt {32} {\rm{ \;}} - 3\sqrt {18} \).
b. Rút gọn biểu thức \(B = \left( {\frac{{x + 2\sqrt x }}{{\sqrt x }} + \sqrt x {\rm{ \;}} - 2} \right):\sqrt x \) với \(x > 0\).
c. Giải phương trình \(\sqrt {{x^2} - 2x + 1} {\rm{ \;}} = 3\).
Câu 2:
a. Giải phương trình \(3{x^2} - 7x + 4 = 0\).
b. Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{3x + y = 9}\\{2x - y = 1}\end{array}} \right.\).
c. Cho phương trình \({x^2} - 2x + m + 3 = 0\) ( \(x\) là ẩn số, \(m\) là tham số). Với giá trị nào của \(m\) thì phương trình có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \(x_1^2 \cdot {x_2} + {x_1} \cdot x_2^2 = {\rm{ \;}} - 4\).
Câu 3: Trong mặt phẳng toạ độ Oxy cho parabol \((P):y = 2{x^2}\) và đường thả̉ng \((d):y = {\rm{ \;}} - 2x + 4\).
a. Vẽ parabol \((P)\) và đường thẳng \((d)\) trên cùng mặt phẳng tọa độ.
b. Tìm tọa độ giao điểm của \((P)\) và \((d)\) bằng phép tính.
Câu 4:
a. Cho tam giác ABC vuông tại A, đường cao AH. Biết AH = 3cm, HC = 4cm. Tính độ dài đoạn thẳng HB, AC và số đo góc C (kết quả làm tròn đến độ).
b. Để xác định chiều cao của một tòa tháp cao tầng (hình vẽ bên), một người đứng tại điểm C cách chân tháp một khoảng CD = 60m, sử dụng giác kế nhìn thấy đỉnh tòa tháp với góc AOB = 60. Hãy tính chiều cao của tòa tháp. Biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế là OC = 1m, (kết quả làm tròn đến hàng đơn vị).
Câu 5: Cho tam giác ABC có ba góc nhọn. Hai đường cao của tam giác ABC và AD, BE cắt nhau tại H.
a) Chứng minh tứ giác CDHE nội tiếp đường tròn.
b) Chứng minh HA.HD = HB.HE.
c) Gọi điểm I là tâm đường tròn ngoại tiếp tứ giác CDHE. Chứng minh IE là tiếp tuyến của đường tròn đường kính AB.
Câu 6: Cho các số thực x, y thoả mãn \(x + y + 2 = 0\). Tìm giá trị lớn nhất của biểu thức
\(A = 3\left( {{x^2} + {y^2}} \right) + 10xy\)
----- HẾT -----
Câu 1 (VD):
Phương pháp:
a) Sử dụng tính chất căn bậc hai.
b) Quy đồng và rút gọn.
c) Sử dụng tính chất căn bậc hai.
Cách giải:
a. Tính giá trị biểu thức \(A = \sqrt {50} + \sqrt {32} - 3\sqrt {18} \).
Ta có \(A = \sqrt {50} + \sqrt {32} - 3\sqrt {18} \)
\(\begin{array}{l} = \sqrt {25.2} + \sqrt {16.2} - 3\sqrt {9.2} \\ = 5\sqrt 2 + 4\sqrt 2 - 9\sqrt 2 \\ = 0\end{array}\)
Vậy A = 0
b. Rút gọn biểu thức \(B = \left( {\frac{{x + 2\sqrt x }}{{\sqrt x }} + \sqrt x - 2} \right):\sqrt x \) với \(x > 0\).
Ta có \(B = \left( {\frac{{x + 2\sqrt x }}{{\sqrt x }} + \sqrt x - 2} \right):\sqrt x \)
\(\begin{array}{l} = \left( {\frac{{\sqrt x \left( {\sqrt x + 2} \right)}}{{\sqrt x }} + \sqrt x - 2} \right):\sqrt x \\ = \left( {\sqrt x + 2 + \sqrt x - 2} \right).\frac{1}{{\sqrt x }}\\ = 2\sqrt x .\frac{1}{{\sqrt x }} = 2\end{array}\)
Vậy B = 2 với \(x > 0\)
c. Giải phương trình \(\sqrt {{x^2} - 2x + 1} = 3\).
ĐKXĐ: Với mọi giá trị của x
Phương trình \(\sqrt {{x^2} - 2x + 1} = 3\)
\(\begin{array}{l} \Leftrightarrow \sqrt {{{\left( {x - 1} \right)}^2}} = 3\\ \Leftrightarrow \left| {x - 1} \right| = 3\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 3\\x - 1 = - 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = - 2\end{array} \right.\left( {TM} \right)\end{array}\)
Vậy tập nghiệm của phương trình là \(S = \left\{ { - 2,4} \right\}\)
Câu 2 (VD):
Phương pháp:
a) \(\Delta = {b^2} - 4.a.c\)
- \(\Delta = 0\) thì phương trình có nghiệm kép \({x_1} = {x_2} = \frac{{ - b}}{{2a}}\)
- \(\Delta < 0\) thì phương trình vô nghiệm
- \(\Delta > 0\)thì phương trình có hai nghiệm phân biệt:
\({x_1} = \frac{{ - b + \sqrt \Delta }}{{2.a}}\)
\({x_2} = \frac{{ - b - \sqrt \Delta }}{{2.a}}\)
b) Sử dụng phương pháp thế hoặc trừ vế.
c) Sử dụng định lí Vi-ét.
Cách giải:
a. Giải phương trình \(3{x^2} - 7x + 4 = 0\).
Xét Phương trình \(3{x^2} - 7x + 4 = 0\) có \(a + b + c = 3 - 7 + 4 = 0\)nên phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = 1\\{x_2} = 4\end{array} \right.\).
Vậy phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = 1\\{x_2} = 4\end{array} \right.\).
b. Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{3x + y = 9}\\{2x - y = 1}\end{array}} \right.\).
Cộng vế với vế, ta có
\(\left\{ {\begin{array}{*{20}{l}}{3x + y = 9}\\{2x - y = 1}\end{array}} \right. \Leftrightarrow \left\{ \begin{array}{l}5x = 10\\y = 2x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 2.2 - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3\end{array} \right.\).
Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {2;3} \right)\).
c. Cho phương trình \({x^2} - 2x + m + 3 = 0\) ( \(x\) là ẩn số, \(m\) là tham số). Với giá trị nào của \(m\) thì phương trình có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \(x_1^2 \cdot {x_2} + {x_1} \cdot x_2^2 = - 4\).
Xét phương trình \({x^2} - 2x + m + 3 = 0\) có \(\Delta ' = {\left( { - 1} \right)^2} - 1.\left( {m + 3} \right) = 1 - m - 3 = - m - 2\)
Để phương trình có hai nghiệm phân biệt thì \(\Delta ' > 0 \Leftrightarrow - m - 2 > 0 \Leftrightarrow m < - 2\).
Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình, áp dụng định lí Vi – ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a} = 2\\{x_1}.{x_2} = \frac{c}{a} = m + 3\end{array} \right.\) (1)
Khi đó để \(x_1^2 \cdot {x_2} + {x_1} \cdot x_2^2 = - 4 \Leftrightarrow {x_1}.{x_2}\left( {{x_1} + {x_2}} \right) = - 4\) (2)
Thay (1) vào (2) ta có:
\(\begin{array}{l}\left( 2 \right) \Leftrightarrow \left( {m + 3} \right)2 = - 4\\ \Leftrightarrow m + 3 = - 2\\ \Leftrightarrow m = - 5\left( {tm} \right).\end{array}\)
Vậy với \(m = - 5\) thì phương trình có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \(x_1^2 \cdot {x_2} + {x_1} \cdot x_2^2 = - 4\).
Câu 3 (VD):
Phương pháp:
a) Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị (thường từ 5 đến 7 giá trị) tương ứng giữa \(x\) và \(y\).
Bước 3: Vẽ đồ thị và kết luận.
b) Cho hai vế của đồ thị bằng nhau rồi giải phương trình tìm giao điểm.
Cách giải:
Trong mặt phẳng toạ độ Oxy cho parabol \((P):y = 2{x^2}\) và đường thả̉ng \((d):y = - 2x + 4\).
a. Vẽ parabol \((P)\) và đường thẳng \((d)\) trên cùng mặt phẳng tọa độ.
* Vẽ đường thẳng \((d)\)
Với \(x = 0 \Rightarrow y = - 2.0 + 4 = 4\)
Với \(y = 0 \Rightarrow 0 = - 2x + 4 \Leftrightarrow 2x = 4 \Leftrightarrow x = 2\)
\( \Rightarrow \) Đồ thị \((d):y = - 2x + 4\)là đường thẳng đi qua 2 điểm \(M\left( {2;0} \right)\) và \(N\left( {0;4} \right)\)
* Vẽ parabol \((P)\)
Ta có bảng giá trị sau:

\( \Rightarrow \) Đồ thị hàm số là đường cong parabol đi qua các điểm \(O\,\left( {0;0} \right);A\left( { - 2;8} \right);\,\,B\left( { - 1;2} \right);C\left( {1;2} \right);\,\,D\left( {2;8} \right)\)
Hệ số \(a = 2 > 0\) nên parabol có bề cong hướng lên. Đồ thị hàm số nhận Oy làm trục đối xứng.
Ta vẽ được đồ thị hàm số \(y = 2{x^2}\) như sau:
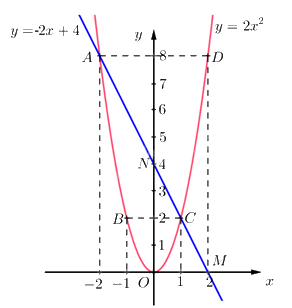
b. Tìm tọa độ giao điểm của \((P)\) và \((d)\) bằng phép tính.
Xét phương trình hoành độ giao điểm của \((P)\) và \((d)\) ta được:
\(\begin{array}{l}2{x^2} = - 2x + 4\\ \Leftrightarrow {x^2} = - x + 2\\ \Leftrightarrow {x^2} + x - 2 = 0\\ \Leftrightarrow {x^2} + 2x - x - 2 = 0\\ \Leftrightarrow x\left( {x + 2} \right) - \left( {x + 2} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 2\end{array} \right.\end{array}\)
Với \(x = 1 \Rightarrow y = {2.1^2} = 2\)
Với \(x = - 2 \Rightarrow y = 2.{\left( { - 2} \right)^2} = 8\)
Vậy \((P)\) và \((d)\)cắt nhau tại 2 giao điểm là: \(A\left( { - 2;8} \right)\)và \(C\left( {1;2} \right)\).
Câu 4 (VD):
Phương pháp:
Sử dụng hệ thức lượng trong tam giác vuông.
Cách giải:
a. Cho tam giác ABC vuông tại A, đường cao AH. Biết AH = 3cm, HC = 4cm. Tính độ dài đoạn thẳng HB, AC và số đo góc C (kết quả làm tròn đến độ).
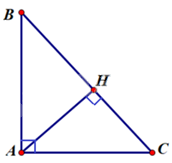
Do tam giác ABC vuông tại A, đường cao AH nên áp dụng hệ thức lượng trong tam giác vuông có:
\(A{H^2} = HB.HC \Rightarrow HB = \frac{{A{H^2}}}{{HC}} = \frac{{{3^2}}}{4} = \frac{9}{4}\) cm
Suy ra \(BC = HB + HC = \frac{9}{4} + 4 = \frac{{25}}{4}\) cm
\( \Rightarrow A{C^2} = HC.BC = 4.\frac{{25}}{4} = 25 \Rightarrow AC = 5\)cm
\( \Rightarrow \sin C = \frac{{AH}}{{AC}} = \frac{3}{5} \Rightarrow \angle C \approx 36,{87^0}\)
b. Để xác định chiều cao của một tòa tháp cao tầng (hình vẽ bên), một người đứng tại điểm C cách chân tháp một khoảng CD = 60m, sử dụng giác kế nhìn thấy đỉnh tòa tháp với góc AOB = 60. Hãy tính chiều cao của tòa tháp. Biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế là OC = 1m, (kết quả làm tròn đến hàng đơn vị).
Do tam giác ABO vuông tại B, góc AOB = \({60^0}\) nên
\(AB = OB.\tan \angle O = CD.\tan {60^0} = 60.\tan {60^0} = 60\sqrt 3 \) m
Lại có BD = CO = 1m
\( \Rightarrow AD = AB + BD = 60\sqrt 3 + 1 \approx 105\) m
Vậy tòa nhà cao khoảng 105 m
Câu 5 (VD):
Cách giải:
Cho tam giác ABC có ba góc nhọn. Hai đường cao của tam giác ABC và AD, BE cắt nhau tại H.
a) Chứng minh tứ giác CDHE nội tiếp đường tròn.
Ta có:
\(\begin{array}{l}\angle HDC = {90^0}\,\,\left( {do\,\,AD \bot BC} \right)\\\angle HEC = {90^0}\,\,\left( {do\,\,BE \bot AC} \right)\\ \Rightarrow \angle HDC + \angle HEC = {90^0} + {90^0} = {180^0}\end{array}\)
Mà 2 góc này ở vị trí đối nhau của tứ giác CDHE.
=> CDHE là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng \({180^0}\)). (đpcm)
b) Chứng minh HA.HD = HB.HE.
Xét \(\Delta AHE\) và \(\Delta BHD\) có:
\(\angle AEH = \angle BDH = {90^0}\,\,\left( {do\,\,BE \bot AC,\,\,AD \bot BC} \right)\)
\(\angle AHE = \angle BHD\) (đối đỉnh)
$\Rightarrow \Delta AHE\backsim \Delta BHD\,\,\left( g.g \right)$
\( \Rightarrow \frac{{HA}}{{HB}} = \frac{{HE}}{{HD}}\) (cặp cạnh tương ứng tỉ lệ) \( \Rightarrow HA.HD = HB.HE\,\,\left( {dpcm} \right)\).
c) Gọi điểm I là tâm đường tròn ngoại tiếp tứ giác CDHE. Chứng minh IE là tiếp tuyến của đường tròn đường kính AB.
Xét tứ giác nội tiếp CDHE có: \(\angle HEC = {90^0}\,\,\left( {gt} \right)\) nên \(\angle HEC\) là góc nội tiếp chắn nửa đường tròn.
\( \Rightarrow HC\) là đường kính của đường tròn ngoại tiếp tứ giác CDHE.
\( \Rightarrow I\) là trung điểm của HC.
Gọi O là trung điểm của AB => O là tâm đường tròn đường kính AB.
Ta cần chứng minh \(OE \bot IE\) tại E.
Vì tam giác AEB vuông tại E có EO là trung tuyến ứng với cạnh huyền AB nên \(OE = \frac{1}{2}AB = OA = OB \Rightarrow E \in \left( O \right)\).
Vì tam giác ADB vuông tại D có DO là trung tuyến ứng với cạnh huyền AB nên \(OD = \frac{1}{2}AB = OA = OB \Rightarrow D \in \left( O \right)\)
Vì CDHE là tứ giác nội tiếp (cmt) nên \(\angle ECH = \angle EDH \Rightarrow \angle ECI = \angle EDA\) (hai góc nội tiếp cùng chắn cung HE).
Mà \(\angle EDA = \angle EBA = \angle EBO\) (hai góc nội tiếp cùng chắn cung EA của (O)).
\( \Rightarrow \angle ECI = \angle EBO\). (1)
Vì tứ giác CDHE nội tiếp đường tròn tâm I đường kính HC nên IE = IC
\( \Rightarrow \Delta IEC\) cân tại I (định nghĩa)
\( \Rightarrow \angle ECI = \angle CEI\) (tính chất tam giác cân). (2)
Vì E thuộc (O) nên OB = OE
\( \Rightarrow \Delta OBE\) cân tại O (định nghĩa)
\( \Rightarrow \angle EBO = \angle BEO\) (tính chất tam giác cân). (3)
Từ (1), (2), (3)
\(\begin{array}{l} \Rightarrow \angle CEI = \angle BEO\\ \Rightarrow \angle CEI + \angle IEH = \angle BEO + \angle IEH\\ \Rightarrow \angle CEH = \angle IEO\\ \Rightarrow {90^0} = \angle IEO\end{array}\)
Vậy \(OE \bot IE\) tại E hay IE là tiếp tuyến của đường tròn (O) đường kính AB (đpcm).
Câu 6 (VD):
Cách giải:
Theo bài ra ta có: \(x + y + 2 = 0 \Leftrightarrow x + y = - 2\).
Ta có:
\(\begin{array}{l}A = 3\left( {{x^2} + {y^2}} \right) + 10xy\\A = 3\left( {{x^2} + {y^2} + 2xy} \right) + 4xy\\A = 3{\left( {x + y} \right)^2} + 4xy\\A = 3.{\left( { - 2} \right)^2} + 4xy\\A = 12 + 4xy\end{array}\)
Ta có: \(xy \le {\left( {\frac{{x + y}}{2}} \right)^2} = {\left( {\frac{{ - 2}}{2}} \right)^2} = 1\).
\( \Rightarrow A \le 12 + 4 = 16\).
Vậy \({A_{\max }} = 16 \Leftrightarrow \left\{ \begin{array}{l}x = y\\x + y + 2 = 0\end{array} \right. \Leftrightarrow x = y = - 1\).
Kỳ thi tuyển sinh vào lớp 10 môn Toán Long An năm 2023 là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Đề thi thường bao gồm các dạng bài tập khác nhau, đòi hỏi học sinh phải có kiến thức vững chắc và kỹ năng giải quyết vấn đề tốt. Năm 2023, đề thi tiếp tục đánh giá khả năng vận dụng kiến thức toán học vào thực tế, cũng như khả năng tư duy logic và sáng tạo của học sinh.
Cấu trúc đề thi thường bao gồm các phần chính sau:
Dưới đây là một số dạng bài tập thường gặp trong đề thi vào 10 môn Toán Long An:
Để ôn thi hiệu quả cho kỳ thi vào 10 môn Toán Long An, các em học sinh cần:
Giaitoan.edu.vn cung cấp đầy đủ các tài liệu ôn thi vào 10 môn Toán Long An năm 2023, bao gồm:
Trước khi bước vào phòng thi, hãy:
Chúc các em học sinh ôn thi tốt và đạt kết quả cao trong kỳ thi tuyển sinh vào lớp 10 môn Toán Long An năm 2023!