Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Bạc Liêu năm 2023. Đây là tài liệu ôn tập vô cùng quan trọng dành cho các em học sinh đang chuẩn bị cho kỳ thi sắp tới.
Chúng tôi cung cấp đầy đủ các đề thi chính thức, đáp án chi tiết và phương pháp giải bài tập hiệu quả. Hãy cùng giaitoan.edu.vn chinh phục kỳ thi vào 10 môn Toán Bạc Liêu năm 2023!
Câu 1: a) Tính giá trị của biểu thức \(A = \sqrt {80} + \sqrt {45} \). b) Rút gọn biểu thức \(B = \left( {\frac{1}{{\sqrt x - 1}} + \frac{3}{{\sqrt x + 1}}} \right):\frac{2}{{\sqrt x + 1}}\) với \(x > 0\) và \(x \ne 1\).
Câu 1:
a) Tính giá trị của biểu thức \(A = \sqrt {80} + \sqrt {45} \).
b) Rút gọn biểu thức \(B = \left( {\frac{1}{{\sqrt x - 1}} + \frac{3}{{\sqrt x + 1}}} \right):\frac{2}{{\sqrt x + 1}}\) với \(x > 0\) và \(x \ne 1\).
Câu 2:
a) Tìm hệ số a để đồ thị hàm số \(y = a{x^2}\)đi qua điểm M(-1;2). Vẽ đồ thị của hàm số \(y = a{x^2}\) với giá trị \(a\) vừa tìm được.
b) Giải hệ phương trình \(\left\{ \begin{array}{l}x - 2y = 4\\2x + y = 3\end{array} \right.\)
Câu 3:
Cho phương trình bậc hai \({x^2} - 2x + m - 2 = 0\) (1), với \(m\) là tham số.
a) Xác định các hệ số a, b, c của phương trình (1).
b) Giải phương trình (1) khi \(m = - 1\).
c) Tìm giá trị của \(m\) để phương trình (1) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(3\left( {x_1^2 + x_2^2} \right) + x_1^2x_2^2 = 11\).
Câu 4:
Trên đường tròn tâm O, đường kính AB = 2R, lấy hai điểm C, D sao cho CD vuông góc với AB tại H (H thuộc đoạn OA, khác O và A). Gọi M là điểm trên đoạn CD (M khác C và D, CM > DM), E là giao điểm của AM với đường tròn (O), N là giao điểm của hai đường thẳng BE và CD.
a) Chứng minh tứ giác MEBH nội tiếp
b) Chứng minh NC. ND = NB. NE
c) Khi AC = R, xác định vị trí của điểm M để 2AM + AE đạt giá trị nhỏ nhất
-----HẾT-----
Câu 1:
a) Tính giá trị của biểu thức \(A = \sqrt {80} + \sqrt {45} \).
b) Rút gọn biểu thức \(B = \left( {\frac{1}{{\sqrt x - 1}} + \frac{3}{{\sqrt x + 1}}} \right):\frac{2}{{\sqrt x + 1}}\) với \(x > 0\) và \(x \ne 1\).
Câu 2:
a) Tìm hệ số a để đồ thị hàm số \(y = a{x^2}\)đi qua điểm M(-1;2). Vẽ đồ thị của hàm số \(y = a{x^2}\) với giá trị \(a\) vừa tìm được.
b) Giải hệ phương trình \(\left\{ \begin{array}{l}x - 2y = 4\\2x + y = 3\end{array} \right.\)
Câu 3:
Cho phương trình bậc hai \({x^2} - 2x + m - 2 = 0\) (1), với \(m\) là tham số.
a) Xác định các hệ số a, b, c của phương trình (1).
b) Giải phương trình (1) khi \(m = - 1\).
c) Tìm giá trị của \(m\) để phương trình (1) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(3\left( {x_1^2 + x_2^2} \right) + x_1^2x_2^2 = 11\).
Câu 4:
Trên đường tròn tâm O, đường kính AB = 2R, lấy hai điểm C, D sao cho CD vuông góc với AB tại H (H thuộc đoạn OA, khác O và A). Gọi M là điểm trên đoạn CD (M khác C và D, CM > DM), E là giao điểm của AM với đường tròn (O), N là giao điểm của hai đường thẳng BE và CD.
a) Chứng minh tứ giác MEBH nội tiếp
b) Chứng minh NC. ND = NB. NE
c) Khi AC = R, xác định vị trí của điểm M để 2AM + AE đạt giá trị nhỏ nhất
-----HẾT-----
Câu 1 (TH):
Phương pháp:
a) Biến đổi \(\sqrt {{A^2}} = \left| A \right|\) và \(\sqrt {A.B} = \sqrt A .\sqrt B \)
b) Tìm mẫu số chung, quy đồng và rút gọn biểu thức
Cách giải:
a) Tính giá trị của biểu thức \(A = \sqrt {80} + \sqrt {45} \).
Ta có:
\(\begin{array}{l}A = \sqrt {80} + \sqrt {45} \\A = \sqrt {16.5} + \sqrt {9.5} \\A = \sqrt {{4^2}.5} + \sqrt {{3^2}.5} \\A = 4\sqrt 5 + 3\sqrt 5 \\A = 7\sqrt 5 \end{array}\)
Vậy \(A = 7\sqrt 5 \).
b) Rút gọn biểu thức \(B = \left( {\frac{1}{{\sqrt x - 1}} + \frac{3}{{\sqrt x + 1}}} \right):\frac{2}{{\sqrt x + 1}}\) với \(x > 0\) và \(x \ne 1\).
Với \(x > 0\) và \(x \ne 1\) ta có:
\(\begin{array}{l}B = \left( {\frac{1}{{\sqrt x - 1}} + \frac{3}{{\sqrt x + 1}}} \right):\frac{2}{{\sqrt x + 1}}\\B = \frac{{\sqrt x + 1 + 3\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}:\frac{2}{{\sqrt x + 1}}\\B = \frac{{\sqrt x + 1 + 3\sqrt x - 3}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}.\frac{{\sqrt x + 1}}{2}\\B = \frac{{4\sqrt x - 2}}{{\sqrt x - 1}}.\frac{1}{2}\\B = \frac{{2\sqrt x - 1}}{{\sqrt x - 1}}\end{array}\)
Vậy \(B = \frac{{2\sqrt x - 1}}{{\sqrt x - 1}}.\)
Câu 2 (TH):
Phương pháp:
a) Thay tọa độ M vào hàm số tìm a, lập bảng vẽ đồ thị hàm số và nhận xét
b) Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số
Cách giải:
a) Tìm hệ số a để đồ thị hàm số \(y = a{x^2}\)đi qua điểm M(-1;2). Vẽ đồ thị của hàm số \(y = a{x^2}\) với giá trị \(a\) vừa tìm được.
Đồ thị hàm số \(y = a{x^2}\)đi qua điểm \(M\left( { - 1;2} \right)\) khi và chỉ khi: \(a.{\left( { - 1} \right)^2} = 2 \Leftrightarrow a = 2\)
Vậy \(a = 2\).
* Vẽ đồ thị hàm số \(y = 2{x^2}\)
Ta có bảng giá trị sau:

=> Đồ thị hàm số là đường cong parabol đi qua các điểm \(O\,\left( {0;0} \right);A\left( { - 1;2} \right);\,\,B\left( {1;2} \right);\,C\left( { - 2;8} \right);\,D\left( {2;8} \right)\).
Hệ số a = 2 > 0 nên parabol có bề cong hướng lên. Đồ thị hàm số nhận Oy làm trục đối xứng.
Ta vẽ được đồ thị hàm số \(y = 2{x^2}\) như sau:
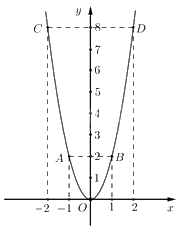
b) Giải hệ phương trình \(\left\{ \begin{array}{l}x - 2y = 4\\2x + y = 3\end{array} \right.\)
Ta có: \(\left\{ \begin{array}{l}x - 2y = 4\\2x + y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 2y = 4\\4x + 2y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x = 10\\y = 3 - 2x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = - 1\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất là: \(\left( {x;y} \right) = \left( {2; - 1} \right)\).
Câu 3 (TH):
Phương pháp:
a) Hệ số a, b, c của phương trình là các hệ số của số hạng \({x^2},x\)và hệ số tự do
b) Thay m = -1 vào phương trình, giải phương trình bằng cách nhẩm nghiệm
c) Tính \(\Delta '\). Cho \(\Delta ' > 0\) tìm m, áp dụng Viet thay vào \(3\left( {x_1^2 + x_2^2} \right) + x_1^2x_2^2 = 11\)
Cách giải:
a) Xác định các hệ số a, b, c của phương trình (1).
Hệ số \(a = 1;\,\,b = - 2;\,\,c = m - 2.\)
b) Giải phương trình (1) khi \(m = - 1\).
Khi \(m = - 1\) phương trình (1) \( \Leftrightarrow {x^2} - 2x - 3 = 0\).
Ta có \(a - b + c = 1 - \left( { - 2} \right) + \left( { - 3} \right) = 0\) nên phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = - 1\\{x_2} = - \frac{c}{a} = 3\end{array} \right.\).
Vậy khi m = -1 thì tập nghiệm của phương trình là \(S = \left\{ { - 1;3} \right\}\).
c) Tìm giá trị của \(m\) để phương trình (1) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(3\left( {x_1^2 + x_2^2} \right) + x_1^2x_2^2 = 11\).
Phương trình (1) có \(\Delta ' = {\left( { - 1} \right)^2} - 1\left( {m - 2} \right) = - m + 3\).
Để phương trình có hai nghiệm thì \(\Delta ' \ge 0 \Leftrightarrow - m + 3 \ge 0 \Leftrightarrow m \le 3\)
Áp dụng định lí Vi – ét ta có:\(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = 2}\\{{x_1}.{x_2} = m - 2}\end{array}} \right.\)
Theo bài ra ta có: \(3\left( {x_1^2 + x_2^2} \right) + x_1^2x_2^2 = 11\)
\( \Leftrightarrow 3\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}.{x_2}} \right] + x_1^2x_2^2 = 11\) (2)
Thay \(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = 2}\\{{x_1}.{x_2} = m - 2}\end{array}} \right.\) vào (2) ta có:
\(\begin{array}{l} \Leftrightarrow 3\left[ {{2^2} - 2\left( {m - 2} \right)} \right] + {\left( {m - 2} \right)^2} = 11\\ \Leftrightarrow 3\left( {8 - 2m} \right) + {m^2} - 4m + 4 = 11\\ \Leftrightarrow {m^2} - 10m + 17 = 0\,\,\left( * \right)\end{array}\)
Ta có: \({\Delta _m}' = {5^2} - 17 = 8 > 0\) nên phương trình (*) có hai nghiệm phân biệt \(\left[ \begin{array}{l}m = 5 + 2\sqrt 2 \,\,\,\left( {ktm} \right)\\m = 5 - 2\sqrt 2 \,\,\,\left( {tm} \right)\end{array} \right.\)
Vậy với \(m = 5 - 2\sqrt 2 \,\) phương trình (1) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(3\left( {x_1^2 + x_2^2} \right) + x_1^2x_2^2 = 11\).
Câu 4 (VD):
Phương pháp:
a) Tổng hai góc đối bằng \({180^0}\)
b) Chứng minh $\Delta NCE\backsim \Delta NBD\left( g.g \right)$
c) Gọi \(HM = x\,\,\left( {0 < x < R} \right)\). Tính AE, AM theo x và áp dụng bất đẳng thức Cô-si
Cách giải:
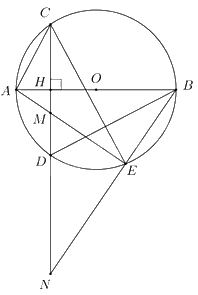
a) Chứng minh tứ giác MEBH nội tiếp
Ta có \(\angle AEB = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
\(\angle MHB = {90^0}\) (do \(CD \bot AB\) tại H) (gt)
\( \Rightarrow \angle MEB + \angle MHB = {90^0} + {90^0} = {180^0}\).
Mà 2 góc này ở vị trí đối diện nên tứ giác MEBH nội tiếp (dhnb)
b) Chứng minh NC. ND = NB. NE
Xét \(\Delta NCE\) và \(\Delta NBD\) có:
\(\angle BNC\) chung
\(\angle NCE = \angle NBD\) (góc nội tiếp cùng chắn cung DE)
$\Rightarrow \Delta NCE\backsim \Delta NBD\left( g.g \right)$
\( \Rightarrow \frac{{NC}}{{NB}} = \frac{{NE}}{{ND}} \Leftrightarrow NC.ND = NE.NB\) (đpcm)
c) Khi AC = R, xác định vị trí của điểm M để 2AM + AE đạt giá trị nhỏ nhất
Xét tam giác OAC có OA = OC = AC = R => Tam giác OAC đều.
\( \Rightarrow \) Đường cao CH đồng thời là đường trung tuyến \( \Rightarrow H\) là trung điểm của OA \( \Rightarrow AH = \frac{1}{2}OA = \frac{R}{2}\).
Đặt \(HM = x\,\,\left( {0 < x < R} \right)\).
Áp dụng định lí Pytago trong tam giác vuông AHM ta có: \(AM = \sqrt {\frac{{{R^2}}}{4} + {x^2}} \Rightarrow 2AM = \sqrt {{R^2} + 4{x^2}} \).
Xét tam giác AHM và tam giác AEB có:
\(\begin{array}{l}\angle BAE\,\,chung\\\angle AHM = \angle AEB = {90^0}\,\,\left( {cmt} \right)\end{array}\)
\(\Rightarrow \Delta AHM\backsim \Delta AEB\,\,\left( g.g \right)\)
\( \Rightarrow \frac{{HM}}{{BE}} = \frac{{AH}}{{AE}} = \frac{{AM}}{{AB}}\) (các cặp cạnh tương ứng tỉ lệ).
\( \Rightarrow AE = \frac{{AH.AB}}{{AM}} = \frac{{\frac{R}{2}.2R}}{{\sqrt {\frac{{{R^2}}}{4} + {x^2}} }} = \frac{{2{R^2}}}{{\sqrt {{R^2} + 4{x^2}} }}\)
\( \Rightarrow 2AM + AE = \sqrt {{R^2} + 4{x^2}} + \frac{{2{R^2}}}{{\sqrt {{R^2} + 4{x^2}} }}\)
Áp dụng BĐT Cô-si ta có:
\(\sqrt {{R^2} + 4{x^2}} + \frac{{2{R^2}}}{{\sqrt {{R^2} + 4{x^2}} }} \ge 2\sqrt {\sqrt {{R^2} + 4{x^2}} .\frac{{2{R^2}}}{{\sqrt {{R^2} + 4{x^2}} }}} = 2\sqrt 2 R\)
Dấu “=” xảy ra
\(\begin{array}{l} \Leftrightarrow \sqrt {{R^2} + 4{x^2}} = \frac{{2{R^2}}}{{\sqrt {{R^2} + 4{x^2}} }}\\ \Leftrightarrow {R^2} + 4{x^2} = 2{R^2} \Leftrightarrow {x^2} = \frac{{{R^2}}}{4} \Leftrightarrow x = \frac{R}{2}\,\,\left( {tm} \right)\end{array}\)
\( \Rightarrow HM = \frac{R}{2} \Rightarrow M\) là trung điểm của HD.
Vậy để 2AM + AE đạt giá trị nhỏ nhất thì M là trung điểm của HD.
Câu 1 (TH):
Phương pháp:
a) Biến đổi \(\sqrt {{A^2}} = \left| A \right|\) và \(\sqrt {A.B} = \sqrt A .\sqrt B \)
b) Tìm mẫu số chung, quy đồng và rút gọn biểu thức
Cách giải:
a) Tính giá trị của biểu thức \(A = \sqrt {80} + \sqrt {45} \).
Ta có:
\(\begin{array}{l}A = \sqrt {80} + \sqrt {45} \\A = \sqrt {16.5} + \sqrt {9.5} \\A = \sqrt {{4^2}.5} + \sqrt {{3^2}.5} \\A = 4\sqrt 5 + 3\sqrt 5 \\A = 7\sqrt 5 \end{array}\)
Vậy \(A = 7\sqrt 5 \).
b) Rút gọn biểu thức \(B = \left( {\frac{1}{{\sqrt x - 1}} + \frac{3}{{\sqrt x + 1}}} \right):\frac{2}{{\sqrt x + 1}}\) với \(x > 0\) và \(x \ne 1\).
Với \(x > 0\) và \(x \ne 1\) ta có:
\(\begin{array}{l}B = \left( {\frac{1}{{\sqrt x - 1}} + \frac{3}{{\sqrt x + 1}}} \right):\frac{2}{{\sqrt x + 1}}\\B = \frac{{\sqrt x + 1 + 3\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}:\frac{2}{{\sqrt x + 1}}\\B = \frac{{\sqrt x + 1 + 3\sqrt x - 3}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}.\frac{{\sqrt x + 1}}{2}\\B = \frac{{4\sqrt x - 2}}{{\sqrt x - 1}}.\frac{1}{2}\\B = \frac{{2\sqrt x - 1}}{{\sqrt x - 1}}\end{array}\)
Vậy \(B = \frac{{2\sqrt x - 1}}{{\sqrt x - 1}}.\)
Câu 2 (TH):
Phương pháp:
a) Thay tọa độ M vào hàm số tìm a, lập bảng vẽ đồ thị hàm số và nhận xét
b) Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số
Cách giải:
a) Tìm hệ số a để đồ thị hàm số \(y = a{x^2}\)đi qua điểm M(-1;2). Vẽ đồ thị của hàm số \(y = a{x^2}\) với giá trị \(a\) vừa tìm được.
Đồ thị hàm số \(y = a{x^2}\)đi qua điểm \(M\left( { - 1;2} \right)\) khi và chỉ khi: \(a.{\left( { - 1} \right)^2} = 2 \Leftrightarrow a = 2\)
Vậy \(a = 2\).
* Vẽ đồ thị hàm số \(y = 2{x^2}\)
Ta có bảng giá trị sau:

=> Đồ thị hàm số là đường cong parabol đi qua các điểm \(O\,\left( {0;0} \right);A\left( { - 1;2} \right);\,\,B\left( {1;2} \right);\,C\left( { - 2;8} \right);\,D\left( {2;8} \right)\).
Hệ số a = 2 > 0 nên parabol có bề cong hướng lên. Đồ thị hàm số nhận Oy làm trục đối xứng.
Ta vẽ được đồ thị hàm số \(y = 2{x^2}\) như sau:
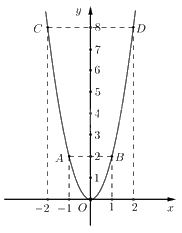
b) Giải hệ phương trình \(\left\{ \begin{array}{l}x - 2y = 4\\2x + y = 3\end{array} \right.\)
Ta có: \(\left\{ \begin{array}{l}x - 2y = 4\\2x + y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 2y = 4\\4x + 2y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x = 10\\y = 3 - 2x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = - 1\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất là: \(\left( {x;y} \right) = \left( {2; - 1} \right)\).
Câu 3 (TH):
Phương pháp:
a) Hệ số a, b, c của phương trình là các hệ số của số hạng \({x^2},x\)và hệ số tự do
b) Thay m = -1 vào phương trình, giải phương trình bằng cách nhẩm nghiệm
c) Tính \(\Delta '\). Cho \(\Delta ' > 0\) tìm m, áp dụng Viet thay vào \(3\left( {x_1^2 + x_2^2} \right) + x_1^2x_2^2 = 11\)
Cách giải:
a) Xác định các hệ số a, b, c của phương trình (1).
Hệ số \(a = 1;\,\,b = - 2;\,\,c = m - 2.\)
b) Giải phương trình (1) khi \(m = - 1\).
Khi \(m = - 1\) phương trình (1) \( \Leftrightarrow {x^2} - 2x - 3 = 0\).
Ta có \(a - b + c = 1 - \left( { - 2} \right) + \left( { - 3} \right) = 0\) nên phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = - 1\\{x_2} = - \frac{c}{a} = 3\end{array} \right.\).
Vậy khi m = -1 thì tập nghiệm của phương trình là \(S = \left\{ { - 1;3} \right\}\).
c) Tìm giá trị của \(m\) để phương trình (1) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(3\left( {x_1^2 + x_2^2} \right) + x_1^2x_2^2 = 11\).
Phương trình (1) có \(\Delta ' = {\left( { - 1} \right)^2} - 1\left( {m - 2} \right) = - m + 3\).
Để phương trình có hai nghiệm thì \(\Delta ' \ge 0 \Leftrightarrow - m + 3 \ge 0 \Leftrightarrow m \le 3\)
Áp dụng định lí Vi – ét ta có:\(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = 2}\\{{x_1}.{x_2} = m - 2}\end{array}} \right.\)
Theo bài ra ta có: \(3\left( {x_1^2 + x_2^2} \right) + x_1^2x_2^2 = 11\)
\( \Leftrightarrow 3\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}.{x_2}} \right] + x_1^2x_2^2 = 11\) (2)
Thay \(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = 2}\\{{x_1}.{x_2} = m - 2}\end{array}} \right.\) vào (2) ta có:
\(\begin{array}{l} \Leftrightarrow 3\left[ {{2^2} - 2\left( {m - 2} \right)} \right] + {\left( {m - 2} \right)^2} = 11\\ \Leftrightarrow 3\left( {8 - 2m} \right) + {m^2} - 4m + 4 = 11\\ \Leftrightarrow {m^2} - 10m + 17 = 0\,\,\left( * \right)\end{array}\)
Ta có: \({\Delta _m}' = {5^2} - 17 = 8 > 0\) nên phương trình (*) có hai nghiệm phân biệt \(\left[ \begin{array}{l}m = 5 + 2\sqrt 2 \,\,\,\left( {ktm} \right)\\m = 5 - 2\sqrt 2 \,\,\,\left( {tm} \right)\end{array} \right.\)
Vậy với \(m = 5 - 2\sqrt 2 \,\) phương trình (1) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(3\left( {x_1^2 + x_2^2} \right) + x_1^2x_2^2 = 11\).
Câu 4 (VD):
Phương pháp:
a) Tổng hai góc đối bằng \({180^0}\)
b) Chứng minh $\Delta NCE\backsim \Delta NBD\left( g.g \right)$
c) Gọi \(HM = x\,\,\left( {0 < x < R} \right)\). Tính AE, AM theo x và áp dụng bất đẳng thức Cô-si
Cách giải:
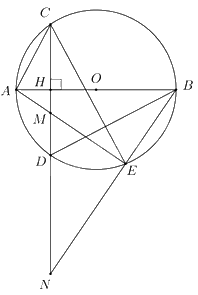
a) Chứng minh tứ giác MEBH nội tiếp
Ta có \(\angle AEB = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
\(\angle MHB = {90^0}\) (do \(CD \bot AB\) tại H) (gt)
\( \Rightarrow \angle MEB + \angle MHB = {90^0} + {90^0} = {180^0}\).
Mà 2 góc này ở vị trí đối diện nên tứ giác MEBH nội tiếp (dhnb)
b) Chứng minh NC. ND = NB. NE
Xét \(\Delta NCE\) và \(\Delta NBD\) có:
\(\angle BNC\) chung
\(\angle NCE = \angle NBD\) (góc nội tiếp cùng chắn cung DE)
$\Rightarrow \Delta NCE\backsim \Delta NBD\left( g.g \right)$
\( \Rightarrow \frac{{NC}}{{NB}} = \frac{{NE}}{{ND}} \Leftrightarrow NC.ND = NE.NB\) (đpcm)
c) Khi AC = R, xác định vị trí của điểm M để 2AM + AE đạt giá trị nhỏ nhất
Xét tam giác OAC có OA = OC = AC = R => Tam giác OAC đều.
\( \Rightarrow \) Đường cao CH đồng thời là đường trung tuyến \( \Rightarrow H\) là trung điểm của OA \( \Rightarrow AH = \frac{1}{2}OA = \frac{R}{2}\).
Đặt \(HM = x\,\,\left( {0 < x < R} \right)\).
Áp dụng định lí Pytago trong tam giác vuông AHM ta có: \(AM = \sqrt {\frac{{{R^2}}}{4} + {x^2}} \Rightarrow 2AM = \sqrt {{R^2} + 4{x^2}} \).
Xét tam giác AHM và tam giác AEB có:
\(\begin{array}{l}\angle BAE\,\,chung\\\angle AHM = \angle AEB = {90^0}\,\,\left( {cmt} \right)\end{array}\)
\(\Rightarrow \Delta AHM\backsim \Delta AEB\,\,\left( g.g \right)\)
\( \Rightarrow \frac{{HM}}{{BE}} = \frac{{AH}}{{AE}} = \frac{{AM}}{{AB}}\) (các cặp cạnh tương ứng tỉ lệ).
\( \Rightarrow AE = \frac{{AH.AB}}{{AM}} = \frac{{\frac{R}{2}.2R}}{{\sqrt {\frac{{{R^2}}}{4} + {x^2}} }} = \frac{{2{R^2}}}{{\sqrt {{R^2} + 4{x^2}} }}\)
\( \Rightarrow 2AM + AE = \sqrt {{R^2} + 4{x^2}} + \frac{{2{R^2}}}{{\sqrt {{R^2} + 4{x^2}} }}\)
Áp dụng BĐT Cô-si ta có:
\(\sqrt {{R^2} + 4{x^2}} + \frac{{2{R^2}}}{{\sqrt {{R^2} + 4{x^2}} }} \ge 2\sqrt {\sqrt {{R^2} + 4{x^2}} .\frac{{2{R^2}}}{{\sqrt {{R^2} + 4{x^2}} }}} = 2\sqrt 2 R\)
Dấu “=” xảy ra
\(\begin{array}{l} \Leftrightarrow \sqrt {{R^2} + 4{x^2}} = \frac{{2{R^2}}}{{\sqrt {{R^2} + 4{x^2}} }}\\ \Leftrightarrow {R^2} + 4{x^2} = 2{R^2} \Leftrightarrow {x^2} = \frac{{{R^2}}}{4} \Leftrightarrow x = \frac{R}{2}\,\,\left( {tm} \right)\end{array}\)
\( \Rightarrow HM = \frac{R}{2} \Rightarrow M\) là trung điểm của HD.
Vậy để 2AM + AE đạt giá trị nhỏ nhất thì M là trung điểm của HD.
Kỳ thi tuyển sinh vào lớp 10 môn Toán tỉnh Bạc Liêu năm 2023 là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Đề thi thường bao gồm các dạng bài tập thuộc chương trình Toán lớp 9, tập trung vào các chủ đề chính như Đại số, Hình học và số học. Việc nắm vững kiến thức cơ bản và luyện tập thường xuyên là chìa khóa để đạt kết quả tốt trong kỳ thi này.
Dựa trên các đề thi trước đây, cấu trúc đề thi vào 10 môn Toán Bạc Liêu thường bao gồm:
Để chuẩn bị tốt nhất cho kỳ thi, các em học sinh cần tập trung vào các chủ đề sau:
Giaitoan.edu.vn cung cấp bộ đề thi vào 10 môn Toán Bạc Liêu năm 2023 chính thức, giúp các em học sinh làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải bài tập. Bên cạnh đó, chúng tôi còn cung cấp đáp án chi tiết và phương pháp giải bài tập hiệu quả, giúp các em hiểu rõ hơn về các kiến thức đã học.
Để đạt kết quả tốt trong kỳ thi vào 10 môn Toán Bạc Liêu, các em học sinh cần áp dụng các phương pháp giải đề thi hiệu quả sau:
Ngoài bộ đề thi vào 10 môn Toán Bạc Liêu năm 2023, các em học sinh có thể tham khảo thêm các tài liệu ôn thi bổ trợ sau:
Trước kỳ thi, các em học sinh cần:
Đề thi vào 10 môn Toán Bạc Liêu năm 2023 là một kỳ thi quan trọng, đòi hỏi sự chuẩn bị kỹ lưỡng và tinh thần quyết tâm cao. Hy vọng với bộ đề thi và các tài liệu ôn thi mà giaitoan.edu.vn cung cấp, các em học sinh sẽ đạt kết quả tốt nhất trong kỳ thi sắp tới.