Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Tiền Giang năm 2023. Đây là tài liệu ôn tập vô cùng quan trọng dành cho các em học sinh đang chuẩn bị cho kỳ thi sắp tới.
Chúng tôi đã tổng hợp đầy đủ các đề thi chính thức, đáp án chi tiết và hướng dẫn giải bài tập để giúp các em nắm vững kiến thức và tự tin làm bài.
Câu 1: 1. Tính giá trị của biểu thức \(A = \sqrt {27} {\rm{ \;}} - \frac{3}{{\sqrt 3 }} - \sqrt 3 \). 2. Giải các phương trình và hệ phương trình sau: a) \({x^2} + 3x - 10 = 0\);
Câu 1:
1. Tính giá trị của biểu thức \(A = \sqrt {27} {\rm{ \;}} - \frac{3}{{\sqrt 3 }} - \sqrt 3 \).
2. Giải các phương trình và hệ phương trình sau:
a) \({x^2} + 3x - 10 = 0\);
b) \({x^4} - 8{x^2} - 9 = 0\);
c) \(\left\{ {\begin{array}{*{20}{l}}{3x + y = 2}\\{x - y = 6}\end{array}} \right.\)
Câu 2: Trong mặt phẳng tọa độ Oxy, cho parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = 2x + 3\).
1. Vẽ parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) trên cùng một mặt phẳng tọa độ.
2. Bằng phép tính, tìm tọa độ các giao điểm của \(\left( P \right)\) và \(\left( d \right)\).
Câu 3:
1. Gọi \({x_1}\) và \({x_2}\) là hai nghiệm của phương trình \({x^2} + x - 10 = 0\). Không giải phương trình, tính giá trị của biểu thức \(A = x_1^2 + x_2^2 - 3{x_1}{x_2}\)
2. Tìm tất cả các giá trị của tham số \(m\) để phương trình \({x^2} + \left( {m + 1} \right)x + \frac{1}{4}{m^2} + 1 = 0\) có hai nghiệm phân biệt.
Câu 4: Một khu vườn hình chữ nhật có diện tích bằng \(150\;{{\rm{m}}^2}\). Hơi khu vườn có chiều dài và chiều rộng bằng bao nhiêu mét, biết rằng chiều dài lơn hơn chiều rộng \(5\;{\rm{m}}\) ?
Câu 5: Cho nửa đường tròn tâm \(O\) đường kính AB. Trên nửa đường tròn đó lấy điểm \(C(C\) khác \(A\) và \(B\) ), kẻ CH vuông góc với AB tại \(H\). Gọi \(K\) là điểm nằm giữa \(C\) và \(H\), tia AK cắt đường tròn tại điểm thứ hai là \(D\).
1. Chứng minh BHKD là một tứ giác nội tiếp.
2. Chứng minh tam giác ACK đồng dạng với tam giác ADC và chứng minh \(AK \cdot AD = A{C^2}\).
Câu 6: Một hình trụ có bán kính đáy bằng \(4\;{\rm{cm}}\), chiều cao bằng \(12\;{\rm{cm}}\). Tính diện tích xung quanh và thể tích của hình trụ đã cho.
----- HẾT -----
Câu 1 (TH):
Phương pháp:
1. Khai căn và tính giá trị biểu thức.
2. a) Tính \(\Delta \) và giải phương trình
b) Đặt \(t = {x^2}\)
c) Giải hệ phương trình bằng phương pháp cộng đại số.
Cách giải:
1.
\(\begin{array}{*{20}{r}}{A = \sqrt {27} {\rm{\;}} - \frac{3}{{\sqrt 3 }} - \sqrt 3 }&{}\\{A = \sqrt {{3^2} \cdot 3} {\rm{\;}} - \frac{{{{(\sqrt 3 )}^2}}}{{\sqrt 3 }} - \sqrt 3 }&{}\\{A = 3\sqrt 3 {\rm{\;}} - \sqrt 3 {\rm{\;}} - \sqrt 3 }&{}\\{A = \left( {3 - 1 - 1} \right)\sqrt 3 }&{}\\{A = \sqrt 3 }&{}\end{array}\)
Vậy \(A = \sqrt 3 \).
2. Giải các phương trình và hệ phương trình sau:
a) \({x^2} + 3x - 10 = 0\)
Ta có: \(\Delta = {3^2} - 4 \cdot 1 \cdot \left( { - 10} \right) = 49 > 0\) nên phương trình có 2 nghiệm phân biệt
\(\left[ {\begin{array}{*{20}{l}}{{x_1} = \frac{{ - 3 + \sqrt {49} }}{{2.1}} = 2}\\{{x_2} = \frac{{ - 3 - \sqrt {49} }}{{2.1}} = {\rm{ \;}} - 5}\end{array}} \right.\)
Vậy tập nghiệm của phương trình là \(S = \left\{ {2; - 5} \right\}\).
b) \({x^4} - 8{x^2} - 9 = 0\).
Đặt \(t = {x^2} \ge 0\), phương trình trở thành \({t^2} - 8t - 9 = 0\).
Ta có \(a - b + c = 1 - \left( { - 8} \right) + \left( { - 9} \right) = 0\) nên phương trình có 2 nghiệm phân biệt
Với \(t = 9 \Rightarrow {x^2} = 9 \Leftrightarrow x = {\rm{ \;}} \pm 3\).
Vạy tập nghiệm của phương trình là \(S = \left\{ { \pm 3} \right\}\).
c) \(\left\{ {\begin{array}{*{20}{l}}{3x + y = 2}\\{x - y = 6}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{l}}{3x + y = 2}\\{x - y = 6}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4x = 8}\\{y = x - 6}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = {\rm{ \;}} - 4}\end{array}} \right.} \right.} \right.\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {2; - 4} \right)\)
Câu 2 (TH):
Phương pháp:
a) Tìm 2 điểm để vẽ đường thẳng d và 5 điểm để vẽ parabol P.
b) Xét phương trình hoành độ giao điểm và tìm 2 nghiệm của phương trình đó.
Cách giải:
a) Vẽ parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) trên cùng một mặt phẳng tọa độ.
Vẽ đường thẳng \(\left( d \right)\) :
Với \(x = 0\) thì \(y = 2.0 + 3 = 3\)
Với \(x = 1\) thì \(y = 2.1 + 3 = 5\)
\( \Rightarrow \) Đồ thị hàm số \(y = 2x + 3\) là đường thẳng đi qua \(M\left( {0;3} \right)\) và \(N\left( {1;5} \right)\)
Vẽ parabol \(\left( P \right)\) :
Ta có bảng giá trị sau:

\( \Rightarrow \) Đồ thị hàm số là đường cong parabol đi qua các điểm \(O\left( {0;0} \right);A\left( { - 2;4} \right);B\left( { - 1;1} \right);C\left( {1;1} \right);D\left( {2;4} \right)\)
Hệ số \(a = 1 > 0\) nên parabol có bể cong hướng lên. Đồ thị hàm số nhận \({\rm{Oy}}\) làm trục đối xứng.
Ta vẽ được đồ thị hàm số \(y = {x^2}\) như sau:
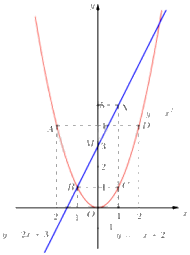
b) Bằng phép tính, tìm tọa độ các giao điểm \(\left( d \right)\) và \(\left( P \right)\).
Xét phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) ta có:
\({x^2} = 2x + 3 \Leftrightarrow {x^2} - 2x - 3 = 0\)
Ta có: \(a - b + c = 1 - \left( { - 2} \right) + \left( { - 3} \right) = 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ {\begin{array}{*{20}{l}}{x = {\rm{ \;}} - 1}\\{x = {\rm{ \;}} - \frac{c}{a} = 3}\end{array}} \right.\).
Với \(x = {\rm{ \;}} - 1\) thì \(y = {( - 1)^2} = 1\)
Với \(x = 3\) thì \(y = {3^2} = 9\)
Vậy \(\left( P \right)\) cắt \(\left( d \right)\) tại 2 điểm có tọa độ là: \(\left( { - 1;1} \right)\) và \(\left( {3;9} \right)\).
Câu 3 (VD):
Phương pháp:
1. Áp dụng hệ thức vi-et \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = {\rm{ \;}} - \frac{b}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\)
2. Phương trình có hai nghiệm phân biệt khi \(\Delta {\rm{ \;}} > 0\)
Cách giải:
1. Do \({x_1},{x_2}\) là hai nghiệm của phương trình \({x^2} + x - 10 = 0\) nên áp dụng hệ thức Vi-et ta có \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = {\rm{ \;}} - 1}\\{{x_1}{x_2} = {\rm{ \;}} - 10}\end{array}} \right.\)
Ta có \(A = x_1^2 + x_2^2 - 3{x_1}{x_2}\)
\(\begin{array}{*{20}{r}}{ = x_1^2 + 2{x_1}{x_2} + x_2^2 - 5{x_1}{x_2}}&\;\\{ = {{\left( {{x_1} + {x_2}} \right)}^2} - 5{x_1}{x_2}}&\;\\{ = {{( - 1)}^2} - 5\left( { - 10} \right)}&\;\\{ = 51}&\;\end{array}\)
Vây \(A = 51\).
2. Ta có \(\Delta = {(m + 1)^2} - 4 \cdot 1 \cdot \left( {\frac{1}{4}{m^2} + 1} \right) = {m^2} + 2m + 1 - {m^2} - 4 = 2m - 3\)
Để phương trình có 2 nghiệm phân biệt thì \(\Delta > 0 \Leftrightarrow 2m - 3 > 0 \Leftrightarrow m > \frac{3}{2}\)
Vậy \(m > \frac{3}{2}\) thì phương trình có 2 nghiệm phân biệt .
Câu 4 (TH):
Phương pháp:
- Gọi chiều dài hình chữ nhật là x, khi đó chiều rộng là x – 5.
- Ta tìm được phương trình là: Chiều dài nhân với chiều rộng bằng 150.
Cách giải:
Gọi chiều dài hình chữ nhật là \(x(x > 5\), mét)
Do chiều dài lớn hơn chiều rộng \(5\;{\rm{m}}\) nên chiều rộng hình chữ nhật là \(x - 5\left( {\;{\rm{m}}} \right)\)
Diện tích hình chữ nhật là \(x\left( {x - 5} \right)\left( {{{\rm{m}}^2}} \right)\)
Do diện tích khu vườn bằng \(150\;{{\rm{m}}^2}\) nên ta có phương trình
\(\begin{array}{*{20}{r}}{}&{x\left( {x - 5} \right) = 150}\\{}&{{x^2} - 5x - 150 = 0}\end{array}\)
Ta có \(\Delta = {( - 5)^2} - 4 \cdot 1 \cdot \left( { - 150} \right) = 625 > 0\) nên phương trình có 2 nghiệm phân biệt
\(\left[ {\begin{array}{*{20}{l}}{{x_1} = \frac{{ - \left( { - 5} \right) + \sqrt {625} }}{2} = 15\left( {{\rm{tm}}} \right)}\\{{x_2} = \frac{{ - \left( { - 5} \right) - \sqrt {625} }}{2} = {\rm{ \;}} - 10\left( {{\rm{ktm}}} \right)}\end{array}} \right.\)
Vậy chiều dài hình chữ nhật là \(15\;{\rm{m}}\), chiều rộng hình chữ nhật là \(10\;{\rm{m}}\).
Câu 5 (VD):
Phương pháp:
1. Tứ giác có tổng hai góc đối bằng \(180^\circ \) là tứ giác nội tiếp.
2. Chứng minh từ đó suy ra điều phải chứng minh.
Cách giải:
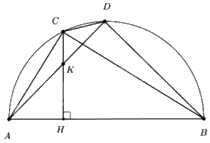
1. Do \(CH \bot AB\left( {gt} \right) \Rightarrow \angle KHB = 90^\circ \)
Ta có \(\angle ADB = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow \angle KHB + \angle KDB = 90^\circ + 90^\circ = 180^\circ \)
Mà hai góc này ở vị trí đối diện nên tứ giác HKDB nội tiếp (dhnb) (đpcm)
2. Ta có \(\angle ACB = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow \angle ACH + \angle HCB = 90^\circ \)
Mà \(\angle HCB + \angle HBC = 90^\circ \) (do vuông tại \({\rm{H}}\) )
\( \Rightarrow \angle ACH = \angle ABC\) (cùng phụ \(\angle HCB)\)
Mà \(\angle ABC = \angle ADC\) (góc nội tiếp cùng chắn cung \({\rm{AC}}\) )
\( \Rightarrow \angle ACH = \angle CDA\;{\rm{hay}}\;\angle ACK = \angle CDA\)
Xét \(\Delta ACK\) và \(\Delta ADC\) có:
\(\angle ACK = \angle CDA\)
\(\angle CAD\) chung
\(\Rightarrow \Delta ACK\backsim \Delta ADC\) (g.g)
\( \Rightarrow \frac{{AC}}{{AD}} = \frac{{AK}}{{AC}} \Leftrightarrow A{C^2} = AD \cdot AK\) (đpcm)
Câu 6 (TH):
Phương pháp:
Áp dụng công thức:
\({S_{{\rm{sq}}}} = 2\pi rh\)
\(V = \pi {r^2}h\)
Cách giải:
Diện tích xung quanh của hình trụ là:
\({S_{{\rm{sq}}}} = 2\pi rh = 2\pi {\rm{ \;}} \cdot 4 \cdot 12 = 96\pi \left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
Thể tích của hình trụ là:
\(V = \pi {r^2}h = \pi {\rm{ \;}} \cdot {4^2} \cdot 12 = 192\pi \left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
Vậy diện tích xung quanh của hình trụ là \(96\pi {\rm{c}}{{\rm{m}}^2}\), thể tích hình trụ là: \(192\pi {\rm{c}}{{\rm{m}}^3}\).
-----HẾT-----
Câu 1:
1. Tính giá trị của biểu thức \(A = \sqrt {27} {\rm{ \;}} - \frac{3}{{\sqrt 3 }} - \sqrt 3 \).
2. Giải các phương trình và hệ phương trình sau:
a) \({x^2} + 3x - 10 = 0\);
b) \({x^4} - 8{x^2} - 9 = 0\);
c) \(\left\{ {\begin{array}{*{20}{l}}{3x + y = 2}\\{x - y = 6}\end{array}} \right.\)
Câu 2: Trong mặt phẳng tọa độ Oxy, cho parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = 2x + 3\).
1. Vẽ parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) trên cùng một mặt phẳng tọa độ.
2. Bằng phép tính, tìm tọa độ các giao điểm của \(\left( P \right)\) và \(\left( d \right)\).
Câu 3:
1. Gọi \({x_1}\) và \({x_2}\) là hai nghiệm của phương trình \({x^2} + x - 10 = 0\). Không giải phương trình, tính giá trị của biểu thức \(A = x_1^2 + x_2^2 - 3{x_1}{x_2}\)
2. Tìm tất cả các giá trị của tham số \(m\) để phương trình \({x^2} + \left( {m + 1} \right)x + \frac{1}{4}{m^2} + 1 = 0\) có hai nghiệm phân biệt.
Câu 4: Một khu vườn hình chữ nhật có diện tích bằng \(150\;{{\rm{m}}^2}\). Hơi khu vườn có chiều dài và chiều rộng bằng bao nhiêu mét, biết rằng chiều dài lơn hơn chiều rộng \(5\;{\rm{m}}\) ?
Câu 5: Cho nửa đường tròn tâm \(O\) đường kính AB. Trên nửa đường tròn đó lấy điểm \(C(C\) khác \(A\) và \(B\) ), kẻ CH vuông góc với AB tại \(H\). Gọi \(K\) là điểm nằm giữa \(C\) và \(H\), tia AK cắt đường tròn tại điểm thứ hai là \(D\).
1. Chứng minh BHKD là một tứ giác nội tiếp.
2. Chứng minh tam giác ACK đồng dạng với tam giác ADC và chứng minh \(AK \cdot AD = A{C^2}\).
Câu 6: Một hình trụ có bán kính đáy bằng \(4\;{\rm{cm}}\), chiều cao bằng \(12\;{\rm{cm}}\). Tính diện tích xung quanh và thể tích của hình trụ đã cho.
----- HẾT -----
Câu 1 (TH):
Phương pháp:
1. Khai căn và tính giá trị biểu thức.
2. a) Tính \(\Delta \) và giải phương trình
b) Đặt \(t = {x^2}\)
c) Giải hệ phương trình bằng phương pháp cộng đại số.
Cách giải:
1.
\(\begin{array}{*{20}{r}}{A = \sqrt {27} {\rm{\;}} - \frac{3}{{\sqrt 3 }} - \sqrt 3 }&{}\\{A = \sqrt {{3^2} \cdot 3} {\rm{\;}} - \frac{{{{(\sqrt 3 )}^2}}}{{\sqrt 3 }} - \sqrt 3 }&{}\\{A = 3\sqrt 3 {\rm{\;}} - \sqrt 3 {\rm{\;}} - \sqrt 3 }&{}\\{A = \left( {3 - 1 - 1} \right)\sqrt 3 }&{}\\{A = \sqrt 3 }&{}\end{array}\)
Vậy \(A = \sqrt 3 \).
2. Giải các phương trình và hệ phương trình sau:
a) \({x^2} + 3x - 10 = 0\)
Ta có: \(\Delta = {3^2} - 4 \cdot 1 \cdot \left( { - 10} \right) = 49 > 0\) nên phương trình có 2 nghiệm phân biệt
\(\left[ {\begin{array}{*{20}{l}}{{x_1} = \frac{{ - 3 + \sqrt {49} }}{{2.1}} = 2}\\{{x_2} = \frac{{ - 3 - \sqrt {49} }}{{2.1}} = {\rm{ \;}} - 5}\end{array}} \right.\)
Vậy tập nghiệm của phương trình là \(S = \left\{ {2; - 5} \right\}\).
b) \({x^4} - 8{x^2} - 9 = 0\).
Đặt \(t = {x^2} \ge 0\), phương trình trở thành \({t^2} - 8t - 9 = 0\).
Ta có \(a - b + c = 1 - \left( { - 8} \right) + \left( { - 9} \right) = 0\) nên phương trình có 2 nghiệm phân biệt
Với \(t = 9 \Rightarrow {x^2} = 9 \Leftrightarrow x = {\rm{ \;}} \pm 3\).
Vạy tập nghiệm của phương trình là \(S = \left\{ { \pm 3} \right\}\).
c) \(\left\{ {\begin{array}{*{20}{l}}{3x + y = 2}\\{x - y = 6}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{l}}{3x + y = 2}\\{x - y = 6}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4x = 8}\\{y = x - 6}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = {\rm{ \;}} - 4}\end{array}} \right.} \right.} \right.\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {2; - 4} \right)\)
Câu 2 (TH):
Phương pháp:
a) Tìm 2 điểm để vẽ đường thẳng d và 5 điểm để vẽ parabol P.
b) Xét phương trình hoành độ giao điểm và tìm 2 nghiệm của phương trình đó.
Cách giải:
a) Vẽ parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) trên cùng một mặt phẳng tọa độ.
Vẽ đường thẳng \(\left( d \right)\) :
Với \(x = 0\) thì \(y = 2.0 + 3 = 3\)
Với \(x = 1\) thì \(y = 2.1 + 3 = 5\)
\( \Rightarrow \) Đồ thị hàm số \(y = 2x + 3\) là đường thẳng đi qua \(M\left( {0;3} \right)\) và \(N\left( {1;5} \right)\)
Vẽ parabol \(\left( P \right)\) :
Ta có bảng giá trị sau:
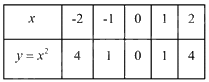
\( \Rightarrow \) Đồ thị hàm số là đường cong parabol đi qua các điểm \(O\left( {0;0} \right);A\left( { - 2;4} \right);B\left( { - 1;1} \right);C\left( {1;1} \right);D\left( {2;4} \right)\)
Hệ số \(a = 1 > 0\) nên parabol có bể cong hướng lên. Đồ thị hàm số nhận \({\rm{Oy}}\) làm trục đối xứng.
Ta vẽ được đồ thị hàm số \(y = {x^2}\) như sau:
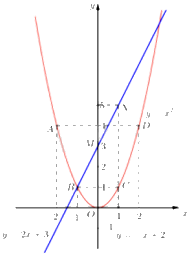
b) Bằng phép tính, tìm tọa độ các giao điểm \(\left( d \right)\) và \(\left( P \right)\).
Xét phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) ta có:
\({x^2} = 2x + 3 \Leftrightarrow {x^2} - 2x - 3 = 0\)
Ta có: \(a - b + c = 1 - \left( { - 2} \right) + \left( { - 3} \right) = 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ {\begin{array}{*{20}{l}}{x = {\rm{ \;}} - 1}\\{x = {\rm{ \;}} - \frac{c}{a} = 3}\end{array}} \right.\).
Với \(x = {\rm{ \;}} - 1\) thì \(y = {( - 1)^2} = 1\)
Với \(x = 3\) thì \(y = {3^2} = 9\)
Vậy \(\left( P \right)\) cắt \(\left( d \right)\) tại 2 điểm có tọa độ là: \(\left( { - 1;1} \right)\) và \(\left( {3;9} \right)\).
Câu 3 (VD):
Phương pháp:
1. Áp dụng hệ thức vi-et \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = {\rm{ \;}} - \frac{b}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\)
2. Phương trình có hai nghiệm phân biệt khi \(\Delta {\rm{ \;}} > 0\)
Cách giải:
1. Do \({x_1},{x_2}\) là hai nghiệm của phương trình \({x^2} + x - 10 = 0\) nên áp dụng hệ thức Vi-et ta có \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = {\rm{ \;}} - 1}\\{{x_1}{x_2} = {\rm{ \;}} - 10}\end{array}} \right.\)
Ta có \(A = x_1^2 + x_2^2 - 3{x_1}{x_2}\)
\(\begin{array}{*{20}{r}}{ = x_1^2 + 2{x_1}{x_2} + x_2^2 - 5{x_1}{x_2}}&\;\\{ = {{\left( {{x_1} + {x_2}} \right)}^2} - 5{x_1}{x_2}}&\;\\{ = {{( - 1)}^2} - 5\left( { - 10} \right)}&\;\\{ = 51}&\;\end{array}\)
Vây \(A = 51\).
2. Ta có \(\Delta = {(m + 1)^2} - 4 \cdot 1 \cdot \left( {\frac{1}{4}{m^2} + 1} \right) = {m^2} + 2m + 1 - {m^2} - 4 = 2m - 3\)
Để phương trình có 2 nghiệm phân biệt thì \(\Delta > 0 \Leftrightarrow 2m - 3 > 0 \Leftrightarrow m > \frac{3}{2}\)
Vậy \(m > \frac{3}{2}\) thì phương trình có 2 nghiệm phân biệt .
Câu 4 (TH):
Phương pháp:
- Gọi chiều dài hình chữ nhật là x, khi đó chiều rộng là x – 5.
- Ta tìm được phương trình là: Chiều dài nhân với chiều rộng bằng 150.
Cách giải:
Gọi chiều dài hình chữ nhật là \(x(x > 5\), mét)
Do chiều dài lớn hơn chiều rộng \(5\;{\rm{m}}\) nên chiều rộng hình chữ nhật là \(x - 5\left( {\;{\rm{m}}} \right)\)
Diện tích hình chữ nhật là \(x\left( {x - 5} \right)\left( {{{\rm{m}}^2}} \right)\)
Do diện tích khu vườn bằng \(150\;{{\rm{m}}^2}\) nên ta có phương trình
\(\begin{array}{*{20}{r}}{}&{x\left( {x - 5} \right) = 150}\\{}&{{x^2} - 5x - 150 = 0}\end{array}\)
Ta có \(\Delta = {( - 5)^2} - 4 \cdot 1 \cdot \left( { - 150} \right) = 625 > 0\) nên phương trình có 2 nghiệm phân biệt
\(\left[ {\begin{array}{*{20}{l}}{{x_1} = \frac{{ - \left( { - 5} \right) + \sqrt {625} }}{2} = 15\left( {{\rm{tm}}} \right)}\\{{x_2} = \frac{{ - \left( { - 5} \right) - \sqrt {625} }}{2} = {\rm{ \;}} - 10\left( {{\rm{ktm}}} \right)}\end{array}} \right.\)
Vậy chiều dài hình chữ nhật là \(15\;{\rm{m}}\), chiều rộng hình chữ nhật là \(10\;{\rm{m}}\).
Câu 5 (VD):
Phương pháp:
1. Tứ giác có tổng hai góc đối bằng \(180^\circ \) là tứ giác nội tiếp.
2. Chứng minh từ đó suy ra điều phải chứng minh.
Cách giải:
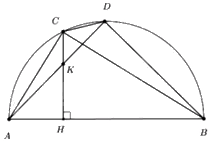
1. Do \(CH \bot AB\left( {gt} \right) \Rightarrow \angle KHB = 90^\circ \)
Ta có \(\angle ADB = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow \angle KHB + \angle KDB = 90^\circ + 90^\circ = 180^\circ \)
Mà hai góc này ở vị trí đối diện nên tứ giác HKDB nội tiếp (dhnb) (đpcm)
2. Ta có \(\angle ACB = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow \angle ACH + \angle HCB = 90^\circ \)
Mà \(\angle HCB + \angle HBC = 90^\circ \) (do vuông tại \({\rm{H}}\) )
\( \Rightarrow \angle ACH = \angle ABC\) (cùng phụ \(\angle HCB)\)
Mà \(\angle ABC = \angle ADC\) (góc nội tiếp cùng chắn cung \({\rm{AC}}\) )
\( \Rightarrow \angle ACH = \angle CDA\;{\rm{hay}}\;\angle ACK = \angle CDA\)
Xét \(\Delta ACK\) và \(\Delta ADC\) có:
\(\angle ACK = \angle CDA\)
\(\angle CAD\) chung
\(\Rightarrow \Delta ACK\backsim \Delta ADC\) (g.g)
\( \Rightarrow \frac{{AC}}{{AD}} = \frac{{AK}}{{AC}} \Leftrightarrow A{C^2} = AD \cdot AK\) (đpcm)
Câu 6 (TH):
Phương pháp:
Áp dụng công thức:
\({S_{{\rm{sq}}}} = 2\pi rh\)
\(V = \pi {r^2}h\)
Cách giải:
Diện tích xung quanh của hình trụ là:
\({S_{{\rm{sq}}}} = 2\pi rh = 2\pi {\rm{ \;}} \cdot 4 \cdot 12 = 96\pi \left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
Thể tích của hình trụ là:
\(V = \pi {r^2}h = \pi {\rm{ \;}} \cdot {4^2} \cdot 12 = 192\pi \left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
Vậy diện tích xung quanh của hình trụ là \(96\pi {\rm{c}}{{\rm{m}}^2}\), thể tích hình trụ là: \(192\pi {\rm{c}}{{\rm{m}}^3}\).
-----HẾT-----
Kỳ thi tuyển sinh vào lớp 10 môn Toán tỉnh Tiền Giang năm 2023 là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Kết quả của kỳ thi này sẽ quyết định việc các em có được vào học tại các trường THPT công lập tốt nhất của tỉnh hay không. Do đó, việc chuẩn bị kỹ lưỡng cho kỳ thi là vô cùng cần thiết.
Đề thi vào 10 môn Toán Tiền Giang năm 2023 thường có cấu trúc tương tự như các năm trước, bao gồm các dạng bài tập sau:
Độ khó của đề thi vào 10 môn Toán Tiền Giang năm 2023 thường ở mức trung bình đến khá. Đề thi thường có các câu hỏi cơ bản để kiểm tra kiến thức nền tảng của học sinh, đồng thời cũng có các câu hỏi nâng cao để phân loại học sinh giỏi. Để đạt được kết quả tốt trong kỳ thi này, các em học sinh cần nắm vững kiến thức cơ bản, rèn luyện kỹ năng giải bài tập, và làm quen với các dạng bài tập thường gặp.
Để ôn thi vào 10 môn Toán Tiền Giang năm 2023 hiệu quả, các em học sinh có thể tham khảo các phương pháp sau:
Có rất nhiều nguồn tài liệu ôn thi vào 10 môn Toán Tiền Giang năm 2023 mà các em học sinh có thể tham khảo, bao gồm:
Trước khi bước vào phòng thi, các em học sinh nên:
Kỳ thi tuyển sinh vào lớp 10 môn Toán Tiền Giang năm 2023 là một kỳ thi quan trọng. Hy vọng rằng với những thông tin và lời khuyên trên, các em học sinh sẽ có sự chuẩn bị tốt nhất và đạt được kết quả cao nhất trong kỳ thi này. Chúc các em thành công!