Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Tây Ninh năm 2023. Đây là tài liệu ôn tập vô cùng quan trọng dành cho các em học sinh đang chuẩn bị cho kỳ thi sắp tới.
Chúng tôi cung cấp đầy đủ các đề thi chính thức, đáp án chi tiết và phương pháp giải bài tập hiệu quả. Hãy cùng giaitoan.edu.vn chinh phục kỳ thi vào 10 môn Toán Tây Ninh một cách tự tin nhất!
Câu 1: Tính giá trị của biểu thức \(P = \sqrt 4 {\rm{ \;}} + {(\sqrt 2 )^2}\) Câu 2: Giải phương trình \({x^2} - 5x + 6 = 0\)
Câu 1: Tính giá trị của biểu thức \(P = \sqrt 4 {\rm{ \;}} + {(\sqrt 2 )^2}\)
Câu 2: Giải phương trình \({x^2} - 5x + 6 = 0\)
Câu 3: Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x - y = 5}\\{2x + y = 4}\end{array}} \right.\)
Câu 4: Vẽ đồ thị của hàm số \(y = {\rm{ \;}} - 2{x^2}\)
Câu 5: Cho tam giác A B C cân tại \(A,AB = AC = 5\) và đường cao \(AH = 3\). Tính độ dài BC.
Câu 6: Trong hệ trục tọa độ Oxy, cho đường thẳng (d): \(y = 5x - 3\). Tìm tọa độ điểm \(M\) thuộc (d) biết điểm \(M\) có hoành độ bằng 4.
Câu 7: Cho phương trình \({x^2} + (m - 8)x + 3m + 9 = 0\). Tìm giá trị của m để phuơng trình đã cho có hai nghiệm phân biệt \({x_1},{x_2}\) thoả mãn \(x_1^2 + x_2^2 = 25\).
Câu 8: Hệ thống cáp treo núi Bà Đen tình Tây Ninh gồm hai tuyến Vân Sơn và Chùa Hang có tổng cộng 191 cabin, mỗi cabin có súc chứa 10 nguời. Nếu tất cả các cabin của hai tuyến đều chứa đủ số nguời theo quy định thì số người ở tuyến Vân Sơn nhiều hơn số người ở tuyến Chùa Hang là 350 người. Tính số cabin của mỗi tuyến.
Câu 9: Cho đường tròn (O) và điểm A nằm ngoài \((O)\). Từ \(A\) vẽ các tiếp tuyến A B, A C với \((O)\) (B và C là các tiếp điểm). Gọi \({\rm{D}}\) là trung điềm của đoạn thẳng \({\rm{AC}},{\rm{BD}}\) cắt \(({\rm{O}})\) tại \({\rm{E}}\) (khác B) và BC cắt \({\rm{OA}}\) tại \({\rm{F}}\). Chứng minh bốn điểm C, D, E, F cùng thuộc một đường tròn.
Câu 10: Cho tam giác ABC vuông tại \(A\), đường cao A H. Gọi M, N lần lượt là trung điểm của HB và HC. Kẻ MK vuông góc với AN tại \(K\), MK cắt AH tại I. Tính \(\frac{{AH}}{{AI}}\).
----- HẾT -----
Câu 1 (NB):
Phương pháp:
Số \(x\)là căn bậc hai của \(a\) nếu \({x^2} = a\).
Cách giải:
Ta có: \(P = \sqrt 4 {\rm{ \;}} + {(\sqrt 2 )^2} = \sqrt {{2^2}} {\rm{ \;}} + 2 = 2 + 2 = 4\).
Vậy \({\rm{P}} = 4\).
Câu 2 (VD):
Phương pháp:
Giải phương trình bậc hai
Bước 1: Tính giá trính của \(\Delta \) với \(\Delta {\rm{ \;}} = {{\rm{b}}^2} - 4{\rm{ac}}\)
Bước 2: Xét tập nghiệm của phương trình bẳng việc sánh giá \(\Delta \) với 0
\(\Delta {\rm{ \;}} < 0 \Rightarrow \) phương trình bậc 2 vô nghiệm
\(\Delta {\rm{ \;}} = 0 \Rightarrow \) phương trình bậc 2 có nghiệm kép \({x_1} = {x_2} = {\rm{ \;}} - \frac{b}{{2a}}\)
\(\Delta {\rm{ \;}} > 0 \Rightarrow \) phương trình (1) có 2 nghiệm phân biệt, ta dùng công thức nghiệm sau: \({x_1} = \frac{{ - b + \sqrt \Delta }}{{2a}};{x_2} = \frac{{ - b - \sqrt \Delta }}{{2a}}\)
Cách giải:
Ta có: \(\Delta {\rm{ \;}} = {( - 5)^2} - 4 \cdot 1 \cdot 6 = 1 > 0\) nên phương trình có 2 nghiệm phân biệt
\(\left[ {\begin{array}{*{20}{l}}{{x_1} = \frac{{5 + \sqrt 1 }}{{2.1}} = 3}\\{{x_2} = \frac{{5 - \sqrt 1 }}{{2.1}} = 2}\end{array}.} \right.\)
Vậy tập nghiệm của phương trình là \(S = \{ 3;2\} \).
Câu 3 (VD):
Phương pháp:
Sử dụng phương pháp thế hoặc trừ vế.
Cách giải:
Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x - y = 5}\\{2x + y = 4}\end{array}} \right.\)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{x - y = 5}\\{2x + y = 4}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3x = 9}\\{y = x - 5}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = 3 - 5 = {\rm{ \;}} - 2}\end{array}} \right.} \right.} \right.\).
Vậy hệ phương trình có nghiệm duy nhất \((x;y) = (3; - 2)\).
Câu 4 (TH):
Phương pháp:
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị (thường từ 5 đến 7 giá trị) tương ứng giữa \(x\) và \(y\).
Bước 3: Vẽ đồ thị và kết luận.
* Chú ý: vì đồ thị hàm số y \( = a{x^2}(a \ne 0)\) luôn đi qua gốc tọa độ \({\rm{O}}\) và nhận trục Oy làm trục đối xứng nên khi vẽ đồ thị của hàm số này, ta chỉ cần tìm một số điểm bên phải trục Oy rồi lấy các điểm đối xứng với chúng qua Oy.
Cách giải:
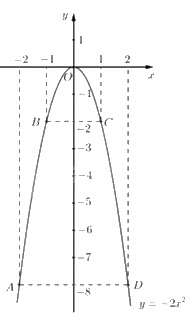
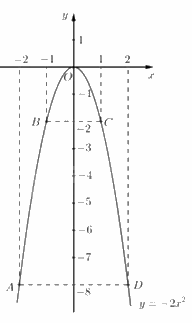
Vẽ đồ thị của hàm số \(y = - 2{x^2}\)
Ta có bảng giá trị sau:

\( \Rightarrow \) Đồ thị hàm số là đường cong parabol đi qua các điểm \(O(0;0);A( - 2; - 8);B( - 1; - 2);C( - 1; - 2);D(2; - 8)\) Hệ số \(a = - 2 < 0\) nên parabol có bề cong hướng lên. Đồ thị hàm số nhận \({\rm{Oy}}\) làm trục đối xứng.
Ta vẽ được đồ thị hàm số \(y = - 2{x^2}\) như sau:
Câu 5 (VD):
Phương pháp:
Sử dụng hệ thức lượng trong tam giác vuông.
Cách giải:
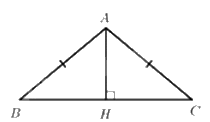
Tam giác \({\rm{ABC}}\) cân tại \({\rm{A}}\) có đường cao \({\rm{AH}}\) nên \({\rm{AH}}\) là trung tuyến (tính chất)
Do đó \({\rm{H}}\) là trung điểm của \({\rm{BC}}\).
Áp dụng định lý Py-ta-go cho tam giác AHB vuông tại \({\rm{H}}\) ta được:
\(A{H^2} + B{H^2} = A{B^2} \Leftrightarrow {3^2} + B{H^2} = {5^2}\)
\( \Leftrightarrow 9 + B{H^2} = 25\)
\( \Leftrightarrow B{H^2} = 16\)
\( \Leftrightarrow BH = 4\)
Suy ra: \(BC = 2.BH = 2.4 = 8(\;{\rm{cm}})\)
Vậy \(BC = 8\;{\rm{cm}}\).
Câu 6 (TH):
Phương pháp:
Thay giá trị của \(x\) vào phương trình đường thẳng.
Cách giải:
Thay \({\rm{x}} = 4\) vào phương trình đường thẳng \(({\rm{d}})\) ta có: \(y = 5.4 - 3 = 20 - 3 = 17\).
Vậy \(M(4;17) \in (d)\).
Câu 7 (VD):
Phương pháp:
Sử dụng định lí Vi – et
Nếu phương trình \(a{x^2} + bx + c = 0(a \ne 0)\) có 2 nghiệm \({x_1},{x_2}\) thì \(\left\{ {\begin{array}{*{20}{l}}{{\rm{S}} = {{\rm{X}}_1} + {{\rm{X}}_2} = \frac{{ - {\rm{b}}}}{{\rm{a}}}}\\{{\rm{P}} = {{\rm{X}}_1} \cdot {{\rm{X}}_2} = \frac{{\rm{c}}}{{\rm{a}}}}\end{array}} \right.\)
Cách giải:
Ta có:
\(\Delta = {(m - 8)^2} - 4 \cdot (3m + 9)\)
\(\Delta = {m^2} - 16m + 64 - 12m - 36\)
\(\Delta = {m^2} - 28m + 28\)
Để phương trình có hai nghiệm phân biệt thì \(\Delta > 0 \Leftrightarrow {m^2} - 28m + 28 > 0\). Khi đó phương trình có hai nghiệm phân biệt \({x_1},{x_2}\).
Khi đó áp dụng hệ thức Vi-ét ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = - m + 8}\\{{x_1}{x_2} = 3m + 9}\end{array}} \right.\).
Khi đó ta có:
\(x_1^2 + x_2^2 = 25 \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 25\)
\( \Leftrightarrow {( - m + 8)^2} - 2(3m + 9) = 25\)
\( \Leftrightarrow {m^2} - 16m + 64 - 6m - 18 = 25\)
\( \Leftrightarrow {m^2} - 22m + 21 = 0\)
Ta có \(a + b + c = 1 + ( - 22) + 21 = 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ {\begin{array}{*{20}{l}}{{m_1} = 1}\\{{m_2} = 21}\end{array}} \right.\).
Đối chiếu (*) ta thấy \({\rm{m}} = 1\) thoả mãn.
Vậy \(m = 1\).
Câu 8 (VD):
Phương pháp:
Giải toán bằng cách lập hệ phương trình.
Cách giải:
Gọi số cabin ở hai tuyến Vân Sơn và Chùa Hang lần lượt là x, y (cabin,\(x,y \in \mathbb{N},0 < x,y < 191\) )
Vi tổng số cabin ở hai tuyến là 191 nên ta có: \(x + y = 191\) (1)
Vì mỗi cabin có sức chứa 10 người và tồng số người ở tuyến Vân Sơn nhiều hơn số người ở tuyến Chùa Hang là \(10x - 10y = 350 \Leftrightarrow x - y = 35\) (2)
Từ (1) và (2) ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{x + y = 191}\\{x - y = 35}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2x = 226}\\{y = x - 35}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 113}\\{y = 78}\end{array}(TM)} \right.} \right.} \right.\)
Vậy tuyến Vân Sơn có 113 cabin, tuyến Chùa Hang có 78 cabin.
Câu 9 (VD):
Cách giải:
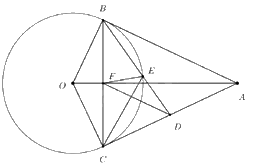
Vì \({\rm{AB}},{\rm{AC}}\) là 2 tiếp tuyến cắt nhau của \(({\rm{O}})\) nên \({\rm{AB}} = {\rm{AC}}\) (tính chất hai tiếp tuyến cắt nhau) \( \Rightarrow A\) thuộc trung trực của \({\rm{BC}}\).
Mà \({\rm{OB}} = {\rm{OC}}\) (cùng bằng bán kính) \( = > {\rm{O}}\) thuộc trung trực của \({\rm{BC}}\).
\( \Rightarrow {\rm{OA}}\) là trung trực \({\rm{BC}}\).
\( \Rightarrow OA \bot BC\) tại \({\rm{F}}\) và \({\rm{F}}\) là trung điểm của \({\rm{BC}}\).
Do \({\rm{F}}\) là trung điểm của \({\rm{BC}}\) và \({\rm{D}}\) là trung điểm của \({\rm{AC}}\) (gt)
\( \Rightarrow \) FD là đường trung bình của \(\Delta ABC\) (định nghĩa)
(tính chất)
\( \Rightarrow \angle FDB = \angle DBA\) (so le trong)
Mà \(\angle ECF = \angle DBA\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \({\rm{BE}}\) )
\( \Rightarrow \angle EDF = \angle ECF( = \angle EBA)\)
Mà \({\rm{D}},{\rm{C}}\) là 2 đỉnh kề nhau cùng nhìn \({\rm{EF}}\) dưới 2 góc bằng nhau
\( \Rightarrow E,F,C,D\) cùng thuộc một đường tròn
\( \Rightarrow ECDF\) là tứ giác nội tiếp (dhnb).
Câu 10 (VDC):
Cách giải:
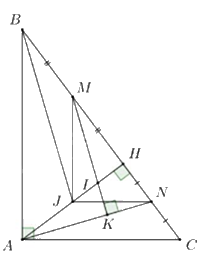
Gọi \({\rm{J}}\) là trung điểm của \({\rm{AH}}\).
Xét tam giác \({\rm{ABH}}\) và tam giác \({\rm{CAH}}\) có:
\(\angle AHB = \angle AHC = 90^\circ ({\rm{ do }}AH \bot BC)\)
\(\angle ABH = \angle CAH\) (cùng phụ với \(\angle CAH\))
$\Rightarrow \Delta ABH\backsim \Delta CAH(g\cdot g)\Rightarrow \frac{AB}{AH}=\frac{AC}{CH}$
\( \Rightarrow \frac{{AB}}{{2AJ}} = \frac{{AC}}{{2CN}} \Rightarrow \frac{{AB}}{{AJ}} = \frac{{AC}}{{CN}}\)
Xét tam giác \({\rm{ABJ}}\) và \({\rm{CAN}}\) có:
\(\angle BAJ = \angle ACN{\rm{ }}\)(cùng phụ với \(\angle HAC\))
\(\frac{{AB}}{{AJ}} = \frac{{AC}}{{CN}}(cmt){\rm{ }}\)
\( \Rightarrow \Delta ABJ = \Delta CAN(c.g.c) \Rightarrow \angle ABJ = \angle CAN\)(Hai goc tương ứng)
Ta có \({\rm{MJ}}\) là đường trung bình của tam giác \({\rm{HAB}}\) (định nghĩa)
\( \Rightarrow {\rm{MJ}}//{\rm{AB}}\) (tính chất đường trung bình)
\( \Rightarrow \angle ABJ = \angle BJM\) (so le trong)
Tương tự: \({\rm{JN}}\) là đường trung bình của tam giác \({\rm{AHC}}\) (định nghĩa)
\( \Rightarrow {\rm{JN}}//{\rm{AC}}\) (tính chất đường trung bình)
\( \Rightarrow \angle CAN = \angle ANJ\) (so le trong)
Ta có \(\left\{ {\begin{array}{*{20}{l}}{MJ//AB({\rm{cmt}})}\\{JN//AC({\rm{cmt}}) \Rightarrow MJ \bot JN \Rightarrow \angle MJN = 90^\circ }\\{AB \bot AC}\end{array}} \right.\)
Xét tứ giác \({\rm{MJKN}}\) có: \(\angle MJN = \angle MKN = 90^\circ \), mà hai đỉnh \({\rm{J}},{\rm{K}}\) kề nhau cùng nhìn \({\rm{MN}}\) dưới hai góc bằng nhau \( \Rightarrow {\rm{MJKN}}\) là tứ giác nội tiếp (dhnb) \( \Rightarrow \angle ANJ = \angle JMK\) (hai góc nội tiếp cùng chắn cung \({\rm{JK}}\) )
Từ (1), (2), (3), (4) \( \Rightarrow \angle BJM = \angle JMK\).
Mà 2 góc này ở vị trí hai góc so le trong bằng nhau \( \Rightarrow {\rm{BJ}}//{\rm{MK}}({\rm{dhnb}}) \Rightarrow {\rm{BJ}}//{\rm{MI}}\).
Xét tam giác \({\rm{BHJ}}\) có: \({\rm{M}}\) là trung điểm của \({\rm{BH}},{\rm{BJ}}//{\rm{MI}}({\rm{cmt}})\)
\( \Rightarrow {\rm{I}}\) là trung điểm của \({\rm{JH}}\) (tính chất đường trung bình của tam giác).
\( \Rightarrow IH = \frac{1}{2}JH = \frac{1}{2} \cdot \frac{1}{2}AH = \frac{1}{4}AH\)
\( \Rightarrow AI = AH - IH = \frac{3}{4}AH \Rightarrow \frac{{AH}}{{AI}} = \frac{4}{3}\)
Câu 1: Tính giá trị của biểu thức \(P = \sqrt 4 {\rm{ \;}} + {(\sqrt 2 )^2}\)
Câu 2: Giải phương trình \({x^2} - 5x + 6 = 0\)
Câu 3: Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x - y = 5}\\{2x + y = 4}\end{array}} \right.\)
Câu 4: Vẽ đồ thị của hàm số \(y = {\rm{ \;}} - 2{x^2}\)
Câu 5: Cho tam giác A B C cân tại \(A,AB = AC = 5\) và đường cao \(AH = 3\). Tính độ dài BC.
Câu 6: Trong hệ trục tọa độ Oxy, cho đường thẳng (d): \(y = 5x - 3\). Tìm tọa độ điểm \(M\) thuộc (d) biết điểm \(M\) có hoành độ bằng 4.
Câu 7: Cho phương trình \({x^2} + (m - 8)x + 3m + 9 = 0\). Tìm giá trị của m để phuơng trình đã cho có hai nghiệm phân biệt \({x_1},{x_2}\) thoả mãn \(x_1^2 + x_2^2 = 25\).
Câu 8: Hệ thống cáp treo núi Bà Đen tình Tây Ninh gồm hai tuyến Vân Sơn và Chùa Hang có tổng cộng 191 cabin, mỗi cabin có súc chứa 10 nguời. Nếu tất cả các cabin của hai tuyến đều chứa đủ số nguời theo quy định thì số người ở tuyến Vân Sơn nhiều hơn số người ở tuyến Chùa Hang là 350 người. Tính số cabin của mỗi tuyến.
Câu 9: Cho đường tròn (O) và điểm A nằm ngoài \((O)\). Từ \(A\) vẽ các tiếp tuyến A B, A C với \((O)\) (B và C là các tiếp điểm). Gọi \({\rm{D}}\) là trung điềm của đoạn thẳng \({\rm{AC}},{\rm{BD}}\) cắt \(({\rm{O}})\) tại \({\rm{E}}\) (khác B) và BC cắt \({\rm{OA}}\) tại \({\rm{F}}\). Chứng minh bốn điểm C, D, E, F cùng thuộc một đường tròn.
Câu 10: Cho tam giác ABC vuông tại \(A\), đường cao A H. Gọi M, N lần lượt là trung điểm của HB và HC. Kẻ MK vuông góc với AN tại \(K\), MK cắt AH tại I. Tính \(\frac{{AH}}{{AI}}\).
----- HẾT -----
Câu 1 (NB):
Phương pháp:
Số \(x\)là căn bậc hai của \(a\) nếu \({x^2} = a\).
Cách giải:
Ta có: \(P = \sqrt 4 {\rm{ \;}} + {(\sqrt 2 )^2} = \sqrt {{2^2}} {\rm{ \;}} + 2 = 2 + 2 = 4\).
Vậy \({\rm{P}} = 4\).
Câu 2 (VD):
Phương pháp:
Giải phương trình bậc hai
Bước 1: Tính giá trính của \(\Delta \) với \(\Delta {\rm{ \;}} = {{\rm{b}}^2} - 4{\rm{ac}}\)
Bước 2: Xét tập nghiệm của phương trình bẳng việc sánh giá \(\Delta \) với 0
\(\Delta {\rm{ \;}} < 0 \Rightarrow \) phương trình bậc 2 vô nghiệm
\(\Delta {\rm{ \;}} = 0 \Rightarrow \) phương trình bậc 2 có nghiệm kép \({x_1} = {x_2} = {\rm{ \;}} - \frac{b}{{2a}}\)
\(\Delta {\rm{ \;}} > 0 \Rightarrow \) phương trình (1) có 2 nghiệm phân biệt, ta dùng công thức nghiệm sau: \({x_1} = \frac{{ - b + \sqrt \Delta }}{{2a}};{x_2} = \frac{{ - b - \sqrt \Delta }}{{2a}}\)
Cách giải:
Ta có: \(\Delta {\rm{ \;}} = {( - 5)^2} - 4 \cdot 1 \cdot 6 = 1 > 0\) nên phương trình có 2 nghiệm phân biệt
\(\left[ {\begin{array}{*{20}{l}}{{x_1} = \frac{{5 + \sqrt 1 }}{{2.1}} = 3}\\{{x_2} = \frac{{5 - \sqrt 1 }}{{2.1}} = 2}\end{array}.} \right.\)
Vậy tập nghiệm của phương trình là \(S = \{ 3;2\} \).
Câu 3 (VD):
Phương pháp:
Sử dụng phương pháp thế hoặc trừ vế.
Cách giải:
Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x - y = 5}\\{2x + y = 4}\end{array}} \right.\)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{x - y = 5}\\{2x + y = 4}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3x = 9}\\{y = x - 5}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = 3 - 5 = {\rm{ \;}} - 2}\end{array}} \right.} \right.} \right.\).
Vậy hệ phương trình có nghiệm duy nhất \((x;y) = (3; - 2)\).
Câu 4 (TH):
Phương pháp:
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị (thường từ 5 đến 7 giá trị) tương ứng giữa \(x\) và \(y\).
Bước 3: Vẽ đồ thị và kết luận.
* Chú ý: vì đồ thị hàm số y \( = a{x^2}(a \ne 0)\) luôn đi qua gốc tọa độ \({\rm{O}}\) và nhận trục Oy làm trục đối xứng nên khi vẽ đồ thị của hàm số này, ta chỉ cần tìm một số điểm bên phải trục Oy rồi lấy các điểm đối xứng với chúng qua Oy.
Cách giải:
Vẽ đồ thị của hàm số \(y = - 2{x^2}\)
Ta có bảng giá trị sau:

\( \Rightarrow \) Đồ thị hàm số là đường cong parabol đi qua các điểm \(O(0;0);A( - 2; - 8);B( - 1; - 2);C( - 1; - 2);D(2; - 8)\) Hệ số \(a = - 2 < 0\) nên parabol có bề cong hướng lên. Đồ thị hàm số nhận \({\rm{Oy}}\) làm trục đối xứng.
Ta vẽ được đồ thị hàm số \(y = - 2{x^2}\) như sau:
Câu 5 (VD):
Phương pháp:
Sử dụng hệ thức lượng trong tam giác vuông.
Cách giải:
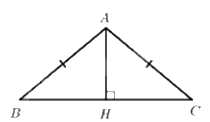
Tam giác \({\rm{ABC}}\) cân tại \({\rm{A}}\) có đường cao \({\rm{AH}}\) nên \({\rm{AH}}\) là trung tuyến (tính chất)
Do đó \({\rm{H}}\) là trung điểm của \({\rm{BC}}\).
Áp dụng định lý Py-ta-go cho tam giác AHB vuông tại \({\rm{H}}\) ta được:
\(A{H^2} + B{H^2} = A{B^2} \Leftrightarrow {3^2} + B{H^2} = {5^2}\)
\( \Leftrightarrow 9 + B{H^2} = 25\)
\( \Leftrightarrow B{H^2} = 16\)
\( \Leftrightarrow BH = 4\)
Suy ra: \(BC = 2.BH = 2.4 = 8(\;{\rm{cm}})\)
Vậy \(BC = 8\;{\rm{cm}}\).
Câu 6 (TH):
Phương pháp:
Thay giá trị của \(x\) vào phương trình đường thẳng.
Cách giải:
Thay \({\rm{x}} = 4\) vào phương trình đường thẳng \(({\rm{d}})\) ta có: \(y = 5.4 - 3 = 20 - 3 = 17\).
Vậy \(M(4;17) \in (d)\).
Câu 7 (VD):
Phương pháp:
Sử dụng định lí Vi – et
Nếu phương trình \(a{x^2} + bx + c = 0(a \ne 0)\) có 2 nghiệm \({x_1},{x_2}\) thì \(\left\{ {\begin{array}{*{20}{l}}{{\rm{S}} = {{\rm{X}}_1} + {{\rm{X}}_2} = \frac{{ - {\rm{b}}}}{{\rm{a}}}}\\{{\rm{P}} = {{\rm{X}}_1} \cdot {{\rm{X}}_2} = \frac{{\rm{c}}}{{\rm{a}}}}\end{array}} \right.\)
Cách giải:
Ta có:
\(\Delta = {(m - 8)^2} - 4 \cdot (3m + 9)\)
\(\Delta = {m^2} - 16m + 64 - 12m - 36\)
\(\Delta = {m^2} - 28m + 28\)
Để phương trình có hai nghiệm phân biệt thì \(\Delta > 0 \Leftrightarrow {m^2} - 28m + 28 > 0\). Khi đó phương trình có hai nghiệm phân biệt \({x_1},{x_2}\).
Khi đó áp dụng hệ thức Vi-ét ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = - m + 8}\\{{x_1}{x_2} = 3m + 9}\end{array}} \right.\).
Khi đó ta có:
\(x_1^2 + x_2^2 = 25 \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 25\)
\( \Leftrightarrow {( - m + 8)^2} - 2(3m + 9) = 25\)
\( \Leftrightarrow {m^2} - 16m + 64 - 6m - 18 = 25\)
\( \Leftrightarrow {m^2} - 22m + 21 = 0\)
Ta có \(a + b + c = 1 + ( - 22) + 21 = 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ {\begin{array}{*{20}{l}}{{m_1} = 1}\\{{m_2} = 21}\end{array}} \right.\).
Đối chiếu (*) ta thấy \({\rm{m}} = 1\) thoả mãn.
Vậy \(m = 1\).
Câu 8 (VD):
Phương pháp:
Giải toán bằng cách lập hệ phương trình.
Cách giải:
Gọi số cabin ở hai tuyến Vân Sơn và Chùa Hang lần lượt là x, y (cabin,\(x,y \in \mathbb{N},0 < x,y < 191\) )
Vi tổng số cabin ở hai tuyến là 191 nên ta có: \(x + y = 191\) (1)
Vì mỗi cabin có sức chứa 10 người và tồng số người ở tuyến Vân Sơn nhiều hơn số người ở tuyến Chùa Hang là \(10x - 10y = 350 \Leftrightarrow x - y = 35\) (2)
Từ (1) và (2) ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{x + y = 191}\\{x - y = 35}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2x = 226}\\{y = x - 35}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 113}\\{y = 78}\end{array}(TM)} \right.} \right.} \right.\)
Vậy tuyến Vân Sơn có 113 cabin, tuyến Chùa Hang có 78 cabin.
Câu 9 (VD):
Cách giải:
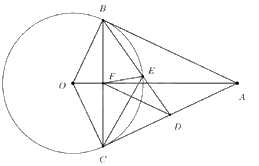
Vì \({\rm{AB}},{\rm{AC}}\) là 2 tiếp tuyến cắt nhau của \(({\rm{O}})\) nên \({\rm{AB}} = {\rm{AC}}\) (tính chất hai tiếp tuyến cắt nhau) \( \Rightarrow A\) thuộc trung trực của \({\rm{BC}}\).
Mà \({\rm{OB}} = {\rm{OC}}\) (cùng bằng bán kính) \( = > {\rm{O}}\) thuộc trung trực của \({\rm{BC}}\).
\( \Rightarrow {\rm{OA}}\) là trung trực \({\rm{BC}}\).
\( \Rightarrow OA \bot BC\) tại \({\rm{F}}\) và \({\rm{F}}\) là trung điểm của \({\rm{BC}}\).
Do \({\rm{F}}\) là trung điểm của \({\rm{BC}}\) và \({\rm{D}}\) là trung điểm của \({\rm{AC}}\) (gt)
\( \Rightarrow \) FD là đường trung bình của \(\Delta ABC\) (định nghĩa)
(tính chất)
\( \Rightarrow \angle FDB = \angle DBA\) (so le trong)
Mà \(\angle ECF = \angle DBA\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \({\rm{BE}}\) )
\( \Rightarrow \angle EDF = \angle ECF( = \angle EBA)\)
Mà \({\rm{D}},{\rm{C}}\) là 2 đỉnh kề nhau cùng nhìn \({\rm{EF}}\) dưới 2 góc bằng nhau
\( \Rightarrow E,F,C,D\) cùng thuộc một đường tròn
\( \Rightarrow ECDF\) là tứ giác nội tiếp (dhnb).
Câu 10 (VDC):
Cách giải:
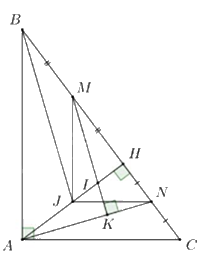
Gọi \({\rm{J}}\) là trung điểm của \({\rm{AH}}\).
Xét tam giác \({\rm{ABH}}\) và tam giác \({\rm{CAH}}\) có:
\(\angle AHB = \angle AHC = 90^\circ ({\rm{ do }}AH \bot BC)\)
\(\angle ABH = \angle CAH\) (cùng phụ với \(\angle CAH\))
$\Rightarrow \Delta ABH\backsim \Delta CAH(g\cdot g)\Rightarrow \frac{AB}{AH}=\frac{AC}{CH}$
\( \Rightarrow \frac{{AB}}{{2AJ}} = \frac{{AC}}{{2CN}} \Rightarrow \frac{{AB}}{{AJ}} = \frac{{AC}}{{CN}}\)
Xét tam giác \({\rm{ABJ}}\) và \({\rm{CAN}}\) có:
\(\angle BAJ = \angle ACN{\rm{ }}\)(cùng phụ với \(\angle HAC\))
\(\frac{{AB}}{{AJ}} = \frac{{AC}}{{CN}}(cmt){\rm{ }}\)
\( \Rightarrow \Delta ABJ = \Delta CAN(c.g.c) \Rightarrow \angle ABJ = \angle CAN\)(Hai goc tương ứng)
Ta có \({\rm{MJ}}\) là đường trung bình của tam giác \({\rm{HAB}}\) (định nghĩa)
\( \Rightarrow {\rm{MJ}}//{\rm{AB}}\) (tính chất đường trung bình)
\( \Rightarrow \angle ABJ = \angle BJM\) (so le trong)
Tương tự: \({\rm{JN}}\) là đường trung bình của tam giác \({\rm{AHC}}\) (định nghĩa)
\( \Rightarrow {\rm{JN}}//{\rm{AC}}\) (tính chất đường trung bình)
\( \Rightarrow \angle CAN = \angle ANJ\) (so le trong)
Ta có \(\left\{ {\begin{array}{*{20}{l}}{MJ//AB({\rm{cmt}})}\\{JN//AC({\rm{cmt}}) \Rightarrow MJ \bot JN \Rightarrow \angle MJN = 90^\circ }\\{AB \bot AC}\end{array}} \right.\)
Xét tứ giác \({\rm{MJKN}}\) có: \(\angle MJN = \angle MKN = 90^\circ \), mà hai đỉnh \({\rm{J}},{\rm{K}}\) kề nhau cùng nhìn \({\rm{MN}}\) dưới hai góc bằng nhau \( \Rightarrow {\rm{MJKN}}\) là tứ giác nội tiếp (dhnb) \( \Rightarrow \angle ANJ = \angle JMK\) (hai góc nội tiếp cùng chắn cung \({\rm{JK}}\) )
Từ (1), (2), (3), (4) \( \Rightarrow \angle BJM = \angle JMK\).
Mà 2 góc này ở vị trí hai góc so le trong bằng nhau \( \Rightarrow {\rm{BJ}}//{\rm{MK}}({\rm{dhnb}}) \Rightarrow {\rm{BJ}}//{\rm{MI}}\).
Xét tam giác \({\rm{BHJ}}\) có: \({\rm{M}}\) là trung điểm của \({\rm{BH}},{\rm{BJ}}//{\rm{MI}}({\rm{cmt}})\)
\( \Rightarrow {\rm{I}}\) là trung điểm của \({\rm{JH}}\) (tính chất đường trung bình của tam giác).
\( \Rightarrow IH = \frac{1}{2}JH = \frac{1}{2} \cdot \frac{1}{2}AH = \frac{1}{4}AH\)
\( \Rightarrow AI = AH - IH = \frac{3}{4}AH \Rightarrow \frac{{AH}}{{AI}} = \frac{4}{3}\)
Kỳ thi tuyển sinh vào lớp 10 môn Toán tại Tây Ninh năm 2023 là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Đề thi thường bao gồm các kiến thức trọng tâm của chương trình Toán lớp 9, tập trung vào các chủ đề như đại số, hình học, số học và các ứng dụng thực tế. Việc nắm vững kiến thức nền tảng và luyện tập thường xuyên là chìa khóa để đạt kết quả tốt trong kỳ thi này.
Cấu trúc đề thi thường bao gồm các dạng bài tập sau:
Để chuẩn bị tốt nhất cho kỳ thi, các em học sinh cần tập trung vào các chủ đề sau:
Việc luyện tập với các đề thi thử và đề thi chính thức của các năm trước là một phương pháp hiệu quả để làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải bài tập và đánh giá năng lực bản thân. Giaitoan.edu.vn cung cấp đầy đủ các đề thi vào 10 môn Toán Tây Ninh năm 2023, đáp án chi tiết và phương pháp giải bài tập hiệu quả.
Để giải đề thi vào 10 môn Toán Tây Ninh năm 2023 một cách hiệu quả, các em học sinh cần:
Ngoài các đề thi, các em học sinh có thể tham khảo các tài liệu ôn thi sau:
Hãy tự tin vào bản thân, chuẩn bị kỹ lưỡng và giữ tâm lý thoải mái trong kỳ thi. Chúc các em học sinh đạt kết quả tốt nhất!
| Trường THPT | Điểm chuẩn (2022) |
|---|---|
| Trường THPT Chuyên Hoàng Lê Kha | 35.0 - 40.0 |
| Trường THPT Tây Ninh | 30.0 - 35.0 |
| Trường THPT Trần Đại Nghĩa | 28.0 - 33.0 |
| *Lưu ý: Điểm chuẩn có thể thay đổi theo từng năm. | |