Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Thanh Hóa năm 2023. Đây là tài liệu ôn tập vô cùng quan trọng dành cho các em học sinh đang chuẩn bị cho kỳ thi sắp tới.
Chúng tôi cung cấp đầy đủ các đề thi chính thức, đáp án chi tiết và phương pháp giải bài tập hiệu quả. Hãy cùng giaitoan.edu.vn chinh phục kỳ thi vào 10 môn Toán Thanh Hóa 2023!
Câu 1: Cho biểu thức \(P = \frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} + 2}} + \frac{{\sqrt x {\rm{ \;}} + 1}}{{\sqrt x {\rm{ \;}} - 2}} - \frac{{2 + 5\sqrt x }}{{x - 4}}\) với \(x \ge 0,x \ne 4\). 1. Rút gọn biểu thức P 2. Tìm tất cả các giá trị của \(x\) để \(P > 1\).
Câu 1: Cho biểu thức \(P = \frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} + 2}} + \frac{{\sqrt x {\rm{ \;}} + 1}}{{\sqrt x {\rm{ \;}} - 2}} - \frac{{2 + 5\sqrt x }}{{x - 4}}\) với \(x \ge 0,x \ne 4\).
1. Rút gọn biểu thức P
2. Tìm tất cả các giá trị của \(x\) để \(P > 1\).
Câu 2:
1. Trong mặt phẳng tọa độ Oxy, cho đường thẳng \((d)\) có phương trình \(y = ax + b\). Tìm a, b để đường thẳng \((d)\) có hệ số góc bằng 3 và đi qua điểm \(M( - 1;2).\)
2. Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{3x + y = 6}\\{x - y = {\rm{ \;}} - 2}\end{array}} \right.\)
Câu 3:
1. Giải phương trình \({x^2} - 3x + 2 = 0\).
2. Cho phương trình \({x^2} - 2mx - {m^2} - 2 = 0\) ( \(m\) là tham số). Tìm các giá trị của \(m\) để phương trình có hai nghiệm \({x_1},{x_2}\) (với \({x_1} < {x_2}\) ) thỏa mãn hệ thức \({x_2} - 2\left| {{x_1}} \right| - 3{x_1}{x_2} = 3{m^2} + 3m + 4\).
Câu 4: Cho đường tròn (O) và một điểm M nằm ngoài đường tròn. Từ điểm M kẻ hai tiếp tuyến MA, MB đến (O) (với A, B là các tiếp điểm). Gọi C là điểm đối xứng với B qua O, đường thẳng MC cắt đường tròn (O) tại D (D khác C).
1. Chứng minh MAOB là tứ giác nội tiếp.
2. Gọi N là giao điểm của hai đường thẳng AD và MO. Chứng minh rằng MN2 = ND.NA.
3. Gọi H là giao điểm của MO và AB. Chứng minh \({\left( {\frac{{HA}}{{HD}}} \right)^2} - \frac{{AC}}{{HN}} = 1\).
Câu 5: Cho các số thực không âm x, y, z thỏa mãn \(4{x^2} + {y^2} + 4{z^2} \le 6y\).
Tìm giá trị nhỏ nhất của biểu thức \(M = \frac{8}{{{{(x + 3)}^2}}} + \frac{{16}}{{{{(y + 4)}^2}}} + \frac{1}{{{{(z + 1)}^2}}} + 2023\).
----- HẾT -----
Câu 1: Cho biểu thức \(P = \frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} + 2}} + \frac{{\sqrt x {\rm{ \;}} + 1}}{{\sqrt x {\rm{ \;}} - 2}} - \frac{{2 + 5\sqrt x }}{{x - 4}}\) với \(x \ge 0,x \ne 4\).
1. Rút gọn biểu thức P
2. Tìm tất cả các giá trị của \(x\) để \(P > 1\).
Câu 2:
1. Trong mặt phẳng tọa độ Oxy, cho đường thẳng \((d)\) có phương trình \(y = ax + b\). Tìm a, b để đường thẳng \((d)\) có hệ số góc bằng 3 và đi qua điểm \(M( - 1;2).\)
2. Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{3x + y = 6}\\{x - y = {\rm{ \;}} - 2}\end{array}} \right.\)
Câu 3:
1. Giải phương trình \({x^2} - 3x + 2 = 0\).
2. Cho phương trình \({x^2} - 2mx - {m^2} - 2 = 0\) ( \(m\) là tham số). Tìm các giá trị của \(m\) để phương trình có hai nghiệm \({x_1},{x_2}\) (với \({x_1} < {x_2}\) ) thỏa mãn hệ thức \({x_2} - 2\left| {{x_1}} \right| - 3{x_1}{x_2} = 3{m^2} + 3m + 4\).
Câu 4: Cho đường tròn (O) và một điểm M nằm ngoài đường tròn. Từ điểm M kẻ hai tiếp tuyến MA, MB đến (O) (với A, B là các tiếp điểm). Gọi C là điểm đối xứng với B qua O, đường thẳng MC cắt đường tròn (O) tại D (D khác C).
1. Chứng minh MAOB là tứ giác nội tiếp.
2. Gọi N là giao điểm của hai đường thẳng AD và MO. Chứng minh rằng MN2 = ND.NA.
3. Gọi H là giao điểm của MO và AB. Chứng minh \({\left( {\frac{{HA}}{{HD}}} \right)^2} - \frac{{AC}}{{HN}} = 1\).
Câu 5: Cho các số thực không âm x, y, z thỏa mãn \(4{x^2} + {y^2} + 4{z^2} \le 6y\).
Tìm giá trị nhỏ nhất của biểu thức \(M = \frac{8}{{{{(x + 3)}^2}}} + \frac{{16}}{{{{(y + 4)}^2}}} + \frac{1}{{{{(z + 1)}^2}}} + 2023\).
----- HẾT -----
Câu 1 (VD):
Phương pháp:
1. Quy đồng và rút gọn.
2. Giải phương trình P > 1.
Cách giải:
1. Rút gọn biểu thức P
Ta có \(P = \frac{{\sqrt x }}{{\sqrt x + 2}} + \frac{{\sqrt x + 1}}{{\sqrt x - 2}} - \frac{{2 + 5\sqrt x }}{{x - 4}}\)
\(\begin{array}{l} = \frac{{\sqrt x \left( {\sqrt x - 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} + \frac{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} - \frac{{2 + 5\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\ = \frac{{x - 2\sqrt x + x + 3\sqrt x + 2 - 2 - 5\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\ = \frac{{2x - 4\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\ = \frac{{2\sqrt x \left( {\sqrt x - 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\ = \frac{{2\sqrt x }}{{\sqrt x + 2}}\end{array}\)
Vậy \(P = \frac{{2\sqrt x }}{{\sqrt x + 2}}\) với \(x \ge 0,x \ne 4\)
2. Tìm tất cả các giá trị của \(x\) để \(P > 1\).
Để \(P > 1\)
\(\frac{{2\sqrt x }}{{\sqrt x + 2}} > 1 \Leftrightarrow 2\sqrt x > \sqrt x + 2\) (do \(\sqrt x + 2\) > 0)
\(\begin{array}{l} \Leftrightarrow \sqrt x > 2\\ \Leftrightarrow x > 4\end{array}\)
Đối chiếu với điều kiện \(x \ge 0,x \ne 4\), để P > 1 thì \(x > 4\)
Câu 2 (VD):
Phương pháp:
1. \(y = ax + b\) có hệ số góc là a.
2. Sử dụng phương pháp thế hoặc trừ vế.
Cách giải:
1. Trong mặt phẳng tọa độ Oxy, cho đường thẳng \((d)\) có phương trình \(y = ax + b\). Tìm a, b để đường thẳng \((d)\) có hệ số góc bằng 3 và đi qua điểm \(M( - 1;2).\)
Vì (d) có hệ số góc bằng 3 nên suy ra: \(a = 3.\)
Khi đó phương trình đường thẳng (d) có dạng \(y = 3x + b\)
Vì (d) đi qua điểm \(M( - 1;2)\) nên thay tọa độ điểm M vào phương trình đường thẳng (d) ta được:
\(2 = 3.\left( { - 1} \right) + b \Leftrightarrow 2 = - 3 + b \Leftrightarrow b = 5\)
Vậy \(a = 3;\,\,b = 5.\)
2. Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{3x + y = 6}\\{x - y = - 2}\end{array}} \right.\)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{3x + y = 6}\\{x - y = - 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4x = 4}\\{y = x + 2}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1}\\{y = 3}\end{array}} \right.} \right.\)
Vậy hệ phương trình có nghiệm duy nhất là: \(\left( {x;y} \right) = \left( {1;3} \right)\).
Câu 3 (NB):
Phương pháp:
1. Bước 1: Tính giá trính của \(\Delta \) với \(\Delta \; = {{\rm{b}}^2} - 4{\rm{ac}}\)
Bước 2: Xét tập nghiệm của phương trình bằng việc sánh giá \(\Delta \) với 0
\(\Delta \; < 0 \Rightarrow \) phương trình bậc 2 vô nghiệm
\(\Delta \; = 0 \Rightarrow \) phương trình bậc 2 có nghiệm kép \({x_1} = {x_2} = \; - \frac{b}{{2a}}\)
\(\Delta \; > 0 \Rightarrow \) phương trình (1) có 2 nghiệm phân biệt, ta dùng công thức nghiệm sau: \({x_{1,2}} = \frac{{ - b \pm \sqrt \Delta {\rm{ \;}}}}{{2a}}\).
2. Sử dụng Vi et.
Cách giải:
1. Giải phương trình \({x^2} - 3x + 2 = 0\).
Xét phương trình \({x^2} - 3x + 2 = 0\) có \(a + b + c = 0\) nên ta có phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = 1\\{x_2} = \frac{c}{a} = 2\end{array} \right.\)
Vậy phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = 1\\{x_2} = 2\end{array} \right.\).
2. Cho phương trình \({x^2} - 2mx - {m^2} - 2 = 0\) ( \(m\) là tham số). Tìm các giá trị của \(m\) để phương trình có hai nghiệm \({x_1},{x_2}\) (với \({x_1} < {x_2}\) ) thỏa mãn hệ thức \({x_2} - 2\left| {{x_1}} \right| - 3{x_1}{x_2} = 3{m^2} + 3m + 4\).
Xét phương trình \({x^2} - 2mx - {m^2} - 2 = 0\) có \(\Delta ' = {\left( { - m} \right)^2} - 1.\left( { - {m^2} - 2} \right) = {m^2} + {m^2} + 2 = 2{m^2} + 2 > 0\) với mọi m.
Áp dụng định lí Vi – ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}{x_2} = - {m^2} - 2\end{array} \right.\) . (2)
Nhận thấy \({x_1}{x_2} = - {m^2} - 2 < 0\) với mọi m nên phương trình có hai nghiệm trái dấu \({x_1} < 0 < {x_2}\).
\(\begin{array}{l}{x_2} - 2\left| {{x_1}} \right| - 3{x_1}{x_2} = 3{m^2} + 3m + 4\\ \Leftrightarrow {x_2} + 2{x_1} - 3{x_1}{x_2} = 3{m^2} + 3m + 4\\ \Leftrightarrow 2{x_1} + {x_2} - 3\left( { - {m^2} - 2} \right) = 3{m^2} + 3m + 4\\ \Leftrightarrow 2{x_1} + {x_2} + 3{m^2} + 6 = 3{m^2} + 3m + 4\\ \Leftrightarrow 2{x_1} + {x_2} = 3m - 2\end{array}\)
Ta có hệ phương trình \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\2{x_1} + {x_2} = 3m - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_1} = m - 2\\{x_2} = 2m - m + 2 = m + 2\end{array} \right.\)
Thay vào \({x_1}{x_2} = - {m^2} - 2\) ta được phương trình
\(\begin{array}{l}\left( {m - 2} \right)\left( {m + 2} \right) = - {m^2} - 2\\ \Leftrightarrow {m^2} - 4 = - {m^2} - 2\\ \Leftrightarrow 2{m^2} = 2\end{array}\)
\(\begin{array}{l} \Leftrightarrow {m^2} = 1\\ \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - 1\end{array} \right.\end{array}\)
Vậy \(\left[ \begin{array}{l}m = 1\\m = - 1\end{array} \right.\) thỏa mãn yêu cầu bài toán.
Câu 4 (VD):
Cách giải:
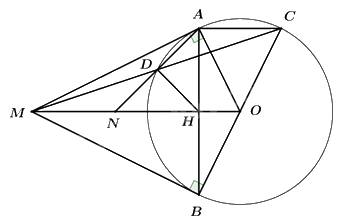
1. Chứng minh MAOB là tứ giác nội tiếp.
Vì MA, MB là tiếp tuyến của (O) (gt) \( \Rightarrow \angle MAO = \angle MBO = {90^0}\).
\( \Rightarrow \angle MAO + \angle MBO = {90^0} + {90^0} = {180^0}\).
Mà A, B là hai đỉnh đối diện của tứ giác MAOB.
Vậy MAOB là tứ giác nội tiếp (dhnb).
2. Gọi N là giao điểm của hai đường thẳng AD và MO. Chứng minh rằng MN2 = ND.NA.
Ta có: \(\angle MDN = \angle ADC\) (đối đỉnh), \(\angle ADC = \angle ABC\) (hai góc nội tiếp cùng chắn cung AC)
\( \Rightarrow \angle MDN = \angle ABC\).
Mà \(\angle ABC = \angle ABO = \angle AMO = \angle AMN\) (hai góc nội tiếp cùng chắn cung AO).
\( \Rightarrow \angle MDN = \angle AMN\).
Xét \(\Delta MND\) và \(\Delta ANM\) có:
\(\begin{array}{l}\angle ANM\,\,chung\\\angle MDN = \angle AMN\,\,\left( {cmt} \right)\end{array}\)
$\Rightarrow \Delta MND\backsim \Delta ANM\,\,\left( g.g \right)$
\( \Rightarrow \frac{{MN}}{{NA}} = \frac{{ND}}{{MN}}\) (cặp cạnh tương ứng tỉ lệ) \( \Rightarrow M{N^2} = ND.NA\,\,\left( {dpcm} \right)\).
3. Gọi H là giao điểm của MO và AB. Chứng minh \({\left( {\frac{{HA}}{{HD}}} \right)^2} - \frac{{AC}}{{HN}} = 1\).
Xét \(\Delta MAD\) và \(\Delta MCA\) có:
\(\angle AMC\) chung
\(\angle MAD = \angle MCA\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AD).
$\Rightarrow \Delta MAD\backsim \Delta MCA\,\,\left( g.g \right)$
\( \Rightarrow \frac{{MA}}{{MC}} = \frac{{MD}}{{MA}}\) (cặp cạnh tương ứng tỉ lệ)
\( \Rightarrow M{A^2} = MC.MD\) (1)
Ta có: \(OA = OB\,\,\left( { = R} \right) \Rightarrow O\) thuộc trung trực của AB.
\(MA = MB\) (tính chất hai tiếp tuyến cắt nhau) \( \Rightarrow M\) thuộc trung trực của AB.
\( \Rightarrow OM\) là trung trực của AB \( \Rightarrow OM \bot AB\) tại H.
Xét tam giác OAM vuông tại A có đường cao AH, áp dụng hệ thức lượng trong tam giác vuông ta có:
\(M{A^2} = MH.MO\) (2)
Từ (1), (2) \( \Rightarrow MC.MD = MH.MO \Rightarrow \frac{{MC}}{{MH}} = \frac{{MO}}{{MD}}\).
Xét \(\Delta MOC\) và \(\Delta MDH\) có:
\(\angle OMC\) chung
\(\frac{{MC}}{{MH}} = \frac{{MO}}{{MD}}\,\,\left( {cmt} \right)\)
$\Rightarrow \Delta MOC\backsim \Delta MDH\,\,\left( g.g \right)$
\( \Rightarrow \angle MHD = \angle MCO\) (hai góc tương ứng)
Mà \(\angle MCO = \angle DCB = \angle DAB\) (hai góc nội tiếp cùng chắn cung DB)
\( \Rightarrow \angle MHD = \angle DAB\).
Mà \(\angle MHD + \angle DHA = \angle AHM = {90^0}\).
\( \Rightarrow \angle DAB + \angle DHA = {90^0}\) \( \Rightarrow \Delta ADH\) vuông tại D (tam giác có tổng hai góc bằng \({90^0}\)).
\( \Rightarrow HD \bot AN\) tại D.
Áp dụng định lí Pytago trong tam giác vuông ADH có: \(H{A^2} = A{D^2} + H{D^2}\).
Biến đổi \({\left( {\frac{{HA}}{{HD}}} \right)^2} - \frac{{AC}}{{HN}} = 1\)ta có:
\(\begin{array}{l}{\left( {\frac{{HA}}{{HD}}} \right)^2} - \frac{{AC}}{{HN}} = 1 \Leftrightarrow \frac{{A{D^2} + H{D^2}}}{{H{D^2}}} = 1 + \frac{{AC}}{{HN}}\\ \Leftrightarrow \frac{{A{D^2}}}{{H{D^2}}} + 1 = 1 + \frac{{AC}}{{HN}} \Leftrightarrow \frac{{A{D^2}}}{{H{D^2}}} = \frac{{AC}}{{HN}}\end{array}\)
Xét tam giác AHN vuông tại H, có đường cao HD ta có: \(H{D^2} = AD.DN\) (hệ thức lượng trong tam giác vuông)
\( \Rightarrow \frac{{A{D^2}}}{{H{D^2}}} = \frac{{AC}}{{HN}} \Leftrightarrow \frac{{A{D^2}}}{{AD.DN}} = \frac{{AC}}{{HN}} \Rightarrow \frac{{AD}}{{DN}} = \frac{{AC}}{{HN}} \Leftrightarrow \frac{{AD}}{{AC}} = \frac{{DN}}{{HN}}\).
Xét \(\Delta ADC\) và \(\Delta NDM\) có:
\(\angle ADC = \angle MDN\) (đối đỉnh)
\(\angle BAC = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow AC \bot AB\). Lại có \(OM \bot AB\,\,\left( {cmt} \right) \Rightarrow OM//AC\) (từ vuông góc đến song song) \( \Rightarrow \angle DAC = \angle DNM\) (so le trong)
$\Rightarrow \Delta ADC\backsim \Delta NDM\,\,\left( g.g \right)$
\( \Rightarrow \frac{{AD}}{{AC}} = \frac{{DN}}{{NM}}\) (cặp cạnh tương ứng tỉ lệ).
Suy ra \({\left( {\frac{{HA}}{{HD}}} \right)^2} - \frac{{AC}}{{HN}} = 1 \Leftrightarrow \frac{{DN}}{{NM}} = \frac{{DN}}{{HN}} \Leftrightarrow NM = HN\)
Do đó ta cần chứng minh \(NM = HN\).
Theo ý 2. ta có: \(M{N^2} = ND.NA\).
Áp dụng hệ thức lượng trong tam giác vuông AHN đường cao HD ta có: \(N{H^2} = ND.NA\).
Vậy \(M{N^2} = N{H^2} \Leftrightarrow MN = NH\). Do đó ta có điều phải chứng minh \({\left( {\frac{{HA}}{{HD}}} \right)^2} - \frac{{AC}}{{HN}} = 1\).
Câu 5 (VDC):
Cách giải:
Áp dụng bất đẳng thức Cosi ta có:
\(\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} \ge 2\sqrt {\frac{1}{{{a^2}}}.\frac{1}{{{b^2}}}} = \frac{2}{{ab}}\)
\(ab \le \frac{{{{\left( {a + b} \right)}^2}}}{4}\)
\( \Rightarrow \frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} \ge \frac{8}{{{{\left( {a + b} \right)}^2}}}\)
Khi đó ta có:
\(M = \frac{8}{{{{(x + 3)}^2}}} + \frac{{16}}{{{{(y + 4)}^2}}} + \frac{1}{{{{(z + 1)}^2}}} + 2023\)
\(\,\,\,\,\,\,\, = \frac{8}{{{{(x + 3)}^2}}} + \frac{1}{{{{\left( {\frac{y}{4} + 1} \right)}^2}}} + \frac{1}{{{{(z + 1)}^2}}} + 2023\)
\(\,\,\,\,\,\,\, \ge \frac{8}{{{{(x + 3)}^2}}} + \frac{8}{{{{\left( {\frac{y}{4} + 1 + z + 1} \right)}^2}}} + 2023\)
\(\,\,\,\,\,\,\, \ge \frac{{64}}{{{{\left( {x + 3 + \frac{y}{4} + 1 + z + 1} \right)}^2}}} + 2023\)
\(\,\,\,\,\,\,\, \ge \frac{{64}}{{{{\left( {x + \frac{y}{4} + z + 5} \right)}^2}}} + 2023\)
Mặt khác, áp dụng bất đẳng thức Cô-si ta có:
\(4{x^2} + 4 \ge 2\sqrt {4{x^2}.4} = 8x\)
\({y^2} + 16 \ge 2\sqrt {{y^2}.16} = 8y\)
\(4{z^2} + 4 \ge 2\sqrt {4{z^2}.4} = 8z\)
Suy ra: \(8x + 8y + 8z \le 4{x^2} + 4 + {y^2} + 16 + 4{z^2} + 4 = 4{x^2} + {y^2} + 4{z^2} + 24\)
Mà: \(4{x^2} + {y^2} + 4{z^2} \le 6y\)
\(\begin{array}{l} \Rightarrow 8x + 8y + 8z \le 6y + 24\\ \Leftrightarrow 8x + 2y + 8z \le 24\\ \Leftrightarrow x + \frac{y}{4} + z \le 3\end{array}\)
\(\begin{array}{l}M \ge \frac{{64}}{{{{\left( {x + \frac{y}{4} + z + 5} \right)}^2}}} + 2023\\\,\,\,\,\,\, = \frac{{64}}{{{{\left( {3 + 5} \right)}^2}}} + 2023 = 2024\end{array}\)
Dấu “=” xảy ra khi và chỉ khi \(x = z = 1;y = 4\)
Vậy giá trị nhỏ nhất của M là 2024 khi \(x = z = 1;y = 4.\)
Câu 1 (VD):
Phương pháp:
1. Quy đồng và rút gọn.
2. Giải phương trình P > 1.
Cách giải:
1. Rút gọn biểu thức P
Ta có \(P = \frac{{\sqrt x }}{{\sqrt x + 2}} + \frac{{\sqrt x + 1}}{{\sqrt x - 2}} - \frac{{2 + 5\sqrt x }}{{x - 4}}\)
\(\begin{array}{l} = \frac{{\sqrt x \left( {\sqrt x - 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} + \frac{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} - \frac{{2 + 5\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\ = \frac{{x - 2\sqrt x + x + 3\sqrt x + 2 - 2 - 5\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\ = \frac{{2x - 4\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\ = \frac{{2\sqrt x \left( {\sqrt x - 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\ = \frac{{2\sqrt x }}{{\sqrt x + 2}}\end{array}\)
Vậy \(P = \frac{{2\sqrt x }}{{\sqrt x + 2}}\) với \(x \ge 0,x \ne 4\)
2. Tìm tất cả các giá trị của \(x\) để \(P > 1\).
Để \(P > 1\)
\(\frac{{2\sqrt x }}{{\sqrt x + 2}} > 1 \Leftrightarrow 2\sqrt x > \sqrt x + 2\) (do \(\sqrt x + 2\) > 0)
\(\begin{array}{l} \Leftrightarrow \sqrt x > 2\\ \Leftrightarrow x > 4\end{array}\)
Đối chiếu với điều kiện \(x \ge 0,x \ne 4\), để P > 1 thì \(x > 4\)
Câu 2 (VD):
Phương pháp:
1. \(y = ax + b\) có hệ số góc là a.
2. Sử dụng phương pháp thế hoặc trừ vế.
Cách giải:
1. Trong mặt phẳng tọa độ Oxy, cho đường thẳng \((d)\) có phương trình \(y = ax + b\). Tìm a, b để đường thẳng \((d)\) có hệ số góc bằng 3 và đi qua điểm \(M( - 1;2).\)
Vì (d) có hệ số góc bằng 3 nên suy ra: \(a = 3.\)
Khi đó phương trình đường thẳng (d) có dạng \(y = 3x + b\)
Vì (d) đi qua điểm \(M( - 1;2)\) nên thay tọa độ điểm M vào phương trình đường thẳng (d) ta được:
\(2 = 3.\left( { - 1} \right) + b \Leftrightarrow 2 = - 3 + b \Leftrightarrow b = 5\)
Vậy \(a = 3;\,\,b = 5.\)
2. Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{3x + y = 6}\\{x - y = - 2}\end{array}} \right.\)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{3x + y = 6}\\{x - y = - 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4x = 4}\\{y = x + 2}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1}\\{y = 3}\end{array}} \right.} \right.\)
Vậy hệ phương trình có nghiệm duy nhất là: \(\left( {x;y} \right) = \left( {1;3} \right)\).
Câu 3 (NB):
Phương pháp:
1. Bước 1: Tính giá trính của \(\Delta \) với \(\Delta \; = {{\rm{b}}^2} - 4{\rm{ac}}\)
Bước 2: Xét tập nghiệm của phương trình bằng việc sánh giá \(\Delta \) với 0
\(\Delta \; < 0 \Rightarrow \) phương trình bậc 2 vô nghiệm
\(\Delta \; = 0 \Rightarrow \) phương trình bậc 2 có nghiệm kép \({x_1} = {x_2} = \; - \frac{b}{{2a}}\)
\(\Delta \; > 0 \Rightarrow \) phương trình (1) có 2 nghiệm phân biệt, ta dùng công thức nghiệm sau: \({x_{1,2}} = \frac{{ - b \pm \sqrt \Delta {\rm{ \;}}}}{{2a}}\).
2. Sử dụng Vi et.
Cách giải:
1. Giải phương trình \({x^2} - 3x + 2 = 0\).
Xét phương trình \({x^2} - 3x + 2 = 0\) có \(a + b + c = 0\) nên ta có phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = 1\\{x_2} = \frac{c}{a} = 2\end{array} \right.\)
Vậy phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = 1\\{x_2} = 2\end{array} \right.\).
2. Cho phương trình \({x^2} - 2mx - {m^2} - 2 = 0\) ( \(m\) là tham số). Tìm các giá trị của \(m\) để phương trình có hai nghiệm \({x_1},{x_2}\) (với \({x_1} < {x_2}\) ) thỏa mãn hệ thức \({x_2} - 2\left| {{x_1}} \right| - 3{x_1}{x_2} = 3{m^2} + 3m + 4\).
Xét phương trình \({x^2} - 2mx - {m^2} - 2 = 0\) có \(\Delta ' = {\left( { - m} \right)^2} - 1.\left( { - {m^2} - 2} \right) = {m^2} + {m^2} + 2 = 2{m^2} + 2 > 0\) với mọi m.
Áp dụng định lí Vi – ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}{x_2} = - {m^2} - 2\end{array} \right.\) . (2)
Nhận thấy \({x_1}{x_2} = - {m^2} - 2 < 0\) với mọi m nên phương trình có hai nghiệm trái dấu \({x_1} < 0 < {x_2}\).
\(\begin{array}{l}{x_2} - 2\left| {{x_1}} \right| - 3{x_1}{x_2} = 3{m^2} + 3m + 4\\ \Leftrightarrow {x_2} + 2{x_1} - 3{x_1}{x_2} = 3{m^2} + 3m + 4\\ \Leftrightarrow 2{x_1} + {x_2} - 3\left( { - {m^2} - 2} \right) = 3{m^2} + 3m + 4\\ \Leftrightarrow 2{x_1} + {x_2} + 3{m^2} + 6 = 3{m^2} + 3m + 4\\ \Leftrightarrow 2{x_1} + {x_2} = 3m - 2\end{array}\)
Ta có hệ phương trình \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\2{x_1} + {x_2} = 3m - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_1} = m - 2\\{x_2} = 2m - m + 2 = m + 2\end{array} \right.\)
Thay vào \({x_1}{x_2} = - {m^2} - 2\) ta được phương trình
\(\begin{array}{l}\left( {m - 2} \right)\left( {m + 2} \right) = - {m^2} - 2\\ \Leftrightarrow {m^2} - 4 = - {m^2} - 2\\ \Leftrightarrow 2{m^2} = 2\end{array}\)
\(\begin{array}{l} \Leftrightarrow {m^2} = 1\\ \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - 1\end{array} \right.\end{array}\)
Vậy \(\left[ \begin{array}{l}m = 1\\m = - 1\end{array} \right.\) thỏa mãn yêu cầu bài toán.
Câu 4 (VD):
Cách giải:
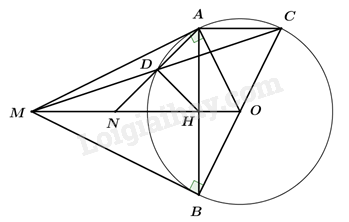
1. Chứng minh MAOB là tứ giác nội tiếp.
Vì MA, MB là tiếp tuyến của (O) (gt) \( \Rightarrow \angle MAO = \angle MBO = {90^0}\).
\( \Rightarrow \angle MAO + \angle MBO = {90^0} + {90^0} = {180^0}\).
Mà A, B là hai đỉnh đối diện của tứ giác MAOB.
Vậy MAOB là tứ giác nội tiếp (dhnb).
2. Gọi N là giao điểm của hai đường thẳng AD và MO. Chứng minh rằng MN2 = ND.NA.
Ta có: \(\angle MDN = \angle ADC\) (đối đỉnh), \(\angle ADC = \angle ABC\) (hai góc nội tiếp cùng chắn cung AC)
\( \Rightarrow \angle MDN = \angle ABC\).
Mà \(\angle ABC = \angle ABO = \angle AMO = \angle AMN\) (hai góc nội tiếp cùng chắn cung AO).
\( \Rightarrow \angle MDN = \angle AMN\).
Xét \(\Delta MND\) và \(\Delta ANM\) có:
\(\begin{array}{l}\angle ANM\,\,chung\\\angle MDN = \angle AMN\,\,\left( {cmt} \right)\end{array}\)
$\Rightarrow \Delta MND\backsim \Delta ANM\,\,\left( g.g \right)$
\( \Rightarrow \frac{{MN}}{{NA}} = \frac{{ND}}{{MN}}\) (cặp cạnh tương ứng tỉ lệ) \( \Rightarrow M{N^2} = ND.NA\,\,\left( {dpcm} \right)\).
3. Gọi H là giao điểm của MO và AB. Chứng minh \({\left( {\frac{{HA}}{{HD}}} \right)^2} - \frac{{AC}}{{HN}} = 1\).
Xét \(\Delta MAD\) và \(\Delta MCA\) có:
\(\angle AMC\) chung
\(\angle MAD = \angle MCA\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AD).
$\Rightarrow \Delta MAD\backsim \Delta MCA\,\,\left( g.g \right)$
\( \Rightarrow \frac{{MA}}{{MC}} = \frac{{MD}}{{MA}}\) (cặp cạnh tương ứng tỉ lệ)
\( \Rightarrow M{A^2} = MC.MD\) (1)
Ta có: \(OA = OB\,\,\left( { = R} \right) \Rightarrow O\) thuộc trung trực của AB.
\(MA = MB\) (tính chất hai tiếp tuyến cắt nhau) \( \Rightarrow M\) thuộc trung trực của AB.
\( \Rightarrow OM\) là trung trực của AB \( \Rightarrow OM \bot AB\) tại H.
Xét tam giác OAM vuông tại A có đường cao AH, áp dụng hệ thức lượng trong tam giác vuông ta có:
\(M{A^2} = MH.MO\) (2)
Từ (1), (2) \( \Rightarrow MC.MD = MH.MO \Rightarrow \frac{{MC}}{{MH}} = \frac{{MO}}{{MD}}\).
Xét \(\Delta MOC\) và \(\Delta MDH\) có:
\(\angle OMC\) chung
\(\frac{{MC}}{{MH}} = \frac{{MO}}{{MD}}\,\,\left( {cmt} \right)\)
$\Rightarrow \Delta MOC\backsim \Delta MDH\,\,\left( g.g \right)$
\( \Rightarrow \angle MHD = \angle MCO\) (hai góc tương ứng)
Mà \(\angle MCO = \angle DCB = \angle DAB\) (hai góc nội tiếp cùng chắn cung DB)
\( \Rightarrow \angle MHD = \angle DAB\).
Mà \(\angle MHD + \angle DHA = \angle AHM = {90^0}\).
\( \Rightarrow \angle DAB + \angle DHA = {90^0}\) \( \Rightarrow \Delta ADH\) vuông tại D (tam giác có tổng hai góc bằng \({90^0}\)).
\( \Rightarrow HD \bot AN\) tại D.
Áp dụng định lí Pytago trong tam giác vuông ADH có: \(H{A^2} = A{D^2} + H{D^2}\).
Biến đổi \({\left( {\frac{{HA}}{{HD}}} \right)^2} - \frac{{AC}}{{HN}} = 1\)ta có:
\(\begin{array}{l}{\left( {\frac{{HA}}{{HD}}} \right)^2} - \frac{{AC}}{{HN}} = 1 \Leftrightarrow \frac{{A{D^2} + H{D^2}}}{{H{D^2}}} = 1 + \frac{{AC}}{{HN}}\\ \Leftrightarrow \frac{{A{D^2}}}{{H{D^2}}} + 1 = 1 + \frac{{AC}}{{HN}} \Leftrightarrow \frac{{A{D^2}}}{{H{D^2}}} = \frac{{AC}}{{HN}}\end{array}\)
Xét tam giác AHN vuông tại H, có đường cao HD ta có: \(H{D^2} = AD.DN\) (hệ thức lượng trong tam giác vuông)
\( \Rightarrow \frac{{A{D^2}}}{{H{D^2}}} = \frac{{AC}}{{HN}} \Leftrightarrow \frac{{A{D^2}}}{{AD.DN}} = \frac{{AC}}{{HN}} \Rightarrow \frac{{AD}}{{DN}} = \frac{{AC}}{{HN}} \Leftrightarrow \frac{{AD}}{{AC}} = \frac{{DN}}{{HN}}\).
Xét \(\Delta ADC\) và \(\Delta NDM\) có:
\(\angle ADC = \angle MDN\) (đối đỉnh)
\(\angle BAC = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow AC \bot AB\). Lại có \(OM \bot AB\,\,\left( {cmt} \right) \Rightarrow OM//AC\) (từ vuông góc đến song song) \( \Rightarrow \angle DAC = \angle DNM\) (so le trong)
$\Rightarrow \Delta ADC\backsim \Delta NDM\,\,\left( g.g \right)$
\( \Rightarrow \frac{{AD}}{{AC}} = \frac{{DN}}{{NM}}\) (cặp cạnh tương ứng tỉ lệ).
Suy ra \({\left( {\frac{{HA}}{{HD}}} \right)^2} - \frac{{AC}}{{HN}} = 1 \Leftrightarrow \frac{{DN}}{{NM}} = \frac{{DN}}{{HN}} \Leftrightarrow NM = HN\)
Do đó ta cần chứng minh \(NM = HN\).
Theo ý 2. ta có: \(M{N^2} = ND.NA\).
Áp dụng hệ thức lượng trong tam giác vuông AHN đường cao HD ta có: \(N{H^2} = ND.NA\).
Vậy \(M{N^2} = N{H^2} \Leftrightarrow MN = NH\). Do đó ta có điều phải chứng minh \({\left( {\frac{{HA}}{{HD}}} \right)^2} - \frac{{AC}}{{HN}} = 1\).
Câu 5 (VDC):
Cách giải:
Áp dụng bất đẳng thức Cosi ta có:
\(\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} \ge 2\sqrt {\frac{1}{{{a^2}}}.\frac{1}{{{b^2}}}} = \frac{2}{{ab}}\)
\(ab \le \frac{{{{\left( {a + b} \right)}^2}}}{4}\)
\( \Rightarrow \frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} \ge \frac{8}{{{{\left( {a + b} \right)}^2}}}\)
Khi đó ta có:
\(M = \frac{8}{{{{(x + 3)}^2}}} + \frac{{16}}{{{{(y + 4)}^2}}} + \frac{1}{{{{(z + 1)}^2}}} + 2023\)
\(\,\,\,\,\,\,\, = \frac{8}{{{{(x + 3)}^2}}} + \frac{1}{{{{\left( {\frac{y}{4} + 1} \right)}^2}}} + \frac{1}{{{{(z + 1)}^2}}} + 2023\)
\(\,\,\,\,\,\,\, \ge \frac{8}{{{{(x + 3)}^2}}} + \frac{8}{{{{\left( {\frac{y}{4} + 1 + z + 1} \right)}^2}}} + 2023\)
\(\,\,\,\,\,\,\, \ge \frac{{64}}{{{{\left( {x + 3 + \frac{y}{4} + 1 + z + 1} \right)}^2}}} + 2023\)
\(\,\,\,\,\,\,\, \ge \frac{{64}}{{{{\left( {x + \frac{y}{4} + z + 5} \right)}^2}}} + 2023\)
Mặt khác, áp dụng bất đẳng thức Cô-si ta có:
\(4{x^2} + 4 \ge 2\sqrt {4{x^2}.4} = 8x\)
\({y^2} + 16 \ge 2\sqrt {{y^2}.16} = 8y\)
\(4{z^2} + 4 \ge 2\sqrt {4{z^2}.4} = 8z\)
Suy ra: \(8x + 8y + 8z \le 4{x^2} + 4 + {y^2} + 16 + 4{z^2} + 4 = 4{x^2} + {y^2} + 4{z^2} + 24\)
Mà: \(4{x^2} + {y^2} + 4{z^2} \le 6y\)
\(\begin{array}{l} \Rightarrow 8x + 8y + 8z \le 6y + 24\\ \Leftrightarrow 8x + 2y + 8z \le 24\\ \Leftrightarrow x + \frac{y}{4} + z \le 3\end{array}\)
\(\begin{array}{l}M \ge \frac{{64}}{{{{\left( {x + \frac{y}{4} + z + 5} \right)}^2}}} + 2023\\\,\,\,\,\,\, = \frac{{64}}{{{{\left( {3 + 5} \right)}^2}}} + 2023 = 2024\end{array}\)
Dấu “=” xảy ra khi và chỉ khi \(x = z = 1;y = 4\)
Vậy giá trị nhỏ nhất của M là 2024 khi \(x = z = 1;y = 4.\)
Kỳ thi tuyển sinh vào lớp 10 môn Toán Thanh Hóa năm 2023 là một kỳ thi quan trọng đánh giá năng lực học tập môn Toán của học sinh THCS trên địa bàn tỉnh. Đề thi thường bao gồm các dạng bài tập khác nhau, đòi hỏi học sinh phải nắm vững kiến thức cơ bản và kỹ năng giải quyết vấn đề.
Cấu trúc đề thi thường bao gồm các phần sau:
Tỷ lệ điểm giữa phần trắc nghiệm và phần tự luận có thể thay đổi tùy theo từng năm.
Các chủ đề thường xuyên xuất hiện trong đề thi vào 10 môn Toán Thanh Hóa bao gồm:
Để ôn thi hiệu quả, học sinh cần:
Giaitoan.edu.vn cung cấp bộ đề thi vào 10 môn Toán Thanh Hóa năm 2023 được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm. Bộ đề thi bao gồm:
Học sinh có thể truy cập website giaitoan.edu.vn để tải bộ đề thi và luyện tập.
Kỳ thi tuyển sinh vào lớp 10 môn Toán Thanh Hóa năm 2023 là một kỳ thi quan trọng. Để đạt kết quả tốt, học sinh cần chuẩn bị kỹ lưỡng và luyện tập thường xuyên. Giaitoan.edu.vn hy vọng bộ đề thi và tài liệu ôn tập của chúng tôi sẽ giúp các em tự tin chinh phục kỳ thi này.