Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Hải Dương năm 2023. Đây là tài liệu ôn tập vô cùng quan trọng dành cho các em học sinh đang chuẩn bị cho kỳ thi sắp tới.
Chúng tôi cung cấp đầy đủ các đề thi chính thức, đáp án chi tiết và phương pháp giải bài tập hiệu quả. Hãy cùng giaitoan.edu.vn chinh phục kỳ thi vào 10 môn Toán một cách tự tin nhất!
Câu 1: Cho biểu thức: \(A = 3\sqrt 8 {\rm{ \;}} - \sqrt {50} {\rm{ \;}} - \sqrt {{{\left( {\sqrt 2 {\rm{ \;}} - 1} \right)}^2}} \) \(B = \left( {\frac{{3\sqrt x {\rm{ \;}} + 6}}{{x - 4}} + \frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} - 2}}} \right):\frac{{x - 9}}{{\sqrt x {\rm{ \;}} - 3}}\) với \(x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 4,{\mkern 1mu} {\mkern 1mu} x \ne 9\) a) Rút gọn biểu thức A và B. b) Tìm x sao cho A – 2B = 3.
Câu 1: Cho biểu thức: \(A = 3\sqrt 8 {\rm{ \;}} - \sqrt {50} {\rm{ \;}} - \sqrt {{{\left( {\sqrt 2 {\rm{ \;}} - 1} \right)}^2}} \)
\(B = \left( {\frac{{3\sqrt x {\rm{ \;}} + 6}}{{x - 4}} + \frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} - 2}}} \right):\frac{{x - 9}}{{\sqrt x {\rm{ \;}} - 3}}\) với \(x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 4,{\mkern 1mu} {\mkern 1mu} x \ne 9\)
a) Rút gọn biểu thức A và B.
b) Tìm x sao cho A – 2B = 3.
Câu 2: 1. Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2(x - 3) + 3(3x + y) = {\rm{ \;}} - 11}\\{(x - 3) - 2(3x + y) = 5}\end{array}} \right.\).
2. Một quyển vở giá 14000 đồng, một hộp bút giá 30000 đồng. Minh muốn mua 01 hộp bút và một số quyển vở.
a) Gọi \(x\left( {x \in {\mathbb{N}^*}} \right)\) là số quyển vở Minh mua, y là số tiền cần trả khi mua x quyền vở và 01 hộp bút. Hãy biểu diễn y theo x.
b) Nếu Minh có 300000 đồng để mua vở và 01 hộp bút thì Minh mua được tối đa bao nhiêu quyển vở?
Câu 3: 1. Cho phương trình \({x^2} - 2\left( {m - 1} \right)x + {m^2} - 9 = 0\)\((1)\)(\(x\) là ẩn, \(m\) là tham số)
a) Giải phương trình (1) khi \(m = {\rm{ \;}} - 3\).
b, Tìm các giá trị của m để phương trình (1) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn điều kiện
2. Một trường học có mảnh vườn hình chữ nhật chu vi là 100m. Nhà trường tiến hành mở rộng mảnh vườn bằng cách tăng chiều dài thêm 5m và chiều rộng thêm 4m, khi đó diện tích tăng 240m2. Tính chiều dài và chiều rộng mảnh vường trước khi mở rộng.
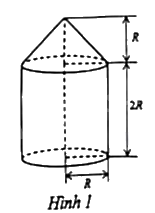
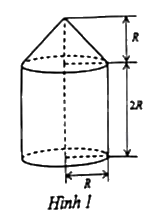
Câu 4: Một chi tiết máy gồm một phần có dạng hình trụ, phần còn lại có dạng hình nón với các kích thước như hình 1. Biết rằng phần hình trụ có chu vi đáy là 37,68cm. Tính thể tích của chi tiết máy đó (lấy \(\pi {\rm{ \;}} \approx 3,14\); kết quả làm tròn đến chữ số thập phân thứ 2).
Câu 5: Cho đường tròn (O;R) và điểm A sao cho OA > 2R, vẽ hai tiếp tuyến AB, AC của đường tròn (B, C là các tiếp điểm), kẻ dây cung BD song song với AC. Đường thẳng AD cắt (O; R) tại điểm E (\(E \ne D\)). Gọi I là trung điểm của DE.
a) Chứng minh năm điểm A, B, I, O, C cùng thuộc một đường tròn.
b) Đường thẳng BC cắt OA, AD lần lượt tại H và K. Gọi F là giao điểm của BE và AC.
Chứng minh AK.AI = AH.AO và tam giác AFE đồng dạng với tam giác BFA.
c) Chứng minh ba đường thẳng AB, CD, FK đồng quy.
Câu 6: Cho các số thực a, b thoả mãn: a > 0, b > 0 và \({(a + b)^3} = 2\left( {1 - {a^2} - {b^2}} \right)\).
Tìm giá trị nhỏ nhất của biểu thức \(M = \frac{1}{{ab}} + \frac{1}{{{a^2} + {b^2}}}\).
----- HẾT -----
Câu 1 (VD):
Cách giải:
a) Rút gọn biểu thức A và B.
+) Ta có:
\(\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} A = 3\sqrt 8 {\rm{ \;}} - \sqrt {50} {\rm{ \;}} - \sqrt {{{\left( {\sqrt 2 {\rm{ \;}} - 1} \right)}^2}} }\\{ \Leftrightarrow A = 3\sqrt {{2^2}.2} {\rm{ \;}} - \sqrt {{5^2}.2} {\rm{ \;}} - \left| {\sqrt 2 {\rm{ \;}} - 1} \right|}\\{ \Leftrightarrow A = 3.2\sqrt 2 {\rm{ \;}} - 5\sqrt 2 {\rm{ \;}} - \left( {\sqrt 2 {\rm{ \;}} - 1} \right){\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} \sqrt 2 {\rm{ \;}} - 1 > 0} \right)}\\{ \Leftrightarrow A = 6\sqrt 2 {\rm{ \;}} - 5\sqrt 2 {\rm{ \;}} - \sqrt 2 {\rm{ \;}} + 1}\\{ \Leftrightarrow A = \left( {6 - 5 - 1} \right)\sqrt 2 {\rm{ \;}} + 1}\\{ \Leftrightarrow A = 1.}\end{array}\)
Vậy A = 1.
+) Với \(x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 4,{\mkern 1mu} {\mkern 1mu} x \ne 9\) ta có:
\(\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} B = \left( {\frac{{3\sqrt x + 6}}{{x - 4}} + \frac{{\sqrt x }}{{\sqrt x - 2}}} \right):\frac{{x - 9}}{{\sqrt x - 3}}}\\{ \Leftrightarrow B = \left( {\frac{{3\left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}} + \frac{{\sqrt x }}{{\sqrt x - 2}}} \right):\frac{{x - 9}}{{\sqrt x - 3}}}\\{ \Leftrightarrow B = \left( {\frac{3}{{\sqrt x - 2}} + \frac{{\sqrt x }}{{\sqrt x - 2}}} \right):\frac{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}{{\sqrt x - 3}}}\\{ \Leftrightarrow B = \frac{{3 + \sqrt x }}{{\sqrt x - 2}}:\left( {\sqrt x + 3} \right)}\\{ \Leftrightarrow B = \frac{{3 + \sqrt x }}{{\sqrt x - 2}}.\frac{1}{{\sqrt x + 3}}}\\{ \Leftrightarrow B = \frac{1}{{\sqrt x - 2}}}\end{array}\)
Vậy với \(x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 4,{\mkern 1mu} {\mkern 1mu} x \ne 9\) thì \(B = \frac{1}{{\sqrt x {\rm{ \;}} - 2}}\).
b) Tìm x sao cho A – 2B = 3.
Ta có
\(\begin{array}{*{20}{l}}{A - 2B = 3}\\{ \Leftrightarrow 1 - 2.\frac{1}{{\sqrt x {\rm{ \;}} - 2}} = 3}\\{ \Leftrightarrow 2.\frac{1}{{\sqrt x {\rm{ \;}} - 2}} = 1 - 3}\\{ \Leftrightarrow 2.\frac{1}{{\sqrt x {\rm{ \;}} - 2}} = {\rm{ \;}} - 2}\\{ \Leftrightarrow \frac{1}{{\sqrt x {\rm{ \;}} - 2}} = {\rm{ \;}} - 1}\\{ \Leftrightarrow \sqrt x {\rm{ \;}} - 2 = {\rm{ \;}} - 1}\\{ \Leftrightarrow \sqrt x {\rm{ \;}} = 1}\\{ \Leftrightarrow x = 1{\mkern 1mu} {\mkern 1mu} \left( {tm} \right)}\end{array}\)
Vậy x = 1.
Câu 2 (VD):
Cách giải:
1. Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2(x - 3) + 3(3x + y) = - 11}\\{(x - 3) - 2(3x + y) = 5}\end{array}} \right.\).
Cách 1:
Đặt: \(\left\{ \begin{array}{l}x - 3 = a\\3x + y = b\end{array} \right.\). Khi đó hệ phương trình trở thành: \(\left\{ {\begin{array}{*{20}{l}}{2a + 3b = - 11}\\{a - 2b = 5}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2a + 3b = - 11}\\{2a - 4b = 10}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 5 + 2b}\\{7b = - 21}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = - 1}\\{b = - 3}\end{array}} \right.\)
Suy ra \(\left\{ \begin{array}{l}x - 3 = - 1\\3x + y = - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = - 3 - 3x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = - 9\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất là: \(\left( {x;y} \right) = \left( {2; - 9} \right)\).
Cách 2:
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{2(x - 3) + 3(3x + y) = - 11}\\{(x - 3) - 2(3x + y) = 5}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2x - 6 + 9x + 3y = - 11}\\{x - 3 - 6x - 2y = 5}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{11x + 3y = - 5}\\{ - 5x - 2y = 8}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{11x + 3y = - 5\,\,\,\,\,\,(1)}\\{y = - \frac{{8 + 5x}}{2} = - 4 - \frac{5}{2}x}\end{array}} \right.\end{array}\)
Thay \(y = - 4 - \frac{5}{2}x\) vào (1) ta có:
\(\begin{array}{l}11x + 3.\left( { - 4 - \frac{5}{2}x} \right) = - 5\\ \Leftrightarrow 11x - 12 - \frac{{15}}{2}x = - 5\\ \Leftrightarrow \frac{7}{2}x = 7\\ \Leftrightarrow x = 2.\end{array}\)
Với \(x = 2\) thì \(y = - 4 - \frac{5}{2}.2 = - 9\).
Vậy hệ phương trình có nghiệm duy nhất là: \(\left( {x;y} \right) = \left( {2; - 9} \right)\).
2. Một quyển vở giá 14000 đồng, một hộp bút giá 30000 đồng. Minh muốn mua 01 hộp bút và một số quyển vở.
a) Gọi \(x\left( {x \in {\mathbb{N}^*}} \right)\) là số quyển vở Minh mua, y là số tiền cần trả khi mua x quyền vở và 01 hộp bút. Hãy biểu diễn y theo x.
Giá tiền khi mua x quyển vở và một hộp bút là: \(14\,000x + 30\,000\) (đồng).
Vì y là số tiền mua x quyển vở và một hộp bút nên \(y = 14\,000x + 30\,000\).
b) Nếu Minh có 300000 đồng để mua vở và 01 hộp bút thì Minh mua được tối đa bao nhiêu quyển vở?
Gọi a \(\left( {a \in \mathbb{N}} \right)\) là số quyển vở tối đa Minh mua.
Số tiền Minh phải trả khi mua 01 hộp bút và a quyển vở là: \(14\,000.a + 30\,000\).
Vì Minh chỉ có 300 000 đồng nên số tiền phải trả nhỏ hơn hoặc bằng 300 000 đồng
Ta có: \(\)
\(\begin{array}{l}14\,000.a + 30\,000 \le 300\,000\\ \Leftrightarrow 14\,000.a \le 300\,000 - 30\,000\\ \Leftrightarrow 14\,000.a \le 270\,000\\ \Leftrightarrow a \le 270\,000:14\,000\\ \Leftrightarrow a \le \frac{{135}}{7} \approx 19,29\end{array}\)
Vậy số vở tối đa Minh có thể mua là 19 quyển.
Câu 3 (VD):
Cách giải:
1. Cho phương trình \({x^2} - 2\left( {m - 1} \right)x + {m^2} - 9 = 0\)\((1)\)(\(x\) là ẩn, \(m\) là tham số)
a) Giải phương trình (1) khi \(m = - 3\).
Thay \(m = - 3\)vào (1) ta được:
\({x^2} - 2\left( { - 3 - 1} \right)x + {\left( { - 3} \right)^2} - 9 = 0\) \( \Leftrightarrow {x^2} + 8x = 0\)
\(\begin{array}{l} \Leftrightarrow x\left( {x + 8} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 8\end{array} \right.\end{array}\)
Vậy với \(m = - 3\)thì phương trình có 2 nghiệm phân biệt\(x = 0\) hoặc \(x = - 8\).
b, Tìm các giá trị của m để phương trình (1) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn điều kiện \({x_1} - {x_2} = 2m - 10\).
+ Phương trình (1) có 2 nghiệm phân biệt \( \Leftrightarrow \Delta ' = {\left[ { - \left( {m - 1} \right)} \right]^2} - {m^2} + 9 > 0\)
\(\begin{array}{l} \Leftrightarrow {m^2} - 2m + 1 - {m^2} + 9 > 0\\ \Leftrightarrow - 2m + 10 > 0\\ \Leftrightarrow m < 5\end{array}\)
Theo hệ thức Vi-ét: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2(m - 1)\\{x_1}.{x_2} = {m^2} - 9\,\,\,(*)\end{array} \right.\)
+ Ta có: \({x_1} + {x_2} = 2(m - 1) \Rightarrow {x_1} = 2(m - 1) - {x_2}\)thay vào \({x_1} - {x_2} = 2m - 10\) ta được:
\(2(m - 1) - {x_2} - {x_2} = 2m - 10\)
\(\begin{array}{l} \Leftrightarrow 2(m - 1) - 2{x_2} = 2\left( {m - 5} \right)\\ \Leftrightarrow m - 1 - {x_2} = m - 5\end{array}\)
\(\begin{array}{l} \Rightarrow {x_2} = 4\\ \Rightarrow {x_1} = 2(m - 1) - 4 = 2m - 6\end{array}\)
Thay vào (*) ta được:
\(\left( {2m - 6} \right).4 = {m^2} - 9\)
\(\begin{array}{l} \Leftrightarrow {m^2} - 8m + 15 = 0\\ \Leftrightarrow {m^2} - 3m - 5m + 15 = 0\\ \Leftrightarrow m\left( {m - 3} \right) - 5\left( {m - 3} \right) = 0\\ \Leftrightarrow \left( {m - 3} \right)\left( {m - 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 3\,\,\,\,(tm)\\m = 5\,\,\,\,(Ktm)\end{array} \right.\end{array}\)
Vậy \(m = 3\)là giá trị cần tìm.
2. Một trường học có mảnh vườn hình chữ nhật chu vi là 100m. Nhà trường tiến hành mở rộng mảnh vườn bằng cách tăng chiều dài thêm 5m và chiều rộng thêm 4m, khi đó diện tích tăng 240m2. Tính chiều dài và chiều rộng mảnh vường trước khi mở rộng.
Gọi chiều dài mảnh vườn trước khi mở rộng là \(x{\rm{ }}\left( m \right)\) (ĐK: 0 < x > 50).
Nửa chu vi mảnh vườn hình chữ nhật là \(100:2 = 50\)(m).
Suy ra, chiều rộng mảnh vườn trước khi mở rộng là: \(50 - x\) (m).
\( \Rightarrow \) Diện tích mảnh vườn trước khi mở rộng là \(x.\left( {50 - x} \right)\)(m2).
Chiều dài mảnh vườn sau khi mở rộng là \(x + 5\) (m).
Chiều rộng mảnh vườn sau khi mở rộng là \(50 - x + 4 = 54 - x\) (m).
Suy ra, diện tích mảnh vườn sau khi mở rộng là \(\left( {x + 5} \right).\left( {54 - x} \right)\)(m2).
Do diện tích sau khi mở rộng tăng 240m2 so với diện tích mảnh vườn ban đầu, nên ta có phương trình:
\(\left( {x + 5} \right).\left( {54 - x} \right) - x.\left( {50 - x} \right) = 240\)
\(\begin{array}{l} \Leftrightarrow 54x - {x^2} + 270 - 5x - 50x + {x^2} = 240\\ \Leftrightarrow - x + 270 = 240\end{array}\)
\( \Rightarrow x = 30\) (TMĐK)
Vậy chiều dài mảnh vườn trước khi mở rộng là 30 m;
Chiều rộng rộng mảnh vườn trước khi mở rộng là 50 – 30 = 20 m.
Câu 4 (NB):
Cách giải:
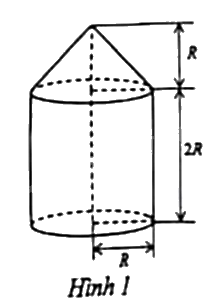
Gọi R là bán kính đường tròn đáy của hình trụ và hình nón.
Ta có đáy hình trụ là hình tròn có chu vi là 37,68 cm nên ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,2\pi R = 37,68\\ \Leftrightarrow 2.3,14.R = 37,68\\ \Leftrightarrow R = \frac{{37,68}}{{2.3,14}} = 6\end{array}\)
Thể tích phần hình trụ là: \({V_{ht}} = \pi {R^2}{h_{ht}} = 3,{14.6^2}.\left( {2.6} \right) = 1356,48\,\,\,(c{m^3})\)
Thể tích phần hình nón là: \({V_{hn}} = \frac{1}{3}\pi {R^2}{h_{hn}} = \frac{1}{3}3,{14.6^2}.6 = 226,08\,\,(c{m^3})\)
Thể tích của chi tiết máy đó là: \(V = {V_{ht}} + {V_{hn}} = 1356,48 + 226,08 = 1582,56\,\,(c{m^3})\)
Vậy thể tích của chi tiết máy là \(1582,56\,\,c{m^3}\).
Câu 5 (VD):
Cách giải:
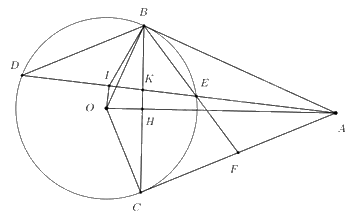
a) Chứng minh năm điểm A, B, I, O, C cùng thuộc một đường tròn.
Do AB, AC là tiếp tuyến nên \(AB \bot OB,AC \bot OC\) (định nghĩa)
\( \Rightarrow \angle ACO = \angle ABO = {90^0}\)\( \Rightarrow \angle ABO + \angle ACO = {90^0} + {90^0} = {180^0}\)
Mà 2 góc này ở vị trí đối diện nên OCAB nội tiếp hay O, C, A, B cùng thuộc một đường tròn (1)
Do I là trung điểm của DE nên \(OI \bot DE\) (tính chất đường kính vuông góc với dây cung)
\( \Rightarrow \angle OIA = {90^0}\)
\( \Rightarrow \angle OIA + \angle OCA = {90^0} + {90^0} = {180^0}\)
Mà 2 góc này ở vị trí đối diện nên OIAC nội tiếp hay O, I, A, C cùng thuộc một đường tròn (2)
Từ (1) và (2) suy ra 5 điểm A, B, I, O, C cùng thuộc một đường tròn (đpcm).
b) Đường thẳng BC cắt OA, AD lần lượt tại H và K. Gọi F là giao điểm của BE và AC. Chứng minh AK.AI = AH.AO và tam giác AFE đồng dạng với tam giác BFA.
Ta có AB = AC (tính chất 2 tiếp tuyến cắt nhau) => A thuộc trung trực của BC
OB = OC (bằng bán kính) => O thuộc trung trực của BC.
\( \Rightarrow \) AO là trung trực của BC hay \(AO \bot BC\) tại H
Xét tam giác ABO vuông tại B, đường cao BH nên:
\(A{B^2} = AH.AO\) (hệ thức lượng trong tam giác vuông) (3)
Ta có \(\angle BIA = \angle BCA\) (hai góc nội tiếp chắn cung AB) \( \Rightarrow \angle BIA = \angle ABC\,\,\left( { = \angle BCA} \right)\).
Xét \(\Delta ABK\) và \(\Delta AIB\) có:
\(\angle BAI\) chung
\(\angle BIA = \angle ABC = \angle ABK\,\,\left( {cmt} \right)\)
\(\Rightarrow \Delta ABK\backsim \Delta AIB\left( g.g \right)\Rightarrow \frac{AB}{AI}=\frac{AK}{AB}\) (cặp cạnh tương ứng tỉ lệ).
\( \Leftrightarrow A{B^2} = AK.AI\) (4)
Từ (3) và (4) suy ra \(AK.AI = AH.AO\,\,\,\left( { = A{B^2}} \right)\) (đpcm)
Do \(BD\parallel AC\left( {gt} \right) \Rightarrow \angle BDA = \angle DAC\) (so le trong)
Mà \(\angle BDA = \angle ABF\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BE)
\( \Rightarrow \angle DAC = \angle ABF\left( { = \angle BDA} \right) = \angle EAF\).
Xét \(\Delta AFE\) và \(\Delta BFA\) có:
\(\angle BFA\) chung
\(\angle EAF = \angle ABF\,\,\left( {cmt} \right)\)
\(\Rightarrow \Delta AFE\backsim \Delta BFA\,\,\left( g.g \right)\) (đpcm)
c) Chứng minh ba đường thẳng AB, CD, FK đồng quy.
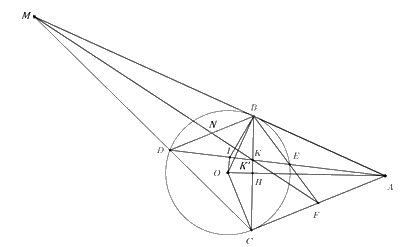
Do \(\Delta AFE\backsim \Delta BFA\,\,\left( cmt \right)\) \( \Rightarrow \frac{{FA}}{{FB}} = \frac{{FE}}{{FA}}\) (cặp cạnh tương ứng tỉ lệ) \( \Rightarrow F{A^2} = FB.FE\)
Xét \(\Delta FEC\) và \(\Delta FCB\) có \(\angle CFB\) chung và \(\angle FCE = \angle CBF\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung CE).
$\Rightarrow \Delta FEC\backsim \Delta FCB\,\,\left( g.g \right)\Rightarrow \frac{FC}{FB}=\frac{FE}{FC}$ (cặp cạnh tương ứng tỉ lệ) \( \Rightarrow F{C^2} = FE.FB\)
\( \Rightarrow FC = FA \Rightarrow F\) là trung điểm của AC.
Gọi M là giao điểm của DC và AB, N là giao điểm của MF và BD.
Do \(BD\parallel AC\left( {gt} \right) \Rightarrow \frac{{DN}}{{FC}} = \frac{{BN}}{{FA}}\,\,\left( { = \frac{{MN}}{{MF}}} \right)\) (định lí Ta-lét).
\( \Rightarrow DN = BN\) (do \(FC = FA\))
Gọi K’ là giao điểm của NF và BC $\Rightarrow \frac{BK'}{CK'}=\frac{BN}{CF}$ (Định lí Ta-lét) (5)
Mà \(\frac{{BN}}{{CF}} = \frac{{2BN}}{{2CF}} = \frac{{BD}}{{AC}} = \frac{{BK}}{{CK}}\) (6)
Từ (5) và (6) suy ra $K,K'$ cùng nằm trên đoạn BC và $\frac{BK}{CK}=\frac{BK'}{CK'}\,\,\,\left( =\frac{BD}{AC} \right)\Rightarrow K\equiv K'$
Chứng tỏ M, N, K, F thẳng hàng hay ba đường thẳng AB, CD, FK đồng quy tại M.
Câu 6 (VD):
Cách giải:
Theo bài ra ta có:
\(\begin{array}{l}{(a + b)^3} = 2\left( {1 - {a^2} - {b^2}} \right)\\ \Leftrightarrow {(a + b)^3} + 2{a^2} + 2{b^2} - 2 = 0\\ \Leftrightarrow {(a + b)^3} + {a^2} + 2ab + {b^2} + {a^2} - 2ab + {b^2} - 2 = 0\\ \Leftrightarrow {(a + b)^3} + {\left( {a + b} \right)^2} + {\left( {a - b} \right)^2} - 2 = 0\\ \Leftrightarrow {(a + b)^3} + {\left( {a + b} \right)^2} - 2 = - {\left( {a - b} \right)^2}\end{array}\)
Vì \({\left( {a - b} \right)^2} \ge 0 \Rightarrow - {\left( {a - b} \right)^2} \le 0\) nên \({(a + b)^3} + {(a + b)^2} - 2 \le 0\) (1)
Đặt \(x = a + b > 0\). Khi đó (1) trở thành:\(\,{x^3} + {x^2} - 2 \le 0\)
\(\begin{array}{l} \Leftrightarrow {x^3} - {x^2} + 2{x^2} - 2x + 2x - 2 \le 0\\ \Leftrightarrow {x^2}\left( {x - 1} \right) + 2x\left( {x - 1} \right) + 2\left( {x - 1} \right) \le 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} + 2x + 2} \right) \le 0\\ \Leftrightarrow \left( {x - 1} \right)\left[ {{{\left( {x + 1} \right)}^2} + 1} \right] \le 0\\ \Leftrightarrow x - 1 \le 0\,\,\left( {do\,\,{{(x + 1)}^2} + 1 > 0\,\,\forall x} \right)\\ \Leftrightarrow x \le 1\end{array}\)
Do \(x > 0\) nên ta có: \(0 < x \le 1\) hay \(0 < a + b \le 1 \Rightarrow 1 \ge {a^2} + {b^2} + 2ab\).
Khi đó:
\(\begin{array}{l}M \ge \left( {{a^2} + {b^2} + 2ab} \right).M = \frac{{{a^2} + {b^2} + 2ab}}{{ab}} + \frac{{{a^2} + {b^2} + 2ab}}{{{a^2} + {b^2}}}\\ \Rightarrow M \ge \frac{{{a^2} + {b^2}}}{{ab}} + 2 + \frac{{2ab}}{{{a^2} + {b^2}}} + 1 = \frac{{{a^2} + {b^2}}}{{ab}} + \frac{{2ab}}{{{a^2} + {b^2}}} + 3 = \frac{{{a^2} + {b^2}}}{{2ab}} + \left( {\frac{{{a^2} + {b^2}}}{{2ab}} + \frac{{2ab}}{{{a^2} + {b^2}}}} \right) + 3\end{array}\)
Theo bất đẳng thức Cô-si ta có:
\({a^2} + {b^2} \ge 2ab \Rightarrow \frac{{{a^2} + {b^2}}}{{2ab}} \ge \frac{{2ab}}{{2ab}} = 1\)
\(\frac{{2ab}}{{{a^2} + {b^2}}} + \frac{{{a^2} + {b^2}}}{{2ab}} \ge 2\sqrt {\frac{{2ab}}{{{a^2} + {b^2}}} \cdot \frac{{{a^2} + {b^2}}}{{2ab}}} = 2\);
Suy ra: \(M \ge 1 + 2 + 3 = 6\)
Dấu “=” xảy ra khi và chỉ khi \(a = b = \frac{1}{2}\).
Vậy giá trị nhỏ nhất của \(M = 6\) khi \(a = b = \frac{1}{2}\).
Câu 1: Cho biểu thức: \(A = 3\sqrt 8 {\rm{ \;}} - \sqrt {50} {\rm{ \;}} - \sqrt {{{\left( {\sqrt 2 {\rm{ \;}} - 1} \right)}^2}} \)
\(B = \left( {\frac{{3\sqrt x {\rm{ \;}} + 6}}{{x - 4}} + \frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} - 2}}} \right):\frac{{x - 9}}{{\sqrt x {\rm{ \;}} - 3}}\) với \(x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 4,{\mkern 1mu} {\mkern 1mu} x \ne 9\)
a) Rút gọn biểu thức A và B.
b) Tìm x sao cho A – 2B = 3.
Câu 2: 1. Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2(x - 3) + 3(3x + y) = {\rm{ \;}} - 11}\\{(x - 3) - 2(3x + y) = 5}\end{array}} \right.\).
2. Một quyển vở giá 14000 đồng, một hộp bút giá 30000 đồng. Minh muốn mua 01 hộp bút và một số quyển vở.
a) Gọi \(x\left( {x \in {\mathbb{N}^*}} \right)\) là số quyển vở Minh mua, y là số tiền cần trả khi mua x quyền vở và 01 hộp bút. Hãy biểu diễn y theo x.
b) Nếu Minh có 300000 đồng để mua vở và 01 hộp bút thì Minh mua được tối đa bao nhiêu quyển vở?
Câu 3: 1. Cho phương trình \({x^2} - 2\left( {m - 1} \right)x + {m^2} - 9 = 0\)\((1)\)(\(x\) là ẩn, \(m\) là tham số)
a) Giải phương trình (1) khi \(m = {\rm{ \;}} - 3\).
b, Tìm các giá trị của m để phương trình (1) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn điều kiện
2. Một trường học có mảnh vườn hình chữ nhật chu vi là 100m. Nhà trường tiến hành mở rộng mảnh vườn bằng cách tăng chiều dài thêm 5m và chiều rộng thêm 4m, khi đó diện tích tăng 240m2. Tính chiều dài và chiều rộng mảnh vường trước khi mở rộng.
Câu 4: Một chi tiết máy gồm một phần có dạng hình trụ, phần còn lại có dạng hình nón với các kích thước như hình 1. Biết rằng phần hình trụ có chu vi đáy là 37,68cm. Tính thể tích của chi tiết máy đó (lấy \(\pi {\rm{ \;}} \approx 3,14\); kết quả làm tròn đến chữ số thập phân thứ 2).
Câu 5: Cho đường tròn (O;R) và điểm A sao cho OA > 2R, vẽ hai tiếp tuyến AB, AC của đường tròn (B, C là các tiếp điểm), kẻ dây cung BD song song với AC. Đường thẳng AD cắt (O; R) tại điểm E (\(E \ne D\)). Gọi I là trung điểm của DE.
a) Chứng minh năm điểm A, B, I, O, C cùng thuộc một đường tròn.
b) Đường thẳng BC cắt OA, AD lần lượt tại H và K. Gọi F là giao điểm của BE và AC.
Chứng minh AK.AI = AH.AO và tam giác AFE đồng dạng với tam giác BFA.
c) Chứng minh ba đường thẳng AB, CD, FK đồng quy.
Câu 6: Cho các số thực a, b thoả mãn: a > 0, b > 0 và \({(a + b)^3} = 2\left( {1 - {a^2} - {b^2}} \right)\).
Tìm giá trị nhỏ nhất của biểu thức \(M = \frac{1}{{ab}} + \frac{1}{{{a^2} + {b^2}}}\).
----- HẾT -----
Câu 1 (VD):
Cách giải:
a) Rút gọn biểu thức A và B.
+) Ta có:
\(\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} A = 3\sqrt 8 {\rm{ \;}} - \sqrt {50} {\rm{ \;}} - \sqrt {{{\left( {\sqrt 2 {\rm{ \;}} - 1} \right)}^2}} }\\{ \Leftrightarrow A = 3\sqrt {{2^2}.2} {\rm{ \;}} - \sqrt {{5^2}.2} {\rm{ \;}} - \left| {\sqrt 2 {\rm{ \;}} - 1} \right|}\\{ \Leftrightarrow A = 3.2\sqrt 2 {\rm{ \;}} - 5\sqrt 2 {\rm{ \;}} - \left( {\sqrt 2 {\rm{ \;}} - 1} \right){\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} \sqrt 2 {\rm{ \;}} - 1 > 0} \right)}\\{ \Leftrightarrow A = 6\sqrt 2 {\rm{ \;}} - 5\sqrt 2 {\rm{ \;}} - \sqrt 2 {\rm{ \;}} + 1}\\{ \Leftrightarrow A = \left( {6 - 5 - 1} \right)\sqrt 2 {\rm{ \;}} + 1}\\{ \Leftrightarrow A = 1.}\end{array}\)
Vậy A = 1.
+) Với \(x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 4,{\mkern 1mu} {\mkern 1mu} x \ne 9\) ta có:
\(\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} B = \left( {\frac{{3\sqrt x + 6}}{{x - 4}} + \frac{{\sqrt x }}{{\sqrt x - 2}}} \right):\frac{{x - 9}}{{\sqrt x - 3}}}\\{ \Leftrightarrow B = \left( {\frac{{3\left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}} + \frac{{\sqrt x }}{{\sqrt x - 2}}} \right):\frac{{x - 9}}{{\sqrt x - 3}}}\\{ \Leftrightarrow B = \left( {\frac{3}{{\sqrt x - 2}} + \frac{{\sqrt x }}{{\sqrt x - 2}}} \right):\frac{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}{{\sqrt x - 3}}}\\{ \Leftrightarrow B = \frac{{3 + \sqrt x }}{{\sqrt x - 2}}:\left( {\sqrt x + 3} \right)}\\{ \Leftrightarrow B = \frac{{3 + \sqrt x }}{{\sqrt x - 2}}.\frac{1}{{\sqrt x + 3}}}\\{ \Leftrightarrow B = \frac{1}{{\sqrt x - 2}}}\end{array}\)
Vậy với \(x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 4,{\mkern 1mu} {\mkern 1mu} x \ne 9\) thì \(B = \frac{1}{{\sqrt x {\rm{ \;}} - 2}}\).
b) Tìm x sao cho A – 2B = 3.
Ta có
\(\begin{array}{*{20}{l}}{A - 2B = 3}\\{ \Leftrightarrow 1 - 2.\frac{1}{{\sqrt x {\rm{ \;}} - 2}} = 3}\\{ \Leftrightarrow 2.\frac{1}{{\sqrt x {\rm{ \;}} - 2}} = 1 - 3}\\{ \Leftrightarrow 2.\frac{1}{{\sqrt x {\rm{ \;}} - 2}} = {\rm{ \;}} - 2}\\{ \Leftrightarrow \frac{1}{{\sqrt x {\rm{ \;}} - 2}} = {\rm{ \;}} - 1}\\{ \Leftrightarrow \sqrt x {\rm{ \;}} - 2 = {\rm{ \;}} - 1}\\{ \Leftrightarrow \sqrt x {\rm{ \;}} = 1}\\{ \Leftrightarrow x = 1{\mkern 1mu} {\mkern 1mu} \left( {tm} \right)}\end{array}\)
Vậy x = 1.
Câu 2 (VD):
Cách giải:
1. Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2(x - 3) + 3(3x + y) = - 11}\\{(x - 3) - 2(3x + y) = 5}\end{array}} \right.\).
Cách 1:
Đặt: \(\left\{ \begin{array}{l}x - 3 = a\\3x + y = b\end{array} \right.\). Khi đó hệ phương trình trở thành: \(\left\{ {\begin{array}{*{20}{l}}{2a + 3b = - 11}\\{a - 2b = 5}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2a + 3b = - 11}\\{2a - 4b = 10}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 5 + 2b}\\{7b = - 21}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = - 1}\\{b = - 3}\end{array}} \right.\)
Suy ra \(\left\{ \begin{array}{l}x - 3 = - 1\\3x + y = - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = - 3 - 3x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = - 9\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất là: \(\left( {x;y} \right) = \left( {2; - 9} \right)\).
Cách 2:
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{2(x - 3) + 3(3x + y) = - 11}\\{(x - 3) - 2(3x + y) = 5}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2x - 6 + 9x + 3y = - 11}\\{x - 3 - 6x - 2y = 5}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{11x + 3y = - 5}\\{ - 5x - 2y = 8}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{11x + 3y = - 5\,\,\,\,\,\,(1)}\\{y = - \frac{{8 + 5x}}{2} = - 4 - \frac{5}{2}x}\end{array}} \right.\end{array}\)
Thay \(y = - 4 - \frac{5}{2}x\) vào (1) ta có:
\(\begin{array}{l}11x + 3.\left( { - 4 - \frac{5}{2}x} \right) = - 5\\ \Leftrightarrow 11x - 12 - \frac{{15}}{2}x = - 5\\ \Leftrightarrow \frac{7}{2}x = 7\\ \Leftrightarrow x = 2.\end{array}\)
Với \(x = 2\) thì \(y = - 4 - \frac{5}{2}.2 = - 9\).
Vậy hệ phương trình có nghiệm duy nhất là: \(\left( {x;y} \right) = \left( {2; - 9} \right)\).
2. Một quyển vở giá 14000 đồng, một hộp bút giá 30000 đồng. Minh muốn mua 01 hộp bút và một số quyển vở.
a) Gọi \(x\left( {x \in {\mathbb{N}^*}} \right)\) là số quyển vở Minh mua, y là số tiền cần trả khi mua x quyền vở và 01 hộp bút. Hãy biểu diễn y theo x.
Giá tiền khi mua x quyển vở và một hộp bút là: \(14\,000x + 30\,000\) (đồng).
Vì y là số tiền mua x quyển vở và một hộp bút nên \(y = 14\,000x + 30\,000\).
b) Nếu Minh có 300000 đồng để mua vở và 01 hộp bút thì Minh mua được tối đa bao nhiêu quyển vở?
Gọi a \(\left( {a \in \mathbb{N}} \right)\) là số quyển vở tối đa Minh mua.
Số tiền Minh phải trả khi mua 01 hộp bút và a quyển vở là: \(14\,000.a + 30\,000\).
Vì Minh chỉ có 300 000 đồng nên số tiền phải trả nhỏ hơn hoặc bằng 300 000 đồng
Ta có: \(\)
\(\begin{array}{l}14\,000.a + 30\,000 \le 300\,000\\ \Leftrightarrow 14\,000.a \le 300\,000 - 30\,000\\ \Leftrightarrow 14\,000.a \le 270\,000\\ \Leftrightarrow a \le 270\,000:14\,000\\ \Leftrightarrow a \le \frac{{135}}{7} \approx 19,29\end{array}\)
Vậy số vở tối đa Minh có thể mua là 19 quyển.
Câu 3 (VD):
Cách giải:
1. Cho phương trình \({x^2} - 2\left( {m - 1} \right)x + {m^2} - 9 = 0\)\((1)\)(\(x\) là ẩn, \(m\) là tham số)
a) Giải phương trình (1) khi \(m = - 3\).
Thay \(m = - 3\)vào (1) ta được:
\({x^2} - 2\left( { - 3 - 1} \right)x + {\left( { - 3} \right)^2} - 9 = 0\) \( \Leftrightarrow {x^2} + 8x = 0\)
\(\begin{array}{l} \Leftrightarrow x\left( {x + 8} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 8\end{array} \right.\end{array}\)
Vậy với \(m = - 3\)thì phương trình có 2 nghiệm phân biệt\(x = 0\) hoặc \(x = - 8\).
b, Tìm các giá trị của m để phương trình (1) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn điều kiện \({x_1} - {x_2} = 2m - 10\).
+ Phương trình (1) có 2 nghiệm phân biệt \( \Leftrightarrow \Delta ' = {\left[ { - \left( {m - 1} \right)} \right]^2} - {m^2} + 9 > 0\)
\(\begin{array}{l} \Leftrightarrow {m^2} - 2m + 1 - {m^2} + 9 > 0\\ \Leftrightarrow - 2m + 10 > 0\\ \Leftrightarrow m < 5\end{array}\)
Theo hệ thức Vi-ét: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2(m - 1)\\{x_1}.{x_2} = {m^2} - 9\,\,\,(*)\end{array} \right.\)
+ Ta có: \({x_1} + {x_2} = 2(m - 1) \Rightarrow {x_1} = 2(m - 1) - {x_2}\)thay vào \({x_1} - {x_2} = 2m - 10\) ta được:
\(2(m - 1) - {x_2} - {x_2} = 2m - 10\)
\(\begin{array}{l} \Leftrightarrow 2(m - 1) - 2{x_2} = 2\left( {m - 5} \right)\\ \Leftrightarrow m - 1 - {x_2} = m - 5\end{array}\)
\(\begin{array}{l} \Rightarrow {x_2} = 4\\ \Rightarrow {x_1} = 2(m - 1) - 4 = 2m - 6\end{array}\)
Thay vào (*) ta được:
\(\left( {2m - 6} \right).4 = {m^2} - 9\)
\(\begin{array}{l} \Leftrightarrow {m^2} - 8m + 15 = 0\\ \Leftrightarrow {m^2} - 3m - 5m + 15 = 0\\ \Leftrightarrow m\left( {m - 3} \right) - 5\left( {m - 3} \right) = 0\\ \Leftrightarrow \left( {m - 3} \right)\left( {m - 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 3\,\,\,\,(tm)\\m = 5\,\,\,\,(Ktm)\end{array} \right.\end{array}\)
Vậy \(m = 3\)là giá trị cần tìm.
2. Một trường học có mảnh vườn hình chữ nhật chu vi là 100m. Nhà trường tiến hành mở rộng mảnh vườn bằng cách tăng chiều dài thêm 5m và chiều rộng thêm 4m, khi đó diện tích tăng 240m2. Tính chiều dài và chiều rộng mảnh vường trước khi mở rộng.
Gọi chiều dài mảnh vườn trước khi mở rộng là \(x{\rm{ }}\left( m \right)\) (ĐK: 0 < x > 50).
Nửa chu vi mảnh vườn hình chữ nhật là \(100:2 = 50\)(m).
Suy ra, chiều rộng mảnh vườn trước khi mở rộng là: \(50 - x\) (m).
\( \Rightarrow \) Diện tích mảnh vườn trước khi mở rộng là \(x.\left( {50 - x} \right)\)(m2).
Chiều dài mảnh vườn sau khi mở rộng là \(x + 5\) (m).
Chiều rộng mảnh vườn sau khi mở rộng là \(50 - x + 4 = 54 - x\) (m).
Suy ra, diện tích mảnh vườn sau khi mở rộng là \(\left( {x + 5} \right).\left( {54 - x} \right)\)(m2).
Do diện tích sau khi mở rộng tăng 240m2 so với diện tích mảnh vườn ban đầu, nên ta có phương trình:
\(\left( {x + 5} \right).\left( {54 - x} \right) - x.\left( {50 - x} \right) = 240\)
\(\begin{array}{l} \Leftrightarrow 54x - {x^2} + 270 - 5x - 50x + {x^2} = 240\\ \Leftrightarrow - x + 270 = 240\end{array}\)
\( \Rightarrow x = 30\) (TMĐK)
Vậy chiều dài mảnh vườn trước khi mở rộng là 30 m;
Chiều rộng rộng mảnh vườn trước khi mở rộng là 50 – 30 = 20 m.
Câu 4 (NB):
Cách giải:
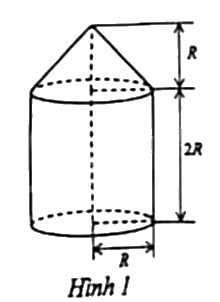
Gọi R là bán kính đường tròn đáy của hình trụ và hình nón.
Ta có đáy hình trụ là hình tròn có chu vi là 37,68 cm nên ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,2\pi R = 37,68\\ \Leftrightarrow 2.3,14.R = 37,68\\ \Leftrightarrow R = \frac{{37,68}}{{2.3,14}} = 6\end{array}\)
Thể tích phần hình trụ là: \({V_{ht}} = \pi {R^2}{h_{ht}} = 3,{14.6^2}.\left( {2.6} \right) = 1356,48\,\,\,(c{m^3})\)
Thể tích phần hình nón là: \({V_{hn}} = \frac{1}{3}\pi {R^2}{h_{hn}} = \frac{1}{3}3,{14.6^2}.6 = 226,08\,\,(c{m^3})\)
Thể tích của chi tiết máy đó là: \(V = {V_{ht}} + {V_{hn}} = 1356,48 + 226,08 = 1582,56\,\,(c{m^3})\)
Vậy thể tích của chi tiết máy là \(1582,56\,\,c{m^3}\).
Câu 5 (VD):
Cách giải:
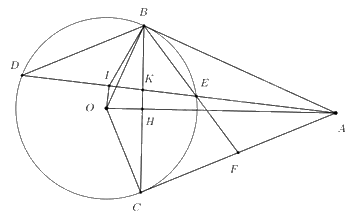
a) Chứng minh năm điểm A, B, I, O, C cùng thuộc một đường tròn.
Do AB, AC là tiếp tuyến nên \(AB \bot OB,AC \bot OC\) (định nghĩa)
\( \Rightarrow \angle ACO = \angle ABO = {90^0}\)\( \Rightarrow \angle ABO + \angle ACO = {90^0} + {90^0} = {180^0}\)
Mà 2 góc này ở vị trí đối diện nên OCAB nội tiếp hay O, C, A, B cùng thuộc một đường tròn (1)
Do I là trung điểm của DE nên \(OI \bot DE\) (tính chất đường kính vuông góc với dây cung)
\( \Rightarrow \angle OIA = {90^0}\)
\( \Rightarrow \angle OIA + \angle OCA = {90^0} + {90^0} = {180^0}\)
Mà 2 góc này ở vị trí đối diện nên OIAC nội tiếp hay O, I, A, C cùng thuộc một đường tròn (2)
Từ (1) và (2) suy ra 5 điểm A, B, I, O, C cùng thuộc một đường tròn (đpcm).
b) Đường thẳng BC cắt OA, AD lần lượt tại H và K. Gọi F là giao điểm của BE và AC. Chứng minh AK.AI = AH.AO và tam giác AFE đồng dạng với tam giác BFA.
Ta có AB = AC (tính chất 2 tiếp tuyến cắt nhau) => A thuộc trung trực của BC
OB = OC (bằng bán kính) => O thuộc trung trực của BC.
\( \Rightarrow \) AO là trung trực của BC hay \(AO \bot BC\) tại H
Xét tam giác ABO vuông tại B, đường cao BH nên:
\(A{B^2} = AH.AO\) (hệ thức lượng trong tam giác vuông) (3)
Ta có \(\angle BIA = \angle BCA\) (hai góc nội tiếp chắn cung AB) \( \Rightarrow \angle BIA = \angle ABC\,\,\left( { = \angle BCA} \right)\).
Xét \(\Delta ABK\) và \(\Delta AIB\) có:
\(\angle BAI\) chung
\(\angle BIA = \angle ABC = \angle ABK\,\,\left( {cmt} \right)\)
\(\Rightarrow \Delta ABK\backsim \Delta AIB\left( g.g \right)\Rightarrow \frac{AB}{AI}=\frac{AK}{AB}\) (cặp cạnh tương ứng tỉ lệ).
\( \Leftrightarrow A{B^2} = AK.AI\) (4)
Từ (3) và (4) suy ra \(AK.AI = AH.AO\,\,\,\left( { = A{B^2}} \right)\) (đpcm)
Do \(BD\parallel AC\left( {gt} \right) \Rightarrow \angle BDA = \angle DAC\) (so le trong)
Mà \(\angle BDA = \angle ABF\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BE)
\( \Rightarrow \angle DAC = \angle ABF\left( { = \angle BDA} \right) = \angle EAF\).
Xét \(\Delta AFE\) và \(\Delta BFA\) có:
\(\angle BFA\) chung
\(\angle EAF = \angle ABF\,\,\left( {cmt} \right)\)
\(\Rightarrow \Delta AFE\backsim \Delta BFA\,\,\left( g.g \right)\) (đpcm)
c) Chứng minh ba đường thẳng AB, CD, FK đồng quy.
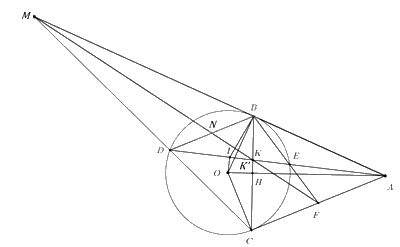
Do \(\Delta AFE\backsim \Delta BFA\,\,\left( cmt \right)\) \( \Rightarrow \frac{{FA}}{{FB}} = \frac{{FE}}{{FA}}\) (cặp cạnh tương ứng tỉ lệ) \( \Rightarrow F{A^2} = FB.FE\)
Xét \(\Delta FEC\) và \(\Delta FCB\) có \(\angle CFB\) chung và \(\angle FCE = \angle CBF\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung CE).
$\Rightarrow \Delta FEC\backsim \Delta FCB\,\,\left( g.g \right)\Rightarrow \frac{FC}{FB}=\frac{FE}{FC}$ (cặp cạnh tương ứng tỉ lệ) \( \Rightarrow F{C^2} = FE.FB\)
\( \Rightarrow FC = FA \Rightarrow F\) là trung điểm của AC.
Gọi M là giao điểm của DC và AB, N là giao điểm của MF và BD.
Do \(BD\parallel AC\left( {gt} \right) \Rightarrow \frac{{DN}}{{FC}} = \frac{{BN}}{{FA}}\,\,\left( { = \frac{{MN}}{{MF}}} \right)\) (định lí Ta-lét).
\( \Rightarrow DN = BN\) (do \(FC = FA\))
Gọi K’ là giao điểm của NF và BC $\Rightarrow \frac{BK'}{CK'}=\frac{BN}{CF}$ (Định lí Ta-lét) (5)
Mà \(\frac{{BN}}{{CF}} = \frac{{2BN}}{{2CF}} = \frac{{BD}}{{AC}} = \frac{{BK}}{{CK}}\) (6)
Từ (5) và (6) suy ra $K,K'$ cùng nằm trên đoạn BC và $\frac{BK}{CK}=\frac{BK'}{CK'}\,\,\,\left( =\frac{BD}{AC} \right)\Rightarrow K\equiv K'$
Chứng tỏ M, N, K, F thẳng hàng hay ba đường thẳng AB, CD, FK đồng quy tại M.
Câu 6 (VD):
Cách giải:
Theo bài ra ta có:
\(\begin{array}{l}{(a + b)^3} = 2\left( {1 - {a^2} - {b^2}} \right)\\ \Leftrightarrow {(a + b)^3} + 2{a^2} + 2{b^2} - 2 = 0\\ \Leftrightarrow {(a + b)^3} + {a^2} + 2ab + {b^2} + {a^2} - 2ab + {b^2} - 2 = 0\\ \Leftrightarrow {(a + b)^3} + {\left( {a + b} \right)^2} + {\left( {a - b} \right)^2} - 2 = 0\\ \Leftrightarrow {(a + b)^3} + {\left( {a + b} \right)^2} - 2 = - {\left( {a - b} \right)^2}\end{array}\)
Vì \({\left( {a - b} \right)^2} \ge 0 \Rightarrow - {\left( {a - b} \right)^2} \le 0\) nên \({(a + b)^3} + {(a + b)^2} - 2 \le 0\) (1)
Đặt \(x = a + b > 0\). Khi đó (1) trở thành:\(\,{x^3} + {x^2} - 2 \le 0\)
\(\begin{array}{l} \Leftrightarrow {x^3} - {x^2} + 2{x^2} - 2x + 2x - 2 \le 0\\ \Leftrightarrow {x^2}\left( {x - 1} \right) + 2x\left( {x - 1} \right) + 2\left( {x - 1} \right) \le 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} + 2x + 2} \right) \le 0\\ \Leftrightarrow \left( {x - 1} \right)\left[ {{{\left( {x + 1} \right)}^2} + 1} \right] \le 0\\ \Leftrightarrow x - 1 \le 0\,\,\left( {do\,\,{{(x + 1)}^2} + 1 > 0\,\,\forall x} \right)\\ \Leftrightarrow x \le 1\end{array}\)
Do \(x > 0\) nên ta có: \(0 < x \le 1\) hay \(0 < a + b \le 1 \Rightarrow 1 \ge {a^2} + {b^2} + 2ab\).
Khi đó:
\(\begin{array}{l}M \ge \left( {{a^2} + {b^2} + 2ab} \right).M = \frac{{{a^2} + {b^2} + 2ab}}{{ab}} + \frac{{{a^2} + {b^2} + 2ab}}{{{a^2} + {b^2}}}\\ \Rightarrow M \ge \frac{{{a^2} + {b^2}}}{{ab}} + 2 + \frac{{2ab}}{{{a^2} + {b^2}}} + 1 = \frac{{{a^2} + {b^2}}}{{ab}} + \frac{{2ab}}{{{a^2} + {b^2}}} + 3 = \frac{{{a^2} + {b^2}}}{{2ab}} + \left( {\frac{{{a^2} + {b^2}}}{{2ab}} + \frac{{2ab}}{{{a^2} + {b^2}}}} \right) + 3\end{array}\)
Theo bất đẳng thức Cô-si ta có:
\({a^2} + {b^2} \ge 2ab \Rightarrow \frac{{{a^2} + {b^2}}}{{2ab}} \ge \frac{{2ab}}{{2ab}} = 1\)
\(\frac{{2ab}}{{{a^2} + {b^2}}} + \frac{{{a^2} + {b^2}}}{{2ab}} \ge 2\sqrt {\frac{{2ab}}{{{a^2} + {b^2}}} \cdot \frac{{{a^2} + {b^2}}}{{2ab}}} = 2\);
Suy ra: \(M \ge 1 + 2 + 3 = 6\)
Dấu “=” xảy ra khi và chỉ khi \(a = b = \frac{1}{2}\).
Vậy giá trị nhỏ nhất của \(M = 6\) khi \(a = b = \frac{1}{2}\).
Kỳ thi tuyển sinh vào lớp 10 môn Toán tại Hải Dương năm 2023 là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Đề thi thường bao gồm các dạng bài tập thuộc chương trình Toán lớp 9, tập trung vào các chủ đề chính như Đại số, Hình học và số học. Việc nắm vững kiến thức cơ bản và luyện tập thường xuyên là chìa khóa để đạt kết quả tốt trong kỳ thi này.
Đề thi thường được chia thành các phần sau:
Tỷ lệ điểm giữa phần trắc nghiệm và phần tự luận có thể thay đổi tùy theo từng năm, nhưng thường phần tự luận chiếm tỷ trọng lớn hơn.
Dưới đây là một số chủ đề thường xuyên xuất hiện trong đề thi vào 10 môn Toán Hải Dương:
Để ôn thi vào 10 môn Toán hiệu quả, các em học sinh cần:
Giaitoan.edu.vn tự hào là một trong những website hàng đầu về giải toán online tại Việt Nam. Chúng tôi cung cấp đầy đủ các tài liệu ôn tập, đề thi thử và đáp án chi tiết cho kỳ thi tuyển sinh vào lớp 10 môn Toán Hải Dương năm 2023. Hãy truy cập giaitoan.edu.vn để được hỗ trợ tốt nhất!
Để giúp các em học sinh làm quen với cấu trúc và độ khó của đề thi, chúng tôi xin giới thiệu một số đề thi tham khảo:
| Đề thi | Năm | Link tải |
|---|---|---|
| Đề thi chính thức | 2023 | [Link đến đề thi 1] |
| Đề thi thử | 2023 | [Link đến đề thi 2] |
| Đề thi năm trước | 2022 | [Link đến đề thi 3] |
Các giáo viên có kinh nghiệm khuyên các em học sinh nên tập trung vào việc nắm vững kiến thức cơ bản, luyện tập thường xuyên và tìm hiểu kỹ cấu trúc đề thi. Ngoài ra, các em cũng nên giữ tâm lý thoải mái và tự tin khi làm bài thi.
Giaitoan.edu.vn chúc các em học sinh đạt kết quả tốt nhất trong kỳ thi tuyển sinh vào lớp 10 môn Toán Hải Dương năm 2023!