Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Quảng Bình năm 2023. Đây là tài liệu ôn tập vô cùng quan trọng dành cho các em học sinh đang chuẩn bị cho kỳ thi sắp tới.
Chúng tôi đã tổng hợp đầy đủ các đề thi chính thức, đáp án chi tiết và hướng dẫn giải bài tập để giúp các em nắm vững kiến thức và tự tin làm bài.
Câu 1: Cho biểu thức \(A = \frac{1}{{\sqrt a {\rm{ \;}} + 3}} + \frac{6}{{a - 9}}\) với \(a \ge 0\) và \(a \ne 9\). 1. Rút gọn biểu thức \(A\). 2. Tìm tất cả các giá trị của \(a\) để \(A = \frac{1}{2}\).
Câu 1: Cho biểu thức \(A = \frac{1}{{\sqrt a {\rm{ \;}} + 3}} + \frac{6}{{a - 9}}\) với \(a \ge 0\) và \(a \ne 9\).
1. Rút gọn biểu thức \(A\).
2. Tìm tất cả các giá trị của \(a\) để \(A = \frac{1}{2}\).
Câu 2: 1. Giải phương trình \({x^2} + 5x - 6 = 0\).
2. Cho phương trình \({x^2} + 5x + m - 3 = 0\) ( \(m\) là tham số).
a. Tìm tất cả các giá trị của \(m\) để phương trình có hai nghiệm.
b. Trong trường hợp phương trình có hai nghiệm \({x_1},{x_2}\), tìm tất cả các giá trị của m để \({x_1},{x_2}\) thỏa mãn hệ thức \(2{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) = 2\).
Câu 3: Với \(x \in \mathbb{R}\),tìm giá trị nhỏ nhất của biểu thức \(P = 4{x^2} - 2|2x - 3| - 12x + 2033\).
Câu 4: Cho nửa đường tròn tâm O đường kính BC và điểm 4 thuộc nửa đường tròn đó, (A khác B và C). Lấy điểm E thuộc cung AB (E khác A và B) sao cho BE < AC, gọi M là giao điểm của AB và CE. Kẻ MH vuông góc với BC tại H.
1. Chứng minh tứ giác ACHM nội tiếp.
2. Chứng minh \(\Delta \)BAE đồng dạng với \(\Delta \)HAM .
3. Gọi K là giao điểm của OE và HA. Chứng minh KE.KO = KA.KH.
----- HẾT -----
Câu 1: Cho biểu thức \(A = \frac{1}{{\sqrt a {\rm{ \;}} + 3}} + \frac{6}{{a - 9}}\) với \(a \ge 0\) và \(a \ne 9\).
1. Rút gọn biểu thức \(A\).
2. Tìm tất cả các giá trị của \(a\) để \(A = \frac{1}{2}\).
Câu 2: 1. Giải phương trình \({x^2} + 5x - 6 = 0\).
2. Cho phương trình \({x^2} + 5x + m - 3 = 0\) ( \(m\) là tham số).
a. Tìm tất cả các giá trị của \(m\) để phương trình có hai nghiệm.
b. Trong trường hợp phương trình có hai nghiệm \({x_1},{x_2}\), tìm tất cả các giá trị của m để \({x_1},{x_2}\) thỏa mãn hệ thức \(2{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) = 2\).
Câu 3: Với \(x \in \mathbb{R}\),tìm giá trị nhỏ nhất của biểu thức \(P = 4{x^2} - 2|2x - 3| - 12x + 2033\).
Câu 4: Cho nửa đường tròn tâm O đường kính BC và điểm 4 thuộc nửa đường tròn đó, (A khác B và C). Lấy điểm E thuộc cung AB (E khác A và B) sao cho BE < AC, gọi M là giao điểm của AB và CE. Kẻ MH vuông góc với BC tại H.
1. Chứng minh tứ giác ACHM nội tiếp.
2. Chứng minh \(\Delta \)BAE đồng dạng với \(\Delta \)HAM .
3. Gọi K là giao điểm của OE và HA. Chứng minh KE.KO = KA.KH.
----- HẾT -----
Câu 1 (VD):
Phương pháp:
1.Sử dụng tính chất căn bậc hai.
2. Giải phương trình với A vừa rút gọn.
Cách giải:
1. Rút gọn biểu thức \(A\).
Với \(a \ge 0\) và \(a \ne 9\) ta có:
\(\begin{array}{l}A = \frac{1}{{\sqrt a + 3}} + \frac{6}{{a - 9}}\\\,\,\,\, = \frac{1}{{\sqrt a + 3}} + \frac{6}{{\left( {\sqrt a + 3} \right)\left( {\sqrt a - 3} \right)}}\\\,\,\, = \frac{{\sqrt a - 3}}{{\left( {\sqrt a + 3} \right)\left( {\sqrt a - 3} \right)}} + \frac{6}{{\left( {\sqrt a + 3} \right)\left( {\sqrt a - 3} \right)}}\\\,\,\, = \frac{{\sqrt a + 3}}{{\left( {\sqrt a + 3} \right)\left( {\sqrt a - 3} \right)}}\\\,\,\, = \frac{1}{{\sqrt a - 3}}\end{array}\)
Vậy \(A = \frac{1}{{\sqrt a - 3}}.\)
2. Tìm tất cả các giá trị của \(a\) để \(A = \frac{1}{2}\).
Với \(a \ge 0\) và \(a \ne 9\) ta có: \(A = \frac{1}{{\sqrt a - 3}}.\)
Vậy với \(a = 5\) thì \(A = \frac{1}{2}\).
Câu 2 (VD):
Phương pháp:
1. Tính \(\Delta {\rm{ \;}} = {b^2} - 4.a.c\)
- \(\Delta {\rm{ \;}} = 0\) thì phương trình có nghiệm kép \({x_1} = {x_2} = \frac{{ - b}}{{2a}}\)
- \(\Delta {\rm{ \;}} < 0\) thì phương trình vô nghiệm
- \(\Delta {\rm{ \;}} > 0\)thì phương trình có hai nghiệm phân biệt:
\({x_1} = \frac{{ - b + \sqrt \Delta {\rm{ \;}}}}{{2.a}}\)
\({x_2} = \frac{{ - b - \sqrt \Delta {\rm{ \;}}}}{{2.a}}\)
2. Sử dụng vi ét.
Cách giải:
1. Giải phương trình \({x^2} + 5x - 6 = 0\).
Xét phương trình \({x^2} + 5x - 6 = 0\) có \(a + b + c = 1 + 5 - 6 = 0\) phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = 1\\{x_2} = - 6\end{array} \right.\)
Vậy phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = 1\\{x_2} = - 6\end{array} \right.\).
2. Cho phương trình \({x^2} + 5x + m - 3 = 0\) ( \(m\) là tham số).
a. Tìm tất cả các giá trị của \(m\) để phương trình có hai nghiệm.
Xét phương trình \({x^2} + 5x + m - 3 = 0\) có \(\Delta = {5^2} - 4.1.\left( {m - 3} \right) = 25 - 4m + 12 = 37 - 4m\)
Để phương trình có hai nghiệm thì \(\Delta \ge 0 \Leftrightarrow 37 - 4m \ge 0 \Leftrightarrow - 4m \ge - 37 \Leftrightarrow m \le \frac{{37}}{4}\).
Vậy phương trình có hai nghiệm khi \(m \le \frac{{37}}{4}\).
b. Trong trường hợp phương trình có hai nghiệm \({x_1},{x_2}\), tìm tất cả các giá trị của \(m\) để \({x_1},{x_2}\) thỏa mãn hệ thức \(2{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) = 2\).
Theo a, phương trình có hai nghiệm khi \(m \le \frac{{37}}{4}\).
Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình.
Áp dụng định lí Vi – ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 5\\{x_1}.{x_2} = m - 3\end{array} \right.\)
Để \(2{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) = 2\)
\(\begin{array}{l}2{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) = 2\\ \Leftrightarrow 2\left( {m - 3} \right) - \left( { - 5} \right) = 2\\ \Leftrightarrow 2m = 3\\ \Leftrightarrow m = \frac{3}{2}\left( {tm} \right).\end{array}\)
Vậy với \(m = \frac{3}{2}\) thì phương trình có hai nghiệm \({x_1},{x_2}\), mãn hệ thức \(2{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) = 2\).
Câu 3 (NB):
Cách giải:
Ta có:
\(\begin{array}{l}P = 4{x^2} - 2|2x - 3| - 12x + 2033\\\,\,\,\,\, = \left( {4{x^2} - 12x + 9} \right) - 2|2x - 3| + 2024\\\,\,\,\,\, = {\left( {2x - 3} \right)^2} - 2|2x - 3| + 2024\end{array}\)
Đặt \(t = |2x - 3| \ge 0\)
Khi đó ta có: \(P = {t^2} - 2t + 2024 = {(t - 1)^2} + 2023\)
Vì \(t \ge 0 \Rightarrow t - 1 \ge - 1 \Rightarrow {(t - 1)^2} \ge 0\) nên \(P \ge 0 + 2023 = 2023\)
Dấu bằng xảy ra khi và chỉ khi \(t - 1 = 0 \Leftrightarrow t = 1\)
Suy ra: \(|2x - 3| = 1 \Leftrightarrow \left[ \begin{array}{l}2x - 3 = 1\\2x - 3 = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x = 4\\2x = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 1\end{array} \right.\)
Vậy giá trị nhỏ nhất của P là \(2023\) khi \(x = 1\) hoặc \(x = 2.\)
Câu 4 (NB):
Cách giải:
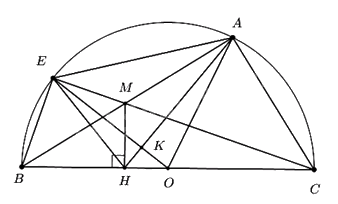
1. Chứng minh tứ giác ACHM nội tiếp.
Ta có \(\angle BAC = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
Mà \(\angle MHC = {90^0}\left( {MH \bot BC} \right)\)
\( \Rightarrow \angle MHC + \angle MAC = {90^0} + {90^0} = {180^0}\)
Mà 2 góc này ở vị trí đối diện nên tứ giác MHCA nội tiếp (dhnb) (đpcm)
2. Chứng minh \(\Delta \)BAE đồng dạng với \(\Delta \)HAM .
Do AMHC nội tiếp (cmt) nên \(\angle MAH = \angle MCH\) (cùng chắn cung MH)
Và \(\angle MHA = \angle MCA\) (cùng chắn cung AM)
Mà \(\angle MCH = \angle ECB = \angle EAB\) (cùng chắn cung EB) và \(\angle ACE = \angle EBA\) (cùng chắn cung AE)
\( \Rightarrow \angle MAH = \angle EAB\left( { = \angle ECB} \right)\) và \(\angle MHA = \angle EBA\left( { = \angle ECA} \right)\)
Xét \(\Delta MHA\) và \(\Delta EBA\) có:
\(\angle MAH = \angle EAB\) (cmt)
\(\angle MHA = \angle EBA\) (cmt)
$\Rightarrow \Delta MAH\backsim \Delta EAB\left( g.g \right)$ (đpcm)
3. Gọi K là giao điểm của OE và HA. Chứng minh KE.KO = KA.KH.
Do MHCA nội tiếp nên \(\angle AHC = \angle AMC\) (cùng chắn cung AC)
Mà \(\angle AMC = \frac{1}{2}\left( {sdcAC + sdcEB} \right) = \frac{1}{2}\left( {{{180}^0} - sdcAE} \right) = \frac{1}{2}\left( {{{180}^0} - \angle EOA} \right) = \frac{1}{2}\left( {\angle AEO + \angle EAO} \right)\)
Mà \(\Delta OEA\) cân do OA = OE nên \(\angle OEA = \angle OAE\)
\( \Rightarrow \angle AMC = \frac{1}{2}.2.\angle OEA = \angle OEA\)
\( \Rightarrow \angle AHO = \angle AEO\left( { = \angle AMC} \right)\)
Xét tứ giác OHEA có \(\angle AHO = \angle AEO\)
Mà H, E là 2 đỉnh kề nhau cùng nhìn OA dưới 2 góc bằng nhau nên OHEA nội tiếp
\( \Rightarrow \angle KAO = \angle KEH\) (cùng chắn cung OH) và \(\angle KOA = \angle KHE\) (cùng chắn cung AE)
Xét \(\Delta KOA\) và \(\Delta KHE\) có:
\(\angle KAO = \angle KEH\left( {cmt} \right)\)
\(\angle KOA = \angle KHE\left( {cmt} \right)\)
$\Rightarrow \Delta KOA\backsim \Delta KHE\left( g.g \right)\Rightarrow \frac{KO}{KH}=\frac{KA}{KE}\Rightarrow KO.KE=KH.KA$ (đpcm)
Câu 1 (VD):
Phương pháp:
1.Sử dụng tính chất căn bậc hai.
2. Giải phương trình với A vừa rút gọn.
Cách giải:
1. Rút gọn biểu thức \(A\).
Với \(a \ge 0\) và \(a \ne 9\) ta có:
\(\begin{array}{l}A = \frac{1}{{\sqrt a + 3}} + \frac{6}{{a - 9}}\\\,\,\,\, = \frac{1}{{\sqrt a + 3}} + \frac{6}{{\left( {\sqrt a + 3} \right)\left( {\sqrt a - 3} \right)}}\\\,\,\, = \frac{{\sqrt a - 3}}{{\left( {\sqrt a + 3} \right)\left( {\sqrt a - 3} \right)}} + \frac{6}{{\left( {\sqrt a + 3} \right)\left( {\sqrt a - 3} \right)}}\\\,\,\, = \frac{{\sqrt a + 3}}{{\left( {\sqrt a + 3} \right)\left( {\sqrt a - 3} \right)}}\\\,\,\, = \frac{1}{{\sqrt a - 3}}\end{array}\)
Vậy \(A = \frac{1}{{\sqrt a - 3}}.\)
2. Tìm tất cả các giá trị của \(a\) để \(A = \frac{1}{2}\).
Với \(a \ge 0\) và \(a \ne 9\) ta có: \(A = \frac{1}{{\sqrt a - 3}}.\)
Vậy với \(a = 5\) thì \(A = \frac{1}{2}\).
Câu 2 (VD):
Phương pháp:
1. Tính \(\Delta {\rm{ \;}} = {b^2} - 4.a.c\)
- \(\Delta {\rm{ \;}} = 0\) thì phương trình có nghiệm kép \({x_1} = {x_2} = \frac{{ - b}}{{2a}}\)
- \(\Delta {\rm{ \;}} < 0\) thì phương trình vô nghiệm
- \(\Delta {\rm{ \;}} > 0\)thì phương trình có hai nghiệm phân biệt:
\({x_1} = \frac{{ - b + \sqrt \Delta {\rm{ \;}}}}{{2.a}}\)
\({x_2} = \frac{{ - b - \sqrt \Delta {\rm{ \;}}}}{{2.a}}\)
2. Sử dụng vi ét.
Cách giải:
1. Giải phương trình \({x^2} + 5x - 6 = 0\).
Xét phương trình \({x^2} + 5x - 6 = 0\) có \(a + b + c = 1 + 5 - 6 = 0\) phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = 1\\{x_2} = - 6\end{array} \right.\)
Vậy phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = 1\\{x_2} = - 6\end{array} \right.\).
2. Cho phương trình \({x^2} + 5x + m - 3 = 0\) ( \(m\) là tham số).
a. Tìm tất cả các giá trị của \(m\) để phương trình có hai nghiệm.
Xét phương trình \({x^2} + 5x + m - 3 = 0\) có \(\Delta = {5^2} - 4.1.\left( {m - 3} \right) = 25 - 4m + 12 = 37 - 4m\)
Để phương trình có hai nghiệm thì \(\Delta \ge 0 \Leftrightarrow 37 - 4m \ge 0 \Leftrightarrow - 4m \ge - 37 \Leftrightarrow m \le \frac{{37}}{4}\).
Vậy phương trình có hai nghiệm khi \(m \le \frac{{37}}{4}\).
b. Trong trường hợp phương trình có hai nghiệm \({x_1},{x_2}\), tìm tất cả các giá trị của \(m\) để \({x_1},{x_2}\) thỏa mãn hệ thức \(2{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) = 2\).
Theo a, phương trình có hai nghiệm khi \(m \le \frac{{37}}{4}\).
Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình.
Áp dụng định lí Vi – ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 5\\{x_1}.{x_2} = m - 3\end{array} \right.\)
Để \(2{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) = 2\)
\(\begin{array}{l}2{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) = 2\\ \Leftrightarrow 2\left( {m - 3} \right) - \left( { - 5} \right) = 2\\ \Leftrightarrow 2m = 3\\ \Leftrightarrow m = \frac{3}{2}\left( {tm} \right).\end{array}\)
Vậy với \(m = \frac{3}{2}\) thì phương trình có hai nghiệm \({x_1},{x_2}\), mãn hệ thức \(2{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) = 2\).
Câu 3 (NB):
Cách giải:
Ta có:
\(\begin{array}{l}P = 4{x^2} - 2|2x - 3| - 12x + 2033\\\,\,\,\,\, = \left( {4{x^2} - 12x + 9} \right) - 2|2x - 3| + 2024\\\,\,\,\,\, = {\left( {2x - 3} \right)^2} - 2|2x - 3| + 2024\end{array}\)
Đặt \(t = |2x - 3| \ge 0\)
Khi đó ta có: \(P = {t^2} - 2t + 2024 = {(t - 1)^2} + 2023\)
Vì \(t \ge 0 \Rightarrow t - 1 \ge - 1 \Rightarrow {(t - 1)^2} \ge 0\) nên \(P \ge 0 + 2023 = 2023\)
Dấu bằng xảy ra khi và chỉ khi \(t - 1 = 0 \Leftrightarrow t = 1\)
Suy ra: \(|2x - 3| = 1 \Leftrightarrow \left[ \begin{array}{l}2x - 3 = 1\\2x - 3 = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x = 4\\2x = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 1\end{array} \right.\)
Vậy giá trị nhỏ nhất của P là \(2023\) khi \(x = 1\) hoặc \(x = 2.\)
Câu 4 (NB):
Cách giải:
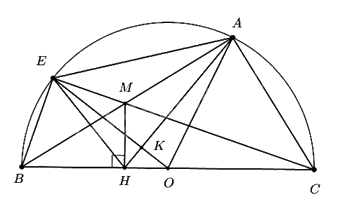
1. Chứng minh tứ giác ACHM nội tiếp.
Ta có \(\angle BAC = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
Mà \(\angle MHC = {90^0}\left( {MH \bot BC} \right)\)
\( \Rightarrow \angle MHC + \angle MAC = {90^0} + {90^0} = {180^0}\)
Mà 2 góc này ở vị trí đối diện nên tứ giác MHCA nội tiếp (dhnb) (đpcm)
2. Chứng minh \(\Delta \)BAE đồng dạng với \(\Delta \)HAM .
Do AMHC nội tiếp (cmt) nên \(\angle MAH = \angle MCH\) (cùng chắn cung MH)
Và \(\angle MHA = \angle MCA\) (cùng chắn cung AM)
Mà \(\angle MCH = \angle ECB = \angle EAB\) (cùng chắn cung EB) và \(\angle ACE = \angle EBA\) (cùng chắn cung AE)
\( \Rightarrow \angle MAH = \angle EAB\left( { = \angle ECB} \right)\) và \(\angle MHA = \angle EBA\left( { = \angle ECA} \right)\)
Xét \(\Delta MHA\) và \(\Delta EBA\) có:
\(\angle MAH = \angle EAB\) (cmt)
\(\angle MHA = \angle EBA\) (cmt)
$\Rightarrow \Delta MAH\backsim \Delta EAB\left( g.g \right)$ (đpcm)
3. Gọi K là giao điểm của OE và HA. Chứng minh KE.KO = KA.KH.
Do MHCA nội tiếp nên \(\angle AHC = \angle AMC\) (cùng chắn cung AC)
Mà \(\angle AMC = \frac{1}{2}\left( {sdcAC + sdcEB} \right) = \frac{1}{2}\left( {{{180}^0} - sdcAE} \right) = \frac{1}{2}\left( {{{180}^0} - \angle EOA} \right) = \frac{1}{2}\left( {\angle AEO + \angle EAO} \right)\)
Mà \(\Delta OEA\) cân do OA = OE nên \(\angle OEA = \angle OAE\)
\( \Rightarrow \angle AMC = \frac{1}{2}.2.\angle OEA = \angle OEA\)
\( \Rightarrow \angle AHO = \angle AEO\left( { = \angle AMC} \right)\)
Xét tứ giác OHEA có \(\angle AHO = \angle AEO\)
Mà H, E là 2 đỉnh kề nhau cùng nhìn OA dưới 2 góc bằng nhau nên OHEA nội tiếp
\( \Rightarrow \angle KAO = \angle KEH\) (cùng chắn cung OH) và \(\angle KOA = \angle KHE\) (cùng chắn cung AE)
Xét \(\Delta KOA\) và \(\Delta KHE\) có:
\(\angle KAO = \angle KEH\left( {cmt} \right)\)
\(\angle KOA = \angle KHE\left( {cmt} \right)\)
$\Rightarrow \Delta KOA\backsim \Delta KHE\left( g.g \right)\Rightarrow \frac{KO}{KH}=\frac{KA}{KE}\Rightarrow KO.KE=KH.KA$ (đpcm)
Kỳ thi tuyển sinh vào lớp 10 môn Toán Quảng Bình năm 2023 là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Để đạt kết quả tốt nhất, việc chuẩn bị kỹ lưỡng là vô cùng cần thiết. Đề thi thường bao gồm các dạng bài tập khác nhau, đòi hỏi học sinh phải có kiến thức vững chắc và kỹ năng giải quyết vấn đề tốt.
Cấu trúc đề thi thường bao gồm các phần sau:
Dưới đây là một số dạng bài tập thường gặp trong đề thi vào 10 môn Toán Quảng Bình:
Để ôn thi hiệu quả, các em cần:
Ngoài bộ đề thi mà chúng tôi cung cấp, các em có thể tham khảo thêm các tài liệu ôn thi sau:
Chúc các em ôn thi tốt và đạt kết quả cao trong kỳ thi tuyển sinh vào lớp 10 môn Toán Quảng Bình năm 2023!
Bài toán: Giải phương trình: 2x + 3 = 7
Giải:
2x + 3 = 7
2x = 7 - 3
2x = 4
x = 2
| Trường THPT | Điểm chuẩn (2022) |
|---|---|
| Trường THPT Chuyên Quảng Bình | 35.0 |
| Trường THPT Quảng Phong | 32.0 |
| Trường THPT Hướng Hóa | 30.0 |
| *Lưu ý: Điểm chuẩn có thể thay đổi theo từng năm. | |