Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Huế năm 2021 chính thức. Đây là tài liệu ôn tập vô cùng quan trọng dành cho các em học sinh đang chuẩn bị cho kỳ thi sắp tới.
Chúng tôi cung cấp đầy đủ các đề thi, đáp án và lời giải chi tiết, giúp các em làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi.
Câu 1 (1,5 điểm): a) Tìm số
Câu 1:
Phương pháp:
a) \(\sqrt {f\left( x \right)} = a\left( {a \ge 0} \right) \Leftrightarrow \left\{ \begin{array}{l}f\left( x \right) \ge 0\\f\left( x \right) = {a^2}\end{array} \right.\)
b) Áp dụng hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)
c) Xác định các hạng tử giống nhau, đơn giản từng phân thức sau đó thực hiện phép toán để rút gọn biểu thức.
Cách giải:
a) Với \(x \ge 0\) ta có \(\sqrt x = 2 \Leftrightarrow {\left( {\sqrt x } \right)^2} = {2^2} \Leftrightarrow x = 4\,\,\left( {tm} \right)\).
Vậy \(x = 4\).
b) Ta có:
\(\begin{array}{l}A = \sqrt {4.5} - \sqrt {9.5} + \sqrt 5 \\A = \sqrt {{2^2}.5} - \sqrt {{3^2}.5} + \sqrt 5 \\A = 2\sqrt 5 - 3\sqrt 5 + \sqrt 5 \\A = 0\end{array}\)
Vậy \(A = 0\).
c) Với \(x > 0,\,\,y > 0\) ta có:
\(\begin{array}{l}P = \dfrac{{x\sqrt x + y\sqrt y }}{{\sqrt x + \sqrt y }} - {\left( {\sqrt x - \sqrt y } \right)^2}\\P = \dfrac{{\left( {\sqrt x + \sqrt y } \right)\left( {x - \sqrt {xy} + y} \right)}}{{\sqrt x + \sqrt y }} - \left( {x - 2\sqrt {xy} + y} \right)\\P = x - \sqrt {xy} + y - x + 2\sqrt {xy} - y\\P = \sqrt {xy} \end{array}\)
Vậy với \(x > 0,\,\,y > 0\) thì \(P = \sqrt {xy} \).
Câu 2:
Phương pháp:
a) Vận dụng phương pháp cộng đại số để giải hệ phương trình.
b) Áp dụng điều kiện của hai đường thẳng song song xác định được điều kiện của hệ số \(a\) và \(b\)
\(\left( d \right)\) đi qua điểm \(M\left( {2; - 3} \right)\) xác định được hệ số \(b\), đối chiếu điều kiện và kết luận.
Cách giải:
a) Ta có: \(\left\{ \begin{array}{l}3x + y = 1\\x - 2y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}6x + 2y = 2\\x - 2y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}7x = 7\\y = 1 - 3x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 1 - 3 = - 2\end{array} \right.\).
Vậy hệ có nghiệm duy nhất \(\left( {x;y} \right) = \left( {1; - 2} \right)\).
b) \(\left( d \right)\) song song với đường thẳng \(\left( {d'} \right)\) nên \(\left\{ \begin{array}{l}a = 2\\b \ne - 1\end{array} \right.\). Thay vào \(\left( d \right)\) ta được \(\left( d \right):y = 2x + b\,\,\left( {b \ne - 1} \right)\).
\(\left( d \right)\) đi qua điểm \(M\left( {2; - 3} \right)\) nên ta có: \( - 3 = 2.2 + b \Leftrightarrow - 3 = 4 + b \Leftrightarrow b = - 3 - 4 = - 7\,\,\left( {tm} \right)\).
Vậy phương trình đường thẳng của \(\left( d \right)\) cần tìm là: \(y = 2x - 7\).
Câu 3:
Phương pháp:
Giải bài toán bằng cách lập phương trình, cụ thể:
Gọi số tấm chắn mà công ty A cần làm trong một ngày theo kế hoạch là \(x\,\,\,\left( {x \in \mathbb{N}*} \right)\) (tấm), từ đó tính được số ngày để hoàn thành \(20000\) tấm theo kế hoạch
Tính được thực tế số tấm chắn mà công ty A làm và thời gian thực tế hoàn thành số tấm chắn làm được.
Lập phương trình, giải phương trình và kết luận.
Cách giải:
Gọi số tấm chắn mà công ty A cần làm trong một ngày theo kế hoạch là \(x\,\,\,\left( {x \in \mathbb{N}*} \right)\) (tấm)
Số ngày để hoàn thành \(20000\) tấm theo kế hoạch là \(\dfrac{{20000}}{x}\)( ngày)
Thực tế: Số tấm chắn mà công ty A làm trong một ngày là \(x + 300\) (tấm chắn)
Tổng số tấm chắn mà công ty A làm theo thực tế là \(20700\)( tấm chắn)
Thời gian thực tế hoàn thành làm \(27000\) tấm chắn là \(\dfrac{{20700}}{{x + 300}}\)( ngày)
Thực tế công ty \(A\) hoàn thành công việc sớm hơn dự định là \(1\)ngày nên ta có phương trình:
\(\dfrac{{20000}}{x} - \dfrac{{20700}}{{x + 300}} = 1\)
\(\begin{array}{l} \Leftrightarrow 20000\left( {x + 300} \right) - 20700x = x\left( {x + 300} \right)\\ \Leftrightarrow 20000x + 6000000 - 20700x = {x^2} + 300x\\ \Leftrightarrow {x^2} + 1000x - 6000000 = 0\\ \Leftrightarrow {x^2} - 2000x + 3000x - 6000000 = 0\\ \Leftrightarrow x\left( {x - 2000} \right) + 3000\left( {x - 2000} \right) = 0\\ \Leftrightarrow \left( {x - 2000} \right)\left( {x + 3000} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 2000 = 0\\x + 3000 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2000\,\,\,\,\,\,\,\left( {tm} \right)\\x = - 3000\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy số tấm chắn mà công ty A thực tế làm một ngày là 2000 tấm chắn .
Câu 4:
Phương pháp:
a) Thay \(m = 2\) vào phương trình của đề bài, nhận thấy đây là phương trình bậc hai ẩn \(x\)
Áp dụng nhận xét \(a + b + c = 0\) thì phương trình bậc hai có hai nghiệm phân biệt \({x_1} = 1\) và \({x_2} = \dfrac{c}{a}\)
b) Phương trình ban đầu có nghiệm \( \Leftrightarrow \Delta \ge 0\) (hoặc \(\Delta ' \ge 0\))
c) Áp dụng hệ thức Vi – ét, tính được \({x_1} + {x_2};{x_1}{x_2}\) theo tham số \(m\)
Biến đổi hệ thức của đề bài để xuất hiện \({x_1} + {x_2};{x_1}{x_2}\), giải phương trình chứa tham số \(m\), đối chiếu điều kiện và kết luận.
Cách giải:
a) Khi \(m = 2\) phương trình (1) trở thành: \({x^2} - 3x + 2 = 0\).
Ta có \(a + b + c = 1 - 3 + 2 = 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ \begin{array}{l}x = 1\\x = \dfrac{c}{a} = 2\end{array} \right.\).
Vậy khi \(m = 2\) thì tập nghiệm của phương trình là \(S = \left\{ {1;2} \right\}\).
b) Để phương trình \(\left( 1 \right)\) có nghiệm thì \(\Delta \ge 0\) \( \Leftrightarrow {3^2} - 4m \ge 0 \Leftrightarrow m \le \dfrac{9}{4}\)
Vậy để phương trình (1) có nghiệm thì \(m \le \dfrac{9}{4}\).
c) Với \(m \le \dfrac{9}{4}\) phương trình có hai nghiệm \({x_1},{x_2}\).
Khi đó áp dụng hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 3\\{x_1}{x_2} = m\end{array} \right.\)
Ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,\,{x_1}^3{x_2} + {x_1}{x_2}^3 - 2{x_1}^2{x_2}^2 = 5\\ \Leftrightarrow {x_1}{x_2}\left( {{x_1}^2 + {x_2}^2} \right) - 2{\left( {{x_1}{x_2}} \right)^2} = 5\\ \Leftrightarrow {x_1}{x_2}\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2}} \right] - 2{\left( {{x_1}{x_2}} \right)^2} = 5\\ \Leftrightarrow {x_1}{x_2}{\left( {{x_1} + {x_2}} \right)^2} - 2{\left( {{x_1}{x_2}} \right)^2} - 2{\left( {{x_1}{x_2}} \right)^2} = 5\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 4{\left( {{x_1}{x_2}} \right)^2} = 5\\ \Leftrightarrow {3^2} - 4{m^2} = 5 \Leftrightarrow 4{m^2} = 4\\ \Leftrightarrow {m^2} = 1 \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - 1\end{array} \right.\,\,\,\left( {tm} \right)\end{array}\)
Vậy \(m \in \left\{ {1; - 1} \right\}\) thỏa mãn yêu cầu bài toán.
Câu 5:
Phương pháp:
a) Vận dụng dấu hiệu nhận biết của tứ giác nội tiếp, chứng minh \(\angle AMO = \angle AIO = {90^0}\) suy ra \(AMIO\) nội tiếp đường tròn đường kính \(OA\) (tứ giác có 2 đỉnh kề cùng nhìn \(OA\) dưới các góc bằng \({90^0}\)).
b) Áp dụng hệ thức lượng trong tam giác vuông và trường hợp đồng dạng cạnh – góc – cạnh của hai tam giác.
c) Gọi \(N \in OA\) sao cho \(\dfrac{{ON}}{{OA}} = \dfrac{2}{3}\), từ đó chứng minh được \(NG//IA\) (định lí Ta – lét đảo)
Chứng minh \(ON\) cố định.
Cách giải:
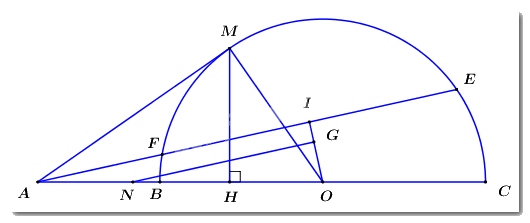
a) Ta có: \(I\) là trung điểm của \(EF\) nên \(OI \bot EF\) (quan hệ vuông góc giữa đường kính và dây cùng)
\( \Rightarrow \angle AIO = {90^0}\).
Mà \(AM\) là tiếp tuyến của nửa đường tròn \(\left( O \right)\) nên \(AM \bot OM\) (định nghĩa) \( \Rightarrow \angle AMO = {90^0}\).
\( \Rightarrow \angle AMO = \angle AIO = {90^0}\)\( \Rightarrow AMIO\) nội tiếp đường tròn đường kính \(OA\) (tứ giác có 2 đỉnh kề cùng nhìn \(OA\) dưới các góc bằng \({90^0}\)).
b) Áp dụng hệ thức lượng trong tam giác \(AMO\) vuông tại \(M\) có \(MH\) là đường cao ta có: \(O{M^2} = OH.OA\)
Mà \(OM = OF \Rightarrow O{F^2} = OH.OA \Rightarrow \dfrac{{OH}}{{OF}} = \dfrac{{OF}}{{OA}}\).
Xét \(\Delta OFH\) và \(\Delta OAF\) ta có:
\(\angle FOA\) chung;
\(\dfrac{{OH}}{{OF}} = \dfrac{{OF}}{{OA}}\,\,\left( {cmt} \right)\);
\( \Rightarrow \Delta OFH \sim \Delta OAF\,\,\,\left( {c.g.c} \right)\,\,\left( {dpcm} \right)\)
c) Gọi \(N \in OA\) sao cho \(\dfrac{{ON}}{{OA}} = \dfrac{2}{3}\), khi đó ta có \(\dfrac{{ON}}{{OA}} = \dfrac{{OG}}{{OI}} = \dfrac{2}{3}\) \( \Rightarrow NG//IA\) (định lí Ta-lét đảo).
Mà \(AI \bot OI\,\,\left( {do\,\,OI \bot EF} \right)\) \( \Rightarrow NG \bot OI\) tại \(G\) \( \Rightarrow \angle OGN = {90^0}\).
\( \Rightarrow G\) thuộc đường tròn đường kính \(ON\).
Vì \(A,\,\,B,\,\,C\) cố định \( \Rightarrow O\) cố định \( \Rightarrow OA\) không đổi \( \Rightarrow ON\) không đổi \( \Rightarrow N\) cố định.
\( \Rightarrow \) Đường tròn đường kính \(ON\) cố định.
Vậy khi điểm E thay đổi trên cung MC thì trọng tâm G của tam giác \(OEF\) luôn nằm trên một đường tròn cố định là đường tròn đường kính \(ON\) với \(ON = \dfrac{2}{3}OA\) (đpcm).
Câu 6:
Phương pháp:
Tính thể tích ban đầu của khúc gỗ: \({V_1} = \pi {r^2}h\) (áp dụng công thức tính thể tích của khối trụ)
Tính thể tích khối gỗ hình nón: \({V_2} = \dfrac{1}{3}\pi {r^2}h\) (áp dụng công thức tính thể tích của khối nón)
Vậy thể tịch khúc gõ còn lại là \(V = {V_1} - {V_2}\)
Cách giải:

Thể tích ban đầu của khúc gỗ là: \({V_1} = \pi {.10^2}.20 = 2000\pi \,\,\left( {c{m^3}} \right)\).
Thể tích khối gỗ hình nón bị tiện bỏ là: \({V_2} = \dfrac{1}{3}\pi {.10^2}.10 = \dfrac{{1000}}{3}\pi \,\,\left( {c{m^3}} \right)\).
Vậy thể tích phần khúc gỗ còn lại là \(V = {V_1} - {V_2} = 2000\pi - \dfrac{{1000}}{3}\pi = \dfrac{{5000}}{3}\pi \approx 5236\,\,\left( {c{m^3}} \right)\).
Câu 1 (1,5 điểm):
a) Tìm số \(x\) không âm, biết \(\sqrt x = 2\).
b) Không sử dụng máy tính cầm tay, tính giá trị của biểu thức \(A = \sqrt {4.5} - \sqrt {9.5} + \sqrt 5 \).
c) Rút gọn biểu thức \(P = \dfrac{{x\sqrt x + y\sqrt y }}{{\sqrt x + \sqrt y }} - {\left( {\sqrt x - \sqrt y } \right)^2}\) với \(x > 0,\,\,y > 0\).
Câu 2 (1,5 điểm):
a) Không sử dụng máy tính cầm tay, giải hệ phương trình \(\left\{ \begin{array}{l}3x + y = 1\\x - 2y = 5\end{array} \right.\)
b) Viết phương trình đường thẳng \(\left( d \right):y = ax + b\,\,\left( {a \ne 0} \right)\), biết rằng đường thẳng \(\left( d \right)\) song song với đường thẳng \(\left( {d'} \right):y = 2x - 1\) và đi qua điểm \(M\left( {2; - 3} \right)\).
Câu 3 (1,0 điểm):
Để phục vụ công tác phòng chống dịch COVID-19, một công ty \(A\) lên kế hoạch trong một thời gian quy định làm \(20000\) tấm chắn bảo hộ để tặng các chốt chống dịch. Do ý thức khẩn trương trong công tác hỗ trợ chống dịch và nhờ cải tiến quy trình làm việc nên mỗi ngày Công ty A làm được nhiều hơn \(300\) tấm so với kế hoạch ban đầu. Vì thế, Công ty A đã hoàn thành kế hoạch sớm hơn đúng một ngày so với thời gian quy định và làm được nhiều hơn \(700\) tấm so với kế hoạch ban đầu. Biết rằng số tấm chắn làm ra trong một ngày là bằng nhau và nguyên cái. Hỏi theo kế hoạch mỗi ngày công ty A cần làm bao nhiêu tắm chắn bảo hộ?
Câu 4 (2,0 điểm):
Cho phương trình \({x^2} - 3x + m = 0\,\,\,\left( 1 \right)\) (\(x\) là ẩn số)
a) Giải phương trình (1) khi \(m = 2\).
b) Tìm các giá trị của \(m\) để phương trình (1) có nghiệm.
c) Tìm các giá trị của \(m\) để phương trình \(\left( 1 \right)\) có hai nghiệm \({x_1},{x_2}\) thỏa mãn đẳng thức:
\({x_1}^3{x_2} + {x_1}{x_2}^3 - 2{x_1}^2{x_2}^2 = 5\)
Câu 5 (3,0 điểm):
Cho ba điểm \(A,B,C\) phân biệt, cố định và thẳng hàng sao cho \(B\) nằm giữa \(A\) và \(C\). Vẽ nửa đường tròn tâm \(O\) đường kính \(BC\). Từ \(A\) kẻ tiếp tuyến \(AM\) đến nửa đường tròn \(\left( O \right)\) (\(M\) là tiếp điểm). Trên cung \(MC\)lấy điểm \(E\) (\(E\) không trùng \(M\) và \(C\)), đường thẳng \(AE\) cắt nửa đường tròn \(\left( O \right)\) tại điểm thứ hai là \(F\) (\(F\) không trùng \(E\)). Gọi \(I\) là trung điểm của đoạn thẳng \(EF\) và \(H\) là hình chiếu vuông góc của \(M\) lên đường thẳng \(BC\). Chứng minh:
a) Tứ giác \(AMIO\) nội tiếp;
b) Hai tam giác \(OFH\) và \(OAF\) đồng dạng với nhau;
c) Trọng tâm G của tam giác \(OEF\) luôn nằm trên một đường tròn cố định khi điểm E thay đổi trên cung MC.
Câu 6 (1,0 điểm):
Một khúc gỗ đặc có dạng hình trụ, bán kính hình tròn đáy là 10 cm, chiều cao bằng 20 cm, người ta tiện bỏ bên trong khúc gỗ một vật dạng hình nón có bán kính hình tròn đáy là 10 cm, chiều cao bằng một nửa chiều cao của khúc gỗ (như hình vẽ bên). Tính thể tích phần khúc gỗ còn lại.

Câu 1 (1,5 điểm):
a) Tìm số \(x\) không âm, biết \(\sqrt x = 2\).
b) Không sử dụng máy tính cầm tay, tính giá trị của biểu thức \(A = \sqrt {4.5} - \sqrt {9.5} + \sqrt 5 \).
c) Rút gọn biểu thức \(P = \dfrac{{x\sqrt x + y\sqrt y }}{{\sqrt x + \sqrt y }} - {\left( {\sqrt x - \sqrt y } \right)^2}\) với \(x > 0,\,\,y > 0\).
Câu 2 (1,5 điểm):
a) Không sử dụng máy tính cầm tay, giải hệ phương trình \(\left\{ \begin{array}{l}3x + y = 1\\x - 2y = 5\end{array} \right.\)
b) Viết phương trình đường thẳng \(\left( d \right):y = ax + b\,\,\left( {a \ne 0} \right)\), biết rằng đường thẳng \(\left( d \right)\) song song với đường thẳng \(\left( {d'} \right):y = 2x - 1\) và đi qua điểm \(M\left( {2; - 3} \right)\).
Câu 3 (1,0 điểm):
Để phục vụ công tác phòng chống dịch COVID-19, một công ty \(A\) lên kế hoạch trong một thời gian quy định làm \(20000\) tấm chắn bảo hộ để tặng các chốt chống dịch. Do ý thức khẩn trương trong công tác hỗ trợ chống dịch và nhờ cải tiến quy trình làm việc nên mỗi ngày Công ty A làm được nhiều hơn \(300\) tấm so với kế hoạch ban đầu. Vì thế, Công ty A đã hoàn thành kế hoạch sớm hơn đúng một ngày so với thời gian quy định và làm được nhiều hơn \(700\) tấm so với kế hoạch ban đầu. Biết rằng số tấm chắn làm ra trong một ngày là bằng nhau và nguyên cái. Hỏi theo kế hoạch mỗi ngày công ty A cần làm bao nhiêu tắm chắn bảo hộ?
Câu 4 (2,0 điểm):
Cho phương trình \({x^2} - 3x + m = 0\,\,\,\left( 1 \right)\) (\(x\) là ẩn số)
a) Giải phương trình (1) khi \(m = 2\).
b) Tìm các giá trị của \(m\) để phương trình (1) có nghiệm.
c) Tìm các giá trị của \(m\) để phương trình \(\left( 1 \right)\) có hai nghiệm \({x_1},{x_2}\) thỏa mãn đẳng thức:
\({x_1}^3{x_2} + {x_1}{x_2}^3 - 2{x_1}^2{x_2}^2 = 5\)
Câu 5 (3,0 điểm):
Cho ba điểm \(A,B,C\) phân biệt, cố định và thẳng hàng sao cho \(B\) nằm giữa \(A\) và \(C\). Vẽ nửa đường tròn tâm \(O\) đường kính \(BC\). Từ \(A\) kẻ tiếp tuyến \(AM\) đến nửa đường tròn \(\left( O \right)\) (\(M\) là tiếp điểm). Trên cung \(MC\)lấy điểm \(E\) (\(E\) không trùng \(M\) và \(C\)), đường thẳng \(AE\) cắt nửa đường tròn \(\left( O \right)\) tại điểm thứ hai là \(F\) (\(F\) không trùng \(E\)). Gọi \(I\) là trung điểm của đoạn thẳng \(EF\) và \(H\) là hình chiếu vuông góc của \(M\) lên đường thẳng \(BC\). Chứng minh:
a) Tứ giác \(AMIO\) nội tiếp;
b) Hai tam giác \(OFH\) và \(OAF\) đồng dạng với nhau;
c) Trọng tâm G của tam giác \(OEF\) luôn nằm trên một đường tròn cố định khi điểm E thay đổi trên cung MC.
Câu 6 (1,0 điểm):
Một khúc gỗ đặc có dạng hình trụ, bán kính hình tròn đáy là 10 cm, chiều cao bằng 20 cm, người ta tiện bỏ bên trong khúc gỗ một vật dạng hình nón có bán kính hình tròn đáy là 10 cm, chiều cao bằng một nửa chiều cao của khúc gỗ (như hình vẽ bên). Tính thể tích phần khúc gỗ còn lại.

Câu 1:
Phương pháp:
a) \(\sqrt {f\left( x \right)} = a\left( {a \ge 0} \right) \Leftrightarrow \left\{ \begin{array}{l}f\left( x \right) \ge 0\\f\left( x \right) = {a^2}\end{array} \right.\)
b) Áp dụng hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)
c) Xác định các hạng tử giống nhau, đơn giản từng phân thức sau đó thực hiện phép toán để rút gọn biểu thức.
Cách giải:
a) Với \(x \ge 0\) ta có \(\sqrt x = 2 \Leftrightarrow {\left( {\sqrt x } \right)^2} = {2^2} \Leftrightarrow x = 4\,\,\left( {tm} \right)\).
Vậy \(x = 4\).
b) Ta có:
\(\begin{array}{l}A = \sqrt {4.5} - \sqrt {9.5} + \sqrt 5 \\A = \sqrt {{2^2}.5} - \sqrt {{3^2}.5} + \sqrt 5 \\A = 2\sqrt 5 - 3\sqrt 5 + \sqrt 5 \\A = 0\end{array}\)
Vậy \(A = 0\).
c) Với \(x > 0,\,\,y > 0\) ta có:
\(\begin{array}{l}P = \dfrac{{x\sqrt x + y\sqrt y }}{{\sqrt x + \sqrt y }} - {\left( {\sqrt x - \sqrt y } \right)^2}\\P = \dfrac{{\left( {\sqrt x + \sqrt y } \right)\left( {x - \sqrt {xy} + y} \right)}}{{\sqrt x + \sqrt y }} - \left( {x - 2\sqrt {xy} + y} \right)\\P = x - \sqrt {xy} + y - x + 2\sqrt {xy} - y\\P = \sqrt {xy} \end{array}\)
Vậy với \(x > 0,\,\,y > 0\) thì \(P = \sqrt {xy} \).
Câu 2:
Phương pháp:
a) Vận dụng phương pháp cộng đại số để giải hệ phương trình.
b) Áp dụng điều kiện của hai đường thẳng song song xác định được điều kiện của hệ số \(a\) và \(b\)
\(\left( d \right)\) đi qua điểm \(M\left( {2; - 3} \right)\) xác định được hệ số \(b\), đối chiếu điều kiện và kết luận.
Cách giải:
a) Ta có: \(\left\{ \begin{array}{l}3x + y = 1\\x - 2y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}6x + 2y = 2\\x - 2y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}7x = 7\\y = 1 - 3x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 1 - 3 = - 2\end{array} \right.\).
Vậy hệ có nghiệm duy nhất \(\left( {x;y} \right) = \left( {1; - 2} \right)\).
b) \(\left( d \right)\) song song với đường thẳng \(\left( {d'} \right)\) nên \(\left\{ \begin{array}{l}a = 2\\b \ne - 1\end{array} \right.\). Thay vào \(\left( d \right)\) ta được \(\left( d \right):y = 2x + b\,\,\left( {b \ne - 1} \right)\).
\(\left( d \right)\) đi qua điểm \(M\left( {2; - 3} \right)\) nên ta có: \( - 3 = 2.2 + b \Leftrightarrow - 3 = 4 + b \Leftrightarrow b = - 3 - 4 = - 7\,\,\left( {tm} \right)\).
Vậy phương trình đường thẳng của \(\left( d \right)\) cần tìm là: \(y = 2x - 7\).
Câu 3:
Phương pháp:
Giải bài toán bằng cách lập phương trình, cụ thể:
Gọi số tấm chắn mà công ty A cần làm trong một ngày theo kế hoạch là \(x\,\,\,\left( {x \in \mathbb{N}*} \right)\) (tấm), từ đó tính được số ngày để hoàn thành \(20000\) tấm theo kế hoạch
Tính được thực tế số tấm chắn mà công ty A làm và thời gian thực tế hoàn thành số tấm chắn làm được.
Lập phương trình, giải phương trình và kết luận.
Cách giải:
Gọi số tấm chắn mà công ty A cần làm trong một ngày theo kế hoạch là \(x\,\,\,\left( {x \in \mathbb{N}*} \right)\) (tấm)
Số ngày để hoàn thành \(20000\) tấm theo kế hoạch là \(\dfrac{{20000}}{x}\)( ngày)
Thực tế: Số tấm chắn mà công ty A làm trong một ngày là \(x + 300\) (tấm chắn)
Tổng số tấm chắn mà công ty A làm theo thực tế là \(20700\)( tấm chắn)
Thời gian thực tế hoàn thành làm \(27000\) tấm chắn là \(\dfrac{{20700}}{{x + 300}}\)( ngày)
Thực tế công ty \(A\) hoàn thành công việc sớm hơn dự định là \(1\)ngày nên ta có phương trình:
\(\dfrac{{20000}}{x} - \dfrac{{20700}}{{x + 300}} = 1\)
\(\begin{array}{l} \Leftrightarrow 20000\left( {x + 300} \right) - 20700x = x\left( {x + 300} \right)\\ \Leftrightarrow 20000x + 6000000 - 20700x = {x^2} + 300x\\ \Leftrightarrow {x^2} + 1000x - 6000000 = 0\\ \Leftrightarrow {x^2} - 2000x + 3000x - 6000000 = 0\\ \Leftrightarrow x\left( {x - 2000} \right) + 3000\left( {x - 2000} \right) = 0\\ \Leftrightarrow \left( {x - 2000} \right)\left( {x + 3000} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 2000 = 0\\x + 3000 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2000\,\,\,\,\,\,\,\left( {tm} \right)\\x = - 3000\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy số tấm chắn mà công ty A thực tế làm một ngày là 2000 tấm chắn .
Câu 4:
Phương pháp:
a) Thay \(m = 2\) vào phương trình của đề bài, nhận thấy đây là phương trình bậc hai ẩn \(x\)
Áp dụng nhận xét \(a + b + c = 0\) thì phương trình bậc hai có hai nghiệm phân biệt \({x_1} = 1\) và \({x_2} = \dfrac{c}{a}\)
b) Phương trình ban đầu có nghiệm \( \Leftrightarrow \Delta \ge 0\) (hoặc \(\Delta ' \ge 0\))
c) Áp dụng hệ thức Vi – ét, tính được \({x_1} + {x_2};{x_1}{x_2}\) theo tham số \(m\)
Biến đổi hệ thức của đề bài để xuất hiện \({x_1} + {x_2};{x_1}{x_2}\), giải phương trình chứa tham số \(m\), đối chiếu điều kiện và kết luận.
Cách giải:
a) Khi \(m = 2\) phương trình (1) trở thành: \({x^2} - 3x + 2 = 0\).
Ta có \(a + b + c = 1 - 3 + 2 = 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ \begin{array}{l}x = 1\\x = \dfrac{c}{a} = 2\end{array} \right.\).
Vậy khi \(m = 2\) thì tập nghiệm của phương trình là \(S = \left\{ {1;2} \right\}\).
b) Để phương trình \(\left( 1 \right)\) có nghiệm thì \(\Delta \ge 0\) \( \Leftrightarrow {3^2} - 4m \ge 0 \Leftrightarrow m \le \dfrac{9}{4}\)
Vậy để phương trình (1) có nghiệm thì \(m \le \dfrac{9}{4}\).
c) Với \(m \le \dfrac{9}{4}\) phương trình có hai nghiệm \({x_1},{x_2}\).
Khi đó áp dụng hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 3\\{x_1}{x_2} = m\end{array} \right.\)
Ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,\,{x_1}^3{x_2} + {x_1}{x_2}^3 - 2{x_1}^2{x_2}^2 = 5\\ \Leftrightarrow {x_1}{x_2}\left( {{x_1}^2 + {x_2}^2} \right) - 2{\left( {{x_1}{x_2}} \right)^2} = 5\\ \Leftrightarrow {x_1}{x_2}\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2}} \right] - 2{\left( {{x_1}{x_2}} \right)^2} = 5\\ \Leftrightarrow {x_1}{x_2}{\left( {{x_1} + {x_2}} \right)^2} - 2{\left( {{x_1}{x_2}} \right)^2} - 2{\left( {{x_1}{x_2}} \right)^2} = 5\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 4{\left( {{x_1}{x_2}} \right)^2} = 5\\ \Leftrightarrow {3^2} - 4{m^2} = 5 \Leftrightarrow 4{m^2} = 4\\ \Leftrightarrow {m^2} = 1 \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - 1\end{array} \right.\,\,\,\left( {tm} \right)\end{array}\)
Vậy \(m \in \left\{ {1; - 1} \right\}\) thỏa mãn yêu cầu bài toán.
Câu 5:
Phương pháp:
a) Vận dụng dấu hiệu nhận biết của tứ giác nội tiếp, chứng minh \(\angle AMO = \angle AIO = {90^0}\) suy ra \(AMIO\) nội tiếp đường tròn đường kính \(OA\) (tứ giác có 2 đỉnh kề cùng nhìn \(OA\) dưới các góc bằng \({90^0}\)).
b) Áp dụng hệ thức lượng trong tam giác vuông và trường hợp đồng dạng cạnh – góc – cạnh của hai tam giác.
c) Gọi \(N \in OA\) sao cho \(\dfrac{{ON}}{{OA}} = \dfrac{2}{3}\), từ đó chứng minh được \(NG//IA\) (định lí Ta – lét đảo)
Chứng minh \(ON\) cố định.
Cách giải:
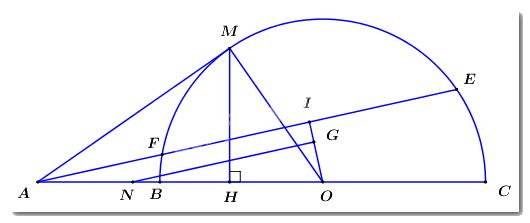
a) Ta có: \(I\) là trung điểm của \(EF\) nên \(OI \bot EF\) (quan hệ vuông góc giữa đường kính và dây cùng)
\( \Rightarrow \angle AIO = {90^0}\).
Mà \(AM\) là tiếp tuyến của nửa đường tròn \(\left( O \right)\) nên \(AM \bot OM\) (định nghĩa) \( \Rightarrow \angle AMO = {90^0}\).
\( \Rightarrow \angle AMO = \angle AIO = {90^0}\)\( \Rightarrow AMIO\) nội tiếp đường tròn đường kính \(OA\) (tứ giác có 2 đỉnh kề cùng nhìn \(OA\) dưới các góc bằng \({90^0}\)).
b) Áp dụng hệ thức lượng trong tam giác \(AMO\) vuông tại \(M\) có \(MH\) là đường cao ta có: \(O{M^2} = OH.OA\)
Mà \(OM = OF \Rightarrow O{F^2} = OH.OA \Rightarrow \dfrac{{OH}}{{OF}} = \dfrac{{OF}}{{OA}}\).
Xét \(\Delta OFH\) và \(\Delta OAF\) ta có:
\(\angle FOA\) chung;
\(\dfrac{{OH}}{{OF}} = \dfrac{{OF}}{{OA}}\,\,\left( {cmt} \right)\);
\( \Rightarrow \Delta OFH \sim \Delta OAF\,\,\,\left( {c.g.c} \right)\,\,\left( {dpcm} \right)\)
c) Gọi \(N \in OA\) sao cho \(\dfrac{{ON}}{{OA}} = \dfrac{2}{3}\), khi đó ta có \(\dfrac{{ON}}{{OA}} = \dfrac{{OG}}{{OI}} = \dfrac{2}{3}\) \( \Rightarrow NG//IA\) (định lí Ta-lét đảo).
Mà \(AI \bot OI\,\,\left( {do\,\,OI \bot EF} \right)\) \( \Rightarrow NG \bot OI\) tại \(G\) \( \Rightarrow \angle OGN = {90^0}\).
\( \Rightarrow G\) thuộc đường tròn đường kính \(ON\).
Vì \(A,\,\,B,\,\,C\) cố định \( \Rightarrow O\) cố định \( \Rightarrow OA\) không đổi \( \Rightarrow ON\) không đổi \( \Rightarrow N\) cố định.
\( \Rightarrow \) Đường tròn đường kính \(ON\) cố định.
Vậy khi điểm E thay đổi trên cung MC thì trọng tâm G của tam giác \(OEF\) luôn nằm trên một đường tròn cố định là đường tròn đường kính \(ON\) với \(ON = \dfrac{2}{3}OA\) (đpcm).
Câu 6:
Phương pháp:
Tính thể tích ban đầu của khúc gỗ: \({V_1} = \pi {r^2}h\) (áp dụng công thức tính thể tích của khối trụ)
Tính thể tích khối gỗ hình nón: \({V_2} = \dfrac{1}{3}\pi {r^2}h\) (áp dụng công thức tính thể tích của khối nón)
Vậy thể tịch khúc gõ còn lại là \(V = {V_1} - {V_2}\)
Cách giải:

Thể tích ban đầu của khúc gỗ là: \({V_1} = \pi {.10^2}.20 = 2000\pi \,\,\left( {c{m^3}} \right)\).
Thể tích khối gỗ hình nón bị tiện bỏ là: \({V_2} = \dfrac{1}{3}\pi {.10^2}.10 = \dfrac{{1000}}{3}\pi \,\,\left( {c{m^3}} \right)\).
Vậy thể tích phần khúc gỗ còn lại là \(V = {V_1} - {V_2} = 2000\pi - \dfrac{{1000}}{3}\pi = \dfrac{{5000}}{3}\pi \approx 5236\,\,\left( {c{m^3}} \right)\).
Kỳ thi tuyển sinh vào lớp 10 tại tỉnh Huế luôn là một kỳ thi quan trọng, đánh dấu bước chuyển mình của học sinh từ bậc trung học cơ sở lên trung học phổ thông. Môn Toán đóng vai trò then chốt trong việc xét tuyển, do đó, việc chuẩn bị kỹ lưỡng là vô cùng cần thiết. Đề thi vào 10 môn Toán Huế năm 2021 tiếp tục duy trì cấu trúc đề thi truyền thống, tập trung vào các kiến thức trọng tâm của chương trình Toán lớp 9.
Đề thi thường bao gồm các dạng bài tập sau:
Năm 2021, đề thi vào 10 môn Toán Huế có độ khó tương đương với các năm trước. Các câu hỏi được thiết kế đa dạng, đòi hỏi học sinh phải nắm vững kiến thức cơ bản, rèn luyện kỹ năng giải toán và có khả năng vận dụng linh hoạt các công thức, định lý đã học.
Đề thi chính thức bao gồm các câu hỏi trắc nghiệm và tự luận. Phần trắc nghiệm thường chiếm khoảng 30-40% tổng số điểm, tập trung vào các kiến thức cơ bản và các công thức thường dùng. Phần tự luận chiếm khoảng 60-70% tổng số điểm, đòi hỏi học sinh phải trình bày lời giải chi tiết, rõ ràng, logic.
Trước khi diễn ra kỳ thi chính thức, các trường THCS thường tổ chức các đề thi thử để giúp học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng làm bài và đánh giá năng lực của bản thân. Các đề thi thử này cũng là một nguồn tài liệu ôn tập hữu ích cho học sinh.
Để đạt kết quả tốt nhất trong kỳ thi vào 10 môn Toán Huế năm 2021, học sinh cần:
Ngoài sách giáo khoa, học sinh có thể tham khảo các tài liệu ôn thi sau:
Giaitoan.edu.vn là một trang web học Toán online uy tín, cung cấp đầy đủ các tài liệu ôn tập, đề thi thử và lời giải chi tiết cho kỳ thi vào 10 môn Toán Huế năm 2021. Chúng tôi cam kết mang đến cho học sinh những trải nghiệm học tập tốt nhất, giúp các em tự tin hơn trong kỳ thi sắp tới.
| Trường THPT | Điểm chuẩn (2021) |
|---|---|
| Quốc Học Huế | 28.0 |
| Hai Bà Trưng | 26.5 |
| Chu Văn An | 25.0 |
| *Lưu ý: Điểm chuẩn có thể thay đổi theo từng năm. | |
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi vào 10 môn Toán Huế năm 2021!