Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp các đề thi thử vào lớp 10 môn Toán chất lượng cao. Đề số 33 là một trong những đề thi được thiết kế để giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi sắp tới.
Đề thi này bao gồm các dạng bài tập đa dạng, từ trắc nghiệm đến tự luận, bao phủ đầy đủ các kiến thức trọng tâm của chương trình Toán lớp 9.
Đề thi vào lớp 10 môn Toán - Đề số 33 có đáp án và lời giải chi tiết
Đề bài
I. TRẮC NGHIỆM KHÁCH QUAN (1,5 điểm)
Câu 1: Tìm tất cả các giá trị của \(x\) để biểu thức \(\sqrt {x - 2} \) có nghĩa.
A. \(x \ge 2\) B. \(x > 2\)
C. \(x \le 2\) D. \(x \ge 0\)
Câu 2: Hàm số nào dưới đây là hàm số bậc nhất?
A. \(y = \sqrt {x + 2} \)
B. \(y = \dfrac{2}{x} + 1\)
C. \(y = - 2x + 1\)
D. \(y = {x^2}\)
Câu 3: Tìm \(m\) biết điểm \(A\left( {1;\; - 2} \right)\) thuộc đường thẳng có phương trình \(y = \left( {2m - 1} \right)x + 3 + m.\)
A. \(m = - \dfrac{4}{3}\)
B. \(m = \dfrac{4}{3}\)
C. \(m = \dfrac{5}{3}\)
D. \(m = - \dfrac{5}{3}\)
Câu 4: Tìm tất cả các giá trị của \(m\) để hàm số \(y = \left( {2m - 1} \right)x + m + 2\) đồng biến trên \(R.\)
A. \(m < \dfrac{1}{2}\)
B. \(m > \dfrac{1}{2}\)
C. \(m > 0\)
D. \(m < 0\)
Câu 5: Hàm số nào dưới đây đồng biến khi \(x < 0\) và nghịch biến khi \(x > 0?\)
A. \(y = - 3x + 1\)
B. \(y = x - 3\)
C. \(y = {x^2}\)
D. \(y = - 3{x^2}\)
Câu 6:Tìm tất cả các giá trị của \(m\) để phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} - 3 = 0\) vô nghiệm.
A. \(m \ge - 2\)
C. \(m > - 2\)
D. \(m < - 2\)
Câu 7: Phương trình nào dưới đây có tổng hai nghiệm bằng 3?
A. \(2{x^2} + 6x + 1 = 0\)
B. \(2{x^2} - 6x + 1 = 0\)
C. \({x^2} - 3x + 4 = 0\)
D. \({x^2} + 3x - 2 = 0\)
Câu 8: Cho tam giác ABC vuông tại A. Khẳng định nào dưới đây đúng?
A. \(\cos B = \dfrac{{AB}}{{BC}}\)
B. \(\cos B = \dfrac{{AC}}{{BC}}\)
C. \(\cos B = \dfrac{{AB}}{{AC}}\)
D. \(\cos B = \dfrac{{AC}}{{AB}}.\)
Câu 9: Khẳng định nào dưới đây sai?
A. Mọi hình vuông đều là tứ giác nội tiếp.
B. Mọi hình chữ nhật đều là tứ giác nội tiếp.
C. Mọi hình thoi đều là tứ giác nội tiếp.
D. Mọi hình thang cân đều là tứ giác nội tiếp.
Câu 10: Cho đường tròn tâm \(O,\) bán kính \(R = 5\;cm\) có dây cung \(AB = 6\;cm.\) Tính khoảng cách \(d\) từ \(O\) tới đường thẳng \(AB.\)
A. \(d = 1\;cm.\)
B. \(d = 2\;cm.\)
D. \(d = \sqrt {34} \;cm.\)
II. TỰ LUẬN: (7,5 điểm)
Câu 1 (1,5 điểm):
Hai bạn Hòa và Bình có 100 quyển sách. Nếu Hòa cho Bình 10 quyển sách thì số quyển sách của Hòa bằng \(\dfrac{3}{2}\) số quyển sách của Bình. Hỏi lúc đầu mỗi bạn có bao nhiêu quyển sách?
Câu 2 (2 điểm):
Trên mặt phẳng tọa độ \(Oxy\) cho đường thẳng \(\left( d \right)\) đi qua \(A\left( {3;\;7} \right)\) và song song với đường thẳng có phương trình \(y = 3x + 1.\)
a) Viết phương trình đường thẳng \(\left( d \right).\)
b) Tìm tọa độ giao điểm của đường thẳng \(\left( d \right)\) và parabol \(\left( P \right):\;\;y = {x^2}.\)
Câu 3 (3 điểm):
Cho đường tròn (O; R) và điểm M cố định nằm ngoài (O; R). Từ M kẻ các tiếp tuyến MA, MB tới (O; R) (A, B là các tiếp điểm). Đường thẳng (d) bất kỳ qua M và cắt (O; R) tại hai điểm phân biệt C, D (C nằm giữa M và D). Gọi N là giao điểm của AB và CD.
a) Chứng minh rằng tứ giác OAMB nội tiếp.
b) Chứng minh rằng \(\Delta ANC\) và \(\Delta DNB\) đồng dạng, \(\Delta AMC\) và \(\Delta DMA\) đồng dạng.
c) Chứng minh rằng:\(\dfrac{{MC}}{{MD}} = \dfrac{{NC}}{{ND}}.\)
d) Xác định vị trí của đường thẳng \(\left( d \right)\) để \(\dfrac{1}{{MD}} + \dfrac{1}{{ND}}\) đạt giá trị nhỏ nhất.
Câu 4 (1 điểm):
Cho \(a,\;b\) là các số thực không âm thỏa mãn \({a^{2018}} + {b^{2018}} = {a^{2020}} + {b^{2020}}.\) Tìm giá trị lớn nhất của biểu thức \(P = {\left( {a + 1} \right)^2} + {\left( {b + 1} \right)^2}.\)
Lời giải chi tiết
1A | 2C | 3A | 4B | 5D |
6D | 7B | 8A | 9C | 10C |
I. PHẦN TRẮC NGHIỆM
Câu 1:
Biểu thức có nghĩa \( \Leftrightarrow x - 2 \ge 0 \Leftrightarrow x \ge 2.\)
Chọn A.
Câu 2:
Theo khái niệm về hàm số bậc nhất thì chỉ có đáp án C đúng.
Chọn C.
Câu 3:
Điểm \(A\left( {1; - 2} \right)\) thuộc đường thẳng \(y = \left( {2m - 1} \right)x + 3 + m\)
\(\begin{array}{l} \Rightarrow - 2 = \left( {2m - 1} \right).1 + 3 + m\\ \Leftrightarrow - 2 = 2m - 1 + 3 + m\\ \Leftrightarrow 3m = - 4\\ \Leftrightarrow m = - \dfrac{4}{3}.\end{array}\)
Chọn A.
Câu 4:
Hàm số đồng biến trên \(R \Leftrightarrow 2m - 1 > 0 \Leftrightarrow m > \dfrac{1}{2}.\)
Chọn B.
Câu 5:
+) Đáp án A: Hàm số là hàm số bậc nhất có \(a = - 3 < 0 \Rightarrow \) hàm số nghịch biến trên \(R \Rightarrow \) loại đáp án A.
+) Đáp án B: Hàm số là hàm số bậc nhất có \(a = 1 > 0 \Rightarrow \) hàm số đồng biến trên \(R \Rightarrow \) loại đáp án B.
+) Đáp án C: Hàm số là hàm số bậc hai có \(a = 1 > 0 \Rightarrow \) hàm số đồng biến khi \(x > 0\) và nghịch biến khi \(x < 0 \Rightarrow \) loại đáp án C.
Chọn D.
Câu 6:
Phương trình đã cho vô nghiệm \( \Leftrightarrow \Delta ' < 0 \Leftrightarrow {\left( {m + 1} \right)^2} - {m^2} + 3 < 0\)
\(\begin{array}{l} \Leftrightarrow {m^2} + 2m + 1 - {m^2} + 3 < 0\\ \Leftrightarrow 2m < - 4\\ \Leftrightarrow m < - 2.\end{array}\)
Chọn D.
Câu 7:
+) Đáp án A: Giả sử phương trình có hai nghiệm \({x_1},\;{x_2}\) thì \({x_1} + {x_2} = - \dfrac{b}{a} = - \dfrac{6}{2} = - 3 \ne 3 \Rightarrow \) loại đáp án A.
+) Đáp án D: Giả sử phương trình có hai nghiệm \({x_1},\;{x_2}\) thì \({x_1} + {x_2} = - \dfrac{b}{a} = - 3 \ne 3 \Rightarrow \) loại đáp án D.
+) Đáp án B: Giả sử phương trình có hai nghiệm \({x_1},\;{x_2}\) ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = S = - \dfrac{b}{a} = \dfrac{6}{2} = 3\\{x_1}{x_2} = P = \dfrac{c}{a} = \dfrac{1}{2}\end{array} \right..\)
Phương trình có hai nghiệm \({x_1},\;{x_2} \Leftrightarrow {S^2} \ge 4P \Leftrightarrow {3^2} \ge 4.\dfrac{1}{2} \Leftrightarrow 9 \ge 2\) (luôn đúng).
\( \Rightarrow \) Đáp án B đúng.
+) Đáp án C: Giả sử phương trình có hai nghiệm \({x_1},\;{x_2}\) ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = S = - \dfrac{b}{a} = 3\\{x_1}{x_2} = P = \dfrac{c}{a} = 4\end{array} \right..\)
Phương trình có hai nghiệm \({x_1},\;{x_2} \Leftrightarrow {S^2} \ge 4P \Leftrightarrow {3^2} \ge 4.4 \Leftrightarrow 9 \ge 16\) (vô lý).
\( \Rightarrow \) Phương trình đã cho vô nghiệm.
\( \Rightarrow \) Đáp án C sai.
Chọn B.
Câu 8:
Ta có: \(\cos B = \dfrac{{AB}}{{BC}}\)
Chọn A.
Câu 9:
Ta có hình vuông, hình chữ nhật và hình thang cân đều là những tứ giác có tổng hai góc đối diện bằng \({180^0}.\)
\( \Rightarrow \) A, B, D đúng.
Chọn C.
Câu 10:
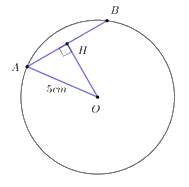
\( \Rightarrow OH = d\) và \(AH = \dfrac{{AB}}{2} = \dfrac{6}{2} = 3cm.\) Gọi \(H\) là hình chiếu của \(O\) trên dây \(AB \Rightarrow OH \bot AB \Rightarrow H\) là trung điểm của \(AB.\) (quan hệ vuông góc giữa đường kính và dây cung).
Áp dụng định lý Pi-ta-go cho tam giác \(AOH\) vuông tại \(H\) ta có:
\(\begin{array}{l}O{H^2} = O{A^2} - A{H^2} = {5^2} - {3^2} = {4^2}\\ \Rightarrow d = OH = 4cm.\end{array}\)
Chọn C.
PHẦN TỰ LUẬN
Câu 1:
Hai bạn Hòa và Bình có 100 quyển sách. Nếu Hòa cho Bình 10 quyển sách thì số quyển sách của Hòa bằng \(\dfrac{3}{2}\) số quyển sách của Bình. Hỏi lúc đầu mỗi bạn có bao nhiêu quyển sách?
Gọi số quyển sách của bạn Hòa là \(x\;\) (quyển sách), \(\left( {10 < x < 100,\;x \in N} \right).\)
Khi đó số quyển sách của Bình là: \(100 - x\) (quyển sách).
Số quyển sách của Hòa sau khi cho Bình \(10\) quyển sách là: \(x - 10\) (quyển sách).
Số quyển sách của Bình sau khi nhận được \(10\) quyển sách từ Hòa là: \(100 - x + 10 = 110 - x\) (quyển sách).
Theo đề bài ta có phương trình:
\(\begin{array}{l}\;\;\;x - 10 = \dfrac{3}{2}\left( {110 - x} \right)\\ \Leftrightarrow 2x - 20 = 330 - 3x\\ \Leftrightarrow 5x = 350\\ \Leftrightarrow x = 70\;\;\left( {tm} \right)\end{array}\)
Vậy lúc đầu Hòa có \(70\) quyển sách và Bình có \(100 - 70 = 30\) quyển sách.
Câu 2:
Trên mặt phẳng tọa độ \(Oxy\) cho đường thẳng \(\left( d \right)\) đi qua \(A\left( {3;\;7} \right)\) và song song với đường thẳng có phương trình \(y = 3x + 1.\)
a) Viết phương trình đường thẳng \(\left( d \right).\)
Giả sử phương trình của đường thẳng \(\left( d \right):\;y = ax + b.\)
Đường thẳng \(\left( d \right)\) song song với đường thẳng \(y = 3x + 1 \Rightarrow \left\{ \begin{array}{l}a = 3\\b \ne 1\end{array} \right..\)
Đường thẳng \(\left( d \right)\) đi qua \(A\left( {3;\;7} \right) \Rightarrow 7 = 3.3 + b \Leftrightarrow b = - 2.\,\,\left( {tm} \right)\)
Vậy phương trình đường thẳng \(\left( d \right):\;\;y = 3x - 2.\)
b) Tìm tọa độ giao điểm của đường thẳng \(\left( d \right)\) và parabol \(\left( P \right):\;\;y = {x^2}.\)
Hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) là nghiệm của p hương trình: \({x^2} = 3x - 2\)
\(\begin{array}{l} \Leftrightarrow {x^2} - 3x + 2 = 0\\ \Leftrightarrow {x^2} - 2x - x + 2 = 0\\ \Leftrightarrow x\left( {x - 2} \right) - \left( {x - 2} \right) = 0\\ \Leftrightarrow \left( {x - 2} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 2 = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2 \Rightarrow y = {2^2} = 4\\x = 1 \Rightarrow y = {1^2} = 1\end{array} \right..\end{array}\)
Vậy \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt \(A\left( {2;\;4} \right)\) và \(B\left( {1;\;1} \right).\)
Câu 3:
Cho đường tròn (O; R) và điểm M cố định nằm ngoài (O; R). Từ M kẻ các tiếp tuyến MA, MB tới (O; R) (A, B là các tiếp điểm). Đường thẳng (d) bất kỳ qua M và cắt (O; R) tại hai điểm phân biệt C, D (C nằm giữa M và D). Gọi N là giao điểm của AB và CD.
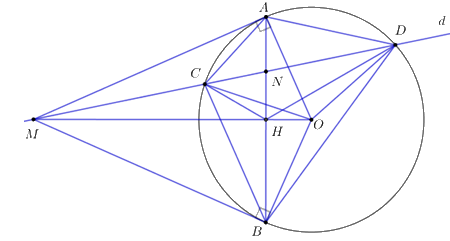
a) Chứng minh rằng tứ giác OAMB nội tiếp.
Vì \(MA,\;\;MB\) là hai tiếp tuyến của \(\left( O \right) \Rightarrow \widehat {MAO} = \widehat {MBO} = {90^0}.\)
Xét tứ giác \(\widehat {MAO} + \widehat {OBM} = {90^0} + {90^0} = {180^0}\) \( \Rightarrow MAOB\) là tứ giác nội tiếp (dhnb).
b) Chứng minh rằng \(\Delta ANC\) và \(\Delta DNB\) đồng dạng, \(\Delta AMC\) và \(\Delta DMA\) đồng dạng.
Xét \(\Delta ANC\)và \(\Delta DNB\) ta có:
\(\widehat {CAN} = \widehat {NDB}\) (hai góc nội tiếp cùng chắn cung \(CB\))
\(\widehat {ANC} = \widehat {DNB}\) (hai góc đối đỉnh).
\( \Rightarrow \Delta ANC \sim \Delta DNB\;\left( {g - g} \right)\;\;\;\;\left( {dpcm} \right).\)
Xét \(\Delta AMC\) và \(\Delta DMA\) ta có:
\(\widehat {AMD}\;\;chung\)
\(\widehat {MAC} = \widehat {MDA}\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(AC\)).
\( \Rightarrow \Delta MAC \sim \Delta MDA\;\;\left( {g - g} \right)\;\;\;\left( {dpcm} \right).\)
c) Chứng minh rằng: \(\dfrac{{MC}}{{MD}} = \dfrac{{NC}}{{ND}}.\)
Ta có: \(\Delta MAC \sim \Delta MDA\;\;\left( {cmt} \right)\\ \Rightarrow \dfrac{{MA}}{{MD}} = \dfrac{{MC}}{{MA}} \Leftrightarrow M{A^2} = MC.MD.\)
Gọi \(H\) là giao điểm của \(AB\) và \(MO \Rightarrow AB \bot MO = \left\{ H \right\}.\) (tính chất hai tiếp tuyến cắt nhau)
Xét tam giác \(MAO\) vuông tại \(A\) và có đường cao \(AH\) có:
\(M{A^2} = MH.MO.\) (hệ thức lượng trong tam giác vuông)
\(\begin{array}{l} \Rightarrow MC.MD = MH.MO\;\left( { = M{A^2}} \right).\\ \Rightarrow \dfrac{{MC}}{{MO}} = \dfrac{{MH}}{{MO}}.\end{array}\)
Xét \(\Delta MCH\) và \(\Delta MOD\) ta có:
\(\begin{array}{l}\dfrac{{MC}}{{MH}} = \dfrac{{MO}}{{MD}}\;\;\left( {cmt} \right)\\\widehat {OMD}\;\;chung\\ \Rightarrow \Delta MCH \sim \Delta MOD\;\;\left( {g - g} \right).\end{array}\)
\( \Rightarrow \widehat {MHC} = \widehat {MDO}\) (hai góc tương ứng).
Xét tứ giác \(CHOD\) ta có: \(\widehat {MHC} = \widehat {CDO}\;\;\left( {cmt} \right)\)
\( \Rightarrow CHOD\) là tứ giác nội tiếp. (góc ngoại tại một đỉnh bằng góc trong tại đỉnh đối diện)
\( \Rightarrow \widehat {DHO} = \widehat {DCO}\) (hai góc nội tiếp cùng chắn cung \(DO\))
Lại có: \(\widehat {ODC} = \widehat {OCD}\) \((\Delta COD\) cân tại \(O)\)
\( \Rightarrow \widehat {DHO} = \widehat {CHM}\left( { = \widehat {CDO}} \right).\)
Mà \(HM \bot HN\;\;\left( {cmt} \right)\)
\( \Rightarrow \widehat {NHC} = \widehat {NHD}\;\left( { = {{90}^0} - \widehat {CHM}} \right)\)
\( \Rightarrow NH\) là tia phân giác trong của \(\widehat {CHD}\) và \(HM\) là tia phân giác ngoài của \(\widehat {CHD}.\)
\( \Rightarrow \dfrac{{MC}}{{MD}} = \dfrac{{NC}}{{ND}}\left( { = \dfrac{{HC}}{{HD}}} \right).\;\;\left( {dpcm} \right)\)
d) Xác định vị trí của đường thẳng \(\left( d \right)\) để \(\dfrac{1}{{MD}} + \dfrac{1}{{ND}}\) đạt giá trị nhỏ nhất.
Xét: \(DC\left( {\dfrac{1}{{MD}} + \dfrac{1}{{ND}}} \right)\)
\(\begin{array}{l} = \dfrac{{CD}}{{MD}} + \dfrac{{CD}}{{ND}} = \dfrac{{MD - CM}}{{MD}} + \dfrac{{CN + ND}}{{ND}}\\ = 1 - \dfrac{{CM}}{{MD}} + 1 + \dfrac{{CN}}{{ND}} = 2 + \dfrac{{CN}}{{DN}} - \dfrac{{MC}}{{MD}} = 2.\\\left( {do\;\;\dfrac{{MC}}{{MD}} = \dfrac{{NC}}{{ND}}} \right)\\ \Rightarrow \dfrac{1}{{MD}} + \dfrac{1}{{ND}} = \dfrac{2}{{CD}}.\end{array}\)
Vì \(CD\) là dây cung \( \Rightarrow CD \le 2R \Rightarrow \dfrac{2}{{CD}} \ge \dfrac{2}{{2R}} \Leftrightarrow \dfrac{2}{{CD}} \ge \dfrac{1}{R}.\)
\( \Rightarrow \dfrac{1}{{MD}} + \dfrac{1}{{ND}} \ge \dfrac{1}{R}.\)
Dấu “=” xảy ra \( \Leftrightarrow CD = 2R\) hay đường thẳng \(d\) đi qua \(O.\)
Vậy để \(\dfrac{1}{{MD}} + \dfrac{1}{{ND}}\) đạt giá trị nhỏ nhất thì đường thẳng \(d\) đi qua \(O.\)
Đề thi vào lớp 10 môn Toán là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Để đạt được kết quả tốt nhất, việc luyện tập thường xuyên với các đề thi thử là vô cùng cần thiết. Đề số 33 mà giaitoan.edu.vn cung cấp được xây dựng dựa trên cấu trúc đề thi chính thức của các trường THPT chuyên và các tỉnh thành trên cả nước.
Đề thi Đề số 33 bao gồm các phần chính sau:
Dưới đây là một số câu hỏi tiêu biểu trong đề thi Đề số 33:
Giải phương trình: 2x2 - 5x + 3 = 0
Hướng dẫn giải: Sử dụng công thức nghiệm của phương trình bậc hai. Tính delta (Δ) = b2 - 4ac = (-5)2 - 4 * 2 * 3 = 25 - 24 = 1. Vì Δ > 0, phương trình có hai nghiệm phân biệt: x1 = (-b + √Δ) / 2a = (5 + 1) / 4 = 1.5 và x2 = (-b - √Δ) / 2a = (5 - 1) / 4 = 1.
Cho tam giác ABC vuông tại A, có AB = 3cm, AC = 4cm. Tính độ dài cạnh BC và diện tích tam giác ABC.
Hướng dẫn giải: Áp dụng định lý Pitago trong tam giác vuông ABC, ta có: BC2 = AB2 + AC2 = 32 + 42 = 9 + 16 = 25. Suy ra BC = √25 = 5cm. Diện tích tam giác ABC là: S = (1/2) * AB * AC = (1/2) * 3 * 4 = 6cm2.
Giải bất phương trình: 3x + 2 > 7
Hướng dẫn giải: Chuyển vế và rút gọn, ta có: 3x > 5. Chia cả hai vế cho 3, ta được: x > 5/3.
Để đạt được kết quả tốt nhất trong kỳ thi vào lớp 10 môn Toán, các em học sinh cần lưu ý những điều sau:
giaitoan.edu.vn cung cấp:
Hãy bắt đầu luyện thi ngay hôm nay với Đề số 33 và các đề thi khác tại giaitoan.edu.vn để tự tin bước vào kỳ thi vào lớp 10 môn Toán!
| Dạng bài | Số lượng câu | Điểm |
|---|---|---|
| Trắc nghiệm | 5 | 2 |
| Tự luận | 5 | 8 |
| Tổng | 10 | 10 |