Chào mừng bạn đến với bài viết phân tích và giải chi tiết Đề số 34 - Đề thi vào lớp 10 môn Toán. Đây là một trong những đề thi thử quan trọng giúp học sinh lớp 9 làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Tại giaitoan.edu.vn, chúng tôi cung cấp không chỉ đề thi mà còn cả lời giải chi tiết, giúp bạn hiểu rõ phương pháp giải và áp dụng vào các bài toán tương tự.
Đề thi vào lớp 10 môn Toán - Đề số 34 có đáp án và lời giải chi tiết
Đề bài
Câu 1 (2 điểm):
a) Bằng các phép biến đổi đại số hãy rút gọn biểu thức: \(A = 2\sqrt 5 + 3\sqrt {45} .\)
b) Giải phương trình \({x^2} - 6x + 5 = 0.\)
Câu 2 (1,5 điểm):
Cho hai hàm số \(y = {x^2}\) và \(y = - x + 2.\)
a) Vẽ đồ thị của hai hàm số này trên cùng một mặt phẳng tọa độ Oxy.
b) Tìm tọa độ giao điểm của hai đồ thị đó bằng phương pháp đại số.
Câu 3 (1,5 điểm):
Cho phương trình \({x^2} - 2x + m + 3 = 0\;\;\;\left( 1 \right)\) (với \(x\) là ẩn, \(m\) là tham số).
a) Tìm tất cả các giá trị của \(m\) để phương trình \(\left( 1 \right)\) có nghiệm.
b) Gọi \({x_1},\;{x_2}\) là nghiệm của phương trình \(\left( 1 \right).\) Tìm tất cả các giá trị của \(m\) để \(x_1^2 + x_2^2 - 3{x_1}{x_2} - 4 = 0.\)
Câu 4 (1,5 điểm):
Một mảnh đất hình chữ nhật có diện tích \(360{m^2}.\) Nếu tăng chiều rộng \(2m\) và giảm chiều dài \(6m\) thì diện tích mảnh đất không đổi. Tính chu vi của mảnh đất lúc đầu.
Câu 5 (3,5 điểm):
Cho đường tròn \(\left( O \right)\) đường kính \(AB = 6cm.\) Gọi \(H\) là điểm thuộc đoạn thẳng \(AB\) sao cho \(AH = 1cm.\) Qua \(H\) vẽ đường thẳng vuông góc với \(AB,\) đường thẳng này cắt đường tròn \(\left( O \right)\) tại C và D. Hai đường thẳng BC và AD cắt nhau tại M. Gọi N là hình chiếu của M trên đường thẳng AB.
a) Chứng minh tứ giác MNAC nội tiếp.
b) Tính độ dài CH và \(\tan \angle ABC\)
c) Chứng minh NC là tiếp tuyến của đường tròn \(\left( O \right)\).
d) Tiếp tuyến tại A của đường tròn \(\left( O \right)\) cắt NC tại E. Chứng minh đường thẳng EB đi qua trung điểm của đoan thẳng CH.
Lời giải chi tiết
Câu 1:
a) Bằng các phép biến đổi đại số hãy rút gọn biểu thức: \(A = 2\sqrt 5 + 3\sqrt {45} .\)
\(A = 2\sqrt 5 + 3\sqrt {45} = 2\sqrt 5 + 3.\sqrt {{3^2}.5}\)\(\, = 2\sqrt 5 + 9\sqrt 5 = 11\sqrt 5 .\)
Vậy \(A = 11\sqrt 5 .\)
b) Giải phương trình \({x^2} - 6x + 5 = 0.\)
\(\begin{array}{l}\;\;\;{x^2} - 6x + 5 = 0 \\\Leftrightarrow {x^2} - 5x - x + 5 = 0\\ \Leftrightarrow x\left( {x - 5} \right) - \left( {x - 5} \right) = 0\\ \Leftrightarrow \left( {x - 5} \right)\left( {x - 1} \right) = 0 \\\Leftrightarrow \left[ \begin{array}{l}x - 5 = 0\\x - 1 = 0\end{array} \right. \\\Leftrightarrow \left[ \begin{array}{l}x = 5\\x = 1\end{array} \right..\end{array}\)
Vậy tập nghiệm của phương trình là: \(S = \left\{ {1;\;5} \right\}.\)
Câu 2:
Cho hai hàm số \(y = {x^2}\) và \(y = - x + 2.\)
a) Vẽ đồ thị của hai hàm số này trên cùng một mặt phẳng tọa độ Oxy.
+) Vẽ đồ thị hàm số: \(\left( d \right):\;\;y = - x + 2.\)
\(x\) | \(0\) | \(2\) |
\(y = - x + 2\) | \(2\) | \(0\) |
Đồ thị hàm số \(y = - x + 2\) là đường thẳng đi qua các điểm \(\left( {0;\;2} \right),\;\left( {2;\;0} \right).\)
+) Vẽ đồ thị hàm số: \(\left( P \right):\;\;y = {x^2}.\)
\(x\) | \( - 2\) | \( - 1\) | \(0\) | \(1\) | \(2\) |
\(y = {x^2}\) | \(4\) | \(1\) | \(0\) | \(1\) | \(4\) |
Đồ thị hàm số \(\left( P \right):\;\;y = {x^2}\) là đường cong đi qua các điểm \(\left( { - 2;\;4} \right),\;\left( { - 1;\;1} \right),\;\left( {0;\;0} \right),\;\left( {1;\;1} \right),\;\left( {2;\;4} \right).\)
Đồ thị hàm số:
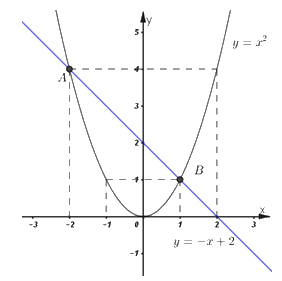
b) Tìm tọa độ giao điểm của hai đồ thị đó bằng phương pháp đại số.
Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình hoành độ giao điểm.
Ta có phương trình hoành độ giao điểm của hai đồ thị là:
\(\begin{array}{l}\;\;\; - x + 2 = {x^2} \Leftrightarrow {x^2} + x - 2 = 0 \\\Leftrightarrow {x^2} + 2x - x - 2 = 0\\ \Leftrightarrow x\left( {x + 2} \right) - \left( {x + 2} \right) = 0\\ \Leftrightarrow \left( {x + 2} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 2 = 0\\x - 1 = 0\end{array} \right. \\\Leftrightarrow \left[ \begin{array}{l}x = - 2 \Rightarrow y = 4\\x = 1 \Rightarrow y = 1\end{array} \right..\end{array}\)
Vậy hai đồ thị cắt nhau tại hai điểm phân biệt \(A\left( { - 2;\;4} \right)\) và \(B\left( {1;\;1} \right).\)
Câu 3:
Cho phương trình \({x^2} - 2x + m + 3 = 0\;\;\;\left( 1 \right)\) (với \(x\) là ẩn, \(m\) là tham số).
a) Tìm tất cả các giá trị của \(m\) để phương trình \(\left( 1 \right)\) có nghiệm.
Phương trình có nghiệm \( \Leftrightarrow \Delta ' \ge 0 \Leftrightarrow 1 - m - 3 \ge 0\) \( \Leftrightarrow m \le - 2.\)
Vậy \(m \le - 2\) thì phương trình đã cho có nghiệm.
b) Gọi \({x_1},\;{x_2}\) là nghiệm của phương trình \(\left( 1 \right).\) Tìm tất cả các giá trị của \(m\) để \(x_1^2 + x_2^2 - 3{x_1}{x_2} - 4 = 0.\)
Với \(m \le - 2\) thì phương trình có hai nghiệm \({x_1},\;{x_2}.\)
Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}{x_2} = m + 3\end{array} \right..\)
Theo đề bài ta có: \(x_1^2 + x_2^2 - 3{x_1}{x_2} - 4 = 0\)
\(\begin{array}{l} \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} - 3{x_1}{x_2} - 4 = 0 \\\Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 5{x_1}{x_2} - 4 = 0\\ \Leftrightarrow 4 - 5\left( {m + 3} \right) - 4 = 0\\ \Leftrightarrow 4 - 5m - 15 - 4 = 0 \\ \Leftrightarrow 5m = - 15\\ \Leftrightarrow m = - 3\;\;\;\left( {tm} \right).\end{array}\)
Vậy \(m = - 3\) thỏa mãn điều kiện bài toán.
Câu 4:
Gọi chiều rộng của mảnh đất đã cho là \(x\;\left( m \right),\;\;\left( {0 < x < 360} \right).\)
Gọi chiều dài của mảnh đất đã cho là: \(y\;\left( m \right),\;\;\left( {6 < y < 360,\;y > x} \right).\)
Khi đó ta có diện tích của mảnh đất là: \(xy = 360\;\;\;\left( 1 \right).\)
Tăng chiều rộng thêm \(2m\) thì chiều rộng mới là: \(x + 2\;\;\left( m \right).\)
Giảm chiều dài đi \(6m\) thì chiều dài mới là: \(y - 6\;\;\left( m \right).\)
Khi đó diện tích mảnh đất không đổi nên ta có phương trình: \(\left( {x + 2} \right)\left( {y - 6} \right) = xy \)
\(\Leftrightarrow 2y - 6x - 12 = 0\;\;\;\;\left( 2 \right).\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{l}xy = 360\\2y - 6x - 12 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}xy = 360\\y = 3x + 6\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}x\left( {3x + 6} \right) = 360\\y = 3x + 6\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}3{x^2} + 6x - 360 = 0\\y = 3x + 6\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x = 10\;\;\;\;\left( {tm} \right)\\x = - 12\;\;\left( {ktm} \right)\end{array} \right.\\y = 3.10 + 6\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 10\\y = 36\;\;\left( {tm} \right)\end{array} \right..\)
Vậy chu vi của mảnh vườn lúc đầu là: \(\left( {10 + 36} \right).2 = 92m.\)
Câu 5:
Cho đường tròn \(\left( O \right)\) đường kính \(AB = 6cm.\) Gọi \(H\) là điểm thuộc đoạn thẳng \(AB\) sao cho \(AH = 1cm.\) Qua \(H\) vẽ đường thẳng vuông góc với \(AB,\) đường thẳng này cắt đường tròn \(\left( O \right)\) tại C và D. Hai đường thẳng BC và AD cắt nhau tại M. Gọi N là hình chiếu của M trên đường thẳng AB.
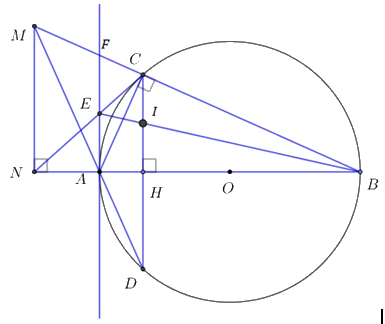
a) Chứng minh tứ giác MNAC nội tiếp.
Do \(\angle ACB\) là góc nội tiếp chắn nửa đường tròn nên \(\angle ACB = {90^0} \Rightarrow \angle ACM = {90^0}\).
Xét tứ giác \(MNAC\) có \(\angle ACM + \angle ANM = {90^0} + {90^0} = {180^0}\)
\( \Rightarrow \) Tứ giác \(MNAC\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).’
b) Tính độ dài CH và \(\tan \angle ABC\)
Ta có: \(BH = AB - AH = 6 - 1 = 5\,\,\left( {cm} \right)\)
Áp dụng hệ thức lượng trong tam giác vuông ABC có: \(A{H^2} = HA.HB = 1.5 = 5 \Rightarrow AH = \sqrt 5 \,\,\left( {cm} \right)\)
\( \Rightarrow \tan \angle ABC = \dfrac{{HA}}{{HB}} = \dfrac{{\sqrt 5 }}{5} = \dfrac{1}{{\sqrt 5 }}\)
c) Chứng minh NC là tiếp tuyến của đường tròn \(\left( O \right)\).
Ta có \(MN \bot AB;\,\,CH \bot AB \Rightarrow MN//CH\)
\( \Rightarrow \angle AMN = \angle ADC\) (so le trong)
Mà \(\angle AMN = \angle ACN\) (hai góc nội tiếp cùng chắn cung AN) \( \Rightarrow \angle ACN = \angle ADC\).
Mà \(\angle ADC\) nội tiếp chắn cung AC, \(\angle ACN\) ở vị trí góc tạo bởi tiếp tuyến và dây cung chắn cung AC.
\( \Rightarrow CN\) là tiếp tuyến của đường tròn \(\left( O \right)\) tại C.
d) Tiếp tuyến tại A của đường tròn \(\left( O \right)\) cắt NC tại E. Chứng minh đường thẳng EB đi qua trung điểm của đoan thẳng CH.
Kéo dài AE cắt BM tại F.
Ta có \(EA = EC\,\,\left( 1 \right)\) (tính chất hai tiếp tuyến cắt nhau) \( \Rightarrow \Delta EAC\) cân tại E \( \Rightarrow \angle EAC = \angle ECA\)
\( \Rightarrow {90^0} - \angle EAC = {90^0} - \angle ECA \)
\(\Leftrightarrow \angle EFC = \angle ECF \) \(\Rightarrow \Delta EFC\) cân tại E \( \Rightarrow EC = EF\) (2)
Từ (1) và (2) \( \Rightarrow EA = EC = EF\)
Ta có \(AF \bot AB\,\left( {gt} \right);\,\,CH \bot AB\,\,\left( {gt} \right) \Rightarrow AF//CH\)
Gọi \(I = BE \cap AF\), áp dụng định lí Ta-let ta có: \(\dfrac{{HI}}{{AE}} = \dfrac{{BI}}{{BE}};\,\,\dfrac{{CI}}{{EF}} = \dfrac{{BI}}{{BE}} \Rightarrow \dfrac{{HI}}{{AE}} = \dfrac{{CI}}{{EF}}\).
Mà \(AE = EF\,\,\left( {cmt} \right) \Rightarrow HI = CI \Rightarrow I\) là trung điểm của HC. (đpcm)
Đề thi vào lớp 10 môn Toán là một bước ngoặt quan trọng trong quá trình học tập của học sinh. Việc làm quen với các dạng bài tập và rèn luyện kỹ năng giải quyết vấn đề là vô cùng cần thiết. Đề số 34 mà chúng ta sẽ cùng phân tích hôm nay là một ví dụ điển hình cho cấu trúc đề thi hiện nay.
Phần đại số thường chiếm khoảng 40-50% tổng số điểm của đề thi. Các dạng bài tập thường gặp bao gồm:
Trong Đề số 34, phần đại số tập trung vào việc giải phương trình bậc hai và hệ phương trình. Để giải quyết tốt phần này, học sinh cần nắm vững các công thức, định lý và kỹ năng biến đổi đại số.
Phần hình học thường chiếm khoảng 30-40% tổng số điểm. Các dạng bài tập thường gặp bao gồm:
Trong Đề số 34, phần hình học yêu cầu học sinh chứng minh các tính chất của tam giác và tính diện tích. Để giải quyết tốt phần này, học sinh cần nắm vững các định lý, tính chất hình học và kỹ năng vẽ hình.
Phần bài toán thực tế thường chiếm khoảng 10-20% tổng số điểm. Đây là phần thi đòi hỏi học sinh phải vận dụng kiến thức đã học vào giải quyết các vấn đề thực tế. Các bài toán này thường có tính ứng dụng cao và đòi hỏi học sinh phải có khả năng tư duy logic và phân tích vấn đề.
Trong Đề số 34, bài toán thực tế liên quan đến việc tính toán diện tích và chi phí xây dựng. Để giải quyết tốt phần này, học sinh cần hiểu rõ đề bài, xác định các yếu tố cần thiết và áp dụng các công thức phù hợp.
Câu 1: (Đại số) Giải phương trình: 2x2 - 5x + 2 = 0
Lời giải:
Phương trình có dạng ax2 + bx + c = 0 với a = 2, b = -5, c = 2.
Tính delta: Δ = b2 - 4ac = (-5)2 - 4 * 2 * 2 = 25 - 16 = 9
Vì Δ > 0, phương trình có hai nghiệm phân biệt:
x1 = (-b + √Δ) / 2a = (5 + 3) / (2 * 2) = 2
x2 = (-b - √Δ) / 2a = (5 - 3) / (2 * 2) = 0.5
Vậy phương trình có hai nghiệm: x1 = 2 và x2 = 0.5
Câu 2: (Hình học) Cho tam giác ABC vuông tại A, có AB = 3cm, AC = 4cm. Tính độ dài cạnh BC.
Lời giải:
Áp dụng định lý Pitago vào tam giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2 = 32 + 42 = 9 + 16 = 25
Suy ra BC = √25 = 5cm
Vậy độ dài cạnh BC là 5cm.
Chúc các em học sinh ôn thi tốt và đạt kết quả cao trong kỳ thi vào lớp 10!