Chào mừng các em học sinh đến với đề tham khảo thi vào 10 môn Toán Hà Nội năm 2025 - Đề số 1 của giaitoan.edu.vn. Đề thi này được biên soạn dựa trên cấu trúc đề thi tuyển sinh vào 10 của các trường THPT chuyên hàng đầu Hà Nội, giúp các em làm quen với dạng đề và rèn luyện kỹ năng giải toán.
Giaitoan.edu.vn cung cấp đầy đủ các đề thi tham khảo, bài giảng online và tài liệu học tập môn Toán, hỗ trợ các em học sinh ôn thi hiệu quả và đạt kết quả cao nhất.
Câu 1: (1,5 điểm) 1) Thành tích chạy $50~m$ của 16 học sinh nam lớp 9A ở một trường THCS (đơn vị: giây) được cho bằng bảng sau:
Câu 1:(1,5 điểm)
1) Thành tích chạy $50~m$ của 16 học sinh nam lớp 9A ở một trường THCS (đơn vị: giây) được cho bằng bảng sau:

Tìm tần số ghép nhóm và tần số tương đối ghép nhóm \([7,5;8,0)\).
2) Đội văn nghệ lớp 9A gồm 2 bạn nam là Hùng, Bình và 3 bạn nữ là Nga, Thảo, Mai. Cô giáo phụ trách đội văn nghệ chọn ngẫu nhiên hai bạn để hát song ca. Tính xác suất của biến cố “Trong hai bạn được chọn có bạn Nga”.
Câu 2:(2 điểm)Cho hai biểu thức: \(A = \frac{{\sqrt x + 1}}{{\sqrt x - 3}}\) và \(B = \left( {\frac{1}{{\sqrt x - 1}} + \frac{{\sqrt x }}{{x - 1}}} \right).\frac{{x - \sqrt x }}{{2\sqrt x + 1}}\) với \(x \ge 0,x \ne 9;x \ne 1\).
1) Tính giá trị của biểu thức \(A\) khi \(x = 25\).
2) Chứng minh \(B = \frac{{\sqrt x }}{{\sqrt x + 1}}\).
3) Xét biểu thức \(P = AB\). Tìm các số nguyên tố \(x\) để \(P < 1\).
Câu 3:(2,5 điểm)
1) Tại một cửa hàng điện máy tủ lạnh được giảm giá \(18\% \) và tivi được giảm giá \(12\% \). Tổng giá niêm yết của hai mặt hàng này là \(45\) triệu đồng, giá sau khi giảm của hai mặt hàng là \(38,64\) triệu đồng. Tìm giá niêm yết của tủ lạnh, tivi.
2) Một người dự định trồng \(216\) cây theo thời gian định trước. Nhưng do thời tiết xấu nên mỗi ngày trồng được ít hơn \(6\) cây, vì thế trồng xong chậm mất \(6\) ngày so với dự kiến. Hỏi theo kế hoạch mỗi ngày người đó trồng được bao nhiêu cây.
3) Phương trình \({x^2} - 5x + k = 0\) có một nghiệm \({x_1} = \frac{{5 - \sqrt {13} }}{2}\). Tính giá trị của biểu thức \(x_1^2{x_2} + {x_1}x_2^2\).
Câu 4:(4 điểm)
1) Một cái thùng dùng để đựng gạo có dạng nửa hình cầu với đường kính \(50cm\), phần gạo vun lên có dạng hình nón cao \(12cm\).
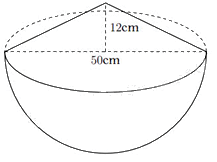
a) Tính thể tích phần gạo trong thùng.
b) Nhà bạn An dùng lon sữa bò dạng hình trụ với bán kính đáy là \(5cm\), chiều cao \(14cm\) dùng để đong gạo mỗi ngày. Biết rằng mỗi ngày nhà An ăn 4 lon gạo và mỗi lần đong thì lượng gạo chiếm \(90\% \) thể tích của lon. Hỏi cần ít nhất bao nhiêu ngày để nhà An có thể ăn hết số gạo trong thùng?
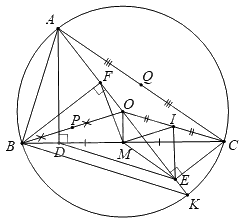
2) Cho đường tròn tâm \((O)\) và dây \(BC\) cố định không đi qua \(O\). Trên cung lớn \(BC\) lấy điểm \(A\) sao cho \(AB < AC\). Kẻ đường kính \(AK,\,E\) là hình chiếu của \(C\) trên \(AK\). \(M\) là trung điểm của \(BC\).
a) Chứng minh bốn \(C,\,E,\,\,M,\,O\) cùng thuộc một đường tròn.
b) Kẻ \(AD \bot BC\) tại \(D\). Chứng minh \(AD.AK = AB.AC\) và \(\Delta MDE\) cân.
c) Gọi \(F\) là hình chiếu của \(B\) trên \(AK\). Chứng minh khi di chuyển trên cung lớn \(BC\) thì tâm đường tròn ngoại tiếp \(\Delta DEF\) là 1 điểm cố định.
Câu 5:(0,5 điểm)
Bác An muốn đặt đóng một chiếc hộp đựng quà lưu niệm có dạng hình hộp chữ nhật với mặt đáy \(ABCD\) là hình vuông như hình dưới đây.
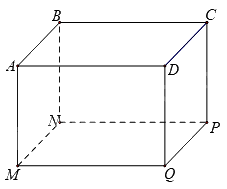
Để món quà trở nên đặc biệt, bác An muốn mạ bốn mặt xung quanh và mặt đáy dưới (mặt \(MNPQ\)) của chiếc hộp bằng kim loại quý (không mạ nắp hộp). Em hãy tìm độ dài cạnh \(MN\) của mặt đáy và chiều cao \(AM\) của hộp quà sao cho tổng diện tích các mặt được mạ kim loại quý của chiếc hộp là nhỏ nhất biết rằng thể tích của chiếc hộp là \(4d{m^3}\).
-------- Hết --------
Câu 1:(1,5 điểm)
1) Thành tích chạy \(50\;m\) của 16 học sinh nam lớp 9A ở một trường THCS (đơn vị: giây) được cho bằng bảng sau:

Tìm tần số ghép nhóm và tần số tương đối ghép nhóm \([7,5;8,0)\).
2) Đội văn nghệ lớp 9A gồm 2 bạn nam là Hùng, Bình và 3 bạn nữ là Nga, Thảo, Mai. Cô giáo phụ trách đội văn nghệ chọn ngẫu nhiên hai bạn để hát song ca. Tính xác suất của biến cố “Trong hai bạn được chọn có bạn Nga”.
Phương pháp
1) - Quan sát bảng số liệu xác định tần số ghép nhóm tương ứng với nhóm \([7,5;8,0)\).
- Tần số tương đối ghép nhóm bằng tỉ số giữa tần số nhóm \([7,5;8,0)\) và tổng số học sinh.
2) - Xác định số kết quả có thể xảy ra.
- Xác định số kết quả thuận lợi cho biến cố “Trong hai bạn được chọn có bạn Nga”.
- Xác suất của biến cố “Trong hai bạn được chọn có bạn Nga” bằng tỉ số giữa số kết quả thuận lợi cho biến cố với số kết quả có thể.
Lời giải
1) Dựa vào bảng ta thấy nhóm \([7,5;8,0)\) có tần số là 6.
Tần số tương đối của nhóm \([7,5;8,0)\) là: \(\frac{6}{{16}}.100\% = 37,5\% \).
2) Có 10 kết quả có thể xảy ra khi chọn ngẫu nhiên hai bạn để hát song ca là: (Hùng và Bình); (Hùng và Nga); (Hùng và Thảo); (Hùng và Mai); (Bình và Nga); (Bình và Thảo); (Bình và Mai); (Nga và Thảo); (Nga và Mai); (Thảo và Mai).
Có 4 kết quả thuận lợi cho biến cố “Trong hai bạn được chọn có bạn Nga” là: (Hùng và Nga); (Bình và Nga); (Nga và Thảo); (Nga và Mai).
Vậy xác suất của biến cố “Trong hai bạn được chọn có bạn Nga” là: \(P = \frac{4}{{10}} = \frac{2}{5}\).
Câu 2:(2 điểm)Cho hai biểu thức: \(A = \frac{{\sqrt x + 1}}{{\sqrt x - 3}}\) và \(B = \left( {\frac{1}{{\sqrt x - 1}} + \frac{{\sqrt x }}{{x - 1}}} \right).\frac{{x - \sqrt x }}{{2\sqrt x + 1}}\) với \(x \ge 0,x \ne 9;x \ne 1\).
1) Tính giá trị của biểu thức \(A\) khi \(x = 25\).
2) Chứng minh \(B = \frac{{\sqrt x }}{{\sqrt x + 1}}\).
3) Xét biểu thức \(P = AB\). Tìm các số nguyên tố \(x\) để \(P < 1\).
Phương pháp
1) Kiểm tra điều kiện của x.
Nếu thỏa mãn, thay \(x = 25\) vào biểu thức \(A\).
2) Kết hợp các tính chất của căn thức bậc hai để rút gọn biểu thức.
3) Rút gọn P sau đó giải bất đẳng thức \(P < 1\). Kết hợp điều kiện để tìm \(x\).
Lời giải
1) Với \(x = 25\) (thỏa mãn điều kiện), ta có:
\(A = \frac{{\sqrt {25} + 1}}{{\sqrt {25} - 3}} = \frac{{5 + 1}}{{5 - 3}} = \frac{6}{2} = 3\)
Vậy \(A = 3\) khi \(x = 25\).
2) Ta có:
\(\begin{array}{l}B = \left( {\frac{1}{{\sqrt x - 1}} + \frac{{\sqrt x }}{{x - 1}}} \right).\frac{{x - \sqrt x }}{{2\sqrt x + 1}}\\ = \left[ {\frac{{\sqrt x + 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} + \frac{{\sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}} \right].\frac{{\sqrt x \left( {\sqrt x - 1} \right)}}{{2\sqrt x + 1}}\\ = \frac{{\sqrt x + 1 + \sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}.\frac{{\sqrt x \left( {\sqrt x - 1} \right)}}{{2\sqrt x + 1}}\\ = \frac{{\left( {2\sqrt x + 1} \right)\sqrt x \left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)\left( {2\sqrt x + 1} \right)}}\\ = \frac{{\sqrt x }}{{\sqrt x + 1}}\end{array}\)
Vậy \(B = \frac{{\sqrt x }}{{\sqrt x + 1}}\).
3) Ta có: \(P = A.B = \frac{{\sqrt x + 1}}{{\sqrt x - 3}}.\frac{{\sqrt x }}{{\sqrt x + 1}} = \frac{{\sqrt x }}{{\sqrt x - 3}}\)
Để \(P < 1\) thì \(\frac{{\sqrt x }}{{\sqrt x - 3}} < 1\)
\(\begin{array}{l}\frac{{\sqrt x }}{{\sqrt x - 3}} - 1 < 0\\\frac{{\sqrt x - \sqrt x + 3}}{{\sqrt x - 3}} < 0\\\frac{3}{{\sqrt x - 3}} < 0\end{array}\)
Vì 3 > 0 nên \(\frac{3}{{\sqrt x - 3}} < 0\) khi \(\sqrt x - 3 < 0\) suy ra \(\sqrt x < 3\) nên \(x < 9\).
Kết hợp với \(x \ge 0,x \ne 9;x \ne 1\) suy ra \(0 \le x < 9\)
Mà \(x\) là số nguyên tố nên \(x \in \left\{ {2;3;5;7} \right\}\).
Vậy \(x \in \left\{ {2;3;5;7} \right\}\) thì \(P < 1\).
Câu 3:(2,5 điểm)
1) Tại một cửa hàng điện máy tủ lạnh được giảm giá \(18\% \) và tivi được giảm giá \(12\% \). Tổng giá niêm yết của hai mặt hàng này là \(45\) triệu đồng, giá sau khi giảm của hai mặt hàng là \(38,64\) triệu đồng. Tìm giá niêm yết của tủ lạnh, tivi.
2) Một người dự định trồng \(216\) cây theo thời gian định trước. Nhưng do thời tiết xấu nên mỗi ngày trồng được ít hơn \(6\) cây, vì thế trồng xong chậm mất \(6\) ngày so với dự kiến. Hỏi theo kế hoạch mỗi ngày người đó trồng được bao nhiêu cây.
3) Phương trình \({x^2} - 5x + k = 0\) có một nghiệm \({x_1} = \frac{{5 - \sqrt {13} }}{2}\). Tính giá trị của biểu thức \(x_1^2{x_2} + {x_1}x_2^2\).
Phương pháp
1) Gọi giá niêm yết của tủ lạnh và ti vi lần lượt là \(x,y\) (triệu đồng) (\(0 < x,y < 45\)).
Lập luận để có hệ phương trình \(\left\{ \begin{array}{l}x + y = 45\\0,18x + 0,12y = 6,36\end{array} \right.\)
Sử dụng phương pháp thế hoặc cộng đại số để tìm \(x,y\).
2) Giả sử theo kế hoạch mỗi ngày người đó trồng được số cây là: \(x\) (cây) (\(x > 6\)).
Biểu diễn số cây thực tế mỗi ngày người đó trồng được.
Từ đó biểu diễn thời gian trồng xong cây theo kế hoạch và thực tế.
Lập phương trình và giải để tìm \(x\).
3) Thay nghiệm \({x_1} = \frac{{5 - \sqrt {13} }}{2}\) vào phương trình để tìm k.
Biến đổi \(x_1^2{x_2} + {x_1}x_2^2\) và áp dụng định lí Viète: \({x_1} + {x_2} = \frac{{ - b}}{a};{x_1}{x_2} = \frac{c}{a}\).
Lời giải
1) Gọi giá niêm yết của tủ lạnh và ti vi lần lượt là \(x,y\) (triệu đồng) (\(0 < x,y < 45\)).
Vì tổng giá niêm yết của hai mặt hàng này là 45 triệu đồng nên \(x + y = 45\) (1)
Số tiền được giảm khi mua hai mặt hàng này là: \(45 - 38,64 = 6,36\) (triệu đồng).
Vì tủ lạnh được giảm giá \(18\% \) và tivi được giảm giá \(12\% \) nên ta có phương trinh: \(18\% x + 12\% y = 6,36\) hay \(0,18x + 0,12y = 6,36\) (2)
Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 45\\0,18x + 0,12y = 6,36\end{array} \right.\) suy ra \(\left\{ \begin{array}{l}x = 16\\y = 29\end{array} \right.\left( {TM} \right)\)
Vậy giá niêm yết của tủ lạnh là 16 triệu đồng, giá niêm yết của ti vi là 29 triệu đồng.
2) Giả sử theo kế hoạch mỗi ngày người đó trồng được số cây là: \(x\) (cây) (\(x > 6\)).
Trên thực tế mỗi ngày người đó trồng được số cây là: \(x - 6\) (cây)
Thời gian người đó trồng xong cây theo kế hoạch là: \(\frac{{216}}{x}\) (ngày).
Thời gian thực tế người đó trồng xong cây trên là: \(\frac{{216}}{{x - 6}}\) (ngày).
Vì thời gian trồng xong chậm 6 ngày so với dự kiến nên ta có phương trình: \(\frac{{216}}{{x - 6}} - \frac{{216}}{x} = 6\)
\(\frac{{216}}{{x - 6}} - \frac{{216}}{x} = 6\)
\(1296 = 6x(x - 6)\)
\(6{x^2} - 36x - 1296 = 0\)
Giải phương trình ta được \(x = 18\) hoặc \(x = - 12\) (loại).
Vậy theo kế hoạch người đó trồng \(18\) cây mỗi ngày.
3) Vì phương trình \({x^2} - 5x + k = 0\) có một nghiệm \({x_1} = \frac{{5 - \sqrt {13} }}{2}\) nên thay \({x_1} = \frac{{5 - \sqrt {13} }}{2}\) vào phương trình, ta được:
\(\begin{array}{l}{\left( {\frac{{5 - \sqrt {13} }}{2}} \right)^2} - 5\left( {\frac{{5 - \sqrt {13} }}{2}} \right) + k = 0\\\frac{{19 - 5\sqrt {13} }}{2} - \frac{{25 - 5\sqrt {13} }}{2} + k = 0\\\frac{{19 - 5\sqrt {13} - 25 + 5\sqrt {13} }}{2} + k = 0\\ - 3 + k = 0\\k = 3\end{array}\)
Do đó phương trình cần tìm là \({x^2} - 5x + 3 = 0\).
Theo định lí Viète ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 5\\{x_1}{x_2} = 3\end{array} \right.\)
Ta có: \(x_1^2{x_2} + {x_1}x_2^2 = {x_1}{x_2}\left( {{x_1} + {x_2}} \right) = 3.5 = 15\).
Câu 4:(4 điểm)
1) Một cái thùng dùng để đựng gạo có dạng nửa hình cầu với đường kính \(50cm\), phần gạo vun lên có dạng hình nón cao \(12cm\).
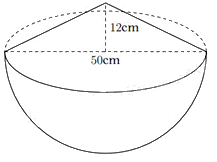
a) Tính thể tích phần gạo trong thùng.
b) Nhà bạn An dùng lon sữa bò dạng hình trụ với bán kính đáy là \(5cm\), chiều cao \(14cm\) dùng để đong gạo mỗi ngày. Biết rằng mỗi ngày nhà An ăn 4 lon gạo và mỗi lần đong thì lượng gạo chiếm \(90\% \) thể tích của lon. Hỏi cần ít nhất bao nhiêu ngày để nhà An có thể ăn hết số gạo trong thùng?
2) Cho đường tròn tâm \((O)\) và dây \(BC\) cố định không đi qua \(O\). Trên cung lớn \(BC\) lấy điểm \(A\) sao cho \(AB < AC\). Kẻ đường kính là hình chiếu của \(C\) trên \(AK\). \(M\) là trung điểm của \(BC\).
a) Chứng minh bốn \(C,\,E,\,\,M,\,O\) cùng thuộc một đường tròn.
b) Kẻ \(AD \bot BC\) tại \(D\). Chứng minh \(AD.AK = AB.AC\) và \(\Delta MDE\) cân.
c) Gọi \(F\) là hình chiếu của \(B\) trên \(AK\). Chứng minh khi di chuyển trên cung lớn \(BC\) thì tâm đường tròn ngoại tiếp \(\Delta DEF\) là 1 điểm cố định.
Phương pháp
1) a) Tính bán kính của hình cầu.
- Thể tích phần gạo nửa hình cầu = \(\frac{1}{2}\) thể tích hình cầu.
Thể tích hình cầu: \({V_c} = \frac{4}{3}\pi {R^3}\).
- Thể tích phần gạo hình nón tính bằng công thức tính thể tích hình nón: \({V_n} = \frac{1}{3}\pi {R^2}h\)
- Thể tích gạo = thể tích phần gạo nửa hình cầu + thể tích phần gạo hình nón.
b) Tính thể tích lon bằng thể tích hình trụ: \({V_t} = \pi {R^2}h\)
Tính thể tích gạo mỗi ngày múc = \(4.90\% .{V_t}\).
Lấy thể tích gạo : thể tích gạo mỗi ngày múc để xác định số ngày ít nhất để dùng hết số gạo trong thùng.
2) a) Chứng minh \(\Delta OMC\) và \(\Delta OEC\) lần lượt vuông tại M và E nên cùng nội tiếp đường tròn đường kính OC.
Gọi I là trung điểm của OC thì \(C,\,E,\,M,\,O\) cùng thuộc một đường tròn (I) đường kính OC (bán kính OI).
b) *Chứng minh \(AD.AK = AB.AC\)
Chứng minh $\Delta DBA\backsim \Delta CK\text{A}$ (g.g) suy ra \(\frac{{AD}}{{AB}} = \frac{{AC}}{{AK}}\) (cặp cạnh tương ứng tỉ lệ) nên \(AD.AK = AB.AC\).
*Chứng minh \(\Delta MDE\)cân.
Để chứng minh \(\Delta MDE\)cân ta chứng minh \(\widehat {MDE} = \widehat {MED}\).
- Lập luận \(\widehat {CAE} = \widehat {CDE}\) và \(\widehat {CBK} = \widehat {CAE}\) suy ra \(\widehat {CBK} = \widehat {CDE}\)
- Lập luận \(\widehat {EMC} = \widehat {EOC}\), \(\widehat {KBC} = \frac{1}{2}\widehat {KOC}\) suy ra \(\widehat {EMC} = 2\widehat {CDE}\)
- Sử dụng tính chất góc ngoài của tam giác \(\Delta MDE\) suy ra \(\widehat {EMC} = 2\widehat {MDE}\)
Do đó \(\widehat {MDE} = \widehat {MED}\).
c) Chứng minh \(\widehat {OBM} = \widehat {MFO}\) và \(\widehat {MEO} = \widehat {MCO}\), mà \(\widehat {OBM} = \widehat {OCM}\) suy ra \(\widehat {MFO} = \widehat {MEO}\).
Do đó \(\Delta EMF\) cân tại \(M\), nên \(ME = MF\).
Mà \(ME = MD\) nên \(MD = ME = MF\)
Suy ra \(M\) là tâm đường tròn ngoại tiếp tam giác \(DEF\).
Mà \(M\) là trung điểm của \(BC\) nên \(M\) là điểm cố định.
Lời giải
1) a) Bán kính của hình cầu là: \(R = \frac{d}{2} = \frac{{50}}{2} = 25{\kern 1pt} {\kern 1pt} \left( {cm} \right)\)
Thể tích phần gạo nửa hình cầu là: \({V_c} = \frac{1}{2} \cdot \frac{4}{3}\pi {R^3} = \frac{1}{2} \cdot \frac{4}{3}\pi {25^3} = \frac{{31{\kern 1pt} 250}}{3}\pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)
Thể tích phần gạo vun lên dạng hình nón là: \({V_n} = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi \cdot {25^2} \cdot 12 = 2500\pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)
Thể tích gạo trong thùng là: \({V_g} = \frac{{31{\kern 1pt} 250}}{3}\pi + 2500\pi = \frac{{38750}}{3}\pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)
b) Thể tích lon là: \(\pi {.5^2}.14 = 350{\kern 1pt} \pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)
Thể tích gạo một ngày múc là: \(4.90\% .350\pi = 1260\pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)
Ta có: \(\frac{{38{\kern 1pt} 750}}{\pi }:1{\kern 1pt} 260\pi \approx 10,3\)
Vậy cần ít nhất 11 ngày để dùng hết số gạo trong thùng.
2)
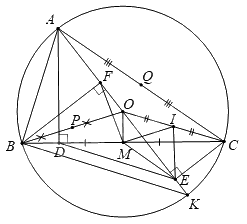
a) Chứng minh bốn \(C,\,E,\,M,\,O\) cùng thuộc một đường tròn.
\(\Delta OBC\) cân tại \(O\), \(M\) là trung điểm của \(BC\) nên \(OM\) vừa là đường trung tuyến vừa là đường cao. Suy ra \(OM \bot BC\) suy ra \(\widehat {OMC} = 90^\circ \).
Tam giác OMC vuông tại \(M\) nên tam giác OMC nội tiếp đường tròn đường kính OC.
Theo bài ra, \(E\) là hình chiếu của \(C\) trên \(AK\) nên \(CE \bot AK\) suy ra \(CE \bot EO\) hay \(\widehat {OEC} = 90^\circ \).
Tam giác OEC vuông tại E nên tam giác OEC nội tiếp đường tròn đường kính OC.
Gọi \(I\) là trung điểm của \(OC\)
Do đó \(C,\,E,\,M,\,O\) cùng thuộc một đường tròn (I) đường kính OC (bán kính OI).
b) *Chứng minh \(AD.AK = AB.AC\)
Xét \(\Delta DBA\) và \(\Delta CK{\rm{A}}\) có
\(\widehat {ADB} = \widehat {ACK} = 90^\circ \)
\(\widehat {ABD} = \widehat {AKC}\) (Hai góc nội tiếp cùng chắn cung )
Nên $\Delta DBA\backsim \Delta CK\text{A}$ (g.g)
Do đó ta có: \(\frac{{AD}}{{AB}} = \frac{{AC}}{{AK}}\) (cặp cạnh tương ứng tỉ lệ)
Hay \(AD.AK = AB.AC\) (đpcm).
*Chứng minh \(\Delta MDE\)cân.
Theo bài ra \(\left\{ \begin{array}{l}AD \bot BC\\AE \bot EC\end{array} \right.\) suy ra \(\left\{ \begin{array}{l}\widehat {ADC} = 90^\circ \\\widehat {AEC} = 90^\circ \end{array} \right.\)
Gọi \(Q\) là trung điểm của \(AC\)
Tam giác ADC và tam giác AEC vuông tại D và E nên nội tiếp đường tròn (Q; AC), suy ra \(QA = QC = QD = QE\)
Suy ra bốn điểm \(A,\,C,\,D,\,E\) cùng thuộc đường tròn \(\left( Q \right)\)
Suy ra \(\widehat {CAE} = \widehat {CDE}\) (Hai góc nội tiếp cùng chắn cung \(CE\)) (1)
Xét \(\left( O \right)\) ta có: \(\widehat {CBK} = \widehat {CAE}\) (Hai góc nội tiếp cùng chắn cung \(CK\) ) (2)
Từ (1) và (2) suy ra \(\widehat {CBK} = \widehat {CDE}\) mà hai góc này ở vị trí đồng vị (3)
Suy ra \(DE//BK\)
Xét đường tròn \(\left( I \right)\) có: \(\widehat {EMC} = \widehat {EOC}\) (Hai góc nội tiếp cùng chắn $\overset\frown{EC}$). (4)
Xét đường tròn \(\left( O \right)\) có: \(\widehat {KBC} = \frac{1}{2}\widehat {KOC}\) (Góc nội tiếp và góc ở tâm cùng chắn \(\overset\frown{KC}\)). (5)
Từ (3); (4) và (5) suy ra \(\widehat {EMC} = 2\widehat {CDE}\).
\(\Delta MDE\) có \(\widehat {EMC} = \widehat {MDE} + \widehat {MED}\) (góc ngoài của tam giác) mà \(\widehat {EMC} = 2\widehat {MDE}\)
Nên \(\widehat {MDE} = \widehat {MED}\). Do đó, \(\Delta MDE\) cân tại \(M\).
c) Gọi \(P\) là trung điểm của \(BO\)
Tam giác BFO và tam giác BMO vuông tại F và M nên nội tiếp đường tròn (P; OP) suy ra \(PB = PO = PF = PM\)
Suy ra bốn điểm \(O,M,B,F\) cùng thuộc đường tròn \(\left( P \right)\)
Nên \(\widehat {OBM} = \widehat {MFO}\) (Hai góc nội tiếp cùng chắn \(\overset\frown{MO}\)).
Xét đường tròn \(\left( I \right)\) có:
\(\widehat {MEO} = \widehat {MCO}\) (Hai góc nội tiếp cùng chắn \(\overset\frown{MO}\)).
Mà \(\widehat {OBM} = \widehat {OCM}\) (\(\Delta OCB\)cân tại \(O\)).
Do đó \(\widehat {MFO} = \widehat {MEO}\) suy ra \(\Delta EMF\) cân tại \(M\), do đó \(ME = MF\).
Mà \(ME = MD\) (Tam giác \(MDE\) cân tại \(M\)).
Suy ra \(MD = ME = MF\).
Suy ra \(M\) là tâm đường tròn ngoại tiếp tam giác \(DEF\).
Mà \(M\) là trung điểm của \(BC\) nên \(M\) là điểm cố định.
Vậy khi \(A\) di chuyển trên cung lớn \(BC\) thì tâm đường tròn ngoại tiếp tam giác \(DEF\) là một điểm cố định.
Câu 5:(0,5 điểm)
Bác An muốn đặt đóng một chiếc hộp đựng quà lưu niệm có dạng hình hộp chữ nhật với mặt đáy \(ABCD\) là hình vuông như hình dưới đây.
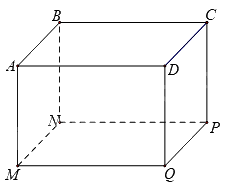
Để món quà trở nên đặc biệt, bác An muốn mạ bốn mặt xung quanh và mặt đáy dưới (mặt \(MNPQ\)) của chiếc hộp bằng kim loại quý (không mạ nắp hộp). Em hãy tìm độ dài cạnh \(MN\) của mặt đáy và chiều cao \(AM\) của hộp quà sao cho tổng diện tích các mặt được mạ kim loại quý của chiếc hộp là nhỏ nhất biết rằng thể tích của chiếc hộp là \(4d{m^3}\).
Phương pháp
Gọi độ dài cạnh \(MN\) là \(x\left( {dm} \right)\) (\(x > 0\))
Gọi độ dài chiều cao \(AM\) là \(h\left( {dm} \right)\) (\(h > 0\))
Biểu diễn \(h\) theo \(x\) dựa vào thể tích của chiếc hộp.
Tính diện tích cần mạ kim loại = diện tích bốn mặt xung quanh và diện tích mặt đáy dưới.
Biến đổi biểu thức bằng cách sử dụng hằng đẳng thức bình phương của một hiệu kết hợp nhóm hạng tử sau đó sử dụng bất đẳng thức Cô – si để tìm giá trị nhỏ nhất của S.
Từ đó tính được \(x,h\).
Lời giải
Gọi độ dài cạnh \(MN\) là \(x\left( {dm} \right)\)(\(x > 0\))
Gọi độ dài chiều cao \(AM\) là \(h\left( {dm} \right)\)(\(h > 0\))
Do thể tích của chiếc hộp là 4dm3 nên ta có: \({x^2}h = 4\)
Suy ra \(h = \frac{4}{{{x^2}}}\)
Diện tích cần mạ kim loại quý của chiếc hộp là:
\(\begin{array}{l}S = {x^2} + 4xh = {x^2} + 4x.\frac{4}{{{x^2}}} = {x^2} + \frac{{16}}{x}\\\,\,\,\, = \left( {{x^2} - 4x + 4} \right) + \left( {4x + \frac{{16}}{x}} \right) - 4 = {\left( {x - 2} \right)^2} + \left( {4x + \frac{{16}}{x}} \right) - 4\end{array}\)
Chứng minh bất đẳng thức Cô – si.
Áp dụng bất đẳng thức Cô – si cho 2 số \(4x > 0\) và \(\frac{{16}}{x} > 0\) và \({\left( {x - 2} \right)^2} \ge 0\) ta có:
\(S \ge 0 + 2\sqrt {4x.\frac{{16}}{{4x}}} - 4 = 0 + 2.8 - 4 = 12\)
Dấu “=” xảy ra khi \(\left\{ \begin{array}{l}x - 2 = 0\\4x = \frac{{16}}{{4x}}\end{array} \right.\)
Ta giải ra được \(x = 2\) từ đó suy ra \(h = \frac{4}{{{2^2}}} = 1\)
Vậy khi độ dài cạnh đáy \(MN = 2dm\) và chiều cao \(AM = 1dm\) thì diện tích cần mạ kim loại quý của chiếc hộp là nhỏ nhất bằng \(12d{m^2}\).
Tải về
Câu 1:(1,5 điểm)
1) Thành tích chạy $50~m$ của 16 học sinh nam lớp 9A ở một trường THCS (đơn vị: giây) được cho bằng bảng sau:

Tìm tần số ghép nhóm và tần số tương đối ghép nhóm \([7,5;8,0)\).
2) Đội văn nghệ lớp 9A gồm 2 bạn nam là Hùng, Bình và 3 bạn nữ là Nga, Thảo, Mai. Cô giáo phụ trách đội văn nghệ chọn ngẫu nhiên hai bạn để hát song ca. Tính xác suất của biến cố “Trong hai bạn được chọn có bạn Nga”.
Câu 2:(2 điểm)Cho hai biểu thức: \(A = \frac{{\sqrt x + 1}}{{\sqrt x - 3}}\) và \(B = \left( {\frac{1}{{\sqrt x - 1}} + \frac{{\sqrt x }}{{x - 1}}} \right).\frac{{x - \sqrt x }}{{2\sqrt x + 1}}\) với \(x \ge 0,x \ne 9;x \ne 1\).
1) Tính giá trị của biểu thức \(A\) khi \(x = 25\).
2) Chứng minh \(B = \frac{{\sqrt x }}{{\sqrt x + 1}}\).
3) Xét biểu thức \(P = AB\). Tìm các số nguyên tố \(x\) để \(P < 1\).
Câu 3:(2,5 điểm)
1) Tại một cửa hàng điện máy tủ lạnh được giảm giá \(18\% \) và tivi được giảm giá \(12\% \). Tổng giá niêm yết của hai mặt hàng này là \(45\) triệu đồng, giá sau khi giảm của hai mặt hàng là \(38,64\) triệu đồng. Tìm giá niêm yết của tủ lạnh, tivi.
2) Một người dự định trồng \(216\) cây theo thời gian định trước. Nhưng do thời tiết xấu nên mỗi ngày trồng được ít hơn \(6\) cây, vì thế trồng xong chậm mất \(6\) ngày so với dự kiến. Hỏi theo kế hoạch mỗi ngày người đó trồng được bao nhiêu cây.
3) Phương trình \({x^2} - 5x + k = 0\) có một nghiệm \({x_1} = \frac{{5 - \sqrt {13} }}{2}\). Tính giá trị của biểu thức \(x_1^2{x_2} + {x_1}x_2^2\).
Câu 4:(4 điểm)
1) Một cái thùng dùng để đựng gạo có dạng nửa hình cầu với đường kính \(50cm\), phần gạo vun lên có dạng hình nón cao \(12cm\).
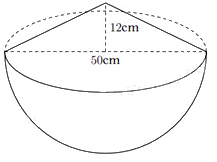
a) Tính thể tích phần gạo trong thùng.
b) Nhà bạn An dùng lon sữa bò dạng hình trụ với bán kính đáy là \(5cm\), chiều cao \(14cm\) dùng để đong gạo mỗi ngày. Biết rằng mỗi ngày nhà An ăn 4 lon gạo và mỗi lần đong thì lượng gạo chiếm \(90\% \) thể tích của lon. Hỏi cần ít nhất bao nhiêu ngày để nhà An có thể ăn hết số gạo trong thùng?
2) Cho đường tròn tâm \((O)\) và dây \(BC\) cố định không đi qua \(O\). Trên cung lớn \(BC\) lấy điểm \(A\) sao cho \(AB < AC\). Kẻ đường kính \(AK,\,E\) là hình chiếu của \(C\) trên \(AK\). \(M\) là trung điểm của \(BC\).
a) Chứng minh bốn \(C,\,E,\,\,M,\,O\) cùng thuộc một đường tròn.
b) Kẻ \(AD \bot BC\) tại \(D\). Chứng minh \(AD.AK = AB.AC\) và \(\Delta MDE\) cân.
c) Gọi \(F\) là hình chiếu của \(B\) trên \(AK\). Chứng minh khi di chuyển trên cung lớn \(BC\) thì tâm đường tròn ngoại tiếp \(\Delta DEF\) là 1 điểm cố định.
Câu 5:(0,5 điểm)
Bác An muốn đặt đóng một chiếc hộp đựng quà lưu niệm có dạng hình hộp chữ nhật với mặt đáy \(ABCD\) là hình vuông như hình dưới đây.
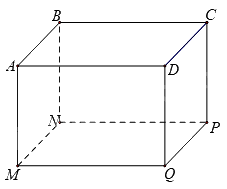
Để món quà trở nên đặc biệt, bác An muốn mạ bốn mặt xung quanh và mặt đáy dưới (mặt \(MNPQ\)) của chiếc hộp bằng kim loại quý (không mạ nắp hộp). Em hãy tìm độ dài cạnh \(MN\) của mặt đáy và chiều cao \(AM\) của hộp quà sao cho tổng diện tích các mặt được mạ kim loại quý của chiếc hộp là nhỏ nhất biết rằng thể tích của chiếc hộp là \(4d{m^3}\).
-------- Hết --------
Câu 1:(1,5 điểm)
1) Thành tích chạy \(50\;m\) của 16 học sinh nam lớp 9A ở một trường THCS (đơn vị: giây) được cho bằng bảng sau:

Tìm tần số ghép nhóm và tần số tương đối ghép nhóm \([7,5;8,0)\).
2) Đội văn nghệ lớp 9A gồm 2 bạn nam là Hùng, Bình và 3 bạn nữ là Nga, Thảo, Mai. Cô giáo phụ trách đội văn nghệ chọn ngẫu nhiên hai bạn để hát song ca. Tính xác suất của biến cố “Trong hai bạn được chọn có bạn Nga”.
Phương pháp
1) - Quan sát bảng số liệu xác định tần số ghép nhóm tương ứng với nhóm \([7,5;8,0)\).
- Tần số tương đối ghép nhóm bằng tỉ số giữa tần số nhóm \([7,5;8,0)\) và tổng số học sinh.
2) - Xác định số kết quả có thể xảy ra.
- Xác định số kết quả thuận lợi cho biến cố “Trong hai bạn được chọn có bạn Nga”.
- Xác suất của biến cố “Trong hai bạn được chọn có bạn Nga” bằng tỉ số giữa số kết quả thuận lợi cho biến cố với số kết quả có thể.
Lời giải
1) Dựa vào bảng ta thấy nhóm \([7,5;8,0)\) có tần số là 6.
Tần số tương đối của nhóm \([7,5;8,0)\) là: \(\frac{6}{{16}}.100\% = 37,5\% \).
2) Có 10 kết quả có thể xảy ra khi chọn ngẫu nhiên hai bạn để hát song ca là: (Hùng và Bình); (Hùng và Nga); (Hùng và Thảo); (Hùng và Mai); (Bình và Nga); (Bình và Thảo); (Bình và Mai); (Nga và Thảo); (Nga và Mai); (Thảo và Mai).
Có 4 kết quả thuận lợi cho biến cố “Trong hai bạn được chọn có bạn Nga” là: (Hùng và Nga); (Bình và Nga); (Nga và Thảo); (Nga và Mai).
Vậy xác suất của biến cố “Trong hai bạn được chọn có bạn Nga” là: \(P = \frac{4}{{10}} = \frac{2}{5}\).
Câu 2:(2 điểm)Cho hai biểu thức: \(A = \frac{{\sqrt x + 1}}{{\sqrt x - 3}}\) và \(B = \left( {\frac{1}{{\sqrt x - 1}} + \frac{{\sqrt x }}{{x - 1}}} \right).\frac{{x - \sqrt x }}{{2\sqrt x + 1}}\) với \(x \ge 0,x \ne 9;x \ne 1\).
1) Tính giá trị của biểu thức \(A\) khi \(x = 25\).
2) Chứng minh \(B = \frac{{\sqrt x }}{{\sqrt x + 1}}\).
3) Xét biểu thức \(P = AB\). Tìm các số nguyên tố \(x\) để \(P < 1\).
Phương pháp
1) Kiểm tra điều kiện của x.
Nếu thỏa mãn, thay \(x = 25\) vào biểu thức \(A\).
2) Kết hợp các tính chất của căn thức bậc hai để rút gọn biểu thức.
3) Rút gọn P sau đó giải bất đẳng thức \(P < 1\). Kết hợp điều kiện để tìm \(x\).
Lời giải
1) Với \(x = 25\) (thỏa mãn điều kiện), ta có:
\(A = \frac{{\sqrt {25} + 1}}{{\sqrt {25} - 3}} = \frac{{5 + 1}}{{5 - 3}} = \frac{6}{2} = 3\)
Vậy \(A = 3\) khi \(x = 25\).
2) Ta có:
\(\begin{array}{l}B = \left( {\frac{1}{{\sqrt x - 1}} + \frac{{\sqrt x }}{{x - 1}}} \right).\frac{{x - \sqrt x }}{{2\sqrt x + 1}}\\ = \left[ {\frac{{\sqrt x + 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} + \frac{{\sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}} \right].\frac{{\sqrt x \left( {\sqrt x - 1} \right)}}{{2\sqrt x + 1}}\\ = \frac{{\sqrt x + 1 + \sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}.\frac{{\sqrt x \left( {\sqrt x - 1} \right)}}{{2\sqrt x + 1}}\\ = \frac{{\left( {2\sqrt x + 1} \right)\sqrt x \left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)\left( {2\sqrt x + 1} \right)}}\\ = \frac{{\sqrt x }}{{\sqrt x + 1}}\end{array}\)
Vậy \(B = \frac{{\sqrt x }}{{\sqrt x + 1}}\).
3) Ta có: \(P = A.B = \frac{{\sqrt x + 1}}{{\sqrt x - 3}}.\frac{{\sqrt x }}{{\sqrt x + 1}} = \frac{{\sqrt x }}{{\sqrt x - 3}}\)
Để \(P < 1\) thì \(\frac{{\sqrt x }}{{\sqrt x - 3}} < 1\)
\(\begin{array}{l}\frac{{\sqrt x }}{{\sqrt x - 3}} - 1 < 0\\\frac{{\sqrt x - \sqrt x + 3}}{{\sqrt x - 3}} < 0\\\frac{3}{{\sqrt x - 3}} < 0\end{array}\)
Vì 3 > 0 nên \(\frac{3}{{\sqrt x - 3}} < 0\) khi \(\sqrt x - 3 < 0\) suy ra \(\sqrt x < 3\) nên \(x < 9\).
Kết hợp với \(x \ge 0,x \ne 9;x \ne 1\) suy ra \(0 \le x < 9\)
Mà \(x\) là số nguyên tố nên \(x \in \left\{ {2;3;5;7} \right\}\).
Vậy \(x \in \left\{ {2;3;5;7} \right\}\) thì \(P < 1\).
Câu 3:(2,5 điểm)
1) Tại một cửa hàng điện máy tủ lạnh được giảm giá \(18\% \) và tivi được giảm giá \(12\% \). Tổng giá niêm yết của hai mặt hàng này là \(45\) triệu đồng, giá sau khi giảm của hai mặt hàng là \(38,64\) triệu đồng. Tìm giá niêm yết của tủ lạnh, tivi.
2) Một người dự định trồng \(216\) cây theo thời gian định trước. Nhưng do thời tiết xấu nên mỗi ngày trồng được ít hơn \(6\) cây, vì thế trồng xong chậm mất \(6\) ngày so với dự kiến. Hỏi theo kế hoạch mỗi ngày người đó trồng được bao nhiêu cây.
3) Phương trình \({x^2} - 5x + k = 0\) có một nghiệm \({x_1} = \frac{{5 - \sqrt {13} }}{2}\). Tính giá trị của biểu thức \(x_1^2{x_2} + {x_1}x_2^2\).
Phương pháp
1) Gọi giá niêm yết của tủ lạnh và ti vi lần lượt là \(x,y\) (triệu đồng) (\(0 < x,y < 45\)).
Lập luận để có hệ phương trình \(\left\{ \begin{array}{l}x + y = 45\\0,18x + 0,12y = 6,36\end{array} \right.\)
Sử dụng phương pháp thế hoặc cộng đại số để tìm \(x,y\).
2) Giả sử theo kế hoạch mỗi ngày người đó trồng được số cây là: \(x\) (cây) (\(x > 6\)).
Biểu diễn số cây thực tế mỗi ngày người đó trồng được.
Từ đó biểu diễn thời gian trồng xong cây theo kế hoạch và thực tế.
Lập phương trình và giải để tìm \(x\).
3) Thay nghiệm \({x_1} = \frac{{5 - \sqrt {13} }}{2}\) vào phương trình để tìm k.
Biến đổi \(x_1^2{x_2} + {x_1}x_2^2\) và áp dụng định lí Viète: \({x_1} + {x_2} = \frac{{ - b}}{a};{x_1}{x_2} = \frac{c}{a}\).
Lời giải
1) Gọi giá niêm yết của tủ lạnh và ti vi lần lượt là \(x,y\) (triệu đồng) (\(0 < x,y < 45\)).
Vì tổng giá niêm yết của hai mặt hàng này là 45 triệu đồng nên \(x + y = 45\) (1)
Số tiền được giảm khi mua hai mặt hàng này là: \(45 - 38,64 = 6,36\) (triệu đồng).
Vì tủ lạnh được giảm giá \(18\% \) và tivi được giảm giá \(12\% \) nên ta có phương trinh: \(18\% x + 12\% y = 6,36\) hay \(0,18x + 0,12y = 6,36\) (2)
Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 45\\0,18x + 0,12y = 6,36\end{array} \right.\) suy ra \(\left\{ \begin{array}{l}x = 16\\y = 29\end{array} \right.\left( {TM} \right)\)
Vậy giá niêm yết của tủ lạnh là 16 triệu đồng, giá niêm yết của ti vi là 29 triệu đồng.
2) Giả sử theo kế hoạch mỗi ngày người đó trồng được số cây là: \(x\) (cây) (\(x > 6\)).
Trên thực tế mỗi ngày người đó trồng được số cây là: \(x - 6\) (cây)
Thời gian người đó trồng xong cây theo kế hoạch là: \(\frac{{216}}{x}\) (ngày).
Thời gian thực tế người đó trồng xong cây trên là: \(\frac{{216}}{{x - 6}}\) (ngày).
Vì thời gian trồng xong chậm 6 ngày so với dự kiến nên ta có phương trình: \(\frac{{216}}{{x - 6}} - \frac{{216}}{x} = 6\)
\(\frac{{216}}{{x - 6}} - \frac{{216}}{x} = 6\)
\(1296 = 6x(x - 6)\)
\(6{x^2} - 36x - 1296 = 0\)
Giải phương trình ta được \(x = 18\) hoặc \(x = - 12\) (loại).
Vậy theo kế hoạch người đó trồng \(18\) cây mỗi ngày.
3) Vì phương trình \({x^2} - 5x + k = 0\) có một nghiệm \({x_1} = \frac{{5 - \sqrt {13} }}{2}\) nên thay \({x_1} = \frac{{5 - \sqrt {13} }}{2}\) vào phương trình, ta được:
\(\begin{array}{l}{\left( {\frac{{5 - \sqrt {13} }}{2}} \right)^2} - 5\left( {\frac{{5 - \sqrt {13} }}{2}} \right) + k = 0\\\frac{{19 - 5\sqrt {13} }}{2} - \frac{{25 - 5\sqrt {13} }}{2} + k = 0\\\frac{{19 - 5\sqrt {13} - 25 + 5\sqrt {13} }}{2} + k = 0\\ - 3 + k = 0\\k = 3\end{array}\)
Do đó phương trình cần tìm là \({x^2} - 5x + 3 = 0\).
Theo định lí Viète ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 5\\{x_1}{x_2} = 3\end{array} \right.\)
Ta có: \(x_1^2{x_2} + {x_1}x_2^2 = {x_1}{x_2}\left( {{x_1} + {x_2}} \right) = 3.5 = 15\).
Câu 4:(4 điểm)
1) Một cái thùng dùng để đựng gạo có dạng nửa hình cầu với đường kính \(50cm\), phần gạo vun lên có dạng hình nón cao \(12cm\).
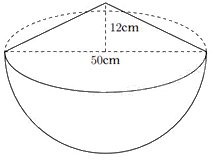
a) Tính thể tích phần gạo trong thùng.
b) Nhà bạn An dùng lon sữa bò dạng hình trụ với bán kính đáy là \(5cm\), chiều cao \(14cm\) dùng để đong gạo mỗi ngày. Biết rằng mỗi ngày nhà An ăn 4 lon gạo và mỗi lần đong thì lượng gạo chiếm \(90\% \) thể tích của lon. Hỏi cần ít nhất bao nhiêu ngày để nhà An có thể ăn hết số gạo trong thùng?
2) Cho đường tròn tâm \((O)\) và dây \(BC\) cố định không đi qua \(O\). Trên cung lớn \(BC\) lấy điểm \(A\) sao cho \(AB < AC\). Kẻ đường kính là hình chiếu của \(C\) trên \(AK\). \(M\) là trung điểm của \(BC\).
a) Chứng minh bốn \(C,\,E,\,\,M,\,O\) cùng thuộc một đường tròn.
b) Kẻ \(AD \bot BC\) tại \(D\). Chứng minh \(AD.AK = AB.AC\) và \(\Delta MDE\) cân.
c) Gọi \(F\) là hình chiếu của \(B\) trên \(AK\). Chứng minh khi di chuyển trên cung lớn \(BC\) thì tâm đường tròn ngoại tiếp \(\Delta DEF\) là 1 điểm cố định.
Phương pháp
1) a) Tính bán kính của hình cầu.
- Thể tích phần gạo nửa hình cầu = \(\frac{1}{2}\) thể tích hình cầu.
Thể tích hình cầu: \({V_c} = \frac{4}{3}\pi {R^3}\).
- Thể tích phần gạo hình nón tính bằng công thức tính thể tích hình nón: \({V_n} = \frac{1}{3}\pi {R^2}h\)
- Thể tích gạo = thể tích phần gạo nửa hình cầu + thể tích phần gạo hình nón.
b) Tính thể tích lon bằng thể tích hình trụ: \({V_t} = \pi {R^2}h\)
Tính thể tích gạo mỗi ngày múc = \(4.90\% .{V_t}\).
Lấy thể tích gạo : thể tích gạo mỗi ngày múc để xác định số ngày ít nhất để dùng hết số gạo trong thùng.
2) a) Chứng minh \(\Delta OMC\) và \(\Delta OEC\) lần lượt vuông tại M và E nên cùng nội tiếp đường tròn đường kính OC.
Gọi I là trung điểm của OC thì \(C,\,E,\,M,\,O\) cùng thuộc một đường tròn (I) đường kính OC (bán kính OI).
b) *Chứng minh \(AD.AK = AB.AC\)
Chứng minh $\Delta DBA\backsim \Delta CK\text{A}$ (g.g) suy ra \(\frac{{AD}}{{AB}} = \frac{{AC}}{{AK}}\) (cặp cạnh tương ứng tỉ lệ) nên \(AD.AK = AB.AC\).
*Chứng minh \(\Delta MDE\)cân.
Để chứng minh \(\Delta MDE\)cân ta chứng minh \(\widehat {MDE} = \widehat {MED}\).
- Lập luận \(\widehat {CAE} = \widehat {CDE}\) và \(\widehat {CBK} = \widehat {CAE}\) suy ra \(\widehat {CBK} = \widehat {CDE}\)
- Lập luận \(\widehat {EMC} = \widehat {EOC}\), \(\widehat {KBC} = \frac{1}{2}\widehat {KOC}\) suy ra \(\widehat {EMC} = 2\widehat {CDE}\)
- Sử dụng tính chất góc ngoài của tam giác \(\Delta MDE\) suy ra \(\widehat {EMC} = 2\widehat {MDE}\)
Do đó \(\widehat {MDE} = \widehat {MED}\).
c) Chứng minh \(\widehat {OBM} = \widehat {MFO}\) và \(\widehat {MEO} = \widehat {MCO}\), mà \(\widehat {OBM} = \widehat {OCM}\) suy ra \(\widehat {MFO} = \widehat {MEO}\).
Do đó \(\Delta EMF\) cân tại \(M\), nên \(ME = MF\).
Mà \(ME = MD\) nên \(MD = ME = MF\)
Suy ra \(M\) là tâm đường tròn ngoại tiếp tam giác \(DEF\).
Mà \(M\) là trung điểm của \(BC\) nên \(M\) là điểm cố định.
Lời giải
1) a) Bán kính của hình cầu là: \(R = \frac{d}{2} = \frac{{50}}{2} = 25{\kern 1pt} {\kern 1pt} \left( {cm} \right)\)
Thể tích phần gạo nửa hình cầu là: \({V_c} = \frac{1}{2} \cdot \frac{4}{3}\pi {R^3} = \frac{1}{2} \cdot \frac{4}{3}\pi {25^3} = \frac{{31{\kern 1pt} 250}}{3}\pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)
Thể tích phần gạo vun lên dạng hình nón là: \({V_n} = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi \cdot {25^2} \cdot 12 = 2500\pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)
Thể tích gạo trong thùng là: \({V_g} = \frac{{31{\kern 1pt} 250}}{3}\pi + 2500\pi = \frac{{38750}}{3}\pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)
b) Thể tích lon là: \(\pi {.5^2}.14 = 350{\kern 1pt} \pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)
Thể tích gạo một ngày múc là: \(4.90\% .350\pi = 1260\pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)
Ta có: \(\frac{{38{\kern 1pt} 750}}{\pi }:1{\kern 1pt} 260\pi \approx 10,3\)
Vậy cần ít nhất 11 ngày để dùng hết số gạo trong thùng.
2)
a) Chứng minh bốn \(C,\,E,\,M,\,O\) cùng thuộc một đường tròn.
\(\Delta OBC\) cân tại \(O\), \(M\) là trung điểm của \(BC\) nên \(OM\) vừa là đường trung tuyến vừa là đường cao. Suy ra \(OM \bot BC\) suy ra \(\widehat {OMC} = 90^\circ \).
Tam giác OMC vuông tại \(M\) nên tam giác OMC nội tiếp đường tròn đường kính OC.
Theo bài ra, \(E\) là hình chiếu của \(C\) trên \(AK\) nên \(CE \bot AK\) suy ra \(CE \bot EO\) hay \(\widehat {OEC} = 90^\circ \).
Tam giác OEC vuông tại E nên tam giác OEC nội tiếp đường tròn đường kính OC.
Gọi \(I\) là trung điểm của \(OC\)
Do đó \(C,\,E,\,M,\,O\) cùng thuộc một đường tròn (I) đường kính OC (bán kính OI).
b) *Chứng minh \(AD.AK = AB.AC\)
Xét \(\Delta DBA\) và \(\Delta CK{\rm{A}}\) có
\(\widehat {ADB} = \widehat {ACK} = 90^\circ \)
\(\widehat {ABD} = \widehat {AKC}\) (Hai góc nội tiếp cùng chắn cung )
Nên $\Delta DBA\backsim \Delta CK\text{A}$ (g.g)
Do đó ta có: \(\frac{{AD}}{{AB}} = \frac{{AC}}{{AK}}\) (cặp cạnh tương ứng tỉ lệ)
Hay \(AD.AK = AB.AC\) (đpcm).
*Chứng minh \(\Delta MDE\)cân.
Theo bài ra \(\left\{ \begin{array}{l}AD \bot BC\\AE \bot EC\end{array} \right.\) suy ra \(\left\{ \begin{array}{l}\widehat {ADC} = 90^\circ \\\widehat {AEC} = 90^\circ \end{array} \right.\)
Gọi \(Q\) là trung điểm của \(AC\)
Tam giác ADC và tam giác AEC vuông tại D và E nên nội tiếp đường tròn (Q; AC), suy ra \(QA = QC = QD = QE\)
Suy ra bốn điểm \(A,\,C,\,D,\,E\) cùng thuộc đường tròn \(\left( Q \right)\)
Suy ra \(\widehat {CAE} = \widehat {CDE}\) (Hai góc nội tiếp cùng chắn cung \(CE\)) (1)
Xét \(\left( O \right)\) ta có: \(\widehat {CBK} = \widehat {CAE}\) (Hai góc nội tiếp cùng chắn cung \(CK\) ) (2)
Từ (1) và (2) suy ra \(\widehat {CBK} = \widehat {CDE}\) mà hai góc này ở vị trí đồng vị (3)
Suy ra \(DE//BK\)
Xét đường tròn \(\left( I \right)\) có: \(\widehat {EMC} = \widehat {EOC}\) (Hai góc nội tiếp cùng chắn $\overset\frown{EC}$). (4)
Xét đường tròn \(\left( O \right)\) có: \(\widehat {KBC} = \frac{1}{2}\widehat {KOC}\) (Góc nội tiếp và góc ở tâm cùng chắn \(\overset\frown{KC}\)). (5)
Từ (3); (4) và (5) suy ra \(\widehat {EMC} = 2\widehat {CDE}\).
\(\Delta MDE\) có \(\widehat {EMC} = \widehat {MDE} + \widehat {MED}\) (góc ngoài của tam giác) mà \(\widehat {EMC} = 2\widehat {MDE}\)
Nên \(\widehat {MDE} = \widehat {MED}\). Do đó, \(\Delta MDE\) cân tại \(M\).
c) Gọi \(P\) là trung điểm của \(BO\)
Tam giác BFO và tam giác BMO vuông tại F và M nên nội tiếp đường tròn (P; OP) suy ra \(PB = PO = PF = PM\)
Suy ra bốn điểm \(O,M,B,F\) cùng thuộc đường tròn \(\left( P \right)\)
Nên \(\widehat {OBM} = \widehat {MFO}\) (Hai góc nội tiếp cùng chắn \(\overset\frown{MO}\)).
Xét đường tròn \(\left( I \right)\) có:
\(\widehat {MEO} = \widehat {MCO}\) (Hai góc nội tiếp cùng chắn \(\overset\frown{MO}\)).
Mà \(\widehat {OBM} = \widehat {OCM}\) (\(\Delta OCB\)cân tại \(O\)).
Do đó \(\widehat {MFO} = \widehat {MEO}\) suy ra \(\Delta EMF\) cân tại \(M\), do đó \(ME = MF\).
Mà \(ME = MD\) (Tam giác \(MDE\) cân tại \(M\)).
Suy ra \(MD = ME = MF\).
Suy ra \(M\) là tâm đường tròn ngoại tiếp tam giác \(DEF\).
Mà \(M\) là trung điểm của \(BC\) nên \(M\) là điểm cố định.
Vậy khi \(A\) di chuyển trên cung lớn \(BC\) thì tâm đường tròn ngoại tiếp tam giác \(DEF\) là một điểm cố định.
Câu 5:(0,5 điểm)
Bác An muốn đặt đóng một chiếc hộp đựng quà lưu niệm có dạng hình hộp chữ nhật với mặt đáy \(ABCD\) là hình vuông như hình dưới đây.
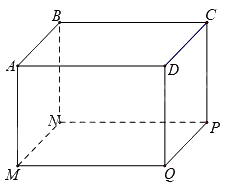
Để món quà trở nên đặc biệt, bác An muốn mạ bốn mặt xung quanh và mặt đáy dưới (mặt \(MNPQ\)) của chiếc hộp bằng kim loại quý (không mạ nắp hộp). Em hãy tìm độ dài cạnh \(MN\) của mặt đáy và chiều cao \(AM\) của hộp quà sao cho tổng diện tích các mặt được mạ kim loại quý của chiếc hộp là nhỏ nhất biết rằng thể tích của chiếc hộp là \(4d{m^3}\).
Phương pháp
Gọi độ dài cạnh \(MN\) là \(x\left( {dm} \right)\) (\(x > 0\))
Gọi độ dài chiều cao \(AM\) là \(h\left( {dm} \right)\) (\(h > 0\))
Biểu diễn \(h\) theo \(x\) dựa vào thể tích của chiếc hộp.
Tính diện tích cần mạ kim loại = diện tích bốn mặt xung quanh và diện tích mặt đáy dưới.
Biến đổi biểu thức bằng cách sử dụng hằng đẳng thức bình phương của một hiệu kết hợp nhóm hạng tử sau đó sử dụng bất đẳng thức Cô – si để tìm giá trị nhỏ nhất của S.
Từ đó tính được \(x,h\).
Lời giải
Gọi độ dài cạnh \(MN\) là \(x\left( {dm} \right)\)(\(x > 0\))
Gọi độ dài chiều cao \(AM\) là \(h\left( {dm} \right)\)(\(h > 0\))
Do thể tích của chiếc hộp là 4dm3 nên ta có: \({x^2}h = 4\)
Suy ra \(h = \frac{4}{{{x^2}}}\)
Diện tích cần mạ kim loại quý của chiếc hộp là:
\(\begin{array}{l}S = {x^2} + 4xh = {x^2} + 4x.\frac{4}{{{x^2}}} = {x^2} + \frac{{16}}{x}\\\,\,\,\, = \left( {{x^2} - 4x + 4} \right) + \left( {4x + \frac{{16}}{x}} \right) - 4 = {\left( {x - 2} \right)^2} + \left( {4x + \frac{{16}}{x}} \right) - 4\end{array}\)
Chứng minh bất đẳng thức Cô – si.
Áp dụng bất đẳng thức Cô – si cho 2 số \(4x > 0\) và \(\frac{{16}}{x} > 0\) và \({\left( {x - 2} \right)^2} \ge 0\) ta có:
\(S \ge 0 + 2\sqrt {4x.\frac{{16}}{{4x}}} - 4 = 0 + 2.8 - 4 = 12\)
Dấu “=” xảy ra khi \(\left\{ \begin{array}{l}x - 2 = 0\\4x = \frac{{16}}{{4x}}\end{array} \right.\)
Ta giải ra được \(x = 2\) từ đó suy ra \(h = \frac{4}{{{2^2}}} = 1\)
Vậy khi độ dài cạnh đáy \(MN = 2dm\) và chiều cao \(AM = 1dm\) thì diện tích cần mạ kim loại quý của chiếc hộp là nhỏ nhất bằng \(12d{m^2}\).
Kỳ thi tuyển sinh vào lớp 10 THPT tại Hà Nội là một bước ngoặt quan trọng trong sự nghiệp học tập của mỗi học sinh. Để chuẩn bị tốt nhất cho kỳ thi này, việc luyện tập với các đề tham khảo là vô cùng cần thiết. Đề tham khảo thi vào 10 môn Toán Hà Nội năm 2025 - Đề số 1 do giaitoan.edu.vn cung cấp là một công cụ hữu ích giúp học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và đánh giá năng lực bản thân.
Đề thi vào 10 môn Toán Hà Nội thường bao gồm các dạng bài tập sau:
Đề số 1 này bao gồm đầy đủ các dạng bài tập trên, được sắp xếp theo mức độ khó tăng dần, giúp học sinh có thể làm quen với các dạng bài tập cơ bản trước khi chuyển sang các bài tập nâng cao.
Để giúp học sinh hiểu rõ hơn về cách giải các bài tập trong đề, giaitoan.edu.vn cung cấp hướng dẫn giải chi tiết cho từng bài tập. Hướng dẫn giải bao gồm các bước giải cụ thể, các công thức và định lý được sử dụng, và các lưu ý quan trọng khi giải bài tập.
Giả sử đề bài yêu cầu giải phương trình: x2 - 5x + 6 = 0
Luyện tập với đề tham khảo thi vào 10 môn Toán Hà Nội năm 2025 - Đề số 1 mang lại nhiều lợi ích cho học sinh:
Để đạt hiệu quả tốt nhất khi luyện tập với đề tham khảo, học sinh nên:
Giaitoan.edu.vn cam kết cung cấp cho học sinh những đề thi tham khảo chất lượng, bài giảng online hấp dẫn và tài liệu học tập hữu ích. Chúng tôi luôn đồng hành cùng học sinh trên con đường chinh phục kỳ thi vào 10 và đạt được ước mơ của mình.
| Dạng bài tập | Tỷ lệ xuất hiện | Mức độ khó |
|---|---|---|
| Phương trình bậc hai | 20% | Trung bình |
| Hình học không gian | 15% | Khó |
| Bất phương trình | 10% | Trung bình |
| Lưu ý: Tỷ lệ xuất hiện và mức độ khó có thể thay đổi tùy theo từng đề thi. | ||