Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Ninh Thuận năm 2021 chính thức. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi sắp tới.
Bộ đề thi này bao gồm các đề thi chính thức của các trường THCS trên địa bàn tỉnh Ninh Thuận, được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm. Các em có thể sử dụng bộ đề này để tự đánh giá năng lực, tìm ra những điểm yếu và tập trung ôn tập.
Bài 1 (2,0 điểm): Giải các phương trình, hệ phương trình:
Bài 1 (2,0 điểm):Giải các phương trình, hệ phương trình:
1) \(2x - 1 = x - \dfrac{1}{3}\) 2) \(\left\{ \begin{array}{l}3x + y = 4\\7x - 5y = - 9\end{array} \right.\)
Bài 2 (2,0 điểm):
1) Vẽ đồ thị \(\left( P \right)\) của hàm số \(y = - \dfrac{1}{4}{x^2}.\)
2) Tìm điều kiện của \(m\) đề đường thẳng \(\left( d \right):\,\,y = - x + m\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ trái dấu.
Bài 3 (2,0 điểm):Bạn Hoàng làm việc tại nhà hàng nọ, bạn ấy được trả tám trăm ngàn đồng cho 40 giờ làm việc tại quán trong một tuần. Mỗi giờ làm thêm trong tuần bạn được trả bằng 150% số tiền mà mỗi giờ bạn ấy được trả trong 40 giờ đầu. Nếu trong tuần đó bạn Hoàng được trả chín trăm hai mươi nghìn đồng thì bạn ấy đã phải làm thêm bao nhiêu giờ?
Bài 4 (4 điểm):Cho tam giác \(ABC\) có các góc \(\angle ABC,\,\,\angle ACB\) nhọn và \(\angle BAC = {60^0}.\) Các đường phân giác trong \(BE,\,\,CF\) của \(\Delta ABC\) cắt nhau tại \(I.\)
1) Chứng minh tứ giác \(AEIF\) nội tiếp.
2) Gọi \(K\) là giao điểm thứ hai \(\left( {K \ne B} \right)\) của đường thẳng \(BC\) với đường tròn ngoại tiếp tam giác \(BFI.\) Chứng minh rằng \(\Delta AFK\) cân tại F.
Bài 1 (2,0 điểm):Giải các phương trình, hệ phương trình:
1) \(2x - 1 = x - \dfrac{1}{3}\) 2) \(\left\{ \begin{array}{l}3x + y = 4\\7x - 5y = - 9\end{array} \right.\)
Bài 2 (2,0 điểm):
1) Vẽ đồ thị \(\left( P \right)\) của hàm số \(y = - \dfrac{1}{4}{x^2}.\)
2) Tìm điều kiện của \(m\) đề đường thẳng \(\left( d \right):\,\,y = - x + m\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ trái dấu.
Bài 3 (2,0 điểm):Bạn Hoàng làm việc tại nhà hàng nọ, bạn ấy được trả tám trăm ngàn đồng cho 40 giờ làm việc tại quán trong một tuần. Mỗi giờ làm thêm trong tuần bạn được trả bằng 150% số tiền mà mỗi giờ bạn ấy được trả trong 40 giờ đầu. Nếu trong tuần đó bạn Hoàng được trả chín trăm hai mươi nghìn đồng thì bạn ấy đã phải làm thêm bao nhiêu giờ?
Bài 4 (4 điểm):Cho tam giác \(ABC\) có các góc \(\angle ABC,\,\,\angle ACB\) nhọn và \(\angle BAC = {60^0}.\) Các đường phân giác trong \(BE,\,\,CF\) của \(\Delta ABC\) cắt nhau tại \(I.\)
1) Chứng minh tứ giác \(AEIF\) nội tiếp.
2) Gọi \(K\) là giao điểm thứ hai \(\left( {K \ne B} \right)\) của đường thẳng \(BC\) với đường tròn ngoại tiếp tam giác \(BFI.\) Chứng minh rằng \(\Delta AFK\) cân tại F.
Bài 1 (TH):
Phương pháp:
1) Đưa phương trình ban đầu về dạng \(ax + b = 0\) để tìm nghiệm của phương trình.
2) Vận dụng phương pháp cộng đại số để tìm nghiệm của hệ phương trình.
Cách giải:
1) \(2x - 1 = x - \dfrac{1}{3}\)
\(\begin{array}{l} \Leftrightarrow 2x - x = - \dfrac{1}{3} + 1\\ \Leftrightarrow x = \dfrac{2}{3}\end{array}\)
Vậy phương trình có nghiệm \(x = \dfrac{2}{3}\).
2) \(\left\{ \begin{array}{l}3x + y = 4\\7x - 5y = - 9\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}15x + 5y = 20\\7x - 5y = - 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}22x = 11\\y = 4 - 3x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{1}{2}\\y = 4 - \dfrac{3}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{1}{2}\\y = \dfrac{5}{2}\end{array} \right.\)
Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {\dfrac{1}{2};\dfrac{5}{2}} \right)\).
Bài 2 (VD):
Phương pháp:
1) Lập bảng giá trị tương ứng của \(x\) và \(y\) sau đó vẽ đồ thị hàm số của hàm số \(\left( P \right)\).
2) Xét phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\)
\(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ trái dấu \( \Leftrightarrow \) phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) có hai nghiệm trái dấu \( \Leftrightarrow ac < 0\)
Cách giải:
1) Ta có bảng giá trị:
\(x\) | \( - 4\) | \( - 2\) | \(0\) | \(2\) | \(4\) |
\(y = - \dfrac{1}{4}{x^2}\) | \( - 4\) | \( - 1\) | \(0\) | \( - 1\) | \( - 4\) |
Vậy đồ thị hàm số \(\left( P \right):\,\,y = - \dfrac{1}{4}{x^2}\) là đường cong đi qua các điểm: \(\left( { - 4;\,\, - 4} \right),\,\,\left( { - 2;\,\, - 1} \right),\,\,\left( {0;\,\,0} \right),\,\,\left( {2;\,\, - 1} \right)\) và \(\left( {4;\,\, - 4} \right).\)
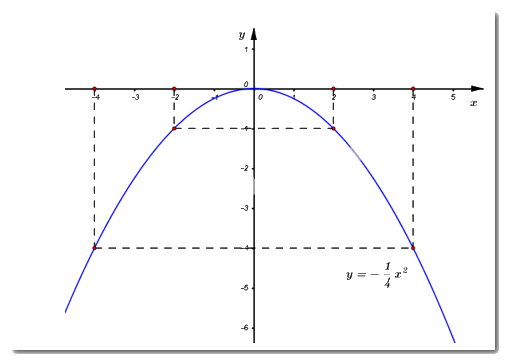
2) Phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right):\)
\( - \dfrac{1}{4}{x^2} = - x + m\) \( \Leftrightarrow {x^2} - 4x + 4m = 0\,\,\,\left( * \right)\)
\(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ trái dấu \( \Leftrightarrow \left( * \right)\) có hai nghiệm trái dấu \( \Leftrightarrow 1.4m < 0 \Leftrightarrow m < 0.\)
Vậy \(m < 0\) thỏa mãn bài toán.
Bài 3 (VD):
Phương pháp:
Giải bài toán bằng cách lập phương trình,cụ thể gọi số giờ bạn Hoàng đã làm thêm trong tuần là \(x\) (giờ) (ĐK: \(x > 0\)), từ giả thiết của đề bài lập phương trình, giải phương trình sau đó đối chiếu điều kiện và kết luận.
Cách giải:
Gọi số giờ bạn Hoàng đã làm thêm trong tuần là \(x\) (giờ) (ĐK: \(x > 0\)).
Bạn Hoàng được trả 800 nghìn đồng cho 40 giờ làm việc trong tuần nên mỗi giờ làm việc trong tuần bạn Hoàng nhận được \(\dfrac{{800}}{{40}} = 20\) (nghìn đồng).
Vì mỗi giờ làm thêm trong tuần Hoàng được trả bằng 150% số tiền mà mỗi giờ bạn ấy được trả trong 40 giờ đầu tiên nên mỗi giờ làm thêm trong tuần Hoàng nhận được \(20.150\% = 30\) (nghìn đồng).
Suy ra tổng số tiền Hoàng nhận được (tính cả làm thêm) trong mỗi tuần là: \(800 + 30x\) (nghìn đồng).
Vì trong tuần đó bạn Hoàng được trả chín trăm hai mươi nghìn đồng nên ta có phương trình
\(800 + 3x = 920 \Leftrightarrow 3x = 120 \Leftrightarrow x = 4\) (thỏa mãn).
Vậy Hoàng đã làm thêm 4 giờ.
Bài 4 (VDC):
Phương pháp:
1) Vận dụng dấu hiệu nhận biết của tứ giác nội tiếp: tứ giác có tổng hai góc đối diện bẳng \({180^0}\) là tứ giác nội tiếp.
2) Vận dụng tính chất của tứ giác nội tiếp, mối quan hệ của góc – đường tròn.
Cách giải:
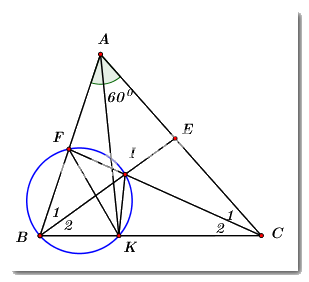
1) Ta có: \(\angle BAC = {60^0}\)
\( \Rightarrow \angle ABC + \angle BCA = {120^0}\) (tổng ba góc trong tam giác bằng \({180^0}\))
\(\begin{array}{l} \Rightarrow \dfrac{1}{2}\left( {\angle ABC + \angle BCA} \right) = {60^0}\\ \Leftrightarrow \angle {B_2} + \angle {C_2} = {60^0}\end{array}\)
\( \Rightarrow \angle BIC = {180^0} - \left( {\angle {B_2} + {C_2}} \right) = {120^0}\) (tổng ba góc trong tam giác bằng \({180^0}\))
\( \Rightarrow \angle FIE = \angle BIC = {120^0}\) (hai góc đối đỉnh)
Xét tứ giác \(AEIF\) ta có:
\(\angle BAC + \angle EIF = {60^0} + {120^0} = {180^0}\)
\( \Rightarrow AEIF\) là tứ giác nội tiếp. (tứ giác có tổng hai góc đối diện bẳng \({180^0}\))
2) Ta có: Tứ giác \(BFIK\) nội tiếp \( \Rightarrow \angle FKB = \angle FIB\) (hai góc nội tiếp cùng chắn cung \(BF\))
\(\begin{array}{l} \Rightarrow \angle FKB = \angle FIB = {180^0} - \angle EIB = {60^0}\\ \Rightarrow \angle FAC = \angle FKB = {60^0}\end{array}\)
\( \Rightarrow AFKC\) là tứ giác nội tiếp. (tứ giác có hai đỉnh kề 1 cạnh nhìn cạnh đối diện dưới các góc bằng nhau).
\( \Rightarrow \angle FAK = FCK\) (hai góc nội tiếp cùng chắn cung \(FK\))
Và \(\angle FKA = \angle FCA\) (hai góc nội tiếp cùng chắn cung \(AF\))
Mà \(\angle FCA = \angle FCK\) (\(CF\) là phân giác góc \(\angle KCA\))
\( \Rightarrow \angle FAK = \angle FKA\,\,\left( { = \angle FCA} \right)\)
\( \Rightarrow \Delta AKF\) cân tại \(F\) (đpcm).
Bài 1 (TH):
Phương pháp:
1) Đưa phương trình ban đầu về dạng \(ax + b = 0\) để tìm nghiệm của phương trình.
2) Vận dụng phương pháp cộng đại số để tìm nghiệm của hệ phương trình.
Cách giải:
1) \(2x - 1 = x - \dfrac{1}{3}\)
\(\begin{array}{l} \Leftrightarrow 2x - x = - \dfrac{1}{3} + 1\\ \Leftrightarrow x = \dfrac{2}{3}\end{array}\)
Vậy phương trình có nghiệm \(x = \dfrac{2}{3}\).
2) \(\left\{ \begin{array}{l}3x + y = 4\\7x - 5y = - 9\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}15x + 5y = 20\\7x - 5y = - 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}22x = 11\\y = 4 - 3x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{1}{2}\\y = 4 - \dfrac{3}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{1}{2}\\y = \dfrac{5}{2}\end{array} \right.\)
Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {\dfrac{1}{2};\dfrac{5}{2}} \right)\).
Bài 2 (VD):
Phương pháp:
1) Lập bảng giá trị tương ứng của \(x\) và \(y\) sau đó vẽ đồ thị hàm số của hàm số \(\left( P \right)\).
2) Xét phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\)
\(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ trái dấu \( \Leftrightarrow \) phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) có hai nghiệm trái dấu \( \Leftrightarrow ac < 0\)
Cách giải:
1) Ta có bảng giá trị:
\(x\) | \( - 4\) | \( - 2\) | \(0\) | \(2\) | \(4\) |
\(y = - \dfrac{1}{4}{x^2}\) | \( - 4\) | \( - 1\) | \(0\) | \( - 1\) | \( - 4\) |
Vậy đồ thị hàm số \(\left( P \right):\,\,y = - \dfrac{1}{4}{x^2}\) là đường cong đi qua các điểm: \(\left( { - 4;\,\, - 4} \right),\,\,\left( { - 2;\,\, - 1} \right),\,\,\left( {0;\,\,0} \right),\,\,\left( {2;\,\, - 1} \right)\) và \(\left( {4;\,\, - 4} \right).\)
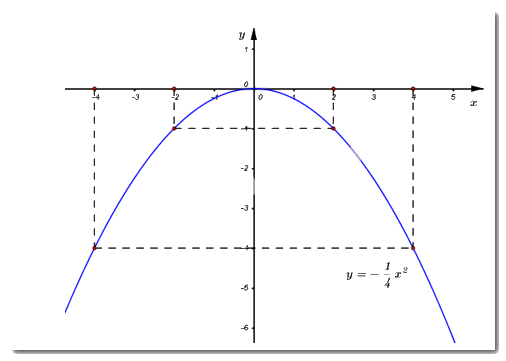
2) Phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right):\)
\( - \dfrac{1}{4}{x^2} = - x + m\) \( \Leftrightarrow {x^2} - 4x + 4m = 0\,\,\,\left( * \right)\)
\(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ trái dấu \( \Leftrightarrow \left( * \right)\) có hai nghiệm trái dấu \( \Leftrightarrow 1.4m < 0 \Leftrightarrow m < 0.\)
Vậy \(m < 0\) thỏa mãn bài toán.
Bài 3 (VD):
Phương pháp:
Giải bài toán bằng cách lập phương trình,cụ thể gọi số giờ bạn Hoàng đã làm thêm trong tuần là \(x\) (giờ) (ĐK: \(x > 0\)), từ giả thiết của đề bài lập phương trình, giải phương trình sau đó đối chiếu điều kiện và kết luận.
Cách giải:
Gọi số giờ bạn Hoàng đã làm thêm trong tuần là \(x\) (giờ) (ĐK: \(x > 0\)).
Bạn Hoàng được trả 800 nghìn đồng cho 40 giờ làm việc trong tuần nên mỗi giờ làm việc trong tuần bạn Hoàng nhận được \(\dfrac{{800}}{{40}} = 20\) (nghìn đồng).
Vì mỗi giờ làm thêm trong tuần Hoàng được trả bằng 150% số tiền mà mỗi giờ bạn ấy được trả trong 40 giờ đầu tiên nên mỗi giờ làm thêm trong tuần Hoàng nhận được \(20.150\% = 30\) (nghìn đồng).
Suy ra tổng số tiền Hoàng nhận được (tính cả làm thêm) trong mỗi tuần là: \(800 + 30x\) (nghìn đồng).
Vì trong tuần đó bạn Hoàng được trả chín trăm hai mươi nghìn đồng nên ta có phương trình
\(800 + 3x = 920 \Leftrightarrow 3x = 120 \Leftrightarrow x = 4\) (thỏa mãn).
Vậy Hoàng đã làm thêm 4 giờ.
Bài 4 (VDC):
Phương pháp:
1) Vận dụng dấu hiệu nhận biết của tứ giác nội tiếp: tứ giác có tổng hai góc đối diện bẳng \({180^0}\) là tứ giác nội tiếp.
2) Vận dụng tính chất của tứ giác nội tiếp, mối quan hệ của góc – đường tròn.
Cách giải:
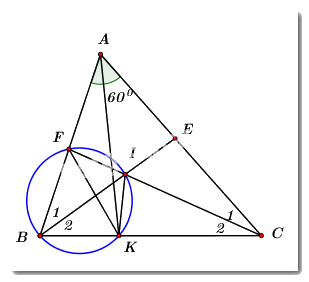
1) Ta có: \(\angle BAC = {60^0}\)
\( \Rightarrow \angle ABC + \angle BCA = {120^0}\) (tổng ba góc trong tam giác bằng \({180^0}\))
\(\begin{array}{l} \Rightarrow \dfrac{1}{2}\left( {\angle ABC + \angle BCA} \right) = {60^0}\\ \Leftrightarrow \angle {B_2} + \angle {C_2} = {60^0}\end{array}\)
\( \Rightarrow \angle BIC = {180^0} - \left( {\angle {B_2} + {C_2}} \right) = {120^0}\) (tổng ba góc trong tam giác bằng \({180^0}\))
\( \Rightarrow \angle FIE = \angle BIC = {120^0}\) (hai góc đối đỉnh)
Xét tứ giác \(AEIF\) ta có:
\(\angle BAC + \angle EIF = {60^0} + {120^0} = {180^0}\)
\( \Rightarrow AEIF\) là tứ giác nội tiếp. (tứ giác có tổng hai góc đối diện bẳng \({180^0}\))
2) Ta có: Tứ giác \(BFIK\) nội tiếp \( \Rightarrow \angle FKB = \angle FIB\) (hai góc nội tiếp cùng chắn cung \(BF\))
\(\begin{array}{l} \Rightarrow \angle FKB = \angle FIB = {180^0} - \angle EIB = {60^0}\\ \Rightarrow \angle FAC = \angle FKB = {60^0}\end{array}\)
\( \Rightarrow AFKC\) là tứ giác nội tiếp. (tứ giác có hai đỉnh kề 1 cạnh nhìn cạnh đối diện dưới các góc bằng nhau).
\( \Rightarrow \angle FAK = FCK\) (hai góc nội tiếp cùng chắn cung \(FK\))
Và \(\angle FKA = \angle FCA\) (hai góc nội tiếp cùng chắn cung \(AF\))
Mà \(\angle FCA = \angle FCK\) (\(CF\) là phân giác góc \(\angle KCA\))
\( \Rightarrow \angle FAK = \angle FKA\,\,\left( { = \angle FCA} \right)\)
\( \Rightarrow \Delta AKF\) cân tại \(F\) (đpcm).
Kỳ thi tuyển sinh vào lớp 10 là một bước ngoặt quan trọng trong quá trình học tập của mỗi học sinh. Để đạt kết quả tốt nhất, việc chuẩn bị kỹ lưỡng là vô cùng cần thiết. Trong đó, việc làm quen với cấu trúc đề thi và luyện tập giải các đề thi thử, đề thi chính thức các năm trước đóng vai trò then chốt. Bài viết này sẽ cung cấp phân tích chi tiết về Đề thi vào 10 môn Toán Ninh Thuận năm 2021, cùng với hướng dẫn giải các bài toán thường gặp, giúp các em học sinh tự tin hơn khi bước vào kỳ thi.
Đề thi vào 10 môn Toán Ninh Thuận năm 2021 thường có cấu trúc tương đối ổn định qua các năm. Đề thi thường bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Phương trình bậc hai là một chủ đề thường xuyên xuất hiện trong đề thi vào 10. Để giải phương trình bậc hai, các em cần nắm vững công thức nghiệm và các điều kiện để phương trình có nghiệm. Ví dụ:
Giải phương trình: 2x2 - 5x + 2 = 0
Δ = (-5)2 - 4 * 2 * 2 = 25 - 16 = 9
x1 = (5 + √9) / (2 * 2) = 2
x2 = (5 - √9) / (2 * 2) = 0.5
Các bài toán chứng minh đẳng thức hình học đòi hỏi các em phải nắm vững các định lý và tính chất của hình học. Ví dụ:
Cho tam giác ABC vuông tại A, có đường cao AH. Chứng minh rằng: AH2 = BH * CH
Chứng minh:
Xét tam giác ABC vuông tại A, có đường cao AH. Ta có:
SABC = 1/2 * AB * AC = 1/2 * BC * AH
=> AB * AC = BC * AH
Xét tam giác AHB vuông tại H, ta có: AB2 = AH2 + BH2
Xét tam giác AHC vuông tại H, ta có: AC2 = AH2 + CH2
=> AB2 + AC2 = 2AH2 + BH2 + CH2
Mà AB2 + AC2 = BC2 (định lý Pitago)
=> BC2 = 2AH2 + BH2 + CH2
=> (BH + CH)2 = 2AH2 + BH2 + CH2
=> BH2 + 2BH * CH + CH2 = 2AH2 + BH2 + CH2
=> 2BH * CH = 2AH2
=> AH2 = BH * CH (đpcm)
Ngoài việc luyện tập các đề thi, các em nên tham khảo thêm các tài liệu ôn thi sau:
Đề thi vào 10 môn Toán Ninh Thuận năm 2021 là một tài liệu quan trọng giúp các em học sinh chuẩn bị tốt nhất cho kỳ thi sắp tới. Hy vọng với những phân tích và hướng dẫn giải trong bài viết này, các em sẽ tự tin hơn và đạt kết quả tốt nhất.