Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Sơn La năm 2023. Đây là tài liệu ôn tập vô cùng quan trọng dành cho các em học sinh đang chuẩn bị cho kỳ thi sắp tới.
Chúng tôi cung cấp đầy đủ các đề thi chính thức, đáp án chi tiết và phương pháp giải bài tập hiệu quả. Hãy cùng giaitoan.edu.vn chinh phục kỳ thi vào 10 môn Toán Sơn La một cách tự tin nhất!
Phần I: Trắc nghiệm (2 điểm) Câu 1: Căn bậc ba của -27 là A. -9 B. -3 C. 9 D. 3
Phần I: Trắc nghiệm (2 điểm)
Câu 1: Căn bậc ba của -27 là
A. -9
B. -3
C. 9
D. 3
Câu 2: Tất cả các giá trị của \(x\) để biểu thức \(P = \sqrt {x - 2} \) có nghĩa là
A. \(x = 2\).
B. \(x \ge 2\).
C. \(x \le 2\).
D. \(x > 2\).
Câu 3: Hàm số \(y = mx - 2\) đồng biến trên \(\mathbb{R}\) khi
A. \(m > 0\).
B. \(m < 0\).
C. \(m = 0\).
D. \(m \ne 0\).
Câu 4: Đồ thị hàm số \(y = 3{x^2}\) đi qua điểm nào dưới đây?
A. \(M\left( {0;0} \right)\).
B. \(N\left( {1;6} \right)\).
C. \(P\left( {1;1} \right)\).
D. \(Q\left( {0;3} \right)\).
Câu 5: Nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x - y = 4}\\{x + 2y = {\rm{ \;}} - 5}\end{array}} \right.\) là
A. \(\left( {1;4} \right)\).
B. \(\left( {1;3} \right)\).
C. \(\left( {1; - 3} \right)\).
D. \(\left( {3;1} \right)\).
Câu 6: Nếu phương trình \(a{x^2} + bx + c = 0\) với \(a \ne 0\) có hai nghiệm \({x_1}\) và \({x_2}\), thì tích \({x_1}{x_2}\) bằng
A. \( - \frac{c}{a}\).
B. \(\frac{b}{a}\).
C. \(\frac{c}{a}\).
D. \( - \frac{b}{a}\).
Câu 7: Cho tam giác ABC vuông tại \(A\) (tham khảo hình vẽ). Khẳng định nào sau đây đúng?
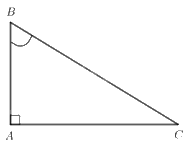
A. \({\rm{cos}}B = \frac{{AC}}{{AB}}\).
B. \({\rm{cos}}B = \frac{{AC}}{{BC}}\).
C. \({\rm{cos}}B = \frac{{AB}}{{AC}}\).
D. \({\rm{cos}}B = \frac{{AB}}{{BC}}\).
Câu 8: Cho đường tròn \(\left( {O;R} \right)\) và đường thẳng \(d\). Gọi \(H\) là hình chiếu vuông góc của \(O\) trên đường thẳng \(d\) (tham khảo hình vẽ). Đường thẳng \(d\) cắt \(\left( {O;R} \right)\) tại hai điểm phân biệt A, B khi
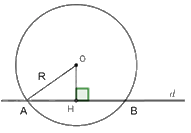
A. \(OH < R\).
B. \(OH = R\).
C. \(OH > R\).
D. \(OH \le R\).
Câu 9: Số đo góc nội tiếp chắn cung \(150^\circ \) bằng
A. \(150^\circ \).
B. \(65^\circ \).
C. \(50^\circ \).
D. \(75^\circ \).
Câu 10: Công thức tính diện tích của hình cầu có bán kính \(R\) là
A. \(S = 4\pi R\).
B. \(S = 4\pi {R^2}\).
C. \(S = \pi {R^2}\).
D. \(S = 3\pi {R^2}\).
Phần II. Tự luận (8 điểm)
Câu 11: Giải các phương trình và hệ phương trình sau:
a)\(2x - 8 = 0\)
b)\({x^2} + 4x + 3 = 0\)
c) \(\left\{ {\begin{array}{*{20}{l}}{x - 2y = 1}\\{3x + 2y = 11}\end{array}} \right.\)
Câu 12:
a) Tính giá trị của biểu thức: \(B = \sqrt {36} {\rm{ \;}} + \sqrt 4 {\rm{ \;}} - \sqrt {25} \).
b) Vẽ đồ thị hàm số: \(y = 3x - 6\).
Câu 13: Cho phương trình \({x^2} - 2(m - 1)x + {m^2} - 3 = 0\) (m là tham số). Tìm m để phương trình đã cho có 2 nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \({x_1} + {x_2} = {x_1}{x_2} - 2\)
Câu 14: Ông Nam sở hữu một mảnh đất hình chữ nhật có chu vi là 60m. Ông Nam định bán mảnh đất đó với giá thị trường là 8 triệu đồng cho một mét vuông. Hãy tính giá tiền của mảnh đất đó biết rằng mảnh đất có chiều dài gấp 2 lần chiều rộng.
Câu 15: Cho đường tròn tâm O đường kính AB. Trên đường tròn (O) lấy điểm C không trùng B sao cho AC > BC. Các tiếp tuyến của đường tròn (O) tại A và C cắt nhau tại D. Gọi H là hình chiếu vuông góc của C trên AB, E là giao điểm của hai đường thẳng OD và AC.
a) Chứng minh tứ giác AOCD nội tiếp.
b) Gọi F là giao điểm của hai đường thẳng CD và AB. Chứng minh CB là tia phân giác của góc HCF.
c) Chứng minh \(AO.AH = 2A{E^2}\)
d) Gọi M là giao điểm của hai đường thẳng BD và CH. Chứng minh M là trung điểm của CH.
Câu 16: Giải hệ phương trình\(\left\{ {\begin{array}{*{20}{l}}{{x^2}\left( {1 + \frac{4}{{{y^2}}}} \right) = 12}\\{2\sqrt {x + 3y + 2} {\rm{ \;}} = 3\sqrt y {\rm{ \;}} + \sqrt {x + 2} }\end{array}} \right.\)
-----HẾT-----
Phần I: Trắc nghiệm
1.B | 2.B | 3.A | 4.A | 5.C | 6.C | 7.D | 8.A | 9.D | 10.B |
Câu 1 (NB):
Phương pháp:
Căn bậc ba của x là số a, sao cho \({a^3} = x\)
Cách giải:
Căn bậc ba của -27 là -3 vì \({( - 3)^3} = - 27\)
Chọn B.
Câu 2 (NB):
Phương pháp:
\(\sqrt {f(x)} \) có nghĩa khi \(f(x) \ge 0\)
Cách giải:
\(P = \sqrt {x - 2} \) có nghĩa khi \(x - 2 \ge 0 \Leftrightarrow x \ge 2\)
Chọn B.
Câu 3 (NB):
Phương pháp:
Hàm số \(y = ax + b(a \ne 0)\) đồng biến trên R khi a > 0.
Cách giải:
Hàm số \(y = mx - 2\) đồng biến trên \(\mathbb{R}\) khi \(m > 0\)
Chọn A.
Câu 4 (NB):
Phương pháp:
Điểm \(A({x_0};{y_0})\) đi qua đồ thị hàm số \(y = a{x^2}(a \ne 0)\) khi \({y_0} = a.{x_0}^2\)
Cách giải:
Đồ thị hàm số \(y = 3{x^2}\) đi qua điểm \(M\left( {0;0} \right)\)
Chọn A.
Câu 5 (NB):
Phương pháp:
Giải hệ phương trình bằng phương pháp cộng đại số.
Cách giải:
\(\left\{ {\begin{array}{*{20}{l}}{x - y = 4}\\{x + 2y = {\rm{ \;}} - 5}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3y = {\rm{ \;}} - 9}\\{x = 4 + y}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = {\rm{ \;}} - 3}\\{x = 4 - 3 = 1}\end{array}} \right.\)
Vậy hệ phương trình có nghiệm \(\left( {1; - 3} \right)\)
Chọn C.
Câu 6 (NB):
Phương pháp:
Hệ thức Vi-ét \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{{ - b}}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\)
Cách giải:
Nếu phương trình \(a{x^2} + bx + c = 0\) với \(a \ne 0\) có hai nghiệm \({x_1}\) và \({x_2}\), thì tích \({x_1}{x_2}\) bằng \(\frac{c}{a}\)
Chọn C.
Câu 7 (NB):
Phương pháp:
Công thức góc lượng giác: tam giác ABC vuông tại \(A\) có \({\rm{cos}}B = \frac{{AB}}{{BC}}\)
Cách giải:
Tam giác ABC vuông tại \(A\) có \({\rm{cos}}B = \frac{{AB}}{{BC}}\)
Chọn D.
Câu 8 (NB):
Phương pháp:
Vị trí tương đối của đường thẳng và đườn tròn:
Đường thẳng \(d\) cắt \(\left( {O;R} \right)\) tại hai điểm phân biệt A, B khi \(OH < R\)
Cách giải:
Đường thẳng \(d\) cắt \(\left( {O;R} \right)\) tại hai điểm phân biệt A, B khi \(OH < R\)
Chọn A.
Câu 9 (NB):
Phương pháp:
Góc nội tiếp bằng một nửa số đo cung bị chắn.
Cách giải:
Số đo góc nội tiếp chắn cung \(150^\circ \) bằng \(75^\circ \)
Chọn D.
Câu 10 (NB):
Phương pháp:
Công thức tính diện tích của hình cầu có bán kính \(R\) là \(S = 4\pi {R^2}\)
Cách giải:
Công thức tính diện tích của hình cầu có bán kính \(R\) là \(S = 4\pi {R^2}\)
Chọn B.
Phần II: Tự luận
Câu 11 (TH):
Phương pháp:
a) Giải phương trình bậc nhất \(ax + b = 0(a \ne 0)\) có nghiệm là \(x = \frac{{ - b}}{a}\)
b) Giải phương trình bậc hai một ẩn bằng cách nhẩm nghiệm \(a - b + c = 0\).
Suy ra PT có nghiệm \(\left[ {\begin{array}{*{20}{l}}{{x_1} = {\rm{ \;}} - 1}\\{{x_2} = \frac{{ - c}}{a}}\end{array}} \right.\)
Cách giải:
a) \(2x - 8 = 0 \Leftrightarrow 2x = 8 \Leftrightarrow x = 4\)
Vậy phương trình có nghiệm duy nhất \(x = 4.\)
b)\({x^2} + 4x + 3 = 0\)
Vì \(a - b + c = 1 - 4 + 3 = 0\) nên phương trình có hai nghiệm phân biệt là: \({x_1} = {\rm{ \;}} - 1\) và \({x_2} = {\rm{ \;}} - \frac{c}{a} = {\rm{ \;}} - 3\)
Vậy phương trình có tập nghiệm là\(S = \left\{ { - 1; - 3} \right\}\).
c) \(\left\{ {\begin{array}{*{20}{l}}{x - 2y = 1}\\{3x + 2y = 11}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4x = 12}\\{2y = x - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3}\\{2y = 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = 1}\end{array}} \right.\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {1;3} \right)\).
Câu 12 (TH):
Phương pháp:
a) Thực hiện tính toán chứa căn bậc hai, \(\sqrt {{a^2}b} {\rm{ \;}} = \left| a \right|\sqrt b \)
b) Cách vẽ đồ thị hàm số \(y = ax + b(a \ne 0)\)
Bước 1: Cho \(x = 0\) thì \(y = b\), ta được điểm \(P(0;b)\) thuộc trục Oy.
Cho \(y = 0\) thì \(x = \frac{{ - b}}{a}\), ta được điểm \(Q\left( {\frac{{ - b}}{a};0} \right)\) thuộc trục hoành Ox.
Bước 2: Vẽ đường thẳng đi qua hai điểm \({\rm{P}}\) và \({\rm{Q}}\) ta được đồ thị hàm số \(y = ax + b\)
Cách giải:
a) Ta có: \(B = \sqrt {36} {\rm{ \;}} + \sqrt 4 {\rm{ \;}} - \sqrt {25} {\rm{ \;}} = \sqrt {{6^2}} {\rm{ \;}} + \sqrt {{2^2}} {\rm{ \;}} - \sqrt {{5^2}} {\rm{ \;}} = 6 + 2 - 5 = 8 - 5 = 3\)
Vậy \(B = 3.\)
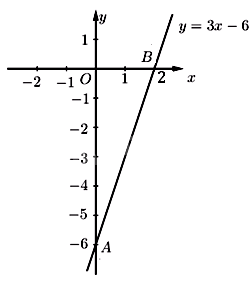
b) Vẽ đồ thị hàm số: \(y = 3x - 6\).
Cho \(x = 0\) thì \(y = 3.0 - 6 = {\rm{ \;}} - 6\)
Cho \(y = 0\) thì \(0 = 3.x - 6 \Leftrightarrow 3x = 6 \Leftrightarrow x = 2\)
Suy ra đồ thị hàm số \(y = 3x - 6\) là đường thẳng đi qua 2 điểm \(A\left( {0; - 6} \right)\) và \(B\left( {2;0} \right)\)
Ta vẽ được đồ thị hàm số như sau:
Câu 13 (TH):
Phương pháp:
Công thức \(\Delta ' = {(b')^2} - ac\) với \(b' = \frac{b}{a}\)
Điều kiện phương trình có hai nghiệm phân biệt \(\Delta {\rm{ \;}} > 0\)
Sử dụng hệ thức Vi-ét \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{{ - b}}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\)
Cách giải:
Ta có \(\Delta ' = {\left( {m - 1} \right)^2} - 1\left( {{m^2} - 3} \right) = {m^2} - 2m + 1 - {m^2} + 3 = {\rm{ \;}} - 2m + 4\)
Để phương trình đã cho có 2 nghiệm phân biệt \({x_1},{x_2}\) thì \(\Delta ' > 0 \Leftrightarrow {\rm{ \;}} - 2m + 4 > 0 \Leftrightarrow m < 2\)
Khi đó theo viet ta có \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 2\left( {m - 1} \right)}\\{{x_1}{x_2} = {m^2} - 3}\end{array}} \right.\)
Để \({x_1} + {x_2} = {x_1}{x_2} - 2\)
\(\begin{array}{*{20}{l}}{ \Rightarrow 2\left( {m - 1} \right) = {m^2} - 3 - 2}\\{ \Leftrightarrow 2m - 2 = {m^2} - 5}\\{ \Leftrightarrow {m^2} - 2m - 3 = 0}\end{array}\)
\( \Leftrightarrow \left( {m - 3} \right)\left( {m + 1} \right) = 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = 3\left( {KTM} \right)}\\{m = {\rm{ \;}} - 1\left( {TM} \right)}\end{array}} \right.\)
Vậy m = -1 thì thỏa mãn bài toán
Câu 14 (TH):
Phương pháp:
Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
Công thức chu vi hình chữ nhật bằng 2 lần tổng chiều dài và chiều rộng.
Cách giải:
Gọi chiều rộng mảnh đất là \(x{\mkern 1mu} \left( {m,{\mkern 1mu} {\mkern 1mu} 0 < x < 30} \right)\).
Vì chiều dài mảnh đất gấp 2 lần chiều rộng nên ta có chiều dài mảnh đất là: \(2x{\mkern 1mu} {\mkern 1mu} \left( m \right)\)
Vì chu vi mảnh đất là 60 nên ta có:
\(2.\left( {x + 2x} \right) = 60 \Leftrightarrow 6x = 60 \Leftrightarrow x = 10\) (TM)
Suy ra chiều dài mảnh đất là 20m, chiều rộng mảnh đất là 10m.
Diện tích mảnh đất là: \(20.10 = 200\left( {{m^2}} \right)\)
Giá tiền của mảnh đất là: \(8.200 = 1600\)(triệu đồng)
Vậy giá tiền của mảnh đất đó là 1600 triệu đồng = 1 600 000 000 đồng.
Câu 15 (VD):
Phương pháp:
a) Chứng minh tứ giác AOCD có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp,
b) Sử dụng tính chất góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BC thì bằng nhau.
Và hai góc cùng phụ với góc thứ 3.
c) Chứng minh $\Delta AEO \backsim \Delta AHC\left( {g.g} \right)$ suy ra các cặp cạnh tương ứng tỉ lệ.
d) Gọi N là giao điểm của AC và BD.
Chứng minh CN là phân giác của \(\angle MCD\), CB là phân giác ngoài tại đỉnh C của \(\Delta CDM\)
Sử dụng tính chất phân giác.
Chứng minh CH // AD, sử dụng định lí Talet.
\( \Rightarrow \frac{{CM}}{{AD}} = \frac{{HM}}{{AD}} \Rightarrow CM = HM \Rightarrow M\)
Cách giải:
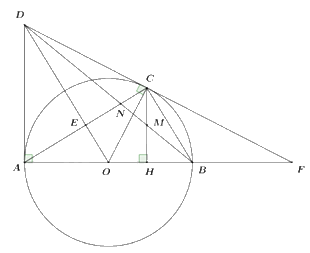
a) Do DA, AC là tiếp tuyến nên \(DA \bot OA,DC \bot OC\)
\( \Rightarrow \angle DAO = \angle DCO = {90^0}\)
Xét tứ giác AOCD có \(\angle DAO + \angle DCO = {90^0} + {90^0} = {180^0}\)
Suy ra AOCD nội tiếp (tổng hai góc đối bằng \({180^0}\)) (dhnb) (đpcm)
b) Ta có \(\angle BCF = \angle FAC\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BC)
\(\angle ACB = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow \angle BCH = \angle BAC\) (cùng phụ với góc CBA)
\( \Rightarrow \angle FCB = \angle BCH\left( { = \angle FAC} \right)\)
\( \Rightarrow BC\) là phân giác của góc HCF
c) Ta có DA = DC (tính chất 2 tiếp tuyến cắt nhau)
\( \Rightarrow \) D thuộc trung trực của AC
OA = OC (cùng bằng bán kính của (O)
\( \Rightarrow \) O thuộc trung trực của AC
\( \Rightarrow DO\) là trung trực của AC.
\( \Rightarrow DO \bot AC\) tại E là trung điểm của AC.
Xét \(\Delta AEO\) và \(\Delta AHC\) có
\(\angle HAC\) chung
\(\angle AEO = \angle AHC\left( { = {{90}^0}} \right)\)
$\Rightarrow \Delta AEO \backsim \Delta AHC\left( {g.g} \right) \Rightarrow \dfrac{{AE}}{{AH}} = \dfrac{{AO}}{{AC}}$ (cặp cạnh tương ứng tỉ lệ).
\( \Rightarrow AO.AH = AE.AC = AE.2AE = 2A{E^2}\).
Vậy \(AO.AH = 2A{E^2}\) (đpcm).
d) Gọi N là giao điểm của AC và BD.
Vì CB là phân giác của góc HCF (theo câu b).
Mà \(\angle ACB = {90^0}{\mkern 1mu} {\mkern 1mu} \left( {cmt} \right) \Rightarrow CB \bot CA\).
Mà \(\angle HCF\) kề bù với \(\angle HCD\).
\( \Rightarrow CA\) là phân giác của góc \(\angle HCD\), CB là phân giác ngoài của \(\angle HCD\).
Áp dụng định lí đường phân giác ta có: \(\frac{{CM}}{{CD}} = \frac{{NM}}{{ND}} = \frac{{BM}}{{BD}}\).
Vì \(\left\{ {\begin{array}{*{20}{l}}{CH \bot AB{\mkern 1mu} {\mkern 1mu} \left( {gt} \right)}\\{AD \bot AB{\mkern 1mu} {\mkern 1mu} \left( {gt} \right)}\end{array}} \right. \Rightarrow CH//AD\) (từ vuông góc đến song song)
\( \Rightarrow \) Áp dụng định lí Ta-lét ta có: \(\frac{{NM}}{{ND}} = \frac{{CM}}{{AD}},{\mkern 1mu} {\mkern 1mu} \frac{{BM}}{{BD}} = \frac{{HM}}{{AD}}\).
\( \Rightarrow \frac{{CM}}{{AD}} = \frac{{HM}}{{AD}} \Rightarrow CM = HM \Rightarrow M\) là trung điểm của CH (đpcm).
Câu 16 (VDC):
Phương pháp:
Đặt \(a = \sqrt {x + 2} ;b = \sqrt y {\mkern 1mu} {\mkern 1mu} \left( {a,b \ge 0} \right)\)
Từ đó giải phương trình tìm a, b.
Suy ra ẩn chính.
Cách giải:
\(\left\{ {\begin{array}{*{20}{l}}{{x^2}\left( {1 + \frac{4}{{{y^2}}}} \right) = 12}&{{\rm{ \;}}}&{(1)}\\{2\sqrt {x + 3y + 2} {\rm{ \;}} = 3\sqrt y {\rm{ \;}} + \sqrt {x + 2} {\rm{ \;}}}&{(2)}&{}\end{array}} \right.\)
(ĐKXĐ: \(x \ge {\rm{ \;}} - 2;y \ge 0\))
Đặt \(a = \sqrt {x + 2} ;b = \sqrt y {\mkern 1mu} {\mkern 1mu} \left( {a,b \ge 0} \right)\)
\(\begin{array}{*{20}{l}}{ \Rightarrow {a^2} = x + 2;{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {b^2} = y}\\{ \Rightarrow x + 3y + 2 = {a^2} + 3{b^2}}\end{array}\)
Khi đó (2) trở thành: \(2\sqrt {{a^2} + 3{b^2}} {\rm{ \;}} = a + 3b\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow 4\left( {{a^2} + 3{b^2}} \right) = {{\left( {a + 3b} \right)}^2}}\\{ \Leftrightarrow 4{a^2} + 12{b^2} = {a^2} + 6ab + 9{b^2}}\\{ \Leftrightarrow 3{a^2} - 6ab + 3{b^2} = 0}\\{ \Leftrightarrow 3{{\left( {a - b} \right)}^2} = 0}\\{ \Leftrightarrow {{\left( {a - b} \right)}^2} = 0}\\{ \Leftrightarrow a - b = 0}\\{ \Leftrightarrow a = b}\\{ \Rightarrow \sqrt {x + 2} {\rm{ \;}} = \sqrt y {\mkern 1mu} }\\{ \Leftrightarrow x + 2 = y}\end{array}\)
Thay vào (1) ta được: \({x^2}\left( {1 + \frac{4}{{{{\left( {x + 2} \right)}^2}}}} \right) = 12\)
\(\begin{array}{l} \Leftrightarrow {x^2}\left[ {{{\left( {x + 2} \right)}^2} + 4} \right] = 12{\left( {x + 2} \right)^2}\\ \Leftrightarrow {x^2}\left( {{x^2} + 4x + 8} \right) = 12\left( {{x^2} + 4x + 4} \right)\\ \Leftrightarrow {x^4} + 4{x^3} + 8{x^2} = 12{x^2} + 48x + 48\\ \Leftrightarrow {x^4} + 4{x^3} - 4{x^2} - 48x - 48 = 0\\ \Leftrightarrow {x^4} + 6{x^3} + 12{x^2} - 2{x^3} - 12{x^2} - 24x - 4{x^2} - 24x - 48 = 0\\ \Leftrightarrow {x^2}\left( {{x^2} + 6x + 12} \right) - 2x\left( {{x^2} + 6x + 12} \right) - 4\left( {{x^2} + 6x + 12} \right) = 0\\ \Leftrightarrow \left( {{x^2} - 2x - 4} \right)\left( {{x^2} + 6x + 12} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}{x^2} - 2x - 4 = 0 \Leftrightarrow x = 1 \pm \sqrt 5 \\{x^2} + 6x + 12 = 0\,(VN)\end{array} \right.\end{array}\)
Với\(x = 1 + \sqrt 5 {\rm{ \;}} \Rightarrow y = 1 + \sqrt 5 {\rm{ \;}} + 2 = 3 + \sqrt 5 \)
Với\(x = 1 - \sqrt 5 {\rm{ \;}} \Rightarrow y = 1 - \sqrt 5 {\rm{ \;}} + 2 = 3 - \sqrt 5 \)
Vậy hệ phương trình có nghiệm là \(\left( {x;y} \right) = \left( {1 + \sqrt 5 ;3 + \sqrt 5 } \right)\) hoặc\(\left( {x;y} \right) = \left( {1 - \sqrt 5 ;3 - \sqrt 5 } \right)\).
Phần I: Trắc nghiệm (2 điểm)
Câu 1: Căn bậc ba của -27 là
A. -9
B. -3
C. 9
D. 3
Câu 2: Tất cả các giá trị của \(x\) để biểu thức \(P = \sqrt {x - 2} \) có nghĩa là
A. \(x = 2\).
B. \(x \ge 2\).
C. \(x \le 2\).
D. \(x > 2\).
Câu 3: Hàm số \(y = mx - 2\) đồng biến trên \(\mathbb{R}\) khi
A. \(m > 0\).
B. \(m < 0\).
C. \(m = 0\).
D. \(m \ne 0\).
Câu 4: Đồ thị hàm số \(y = 3{x^2}\) đi qua điểm nào dưới đây?
A. \(M\left( {0;0} \right)\).
B. \(N\left( {1;6} \right)\).
C. \(P\left( {1;1} \right)\).
D. \(Q\left( {0;3} \right)\).
Câu 5: Nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x - y = 4}\\{x + 2y = {\rm{ \;}} - 5}\end{array}} \right.\) là
A. \(\left( {1;4} \right)\).
B. \(\left( {1;3} \right)\).
C. \(\left( {1; - 3} \right)\).
D. \(\left( {3;1} \right)\).
Câu 6: Nếu phương trình \(a{x^2} + bx + c = 0\) với \(a \ne 0\) có hai nghiệm \({x_1}\) và \({x_2}\), thì tích \({x_1}{x_2}\) bằng
A. \( - \frac{c}{a}\).
B. \(\frac{b}{a}\).
C. \(\frac{c}{a}\).
D. \( - \frac{b}{a}\).
Câu 7: Cho tam giác ABC vuông tại \(A\) (tham khảo hình vẽ). Khẳng định nào sau đây đúng?
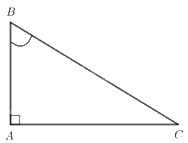
A. \({\rm{cos}}B = \frac{{AC}}{{AB}}\).
B. \({\rm{cos}}B = \frac{{AC}}{{BC}}\).
C. \({\rm{cos}}B = \frac{{AB}}{{AC}}\).
D. \({\rm{cos}}B = \frac{{AB}}{{BC}}\).
Câu 8: Cho đường tròn \(\left( {O;R} \right)\) và đường thẳng \(d\). Gọi \(H\) là hình chiếu vuông góc của \(O\) trên đường thẳng \(d\) (tham khảo hình vẽ). Đường thẳng \(d\) cắt \(\left( {O;R} \right)\) tại hai điểm phân biệt A, B khi
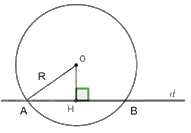
A. \(OH < R\).
B. \(OH = R\).
C. \(OH > R\).
D. \(OH \le R\).
Câu 9: Số đo góc nội tiếp chắn cung \(150^\circ \) bằng
A. \(150^\circ \).
B. \(65^\circ \).
C. \(50^\circ \).
D. \(75^\circ \).
Câu 10: Công thức tính diện tích của hình cầu có bán kính \(R\) là
A. \(S = 4\pi R\).
B. \(S = 4\pi {R^2}\).
C. \(S = \pi {R^2}\).
D. \(S = 3\pi {R^2}\).
Phần II. Tự luận (8 điểm)
Câu 11: Giải các phương trình và hệ phương trình sau:
a)\(2x - 8 = 0\)
b)\({x^2} + 4x + 3 = 0\)
c) \(\left\{ {\begin{array}{*{20}{l}}{x - 2y = 1}\\{3x + 2y = 11}\end{array}} \right.\)
Câu 12:
a) Tính giá trị của biểu thức: \(B = \sqrt {36} {\rm{ \;}} + \sqrt 4 {\rm{ \;}} - \sqrt {25} \).
b) Vẽ đồ thị hàm số: \(y = 3x - 6\).
Câu 13: Cho phương trình \({x^2} - 2(m - 1)x + {m^2} - 3 = 0\) (m là tham số). Tìm m để phương trình đã cho có 2 nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \({x_1} + {x_2} = {x_1}{x_2} - 2\)
Câu 14: Ông Nam sở hữu một mảnh đất hình chữ nhật có chu vi là 60m. Ông Nam định bán mảnh đất đó với giá thị trường là 8 triệu đồng cho một mét vuông. Hãy tính giá tiền của mảnh đất đó biết rằng mảnh đất có chiều dài gấp 2 lần chiều rộng.
Câu 15: Cho đường tròn tâm O đường kính AB. Trên đường tròn (O) lấy điểm C không trùng B sao cho AC > BC. Các tiếp tuyến của đường tròn (O) tại A và C cắt nhau tại D. Gọi H là hình chiếu vuông góc của C trên AB, E là giao điểm của hai đường thẳng OD và AC.
a) Chứng minh tứ giác AOCD nội tiếp.
b) Gọi F là giao điểm của hai đường thẳng CD và AB. Chứng minh CB là tia phân giác của góc HCF.
c) Chứng minh \(AO.AH = 2A{E^2}\)
d) Gọi M là giao điểm của hai đường thẳng BD và CH. Chứng minh M là trung điểm của CH.
Câu 16: Giải hệ phương trình\(\left\{ {\begin{array}{*{20}{l}}{{x^2}\left( {1 + \frac{4}{{{y^2}}}} \right) = 12}\\{2\sqrt {x + 3y + 2} {\rm{ \;}} = 3\sqrt y {\rm{ \;}} + \sqrt {x + 2} }\end{array}} \right.\)
-----HẾT-----
Phần I: Trắc nghiệm
1.B | 2.B | 3.A | 4.A | 5.C | 6.C | 7.D | 8.A | 9.D | 10.B |
Câu 1 (NB):
Phương pháp:
Căn bậc ba của x là số a, sao cho \({a^3} = x\)
Cách giải:
Căn bậc ba của -27 là -3 vì \({( - 3)^3} = - 27\)
Chọn B.
Câu 2 (NB):
Phương pháp:
\(\sqrt {f(x)} \) có nghĩa khi \(f(x) \ge 0\)
Cách giải:
\(P = \sqrt {x - 2} \) có nghĩa khi \(x - 2 \ge 0 \Leftrightarrow x \ge 2\)
Chọn B.
Câu 3 (NB):
Phương pháp:
Hàm số \(y = ax + b(a \ne 0)\) đồng biến trên R khi a > 0.
Cách giải:
Hàm số \(y = mx - 2\) đồng biến trên \(\mathbb{R}\) khi \(m > 0\)
Chọn A.
Câu 4 (NB):
Phương pháp:
Điểm \(A({x_0};{y_0})\) đi qua đồ thị hàm số \(y = a{x^2}(a \ne 0)\) khi \({y_0} = a.{x_0}^2\)
Cách giải:
Đồ thị hàm số \(y = 3{x^2}\) đi qua điểm \(M\left( {0;0} \right)\)
Chọn A.
Câu 5 (NB):
Phương pháp:
Giải hệ phương trình bằng phương pháp cộng đại số.
Cách giải:
\(\left\{ {\begin{array}{*{20}{l}}{x - y = 4}\\{x + 2y = {\rm{ \;}} - 5}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3y = {\rm{ \;}} - 9}\\{x = 4 + y}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = {\rm{ \;}} - 3}\\{x = 4 - 3 = 1}\end{array}} \right.\)
Vậy hệ phương trình có nghiệm \(\left( {1; - 3} \right)\)
Chọn C.
Câu 6 (NB):
Phương pháp:
Hệ thức Vi-ét \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{{ - b}}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\)
Cách giải:
Nếu phương trình \(a{x^2} + bx + c = 0\) với \(a \ne 0\) có hai nghiệm \({x_1}\) và \({x_2}\), thì tích \({x_1}{x_2}\) bằng \(\frac{c}{a}\)
Chọn C.
Câu 7 (NB):
Phương pháp:
Công thức góc lượng giác: tam giác ABC vuông tại \(A\) có \({\rm{cos}}B = \frac{{AB}}{{BC}}\)
Cách giải:
Tam giác ABC vuông tại \(A\) có \({\rm{cos}}B = \frac{{AB}}{{BC}}\)
Chọn D.
Câu 8 (NB):
Phương pháp:
Vị trí tương đối của đường thẳng và đườn tròn:
Đường thẳng \(d\) cắt \(\left( {O;R} \right)\) tại hai điểm phân biệt A, B khi \(OH < R\)
Cách giải:
Đường thẳng \(d\) cắt \(\left( {O;R} \right)\) tại hai điểm phân biệt A, B khi \(OH < R\)
Chọn A.
Câu 9 (NB):
Phương pháp:
Góc nội tiếp bằng một nửa số đo cung bị chắn.
Cách giải:
Số đo góc nội tiếp chắn cung \(150^\circ \) bằng \(75^\circ \)
Chọn D.
Câu 10 (NB):
Phương pháp:
Công thức tính diện tích của hình cầu có bán kính \(R\) là \(S = 4\pi {R^2}\)
Cách giải:
Công thức tính diện tích của hình cầu có bán kính \(R\) là \(S = 4\pi {R^2}\)
Chọn B.
Phần II: Tự luận
Câu 11 (TH):
Phương pháp:
a) Giải phương trình bậc nhất \(ax + b = 0(a \ne 0)\) có nghiệm là \(x = \frac{{ - b}}{a}\)
b) Giải phương trình bậc hai một ẩn bằng cách nhẩm nghiệm \(a - b + c = 0\).
Suy ra PT có nghiệm \(\left[ {\begin{array}{*{20}{l}}{{x_1} = {\rm{ \;}} - 1}\\{{x_2} = \frac{{ - c}}{a}}\end{array}} \right.\)
Cách giải:
a) \(2x - 8 = 0 \Leftrightarrow 2x = 8 \Leftrightarrow x = 4\)
Vậy phương trình có nghiệm duy nhất \(x = 4.\)
b)\({x^2} + 4x + 3 = 0\)
Vì \(a - b + c = 1 - 4 + 3 = 0\) nên phương trình có hai nghiệm phân biệt là: \({x_1} = {\rm{ \;}} - 1\) và \({x_2} = {\rm{ \;}} - \frac{c}{a} = {\rm{ \;}} - 3\)
Vậy phương trình có tập nghiệm là\(S = \left\{ { - 1; - 3} \right\}\).
c) \(\left\{ {\begin{array}{*{20}{l}}{x - 2y = 1}\\{3x + 2y = 11}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4x = 12}\\{2y = x - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3}\\{2y = 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = 1}\end{array}} \right.\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {1;3} \right)\).
Câu 12 (TH):
Phương pháp:
a) Thực hiện tính toán chứa căn bậc hai, \(\sqrt {{a^2}b} {\rm{ \;}} = \left| a \right|\sqrt b \)
b) Cách vẽ đồ thị hàm số \(y = ax + b(a \ne 0)\)
Bước 1: Cho \(x = 0\) thì \(y = b\), ta được điểm \(P(0;b)\) thuộc trục Oy.
Cho \(y = 0\) thì \(x = \frac{{ - b}}{a}\), ta được điểm \(Q\left( {\frac{{ - b}}{a};0} \right)\) thuộc trục hoành Ox.
Bước 2: Vẽ đường thẳng đi qua hai điểm \({\rm{P}}\) và \({\rm{Q}}\) ta được đồ thị hàm số \(y = ax + b\)
Cách giải:
a) Ta có: \(B = \sqrt {36} {\rm{ \;}} + \sqrt 4 {\rm{ \;}} - \sqrt {25} {\rm{ \;}} = \sqrt {{6^2}} {\rm{ \;}} + \sqrt {{2^2}} {\rm{ \;}} - \sqrt {{5^2}} {\rm{ \;}} = 6 + 2 - 5 = 8 - 5 = 3\)
Vậy \(B = 3.\)
b) Vẽ đồ thị hàm số: \(y = 3x - 6\).
Cho \(x = 0\) thì \(y = 3.0 - 6 = {\rm{ \;}} - 6\)
Cho \(y = 0\) thì \(0 = 3.x - 6 \Leftrightarrow 3x = 6 \Leftrightarrow x = 2\)
Suy ra đồ thị hàm số \(y = 3x - 6\) là đường thẳng đi qua 2 điểm \(A\left( {0; - 6} \right)\) và \(B\left( {2;0} \right)\)
Ta vẽ được đồ thị hàm số như sau:
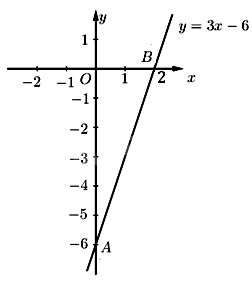
Câu 13 (TH):
Phương pháp:
Công thức \(\Delta ' = {(b')^2} - ac\) với \(b' = \frac{b}{a}\)
Điều kiện phương trình có hai nghiệm phân biệt \(\Delta {\rm{ \;}} > 0\)
Sử dụng hệ thức Vi-ét \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{{ - b}}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\)
Cách giải:
Ta có \(\Delta ' = {\left( {m - 1} \right)^2} - 1\left( {{m^2} - 3} \right) = {m^2} - 2m + 1 - {m^2} + 3 = {\rm{ \;}} - 2m + 4\)
Để phương trình đã cho có 2 nghiệm phân biệt \({x_1},{x_2}\) thì \(\Delta ' > 0 \Leftrightarrow {\rm{ \;}} - 2m + 4 > 0 \Leftrightarrow m < 2\)
Khi đó theo viet ta có \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 2\left( {m - 1} \right)}\\{{x_1}{x_2} = {m^2} - 3}\end{array}} \right.\)
Để \({x_1} + {x_2} = {x_1}{x_2} - 2\)
\(\begin{array}{*{20}{l}}{ \Rightarrow 2\left( {m - 1} \right) = {m^2} - 3 - 2}\\{ \Leftrightarrow 2m - 2 = {m^2} - 5}\\{ \Leftrightarrow {m^2} - 2m - 3 = 0}\end{array}\)
\( \Leftrightarrow \left( {m - 3} \right)\left( {m + 1} \right) = 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = 3\left( {KTM} \right)}\\{m = {\rm{ \;}} - 1\left( {TM} \right)}\end{array}} \right.\)
Vậy m = -1 thì thỏa mãn bài toán
Câu 14 (TH):
Phương pháp:
Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
Công thức chu vi hình chữ nhật bằng 2 lần tổng chiều dài và chiều rộng.
Cách giải:
Gọi chiều rộng mảnh đất là \(x{\mkern 1mu} \left( {m,{\mkern 1mu} {\mkern 1mu} 0 < x < 30} \right)\).
Vì chiều dài mảnh đất gấp 2 lần chiều rộng nên ta có chiều dài mảnh đất là: \(2x{\mkern 1mu} {\mkern 1mu} \left( m \right)\)
Vì chu vi mảnh đất là 60 nên ta có:
\(2.\left( {x + 2x} \right) = 60 \Leftrightarrow 6x = 60 \Leftrightarrow x = 10\) (TM)
Suy ra chiều dài mảnh đất là 20m, chiều rộng mảnh đất là 10m.
Diện tích mảnh đất là: \(20.10 = 200\left( {{m^2}} \right)\)
Giá tiền của mảnh đất là: \(8.200 = 1600\)(triệu đồng)
Vậy giá tiền của mảnh đất đó là 1600 triệu đồng = 1 600 000 000 đồng.
Câu 15 (VD):
Phương pháp:
a) Chứng minh tứ giác AOCD có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp,
b) Sử dụng tính chất góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BC thì bằng nhau.
Và hai góc cùng phụ với góc thứ 3.
c) Chứng minh $\Delta AEO \backsim \Delta AHC\left( {g.g} \right)$ suy ra các cặp cạnh tương ứng tỉ lệ.
d) Gọi N là giao điểm của AC và BD.
Chứng minh CN là phân giác của \(\angle MCD\), CB là phân giác ngoài tại đỉnh C của \(\Delta CDM\)
Sử dụng tính chất phân giác.
Chứng minh CH // AD, sử dụng định lí Talet.
\( \Rightarrow \frac{{CM}}{{AD}} = \frac{{HM}}{{AD}} \Rightarrow CM = HM \Rightarrow M\)
Cách giải:
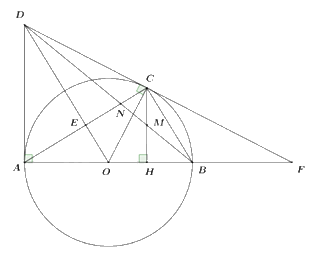
a) Do DA, AC là tiếp tuyến nên \(DA \bot OA,DC \bot OC\)
\( \Rightarrow \angle DAO = \angle DCO = {90^0}\)
Xét tứ giác AOCD có \(\angle DAO + \angle DCO = {90^0} + {90^0} = {180^0}\)
Suy ra AOCD nội tiếp (tổng hai góc đối bằng \({180^0}\)) (dhnb) (đpcm)
b) Ta có \(\angle BCF = \angle FAC\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BC)
\(\angle ACB = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow \angle BCH = \angle BAC\) (cùng phụ với góc CBA)
\( \Rightarrow \angle FCB = \angle BCH\left( { = \angle FAC} \right)\)
\( \Rightarrow BC\) là phân giác của góc HCF
c) Ta có DA = DC (tính chất 2 tiếp tuyến cắt nhau)
\( \Rightarrow \) D thuộc trung trực của AC
OA = OC (cùng bằng bán kính của (O)
\( \Rightarrow \) O thuộc trung trực của AC
\( \Rightarrow DO\) là trung trực của AC.
\( \Rightarrow DO \bot AC\) tại E là trung điểm của AC.
Xét \(\Delta AEO\) và \(\Delta AHC\) có
\(\angle HAC\) chung
\(\angle AEO = \angle AHC\left( { = {{90}^0}} \right)\)
$\Rightarrow \Delta AEO \backsim \Delta AHC\left( {g.g} \right) \Rightarrow \dfrac{{AE}}{{AH}} = \dfrac{{AO}}{{AC}}$ (cặp cạnh tương ứng tỉ lệ).
\( \Rightarrow AO.AH = AE.AC = AE.2AE = 2A{E^2}\).
Vậy \(AO.AH = 2A{E^2}\) (đpcm).
d) Gọi N là giao điểm của AC và BD.
Vì CB là phân giác của góc HCF (theo câu b).
Mà \(\angle ACB = {90^0}{\mkern 1mu} {\mkern 1mu} \left( {cmt} \right) \Rightarrow CB \bot CA\).
Mà \(\angle HCF\) kề bù với \(\angle HCD\).
\( \Rightarrow CA\) là phân giác của góc \(\angle HCD\), CB là phân giác ngoài của \(\angle HCD\).
Áp dụng định lí đường phân giác ta có: \(\frac{{CM}}{{CD}} = \frac{{NM}}{{ND}} = \frac{{BM}}{{BD}}\).
Vì \(\left\{ {\begin{array}{*{20}{l}}{CH \bot AB{\mkern 1mu} {\mkern 1mu} \left( {gt} \right)}\\{AD \bot AB{\mkern 1mu} {\mkern 1mu} \left( {gt} \right)}\end{array}} \right. \Rightarrow CH//AD\) (từ vuông góc đến song song)
\( \Rightarrow \) Áp dụng định lí Ta-lét ta có: \(\frac{{NM}}{{ND}} = \frac{{CM}}{{AD}},{\mkern 1mu} {\mkern 1mu} \frac{{BM}}{{BD}} = \frac{{HM}}{{AD}}\).
\( \Rightarrow \frac{{CM}}{{AD}} = \frac{{HM}}{{AD}} \Rightarrow CM = HM \Rightarrow M\) là trung điểm của CH (đpcm).
Câu 16 (VDC):
Phương pháp:
Đặt \(a = \sqrt {x + 2} ;b = \sqrt y {\mkern 1mu} {\mkern 1mu} \left( {a,b \ge 0} \right)\)
Từ đó giải phương trình tìm a, b.
Suy ra ẩn chính.
Cách giải:
\(\left\{ {\begin{array}{*{20}{l}}{{x^2}\left( {1 + \frac{4}{{{y^2}}}} \right) = 12}&{{\rm{ \;}}}&{(1)}\\{2\sqrt {x + 3y + 2} {\rm{ \;}} = 3\sqrt y {\rm{ \;}} + \sqrt {x + 2} {\rm{ \;}}}&{(2)}&{}\end{array}} \right.\)
(ĐKXĐ: \(x \ge {\rm{ \;}} - 2;y \ge 0\))
Đặt \(a = \sqrt {x + 2} ;b = \sqrt y {\mkern 1mu} {\mkern 1mu} \left( {a,b \ge 0} \right)\)
\(\begin{array}{*{20}{l}}{ \Rightarrow {a^2} = x + 2;{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {b^2} = y}\\{ \Rightarrow x + 3y + 2 = {a^2} + 3{b^2}}\end{array}\)
Khi đó (2) trở thành: \(2\sqrt {{a^2} + 3{b^2}} {\rm{ \;}} = a + 3b\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow 4\left( {{a^2} + 3{b^2}} \right) = {{\left( {a + 3b} \right)}^2}}\\{ \Leftrightarrow 4{a^2} + 12{b^2} = {a^2} + 6ab + 9{b^2}}\\{ \Leftrightarrow 3{a^2} - 6ab + 3{b^2} = 0}\\{ \Leftrightarrow 3{{\left( {a - b} \right)}^2} = 0}\\{ \Leftrightarrow {{\left( {a - b} \right)}^2} = 0}\\{ \Leftrightarrow a - b = 0}\\{ \Leftrightarrow a = b}\\{ \Rightarrow \sqrt {x + 2} {\rm{ \;}} = \sqrt y {\mkern 1mu} }\\{ \Leftrightarrow x + 2 = y}\end{array}\)
Thay vào (1) ta được: \({x^2}\left( {1 + \frac{4}{{{{\left( {x + 2} \right)}^2}}}} \right) = 12\)
\(\begin{array}{l} \Leftrightarrow {x^2}\left[ {{{\left( {x + 2} \right)}^2} + 4} \right] = 12{\left( {x + 2} \right)^2}\\ \Leftrightarrow {x^2}\left( {{x^2} + 4x + 8} \right) = 12\left( {{x^2} + 4x + 4} \right)\\ \Leftrightarrow {x^4} + 4{x^3} + 8{x^2} = 12{x^2} + 48x + 48\\ \Leftrightarrow {x^4} + 4{x^3} - 4{x^2} - 48x - 48 = 0\\ \Leftrightarrow {x^4} + 6{x^3} + 12{x^2} - 2{x^3} - 12{x^2} - 24x - 4{x^2} - 24x - 48 = 0\\ \Leftrightarrow {x^2}\left( {{x^2} + 6x + 12} \right) - 2x\left( {{x^2} + 6x + 12} \right) - 4\left( {{x^2} + 6x + 12} \right) = 0\\ \Leftrightarrow \left( {{x^2} - 2x - 4} \right)\left( {{x^2} + 6x + 12} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}{x^2} - 2x - 4 = 0 \Leftrightarrow x = 1 \pm \sqrt 5 \\{x^2} + 6x + 12 = 0\,(VN)\end{array} \right.\end{array}\)
Với\(x = 1 + \sqrt 5 {\rm{ \;}} \Rightarrow y = 1 + \sqrt 5 {\rm{ \;}} + 2 = 3 + \sqrt 5 \)
Với\(x = 1 - \sqrt 5 {\rm{ \;}} \Rightarrow y = 1 - \sqrt 5 {\rm{ \;}} + 2 = 3 - \sqrt 5 \)
Vậy hệ phương trình có nghiệm là \(\left( {x;y} \right) = \left( {1 + \sqrt 5 ;3 + \sqrt 5 } \right)\) hoặc\(\left( {x;y} \right) = \left( {1 - \sqrt 5 ;3 - \sqrt 5 } \right)\).
Kỳ thi tuyển sinh vào lớp 10 môn Toán tỉnh Sơn La năm 2023 là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Đề thi thường bao gồm các dạng bài tập thuộc nhiều chủ đề khác nhau, đòi hỏi học sinh phải có kiến thức vững chắc và kỹ năng giải quyết vấn đề tốt. Việc nắm vững cấu trúc đề thi, các dạng bài tập thường gặp và phương pháp giải quyết hiệu quả là chìa khóa để đạt kết quả cao trong kỳ thi này.
Thông thường, đề thi vào 10 môn Toán Sơn La năm 2023 có cấu trúc gồm hai phần chính:
Để giải đề thi vào 10 môn Toán Sơn La năm 2023 hiệu quả, các em học sinh cần:
Việc luyện tập với đề thi vào 10 môn Toán Sơn La năm 2023 mang lại nhiều lợi ích cho các em học sinh:
Giaitoan.edu.vn là một website học toán online uy tín, cung cấp đầy đủ các tài liệu ôn tập, đề thi thử và bài giảng chất lượng cao. Chúng tôi cam kết đồng hành cùng các em trên con đường chinh phục kỳ thi vào 10 môn Toán Sơn La năm 2023. Hãy truy cập giaitoan.edu.vn để khám phá thêm nhiều tài liệu hữu ích và phương pháp học tập hiệu quả!
Ngoài việc luyện tập với đề thi, các em học sinh cũng cần chú ý đến các yếu tố sau:
Đề thi vào 10 môn Toán Sơn La năm 2023 là một kỳ thi quan trọng, đòi hỏi sự chuẩn bị kỹ lưỡng và nỗ lực không ngừng. Hy vọng với những thông tin và phương pháp giải đề thi hiệu quả mà giaitoan.edu.vn cung cấp, các em học sinh sẽ đạt kết quả tốt nhất trong kỳ thi sắp tới.