Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Bình Phước năm 2020. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi sắp tới.
Bộ đề thi này bao gồm các đề thi chính thức của kỳ thi tuyển sinh vào lớp 10 môn Toán Bình Phước năm 2020, được chúng tôi tổng hợp và cung cấp kèm theo đáp án chi tiết, giúp các em tự học và kiểm tra kiến thức một cách hiệu quả.
Câu 1: 1. Tính giá trị của biểu thức sau:
Câu 1:
1. Tính giá trị của biểu thức sau:
\(A = \sqrt {64} - \sqrt {49} \) \(B = \sqrt {{{\left( {4 + \sqrt 7 } \right)}^2}} - \sqrt 7 \)
2. Cho biểu thức \(Q = \dfrac{{x + 2\sqrt x }}{{\sqrt x + 2}} - 3\,\,\left( {x \ge 0} \right)\)
a) Rút gọn biểu thức \(Q\).
b) Tìm giá trị của x để biểu thức \(Q = 2\).
Câu 2:
1. Cho parabol \(\left( P \right):\,\,\,y = {x^2}\) và đường thẳng \(\left( d \right):\,\,\,y = 2x + 3\)
a) Vẽ parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) trên cùng một mặt phẳng tọa độ \(Oxy.\)
b) Tìm tọa độ giao điểm của parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) bằng phép tính.
2) Không sử dụng máy tính, giải hệ phương trình sau: \(\left\{ \begin{array}{l}2x - 3y = 3\\x + 3y = 6\end{array} \right..\)
Câu 3:
1. Cho phương trình ẩn x: \({x^2} - 5x + \left( {m - 2} \right) = 0\,\,\,\left( 1 \right)\).
a) Giải phương trình (1) với \(m = 6\).
b) Tìm m để phương trình (1) có hai nghiệm dương phân biệt \({x_1},\,\,{x_2}\) thỏa mãn hệ thức \(\dfrac{1}{{\sqrt {{x_1}} }} + \dfrac{1}{{\sqrt {{x_2}} }} = \dfrac{3}{2}\).
2. Một thửa đất hình chữ nhật có chiều dài hơn chiều rộng 4m và có diện tích là \(320{m^2}\). Tính chu vi thửa đất đó.
Câu 4:
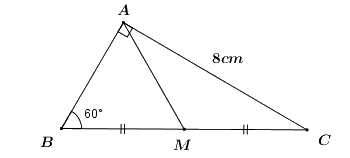
Cho tam giác \(ABC\) vuông tại \(A\), có cạnh \(AC = 8\,\,cm\), \(\angle B = {60^0}\). Tính số đo góc \(\angle C\) và độ dài các cạnh \(AB,\,\,BC\), đường trung tuyến \(AM\) của tam giác \(ABC\).
Câu 5:
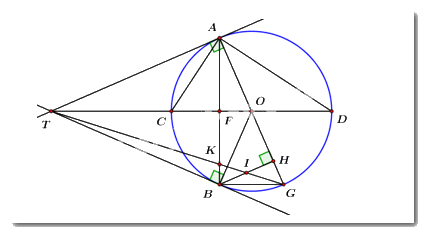
Từ một điểm \(T\) ở bên ngoài đường tròn \(\left( O \right).\) Vẽ hai tiếp tuyến \(TA,\,\,TB\) với đường tròn (\(A,\,\,B\) là hai tiếp điểm). Tia \(TO\) cắt \(\left( O \right)\) tại hai điểm phân biệt \(C\) và \(D\) (\(C\) nằm giữa \(T\) và \(O\)) vắt cắt đoạn thẳng \(AB\) tại \(F.\)
a) Chứng minh: Tứ giác \(TAOB\) nội tiếp.
b) Chứng minh: \(TC.TD = TF.TO.\)
c) Vẽ đường kính \(AG\) của đường tròn \(\left( O \right).\) Gọi \(H\) là chân đường vuông góc kẻ từ điểm \(B\) đến \(AG,\,\,I\) là giao điểm của \(TG\) và \(BH.\) Chứng minh \(I\) là trung điểm của \(BH.\)
Câu 1 (2,0 điểm)
Cách giải:
1. Tính giá trị của biểu thức sau:
\(A = \sqrt {64} - \sqrt {49} \) \(B = \sqrt {{{\left( {4 + \sqrt 7 } \right)}^2}} - \sqrt 7 \)
+ Tính giá trị biểu thức A:
\(\begin{array}{l}A = \sqrt {64} - \sqrt {49} \\A = \sqrt {{8^2}} - \sqrt {{7^2}} \\A = 8 - 7\\A = 1\end{array}\)
Vậy \(A = 1\).
+ Tính giá trị biểu thức B:
\(\begin{array}{l}B = \sqrt {{{\left( {4 + \sqrt 7 } \right)}^2}} - \sqrt 7 \\B = \left| {4 + \sqrt 7 } \right| - \sqrt 7 \\B = 4 + \sqrt 7 - \sqrt 7 \,\,\left( {Do\,\,4 + \sqrt 7 > 0} \right)\\B = 4\end{array}\)
Vậy \(B = 4\).
2. Cho biểu thức \(Q = \dfrac{{x + 2\sqrt x }}{{\sqrt x + 2}} - 3\,\,\left( {x \ge 0} \right)\)
a) Rút gọn biểu thức \(Q\).
Với \(x \ge 0\) ta có:
\(\begin{array}{l}Q = \dfrac{{x + 2\sqrt x }}{{\sqrt x + 2}} - 3\\Q = \dfrac{{\sqrt x \left( {\sqrt x + 2} \right)}}{{\sqrt x + 2}} - 3\\Q = \sqrt x - 3\end{array}\)
Vậy với \(x \ge 0\) thì \(Q = \sqrt x - 3\).
b) Tìm giá trị của x để biểu thức \(Q = 2\).
Ta có: \(Q = 2 \Leftrightarrow \sqrt x - 3 = 2 \Leftrightarrow \sqrt x = 5 \Leftrightarrow x = 25\,\,\left( {tm} \right)\).
Vậy để \(Q = 2\) thì \(x = 25\).
Câu 2 (2điểm)
Cách giải:
1. Cho parabol \(\left( P \right):\,\,\,y = {x^2}\) và đường thẳng \(\left( d \right):\,\,\,y = 2x + 3\)
a) Vẽ parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) trên cùng một mặt phẳng tọa độ \(Oxy.\)
+) Vẽ parabol \(\left( P \right):\,\,y = {x^2}\)
Ta có bảng giá trị:
\(x\) | \( - 2\) | \( - 1\) | \(0\) | \(1\) | \(2\) |
\(y = {x^2}\) | \(4\) | \(1\) | \(0\) | \(1\) | \(4\) |
Vậy \(\left( P \right):\,\,y = {x^2}\) là đường cong đi qua các điểm: \(\left( { - 2;\,\,4} \right),\,\,\left( { - 1;\,\,1} \right),\,\,\left( {0;\,\,0} \right),\,\,\left( {1;\,\,1} \right),\,\,\left( {2;\,\,4} \right).\)
+) Vẽ đường thẳng \(\left( d \right):\,\,y = 2x + 3\).
Ta có bảng giá trị:
\(x\) | \(0\) | \( - 1\) |
\(y = 2x + 3\) | \(3\) | \(1\) |
Vậy \(\left( d \right):\,\,\,y = 2x + 3\) là đường thẳng đi qua các điểm \(\left( {0;\,\,3} \right)\) và \(\left( { - 1;\,\,1} \right).\)
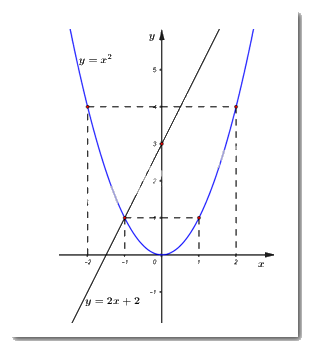
b) Tìm tọa độ giao điểm của parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) bằng phép tính.
Xét phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) ta có:
\(\begin{array}{l}\,\,\,\,\,\,{x^2} = 2x + 3\\ \Leftrightarrow {x^2} - 2x - 3 = 0\\ \Leftrightarrow {x^2} - 3x + x - 3 = 0\\ \Leftrightarrow x\left( {x - 3} \right) + \left( {x - 3} \right) = 0\\ \Leftrightarrow \left( {x - 3} \right)\left( {x + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 3 = 0\\x + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = - 1\end{array} \right.\end{array}\)
+) Với \(x = 3 \Rightarrow y = {3^2} = 9\).
+) Với \(x = - 1 \Rightarrow y = {\left( { - 1} \right)^2} = 1.\)
Vậy \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt có tọa độ là \(\left( {3;\,\,9} \right)\) và \(\left( { - 1;\,\,1} \right).\)
2) Không sử dụng máy tính, giải hệ phương trình sau: \(\left\{ \begin{array}{l}2x - 3y = 3\\x + 3y = 6\end{array} \right..\)
\(\left\{ \begin{array}{l}2x - 3y = 3\\x + 3y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x = 9\\x + 3y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\3 + 3y = 6\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = 3\\3y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 1\end{array} \right.\).
Vậy hệ phương trình có nghiệm duy nhất \(\left( {3;\,\,1} \right).\)
Câu 3 (2,5 điểm)
Cách giải:
1. Cho phương trình ẩn x: \({x^2} - 5x + \left( {m - 2} \right) = 0\,\,\,\left( 1 \right)\).
a) Giải phương trình (1) với \(m = 6\).
Với \(m = 6\) thì phương trình (1) trở thành:
\(\begin{array}{l}\,\,\,\,\,\,{x^2} - 5x + 4 = 0\\ \Leftrightarrow {x^2} - x - 4x + 4 = 0\\ \Leftrightarrow \left( {{x^2} - x} \right) - \left( {4x - 4} \right) = 0\\ \Leftrightarrow x\left( {x - 1} \right) - 4\left( {x - 1} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 4\end{array} \right.\end{array}\)
Vậy với \(m = 6\) thì tập nghiệm của phương trình là \(S = \left\{ {1;4} \right\}\).
b) Tìm m để phương trình (1) có hai nghiệm dương phân biệt \({x_1},\,\,{x_2}\) thỏa mãn hệ thức \(\dfrac{1}{{\sqrt {{x_1}} }} + \dfrac{1}{{\sqrt {{x_2}} }} = \dfrac{3}{2}\).
Để phương trình (1) có hai nghiệm dương phân biệt \({x_1},\,\,{x_2}\) thì \(\left\{ \begin{array}{l}\Delta > 0\\S > 0\\P > 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{\left( { - 5} \right)^2} - 4\left( {m - 2} \right) > 0\\5 > 0\,\,\left( {luon\,\,dung} \right)\\m - 2 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}25 - 4m + 8 > 0\\m > 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}33 - 4m > 0\\m > 2\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}m < \dfrac{{33}}{4}\\m > 2\end{array} \right. \Leftrightarrow 2 < m < \dfrac{{33}}{4}\).
Khi đó áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 5\\{x_1}{x_2} = m - 2\end{array} \right.\).
Theo bài ra ta có:
\(\begin{array}{l}\dfrac{1}{{\sqrt {{x_1}} }} + \dfrac{1}{{\sqrt {{x_2}} }} = \dfrac{3}{2}\\ \Leftrightarrow \dfrac{{\sqrt {{x_1}} + \sqrt {{x_2}} }}{{\sqrt {{x_1}{x_2}} }} = \dfrac{3}{2}\\ \Leftrightarrow 2\left( {\sqrt {{x_1}} + \sqrt {{x_2}} } \right) = 3\sqrt {{x_1}{x_2}} \\ \Leftrightarrow 4\left( {{x_1} + {x_2} + 2\sqrt {{x_1}{x_2}} } \right) = 9{x_1}{x_2}\\ \Leftrightarrow 4\left( {5 + 2\sqrt {m - 2} } \right) = 9\left( {m - 2} \right)\\ \Leftrightarrow 9\left( {m - 2} \right) - 8\sqrt {m - 2} - 20 = 0\,\,\,\left( * \right)\end{array}\)
Đặt \(t = \sqrt {m - 2} \,\,\left( {t \ge 0} \right)\), phương trình (*) trở thành:
\(\begin{array}{l}\,\,\,\,\,9{t^2} - 8t - 20 = 0\\ \Leftrightarrow 9{t^2} - 18t + 10t - 20 = 0\\ \Leftrightarrow \left( {9{t^2} - 18t} \right) + \left( {10t - 20} \right) = 0\\ \Leftrightarrow 9t\left( {t - 2} \right) + 10\left( {t - 2} \right) = 0\\ \Leftrightarrow \left( {t - 2} \right)\left( {9t + 10} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}t - 2 = 0\\9t + 10 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = 2\,\,\,\,\,\,\,\,\,\,\,\left( {tm} \right)\\t = - \dfrac{{10}}{9}\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Với \(t = 2\) \( \Rightarrow \sqrt {m - 2} = 2 \Leftrightarrow m - 2 = 4 \Leftrightarrow m = 6\,\,\left( {tm} \right)\).
Vậy \(m = 6\).
2. Một thửa đất hình chữ nhật có chiều dài hơn chiều rộng 4m và có diện tích là \(320{m^2}\). Tính chu vi thửa đất đó.
Gọi chiều rộng thửa đất là \(x\,\,\left( m \right)\) (ĐK: \(x > 0\)) \( \Rightarrow \) Chiều dài thửa đất là \(x + 4\,\,\left( m \right)\).
Vì thửa đất có diện tích là \(320{m^2}\) nên ta có phương trình:
\(\begin{array}{l}x\left( {x + 4} \right) = 320\\ \Leftrightarrow {x^2} + 4x - 320 = 0\\ \Leftrightarrow {x^2} - 16x + 20x - 320 = 0\\ \Leftrightarrow \left( {{x^2} - 16x} \right) + \left( {20x - 320} \right) = 0\\ \Leftrightarrow x\left( {x - 16} \right) + 20\left( {x - 16} \right) = 0\\ \Leftrightarrow \left( {x - 16} \right)\left( {x + 20} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 16 = 0\\x + 20 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 16\,\,\,\,\,\,\left( {tm} \right)\\x = - 20\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
\( \Rightarrow \) Chiều rộng thửa đất là \(16m\), chiều dài thửa đất là \(16 + 4 = 20m\).
Vậy chu vi thửa đất đó là: \(\left( {16 + 20} \right).2 = 72\,\,\left( m \right)\).
Câu 4 (2,5 điểm)
Cách giải:
Cho tam giác \(ABC\) vuông tại \(A\), có cạnh \(AC = 8\,\,cm\), \(\angle B = {60^0}\). Tính số đo góc \(\angle C\) và độ dài các cạnh \(AB,\,\,BC\), đường trung tuyến \(AM\) của tam giác \(ABC\).
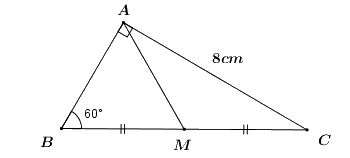
Vì \(\Delta ABC\) vuông tại \(A\) nên \(\angle B + \angle C = {90^0}\) (hai góc nhọn trong tam giác vuông phụ nhau).
\( \Rightarrow \angle C = {90^0} - \angle B = {90^0} - {60^0} = {30^0}\).
Ta có:
\(\tan {60^0} = \dfrac{{AC}}{{AB}} \Rightarrow AB = \dfrac{{AC}}{{\tan {{60}^0}}} = \dfrac{8}{{\sqrt 3 }} = \dfrac{{8\sqrt 3 }}{3}\,\,\left( {cm} \right)\).
\(\sin {60^0} = \dfrac{{AC}}{{BC}} \Rightarrow BC = \dfrac{{AC}}{{\sin {{60}^0}}} = \dfrac{8}{{\dfrac{{\sqrt 3 }}{2}}} = \dfrac{{16\sqrt 3 }}{3}\,\,\left( {cm} \right)\).
Tam giác \(ABC\) vuông tại \(A\) có đường trung tuyến \(AM\) ứng với cạnh huyền \(BC\) nên
\(AM = \dfrac{1}{2}BC = \dfrac{1}{2}.\dfrac{{16\sqrt 3 }}{3} = \dfrac{{8\sqrt 3 }}{3}\).
Vậy \(\angle C = {30^0},\,\,AB = AM = \dfrac{{8\sqrt 3 }}{3}cm,\,\,BC = \dfrac{{16\sqrt 3 }}{3}\,cm\).
Câu 5 (2,5 điểm)
Cách giải:
Từ một điểm \(T\) ở bên ngoài đường tròn \(\left( O \right).\) Vẽ hai tiếp tuyến \(TA,\,\,TB\) với đường tròn (\(A,\,\,B\) là hai tiếp điểm). Tia \(TO\) cắt \(\left( O \right)\) tại hai điểm phân biệt \(C\) và \(D\) (\(C\) nằm giữa \(T\) và \(O\)) vắt cắt đoạn thẳng \(AB\) tại \(F.\)
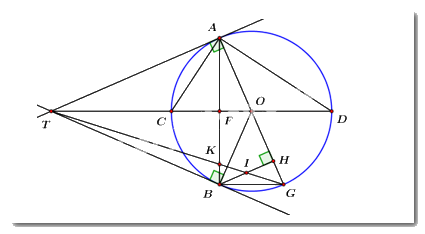
a) Chứng minh: Tứ giác \(TAOB\) nội tiếp.
Ta có: \(TA,\,\,TB\) là hai tiếp tuyến của \(\left( O \right)\) tại \(A,\,\,B\) (gt).
\( \Rightarrow \left\{ \begin{array}{l}TA \bot OA\\TB \bot OB\end{array} \right.\) \( \Rightarrow \angle TAO = \angle TBO = {90^0}\).
Xét tứ giác \(TAOB\) ta có: \(\angle TAO + \angle TBO = {90^0} + {90^0} = {180^0}\).
Mà hai góc này là hai góc đối diện
\( \Rightarrow TAOB\) là tứ giác nội tiếp (dhnb).
b) Chứng minh: \(TC.TD = TF.TO.\)
Ta có: \(OA = OB = R\) \( \Rightarrow O\) thuộc đường trung trực của \(AB.\)
\(TA = TB\,\) (tính chất hai tiếp tuyến cắt nhau) \( \Rightarrow T\) thuộc đường trung trực của \(AB.\)
\( \Rightarrow TO\) là đường trung trực của \(AB.\)
\( \Rightarrow TO \bot AB = \left\{ F \right\}\)
Áp dụng hệ thức lượng cho \(\Delta TAO\) vuông tại \(A\) có đường cao \(AF\) ta có: \(T{A^2} = TF.TO\,\,\,\left( 1 \right)\)
Xét \(\Delta TAC\) và \(\Delta TDA\) ta có:
\(\angle T\) chung;
\(\angle TDA = \angle TAC\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(AC\)).
\( \Rightarrow \Delta TAC \sim \Delta TDA\,\,\,\left( {g - g} \right)\)
\( \Rightarrow \dfrac{{TA}}{{TD}} = \dfrac{{TC}}{{TA}} \Leftrightarrow T{A^2} = TC.TD\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow TF.TO = TC.TD\,\,\,\left( { = T{A^2}} \right)\,\,\,\left( {dpcm} \right).\)
c) Vẽ đường kính \(AG\) của đường tròn \(\left( O \right).\) Gọi \(H\) là chân đường vuông góc kẻ từ điểm \(B\) đến \(AG,\,\,I\) là giao điểm của \(TG\) và \(BH.\) Chứng minh \(I\) là trung điểm của \(BH.\)
Gọi \(AB \cap TG = \left\{ K \right\}\).
Ta có: \(\left\{ \begin{array}{l}AT \bot OA \Rightarrow AT \bot AG\\BH \bot AG\end{array} \right. \Rightarrow BH\parallel AT\) (từ vuông góc đến song song).
\( \Rightarrow \angle ABH = \angle TAB\) (so le trong).
Mà \(TA = TB\) (tính chất 2 tiếp tuyến cắt nhau) nên \(\Delta TAB\) cân tại \(T\) \( \Rightarrow \angle TAB = \angle TBA\).
\( \Rightarrow \angle ABH = \angle TBA\)
\( \Rightarrow BK\) là phân giác của \(\angle TBH\).
Ta có: \(\angle ABG = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow BA \bot BG\) hay \(BK \bot BG\).
Do đó \(BG\) là phân giác ngoài của \(\angle TBH\).
Áp dụng định lí đường phân giác ta có: \(\dfrac{{BI}}{{BT}} = \dfrac{{KI}}{{KT}} = \dfrac{{GI}}{{GT}}\).
Lại có: \(\dfrac{{KI}}{{KT}} = \dfrac{{BI}}{{AT}};\,\,\dfrac{{GI}}{{GT}} = \dfrac{{IH}}{{AT}}\) (định lí Ta-lét)
Do đó \(\dfrac{{BI}}{{AT}} = \dfrac{{IH}}{{AT}} \Rightarrow BI = IH\).
Vậy \(I\) là trung điểm của \(BH\) (đpcm).
Câu 1:
1. Tính giá trị của biểu thức sau:
\(A = \sqrt {64} - \sqrt {49} \) \(B = \sqrt {{{\left( {4 + \sqrt 7 } \right)}^2}} - \sqrt 7 \)
2. Cho biểu thức \(Q = \dfrac{{x + 2\sqrt x }}{{\sqrt x + 2}} - 3\,\,\left( {x \ge 0} \right)\)
a) Rút gọn biểu thức \(Q\).
b) Tìm giá trị của x để biểu thức \(Q = 2\).
Câu 2:
1. Cho parabol \(\left( P \right):\,\,\,y = {x^2}\) và đường thẳng \(\left( d \right):\,\,\,y = 2x + 3\)
a) Vẽ parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) trên cùng một mặt phẳng tọa độ \(Oxy.\)
b) Tìm tọa độ giao điểm của parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) bằng phép tính.
2) Không sử dụng máy tính, giải hệ phương trình sau: \(\left\{ \begin{array}{l}2x - 3y = 3\\x + 3y = 6\end{array} \right..\)
Câu 3:
1. Cho phương trình ẩn x: \({x^2} - 5x + \left( {m - 2} \right) = 0\,\,\,\left( 1 \right)\).
a) Giải phương trình (1) với \(m = 6\).
b) Tìm m để phương trình (1) có hai nghiệm dương phân biệt \({x_1},\,\,{x_2}\) thỏa mãn hệ thức \(\dfrac{1}{{\sqrt {{x_1}} }} + \dfrac{1}{{\sqrt {{x_2}} }} = \dfrac{3}{2}\).
2. Một thửa đất hình chữ nhật có chiều dài hơn chiều rộng 4m và có diện tích là \(320{m^2}\). Tính chu vi thửa đất đó.
Câu 4:
Cho tam giác \(ABC\) vuông tại \(A\), có cạnh \(AC = 8\,\,cm\), \(\angle B = {60^0}\). Tính số đo góc \(\angle C\) và độ dài các cạnh \(AB,\,\,BC\), đường trung tuyến \(AM\) của tam giác \(ABC\).
Câu 5:
Từ một điểm \(T\) ở bên ngoài đường tròn \(\left( O \right).\) Vẽ hai tiếp tuyến \(TA,\,\,TB\) với đường tròn (\(A,\,\,B\) là hai tiếp điểm). Tia \(TO\) cắt \(\left( O \right)\) tại hai điểm phân biệt \(C\) và \(D\) (\(C\) nằm giữa \(T\) và \(O\)) vắt cắt đoạn thẳng \(AB\) tại \(F.\)
a) Chứng minh: Tứ giác \(TAOB\) nội tiếp.
b) Chứng minh: \(TC.TD = TF.TO.\)
c) Vẽ đường kính \(AG\) của đường tròn \(\left( O \right).\) Gọi \(H\) là chân đường vuông góc kẻ từ điểm \(B\) đến \(AG,\,\,I\) là giao điểm của \(TG\) và \(BH.\) Chứng minh \(I\) là trung điểm của \(BH.\)
Câu 1 (2,0 điểm)
Cách giải:
1. Tính giá trị của biểu thức sau:
\(A = \sqrt {64} - \sqrt {49} \) \(B = \sqrt {{{\left( {4 + \sqrt 7 } \right)}^2}} - \sqrt 7 \)
+ Tính giá trị biểu thức A:
\(\begin{array}{l}A = \sqrt {64} - \sqrt {49} \\A = \sqrt {{8^2}} - \sqrt {{7^2}} \\A = 8 - 7\\A = 1\end{array}\)
Vậy \(A = 1\).
+ Tính giá trị biểu thức B:
\(\begin{array}{l}B = \sqrt {{{\left( {4 + \sqrt 7 } \right)}^2}} - \sqrt 7 \\B = \left| {4 + \sqrt 7 } \right| - \sqrt 7 \\B = 4 + \sqrt 7 - \sqrt 7 \,\,\left( {Do\,\,4 + \sqrt 7 > 0} \right)\\B = 4\end{array}\)
Vậy \(B = 4\).
2. Cho biểu thức \(Q = \dfrac{{x + 2\sqrt x }}{{\sqrt x + 2}} - 3\,\,\left( {x \ge 0} \right)\)
a) Rút gọn biểu thức \(Q\).
Với \(x \ge 0\) ta có:
\(\begin{array}{l}Q = \dfrac{{x + 2\sqrt x }}{{\sqrt x + 2}} - 3\\Q = \dfrac{{\sqrt x \left( {\sqrt x + 2} \right)}}{{\sqrt x + 2}} - 3\\Q = \sqrt x - 3\end{array}\)
Vậy với \(x \ge 0\) thì \(Q = \sqrt x - 3\).
b) Tìm giá trị của x để biểu thức \(Q = 2\).
Ta có: \(Q = 2 \Leftrightarrow \sqrt x - 3 = 2 \Leftrightarrow \sqrt x = 5 \Leftrightarrow x = 25\,\,\left( {tm} \right)\).
Vậy để \(Q = 2\) thì \(x = 25\).
Câu 2 (2điểm)
Cách giải:
1. Cho parabol \(\left( P \right):\,\,\,y = {x^2}\) và đường thẳng \(\left( d \right):\,\,\,y = 2x + 3\)
a) Vẽ parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) trên cùng một mặt phẳng tọa độ \(Oxy.\)
+) Vẽ parabol \(\left( P \right):\,\,y = {x^2}\)
Ta có bảng giá trị:
\(x\) | \( - 2\) | \( - 1\) | \(0\) | \(1\) | \(2\) |
\(y = {x^2}\) | \(4\) | \(1\) | \(0\) | \(1\) | \(4\) |
Vậy \(\left( P \right):\,\,y = {x^2}\) là đường cong đi qua các điểm: \(\left( { - 2;\,\,4} \right),\,\,\left( { - 1;\,\,1} \right),\,\,\left( {0;\,\,0} \right),\,\,\left( {1;\,\,1} \right),\,\,\left( {2;\,\,4} \right).\)
+) Vẽ đường thẳng \(\left( d \right):\,\,y = 2x + 3\).
Ta có bảng giá trị:
\(x\) | \(0\) | \( - 1\) |
\(y = 2x + 3\) | \(3\) | \(1\) |
Vậy \(\left( d \right):\,\,\,y = 2x + 3\) là đường thẳng đi qua các điểm \(\left( {0;\,\,3} \right)\) và \(\left( { - 1;\,\,1} \right).\)
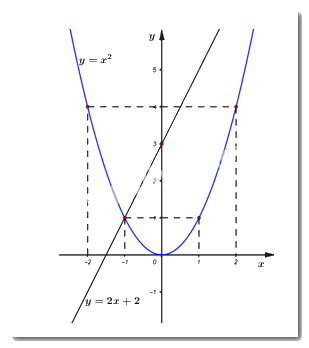
b) Tìm tọa độ giao điểm của parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) bằng phép tính.
Xét phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) ta có:
\(\begin{array}{l}\,\,\,\,\,\,{x^2} = 2x + 3\\ \Leftrightarrow {x^2} - 2x - 3 = 0\\ \Leftrightarrow {x^2} - 3x + x - 3 = 0\\ \Leftrightarrow x\left( {x - 3} \right) + \left( {x - 3} \right) = 0\\ \Leftrightarrow \left( {x - 3} \right)\left( {x + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 3 = 0\\x + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = - 1\end{array} \right.\end{array}\)
+) Với \(x = 3 \Rightarrow y = {3^2} = 9\).
+) Với \(x = - 1 \Rightarrow y = {\left( { - 1} \right)^2} = 1.\)
Vậy \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt có tọa độ là \(\left( {3;\,\,9} \right)\) và \(\left( { - 1;\,\,1} \right).\)
2) Không sử dụng máy tính, giải hệ phương trình sau: \(\left\{ \begin{array}{l}2x - 3y = 3\\x + 3y = 6\end{array} \right..\)
\(\left\{ \begin{array}{l}2x - 3y = 3\\x + 3y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x = 9\\x + 3y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\3 + 3y = 6\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = 3\\3y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 1\end{array} \right.\).
Vậy hệ phương trình có nghiệm duy nhất \(\left( {3;\,\,1} \right).\)
Câu 3 (2,5 điểm)
Cách giải:
1. Cho phương trình ẩn x: \({x^2} - 5x + \left( {m - 2} \right) = 0\,\,\,\left( 1 \right)\).
a) Giải phương trình (1) với \(m = 6\).
Với \(m = 6\) thì phương trình (1) trở thành:
\(\begin{array}{l}\,\,\,\,\,\,{x^2} - 5x + 4 = 0\\ \Leftrightarrow {x^2} - x - 4x + 4 = 0\\ \Leftrightarrow \left( {{x^2} - x} \right) - \left( {4x - 4} \right) = 0\\ \Leftrightarrow x\left( {x - 1} \right) - 4\left( {x - 1} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 4\end{array} \right.\end{array}\)
Vậy với \(m = 6\) thì tập nghiệm của phương trình là \(S = \left\{ {1;4} \right\}\).
b) Tìm m để phương trình (1) có hai nghiệm dương phân biệt \({x_1},\,\,{x_2}\) thỏa mãn hệ thức \(\dfrac{1}{{\sqrt {{x_1}} }} + \dfrac{1}{{\sqrt {{x_2}} }} = \dfrac{3}{2}\).
Để phương trình (1) có hai nghiệm dương phân biệt \({x_1},\,\,{x_2}\) thì \(\left\{ \begin{array}{l}\Delta > 0\\S > 0\\P > 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{\left( { - 5} \right)^2} - 4\left( {m - 2} \right) > 0\\5 > 0\,\,\left( {luon\,\,dung} \right)\\m - 2 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}25 - 4m + 8 > 0\\m > 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}33 - 4m > 0\\m > 2\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}m < \dfrac{{33}}{4}\\m > 2\end{array} \right. \Leftrightarrow 2 < m < \dfrac{{33}}{4}\).
Khi đó áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 5\\{x_1}{x_2} = m - 2\end{array} \right.\).
Theo bài ra ta có:
\(\begin{array}{l}\dfrac{1}{{\sqrt {{x_1}} }} + \dfrac{1}{{\sqrt {{x_2}} }} = \dfrac{3}{2}\\ \Leftrightarrow \dfrac{{\sqrt {{x_1}} + \sqrt {{x_2}} }}{{\sqrt {{x_1}{x_2}} }} = \dfrac{3}{2}\\ \Leftrightarrow 2\left( {\sqrt {{x_1}} + \sqrt {{x_2}} } \right) = 3\sqrt {{x_1}{x_2}} \\ \Leftrightarrow 4\left( {{x_1} + {x_2} + 2\sqrt {{x_1}{x_2}} } \right) = 9{x_1}{x_2}\\ \Leftrightarrow 4\left( {5 + 2\sqrt {m - 2} } \right) = 9\left( {m - 2} \right)\\ \Leftrightarrow 9\left( {m - 2} \right) - 8\sqrt {m - 2} - 20 = 0\,\,\,\left( * \right)\end{array}\)
Đặt \(t = \sqrt {m - 2} \,\,\left( {t \ge 0} \right)\), phương trình (*) trở thành:
\(\begin{array}{l}\,\,\,\,\,9{t^2} - 8t - 20 = 0\\ \Leftrightarrow 9{t^2} - 18t + 10t - 20 = 0\\ \Leftrightarrow \left( {9{t^2} - 18t} \right) + \left( {10t - 20} \right) = 0\\ \Leftrightarrow 9t\left( {t - 2} \right) + 10\left( {t - 2} \right) = 0\\ \Leftrightarrow \left( {t - 2} \right)\left( {9t + 10} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}t - 2 = 0\\9t + 10 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = 2\,\,\,\,\,\,\,\,\,\,\,\left( {tm} \right)\\t = - \dfrac{{10}}{9}\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Với \(t = 2\) \( \Rightarrow \sqrt {m - 2} = 2 \Leftrightarrow m - 2 = 4 \Leftrightarrow m = 6\,\,\left( {tm} \right)\).
Vậy \(m = 6\).
2. Một thửa đất hình chữ nhật có chiều dài hơn chiều rộng 4m và có diện tích là \(320{m^2}\). Tính chu vi thửa đất đó.
Gọi chiều rộng thửa đất là \(x\,\,\left( m \right)\) (ĐK: \(x > 0\)) \( \Rightarrow \) Chiều dài thửa đất là \(x + 4\,\,\left( m \right)\).
Vì thửa đất có diện tích là \(320{m^2}\) nên ta có phương trình:
\(\begin{array}{l}x\left( {x + 4} \right) = 320\\ \Leftrightarrow {x^2} + 4x - 320 = 0\\ \Leftrightarrow {x^2} - 16x + 20x - 320 = 0\\ \Leftrightarrow \left( {{x^2} - 16x} \right) + \left( {20x - 320} \right) = 0\\ \Leftrightarrow x\left( {x - 16} \right) + 20\left( {x - 16} \right) = 0\\ \Leftrightarrow \left( {x - 16} \right)\left( {x + 20} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 16 = 0\\x + 20 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 16\,\,\,\,\,\,\left( {tm} \right)\\x = - 20\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
\( \Rightarrow \) Chiều rộng thửa đất là \(16m\), chiều dài thửa đất là \(16 + 4 = 20m\).
Vậy chu vi thửa đất đó là: \(\left( {16 + 20} \right).2 = 72\,\,\left( m \right)\).
Câu 4 (2,5 điểm)
Cách giải:
Cho tam giác \(ABC\) vuông tại \(A\), có cạnh \(AC = 8\,\,cm\), \(\angle B = {60^0}\). Tính số đo góc \(\angle C\) và độ dài các cạnh \(AB,\,\,BC\), đường trung tuyến \(AM\) của tam giác \(ABC\).
Vì \(\Delta ABC\) vuông tại \(A\) nên \(\angle B + \angle C = {90^0}\) (hai góc nhọn trong tam giác vuông phụ nhau).
\( \Rightarrow \angle C = {90^0} - \angle B = {90^0} - {60^0} = {30^0}\).
Ta có:
\(\tan {60^0} = \dfrac{{AC}}{{AB}} \Rightarrow AB = \dfrac{{AC}}{{\tan {{60}^0}}} = \dfrac{8}{{\sqrt 3 }} = \dfrac{{8\sqrt 3 }}{3}\,\,\left( {cm} \right)\).
\(\sin {60^0} = \dfrac{{AC}}{{BC}} \Rightarrow BC = \dfrac{{AC}}{{\sin {{60}^0}}} = \dfrac{8}{{\dfrac{{\sqrt 3 }}{2}}} = \dfrac{{16\sqrt 3 }}{3}\,\,\left( {cm} \right)\).
Tam giác \(ABC\) vuông tại \(A\) có đường trung tuyến \(AM\) ứng với cạnh huyền \(BC\) nên
\(AM = \dfrac{1}{2}BC = \dfrac{1}{2}.\dfrac{{16\sqrt 3 }}{3} = \dfrac{{8\sqrt 3 }}{3}\).
Vậy \(\angle C = {30^0},\,\,AB = AM = \dfrac{{8\sqrt 3 }}{3}cm,\,\,BC = \dfrac{{16\sqrt 3 }}{3}\,cm\).
Câu 5 (2,5 điểm)
Cách giải:
Từ một điểm \(T\) ở bên ngoài đường tròn \(\left( O \right).\) Vẽ hai tiếp tuyến \(TA,\,\,TB\) với đường tròn (\(A,\,\,B\) là hai tiếp điểm). Tia \(TO\) cắt \(\left( O \right)\) tại hai điểm phân biệt \(C\) và \(D\) (\(C\) nằm giữa \(T\) và \(O\)) vắt cắt đoạn thẳng \(AB\) tại \(F.\)
a) Chứng minh: Tứ giác \(TAOB\) nội tiếp.
Ta có: \(TA,\,\,TB\) là hai tiếp tuyến của \(\left( O \right)\) tại \(A,\,\,B\) (gt).
\( \Rightarrow \left\{ \begin{array}{l}TA \bot OA\\TB \bot OB\end{array} \right.\) \( \Rightarrow \angle TAO = \angle TBO = {90^0}\).
Xét tứ giác \(TAOB\) ta có: \(\angle TAO + \angle TBO = {90^0} + {90^0} = {180^0}\).
Mà hai góc này là hai góc đối diện
\( \Rightarrow TAOB\) là tứ giác nội tiếp (dhnb).
b) Chứng minh: \(TC.TD = TF.TO.\)
Ta có: \(OA = OB = R\) \( \Rightarrow O\) thuộc đường trung trực của \(AB.\)
\(TA = TB\,\) (tính chất hai tiếp tuyến cắt nhau) \( \Rightarrow T\) thuộc đường trung trực của \(AB.\)
\( \Rightarrow TO\) là đường trung trực của \(AB.\)
\( \Rightarrow TO \bot AB = \left\{ F \right\}\)
Áp dụng hệ thức lượng cho \(\Delta TAO\) vuông tại \(A\) có đường cao \(AF\) ta có: \(T{A^2} = TF.TO\,\,\,\left( 1 \right)\)
Xét \(\Delta TAC\) và \(\Delta TDA\) ta có:
\(\angle T\) chung;
\(\angle TDA = \angle TAC\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(AC\)).
\( \Rightarrow \Delta TAC \sim \Delta TDA\,\,\,\left( {g - g} \right)\)
\( \Rightarrow \dfrac{{TA}}{{TD}} = \dfrac{{TC}}{{TA}} \Leftrightarrow T{A^2} = TC.TD\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow TF.TO = TC.TD\,\,\,\left( { = T{A^2}} \right)\,\,\,\left( {dpcm} \right).\)
c) Vẽ đường kính \(AG\) của đường tròn \(\left( O \right).\) Gọi \(H\) là chân đường vuông góc kẻ từ điểm \(B\) đến \(AG,\,\,I\) là giao điểm của \(TG\) và \(BH.\) Chứng minh \(I\) là trung điểm của \(BH.\)
Gọi \(AB \cap TG = \left\{ K \right\}\).
Ta có: \(\left\{ \begin{array}{l}AT \bot OA \Rightarrow AT \bot AG\\BH \bot AG\end{array} \right. \Rightarrow BH\parallel AT\) (từ vuông góc đến song song).
\( \Rightarrow \angle ABH = \angle TAB\) (so le trong).
Mà \(TA = TB\) (tính chất 2 tiếp tuyến cắt nhau) nên \(\Delta TAB\) cân tại \(T\) \( \Rightarrow \angle TAB = \angle TBA\).
\( \Rightarrow \angle ABH = \angle TBA\)
\( \Rightarrow BK\) là phân giác của \(\angle TBH\).
Ta có: \(\angle ABG = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow BA \bot BG\) hay \(BK \bot BG\).
Do đó \(BG\) là phân giác ngoài của \(\angle TBH\).
Áp dụng định lí đường phân giác ta có: \(\dfrac{{BI}}{{BT}} = \dfrac{{KI}}{{KT}} = \dfrac{{GI}}{{GT}}\).
Lại có: \(\dfrac{{KI}}{{KT}} = \dfrac{{BI}}{{AT}};\,\,\dfrac{{GI}}{{GT}} = \dfrac{{IH}}{{AT}}\) (định lí Ta-lét)
Do đó \(\dfrac{{BI}}{{AT}} = \dfrac{{IH}}{{AT}} \Rightarrow BI = IH\).
Vậy \(I\) là trung điểm của \(BH\) (đpcm).
Kỳ thi tuyển sinh vào lớp 10 môn Toán tỉnh Bình Phước năm 2020 là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Để chuẩn bị tốt nhất cho kỳ thi này, việc nắm vững cấu trúc đề thi, các dạng bài tập thường gặp và phương pháp giải quyết là vô cùng cần thiết. Bài viết này sẽ cung cấp cho các em một cái nhìn tổng quan về đề thi vào 10 môn Toán Bình Phước năm 2020, cùng với những phân tích chi tiết và hướng dẫn giải các bài tập điển hình.
Đề thi vào 10 môn Toán Bình Phước năm 2020 thường bao gồm các phần sau:
Trong đề thi vào 10 môn Toán Bình Phước năm 2020, các em học sinh thường gặp các dạng bài tập sau:
Ví dụ 1: Giải phương trình 2x + 3 = 7
Giải:
2x + 3 = 7
2x = 7 - 3
2x = 4
x = 2
Ví dụ 2: Chứng minh bất đẳng thức a2 + b2 ≥ 2ab với mọi số thực a, b.
Giải:
Ta có: (a - b)2 ≥ 0 với mọi số thực a, b.
Khai triển biểu thức, ta được: a2 - 2ab + b2 ≥ 0
Suy ra: a2 + b2 ≥ 2ab
Để ôn thi vào 10 môn Toán Bình Phước năm 2020 hiệu quả, các em học sinh nên:
Ngoài bộ đề thi vào 10 môn Toán Bình Phước năm 2020 mà Giaitoan.edu.vn cung cấp, các em học sinh có thể tham khảo thêm các tài liệu sau:
Chúc các em học sinh ôn thi tốt và đạt kết quả cao trong kỳ thi tuyển sinh vào lớp 10 môn Toán tỉnh Bình Phước năm 2020!