Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Lạng Sơn năm 2023. Đây là tài liệu ôn tập vô cùng quan trọng dành cho các em học sinh đang chuẩn bị cho kỳ thi sắp tới.
Chúng tôi cung cấp đầy đủ các đề thi chính thức, đáp án chi tiết và phương pháp giải bài tập hiệu quả. Hy vọng với bộ tài liệu này, các em sẽ tự tin hơn và đạt kết quả tốt nhất trong kỳ thi tuyển sinh.
Câu 1: a) Tính giá trị các biểu thức sau: \(A = \sqrt {36} {\rm{ \;}} - \sqrt 4 \) \(B = \sqrt {{{(4 - \sqrt {15} )}^2}} {\rm{ \;}} + \sqrt {15} \) \(C = \frac{{\sqrt {12} {\rm{ \;}} + \sqrt {27} }}{{\sqrt 3 }}\)
Câu 1: a) Tính giá trị các biểu thức sau:
\(A = \sqrt {36} {\rm{ \;}} - \sqrt 4 \)
\(B = \sqrt {{{(4 - \sqrt {15} )}^2}} {\rm{ \;}} + \sqrt {15} \)
\(C = \frac{{\sqrt {12} {\rm{ \;}} + \sqrt {27} }}{{\sqrt 3 }}\)
b) Cho biểu thức: \(P = \left( {\frac{1}{{\sqrt x {\rm{ \;}} - 3}} + \frac{1}{{x - 9}}} \right):\frac{{\sqrt x {\rm{ \;}} + 4}}{{\sqrt x {\rm{ \;}} + 3}}\) với \(x \ge 0;x \ne 9\).
1) Rút gọn biểu thức \(P\).
2) Tìm giá trị của \(x\) để \(P = \frac{1}{2}\).
Câu 2: a) Vẽ đường thẳng \((d):y = 3x - 2\)
b) Tìm tọa độ giao điểm của đồ thị hàm số \((P):y = {x^2}\) với đường thẳng \((d):y = 3x - 2\).
Câu 3: a) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y = 5}\\{3x - 2y = 5}\end{array}} \right.\).
b) Giải phương trình \({x^2} - 9x + 14 = 0\).
c) Cho phương trình \({x^2} - (m + 2)x + m - 3 = 0(*)\), với \(m\) là tham số.
1) Chứng minh rằng phương trình \(\left( * \right)\) luôn có hai nghiệm phân biệt với mọi \(m\).
2) Tìm \(m\) để phương trình \(\left( * \right)\) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \({x_1} + {x_2} + 2{x_1}{x_2} > 5\).
Câu 4: Cho tam giác ABC không cân và có ba góc nhọn. Các đường cao AD, BE, CF cắt nhau tại H (với \(D \in BC\), \(E \in CA\), \(F \in AB\)).
a) Chứng minh rằng tứ giác AFHE nội tiếp.
b) Chứng minh rằng $\Delta EAD\backsim \Delta EFC$.
c) Kẻ DE cắt đường tròn đường kính AC tại M \(\left( {M \ne D} \right)\); DF cắt đường tròn đường kính AB tại N \(\left( {N \ne D} \right)\). Gọi \(K = FM \cap EN\). Chứng minh rằng AF = AM và đường thẳng EF đi qua trung điểm của đoạn thẳng HK.
Câu 5: Cho các số thực dương a, b, c thoả mãn a + b + c = 3. Chứng minh rằng:
\(\frac{{{a^3}}}{{{a^2} + b}} + \frac{{{b^3}}}{{{b^2} + c}} + \frac{{{c^3}}}{{{c^2} + a}} \ge \frac{3}{2}\)
----- HẾT -----
Câu 1 (VD):
Phương pháp:
a) Sử dụng tính chất căn bậc hai.
b) Quy đồng và rút gọn.
Cách giải:
a) Tính giá trị các biểu thức sau:
\(A = \sqrt {36} {\rm{ \;}} - \sqrt 4 \)
\(B = \sqrt {{{(4 - \sqrt {15} )}^2}} {\rm{ \;}} + \sqrt {15} \)
\(C = \frac{{\sqrt {12} {\rm{ \;}} + \sqrt {27} }}{{\sqrt 3 }}\)
Ta có \(A = \sqrt {36} - \sqrt 4 = \sqrt {{6^2}} - \sqrt {{2^2}} = 6 - 2 = 4\)
\(B = \sqrt {{{(4 - \sqrt {15} )}^2}} + \sqrt {15} = \left| {4 - \sqrt {15} } \right| + \sqrt {15} = 4 - \sqrt {15} + \sqrt {15} = 4\)
\(C = \frac{{\sqrt {12} + \sqrt {27} }}{{\sqrt 3 }} = \frac{{\sqrt {4.3} + \sqrt {9.3} }}{{\sqrt 3 }} = \frac{{2\sqrt 3 + 3\sqrt 3 }}{{\sqrt 3 }} = \frac{{5\sqrt 3 }}{{\sqrt 3 }} = 5\)
Vậy A = 4, B = 4, C = 5.
b) Cho biểu thức: \(P = \left( {\frac{1}{{\sqrt x - 3}} + \frac{1}{{x - 9}}} \right):\frac{{\sqrt x + 4}}{{\sqrt x + 3}}\) với \(x \ge 0;x \ne 9\).
1) Rút gọn biểu thức \(P\).
Ta có \(P = \left( {\frac{1}{{\sqrt x - 3}} + \frac{1}{{x - 9}}} \right):\frac{{\sqrt x + 4}}{{\sqrt x + 3}}\)
\(\begin{array}{l} = \left( {\frac{1}{{\sqrt x - 3}} + \frac{1}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}} \right).\frac{{\sqrt x + 3}}{{\sqrt x + 4}}\\ = \left( {\frac{{\sqrt x + 3}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} + \frac{1}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}} \right).\frac{{\sqrt x + 3}}{{\sqrt x + 4}}\\ = \frac{{\sqrt x + 4}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}.\frac{{\sqrt x + 3}}{{\sqrt x + 4}}\\ = \frac{1}{{\sqrt x - 3}}\end{array}\)
Vậy \(P = \frac{1}{{\sqrt x - 3}}\) với \(x \ge 0;x \ne 9\).
2) Tìm giá trị của \(x\) để \(P = \frac{1}{2}\).
Ta có \(P = \frac{1}{{\sqrt x - 3}}\) với \(x \ge 0;x \ne 9\).
Để \(P = \frac{1}{2}\)
\(\begin{array}{l} \Leftrightarrow \frac{1}{{\sqrt x - 3}} = \frac{1}{2}\\ \Leftrightarrow \sqrt x - 3 = 2\\ \Leftrightarrow \sqrt x = 5\\ \Leftrightarrow x = 25\left( {TM} \right)\end{array}\)
Vậy để \(P = \frac{1}{2}\) thì \(x = 25\).
Câu 2 (VD):
Phương pháp:
a) Lấy hai điểm mà đồ thị đi qua, kẻ đường thẳng qua hai điểm đó.
b) Cho hai vế của đồ thị bằng nhau rồi giải phương trình tìm giao điểm.
Cách giải:
a) Vẽ đường thẳng \((d):y = 3x - 2\)
Với \(x = 0 \Rightarrow y = 3.0 - 2 = - 2\)
Với \(x = 1 \Rightarrow y = 3.1 - 2 = 1\)
Vẽ đường thẳng đi qua 2 điểm: \(A\left( {0; - 2} \right)\) và \(B\left( {1;1} \right)\) ta được đồ thị \((d):y = 3x - 2\) như sau:
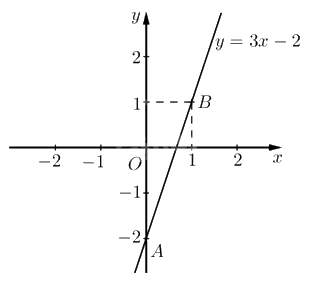
b) Tìm tọa độ giao điểm của đồ thị hàm số \((P):y = {x^2}\) với đường thẳng \((d):y = 3x - 2\).
Xét phương trình hoành độ giao điểm của (P) và (d) ta được:
\(\begin{array}{l}{x^2} = 3x - 2\\ \Leftrightarrow {x^2} - 3x + 2 = 0\\ \Leftrightarrow {x^2} - x - 2x + 2 = 0\\ \Leftrightarrow x\left( {x - 1} \right) - 2\left( {x - 1} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\end{array}\)
Với \(x = 1 \Rightarrow y = {1^2} = 1\)
Với \(x = 2 \Rightarrow y = {2^2} = 4\)
Vậy (d) và (P) cắt nhau tại 2 giao điểm là: \(\left( {1;1} \right)\) và \(\left( {2;4} \right)\)
Câu 3 (VD):
Phương pháp:
a) Sử dụng phương pháp thế hoặc trừ vế.
b) \(\Delta = {b^2} - 4.a.c\)
- \(\Delta = 0\) thì phương trình có nghiệm kép \({x_1} = {x_2} = \frac{{ - b}}{{2a}}\)
- \(\Delta < 0\) thì phương trình vô nghiệm
- \(\Delta > 0\)thì phương trình có hai nghiệm phân biệt:
\({x_1} = \frac{{ - b + \sqrt \Delta }}{{2.a}}\)
\({x_2} = \frac{{ - b - \sqrt \Delta }}{{2.a}}\)
Cách giải:
a) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y = 5}\\{3x - 2y = 5}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{l}}{x + y = 5}\\{3x - 2y = 5}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2x + 2y = 10}\\{3x - 2y = 5}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x + y = 5}\\{5x = 15}\end{array} \Leftrightarrow } \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = 5 - x}\\{x = 3}\end{array} \Leftrightarrow } \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = 2}\\{x = 3}\end{array}} \right.\)
Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {3;2} \right)\).
b) Giải phương trình \({x^2} - 9x + 14 = 0\).
phương trình \({x^2} - 9x + 14 = 0\) có \(\Delta = {\left( { - 9} \right)^2} - 4.1.14 = 81 - 56 = 25 > 0\) phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = \frac{{9 - \sqrt {25} }}{{2.1}} = 2\\{x_2} = \frac{{9 + \sqrt {25} }}{{2.1}} = 7\end{array} \right.\)
Vậy phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = 2\\{x_2} = 7\end{array} \right.\).
c) Cho phương trình \({x^2} - (m + 2)x + m - 3 = 0(*)\), với \(m\) là tham số.
1) Chứng minh rằng phương trình \(\left( * \right)\) luôn có hai nghiệm phân biệt với mọi \(m\).
Phương trình \({x^2} - (m + 2)x + m - 3 = 0(*)\) có \(\Delta = {\left[ { - \left( {m + 2} \right)} \right]^2} - 4.1.\left( {m - 3} \right) = {m^2} + 4m + 4 - 4m + 12 = {m^2} + 16 > 0\) với mọi m.
Vậy phương trình \(\left( * \right)\) luôn có hai nghiệm phân biệt với mọi \(m\).
2) Tìm \(m\) để phương trình \(\left( * \right)\) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \({x_1} + {x_2} + 2{x_1}{x_2} > 5\).
Gọi \({x_1},{x_2}\) là nghiệm của \({x_1},{x_2}\).
Áp dụng định lí Vi – ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m + 2\\{x_1}.{x_2} = m - 3\end{array} \right.\) thay vào \({x_1} + {x_2} + 2{x_1}{x_2} > 5\) ta có:
\(\begin{array}{l}m + 2 + 2\left( {m - 3} \right) > 5\\ \Leftrightarrow 3m - 4 > 5\\ \Leftrightarrow m > 3.\end{array}\)
Vậy với \(m > 3\) thì phương trình \(\left( * \right)\) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \({x_1} + {x_2} + 2{x_1}{x_2} > 5\).
Câu 4 (VD):
Cách giải:
a) Chứng minh rằng tứ giác AFHE nội tiếp.
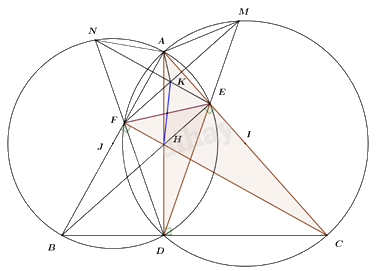
Ta có: \(\angle AFH = \angle AEH = {90^0}\) (do \(BE \bot AC,\,\,CF \bot AB\)).
\( \Rightarrow \angle AFH + \angle AEH = {90^0} + {90^0} = {180^0}\).
Mà 2 đỉnh E, F là hai đỉnh đối diện của tứ giác AFEH.
Vậy AFEH là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\)).
b) Chứng minh rằng $\Delta EAD\backsim \Delta EFC$.
Xét tứ giác CDHE có:
\(\begin{array}{l}\angle CEH = \angle CDH = {90^0}\,\,\left( {do\,\,AD \bot BC,\,\,BE \bot AC} \right)\\ \Rightarrow \angle CEH + \angle CDH = {90^0} + {90^0} = {180^0}\end{array}\)
Mà 2 đỉnh E, D là hai đỉnh đối diện của tứ giác CDHE.
\( \Rightarrow \) CDHE là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\)).
\( \Rightarrow \angle HCE = \angle HDE\) (hai góc nội tiếp cùng chắn cung HE).
\( \Rightarrow \angle FCE = \angle ADE\).
Vì AFEH nội tiếp (cmt) \( \Rightarrow \angle HAE = \angle HFE\) (hai góc nội tiếp cùng chắn cung HE).
\( \Rightarrow \angle DAE = \angle CFE\)
Xét \(\Delta EAD\) và \(\Delta EFC\) có:
\(\begin{align}\angle ADE=\angle FCE\,\,\left( cmt \right) \\ \angle DAE=\angle CFE\,\,\left( cmt \right) \\ \Rightarrow \Delta EAD\backsim \Delta EFC\,\,\left( g.g \right)\,\,\left( dpcm \right) \end{align}\)
c) Kẻ DE cắt đường tròn đường kính AC tại M \(\left( {M \ne D} \right)\); DF cắt đường tròn đường kính AB tại N \(\left( {N \ne D} \right)\). Gọi \(K = FM \cap EN\). Chứng minh rằng AF = AM và đường thẳng EF đi qua trung điểm của đoạn thẳng HK.
+) Chứng minh AF = AM.
Xét đường tròn đường kính AC ta có:
\(\angle AMF = \angle ACF\) (hai góc nội tiếp cùng chắn cung AF).
\(\angle AFM = \angle ADM\) (hai góc nội tiếp cùng chắn cung AM).
Mà \(\angle FCE = \angle ADE\,\,\left( {cmt} \right) \Rightarrow \angle ACF = \angle ADM\).
\( \Rightarrow \angle AMF = \angle AFM \Rightarrow \Delta AMF\) cân tại A (định nghĩa) \( \Rightarrow AF = AM\) (tính chất tam giác cân) (đpcm).
+) Chứng minh đường thẳng EF đi qua trung điểm của đoạn thẳng HK.
Xét tứ giác BDHF có: \(\angle BFH = \angle BDH = {90^0}\,\,\left( {do\,\,CF \bot AB,\,\,AD \bot BC} \right)\)
\( \Rightarrow \angle BFH + \angle BDH = {90^0} + {90^0} = {180^0}\)
Mà 2 đỉnh F, D là hai đỉnh đối diện của tứ giác BDHF
\( \Rightarrow \) BDHF là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\)).
\( \Rightarrow \angle FBH = \angle FDH\) (hai góc nội tiếp cùng chắn cung FH)
\( \Rightarrow \angle ABE = \angle ADN\).
Tương tự xét đường tròn đường kính AB ta có:
\(\angle ANE = \angle ABE\) (hai góc nội tiếp cùng chắn cung AE).
\(\angle AEN = \angle ADN\) (hai góc nội tiếp cùng chắn cung AN).
Mà \(\angle ABE = \angle AND\,\,\left( {cmt} \right) \Rightarrow \angle ANE = \angle AEN \Rightarrow \Delta ANE\) cân tại A (định nghĩa)
\( \Rightarrow AE = AN\) (tính chất tam giác cân)
Gọi I, J lần lượt là trung điểm của AC và AB
=> I, J lần lượt là tâm đường tròn đường kính AC và đường tròn đường kính AB.
Vì AM = AF (cmt) \( \Rightarrow A\) thuộc trung trực của FM.
Vì IM = IF (do I là tâm đường tròn đường kính AC) \( \Rightarrow I\) thuộc trung trực của FM.
\( \Rightarrow IA\) là trung trực của FM \( \Rightarrow IA \bot FM \Rightarrow FK \bot AC\).
Mà \(HE \bot AC\,\,\left( {do\,\,BE \bot AC} \right)\).
\( \Rightarrow \) FK // HE (từ vuông góc đến song song) (1)
Vì AE = AN (cmt) \( \Rightarrow A\) thuộc trung trực của EN.
Vì JE = JN (do J là tâm đường tròn đường kính AB) \( \Rightarrow J\) thuộc trung trực của AN.
\( \Rightarrow JA\) là trung trực của EN \( \Rightarrow JA \bot EN \Rightarrow EK \bot AB\).
Mà \(HF \bot AB\,\,\left( {do\,\,CF \bot AB} \right)\)
\( \Rightarrow \) EK // HF (từ vuông góc đến song song) (2)
Từ (1) và (2) => EHFK là hình bình hành (dhnb)
=> Hai đường chéo EF và HK cắt nhau tại trung điểm mỗi đường.
Vậy EF đi qua trung điểm của HK (đpcm).
Câu 5 (VDC):
Phương pháp:
Áp dụng BĐT Cô-si.
Cách giải:
Ta có:
\(\frac{{{a^3}}}{{{a^2} + b}} = \frac{{a\left( {{a^2} + b} \right) - ab}}{{{a^2} + b}} = a - \frac{{ab}}{{{a^2} + b}}\)
Áp dụng BĐT Cô-si ta có: \({a^2} + b \ge 2\sqrt {{a^2}b} = 2a\sqrt b \).
\(\begin{array}{l} \Rightarrow \frac{{ab}}{{{a^2} + b}} \le \frac{{ab}}{{2a\sqrt b }} = \frac{{\sqrt b }}{2}\\ \Rightarrow a - \frac{{ab}}{{{a^2} + b}} \ge a - \frac{{\sqrt b }}{2}\\ \Rightarrow \frac{{{a^3}}}{{{a^2} + b}} \ge a - \frac{{\sqrt b }}{2}\end{array}\)
Chứng minh tương tự ta có:
\(\begin{array}{l}\frac{{{b^3}}}{{{b^2} + c}} \ge b - \frac{{\sqrt c }}{2}\\\frac{{{c^3}}}{{{c^2} + a}} \ge c - \frac{{\sqrt a }}{2}\end{array}\)
Cộng vế theo vế ba bất phương trình ta được:
\(\frac{{{a^3}}}{{{a^2} + b}} + \frac{{{b^3}}}{{{b^2} + c}} + \frac{{{c^3}}}{{{c^2} + a}} \ge \left( {a + b + c} \right) - \frac{{\sqrt a + \sqrt b + \sqrt c }}{2} = 3 - \frac{{\sqrt a + \sqrt b + \sqrt c }}{2}\)
Áp dụng BĐT Bunhiacopxki ta có:
\({\left( {\sqrt a + \sqrt b + \sqrt c } \right)^2} \le 3\left( {a + b + c} \right) = 3.3 = 9 \Rightarrow \sqrt a + \sqrt b + \sqrt c \le 3\).
Vậy \(\frac{{{a^3}}}{{{a^2} + b}} + \frac{{{b^3}}}{{{b^2} + c}} + \frac{{{c^3}}}{{{c^2} + a}} \ge 3 - \frac{3}{2} = \frac{3}{2}\,\,\left( {dpcm} \right)\).
Câu 1: a) Tính giá trị các biểu thức sau:
\(A = \sqrt {36} {\rm{ \;}} - \sqrt 4 \)
\(B = \sqrt {{{(4 - \sqrt {15} )}^2}} {\rm{ \;}} + \sqrt {15} \)
\(C = \frac{{\sqrt {12} {\rm{ \;}} + \sqrt {27} }}{{\sqrt 3 }}\)
b) Cho biểu thức: \(P = \left( {\frac{1}{{\sqrt x {\rm{ \;}} - 3}} + \frac{1}{{x - 9}}} \right):\frac{{\sqrt x {\rm{ \;}} + 4}}{{\sqrt x {\rm{ \;}} + 3}}\) với \(x \ge 0;x \ne 9\).
1) Rút gọn biểu thức \(P\).
2) Tìm giá trị của \(x\) để \(P = \frac{1}{2}\).
Câu 2: a) Vẽ đường thẳng \((d):y = 3x - 2\)
b) Tìm tọa độ giao điểm của đồ thị hàm số \((P):y = {x^2}\) với đường thẳng \((d):y = 3x - 2\).
Câu 3: a) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y = 5}\\{3x - 2y = 5}\end{array}} \right.\).
b) Giải phương trình \({x^2} - 9x + 14 = 0\).
c) Cho phương trình \({x^2} - (m + 2)x + m - 3 = 0(*)\), với \(m\) là tham số.
1) Chứng minh rằng phương trình \(\left( * \right)\) luôn có hai nghiệm phân biệt với mọi \(m\).
2) Tìm \(m\) để phương trình \(\left( * \right)\) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \({x_1} + {x_2} + 2{x_1}{x_2} > 5\).
Câu 4: Cho tam giác ABC không cân và có ba góc nhọn. Các đường cao AD, BE, CF cắt nhau tại H (với \(D \in BC\), \(E \in CA\), \(F \in AB\)).
a) Chứng minh rằng tứ giác AFHE nội tiếp.
b) Chứng minh rằng $\Delta EAD\backsim \Delta EFC$.
c) Kẻ DE cắt đường tròn đường kính AC tại M \(\left( {M \ne D} \right)\); DF cắt đường tròn đường kính AB tại N \(\left( {N \ne D} \right)\). Gọi \(K = FM \cap EN\). Chứng minh rằng AF = AM và đường thẳng EF đi qua trung điểm của đoạn thẳng HK.
Câu 5: Cho các số thực dương a, b, c thoả mãn a + b + c = 3. Chứng minh rằng:
\(\frac{{{a^3}}}{{{a^2} + b}} + \frac{{{b^3}}}{{{b^2} + c}} + \frac{{{c^3}}}{{{c^2} + a}} \ge \frac{3}{2}\)
----- HẾT -----
Câu 1 (VD):
Phương pháp:
a) Sử dụng tính chất căn bậc hai.
b) Quy đồng và rút gọn.
Cách giải:
a) Tính giá trị các biểu thức sau:
\(A = \sqrt {36} {\rm{ \;}} - \sqrt 4 \)
\(B = \sqrt {{{(4 - \sqrt {15} )}^2}} {\rm{ \;}} + \sqrt {15} \)
\(C = \frac{{\sqrt {12} {\rm{ \;}} + \sqrt {27} }}{{\sqrt 3 }}\)
Ta có \(A = \sqrt {36} - \sqrt 4 = \sqrt {{6^2}} - \sqrt {{2^2}} = 6 - 2 = 4\)
\(B = \sqrt {{{(4 - \sqrt {15} )}^2}} + \sqrt {15} = \left| {4 - \sqrt {15} } \right| + \sqrt {15} = 4 - \sqrt {15} + \sqrt {15} = 4\)
\(C = \frac{{\sqrt {12} + \sqrt {27} }}{{\sqrt 3 }} = \frac{{\sqrt {4.3} + \sqrt {9.3} }}{{\sqrt 3 }} = \frac{{2\sqrt 3 + 3\sqrt 3 }}{{\sqrt 3 }} = \frac{{5\sqrt 3 }}{{\sqrt 3 }} = 5\)
Vậy A = 4, B = 4, C = 5.
b) Cho biểu thức: \(P = \left( {\frac{1}{{\sqrt x - 3}} + \frac{1}{{x - 9}}} \right):\frac{{\sqrt x + 4}}{{\sqrt x + 3}}\) với \(x \ge 0;x \ne 9\).
1) Rút gọn biểu thức \(P\).
Ta có \(P = \left( {\frac{1}{{\sqrt x - 3}} + \frac{1}{{x - 9}}} \right):\frac{{\sqrt x + 4}}{{\sqrt x + 3}}\)
\(\begin{array}{l} = \left( {\frac{1}{{\sqrt x - 3}} + \frac{1}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}} \right).\frac{{\sqrt x + 3}}{{\sqrt x + 4}}\\ = \left( {\frac{{\sqrt x + 3}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} + \frac{1}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}} \right).\frac{{\sqrt x + 3}}{{\sqrt x + 4}}\\ = \frac{{\sqrt x + 4}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}.\frac{{\sqrt x + 3}}{{\sqrt x + 4}}\\ = \frac{1}{{\sqrt x - 3}}\end{array}\)
Vậy \(P = \frac{1}{{\sqrt x - 3}}\) với \(x \ge 0;x \ne 9\).
2) Tìm giá trị của \(x\) để \(P = \frac{1}{2}\).
Ta có \(P = \frac{1}{{\sqrt x - 3}}\) với \(x \ge 0;x \ne 9\).
Để \(P = \frac{1}{2}\)
\(\begin{array}{l} \Leftrightarrow \frac{1}{{\sqrt x - 3}} = \frac{1}{2}\\ \Leftrightarrow \sqrt x - 3 = 2\\ \Leftrightarrow \sqrt x = 5\\ \Leftrightarrow x = 25\left( {TM} \right)\end{array}\)
Vậy để \(P = \frac{1}{2}\) thì \(x = 25\).
Câu 2 (VD):
Phương pháp:
a) Lấy hai điểm mà đồ thị đi qua, kẻ đường thẳng qua hai điểm đó.
b) Cho hai vế của đồ thị bằng nhau rồi giải phương trình tìm giao điểm.
Cách giải:
a) Vẽ đường thẳng \((d):y = 3x - 2\)
Với \(x = 0 \Rightarrow y = 3.0 - 2 = - 2\)
Với \(x = 1 \Rightarrow y = 3.1 - 2 = 1\)
Vẽ đường thẳng đi qua 2 điểm: \(A\left( {0; - 2} \right)\) và \(B\left( {1;1} \right)\) ta được đồ thị \((d):y = 3x - 2\) như sau:

b) Tìm tọa độ giao điểm của đồ thị hàm số \((P):y = {x^2}\) với đường thẳng \((d):y = 3x - 2\).
Xét phương trình hoành độ giao điểm của (P) và (d) ta được:
\(\begin{array}{l}{x^2} = 3x - 2\\ \Leftrightarrow {x^2} - 3x + 2 = 0\\ \Leftrightarrow {x^2} - x - 2x + 2 = 0\\ \Leftrightarrow x\left( {x - 1} \right) - 2\left( {x - 1} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\end{array}\)
Với \(x = 1 \Rightarrow y = {1^2} = 1\)
Với \(x = 2 \Rightarrow y = {2^2} = 4\)
Vậy (d) và (P) cắt nhau tại 2 giao điểm là: \(\left( {1;1} \right)\) và \(\left( {2;4} \right)\)
Câu 3 (VD):
Phương pháp:
a) Sử dụng phương pháp thế hoặc trừ vế.
b) \(\Delta = {b^2} - 4.a.c\)
- \(\Delta = 0\) thì phương trình có nghiệm kép \({x_1} = {x_2} = \frac{{ - b}}{{2a}}\)
- \(\Delta < 0\) thì phương trình vô nghiệm
- \(\Delta > 0\)thì phương trình có hai nghiệm phân biệt:
\({x_1} = \frac{{ - b + \sqrt \Delta }}{{2.a}}\)
\({x_2} = \frac{{ - b - \sqrt \Delta }}{{2.a}}\)
Cách giải:
a) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y = 5}\\{3x - 2y = 5}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{l}}{x + y = 5}\\{3x - 2y = 5}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2x + 2y = 10}\\{3x - 2y = 5}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x + y = 5}\\{5x = 15}\end{array} \Leftrightarrow } \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = 5 - x}\\{x = 3}\end{array} \Leftrightarrow } \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = 2}\\{x = 3}\end{array}} \right.\)
Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {3;2} \right)\).
b) Giải phương trình \({x^2} - 9x + 14 = 0\).
phương trình \({x^2} - 9x + 14 = 0\) có \(\Delta = {\left( { - 9} \right)^2} - 4.1.14 = 81 - 56 = 25 > 0\) phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = \frac{{9 - \sqrt {25} }}{{2.1}} = 2\\{x_2} = \frac{{9 + \sqrt {25} }}{{2.1}} = 7\end{array} \right.\)
Vậy phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = 2\\{x_2} = 7\end{array} \right.\).
c) Cho phương trình \({x^2} - (m + 2)x + m - 3 = 0(*)\), với \(m\) là tham số.
1) Chứng minh rằng phương trình \(\left( * \right)\) luôn có hai nghiệm phân biệt với mọi \(m\).
Phương trình \({x^2} - (m + 2)x + m - 3 = 0(*)\) có \(\Delta = {\left[ { - \left( {m + 2} \right)} \right]^2} - 4.1.\left( {m - 3} \right) = {m^2} + 4m + 4 - 4m + 12 = {m^2} + 16 > 0\) với mọi m.
Vậy phương trình \(\left( * \right)\) luôn có hai nghiệm phân biệt với mọi \(m\).
2) Tìm \(m\) để phương trình \(\left( * \right)\) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \({x_1} + {x_2} + 2{x_1}{x_2} > 5\).
Gọi \({x_1},{x_2}\) là nghiệm của \({x_1},{x_2}\).
Áp dụng định lí Vi – ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m + 2\\{x_1}.{x_2} = m - 3\end{array} \right.\) thay vào \({x_1} + {x_2} + 2{x_1}{x_2} > 5\) ta có:
\(\begin{array}{l}m + 2 + 2\left( {m - 3} \right) > 5\\ \Leftrightarrow 3m - 4 > 5\\ \Leftrightarrow m > 3.\end{array}\)
Vậy với \(m > 3\) thì phương trình \(\left( * \right)\) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \({x_1} + {x_2} + 2{x_1}{x_2} > 5\).
Câu 4 (VD):
Cách giải:
a) Chứng minh rằng tứ giác AFHE nội tiếp.
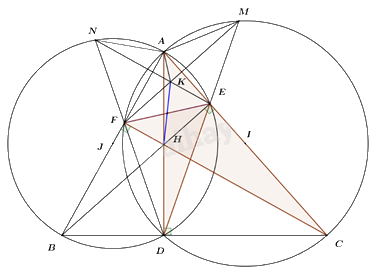
Ta có: \(\angle AFH = \angle AEH = {90^0}\) (do \(BE \bot AC,\,\,CF \bot AB\)).
\( \Rightarrow \angle AFH + \angle AEH = {90^0} + {90^0} = {180^0}\).
Mà 2 đỉnh E, F là hai đỉnh đối diện của tứ giác AFEH.
Vậy AFEH là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\)).
b) Chứng minh rằng $\Delta EAD\backsim \Delta EFC$.
Xét tứ giác CDHE có:
\(\begin{array}{l}\angle CEH = \angle CDH = {90^0}\,\,\left( {do\,\,AD \bot BC,\,\,BE \bot AC} \right)\\ \Rightarrow \angle CEH + \angle CDH = {90^0} + {90^0} = {180^0}\end{array}\)
Mà 2 đỉnh E, D là hai đỉnh đối diện của tứ giác CDHE.
\( \Rightarrow \) CDHE là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\)).
\( \Rightarrow \angle HCE = \angle HDE\) (hai góc nội tiếp cùng chắn cung HE).
\( \Rightarrow \angle FCE = \angle ADE\).
Vì AFEH nội tiếp (cmt) \( \Rightarrow \angle HAE = \angle HFE\) (hai góc nội tiếp cùng chắn cung HE).
\( \Rightarrow \angle DAE = \angle CFE\)
Xét \(\Delta EAD\) và \(\Delta EFC\) có:
\(\begin{align}\angle ADE=\angle FCE\,\,\left( cmt \right) \\ \angle DAE=\angle CFE\,\,\left( cmt \right) \\ \Rightarrow \Delta EAD\backsim \Delta EFC\,\,\left( g.g \right)\,\,\left( dpcm \right) \end{align}\)
c) Kẻ DE cắt đường tròn đường kính AC tại M \(\left( {M \ne D} \right)\); DF cắt đường tròn đường kính AB tại N \(\left( {N \ne D} \right)\). Gọi \(K = FM \cap EN\). Chứng minh rằng AF = AM và đường thẳng EF đi qua trung điểm của đoạn thẳng HK.
+) Chứng minh AF = AM.
Xét đường tròn đường kính AC ta có:
\(\angle AMF = \angle ACF\) (hai góc nội tiếp cùng chắn cung AF).
\(\angle AFM = \angle ADM\) (hai góc nội tiếp cùng chắn cung AM).
Mà \(\angle FCE = \angle ADE\,\,\left( {cmt} \right) \Rightarrow \angle ACF = \angle ADM\).
\( \Rightarrow \angle AMF = \angle AFM \Rightarrow \Delta AMF\) cân tại A (định nghĩa) \( \Rightarrow AF = AM\) (tính chất tam giác cân) (đpcm).
+) Chứng minh đường thẳng EF đi qua trung điểm của đoạn thẳng HK.
Xét tứ giác BDHF có: \(\angle BFH = \angle BDH = {90^0}\,\,\left( {do\,\,CF \bot AB,\,\,AD \bot BC} \right)\)
\( \Rightarrow \angle BFH + \angle BDH = {90^0} + {90^0} = {180^0}\)
Mà 2 đỉnh F, D là hai đỉnh đối diện của tứ giác BDHF
\( \Rightarrow \) BDHF là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\)).
\( \Rightarrow \angle FBH = \angle FDH\) (hai góc nội tiếp cùng chắn cung FH)
\( \Rightarrow \angle ABE = \angle ADN\).
Tương tự xét đường tròn đường kính AB ta có:
\(\angle ANE = \angle ABE\) (hai góc nội tiếp cùng chắn cung AE).
\(\angle AEN = \angle ADN\) (hai góc nội tiếp cùng chắn cung AN).
Mà \(\angle ABE = \angle AND\,\,\left( {cmt} \right) \Rightarrow \angle ANE = \angle AEN \Rightarrow \Delta ANE\) cân tại A (định nghĩa)
\( \Rightarrow AE = AN\) (tính chất tam giác cân)
Gọi I, J lần lượt là trung điểm của AC và AB
=> I, J lần lượt là tâm đường tròn đường kính AC và đường tròn đường kính AB.
Vì AM = AF (cmt) \( \Rightarrow A\) thuộc trung trực của FM.
Vì IM = IF (do I là tâm đường tròn đường kính AC) \( \Rightarrow I\) thuộc trung trực của FM.
\( \Rightarrow IA\) là trung trực của FM \( \Rightarrow IA \bot FM \Rightarrow FK \bot AC\).
Mà \(HE \bot AC\,\,\left( {do\,\,BE \bot AC} \right)\).
\( \Rightarrow \) FK // HE (từ vuông góc đến song song) (1)
Vì AE = AN (cmt) \( \Rightarrow A\) thuộc trung trực của EN.
Vì JE = JN (do J là tâm đường tròn đường kính AB) \( \Rightarrow J\) thuộc trung trực của AN.
\( \Rightarrow JA\) là trung trực của EN \( \Rightarrow JA \bot EN \Rightarrow EK \bot AB\).
Mà \(HF \bot AB\,\,\left( {do\,\,CF \bot AB} \right)\)
\( \Rightarrow \) EK // HF (từ vuông góc đến song song) (2)
Từ (1) và (2) => EHFK là hình bình hành (dhnb)
=> Hai đường chéo EF và HK cắt nhau tại trung điểm mỗi đường.
Vậy EF đi qua trung điểm của HK (đpcm).
Câu 5 (VDC):
Phương pháp:
Áp dụng BĐT Cô-si.
Cách giải:
Ta có:
\(\frac{{{a^3}}}{{{a^2} + b}} = \frac{{a\left( {{a^2} + b} \right) - ab}}{{{a^2} + b}} = a - \frac{{ab}}{{{a^2} + b}}\)
Áp dụng BĐT Cô-si ta có: \({a^2} + b \ge 2\sqrt {{a^2}b} = 2a\sqrt b \).
\(\begin{array}{l} \Rightarrow \frac{{ab}}{{{a^2} + b}} \le \frac{{ab}}{{2a\sqrt b }} = \frac{{\sqrt b }}{2}\\ \Rightarrow a - \frac{{ab}}{{{a^2} + b}} \ge a - \frac{{\sqrt b }}{2}\\ \Rightarrow \frac{{{a^3}}}{{{a^2} + b}} \ge a - \frac{{\sqrt b }}{2}\end{array}\)
Chứng minh tương tự ta có:
\(\begin{array}{l}\frac{{{b^3}}}{{{b^2} + c}} \ge b - \frac{{\sqrt c }}{2}\\\frac{{{c^3}}}{{{c^2} + a}} \ge c - \frac{{\sqrt a }}{2}\end{array}\)
Cộng vế theo vế ba bất phương trình ta được:
\(\frac{{{a^3}}}{{{a^2} + b}} + \frac{{{b^3}}}{{{b^2} + c}} + \frac{{{c^3}}}{{{c^2} + a}} \ge \left( {a + b + c} \right) - \frac{{\sqrt a + \sqrt b + \sqrt c }}{2} = 3 - \frac{{\sqrt a + \sqrt b + \sqrt c }}{2}\)
Áp dụng BĐT Bunhiacopxki ta có:
\({\left( {\sqrt a + \sqrt b + \sqrt c } \right)^2} \le 3\left( {a + b + c} \right) = 3.3 = 9 \Rightarrow \sqrt a + \sqrt b + \sqrt c \le 3\).
Vậy \(\frac{{{a^3}}}{{{a^2} + b}} + \frac{{{b^3}}}{{{b^2} + c}} + \frac{{{c^3}}}{{{c^2} + a}} \ge 3 - \frac{3}{2} = \frac{3}{2}\,\,\left( {dpcm} \right)\).
Kỳ thi tuyển sinh vào lớp 10 là một bước ngoặt quan trọng trong quá trình học tập của mỗi học sinh. Để giúp các em học sinh tỉnh Lạng Sơn chuẩn bị tốt nhất cho kỳ thi này, giaitoan.edu.vn xin giới thiệu bộ đề thi vào 10 môn Toán Lạng Sơn năm 2023, kèm theo phân tích chi tiết và hướng dẫn ôn tập.
Đề thi vào 10 môn Toán Lạng Sơn năm 2023 thường có cấu trúc tương tự như các năm trước, bao gồm các dạng bài tập sau:
Độ khó của đề thi thường ở mức trung bình, đòi hỏi học sinh phải nắm vững kiến thức cơ bản và có khả năng vận dụng linh hoạt vào giải quyết các bài toán.
Chúng tôi đã thu thập và phân tích chi tiết các đề thi vào 10 môn Toán Lạng Sơn năm 2023, bao gồm:
Qua phân tích, chúng tôi nhận thấy rằng các đề thi thường tập trung vào các chủ đề sau:
Để đạt kết quả tốt nhất trong kỳ thi vào 10 môn Toán Lạng Sơn năm 2023, các em học sinh cần có một kế hoạch ôn tập khoa học và hiệu quả. Dưới đây là một số gợi ý:
Giaitoan.edu.vn là một nền tảng học toán online uy tín và chất lượng, cung cấp cho học sinh các khóa học và tài liệu ôn tập hiệu quả. Khi luyện thi vào 10 môn Toán tại giaitoan.edu.vn, các em sẽ được hưởng những lợi ích sau:
Kỳ thi vào 10 môn Toán Lạng Sơn năm 2023 là một kỳ thi quan trọng, đòi hỏi các em học sinh phải chuẩn bị kỹ lưỡng. Hy vọng với bộ đề thi và hướng dẫn ôn tập mà giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn và đạt kết quả tốt nhất trong kỳ thi sắp tới. Chúc các em thành công!