Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Quảng Ninh năm 2023. Đây là tài liệu ôn tập vô cùng quan trọng dành cho các em học sinh đang chuẩn bị cho kỳ thi sắp tới.
Chúng tôi cung cấp đầy đủ các đề thi chính thức, đáp án chi tiết và phương pháp giải bài tập hiệu quả, giúp các em tự tin đối mặt với mọi dạng bài thi.
Câu 1: a) Thực hiện phép tính \(2\sqrt 9 {\rm{ \;}} - \sqrt {16} \). b) Xác định hệ số a của đồ thị hàm số \(y = a{x^2}\) đi qua điểm A(1;2). c) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2x + y = 7}\\{x - 2y = {\rm{ \;}} - 4}\end{array}} \right.\) d) Rút gọn biểu thức \(P = \left( {\frac{1}{{\sqrt x {\rm{ \;}} - 3}} + \frac{2}{{\sqrt x {\rm{ \;}} + 3}}} \right):\frac{{\sqrt x {\rm{ \;}} - 1}}{{\sqrt x {\rm{ \;}} - 3}}\) với \(x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 1,{\mkern 1mu
Câu 1: a) Thực hiện phép tính \(2\sqrt 9 {\rm{ \;}} - \sqrt {16} \).
b) Xác định hệ số a của đồ thị hàm số \(y = a{x^2}\) đi qua điểm A(1;2).
c) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2x + y = 7}\\{x - 2y = {\rm{ \;}} - 4}\end{array}} \right.\)
d) Rút gọn biểu thức \(P = \left( {\frac{1}{{\sqrt x {\rm{ \;}} - 3}} + \frac{2}{{\sqrt x {\rm{ \;}} + 3}}} \right):\frac{{\sqrt x {\rm{ \;}} - 1}}{{\sqrt x {\rm{ \;}} - 3}}\) với \(x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 1,{\mkern 1mu} {\mkern 1mu} x \ne 9\).
Câu 2: Cho phuơng trình \({x^2} - 2(m + 1)x - 9 = 0\), với \(m\) là tham số.)
a) Giải phương trình khi \(m = 3\);
b) Tìm các giá trị của \(m\) để phuơng trình có nghiệm \(x = 2\);
c) Tìm các giá trị của \(m\) để phuơng trình có hai nghiệm phân biệt \({x_1},{x_2}\) sao cho \({x_1} < {x_2}\) và \(\left| {{x_1}} \right| - \left| {{x_2}} \right| = {\rm{ \;}} - 6\).
Câu 3: Hai địa điểm A và B cách nhau 280 km. Hai ô tô cùng xuất phát từ A đến B. Biết vận tốc của xe thứ nhất lớn hơn vận tốc của xe thứ hai 10 km/h và xe thứ nhất đến B sớm hơn xe thứ hai 30 phút. Tính vận tốc mỗi xe?
Câu 4: Cho nửa đuờng tròn tâm \(O\), đuờng kính BC. Trên nửa đường tròn (O) lấy A (A khác B và \(C\)), gọi \(H\) là hình chiếu của \(A\) trên B C. Trên cung AC của nửa đường tròn (O) lấy điểm D (D khác \(A\) và \(C\)), gọi \(E\) là hình chiếu của \(A\) trên BD, I là giao điểm của hai đường thằng AH và BD.
a) Chứng minh tứ giác ABHE nội tiếp;
b) Chứng minh BI.BD = BH.BC.
c) Chứng minh hai tam giác AHE và ACD đồng dạng;
d) Hai đường thẳng AE và DH cắt nhau tại \(F\). Chứng minh \(IF//AD\).
Câu 5: Một người thợ cơ khí cần cắt vừa đủ một cây sắt dài 100 dm thành các đoạn để hàn lại thành khung một hình lập phương và một hình hộp chữ nhật. Biết hình hộp chữ nhật có chiều dài gấp 6 lần chiều rộng và chiều cao bằng chiều rộng (hình vẽ minh họa). Tìm độ dài của các đoạn sắt sao cho tổng thể tích cùa hai hình thu được nhỏ nhất?
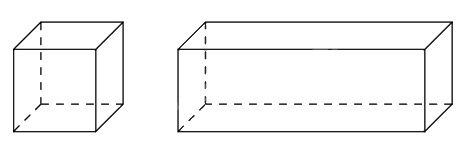
-----HẾT-----
Câu 1 (TH):
Phương pháp:
a) Khai phương căn bậc hai
b) Thay tọa độ A vào hàm số tìm a
c) Giải hệ bằng phương pháp thế hoặc cộng đại số
d) Tìm mẫu số chung quy đồng và rút gọn biểu thức.
Cách giải:
a) Thực hiện phép tính \(2\sqrt 9 {\rm{ \;}} - \sqrt {16} \).
\(\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} 2\sqrt 9 {\rm{ \;}} - \sqrt {16} }\\{ = 2.\sqrt {{3^2}} {\rm{ \;}} - \sqrt {{4^2}} }\\{ = 2.3 - 4}\\{ = 6 - 4}\\{ = 2}\end{array}\)
b) Xác định hệ số a của đồ thị hàm số \(y = a{x^2}\) đi qua điểm A(1;2).
Thay x = 1, y = 2 vào hàm số \(y = a{x^2}\) ta có: \(2 = a{.1^2} \Leftrightarrow a = 2.\)
Vậy a = 2.
c) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2x + y = 7}\\{x - 2y = {\rm{ \;}} - 4}\end{array}} \right.\)
\(\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{2x + y = 7}\\{x - 2y = - 4}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2x + y = 7}\\{x = 2y - 4}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2\left( {2y - 4} \right) + y = 7}\\{x = 2y - 4}\end{array}} \right.}\\{ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4y - 8 + y = 7}\\{x = 2y - 4}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{5y = 15}\\{x = 2y - 4}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = 3}\\{x = 2y - 4}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = 3}\end{array}} \right.}\end{array}\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {2;3} \right)\).
d) Rút gọn biểu thức \(P = \left( {\frac{1}{{\sqrt x {\rm{ \;}} - 3}} + \frac{2}{{\sqrt x {\rm{ \;}} + 3}}} \right):\frac{{\sqrt x {\rm{ \;}} - 1}}{{\sqrt x {\rm{ \;}} - 3}}\) với \(x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 1,{\mkern 1mu} {\mkern 1mu} x \ne 9\).
Với \(x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 1,{\mkern 1mu} {\mkern 1mu} x \ne 9\) ta có:
\(\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} P = \left( {\frac{1}{{\sqrt x - 3}} + \frac{2}{{\sqrt x + 3}}} \right):\frac{{\sqrt x - 1}}{{\sqrt x - 3}}}\\{ \Leftrightarrow P = \frac{{\sqrt x + 3 + 2\left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}:\frac{{\sqrt x - 1}}{{\sqrt x - 3}}}\\{ \Leftrightarrow P = \frac{{\sqrt x + 3 + 2\sqrt x - 6}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}.\frac{{\sqrt x - 3}}{{\sqrt x - 1}}}\\{ \Leftrightarrow P = \frac{{3\sqrt x - 3}}{{\sqrt x + 3}}.\frac{1}{{\sqrt x - 1}}}\\{ \Leftrightarrow P = \frac{{3\left( {\sqrt x - 1} \right)}}{{\sqrt x + 3}}.\frac{1}{{\sqrt x - 1}}}\\{ \Leftrightarrow P = \frac{3}{{\sqrt x + 3}}}\end{array}\)
Vậy với \(x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 1,{\mkern 1mu} {\mkern 1mu} x \ne 9\) thì \(P = \frac{3}{{\sqrt x {\rm{ \;}} + 3}}\).
Câu 2 (TH):
Phương pháp:
a) Thay m = 3 vào phương trình và giải phương trình bậc 2
b) Thay x = 2 vào phương trình tìm m
c) Chứng minh phương trình luôn có 2 nghiệm trái dấu và sử dụng hệ thức viet
Cách giải:
a) Giải phương trình khi \(m = 3\);
Khi \(m = 3\) phương trình trở thành: \({x^2} - 8x - 9 = 0\), ta có: \({\Delta ^\prime } = {( - 4)^2} - 1.( - 9) = 25 > 0\)
Suy ra phương trình có hai nghiệm phân biệt:
\(\left[ {\begin{array}{*{20}{l}}{{x_1} = \frac{{4 + \sqrt {25} }}{1} = 9}\\{{x_2} = \frac{{4 - \sqrt {25} }}{1} = {\rm{ \;}} - 1}\end{array}.} \right.\)
b) Tìm các giá trị của \(m\) để phuơng trình có nghiệm \(x = 2\);
Phương trình có nghiệm \(x = 2\) nên thay \(x = 2\) vào phương trình ta có:
\(\begin{array}{*{20}{l}}{{2^2} - 2(m + 1)2 - 9 = 0}\\{ \Leftrightarrow 4 - 4m - 4 - 9 = 0}\\{ \Leftrightarrow {\rm{ \;}} - 4m - 9 = 0 \Leftrightarrow m = {\rm{ \;}} - \frac{9}{4}}\end{array}\)
Vậy để phương trình có nghiệm \(x = 2\) thì \(m = {\rm{ \;}} - \frac{9}{4}\).
c) Tìm các giá trị của \(m\) để phuơng trình có hai nghiệm phân biệt \({x_1},{x_2}\) sao cho \({x_1} < {x_2}\) và \(\left| {{x_1}} \right| - \left| {{x_2}} \right| = {\rm{ \;}} - 6\).
Xét phương trình \({x^2} - 2(m + 1)x - 9 = 0\) có \(a.c = {\rm{ \;}} - 9 < 0\) nên phương trình luôn có 2 nghiệm trái dấu \({x_1},{x_2}\) Áp dụng hệ thức viet ta có \({x_1} + {x_2} = 2(m + 1)\)
Do \({x_1} < {x_2} \Rightarrow {x_1} < 0 < {x_2}\)
Để \(\left| {{x_1}} \right| - \left| {{x_2}} \right| = {\rm{ \;}} - 6\)
\(\begin{array}{*{20}{l}}{ - {x_1} - {x_2} = {\rm{ \;}} - 6}\\{ \Leftrightarrow {\rm{ \;}} - \left( {{x_1} + {x_2}} \right) = {\rm{ \;}} - 6}\\{ \Leftrightarrow {x_1} + {x_2} = 6}\\{ \Leftrightarrow 2(m + 1) = 6}\\{ \Leftrightarrow m + 1 = 3 \Leftrightarrow m = 2}\end{array}\)
Vậy với \(m = 2\) thì phương trình có hai nghiệm phân biệt \({x_1},{x_2}\) sao cho \({x_1} < {x_2}\) và \(\left| {{x_1}} \right| - \left| {{x_2}} \right| = {\rm{ \;}} - 6\).
Câu 3 (VD):
Phương pháp:
Gọi vận tốc của xe thứ hai là \(x\) (km/h, \(x > 0\)).
Biểu diễn vận tốc, thời gian của 2 xe theo x và lập phương trình tìm x.
Cách giải:
Gọi vận tốc của xe thứ hai là \(x\) (km/h, \(x > 0\)).
Vì vận tốc của xe thứ nhất lớn hơn vận tốc của xe thứ hai là 10 km/h nên vận tốc của xe thứ nhất là \(x + 10\) (km/h)
Thời gian xe thứ nhất đi từ A đến B là: \(\frac{{280}}{{x + 10}}\) (giờ)
Thời gian xe thứ hai đi từ A đến B là: \(\frac{{280}}{x}\) (giờ)
Vì xe thứ nhất đến B sớm hơn xe thứ hai 30 phút = \(\frac{1}{2}\)giờ nên ta có:
\(\frac{{280}}{x} - \frac{{280}}{{x + 10}} = \frac{1}{2}\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow \frac{{560\left( {x + 10} \right)}}{{2x\left( {x + 10} \right)}} - \frac{{560x}}{{2x\left( {x + 10} \right)}} = \frac{{x\left( {x + 10} \right)}}{{2x\left( {x + 10} \right)}}}\\{ \Leftrightarrow 560\left( {x + 10} \right) - 560x = x\left( {x + 10} \right)}\\{ \Leftrightarrow 560x + 5600 - 560x = {x^2} + 10x}\\{ \Leftrightarrow {x^2} + 10x - 5600 = 0}\\{ \Leftrightarrow {x^2} - 70x + 80x - 5600 = 0}\\{ \Leftrightarrow x\left( {x - 70} \right) + 80\left( {x - 70} \right) = 0}\\{ \Leftrightarrow \left( {x + 80} \right)\left( {x - 70} \right) = 0}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x + 80 = 0}\\{x - 70 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 80{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} (KTM)}\\{x = 70{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} (TM)}\end{array}} \right.}\end{array}\)
Vậy vận tốc xe thứ nhất là 80km/h, vận tốc xe thứ hai là 70km/h.
Câu 4 (VD):
Phương pháp:
a) Sử dụng tính chất hai góc kề nhau cùng nhìn một cạnh dưới 2 góc bằng nhau
b) Chứng minh $\Delta BIH\backsim \Delta BCD\,\,(g\cdot g)$
c) Chứng minh $\Delta AEH\backsim \Delta ADC(g.g)\,\,$
d) Chứng minh I là trực tâm của tam giác \({\rm{SAB}}\) và sử dụng định lý Talet
Cách giải:
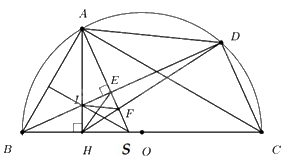
a) Chứng minh tứ giác ABHE nội tiếp;
Do \(AH \bot BC(gt),\,\,AE \bot BD(gt) \Rightarrow \angle AHB = \angle AEB = {90^0}\)
Mà \({\rm{E}},{\rm{H}}\) là 2 đỉnh kề nhau, cùng nhìn \({\rm{AD}}\) dưới 2 góc bằng nhau nên \({\rm{A}},{\rm{E}},{\rm{H}},{\rm{B}}\) cùng thuộc một đường tròn (dhnb)
Hay tứ giác ABHE nội tiếp (đpcm).
b) Chứng minh BI.BD = BH.BC.
Ta có \(\angle BDC = {90^0}\) (góc nội tiếp chắn nửa đường tròn).
Xét \(\Delta BIH\) và \(\Delta BCD\) có:
\(\angle CBD\) chung
\(\angle BHI = \angle BDC = {90^0}\)
$\Rightarrow \Delta BIH\backsim \Delta BCD(g\cdot g)$
\( \Rightarrow \frac{{BI}}{{BC}} = \frac{{BH}}{{BD}}\) (cặp cạnh tương ứng tỉ lệ)
\( \Rightarrow BI.BD = BH.BC{\mkern 1mu} {\mkern 1mu} (dpcm)\)
c) Chứng minh hai tam giác AHE và ACD đồng dạng;
Do ABHE nội tiếp (cmt) nên \(\angle AHE = \angle ABE\) (hai góc nội tiếp cùng chắn cung AE).
Mà \(\angle ABE = \angle ACD\) (hai góc nội tiếp cùng chắn cung AD).
\( \Rightarrow \angle AHE = \angle ACD\)
Do ABHE nội tiếp (cmt) nên \(\angle HAE = \angle HBE = \angle CBD\) (hai góc nội tiếp cùng chắn cung HE).
Lại có tứ giác ABCD nội tiếp \((O) \Rightarrow \angle CBD = \angle CAD\) (hai góc nội tiếp cùng chắn cung \({\rm{CD}}\) )
\( \Rightarrow \angle HAE = \angle CAD\)
Xét tam giác \({\rm{AHE}}\) và tam giác \({\rm{ACD}}\) có:
$\begin{array}{*{35}{l}}\angle AHE=\angle ACD(\text{cmt}) \\\angle HAE=\angle CAD(\text{cmt}) \\ \Rightarrow \Delta AEH\backsim \Delta ADC(g.g)(\text{dpcm}) \end{array}$
d) Hai đường thẳng AE và DH cắt nhau tại \(F\). Chứng minh \(IF//AD\).
Xét tam giác \({\rm{SAB}}\) có: \(\left\{ {\begin{array}{*{20}{l}}{AH \bot SB}\\{BE \bot SA}\\{AH \cap BE = \{ I\} }\end{array} \Rightarrow I} \right.\) là trực tâm của tam giác \({\rm{SAB}}\).
\( \Rightarrow SI \bot AB\) (SI là đường cao thứ ba).
Mà \(\angle BAC = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow AC \bot AB\).
\( \Rightarrow SI//AC\) (từ vuông góc đến song song).
\( \Rightarrow \frac{{SI}}{{AC}} = \frac{{SH}}{{HC}}(\) định lí Ta-lét ).
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{SF \bot BD({\rm{do}}AE \bot BD)}\\{CD \bot BD\left( {\angle BDC = 90^\circ } \right)}\end{array} \Rightarrow SF//CD} \right.\) (từ vuông góc đến song song).
\( \Rightarrow \frac{{SH}}{{HC}} = \frac{{SF}}{{CD}}(\) định lí Ta-lét)
Từ (1) và (2) \( \Rightarrow \frac{{SI}}{{AC}} = \frac{{SF}}{{CD}}\)
Lại có: \({\rm{IS}}//{\rm{AC}}{\mkern 1mu} {\mkern 1mu} ({\rm{cmt}}) \Rightarrow \angle ISF = \angle SAC\) (hai góc so le trong bằng nhau)
\({\rm{SA}}//{\rm{CD}}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} ({\rm{SF}}//{\rm{CD}}) \Rightarrow \angle SAC = \angle ACD\) (hai góc so le trong bằng nhau)
\( \Rightarrow \angle ISF = \angle ACD\)
Từ (3) và (4) $\Rightarrow \Delta ISF\backsim \Delta ACD$ (c.g.c) \( \Rightarrow \angle IFS = \angle ADC\) (hai góc tương ứng)
Ta có:
\(\angle IFA = {180^0} - \angle IFS = {180^0} - \angle ADC = \angle DAC + \angle ACD = \angle DAC + \angle SAC = \angle SAD\)
Mà hai góc này ở vị trí hai góc so le trong bằng nhau.
Vậy IF // AD (đpcm).
Câu 5 (VDC):
Cách giải:
Gọi cạnh hình lập phương bằng x (dm) (ĐK: x > 0).
=> Hình hộp chữ nhật có: Chiều cao = chiều rộng = y (dm) (ĐK: y > 0).
=> Chiều dài hình hộp chữ nhật bằng 6y (dm).
Hình lập phương có 12 cạnh có độ dài bằng x (dm).
Hình hộp chữ nhật có 8 cạnh có độ dài bằng y (dm) và 4 cạnh có độ dài 6y (dm).
Người thợ cắt vừa đủ một cây sắt dài 100m nên ta có:
\(12x + 8y + 4.6y = 100 \Leftrightarrow 12x + 32y = 100 \Leftrightarrow 3x + 8y = 25 \Leftrightarrow x = \frac{{25 - 8y}}{3}\)
Thể tích khối lập phương là \({V_1} = {x^3}\).
Thể tích khối hộp chữ nhật là \({V_2} = y.y.6y = 6{y^3}\).
Tổng thể tích hai hình là: \(V = {V_1} + {V_2} = {x^3} + 6{y^3}\).
Ta có: \({x^3} + {3^3} + {3^3} \ge 3\sqrt[3]{{{x^3} \cdot {3^3} \cdot {3^3}}} = 27x\)
\(6\left( {{y^3} + {2^3} + {2^3}} \right) \ge 6 \cdot 3 \cdot \sqrt[3]{{{y^3} \cdot {2^3} \cdot {2^3}}} = 72y\)
Cộng vế theo vế hai bất phương trình ta được:
\(\begin{array}{*{20}{l}}{{x^3} + 6{y^3} + 150 \ge 27x + 72y}\\{ \Leftrightarrow V + 150 \ge 9(3x + 8y)}\\{ \Leftrightarrow V + 150 \ge 9.25}\\{ \Leftrightarrow V + 150 \ge 225}\\{ \Leftrightarrow V \ge 75}\end{array}\)
Dấu “=” xảy ra \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = 2}\end{array}} \right.\).
Vậy tổng thể tích của hai hình thu được nhỏ nhất bằng \(75{\rm{d}}{{\rm{m}}^3}\) khi độ dài cạnh hình lập phương bằng \(3{\rm{dm}}\), độ dài chiều rộng và chiều cao hình hộp chữ nhật bằng \(2{\rm{dm}}\), chiều dài hình hộp chữ nhật bằng \(12{\rm{dm}}\).
Câu 1: a) Thực hiện phép tính \(2\sqrt 9 {\rm{ \;}} - \sqrt {16} \).
b) Xác định hệ số a của đồ thị hàm số \(y = a{x^2}\) đi qua điểm A(1;2).
c) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2x + y = 7}\\{x - 2y = {\rm{ \;}} - 4}\end{array}} \right.\)
d) Rút gọn biểu thức \(P = \left( {\frac{1}{{\sqrt x {\rm{ \;}} - 3}} + \frac{2}{{\sqrt x {\rm{ \;}} + 3}}} \right):\frac{{\sqrt x {\rm{ \;}} - 1}}{{\sqrt x {\rm{ \;}} - 3}}\) với \(x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 1,{\mkern 1mu} {\mkern 1mu} x \ne 9\).
Câu 2: Cho phuơng trình \({x^2} - 2(m + 1)x - 9 = 0\), với \(m\) là tham số.)
a) Giải phương trình khi \(m = 3\);
b) Tìm các giá trị của \(m\) để phuơng trình có nghiệm \(x = 2\);
c) Tìm các giá trị của \(m\) để phuơng trình có hai nghiệm phân biệt \({x_1},{x_2}\) sao cho \({x_1} < {x_2}\) và \(\left| {{x_1}} \right| - \left| {{x_2}} \right| = {\rm{ \;}} - 6\).
Câu 3: Hai địa điểm A và B cách nhau 280 km. Hai ô tô cùng xuất phát từ A đến B. Biết vận tốc của xe thứ nhất lớn hơn vận tốc của xe thứ hai 10 km/h và xe thứ nhất đến B sớm hơn xe thứ hai 30 phút. Tính vận tốc mỗi xe?
Câu 4: Cho nửa đuờng tròn tâm \(O\), đuờng kính BC. Trên nửa đường tròn (O) lấy A (A khác B và \(C\)), gọi \(H\) là hình chiếu của \(A\) trên B C. Trên cung AC của nửa đường tròn (O) lấy điểm D (D khác \(A\) và \(C\)), gọi \(E\) là hình chiếu của \(A\) trên BD, I là giao điểm của hai đường thằng AH và BD.
a) Chứng minh tứ giác ABHE nội tiếp;
b) Chứng minh BI.BD = BH.BC.
c) Chứng minh hai tam giác AHE và ACD đồng dạng;
d) Hai đường thẳng AE và DH cắt nhau tại \(F\). Chứng minh \(IF//AD\).
Câu 5: Một người thợ cơ khí cần cắt vừa đủ một cây sắt dài 100 dm thành các đoạn để hàn lại thành khung một hình lập phương và một hình hộp chữ nhật. Biết hình hộp chữ nhật có chiều dài gấp 6 lần chiều rộng và chiều cao bằng chiều rộng (hình vẽ minh họa). Tìm độ dài của các đoạn sắt sao cho tổng thể tích cùa hai hình thu được nhỏ nhất?
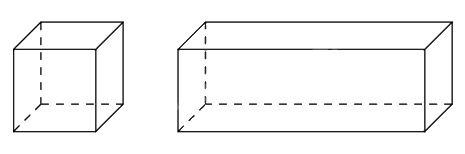
-----HẾT-----
Câu 1 (TH):
Phương pháp:
a) Khai phương căn bậc hai
b) Thay tọa độ A vào hàm số tìm a
c) Giải hệ bằng phương pháp thế hoặc cộng đại số
d) Tìm mẫu số chung quy đồng và rút gọn biểu thức.
Cách giải:
a) Thực hiện phép tính \(2\sqrt 9 {\rm{ \;}} - \sqrt {16} \).
\(\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} 2\sqrt 9 {\rm{ \;}} - \sqrt {16} }\\{ = 2.\sqrt {{3^2}} {\rm{ \;}} - \sqrt {{4^2}} }\\{ = 2.3 - 4}\\{ = 6 - 4}\\{ = 2}\end{array}\)
b) Xác định hệ số a của đồ thị hàm số \(y = a{x^2}\) đi qua điểm A(1;2).
Thay x = 1, y = 2 vào hàm số \(y = a{x^2}\) ta có: \(2 = a{.1^2} \Leftrightarrow a = 2.\)
Vậy a = 2.
c) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2x + y = 7}\\{x - 2y = {\rm{ \;}} - 4}\end{array}} \right.\)
\(\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{2x + y = 7}\\{x - 2y = - 4}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2x + y = 7}\\{x = 2y - 4}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2\left( {2y - 4} \right) + y = 7}\\{x = 2y - 4}\end{array}} \right.}\\{ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4y - 8 + y = 7}\\{x = 2y - 4}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{5y = 15}\\{x = 2y - 4}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = 3}\\{x = 2y - 4}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = 3}\end{array}} \right.}\end{array}\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {2;3} \right)\).
d) Rút gọn biểu thức \(P = \left( {\frac{1}{{\sqrt x {\rm{ \;}} - 3}} + \frac{2}{{\sqrt x {\rm{ \;}} + 3}}} \right):\frac{{\sqrt x {\rm{ \;}} - 1}}{{\sqrt x {\rm{ \;}} - 3}}\) với \(x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 1,{\mkern 1mu} {\mkern 1mu} x \ne 9\).
Với \(x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 1,{\mkern 1mu} {\mkern 1mu} x \ne 9\) ta có:
\(\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} P = \left( {\frac{1}{{\sqrt x - 3}} + \frac{2}{{\sqrt x + 3}}} \right):\frac{{\sqrt x - 1}}{{\sqrt x - 3}}}\\{ \Leftrightarrow P = \frac{{\sqrt x + 3 + 2\left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}:\frac{{\sqrt x - 1}}{{\sqrt x - 3}}}\\{ \Leftrightarrow P = \frac{{\sqrt x + 3 + 2\sqrt x - 6}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}.\frac{{\sqrt x - 3}}{{\sqrt x - 1}}}\\{ \Leftrightarrow P = \frac{{3\sqrt x - 3}}{{\sqrt x + 3}}.\frac{1}{{\sqrt x - 1}}}\\{ \Leftrightarrow P = \frac{{3\left( {\sqrt x - 1} \right)}}{{\sqrt x + 3}}.\frac{1}{{\sqrt x - 1}}}\\{ \Leftrightarrow P = \frac{3}{{\sqrt x + 3}}}\end{array}\)
Vậy với \(x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 1,{\mkern 1mu} {\mkern 1mu} x \ne 9\) thì \(P = \frac{3}{{\sqrt x {\rm{ \;}} + 3}}\).
Câu 2 (TH):
Phương pháp:
a) Thay m = 3 vào phương trình và giải phương trình bậc 2
b) Thay x = 2 vào phương trình tìm m
c) Chứng minh phương trình luôn có 2 nghiệm trái dấu và sử dụng hệ thức viet
Cách giải:
a) Giải phương trình khi \(m = 3\);
Khi \(m = 3\) phương trình trở thành: \({x^2} - 8x - 9 = 0\), ta có: \({\Delta ^\prime } = {( - 4)^2} - 1.( - 9) = 25 > 0\)
Suy ra phương trình có hai nghiệm phân biệt:
\(\left[ {\begin{array}{*{20}{l}}{{x_1} = \frac{{4 + \sqrt {25} }}{1} = 9}\\{{x_2} = \frac{{4 - \sqrt {25} }}{1} = {\rm{ \;}} - 1}\end{array}.} \right.\)
b) Tìm các giá trị của \(m\) để phuơng trình có nghiệm \(x = 2\);
Phương trình có nghiệm \(x = 2\) nên thay \(x = 2\) vào phương trình ta có:
\(\begin{array}{*{20}{l}}{{2^2} - 2(m + 1)2 - 9 = 0}\\{ \Leftrightarrow 4 - 4m - 4 - 9 = 0}\\{ \Leftrightarrow {\rm{ \;}} - 4m - 9 = 0 \Leftrightarrow m = {\rm{ \;}} - \frac{9}{4}}\end{array}\)
Vậy để phương trình có nghiệm \(x = 2\) thì \(m = {\rm{ \;}} - \frac{9}{4}\).
c) Tìm các giá trị của \(m\) để phuơng trình có hai nghiệm phân biệt \({x_1},{x_2}\) sao cho \({x_1} < {x_2}\) và \(\left| {{x_1}} \right| - \left| {{x_2}} \right| = {\rm{ \;}} - 6\).
Xét phương trình \({x^2} - 2(m + 1)x - 9 = 0\) có \(a.c = {\rm{ \;}} - 9 < 0\) nên phương trình luôn có 2 nghiệm trái dấu \({x_1},{x_2}\) Áp dụng hệ thức viet ta có \({x_1} + {x_2} = 2(m + 1)\)
Do \({x_1} < {x_2} \Rightarrow {x_1} < 0 < {x_2}\)
Để \(\left| {{x_1}} \right| - \left| {{x_2}} \right| = {\rm{ \;}} - 6\)
\(\begin{array}{*{20}{l}}{ - {x_1} - {x_2} = {\rm{ \;}} - 6}\\{ \Leftrightarrow {\rm{ \;}} - \left( {{x_1} + {x_2}} \right) = {\rm{ \;}} - 6}\\{ \Leftrightarrow {x_1} + {x_2} = 6}\\{ \Leftrightarrow 2(m + 1) = 6}\\{ \Leftrightarrow m + 1 = 3 \Leftrightarrow m = 2}\end{array}\)
Vậy với \(m = 2\) thì phương trình có hai nghiệm phân biệt \({x_1},{x_2}\) sao cho \({x_1} < {x_2}\) và \(\left| {{x_1}} \right| - \left| {{x_2}} \right| = {\rm{ \;}} - 6\).
Câu 3 (VD):
Phương pháp:
Gọi vận tốc của xe thứ hai là \(x\) (km/h, \(x > 0\)).
Biểu diễn vận tốc, thời gian của 2 xe theo x và lập phương trình tìm x.
Cách giải:
Gọi vận tốc của xe thứ hai là \(x\) (km/h, \(x > 0\)).
Vì vận tốc của xe thứ nhất lớn hơn vận tốc của xe thứ hai là 10 km/h nên vận tốc của xe thứ nhất là \(x + 10\) (km/h)
Thời gian xe thứ nhất đi từ A đến B là: \(\frac{{280}}{{x + 10}}\) (giờ)
Thời gian xe thứ hai đi từ A đến B là: \(\frac{{280}}{x}\) (giờ)
Vì xe thứ nhất đến B sớm hơn xe thứ hai 30 phút = \(\frac{1}{2}\)giờ nên ta có:
\(\frac{{280}}{x} - \frac{{280}}{{x + 10}} = \frac{1}{2}\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow \frac{{560\left( {x + 10} \right)}}{{2x\left( {x + 10} \right)}} - \frac{{560x}}{{2x\left( {x + 10} \right)}} = \frac{{x\left( {x + 10} \right)}}{{2x\left( {x + 10} \right)}}}\\{ \Leftrightarrow 560\left( {x + 10} \right) - 560x = x\left( {x + 10} \right)}\\{ \Leftrightarrow 560x + 5600 - 560x = {x^2} + 10x}\\{ \Leftrightarrow {x^2} + 10x - 5600 = 0}\\{ \Leftrightarrow {x^2} - 70x + 80x - 5600 = 0}\\{ \Leftrightarrow x\left( {x - 70} \right) + 80\left( {x - 70} \right) = 0}\\{ \Leftrightarrow \left( {x + 80} \right)\left( {x - 70} \right) = 0}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x + 80 = 0}\\{x - 70 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 80{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} (KTM)}\\{x = 70{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} (TM)}\end{array}} \right.}\end{array}\)
Vậy vận tốc xe thứ nhất là 80km/h, vận tốc xe thứ hai là 70km/h.
Câu 4 (VD):
Phương pháp:
a) Sử dụng tính chất hai góc kề nhau cùng nhìn một cạnh dưới 2 góc bằng nhau
b) Chứng minh $\Delta BIH\backsim \Delta BCD\,\,(g\cdot g)$
c) Chứng minh $\Delta AEH\backsim \Delta ADC(g.g)\,\,$
d) Chứng minh I là trực tâm của tam giác \({\rm{SAB}}\) và sử dụng định lý Talet
Cách giải:
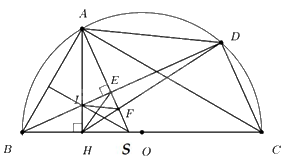
a) Chứng minh tứ giác ABHE nội tiếp;
Do \(AH \bot BC(gt),\,\,AE \bot BD(gt) \Rightarrow \angle AHB = \angle AEB = {90^0}\)
Mà \({\rm{E}},{\rm{H}}\) là 2 đỉnh kề nhau, cùng nhìn \({\rm{AD}}\) dưới 2 góc bằng nhau nên \({\rm{A}},{\rm{E}},{\rm{H}},{\rm{B}}\) cùng thuộc một đường tròn (dhnb)
Hay tứ giác ABHE nội tiếp (đpcm).
b) Chứng minh BI.BD = BH.BC.
Ta có \(\angle BDC = {90^0}\) (góc nội tiếp chắn nửa đường tròn).
Xét \(\Delta BIH\) và \(\Delta BCD\) có:
\(\angle CBD\) chung
\(\angle BHI = \angle BDC = {90^0}\)
$\Rightarrow \Delta BIH\backsim \Delta BCD(g\cdot g)$
\( \Rightarrow \frac{{BI}}{{BC}} = \frac{{BH}}{{BD}}\) (cặp cạnh tương ứng tỉ lệ)
\( \Rightarrow BI.BD = BH.BC{\mkern 1mu} {\mkern 1mu} (dpcm)\)
c) Chứng minh hai tam giác AHE và ACD đồng dạng;
Do ABHE nội tiếp (cmt) nên \(\angle AHE = \angle ABE\) (hai góc nội tiếp cùng chắn cung AE).
Mà \(\angle ABE = \angle ACD\) (hai góc nội tiếp cùng chắn cung AD).
\( \Rightarrow \angle AHE = \angle ACD\)
Do ABHE nội tiếp (cmt) nên \(\angle HAE = \angle HBE = \angle CBD\) (hai góc nội tiếp cùng chắn cung HE).
Lại có tứ giác ABCD nội tiếp \((O) \Rightarrow \angle CBD = \angle CAD\) (hai góc nội tiếp cùng chắn cung \({\rm{CD}}\) )
\( \Rightarrow \angle HAE = \angle CAD\)
Xét tam giác \({\rm{AHE}}\) và tam giác \({\rm{ACD}}\) có:
$\begin{array}{*{35}{l}}\angle AHE=\angle ACD(\text{cmt}) \\\angle HAE=\angle CAD(\text{cmt}) \\ \Rightarrow \Delta AEH\backsim \Delta ADC(g.g)(\text{dpcm}) \end{array}$
d) Hai đường thẳng AE và DH cắt nhau tại \(F\). Chứng minh \(IF//AD\).
Xét tam giác \({\rm{SAB}}\) có: \(\left\{ {\begin{array}{*{20}{l}}{AH \bot SB}\\{BE \bot SA}\\{AH \cap BE = \{ I\} }\end{array} \Rightarrow I} \right.\) là trực tâm của tam giác \({\rm{SAB}}\).
\( \Rightarrow SI \bot AB\) (SI là đường cao thứ ba).
Mà \(\angle BAC = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow AC \bot AB\).
\( \Rightarrow SI//AC\) (từ vuông góc đến song song).
\( \Rightarrow \frac{{SI}}{{AC}} = \frac{{SH}}{{HC}}(\) định lí Ta-lét ).
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{SF \bot BD({\rm{do}}AE \bot BD)}\\{CD \bot BD\left( {\angle BDC = 90^\circ } \right)}\end{array} \Rightarrow SF//CD} \right.\) (từ vuông góc đến song song).
\( \Rightarrow \frac{{SH}}{{HC}} = \frac{{SF}}{{CD}}(\) định lí Ta-lét)
Từ (1) và (2) \( \Rightarrow \frac{{SI}}{{AC}} = \frac{{SF}}{{CD}}\)
Lại có: \({\rm{IS}}//{\rm{AC}}{\mkern 1mu} {\mkern 1mu} ({\rm{cmt}}) \Rightarrow \angle ISF = \angle SAC\) (hai góc so le trong bằng nhau)
\({\rm{SA}}//{\rm{CD}}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} ({\rm{SF}}//{\rm{CD}}) \Rightarrow \angle SAC = \angle ACD\) (hai góc so le trong bằng nhau)
\( \Rightarrow \angle ISF = \angle ACD\)
Từ (3) và (4) $\Rightarrow \Delta ISF\backsim \Delta ACD$ (c.g.c) \( \Rightarrow \angle IFS = \angle ADC\) (hai góc tương ứng)
Ta có:
\(\angle IFA = {180^0} - \angle IFS = {180^0} - \angle ADC = \angle DAC + \angle ACD = \angle DAC + \angle SAC = \angle SAD\)
Mà hai góc này ở vị trí hai góc so le trong bằng nhau.
Vậy IF // AD (đpcm).
Câu 5 (VDC):
Cách giải:
Gọi cạnh hình lập phương bằng x (dm) (ĐK: x > 0).
=> Hình hộp chữ nhật có: Chiều cao = chiều rộng = y (dm) (ĐK: y > 0).
=> Chiều dài hình hộp chữ nhật bằng 6y (dm).
Hình lập phương có 12 cạnh có độ dài bằng x (dm).
Hình hộp chữ nhật có 8 cạnh có độ dài bằng y (dm) và 4 cạnh có độ dài 6y (dm).
Người thợ cắt vừa đủ một cây sắt dài 100m nên ta có:
\(12x + 8y + 4.6y = 100 \Leftrightarrow 12x + 32y = 100 \Leftrightarrow 3x + 8y = 25 \Leftrightarrow x = \frac{{25 - 8y}}{3}\)
Thể tích khối lập phương là \({V_1} = {x^3}\).
Thể tích khối hộp chữ nhật là \({V_2} = y.y.6y = 6{y^3}\).
Tổng thể tích hai hình là: \(V = {V_1} + {V_2} = {x^3} + 6{y^3}\).
Ta có: \({x^3} + {3^3} + {3^3} \ge 3\sqrt[3]{{{x^3} \cdot {3^3} \cdot {3^3}}} = 27x\)
\(6\left( {{y^3} + {2^3} + {2^3}} \right) \ge 6 \cdot 3 \cdot \sqrt[3]{{{y^3} \cdot {2^3} \cdot {2^3}}} = 72y\)
Cộng vế theo vế hai bất phương trình ta được:
\(\begin{array}{*{20}{l}}{{x^3} + 6{y^3} + 150 \ge 27x + 72y}\\{ \Leftrightarrow V + 150 \ge 9(3x + 8y)}\\{ \Leftrightarrow V + 150 \ge 9.25}\\{ \Leftrightarrow V + 150 \ge 225}\\{ \Leftrightarrow V \ge 75}\end{array}\)
Dấu “=” xảy ra \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = 2}\end{array}} \right.\).
Vậy tổng thể tích của hai hình thu được nhỏ nhất bằng \(75{\rm{d}}{{\rm{m}}^3}\) khi độ dài cạnh hình lập phương bằng \(3{\rm{dm}}\), độ dài chiều rộng và chiều cao hình hộp chữ nhật bằng \(2{\rm{dm}}\), chiều dài hình hộp chữ nhật bằng \(12{\rm{dm}}\).
Kỳ thi tuyển sinh vào lớp 10 môn Toán Quảng Ninh năm 2023 là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Để đạt kết quả tốt nhất, việc nắm vững kiến thức, kỹ năng và làm quen với cấu trúc đề thi là vô cùng cần thiết. Bài viết này sẽ cung cấp thông tin chi tiết về kỳ thi, các dạng bài thường gặp, phương pháp giải và những lưu ý quan trọng để giúp các em chuẩn bị tốt nhất.
Đề thi vào 10 môn Toán Quảng Ninh thường bao gồm các dạng bài sau:
Tỷ lệ phân bổ điểm giữa các phần thường khá cân bằng, tuy nhiên, có thể có sự thay đổi nhỏ tùy theo từng năm.
Dưới đây là một số dạng bài tập thường gặp trong đề thi vào 10 môn Toán Quảng Ninh:
Để giải đề thi vào 10 môn Toán Quảng Ninh hiệu quả, các em cần:
Dưới đây là một số lưu ý quan trọng dành cho các em khi làm bài thi:
Giaitoan.edu.vn cung cấp đầy đủ các tài liệu ôn thi và luyện đề thi vào 10 môn Toán Quảng Ninh năm 2023, bao gồm:
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi tuyển sinh vào lớp 10 môn Toán Quảng Ninh năm 2023!