Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Quảng Ninh năm 2019 chính thức. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi sắp tới.
Bộ đề thi này bao gồm các đề thi chính thức của các trường THPT chuyên và không chuyên trên địa bàn tỉnh Quảng Ninh, được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm của Giaitoan.edu.vn.
Câu 1 (2 điểm): 1. Thực hiện phép tính:
Câu 1 (2 điểm):
1. Thực hiện phép tính: \(2\sqrt 9 - 3\sqrt 4 .\)
2. Rút gọn biểu thức: \(\sqrt {\dfrac{{28{{\left( {a - 2} \right)}^2}}}{7}} ,\) với \(a > 2.\)
3. Tìm tọa độ các giao điểm của đồ thị hàm số \(y = {x^2}\) và đồ thị hàm số \(y = 3x - 2.\)
Câu 2 (2 điểm): Cho phương trình \({x^2} + 2x + m - 1 = 0,\) với \(m\) là tham số.
1. Giải phương trình với \(m = 1.\)
2. Tìm giá trị của \(m\) để phương trình đã cho có hai nghiệm phân biệt \({x_1}\) và \({x_2}\) thỏa mãn \(x_1^3 + x_2^3 - 6{x_1}{x_2} = 4\left( {m - {m^2}} \right).\)
Câu 3 (2 điểm): Hai người thợ cùng làm một công việc trong 9 ngày thì làm xong. Mỗi ngày, lượng công việc của người thứ hai làm được nhiều gấp 3 lần lượng công việc của người thứ nhất. Hỏi nếu làm một mình thì mỗi người làm xong công việc đó trong bao nhiêu ngày?
Câu 4 (3,5 điểm): Cho đường tròn \(\left( {O;\,\,R} \right),\) hai đường kính \(AB\) và \(CD\) vuông góc với nhau. \(E\) là điểm thuộc cung nhỏ \(BC\,\,\,\left( {E \ne B,\,\,C} \right),\) tiếp tuyến của đường tròn \(\left( {O;\,\,R} \right)\) tại \(E\) cắt đường thẳng \(AB\) tại \(I.\) Gọi \(F\) là giao điểm của \(DE\) và \(AB,\,\,K\) là điểm thuộc đường thẳng \(IE\) sao cho \(KF\) vuông góc với \(AB.\)
a) Chứng minh tứ giác \(OKEF\) nội tiếp.
b) Chứng minh \(\angle OKF = \angle ODF.\)
c) Chứng minh \(DE.DF = 2{R^2}.\)
d) Gọi \(M\) là giao điểm của \(OK\) với \(CF,\) tính \(\tan \angle MDC\) khi \(\angle EIB = {45^0}.\)
Câu 5 (0,5 điểm): Cho \(x,\,y,\,\,z\) là các số thực dương thỏa mãn \(x + y + z \le 1.\) Tìm giá trị nhỏ nhất của biểu thức: \(P = \dfrac{1}{{{x^2} + {y^2} + {z^2}}} + \dfrac{{2019}}{{xy + yz + zx}}.\)
Câu 1:
Phương pháp:
1, 2. Sử dụng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right..\)
3. Giải phương trình hoành độ giao điểm của hai đồ thị hàm số để tìm hoành độ giao điểm rồi thế vào 1 trong 2 công thức hàm số để tìm tung độ giao điểm rồi kết luận.
Cách giải:
1. Thực hiện phép tính: \(2\sqrt 9 - 3\sqrt 4 .\)
Ta có: \(2\sqrt 9 - 3\sqrt 4 = 2\sqrt {{3^2}} - 3\sqrt {{2^2}} = 2.3 - 3.2 = 0.\)
2. Rút gọn biểu thức: \(\sqrt {\dfrac{{28{{\left( {a - 2} \right)}^2}}}{7}} ,\) với \(a > 2.\)
\(\sqrt {\dfrac{{28{{\left( {a - 2} \right)}^2}}}{7}} = \sqrt {4{{\left( {a - 2} \right)}^2}} = \sqrt {{{\left[ {2\left( {a - 2} \right)} \right]}^2}} = \left| {2\left( {a - 2} \right)} \right| = 2\left( {a - 2} \right) = 2a - 4.\,\,\,\,\left( {do\,\,\,a > 2 \Rightarrow a - 2 > 0} \right).\)
Vậy với \(a > 2\) thì \(\sqrt {\dfrac{{28{{\left( {a - 2} \right)}^2}}}{7}} = 2a - 4.\)
3. Tìm tọa độ các giao điểm của đồ thị hàm số \(y = {x^2}\) và đồ thị hàm số \(y = 3x - 2.\)
Xét phương trình hoành độ giao điểm của hai đồ thị hàm số ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,{x^2} = 3x - 2\\ \Leftrightarrow {x^2} - 3x + 2 = 0 \Leftrightarrow {x^2} - 2x - x - 2 = 0\\ \Leftrightarrow x\left( {x - 2} \right) - \left( {x - 2} \right) = 0 \Leftrightarrow \left( {x - 2} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 2 = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2 \Rightarrow y = {2^2} = 4 \Rightarrow A\left( {2;\,\,4} \right)\\x = 1 \Rightarrow y = {1^2} = 1 \Rightarrow B\left( {1;\,\,1} \right)\end{array} \right..\end{array}\)
Vậy hai đồ thị hàm số cắt nhau tại hai điểm phân biệt \(A\left( {2;\,\,4} \right),\,\,B\left( {1;\,\,1} \right).\)
Câu 2:
Phương pháp:
1. Thay \(m = 1\) vào phương trình bài cho rồi giải phương trình bậc hai.
2) Phương trình đã cho có hai nghiệm phân biệt \( \Leftrightarrow \Delta > 0.\)
Áp dụng hệ thức Vi-ét và biến đổi biểu thức bài cho để tìm \(m.\) Đối chiếu với điều kiện rồi kết luận giá trị của \(m.\)
Cách giải:
1) Giải phương trình với \(m = 1\) .
Với \(m = 1\) ta có phương trình: \({x^2} + 2x = 0 \Leftrightarrow x\left( {x + 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 2\end{array} \right..\)
Vậy với \(m = 1\) phương trình có tập nghiệm \(S = \left\{ { - 2;\,\,0} \right\}.\)
2) Tìm giá trị của \(m\) để phương trình đã cho có hai nghiệm phân biệt \({x_1}\) và \({x_2}\) thỏa mãn \(x_1^3 + x_2^3 - 6{x_1}{x_2} = 4\left( {m - {m^2}} \right)\)
Phương trình:\({x^2} + 2x + m - 1 = 0\)
Có: \(\Delta ' = {1^2} - \left( {m - 1} \right) = 2 - m\)
Phương trình có hai nghiệm phân biệt \({x_1}\) và \({x_2} \Leftrightarrow \Delta ' > 0 \Leftrightarrow 2 - m > 0 \Leftrightarrow m < 2\)
Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 2\\{x_1}{x_2} = m - 1\end{array} \right..\)
Theo đề bài ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,x_1^3 + x_2^3 - 6{x_1}{x_2} = 4\left( {m - {m^2}} \right)\\ \Leftrightarrow \left( {{x_1} + {x_2}} \right)\left( {x_1^2 - {x_1}{x_2} + x_2^2} \right) - 6{x_1}{x_2} = 4\left( {m - {m^2}} \right)\\ \Leftrightarrow \left( {{x_1} + {x_2}} \right)\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 3{x_1}{x_2}} \right] - 6{x_1}{x_2} = 4\left( {m - {m^2}} \right)\\ \Leftrightarrow \left( { - 2} \right)\left[ {{{\left( { - 2} \right)}^2} - 3\left( {m - 1} \right)} \right] - 6\left( {m - 1} \right) = 4m - 4{m^2}\\ \Leftrightarrow \left( { - 2} \right)\left( {7 - 3m} \right) - 6m + 6 = 4m - 4{m^2}\\ \Leftrightarrow - 14 + 6m - 6m + 6 - 4m + 4{m^2} = 0\\ \Leftrightarrow {m^2} - m - 2 = 0\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array}\)
Có \(a = 1;\,\,b = - 1;\,\,c = - 2 \Rightarrow a - b + c = 0\) . Khi đó phương trình (2) có hai nghiệm phân biệt là: \({m_1} = - 1;{m_2} = 2\)
Kết hợp với điều kiện \(m < 2\) ta thấy \(m = - 1\) thỏa mãn.
Vậy \(m = - 1\) thỏa mãn bài toán.
Câu 3:
Phương pháp:
Gọi thời gian người thứ nhất làm một mình xong công việc là \(x\) (ngày) \(\left( {x > 0} \right)\).
Thời gian người thứ hai làm một mình xong công việc là \(y\) (ngày) \(\left( {y > 0} \right)\).
Biểu diễn các đại lượng chưa biết thông qua ẩn \(x,\,\,y\) và các đại lượng đã biết.
Dựa vào giả thiết để lập phương trình hoặc hệ phương trình. Giải phương trình hoặc hệ phương trình vừa lập được. Đối chiếu với điều kiện rồi kết luận.
Cách giải:
Gọi thời gian người thứ nhất làm một mình xong công việc là \(x\) (ngày) \(\left( {x > 0} \right)\).
Thời gian người thứ hai làm một mình xong công việc là \(y\) (ngày) \(\left( {y > 0} \right)\).
\( \Rightarrow \) Mỗi ngày người thứ nhất làm được \(\dfrac{1}{x}\) (công việc).
Mỗi ngày người thứ hai làm được \(\dfrac{1}{y}\) (công việc).
Vì hai người cùng làm một công việc trong 9 ngày thì xong nên mỗi ngày hai người làm chung được \(\dfrac{1}{9}\) công việc, do đó ta có phương trình: \(\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{9}\,\,\left( 1 \right)\).
Lại có mỗi ngày, lượng công việc của người thứ hai làm được gấp ba lần lượng công việc của người thứ nhất nên ta có phương trình: \(\dfrac{1}{y} = \dfrac{3}{x}\,\,\left( 2 \right)\).
Từ (1), (2) ta có hệ phương trình
\(\left\{ \begin{array}{l}\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{9}\\\dfrac{3}{x} = \dfrac{1}{y}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{1}{x} + \dfrac{3}{x} = \dfrac{1}{9}\\\dfrac{3}{x} = \dfrac{1}{y}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{4}{x} = \dfrac{1}{9}\\\dfrac{3}{x} = \dfrac{1}{y}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 36\,\,\,\,\left( {tm} \right)\\\dfrac{1}{y} = \dfrac{3}{{36}} = \dfrac{1}{{12}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 36\,\,\left( {tm} \right)\\y = 12\,\,\,\left( {tm} \right)\end{array} \right.\)
Vậy người thứ nhất làm một mình xong công việc hết 36 ngày và người thứ nhất làm một mình xong công việc hết 12 ngày.
Câu 4:
Cách giải:
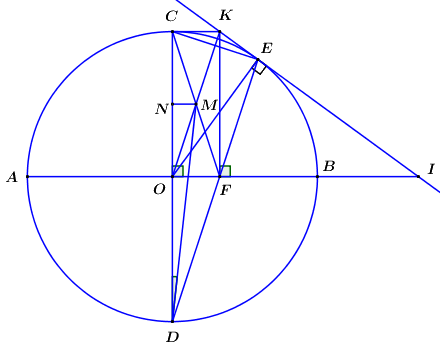
a. Chứng minh tứ giác \(OKEF\) nội tiếp.
Do \(EK\) là tiếp tuyến của \(\left( O \right) \Rightarrow \angle OEK = {90^0}\).
Lại có \(\angle OFK = {90^0}\,\,\left( {gt} \right) \Rightarrow \) Tứ giác \(OKEF\) có 2 đỉnh \(E,\,\,F\) kề nhau cùng nhìn \(OK\) dưới góc \({90^0}\).
\( \Rightarrow E,\,\,F\) thuộc đường tròn đường kính \(OK\) hay tứ giác \(OKEF\) nội tiếp.
b. Chứng minh \(\angle OKF = \angle ODF\).
Tứ giác \(OKEF\) nội tiếp (cmt) \( \Rightarrow \angle OKF = \angle OEF\) (hai góc nội tiếp cùng chắn cung \(OF\)).
Ta có \(OE = OD\,\,\left( { = R} \right) \Rightarrow \Delta ODE\) cân tại \(O \Rightarrow \angle OEF = \angle ODF\).
\( \Rightarrow \angle OKF = \angle ODF\,\,\left( { = \angle OKF} \right)\).
c. Chứng minh \(DE.DF = 2{R^2}\).
Nối \(CE\). Ta có \(\angle DEC = {90^0}\) (góc nội tiếp chắn nửa đường tròn).
Xét tam giác \(DOF\) và tam giác \(DEC\) có :
\(\angle CDE\) chung;
\(\angle DOF = \angle DEC = {90^0}\) ;
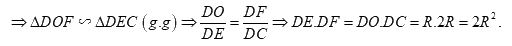
d. Gọi \(M\) là giao điểm của \(OK\) với \(CF\), tính \(\tan \angle MDC\) khi \(\angle EIB = {45^0}\).
Ta có \(AB\) là trung trực của \(CD\). Mà \(F \in AB \Rightarrow FC = FD \Rightarrow \Delta FCD\) cân tại \(F \Rightarrow \angle ODF = \angle OCF\).
Mà \(\angle OKF = \angle ODF\)(cmt) \( \Rightarrow \angle OCF = \angle OKF \Rightarrow \) Tứ giác \(OCKF\) là tứ giác nội tiếp (Tứ giác có 2 đỉnh kề nhau cùng nhìn 1 cạnh dưới các góc bằng nhau).
Mà tứ giác \(OKEF\) nội tiếp đường tròn đường kính \(OK\).
\( \Rightarrow O,\,\,C,\,\,K,\,\,E,\,\,F\) cùng thuộc đường tròn đường kinh \(OK \Rightarrow \angle OCK = {90^0}\) (góc nội tiếp chắn nửa đường tròn).
Xét tứ giác \(OCKF\) có : \(\angle OCK = \angle COF = \angle OFK = {90^0} \Rightarrow \) Tứ giác \(OCKF\) là hình chữ nhật (Tứ giác có 3 góc vuông). Mà \(M = OK \cap CF \Rightarrow \) M là trung điểm của \(OK,\,\,CF\).
Gọi \(N\) là trung điểm của \(OC\) \( \Rightarrow MN\) là đường trung bình của tam giác \(OCF\)\( \Rightarrow MN = \dfrac{1}{2}OF\) và \(MN//OF \Rightarrow MN \bot OC\).
Xét tam giác vuông \(OEI\) có : \(\sin {45^0} = \dfrac{{OE}}{{OI}} \Rightarrow OI = \dfrac{{OE}}{{\sin {{45}^0}}} = \dfrac{R}{{\dfrac{{\sqrt 2 }}{2}}} = R\sqrt 2 \).
\(OCKF\) là hình chữ nhật \( \Rightarrow KF = OC = R\).
Xét tam giác vuông \(IKF\) có \(\angle EIB = \angle KIF = {45^0} \Rightarrow \Delta IKF\) vuông cân tại \(F \Rightarrow IF = KF = R\).
\( \Rightarrow OF = OI - IF = R\sqrt 2 - R = R\left( {\sqrt 2 - 1} \right)\).
\( \Rightarrow MN = \dfrac{1}{2}OF = \dfrac{{R\left( {\sqrt 2 - 1} \right)}}{2}\).
Ta có: \(DN = OD + ON = R + \dfrac{R}{2} = \dfrac{{3R}}{2}\).
Xét tam giác vuông \(DMN\) (\(MN \bot OC \Rightarrow MN \bot DN\)) có:
\(\tan \angle MDN = \dfrac{{MN}}{{DN}} = \dfrac{{\dfrac{{R\left( {\sqrt 2 - 1} \right)}}{2}}}{{\dfrac{{3R}}{2}}} = \dfrac{{\sqrt 2 - 1}}{3} = \tan \angle MDC\)
Vậy \(\tan \angle MDC = \dfrac{{\sqrt 2 - 1}}{3}\).
Câu 5: Cho \(x,\,\,y,\,\,z\) là các số dương thỏa mãn \(x + y + z \le 1\) . Tính giá trị nhỏ nhất của biểu thức
\(P = \dfrac{1}{{{x^2} + {y^2} + {z^2}}} + \dfrac{{2019}}{{xy + yz + zx}}\).
Cách giải:
Ta chứng minh BĐT phụ : \(\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z} \ge \dfrac{9}{{x + y + z}}\).
Áp dụng BĐT Cosi cho các số dương \(\dfrac{1}{x};\dfrac{1}{y};\dfrac{1}{z}\) và \(x;y;z\)
\(\begin{array}{l}\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right)\left( {x + y + z} \right) \ge 3\sqrt[3]{{\dfrac{1}{x}.\dfrac{1}{y}.\dfrac{1}{z}}}.3\sqrt[3]{{xyz}} = 9\\ \Leftrightarrow \dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z} \ge \dfrac{9}{{x + y + z}}\end{array}\)
Dấu "=" xảy ra khi và chỉ khi \(\left\{ \begin{array}{l}\dfrac{1}{x} = \dfrac{1}{y} = \dfrac{1}{z}\\x = y = z\end{array} \right. \Leftrightarrow x = y = z\).
Ta có:
\(\begin{array}{l}P = \dfrac{1}{{{x^2} + {y^2} + {z^2}}} + \dfrac{{2019}}{{xy + yz + zx}}\\P = \dfrac{1}{{{x^2} + {y^2} + {z^2}}} + \dfrac{1}{{xy + yz + zx}} + \dfrac{1}{{xy + yz + zx}} + \dfrac{{2017}}{{xy + yz + zx}}\\P \ge \dfrac{9}{{{x^2} + {y^2} + {z^2} + 2\left( {xy + yz + zx} \right)}} + \dfrac{{2017}}{{xy + yz + zx}}\\P \ge \dfrac{9}{{{{\left( {x + y + z} \right)}^2}}} + \dfrac{{2017}}{{xy + yz + zx}}\end{array}\)
Ta có:
\(\begin{array}{l}1 \ge {\left( {x + y + z} \right)^2} = {x^2} + {y^2} + {z^2} + 2\left( {xy + yz + xz} \right) \ge \dfrac{{{{\left( {x + y + z} \right)}^2}}}{3} + 2\left( {xy + yz + xz} \right)\\ \Rightarrow 2\left( {xy + yz + xz} \right) \le \dfrac{{2{{\left( {x + y + z} \right)}^2}}}{3} \le \dfrac{2}{3} \Rightarrow xy + yz + xz \le \dfrac{1}{3}\\ \Rightarrow \dfrac{{2017}}{{xy + yz + xz}} \ge 2017.3 = 6051\\x + y + z \le 1 \Leftrightarrow {\left( {x + y + z} \right)^2} \le 1 \Rightarrow \dfrac{9}{{{{\left( {x + y + z} \right)}^2}}} \ge 9\\ \Rightarrow \dfrac{9}{{{{\left( {x + y + z} \right)}^2}}} + \dfrac{{2017}}{{xy + yz + xz}} \ge 9 + 6051 = 6060\\ \Rightarrow P \ge \dfrac{9}{{{{\left( {x + y + z} \right)}^2}}} + \dfrac{{2017}}{{xy + yz + xz}} \ge 6060\end{array}\)
Dấu "=" xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}{x^2} + {y^2} + {z^2} = xy + yz + zx\\x + y + z = 1\\xy + yz + zx = \dfrac{1}{3}\\x,y,z > 0\\x = y = z\end{array} \right. \Leftrightarrow x = y = z = \dfrac{1}{3}\).
Vậy \(P\) đạt giá trị nhỏ nhất bằng \(6060\) khi \(x = y = z = \dfrac{1}{3}.\)
Câu 1 (2 điểm):
1. Thực hiện phép tính: \(2\sqrt 9 - 3\sqrt 4 .\)
2. Rút gọn biểu thức: \(\sqrt {\dfrac{{28{{\left( {a - 2} \right)}^2}}}{7}} ,\) với \(a > 2.\)
3. Tìm tọa độ các giao điểm của đồ thị hàm số \(y = {x^2}\) và đồ thị hàm số \(y = 3x - 2.\)
Câu 2 (2 điểm): Cho phương trình \({x^2} + 2x + m - 1 = 0,\) với \(m\) là tham số.
1. Giải phương trình với \(m = 1.\)
2. Tìm giá trị của \(m\) để phương trình đã cho có hai nghiệm phân biệt \({x_1}\) và \({x_2}\) thỏa mãn \(x_1^3 + x_2^3 - 6{x_1}{x_2} = 4\left( {m - {m^2}} \right).\)
Câu 3 (2 điểm): Hai người thợ cùng làm một công việc trong 9 ngày thì làm xong. Mỗi ngày, lượng công việc của người thứ hai làm được nhiều gấp 3 lần lượng công việc của người thứ nhất. Hỏi nếu làm một mình thì mỗi người làm xong công việc đó trong bao nhiêu ngày?
Câu 4 (3,5 điểm): Cho đường tròn \(\left( {O;\,\,R} \right),\) hai đường kính \(AB\) và \(CD\) vuông góc với nhau. \(E\) là điểm thuộc cung nhỏ \(BC\,\,\,\left( {E \ne B,\,\,C} \right),\) tiếp tuyến của đường tròn \(\left( {O;\,\,R} \right)\) tại \(E\) cắt đường thẳng \(AB\) tại \(I.\) Gọi \(F\) là giao điểm của \(DE\) và \(AB,\,\,K\) là điểm thuộc đường thẳng \(IE\) sao cho \(KF\) vuông góc với \(AB.\)
a) Chứng minh tứ giác \(OKEF\) nội tiếp.
b) Chứng minh \(\angle OKF = \angle ODF.\)
c) Chứng minh \(DE.DF = 2{R^2}.\)
d) Gọi \(M\) là giao điểm của \(OK\) với \(CF,\) tính \(\tan \angle MDC\) khi \(\angle EIB = {45^0}.\)
Câu 5 (0,5 điểm): Cho \(x,\,y,\,\,z\) là các số thực dương thỏa mãn \(x + y + z \le 1.\) Tìm giá trị nhỏ nhất của biểu thức: \(P = \dfrac{1}{{{x^2} + {y^2} + {z^2}}} + \dfrac{{2019}}{{xy + yz + zx}}.\)
Câu 1:
Phương pháp:
1, 2. Sử dụng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right..\)
3. Giải phương trình hoành độ giao điểm của hai đồ thị hàm số để tìm hoành độ giao điểm rồi thế vào 1 trong 2 công thức hàm số để tìm tung độ giao điểm rồi kết luận.
Cách giải:
1. Thực hiện phép tính: \(2\sqrt 9 - 3\sqrt 4 .\)
Ta có: \(2\sqrt 9 - 3\sqrt 4 = 2\sqrt {{3^2}} - 3\sqrt {{2^2}} = 2.3 - 3.2 = 0.\)
2. Rút gọn biểu thức: \(\sqrt {\dfrac{{28{{\left( {a - 2} \right)}^2}}}{7}} ,\) với \(a > 2.\)
\(\sqrt {\dfrac{{28{{\left( {a - 2} \right)}^2}}}{7}} = \sqrt {4{{\left( {a - 2} \right)}^2}} = \sqrt {{{\left[ {2\left( {a - 2} \right)} \right]}^2}} = \left| {2\left( {a - 2} \right)} \right| = 2\left( {a - 2} \right) = 2a - 4.\,\,\,\,\left( {do\,\,\,a > 2 \Rightarrow a - 2 > 0} \right).\)
Vậy với \(a > 2\) thì \(\sqrt {\dfrac{{28{{\left( {a - 2} \right)}^2}}}{7}} = 2a - 4.\)
3. Tìm tọa độ các giao điểm của đồ thị hàm số \(y = {x^2}\) và đồ thị hàm số \(y = 3x - 2.\)
Xét phương trình hoành độ giao điểm của hai đồ thị hàm số ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,{x^2} = 3x - 2\\ \Leftrightarrow {x^2} - 3x + 2 = 0 \Leftrightarrow {x^2} - 2x - x - 2 = 0\\ \Leftrightarrow x\left( {x - 2} \right) - \left( {x - 2} \right) = 0 \Leftrightarrow \left( {x - 2} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 2 = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2 \Rightarrow y = {2^2} = 4 \Rightarrow A\left( {2;\,\,4} \right)\\x = 1 \Rightarrow y = {1^2} = 1 \Rightarrow B\left( {1;\,\,1} \right)\end{array} \right..\end{array}\)
Vậy hai đồ thị hàm số cắt nhau tại hai điểm phân biệt \(A\left( {2;\,\,4} \right),\,\,B\left( {1;\,\,1} \right).\)
Câu 2:
Phương pháp:
1. Thay \(m = 1\) vào phương trình bài cho rồi giải phương trình bậc hai.
2) Phương trình đã cho có hai nghiệm phân biệt \( \Leftrightarrow \Delta > 0.\)
Áp dụng hệ thức Vi-ét và biến đổi biểu thức bài cho để tìm \(m.\) Đối chiếu với điều kiện rồi kết luận giá trị của \(m.\)
Cách giải:
1) Giải phương trình với \(m = 1\) .
Với \(m = 1\) ta có phương trình: \({x^2} + 2x = 0 \Leftrightarrow x\left( {x + 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 2\end{array} \right..\)
Vậy với \(m = 1\) phương trình có tập nghiệm \(S = \left\{ { - 2;\,\,0} \right\}.\)
2) Tìm giá trị của \(m\) để phương trình đã cho có hai nghiệm phân biệt \({x_1}\) và \({x_2}\) thỏa mãn \(x_1^3 + x_2^3 - 6{x_1}{x_2} = 4\left( {m - {m^2}} \right)\)
Phương trình:\({x^2} + 2x + m - 1 = 0\)
Có: \(\Delta ' = {1^2} - \left( {m - 1} \right) = 2 - m\)
Phương trình có hai nghiệm phân biệt \({x_1}\) và \({x_2} \Leftrightarrow \Delta ' > 0 \Leftrightarrow 2 - m > 0 \Leftrightarrow m < 2\)
Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 2\\{x_1}{x_2} = m - 1\end{array} \right..\)
Theo đề bài ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,x_1^3 + x_2^3 - 6{x_1}{x_2} = 4\left( {m - {m^2}} \right)\\ \Leftrightarrow \left( {{x_1} + {x_2}} \right)\left( {x_1^2 - {x_1}{x_2} + x_2^2} \right) - 6{x_1}{x_2} = 4\left( {m - {m^2}} \right)\\ \Leftrightarrow \left( {{x_1} + {x_2}} \right)\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 3{x_1}{x_2}} \right] - 6{x_1}{x_2} = 4\left( {m - {m^2}} \right)\\ \Leftrightarrow \left( { - 2} \right)\left[ {{{\left( { - 2} \right)}^2} - 3\left( {m - 1} \right)} \right] - 6\left( {m - 1} \right) = 4m - 4{m^2}\\ \Leftrightarrow \left( { - 2} \right)\left( {7 - 3m} \right) - 6m + 6 = 4m - 4{m^2}\\ \Leftrightarrow - 14 + 6m - 6m + 6 - 4m + 4{m^2} = 0\\ \Leftrightarrow {m^2} - m - 2 = 0\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array}\)
Có \(a = 1;\,\,b = - 1;\,\,c = - 2 \Rightarrow a - b + c = 0\) . Khi đó phương trình (2) có hai nghiệm phân biệt là: \({m_1} = - 1;{m_2} = 2\)
Kết hợp với điều kiện \(m < 2\) ta thấy \(m = - 1\) thỏa mãn.
Vậy \(m = - 1\) thỏa mãn bài toán.
Câu 3:
Phương pháp:
Gọi thời gian người thứ nhất làm một mình xong công việc là \(x\) (ngày) \(\left( {x > 0} \right)\).
Thời gian người thứ hai làm một mình xong công việc là \(y\) (ngày) \(\left( {y > 0} \right)\).
Biểu diễn các đại lượng chưa biết thông qua ẩn \(x,\,\,y\) và các đại lượng đã biết.
Dựa vào giả thiết để lập phương trình hoặc hệ phương trình. Giải phương trình hoặc hệ phương trình vừa lập được. Đối chiếu với điều kiện rồi kết luận.
Cách giải:
Gọi thời gian người thứ nhất làm một mình xong công việc là \(x\) (ngày) \(\left( {x > 0} \right)\).
Thời gian người thứ hai làm một mình xong công việc là \(y\) (ngày) \(\left( {y > 0} \right)\).
\( \Rightarrow \) Mỗi ngày người thứ nhất làm được \(\dfrac{1}{x}\) (công việc).
Mỗi ngày người thứ hai làm được \(\dfrac{1}{y}\) (công việc).
Vì hai người cùng làm một công việc trong 9 ngày thì xong nên mỗi ngày hai người làm chung được \(\dfrac{1}{9}\) công việc, do đó ta có phương trình: \(\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{9}\,\,\left( 1 \right)\).
Lại có mỗi ngày, lượng công việc của người thứ hai làm được gấp ba lần lượng công việc của người thứ nhất nên ta có phương trình: \(\dfrac{1}{y} = \dfrac{3}{x}\,\,\left( 2 \right)\).
Từ (1), (2) ta có hệ phương trình
\(\left\{ \begin{array}{l}\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{9}\\\dfrac{3}{x} = \dfrac{1}{y}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{1}{x} + \dfrac{3}{x} = \dfrac{1}{9}\\\dfrac{3}{x} = \dfrac{1}{y}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{4}{x} = \dfrac{1}{9}\\\dfrac{3}{x} = \dfrac{1}{y}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 36\,\,\,\,\left( {tm} \right)\\\dfrac{1}{y} = \dfrac{3}{{36}} = \dfrac{1}{{12}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 36\,\,\left( {tm} \right)\\y = 12\,\,\,\left( {tm} \right)\end{array} \right.\)
Vậy người thứ nhất làm một mình xong công việc hết 36 ngày và người thứ nhất làm một mình xong công việc hết 12 ngày.
Câu 4:
Cách giải:
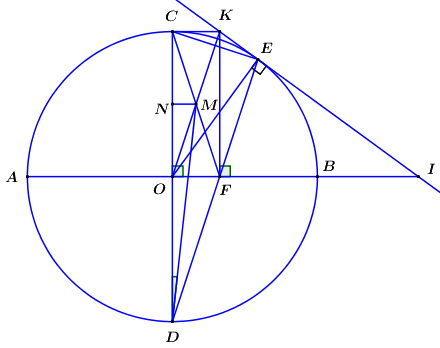
a. Chứng minh tứ giác \(OKEF\) nội tiếp.
Do \(EK\) là tiếp tuyến của \(\left( O \right) \Rightarrow \angle OEK = {90^0}\).
Lại có \(\angle OFK = {90^0}\,\,\left( {gt} \right) \Rightarrow \) Tứ giác \(OKEF\) có 2 đỉnh \(E,\,\,F\) kề nhau cùng nhìn \(OK\) dưới góc \({90^0}\).
\( \Rightarrow E,\,\,F\) thuộc đường tròn đường kính \(OK\) hay tứ giác \(OKEF\) nội tiếp.
b. Chứng minh \(\angle OKF = \angle ODF\).
Tứ giác \(OKEF\) nội tiếp (cmt) \( \Rightarrow \angle OKF = \angle OEF\) (hai góc nội tiếp cùng chắn cung \(OF\)).
Ta có \(OE = OD\,\,\left( { = R} \right) \Rightarrow \Delta ODE\) cân tại \(O \Rightarrow \angle OEF = \angle ODF\).
\( \Rightarrow \angle OKF = \angle ODF\,\,\left( { = \angle OKF} \right)\).
c. Chứng minh \(DE.DF = 2{R^2}\).
Nối \(CE\). Ta có \(\angle DEC = {90^0}\) (góc nội tiếp chắn nửa đường tròn).
Xét tam giác \(DOF\) và tam giác \(DEC\) có :
\(\angle CDE\) chung;
\(\angle DOF = \angle DEC = {90^0}\) ;
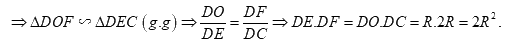
d. Gọi \(M\) là giao điểm của \(OK\) với \(CF\), tính \(\tan \angle MDC\) khi \(\angle EIB = {45^0}\).
Ta có \(AB\) là trung trực của \(CD\). Mà \(F \in AB \Rightarrow FC = FD \Rightarrow \Delta FCD\) cân tại \(F \Rightarrow \angle ODF = \angle OCF\).
Mà \(\angle OKF = \angle ODF\)(cmt) \( \Rightarrow \angle OCF = \angle OKF \Rightarrow \) Tứ giác \(OCKF\) là tứ giác nội tiếp (Tứ giác có 2 đỉnh kề nhau cùng nhìn 1 cạnh dưới các góc bằng nhau).
Mà tứ giác \(OKEF\) nội tiếp đường tròn đường kính \(OK\).
\( \Rightarrow O,\,\,C,\,\,K,\,\,E,\,\,F\) cùng thuộc đường tròn đường kinh \(OK \Rightarrow \angle OCK = {90^0}\) (góc nội tiếp chắn nửa đường tròn).
Xét tứ giác \(OCKF\) có : \(\angle OCK = \angle COF = \angle OFK = {90^0} \Rightarrow \) Tứ giác \(OCKF\) là hình chữ nhật (Tứ giác có 3 góc vuông). Mà \(M = OK \cap CF \Rightarrow \) M là trung điểm của \(OK,\,\,CF\).
Gọi \(N\) là trung điểm của \(OC\) \( \Rightarrow MN\) là đường trung bình của tam giác \(OCF\)\( \Rightarrow MN = \dfrac{1}{2}OF\) và \(MN//OF \Rightarrow MN \bot OC\).
Xét tam giác vuông \(OEI\) có : \(\sin {45^0} = \dfrac{{OE}}{{OI}} \Rightarrow OI = \dfrac{{OE}}{{\sin {{45}^0}}} = \dfrac{R}{{\dfrac{{\sqrt 2 }}{2}}} = R\sqrt 2 \).
\(OCKF\) là hình chữ nhật \( \Rightarrow KF = OC = R\).
Xét tam giác vuông \(IKF\) có \(\angle EIB = \angle KIF = {45^0} \Rightarrow \Delta IKF\) vuông cân tại \(F \Rightarrow IF = KF = R\).
\( \Rightarrow OF = OI - IF = R\sqrt 2 - R = R\left( {\sqrt 2 - 1} \right)\).
\( \Rightarrow MN = \dfrac{1}{2}OF = \dfrac{{R\left( {\sqrt 2 - 1} \right)}}{2}\).
Ta có: \(DN = OD + ON = R + \dfrac{R}{2} = \dfrac{{3R}}{2}\).
Xét tam giác vuông \(DMN\) (\(MN \bot OC \Rightarrow MN \bot DN\)) có:
\(\tan \angle MDN = \dfrac{{MN}}{{DN}} = \dfrac{{\dfrac{{R\left( {\sqrt 2 - 1} \right)}}{2}}}{{\dfrac{{3R}}{2}}} = \dfrac{{\sqrt 2 - 1}}{3} = \tan \angle MDC\)
Vậy \(\tan \angle MDC = \dfrac{{\sqrt 2 - 1}}{3}\).
Câu 5: Cho \(x,\,\,y,\,\,z\) là các số dương thỏa mãn \(x + y + z \le 1\) . Tính giá trị nhỏ nhất của biểu thức
\(P = \dfrac{1}{{{x^2} + {y^2} + {z^2}}} + \dfrac{{2019}}{{xy + yz + zx}}\).
Cách giải:
Ta chứng minh BĐT phụ : \(\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z} \ge \dfrac{9}{{x + y + z}}\).
Áp dụng BĐT Cosi cho các số dương \(\dfrac{1}{x};\dfrac{1}{y};\dfrac{1}{z}\) và \(x;y;z\)
\(\begin{array}{l}\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right)\left( {x + y + z} \right) \ge 3\sqrt[3]{{\dfrac{1}{x}.\dfrac{1}{y}.\dfrac{1}{z}}}.3\sqrt[3]{{xyz}} = 9\\ \Leftrightarrow \dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z} \ge \dfrac{9}{{x + y + z}}\end{array}\)
Dấu "=" xảy ra khi và chỉ khi \(\left\{ \begin{array}{l}\dfrac{1}{x} = \dfrac{1}{y} = \dfrac{1}{z}\\x = y = z\end{array} \right. \Leftrightarrow x = y = z\).
Ta có:
\(\begin{array}{l}P = \dfrac{1}{{{x^2} + {y^2} + {z^2}}} + \dfrac{{2019}}{{xy + yz + zx}}\\P = \dfrac{1}{{{x^2} + {y^2} + {z^2}}} + \dfrac{1}{{xy + yz + zx}} + \dfrac{1}{{xy + yz + zx}} + \dfrac{{2017}}{{xy + yz + zx}}\\P \ge \dfrac{9}{{{x^2} + {y^2} + {z^2} + 2\left( {xy + yz + zx} \right)}} + \dfrac{{2017}}{{xy + yz + zx}}\\P \ge \dfrac{9}{{{{\left( {x + y + z} \right)}^2}}} + \dfrac{{2017}}{{xy + yz + zx}}\end{array}\)
Ta có:
\(\begin{array}{l}1 \ge {\left( {x + y + z} \right)^2} = {x^2} + {y^2} + {z^2} + 2\left( {xy + yz + xz} \right) \ge \dfrac{{{{\left( {x + y + z} \right)}^2}}}{3} + 2\left( {xy + yz + xz} \right)\\ \Rightarrow 2\left( {xy + yz + xz} \right) \le \dfrac{{2{{\left( {x + y + z} \right)}^2}}}{3} \le \dfrac{2}{3} \Rightarrow xy + yz + xz \le \dfrac{1}{3}\\ \Rightarrow \dfrac{{2017}}{{xy + yz + xz}} \ge 2017.3 = 6051\\x + y + z \le 1 \Leftrightarrow {\left( {x + y + z} \right)^2} \le 1 \Rightarrow \dfrac{9}{{{{\left( {x + y + z} \right)}^2}}} \ge 9\\ \Rightarrow \dfrac{9}{{{{\left( {x + y + z} \right)}^2}}} + \dfrac{{2017}}{{xy + yz + xz}} \ge 9 + 6051 = 6060\\ \Rightarrow P \ge \dfrac{9}{{{{\left( {x + y + z} \right)}^2}}} + \dfrac{{2017}}{{xy + yz + xz}} \ge 6060\end{array}\)
Dấu "=" xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}{x^2} + {y^2} + {z^2} = xy + yz + zx\\x + y + z = 1\\xy + yz + zx = \dfrac{1}{3}\\x,y,z > 0\\x = y = z\end{array} \right. \Leftrightarrow x = y = z = \dfrac{1}{3}\).
Vậy \(P\) đạt giá trị nhỏ nhất bằng \(6060\) khi \(x = y = z = \dfrac{1}{3}.\)
Kỳ thi tuyển sinh vào lớp 10 môn Toán Quảng Ninh năm 2019 được đánh giá là một kỳ thi có độ khó vừa phải, tập trung vào các kiến thức cơ bản của chương trình Toán THCS. Tuy nhiên, để đạt được kết quả cao, học sinh cần phải nắm vững kiến thức, rèn luyện kỹ năng giải toán và có phương pháp ôn thi hiệu quả.
Đề thi thường bao gồm các dạng bài tập sau:
Dưới đây là một số đề thi tham khảo vào 10 môn Toán Quảng Ninh năm 2019:
Để giải đề thi vào 10 môn Toán Quảng Ninh 2019 hiệu quả, học sinh cần:
Giaitoan.edu.vn cung cấp các khóa học luyện thi vào 10 môn Toán Quảng Ninh 2019 chất lượng cao, được thiết kế bởi đội ngũ giáo viên giàu kinh nghiệm. Các khóa học này bao gồm:
Ngoài bộ đề thi vào 10 môn Toán Quảng Ninh năm 2019, học sinh có thể tham khảo thêm các tài liệu sau:
Chúc các em học sinh ôn thi tốt và đạt được kết quả cao trong kỳ thi tuyển sinh vào lớp 10 môn Toán Quảng Ninh năm 2019!