Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Bình Phước năm 2023. Đây là tài liệu ôn tập vô cùng quan trọng dành cho các em học sinh đang chuẩn bị cho kỳ thi sắp tới.
Chúng tôi đã tổng hợp đầy đủ các đề thi chính thức, đáp án chi tiết và hướng dẫn giải bài tập để giúp các em nắm vững kiến thức và tự tin làm bài.
Câu 1: 1. Tính giá trị của các biểu thức sau: \(A = \sqrt {16} {\rm{ \;}} + \sqrt 9 \) \(B = \sqrt 7 {\rm{ \;}} + \sqrt {{{\left( {4 - \sqrt 7 } \right)}^2}} \) 2. Cho biểu thức \(P = \frac{{x - 9}}{{\sqrt x {\rm{ \;}} + 3}} + \sqrt x {\rm{ \;}} + 2\) với \(x \ge 0\).
Câu 1: 1. Tính giá trị của các biểu thức sau:
\(A = \sqrt {16} {\rm{ \;}} + \sqrt 9 \)
\(B = \sqrt 7 {\rm{ \;}} + \sqrt {{{\left( {4 - \sqrt 7 } \right)}^2}} \)
2. Cho biểu thức \(P = \frac{{x - 9}}{{\sqrt x {\rm{ \;}} + 3}} + \sqrt x {\rm{ \;}} + 2\) với \(x \ge 0\).
a) Rút gọn biểu thức \(P.\)
b) Tính giá trị của biểu thức \(P\) khi \(x = 4\).
Câu 2: 1. Cho Parabol \(\left( P \right):y = {\rm{ \;}} - {x^2}\) và đường thẳng \((d):y = x - 2\).
a) Vẽ Parabol \((P)\) và đường thẳng \((d)\)trên cùng một hệ trục toạ độ \(Oxy.\)
b) Tìm toạ độ giao điểm của Parabol \((P)\) và đường thẳng \((d)\) bằng phép tính.
2. Không sử dụng máy tính, giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{2x + y = 5}\\{x - 3y = {\rm{ \;}} - 1}\end{array}} \right..\)
Câu 3: 1. Cho phương trình \({x^2} - 2x + m - 3 = 0\) (\(m\) là tham số).
a) Giải phương trình khi \(m = 0.\)
b) Tìm \(m\) để phương trình có hai nghiệm \({x_1},{\mkern 1mu} {\mkern 1mu} {x_2}\) sao cho biểu thức \(P = x_1^2 + x_2^2 + {\left( {{x_1}{x_2}} \right)^2}\) đạt giá trị nhỏ nhất.
2. Một mảnh vườn hình chữ nhật có diện tích \(600{\mkern 1mu} {{\rm{m}}^2}.\) Biết rằng nếu tăng chiều dài \(10{\mkern 1mu} {\rm{m}}\) và giảm chiều rộng \(5{\mkern 1mu} {\rm{m}}\) thì diện tích không đổi. Tính chiều dài và chiều rộng của mảnh vườn.
Câu 4: Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH.\) Biết rằng \(AB = 3\,{\rm{cm}}\), \(\widehat C = 30^\circ .\)
a) Tính \(\widehat B,\,\,AC,\,\,AH.\)
b) Trên cạnh \(BC\)lấy điểm \(M\) sao cho \(MC = 2MB,\) tính diện tích tam giác \(AMC.\)
Câu 5: Cho đường tròn \((O)\) đường kính \(AB\), lấy điểm \(C\) thuộc \((O)\)(\(C\) khác \(A\) và \(B\)), tiếp tuyến của đường tròn \((O)\) tại \(B\) cắt \(AC\) ở \(K.\) Từ \(K\) kẻ tiếp tuyến \(KD\) với đường tròn \((O)\)(\(D\) là tiếp điểm khác \(B\)).
a) Chứng minh tứ giác \(BODK\) nội tiếp.
b) Biết \(OK\)cắt \(BD\) tại \(I.\) Chứng minh rằng \(OI \bot BD\) và \(KC \cdot KA = KI \cdot KO.\)
c) Gọi \(E\) là trung điểm của \(AC,\) kẻ đường kính \(CF\) của đường tròn \((O),\) \(FE\) cắt \(AI\) tại \(H.\) Chứng minh rằng \(H\) là trung điểm của \(AI\).
-----HẾT-----
Câu 1: 1. Tính giá trị của các biểu thức sau:
\(A = \sqrt {16} {\rm{ \;}} + \sqrt 9 \)
\(B = \sqrt 7 {\rm{ \;}} + \sqrt {{{\left( {4 - \sqrt 7 } \right)}^2}} \)
2. Cho biểu thức \(P = \frac{{x - 9}}{{\sqrt x {\rm{ \;}} + 3}} + \sqrt x {\rm{ \;}} + 2\) với \(x \ge 0\).
a) Rút gọn biểu thức \(P.\)
b) Tính giá trị của biểu thức \(P\) khi \(x = 4\).
Câu 2: 1. Cho Parabol \(\left( P \right):y = {\rm{ \;}} - {x^2}\) và đường thẳng \((d):y = x - 2\).
a) Vẽ Parabol \((P)\) và đường thẳng \((d)\)trên cùng một hệ trục toạ độ \(Oxy.\)
b) Tìm toạ độ giao điểm của Parabol \((P)\) và đường thẳng \((d)\) bằng phép tính.
2. Không sử dụng máy tính, giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{2x + y = 5}\\{x - 3y = {\rm{ \;}} - 1}\end{array}} \right..\)
Câu 3: 1. Cho phương trình \({x^2} - 2x + m - 3 = 0\) (\(m\) là tham số).
a) Giải phương trình khi \(m = 0.\)
b) Tìm \(m\) để phương trình có hai nghiệm \({x_1},{\mkern 1mu} {\mkern 1mu} {x_2}\) sao cho biểu thức \(P = x_1^2 + x_2^2 + {\left( {{x_1}{x_2}} \right)^2}\) đạt giá trị nhỏ nhất.
2. Một mảnh vườn hình chữ nhật có diện tích \(600{\mkern 1mu} {{\rm{m}}^2}.\) Biết rằng nếu tăng chiều dài \(10{\mkern 1mu} {\rm{m}}\) và giảm chiều rộng \(5{\mkern 1mu} {\rm{m}}\) thì diện tích không đổi. Tính chiều dài và chiều rộng của mảnh vườn.
Câu 4: Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH.\) Biết rằng \(AB = 3\,{\rm{cm}}\), \(\widehat C = 30^\circ .\)
a) Tính \(\widehat B,\,\,AC,\,\,AH.\)
b) Trên cạnh \(BC\)lấy điểm \(M\) sao cho \(MC = 2MB,\) tính diện tích tam giác \(AMC.\)
Câu 5: Cho đường tròn \((O)\) đường kính \(AB\), lấy điểm \(C\) thuộc \((O)\)(\(C\) khác \(A\) và \(B\)), tiếp tuyến của đường tròn \((O)\) tại \(B\) cắt \(AC\) ở \(K.\) Từ \(K\) kẻ tiếp tuyến \(KD\) với đường tròn \((O)\)(\(D\) là tiếp điểm khác \(B\)).
a) Chứng minh tứ giác \(BODK\) nội tiếp.
b) Biết \(OK\)cắt \(BD\) tại \(I.\) Chứng minh rằng \(OI \bot BD\) và \(KC \cdot KA = KI \cdot KO.\)
c) Gọi \(E\) là trung điểm của \(AC,\) kẻ đường kính \(CF\) của đường tròn \((O),\) \(FE\) cắt \(AI\) tại \(H.\) Chứng minh rằng \(H\) là trung điểm của \(AI\).
-----HẾT-----
Câu 1 (TH):
Phương pháp:
1. Khai căn và thực hiện phép tính.
2. a) Tách tử thành hằng đẳng thức và rút gọn.
b) Thay \(x = 4\) vào biểu thức đã rút gọn ở câu a để tính.
Cách giải:
1. \(A = \sqrt {16} {\rm{ \;}} + \sqrt 9 {\rm{ \;}} = \sqrt {{4^2}} {\rm{ \;}} + \sqrt {{3^2}} {\rm{ \;}} = 4 + 3 = 7\)
\(B = \sqrt 7 {\rm{ \;}} + \sqrt {{{(4 - \sqrt 7 )}^2}} {\rm{ \;}} = \sqrt 7 {\rm{ \;}} + 4 - \sqrt 7 {\rm{ \;}} = 4(\;{\rm{Do}}\;4 - \sqrt 7 {\rm{ \;}} > 0)\)
Vậy \(A = 7;B = 4\).
a) Rút gọn biểu thức \(P\).
Với \(x \ge 0\) ta có:
P = \( = \frac{{x - 9}}{{\sqrt x {\rm{ \;}} + 3}} + \sqrt x {\rm{ \;}} + 2\)
\(\; = \frac{{\left( {\sqrt x {\rm{ \;}} + 3} \right)\left( {\sqrt x {\rm{ \;}} - 3} \right)}}{{\sqrt x {\rm{ \;}} + 3}} + \sqrt x {\rm{ \;}} + 2\)
\(\; = \sqrt x {\rm{ \;}} - 3 + \sqrt x {\rm{ \;}} + 2\)
\(\; = 2\sqrt x {\rm{ \;}} - 1\)
Vậy với \(x \ge 0\) thì \(P = 2\sqrt x {\rm{ \;}} - 1\).
b) Tính giá trị của biểu thức \(P\) khi \(x = 4\).
Với \(x = 4\) (thoả mãn điều kiện) ta được: \(P = 2\sqrt 4 {\rm{ \;}} - 1 = 2\sqrt {{2^2}} {\rm{ \;}} - 1 = 2.2 - 1 = 4 - 1 = 3\).
Vậy với \(x = 4\) thì \(P = 3\).
Câu 2 (TH):
Phương pháp:
1. a) Chọn 5 điểm để vẽ Parabol (P) và chọn 2 điểm để vẽ đường thẳng (d).
b) Xét phương trình hoành độ và giải phương trình.
2. Giải hệ phương trình bằng phương pháp thế.
Cách giải:
1. Cho Parabol \(\left( P \right):y = {\rm{ \;}} - {x^2}\) và dường thẳng \(\left( d \right):y = x - 2\).
a) Vẽ Parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) trên cùng một hệ trục toạ dộ Oxy.
*Vẽ đồ thị hàm số \(y = {\rm{ \;}} - {x^2}\)
Tập xác định \(D = \mathbb{R}\).
Bảng giá trị
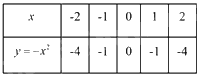
Ta có \(a = {\rm{ \;}} - 1 < 0\) đồ thị hàm số là Parabol có đường cong hướng xuống dưới.
Qua 5 điểm có tọa độ \(A\left( { - 2;4} \right);B\left( { - 1;1} \right);O\left( {0;0} \right);C\left( {1;1} \right);D\left( {2;4} \right)\).
*Vẽ đồ thị hàm số \(y = x - 2\)
Ta có bảng giá trị:

Đồ thị hàm số \(y = x - 2\) là đường thẳng đi qua hai điểm \(\left( {0; - 2} \right)\) và \(\left( {2;0} \right)\).
Ta vẽ được đồ thị \(\left( {\rm{d}} \right)\) và \(\left( {\rm{P}} \right)\) trên cùng hệ trục toạ độ \({\rm{Oxy}}\) như sau:
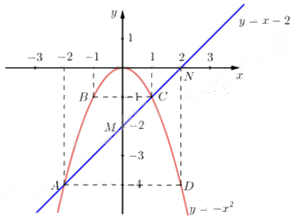
b) Tìm tọa độ giao điểm của Parabol \(\left( P \right)\) và duờng thằng \(\left( d \right)\) bằng phép tính.
Hoành độ giao điểm của \(\left( {\rm{P}} \right)\) và \(\left( {\rm{d}} \right)\) là nghiệm của phương trình
\( - {x^2} = x - 2 \Leftrightarrow {\rm{ \;}} - {x^2} - x + 2 = 0\)
Ta thấy \(a + b + c = 0\) nên phương trình có hai nghiệm \(\left[ {\begin{array}{*{20}{l}}{{x_1} = 1}\\{{x_2} = {\rm{ \;}} - 2}\end{array}} \right.\).
Với \({\rm{x}} = 1\) thì \({\rm{y}} = 1 - 2 = {\rm{ \;}} - 1\) suy ra \(E\left( {1; - 1} \right)\) là giao điểm.
Với \({\rm{x}} = {\rm{ \;}} - 2\) thì \({\rm{y}} = {\rm{ \;}} - 2 - 2 = {\rm{ \;}} - 4\) suy ra \(F\left( { - 2; - 4} \right)\) là giao điểm.
Vậy giao điểm của \(\left( {\rm{P}} \right)\) và \(\left( {\rm{d}} \right)\) là \(E\left( {1; - 1} \right);F\left( { - 2; - 4} \right)\).
2. Không sử dụng máy tính, giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{2x + y = 5}\\{x - 3y = {\rm{ \;}} - 1}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{l}}{2x + y = 5}\\{x - 3y = {\rm{ \;}} - 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2x + y = 5}\\{x = {\rm{ \;}} - 1 + 3y}\end{array}} \right.} \right.\)
Thay (2) vào (1) ta có:
\( \Leftrightarrow 2\left( { - 1 + 3y} \right) + y = 5\)
\( \Leftrightarrow {\rm{ \;}} - 2 + 6y + y = 5\)
\( \Leftrightarrow 7y = 7\)
\( \Leftrightarrow y = 1\)
Thay \(y = 1\) vào (2) ta có: \(x = {\rm{ \;}} - 1 + 3.1 = 2\)
Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {2;1} \right)\).
Câu 3 (VD):
Phương pháp:
1. a) Thay \(m = 0\) vào phương trình ban đầu để giải.
b) Áp dụng hệ thức vi-et \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = {\rm{ \;}} - \frac{b}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\)
2. Gọi chiều rộng ban đầu là x, từ đó tìm được chiều rộng và chiều dài lúc sau. Diện tích không đổi nên phương trình là chiều dài nhân với chiều rộng bằng 600.
Cách giải:
1. Cho phương trình \({x^2} - 2x + m - 3 = 0\) (m là tham số).
a) Giải phương trình khi \(m = 0\).
Với \(m = 0\) ta có: \({x^2} - 2x - 3 = 0\)
Vi \(a - b + c = 1 - \left( { - 2} \right) - 3 = 0\) nên phương trình có 1 nghiệm là \({x_1} = {\rm{ \;}} - 1\) và \({x_2} = \frac{c}{a} = 3\).
Vậy với \(m = 0\) thì phương trình có tập nghiệm là: \(S = \left\{ { - 1;3} \right\}\).
b) Tìm \(m\) để phương trình có hai nghiệm \({x_1},{x_2}\) sao cho biểu thức \(P = {x_1}{\;^2} + {x_1}{\;^2} + {\left( {{x_1}{x_2}} \right)^2}\) dạt giá trị nhỏ nhất.
Xét phương trình \({x^2} - 2x + m - 3 = 0\) :
Ta có: \(\Delta ' = {1^2} - \left( {m - 3} \right) = 4 - m\)
Phương trình có 2 nghiệm khi và chi khi \(\Delta ' \ge 0 \Leftrightarrow 4 - m \ge 0 \Leftrightarrow m \le 4\)
Khi đó, theo hệ thức Vi-ét ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 2}\\{{x_1}{x_2} = m - 3}\end{array}} \right.\)
Từ giả thiết: \(P = x_1^2 + x_1^2 + {\left( {{x_1}{x_2}} \right)^2} = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} + {\left( {{x_1}{x_2}} \right)^2}\)
Suy ra:
P = \( = {2^2} - 2\left( {m - 3} \right) + {(m - 3)^2}\)
\( = 4 - 2m + 6 + {m^2} - 6m + 9\)
\( = {m^2} - 8m + 19\)
\( = {m^2} - 8m + 16 + 3\)
\( = {(m - 4)^2} + 3 \ge 3\)
Suy ra giá trị nhỏ nhất của \(P\) là 3 khi và chỉ khi \({(m - 4)^2} = 0 \Leftrightarrow m - 4 = 0 \Leftrightarrow m = 4\).
Vậy với \(m = 4\) thì biểu thức \(P = x_1^2 + x_1^2 + {\left( {{x_1}{x_2}} \right)^2}\) đạt giá trị nhỏ nhất bằng 3.
2. Gọi chiều rộng khu vườn hình chữ nhật là \(x{\mkern 1mu} {\mkern 1mu} \left( {\rm{m}} \right),\) \(x > 5.\)
Suy ra chiều dài khu vườn là \(\frac{{600}}{x}{\mkern 1mu} {\mkern 1mu} \left( {\rm{m}} \right).\)
Chiều dài khu vườn sau khi tăng là \(\frac{{600}}{x} + 10{\mkern 1mu} {\mkern 1mu} \left( {\rm{m}} \right).\)
Chiều rộng khu vườn sau khi giảm là \(x - 5{\mkern 1mu} \left( {\rm{m}} \right).\)
Diện tích khu vườn sau khi tăng chiều dài \(10{\mkern 1mu} {\rm{m}}\) và giảm chiều rộng \(5{\mkern 1mu} {\rm{m}}\) thì không đổi nên ta có phương trình
\(\left( {\frac{{600}}{x} + 10} \right)\left( {x - 5} \right) = 600.\)
\( \Leftrightarrow \left( {600 + 10x} \right)\left( {x - 5} \right) = 600x \Leftrightarrow 10{x^2} - 50x - 3000 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 20}\\{x = {\rm{ \;}} - 15{\mkern 1mu} \left( {\rm{L}} \right)}\end{array}} \right..\)
Vậy chiều dài mảnh vườn là \(30{\mkern 1mu} {\mkern 1mu} \left( {\rm{m}} \right),\) chiều rộng mảnh vườn là \(20{\mkern 1mu} {\mkern 1mu} \left( {\rm{m}} \right).\)
Câu 4 (TH):
Phương pháp:
a) Áp dụng tỉ số lượng giác trong tam giác vuông.
b) \({S_{AMC}} = \frac{1}{2}AH \cdot MC\)
Cách giải:
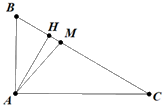
a) Ta có \(\angle B = 60^\circ \)
Ta có \(\sin \angle C = \frac{{AB}}{{BC}} \Rightarrow BC = \frac{{AB}}{{\sin \angle C}} = \frac{3}{{\frac{1}{2}}} = 6{\mkern 1mu} {\mkern 1mu} \left( {{\rm{cm}}} \right).\)
Ta có \(AC = \sqrt {B{C^2} - A{B^2}} {\rm{ \;}} = \sqrt {{6^2} - {3^2}} {\rm{ \;}} = 3\sqrt 3 {\mkern 1mu} {\mkern 1mu} \left( {{\rm{cm}}} \right).\)
\(AH \cdot BC = AB \cdot AC \Leftrightarrow AH = \frac{{AB \cdot AC}}{{BC}} = \frac{{3 \cdot 3\sqrt 3 }}{6} = \frac{{3\sqrt 3 }}{2}{\mkern 1mu} \left( {{\rm{cm}}} \right).\)
b) \({S_{AMC}} = \frac{1}{2}AH \cdot MC = \frac{1}{2}AH \cdot \frac{2}{3}BC = \frac{1}{2} \cdot \frac{{3\sqrt 3 }}{2} \cdot \frac{2}{3} \cdot 6 = 3\sqrt 3 {\mkern 1mu} \left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
Câu 5 (VD):
Phương pháp:
a) Tứ giác có tổng hai góc đối bằng \(180^\circ \) là tứ giác nội tiếp.
b) Áp dụng hệ thức lượng trong tam giác vuông để chứng minh \(K{B^2} = KC.KA\) và \(K{B^2} = KI \cdot KO.\)
c) Chứng minh \(E\) là trung điểm của \(AC\) và \({\rm{EF}}\,{\rm{//}}\,{\rm{CI}}\) từ đó suy ra \(H\) là trung điểm của \(AI\).
Cách giải:
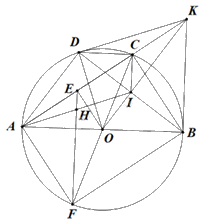
a) Ta có \(\widehat {OBK} = \widehat {ODK} = 90^\circ .\)
\( \Rightarrow \widehat {OBK} + \widehat {ODK} = 180^\circ .\)
Do đó tứ giác \(BODK\) nội tiếp
b) Ta có \(KB = KD\) (tính chất hai tiếp tuyến cắt nhau)
Ta lại có \(OB = OD\) nên \(OK\) là đường trung trực của \(BD\). Suy ra\(KO \bot BD \Rightarrow OI \bot BD.\)
Xét tam giác \(ABK\) vuông tại \(B\) nên \(K{B^2} = KC.KA.\)
Xét tam giác \(OBK\) vuông tại \(B\) nên \(K{B^2} = KI \cdot KO.\)
Suy ra \(KC.KA = KI.KO.\) (đpcm)
c) Xét tam giác \(KCI\) và tam giác \(KOA\) ta có góc \(K\) chung, \(KC \cdot KA = KI \cdot KO \Leftrightarrow \frac{{KC}}{{KI}} = \frac{{KO}}{{KA}}\).
Suy ra tam giác \(KCI\) và tam giác \(KOA\) đồng dạng với nhau. Suy ra \(\widehat {KCI} = \widehat {KOA}\). (*)
Xét tam giác \(ACF\) và \(BAK\) có \(\widehat {KBA} = \widehat {C{\rm{AF}}} = 90^\circ .\) (1)
Mà tam giác \(O{\rm{AC}}\) cân tại \(O\) nên \(\widehat {OAC} = \widehat {OCA}\) (2)
Từ (1) và (2) suy ra \(\Delta ACF\) đồng dạng với \(\Delta BAK\) suy ra \(\frac{{BA}}{{BK}} = \frac{{AC}}{{{\rm{AF}}}} \Leftrightarrow \frac{{2BO}}{{BK}} = \frac{{2AE}}{{{\rm{AF}}}} \Leftrightarrow \frac{{BK}}{{{\rm{AF}}}} = \frac{{BO}}{{AE}}\).
Xét tam giác \(AEF\) và \(BOK\) ta có \(\widehat {KBO} = \widehat {E{\rm{AF}}} = 90^\circ \) và \(\frac{{BK}}{{{\rm{AF}}}} = \frac{{BO}}{{AE}}\)
Nên \(\Delta AEF\) đồng dạng với \(\Delta BOK\) suy ra
\(\widehat {AEF} = \widehat {BOK} \Rightarrow \widehat {K{\rm{EF}}} = \widehat {KOA}\)( cùng bù với \(\widehat {AEF}\)) (**)
Từ (*) và (**) ta có \(\widehat {KCI} = \widehat {K{\rm{EF}}}\) suy ra \({\rm{EF}}\,{\rm{//}}\,{\rm{CI}}\).
Xét tam giác \(ACI\) có \(E\) là trung điểm của \(AC\) và \({\rm{EF}}\,{\rm{//}}\,{\rm{CI}}\) nên \(H\) là trung điểm của \(AI\).
-----HẾT-----
Câu 1 (TH):
Phương pháp:
1. Khai căn và thực hiện phép tính.
2. a) Tách tử thành hằng đẳng thức và rút gọn.
b) Thay \(x = 4\) vào biểu thức đã rút gọn ở câu a để tính.
Cách giải:
1. \(A = \sqrt {16} {\rm{ \;}} + \sqrt 9 {\rm{ \;}} = \sqrt {{4^2}} {\rm{ \;}} + \sqrt {{3^2}} {\rm{ \;}} = 4 + 3 = 7\)
\(B = \sqrt 7 {\rm{ \;}} + \sqrt {{{(4 - \sqrt 7 )}^2}} {\rm{ \;}} = \sqrt 7 {\rm{ \;}} + 4 - \sqrt 7 {\rm{ \;}} = 4(\;{\rm{Do}}\;4 - \sqrt 7 {\rm{ \;}} > 0)\)
Vậy \(A = 7;B = 4\).
a) Rút gọn biểu thức \(P\).
Với \(x \ge 0\) ta có:
P = \( = \frac{{x - 9}}{{\sqrt x {\rm{ \;}} + 3}} + \sqrt x {\rm{ \;}} + 2\)
\(\; = \frac{{\left( {\sqrt x {\rm{ \;}} + 3} \right)\left( {\sqrt x {\rm{ \;}} - 3} \right)}}{{\sqrt x {\rm{ \;}} + 3}} + \sqrt x {\rm{ \;}} + 2\)
\(\; = \sqrt x {\rm{ \;}} - 3 + \sqrt x {\rm{ \;}} + 2\)
\(\; = 2\sqrt x {\rm{ \;}} - 1\)
Vậy với \(x \ge 0\) thì \(P = 2\sqrt x {\rm{ \;}} - 1\).
b) Tính giá trị của biểu thức \(P\) khi \(x = 4\).
Với \(x = 4\) (thoả mãn điều kiện) ta được: \(P = 2\sqrt 4 {\rm{ \;}} - 1 = 2\sqrt {{2^2}} {\rm{ \;}} - 1 = 2.2 - 1 = 4 - 1 = 3\).
Vậy với \(x = 4\) thì \(P = 3\).
Câu 2 (TH):
Phương pháp:
1. a) Chọn 5 điểm để vẽ Parabol (P) và chọn 2 điểm để vẽ đường thẳng (d).
b) Xét phương trình hoành độ và giải phương trình.
2. Giải hệ phương trình bằng phương pháp thế.
Cách giải:
1. Cho Parabol \(\left( P \right):y = {\rm{ \;}} - {x^2}\) và dường thẳng \(\left( d \right):y = x - 2\).
a) Vẽ Parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) trên cùng một hệ trục toạ dộ Oxy.
*Vẽ đồ thị hàm số \(y = {\rm{ \;}} - {x^2}\)
Tập xác định \(D = \mathbb{R}\).
Bảng giá trị
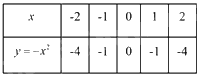
Ta có \(a = {\rm{ \;}} - 1 < 0\) đồ thị hàm số là Parabol có đường cong hướng xuống dưới.
Qua 5 điểm có tọa độ \(A\left( { - 2;4} \right);B\left( { - 1;1} \right);O\left( {0;0} \right);C\left( {1;1} \right);D\left( {2;4} \right)\).
*Vẽ đồ thị hàm số \(y = x - 2\)
Ta có bảng giá trị:

Đồ thị hàm số \(y = x - 2\) là đường thẳng đi qua hai điểm \(\left( {0; - 2} \right)\) và \(\left( {2;0} \right)\).
Ta vẽ được đồ thị \(\left( {\rm{d}} \right)\) và \(\left( {\rm{P}} \right)\) trên cùng hệ trục toạ độ \({\rm{Oxy}}\) như sau:
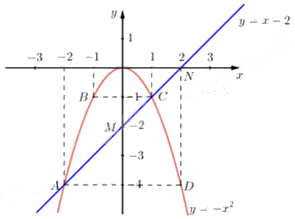
b) Tìm tọa độ giao điểm của Parabol \(\left( P \right)\) và duờng thằng \(\left( d \right)\) bằng phép tính.
Hoành độ giao điểm của \(\left( {\rm{P}} \right)\) và \(\left( {\rm{d}} \right)\) là nghiệm của phương trình
\( - {x^2} = x - 2 \Leftrightarrow {\rm{ \;}} - {x^2} - x + 2 = 0\)
Ta thấy \(a + b + c = 0\) nên phương trình có hai nghiệm \(\left[ {\begin{array}{*{20}{l}}{{x_1} = 1}\\{{x_2} = {\rm{ \;}} - 2}\end{array}} \right.\).
Với \({\rm{x}} = 1\) thì \({\rm{y}} = 1 - 2 = {\rm{ \;}} - 1\) suy ra \(E\left( {1; - 1} \right)\) là giao điểm.
Với \({\rm{x}} = {\rm{ \;}} - 2\) thì \({\rm{y}} = {\rm{ \;}} - 2 - 2 = {\rm{ \;}} - 4\) suy ra \(F\left( { - 2; - 4} \right)\) là giao điểm.
Vậy giao điểm của \(\left( {\rm{P}} \right)\) và \(\left( {\rm{d}} \right)\) là \(E\left( {1; - 1} \right);F\left( { - 2; - 4} \right)\).
2. Không sử dụng máy tính, giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{2x + y = 5}\\{x - 3y = {\rm{ \;}} - 1}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{l}}{2x + y = 5}\\{x - 3y = {\rm{ \;}} - 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2x + y = 5}\\{x = {\rm{ \;}} - 1 + 3y}\end{array}} \right.} \right.\)
Thay (2) vào (1) ta có:
\( \Leftrightarrow 2\left( { - 1 + 3y} \right) + y = 5\)
\( \Leftrightarrow {\rm{ \;}} - 2 + 6y + y = 5\)
\( \Leftrightarrow 7y = 7\)
\( \Leftrightarrow y = 1\)
Thay \(y = 1\) vào (2) ta có: \(x = {\rm{ \;}} - 1 + 3.1 = 2\)
Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {2;1} \right)\).
Câu 3 (VD):
Phương pháp:
1. a) Thay \(m = 0\) vào phương trình ban đầu để giải.
b) Áp dụng hệ thức vi-et \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = {\rm{ \;}} - \frac{b}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\)
2. Gọi chiều rộng ban đầu là x, từ đó tìm được chiều rộng và chiều dài lúc sau. Diện tích không đổi nên phương trình là chiều dài nhân với chiều rộng bằng 600.
Cách giải:
1. Cho phương trình \({x^2} - 2x + m - 3 = 0\) (m là tham số).
a) Giải phương trình khi \(m = 0\).
Với \(m = 0\) ta có: \({x^2} - 2x - 3 = 0\)
Vi \(a - b + c = 1 - \left( { - 2} \right) - 3 = 0\) nên phương trình có 1 nghiệm là \({x_1} = {\rm{ \;}} - 1\) và \({x_2} = \frac{c}{a} = 3\).
Vậy với \(m = 0\) thì phương trình có tập nghiệm là: \(S = \left\{ { - 1;3} \right\}\).
b) Tìm \(m\) để phương trình có hai nghiệm \({x_1},{x_2}\) sao cho biểu thức \(P = {x_1}{\;^2} + {x_1}{\;^2} + {\left( {{x_1}{x_2}} \right)^2}\) dạt giá trị nhỏ nhất.
Xét phương trình \({x^2} - 2x + m - 3 = 0\) :
Ta có: \(\Delta ' = {1^2} - \left( {m - 3} \right) = 4 - m\)
Phương trình có 2 nghiệm khi và chi khi \(\Delta ' \ge 0 \Leftrightarrow 4 - m \ge 0 \Leftrightarrow m \le 4\)
Khi đó, theo hệ thức Vi-ét ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 2}\\{{x_1}{x_2} = m - 3}\end{array}} \right.\)
Từ giả thiết: \(P = x_1^2 + x_1^2 + {\left( {{x_1}{x_2}} \right)^2} = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} + {\left( {{x_1}{x_2}} \right)^2}\)
Suy ra:
P = \( = {2^2} - 2\left( {m - 3} \right) + {(m - 3)^2}\)
\( = 4 - 2m + 6 + {m^2} - 6m + 9\)
\( = {m^2} - 8m + 19\)
\( = {m^2} - 8m + 16 + 3\)
\( = {(m - 4)^2} + 3 \ge 3\)
Suy ra giá trị nhỏ nhất của \(P\) là 3 khi và chỉ khi \({(m - 4)^2} = 0 \Leftrightarrow m - 4 = 0 \Leftrightarrow m = 4\).
Vậy với \(m = 4\) thì biểu thức \(P = x_1^2 + x_1^2 + {\left( {{x_1}{x_2}} \right)^2}\) đạt giá trị nhỏ nhất bằng 3.
2. Gọi chiều rộng khu vườn hình chữ nhật là \(x{\mkern 1mu} {\mkern 1mu} \left( {\rm{m}} \right),\) \(x > 5.\)
Suy ra chiều dài khu vườn là \(\frac{{600}}{x}{\mkern 1mu} {\mkern 1mu} \left( {\rm{m}} \right).\)
Chiều dài khu vườn sau khi tăng là \(\frac{{600}}{x} + 10{\mkern 1mu} {\mkern 1mu} \left( {\rm{m}} \right).\)
Chiều rộng khu vườn sau khi giảm là \(x - 5{\mkern 1mu} \left( {\rm{m}} \right).\)
Diện tích khu vườn sau khi tăng chiều dài \(10{\mkern 1mu} {\rm{m}}\) và giảm chiều rộng \(5{\mkern 1mu} {\rm{m}}\) thì không đổi nên ta có phương trình
\(\left( {\frac{{600}}{x} + 10} \right)\left( {x - 5} \right) = 600.\)
\( \Leftrightarrow \left( {600 + 10x} \right)\left( {x - 5} \right) = 600x \Leftrightarrow 10{x^2} - 50x - 3000 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 20}\\{x = {\rm{ \;}} - 15{\mkern 1mu} \left( {\rm{L}} \right)}\end{array}} \right..\)
Vậy chiều dài mảnh vườn là \(30{\mkern 1mu} {\mkern 1mu} \left( {\rm{m}} \right),\) chiều rộng mảnh vườn là \(20{\mkern 1mu} {\mkern 1mu} \left( {\rm{m}} \right).\)
Câu 4 (TH):
Phương pháp:
a) Áp dụng tỉ số lượng giác trong tam giác vuông.
b) \({S_{AMC}} = \frac{1}{2}AH \cdot MC\)
Cách giải:
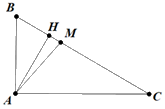
a) Ta có \(\angle B = 60^\circ \)
Ta có \(\sin \angle C = \frac{{AB}}{{BC}} \Rightarrow BC = \frac{{AB}}{{\sin \angle C}} = \frac{3}{{\frac{1}{2}}} = 6{\mkern 1mu} {\mkern 1mu} \left( {{\rm{cm}}} \right).\)
Ta có \(AC = \sqrt {B{C^2} - A{B^2}} {\rm{ \;}} = \sqrt {{6^2} - {3^2}} {\rm{ \;}} = 3\sqrt 3 {\mkern 1mu} {\mkern 1mu} \left( {{\rm{cm}}} \right).\)
\(AH \cdot BC = AB \cdot AC \Leftrightarrow AH = \frac{{AB \cdot AC}}{{BC}} = \frac{{3 \cdot 3\sqrt 3 }}{6} = \frac{{3\sqrt 3 }}{2}{\mkern 1mu} \left( {{\rm{cm}}} \right).\)
b) \({S_{AMC}} = \frac{1}{2}AH \cdot MC = \frac{1}{2}AH \cdot \frac{2}{3}BC = \frac{1}{2} \cdot \frac{{3\sqrt 3 }}{2} \cdot \frac{2}{3} \cdot 6 = 3\sqrt 3 {\mkern 1mu} \left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
Câu 5 (VD):
Phương pháp:
a) Tứ giác có tổng hai góc đối bằng \(180^\circ \) là tứ giác nội tiếp.
b) Áp dụng hệ thức lượng trong tam giác vuông để chứng minh \(K{B^2} = KC.KA\) và \(K{B^2} = KI \cdot KO.\)
c) Chứng minh \(E\) là trung điểm của \(AC\) và \({\rm{EF}}\,{\rm{//}}\,{\rm{CI}}\) từ đó suy ra \(H\) là trung điểm của \(AI\).
Cách giải:
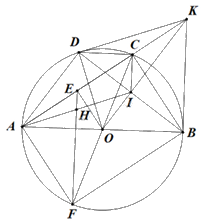
a) Ta có \(\widehat {OBK} = \widehat {ODK} = 90^\circ .\)
\( \Rightarrow \widehat {OBK} + \widehat {ODK} = 180^\circ .\)
Do đó tứ giác \(BODK\) nội tiếp
b) Ta có \(KB = KD\) (tính chất hai tiếp tuyến cắt nhau)
Ta lại có \(OB = OD\) nên \(OK\) là đường trung trực của \(BD\). Suy ra\(KO \bot BD \Rightarrow OI \bot BD.\)
Xét tam giác \(ABK\) vuông tại \(B\) nên \(K{B^2} = KC.KA.\)
Xét tam giác \(OBK\) vuông tại \(B\) nên \(K{B^2} = KI \cdot KO.\)
Suy ra \(KC.KA = KI.KO.\) (đpcm)
c) Xét tam giác \(KCI\) và tam giác \(KOA\) ta có góc \(K\) chung, \(KC \cdot KA = KI \cdot KO \Leftrightarrow \frac{{KC}}{{KI}} = \frac{{KO}}{{KA}}\).
Suy ra tam giác \(KCI\) và tam giác \(KOA\) đồng dạng với nhau. Suy ra \(\widehat {KCI} = \widehat {KOA}\). (*)
Xét tam giác \(ACF\) và \(BAK\) có \(\widehat {KBA} = \widehat {C{\rm{AF}}} = 90^\circ .\) (1)
Mà tam giác \(O{\rm{AC}}\) cân tại \(O\) nên \(\widehat {OAC} = \widehat {OCA}\) (2)
Từ (1) và (2) suy ra \(\Delta ACF\) đồng dạng với \(\Delta BAK\) suy ra \(\frac{{BA}}{{BK}} = \frac{{AC}}{{{\rm{AF}}}} \Leftrightarrow \frac{{2BO}}{{BK}} = \frac{{2AE}}{{{\rm{AF}}}} \Leftrightarrow \frac{{BK}}{{{\rm{AF}}}} = \frac{{BO}}{{AE}}\).
Xét tam giác \(AEF\) và \(BOK\) ta có \(\widehat {KBO} = \widehat {E{\rm{AF}}} = 90^\circ \) và \(\frac{{BK}}{{{\rm{AF}}}} = \frac{{BO}}{{AE}}\)
Nên \(\Delta AEF\) đồng dạng với \(\Delta BOK\) suy ra
\(\widehat {AEF} = \widehat {BOK} \Rightarrow \widehat {K{\rm{EF}}} = \widehat {KOA}\)( cùng bù với \(\widehat {AEF}\)) (**)
Từ (*) và (**) ta có \(\widehat {KCI} = \widehat {K{\rm{EF}}}\) suy ra \({\rm{EF}}\,{\rm{//}}\,{\rm{CI}}\).
Xét tam giác \(ACI\) có \(E\) là trung điểm của \(AC\) và \({\rm{EF}}\,{\rm{//}}\,{\rm{CI}}\) nên \(H\) là trung điểm của \(AI\).
-----HẾT-----
Kỳ thi tuyển sinh vào lớp 10 môn Toán Bình Phước năm 2023 là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Để đạt kết quả tốt nhất, việc chuẩn bị kỹ lưỡng là vô cùng cần thiết. Đề thi thường bao gồm các dạng bài tập thuộc chương trình Toán lớp 9, tập trung vào các chủ đề chính như đại số, hình học và số học.
Cấu trúc đề thi thường bao gồm các phần sau:
Tỷ lệ điểm giữa phần trắc nghiệm và phần tự luận có thể thay đổi tùy theo từng năm, nhưng thường phần tự luận chiếm tỷ trọng lớn hơn.
Để chuẩn bị tốt nhất cho kỳ thi, các em học sinh cần tập trung vào các chủ đề sau:
Ngoài ra, các em cũng nên ôn tập lại các kiến thức về toán học thực tế và các bài toán ứng dụng.
Một trong những cách hiệu quả nhất để chuẩn bị cho kỳ thi là luyện tập với các đề thi năm trước. Điều này giúp các em làm quen với cấu trúc đề thi, dạng bài tập và phân bổ thời gian hợp lý.
Giaitoan.edu.vn cung cấp đầy đủ các đề thi vào 10 môn Toán Bình Phước các năm trước, kèm theo đáp án chi tiết và hướng dẫn giải bài tập. Các em có thể tải về và luyện tập ngay hôm nay.
Ngoài các đề thi, các em học sinh cũng có thể tham khảo các tài liệu ôn tập hữu ích sau:
Các giáo viên có kinh nghiệm thường khuyên các em học sinh nên:
Giaitoan.edu.vn là một trang web học toán online uy tín, cung cấp đầy đủ các tài liệu ôn tập, đề thi và bài giảng chất lượng cao. Chúng tôi luôn đồng hành cùng các em trên con đường chinh phục kiến thức và đạt được thành công trong kỳ thi tuyển sinh vào lớp 10.
| Năm | Link đề thi | Đáp án |
|---|---|---|
| 2022 | Link đề thi 2022 | Đáp án 2022 |
| 2021 | Link đề thi 2021 | Đáp án 2021 |
| 2020 | Link đề thi 2020 | Đáp án 2020 |
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi tuyển sinh vào lớp 10 môn Toán Bình Phước năm 2023!