Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh An Giang năm 2018 chính thức. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi sắp tới.
Đề thi vào 10 môn Toán An Giang năm 2018 được biên soạn theo chuẩn kiến thức và kỹ năng của chương trình THCS, bao gồm các dạng bài tập thường gặp như đại số, hình học, số học và các bài toán thực tế.
Bài 1. (3,0 điểm) Giải các phương trình và hệ phương trình sau đây
Bài 1.
Phương pháp:
a.Giải phương trình bậc nhất một ẩn: \(ax + b = 0 \Leftrightarrow x = - \dfrac{b}{a}\)
b.Giải hệ phương trình bằng phương pháp thế và cộng đại số.
c. Giải phương trình bậc hai: sử dụng biệt thức \(\Delta = {b^2} - 4ac\left( {\Delta ' = b{'^2} - ac} \right)\) Cách giải:
a.
\(\begin{array}{l}\sqrt 3 x - \sqrt 2 x = \sqrt 3 + \sqrt 2 \\ \Leftrightarrow \left( {\sqrt 3 - \sqrt 2 } \right)x = \sqrt 3 + \sqrt 2 \\ \Leftrightarrow x = \dfrac{{\sqrt 3 + \sqrt 2 }}{{\sqrt 3 - \sqrt 2 }}\\ \Leftrightarrow x = \dfrac{{{{\left( {\sqrt 3 + \sqrt 2 } \right)}^2}}}{{3 - 2}}\\ \Leftrightarrow x = 5 + 2\sqrt 6 \end{array}\)
b.\(\left\{ \begin{array}{l}x + y = 101\\ - x + y = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2y = 100\\x = y + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 50\\x = y + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 50\\x = 51\end{array} \right.\)
Vậy hệ phương trình có nghiệm là \(\left( {x;y} \right) = \left( {51;50} \right)\)
c.\({x^2} + 2\sqrt 3 x + 2 = 0\)
Ta có: \(a = 1;b' = \sqrt 3 ;c = 2\)
\(\Delta ' = {\left( {\sqrt 3 } \right)^2} - 2 = 1 > 0\)
Khi đó phương trình có hai nghiệm phân biệt là: \(\left[ \begin{array}{l}{x_1} = - \sqrt 3 - 1\\{x_2} = - \sqrt 3 + 1\end{array} \right.\)
Vậy phương trình đã cho có 2 nghiệm phân biệt là: \(S = \left\{ { - \sqrt 3 - 1; - \sqrt 3 + 1} \right\}\)
Bài 2.
Phương pháp:
a.Lập bảng giá trị
b. (d) cắt trục hoành tại điểm có hoành độ bằng 1 nên điểm đó có tọa độ là (1;0) sau đó thay vào phương trình đường thẳng (d) ta được 1 phương trình theo a, b. (pt1)
(d) cắt (P) tại điểm có hoành độ bằng 2 nên thay x = 2 vào phương trình hoành độ giao điểm của (d) và (P) ta được phương trình thứ 2 theo a, b. (pt2)
Kết hợp (1) và (2) ta giải hệ phương trình tìm được a, b.
Cách giải:
Cho hàm số \(y = 0,5.{x^2}\) có đồ thị là Parabol (P)
a.Vẽ đồ thị (P) của hàm số đã cho
Ta có bảng giá trị
\(x\) | -4 | -2 | 0 | 2 | 4 |
\(y = 0,5{x^2}\) | 8 | 2 | 0 | 2 | 8 |
Đồ thị hàm số (P) có hình dạng đường cong đi qua các điểm \(\left( {0;\;0} \right),\;\;\left( { - 2;\;2} \right),\,\left( { - 4;8} \right),\;\;\left( {2;\;2} \right),\,\,\left( {4;8} \right)\)
Vẽ đồ thị:
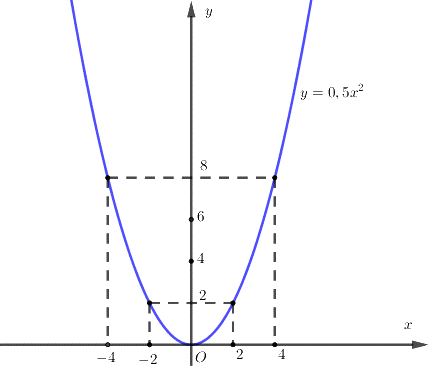
b.Xác định hệ số a; b của đường thẳng (d): \(y = ax + b\) , biết (d) cắt trục hoành tại điểm có hoành độ bằng 1 và (d) cắt (P) tại điểm có hoành độ bằng 2. Chứng tỏ (P) và (d) tiếp xúc nhau.
Ta có: (d) cắt trục hoành tại điểm có hoành độ bằng 1 nên\(A\left( {1;0} \right)\) . Thay tọa độ của điểm A vào phương trình đường thẳng (d) ta có: \(a + b = 0\,\,\left( 1 \right)\)
Hoành độ giao điểm của (d) và (P) là nghiệm của phương trình:
\(0,5{x^2} = ax + b \Leftrightarrow 0,5{x^2} - ax + b = 0\) (*)
Theo đề ra ta có: (d) cắt (P) tại điểm có hoành độ bằng 2 nên x = 2 là nghiệm của phương trình (*)
\(0,{5.2^2} - a.2 + b = 0 \Leftrightarrow 2a - b = 2\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) ta có hệ phương trình
\(\left\{ \begin{array}{l}a + b = 0\\2a - b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3a = 2\\b = - a\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{2}{3}\\b = - \dfrac{2}{3}\end{array} \right.\)
Vậy \(a = \dfrac{2}{3};b = - \dfrac{2}{3}\) thỏa mãn yêu cầu bài toán.
Bài 3.
Phương pháp:
a.Tìm m để phương trình có nghiệm bằng \( - 2\). Ta thay \(x = - 2\) vào phương trình sau đó tìm m.
Tìm nghiệm còn lại ứng với m vừa tìm được. Sau khi tìm được m ta thay m vào phương trình bậc hai sau đó sử dụng công thức nghiệm để tìm nghiệm của phương trình.
b.Áp dụng hệ thức Viet cho phương trình bậc hai và kết hợp với A để tìm m. Hệ thức Viet: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\)
Cách giải:
Cho phương trình bậc hai \({x^2} - 3x + m = 0\)(1) (m là tham số).
a. Tìm m để phương trình có nghiệm bằng \( - 2\) . Tính nghiệm còn lại ứng với m vừa tìm được.
Phương trình có nghiệm bằng \( - 2\) nên thay \(x = - 2\) vào phương trình ta được:
\({\left( { - 2} \right)^2} - 3.\left( { - 2} \right) + m = 0 \Leftrightarrow m = - 10\)
Với \(m = - 10\) phương trình (1) trở thành:
\({x^2} - 3x - 10 = 0\) (2)
Ta có: \(\Delta = {\left( { - 3} \right)^2} + 4.10 = 49 > 0\) Khi đó phương trình (2) sẽ có hai nghiệm phân biệt:
\(\left[ \begin{array}{l}{x_1} = \dfrac{{3 - 7}}{2} = - 2\\{x_2} = \dfrac{{3 + 7}}{2} = 5\end{array} \right.\)
Vậy nghiệm còn lại của phương trình đã cho khi m = -10 là x = 5.
b.Gọi \({x_1};{x_2}\) là hai nghiệm của phương trình đã cho. Tìm giá trị nhỏ nhất của \(A = x_1^2 + x_2^2 - 3{x_1}{x_2}\)
Phương trình có hai nghiệm khi và chỉ khi: \(\Delta \ge 0 \Leftrightarrow 9 - 4m \ge 0 \Leftrightarrow m \le \dfrac{9}{4}\)
Áp dụng Viet cho phương trình (1) ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 3\\{x_1}{x_2} = m\end{array} \right.\)
Từ A ta có:
\(\begin{array}{l}A = x_1^2 + x_2^2 - 3{x_1}{x_2}\\ = {\left( {{x_1} + {x_2}} \right)^2} - 5{x_1}{x_2}\\ = 9 - 5m\end{array}\)
Ta có:
\(m \le \dfrac{9}{4} \Rightarrow - 5m \ge - 5.\dfrac{9}{4} \Rightarrow 9 - 5m \ge 9 - 5.\dfrac{9}{4} = - \dfrac{9}{4} \Rightarrow A \ge \dfrac{{ - 9}}{4}\)
Vậy giá trị nhỏ nhất của A bằng \(\dfrac{{ - 9}}{4}\) dấu “=” xảy ra khi và chỉ khi: \(m = \dfrac{9}{4}\)
Bài 4.
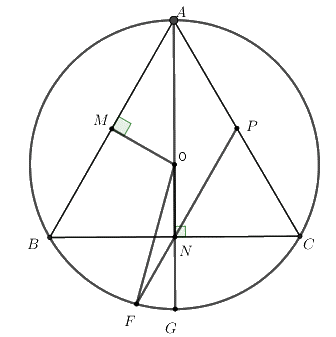
a) Chứng minh tứ giác BMON nội tiếp được đường tròn.
Vì \(\Delta ABC\) là tam giác đều, \(M,\;N\) lần lượt là trung điểm của \(AB,\;BC\) \( \Rightarrow \left\{ \begin{array}{l}OM \bot AB\\ON \bot BC\end{array} \right. \Rightarrow \widehat {OMB} = \widehat {ONB} = {90^0}\) (đường trung tuyến đồng thời là đường cao)
Xét tứ giác \(BMON\) ta có: \(\widehat {OMB} + \widehat {ONB} = {90^0} + {90^0} = {180^0}.\)
\( \Rightarrow BMON\) là tứ giác nội tiếp (tổng hai góc đối diện có tổng bằng \({180^0}\)).
b) Kéo dài AN cắt đường tròn (O) tại G (khác A). Chứng minh ON = NG.
Ta có \(O\) là trọng tâm tâm tam giác \(ABC\) (gt)
\( \Rightarrow ON = \dfrac{1}{2}OA = \dfrac{1}{2}R.\) (tính chất đường trung tuyến trong tam giác)
Lại có:\(OG = ON + NG\)
\(\begin{array}{l} \Rightarrow R = \dfrac{R}{2} + NG \Leftrightarrow NG = \dfrac{R}{2}.\\ \Rightarrow NO = NG = \dfrac{R}{2}.\;\;\left( {dpcm} \right)\end{array}\)
c) PN cắt cung nhỏ của đường tròn (O) tại điểm F. Tính số đo của góc \(\widehat {OFP}\) .
Gọi \(E = OC \cap PN\) ta có \(OC \bot AB\) (do tam giác ABC đều) ;
\(NP//AB\) (do NP là đường trung bình của tam giác ABC.
\( \Rightarrow OC \bot NP\) tại E \( \Rightarrow \Delta OEF\) vuông tại E.
Xét tam giác vuông ONC có : \(O{N^2} = OE.OC \Rightarrow OE = \dfrac{{O{N^2}}}{{OC}} = \dfrac{{{R^2}}}{{4R}} = \dfrac{R}{4}\)
Xét tam giác vuông \(OEF\) có \(\sin \widehat {OFE} = \sin \widehat {OFP} = \dfrac{{OE}}{{ON}} = \dfrac{{\dfrac{R}{4}}}{R} = \dfrac{1}{4} \Rightarrow \widehat {OFP} = \arcsin \dfrac{1}{4} \approx {14^0}28'\)
Câu 5.
Phương pháp:
Sử dụng công thức tính độ dài của cung tròn \({n^0}\) là: \(l = \dfrac{{\pi .R.{n^0}}}{{{{180}^0}}}\)
Cách giải :
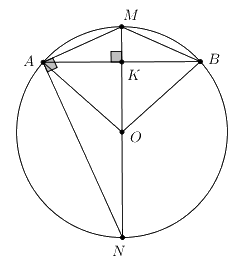
Giả sử AMB là cung tròn của đường tròn tâm O. Vẽ đường kính MN.
M là điểm chính giữa của cung AB \( \Rightarrow OM \bot AB\) và K là trung điểm của AB
\( \Rightarrow AK = \dfrac{1}{2}AB = 15\,\left( m \right)\).
Ta có \(\widehat {MAN} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \Delta AMN\) vuông tại A.
Áp dụng hệ thức lượng trong tam giác vuông AMN có:
\(A{K^2} = KM.KN \Leftrightarrow {15^2} = 5.KN \Leftrightarrow KN = 45\,\,\left( m \right)\)
\( \Rightarrow MN = KM + KN = 5 + 45 = 50\,\,\left( m \right)\)
\( \Rightarrow \) Bán kính đường tròn tâm O là \(R = 25m\).
Xét tam giác vuông ANK có \(\tan \widehat {ANK} = \dfrac{{AK}}{{KN}} = \dfrac{{15}}{{45}} = \dfrac{1}{3} \Rightarrow \widehat {ANK} = \arctan \dfrac{1}{3}\)
\( \Rightarrow \widehat {AOK} = 2\widehat {ANK} = 2\arctan \dfrac{1}{3}\) (góc ở tâm và góc nội tiếp cùng chắn cung AM).
Xét tam giác OAB có \(OA = OB \Rightarrow \Delta OAB\) cân tại O \( \Rightarrow \) Đường cao OK đồng thời là phân giác
\( \Rightarrow \widehat {AOB} = 2\widehat {AOK} = 4\arctan \dfrac{1}{3} \approx 73,{7^0}\).
Vậy độ dài cung AMB là \(l = \dfrac{{\pi .R.{n^0}}}{{{{180}^0}}} = \dfrac{{\pi .25.73,7}}{{180}} \approx 32,18\,\,\left( m \right)\).
Bài 1. (3,0 điểm) Giải các phương trình và hệ phương trình sau đây
a.\(\sqrt 3 x - \sqrt 2 x = \sqrt 3 + \sqrt 2 \) b.\(\left\{ \begin{array}{l}x + y = 101\\ - x + y = - 1\end{array} \right.\)
c.\({x^2} + 2\sqrt 3 x + 2 = 0\)
Bài 2. (2,0 điểm) Cho hàm số \(y = 0,5.{x^2}\) có đồ thị là Parabol (P)
a.Vẽ đồ thị (P) của hàm số đã cho
b.Xác định hệ số a; b của đường thẳng (d): \(y = ax + b\) , biết (d) cắt trục hoành tại điểm có hoành độ bằng 1 và (d) cắt (P) tại điểm có hoành độ bằng 2. Chứng tỏ (P) và (d) tiếp xúc nhau.
Bài 3. (1,5 điểm) Cho phương trình bậc hai \({x^2} - 3x + m = 0\) (m là tham số).
a.Tìm m để phương trình có nghiệm bằng \( - 2\) . Tính nghiệm còn lại ứng với m vừa tìm được.
b.Gọi \({x_1};{x_2}\) là hai nghiệm của phương trình đã cho. Tìm giá trị nhỏ nhất của \(A = x_1^2 + x_2^2 - 3{x_1}{x_2}\)
Bài 4. (2,5 điểm). Cho tam giác đều ABC nội tiếp trong đường tròn tâm O. Gọi M, N, P lần lượt là trung điểm của AB, BC, CA.
a.Chứng minh tứ giác BMON nội tiếp được đường tròn.
b.Kéo dài AN cắt đường tròn (O) tại G (khác A). Chứng minh ON = NG.
b.PN cắt cung nhỏ của đường tròn (O) tại điểm F. Tính số đo của góc \(\widehat {OFP}\) .
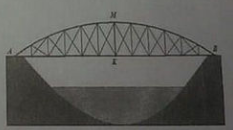
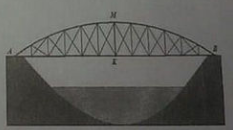
Bài 5 (1,0 điểm) Cầu vòm là một dạng cầu đẹp bởi hình dáng cầu được uốn lượn theo một cung tròn tạo sự hài hòa trong thiết kế cảnh quan, đặc biệt là các khu đô thị có dòng sông chảy qua, tạo được một điểm nhấn của công trình giao thông hiện đại. Một chiếc cầu vòm được thiết kế như hình vẽ bên, vòm cầu là một cung tròn AMB. Độ dài đoạn AB bằng 30m, khoảng cách từ vị trí cao nhất ở giữa vòm cầu so với sàn mặt cầu là đoạn MK có độ dài 5m. Tính chiều dài vòm cầu.
Bài 1. (3,0 điểm) Giải các phương trình và hệ phương trình sau đây
a.\(\sqrt 3 x - \sqrt 2 x = \sqrt 3 + \sqrt 2 \) b.\(\left\{ \begin{array}{l}x + y = 101\\ - x + y = - 1\end{array} \right.\)
c.\({x^2} + 2\sqrt 3 x + 2 = 0\)
Bài 2. (2,0 điểm) Cho hàm số \(y = 0,5.{x^2}\) có đồ thị là Parabol (P)
a.Vẽ đồ thị (P) của hàm số đã cho
b.Xác định hệ số a; b của đường thẳng (d): \(y = ax + b\) , biết (d) cắt trục hoành tại điểm có hoành độ bằng 1 và (d) cắt (P) tại điểm có hoành độ bằng 2. Chứng tỏ (P) và (d) tiếp xúc nhau.
Bài 3. (1,5 điểm) Cho phương trình bậc hai \({x^2} - 3x + m = 0\) (m là tham số).
a.Tìm m để phương trình có nghiệm bằng \( - 2\) . Tính nghiệm còn lại ứng với m vừa tìm được.
b.Gọi \({x_1};{x_2}\) là hai nghiệm của phương trình đã cho. Tìm giá trị nhỏ nhất của \(A = x_1^2 + x_2^2 - 3{x_1}{x_2}\)
Bài 4. (2,5 điểm). Cho tam giác đều ABC nội tiếp trong đường tròn tâm O. Gọi M, N, P lần lượt là trung điểm của AB, BC, CA.
a.Chứng minh tứ giác BMON nội tiếp được đường tròn.
b.Kéo dài AN cắt đường tròn (O) tại G (khác A). Chứng minh ON = NG.
b.PN cắt cung nhỏ của đường tròn (O) tại điểm F. Tính số đo của góc \(\widehat {OFP}\) .
Bài 5 (1,0 điểm) Cầu vòm là một dạng cầu đẹp bởi hình dáng cầu được uốn lượn theo một cung tròn tạo sự hài hòa trong thiết kế cảnh quan, đặc biệt là các khu đô thị có dòng sông chảy qua, tạo được một điểm nhấn của công trình giao thông hiện đại. Một chiếc cầu vòm được thiết kế như hình vẽ bên, vòm cầu là một cung tròn AMB. Độ dài đoạn AB bằng 30m, khoảng cách từ vị trí cao nhất ở giữa vòm cầu so với sàn mặt cầu là đoạn MK có độ dài 5m. Tính chiều dài vòm cầu.
Bài 1.
Phương pháp:
a.Giải phương trình bậc nhất một ẩn: \(ax + b = 0 \Leftrightarrow x = - \dfrac{b}{a}\)
b.Giải hệ phương trình bằng phương pháp thế và cộng đại số.
c. Giải phương trình bậc hai: sử dụng biệt thức \(\Delta = {b^2} - 4ac\left( {\Delta ' = b{'^2} - ac} \right)\) Cách giải:
a.
\(\begin{array}{l}\sqrt 3 x - \sqrt 2 x = \sqrt 3 + \sqrt 2 \\ \Leftrightarrow \left( {\sqrt 3 - \sqrt 2 } \right)x = \sqrt 3 + \sqrt 2 \\ \Leftrightarrow x = \dfrac{{\sqrt 3 + \sqrt 2 }}{{\sqrt 3 - \sqrt 2 }}\\ \Leftrightarrow x = \dfrac{{{{\left( {\sqrt 3 + \sqrt 2 } \right)}^2}}}{{3 - 2}}\\ \Leftrightarrow x = 5 + 2\sqrt 6 \end{array}\)
b.\(\left\{ \begin{array}{l}x + y = 101\\ - x + y = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2y = 100\\x = y + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 50\\x = y + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 50\\x = 51\end{array} \right.\)
Vậy hệ phương trình có nghiệm là \(\left( {x;y} \right) = \left( {51;50} \right)\)
c.\({x^2} + 2\sqrt 3 x + 2 = 0\)
Ta có: \(a = 1;b' = \sqrt 3 ;c = 2\)
\(\Delta ' = {\left( {\sqrt 3 } \right)^2} - 2 = 1 > 0\)
Khi đó phương trình có hai nghiệm phân biệt là: \(\left[ \begin{array}{l}{x_1} = - \sqrt 3 - 1\\{x_2} = - \sqrt 3 + 1\end{array} \right.\)
Vậy phương trình đã cho có 2 nghiệm phân biệt là: \(S = \left\{ { - \sqrt 3 - 1; - \sqrt 3 + 1} \right\}\)
Bài 2.
Phương pháp:
a.Lập bảng giá trị
b. (d) cắt trục hoành tại điểm có hoành độ bằng 1 nên điểm đó có tọa độ là (1;0) sau đó thay vào phương trình đường thẳng (d) ta được 1 phương trình theo a, b. (pt1)
(d) cắt (P) tại điểm có hoành độ bằng 2 nên thay x = 2 vào phương trình hoành độ giao điểm của (d) và (P) ta được phương trình thứ 2 theo a, b. (pt2)
Kết hợp (1) và (2) ta giải hệ phương trình tìm được a, b.
Cách giải:
Cho hàm số \(y = 0,5.{x^2}\) có đồ thị là Parabol (P)
a.Vẽ đồ thị (P) của hàm số đã cho
Ta có bảng giá trị
\(x\) | -4 | -2 | 0 | 2 | 4 |
\(y = 0,5{x^2}\) | 8 | 2 | 0 | 2 | 8 |
Đồ thị hàm số (P) có hình dạng đường cong đi qua các điểm \(\left( {0;\;0} \right),\;\;\left( { - 2;\;2} \right),\,\left( { - 4;8} \right),\;\;\left( {2;\;2} \right),\,\,\left( {4;8} \right)\)
Vẽ đồ thị:
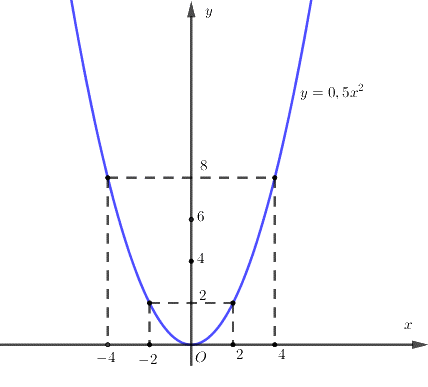
b.Xác định hệ số a; b của đường thẳng (d): \(y = ax + b\) , biết (d) cắt trục hoành tại điểm có hoành độ bằng 1 và (d) cắt (P) tại điểm có hoành độ bằng 2. Chứng tỏ (P) và (d) tiếp xúc nhau.
Ta có: (d) cắt trục hoành tại điểm có hoành độ bằng 1 nên\(A\left( {1;0} \right)\) . Thay tọa độ của điểm A vào phương trình đường thẳng (d) ta có: \(a + b = 0\,\,\left( 1 \right)\)
Hoành độ giao điểm của (d) và (P) là nghiệm của phương trình:
\(0,5{x^2} = ax + b \Leftrightarrow 0,5{x^2} - ax + b = 0\) (*)
Theo đề ra ta có: (d) cắt (P) tại điểm có hoành độ bằng 2 nên x = 2 là nghiệm của phương trình (*)
\(0,{5.2^2} - a.2 + b = 0 \Leftrightarrow 2a - b = 2\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) ta có hệ phương trình
\(\left\{ \begin{array}{l}a + b = 0\\2a - b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3a = 2\\b = - a\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{2}{3}\\b = - \dfrac{2}{3}\end{array} \right.\)
Vậy \(a = \dfrac{2}{3};b = - \dfrac{2}{3}\) thỏa mãn yêu cầu bài toán.
Bài 3.
Phương pháp:
a.Tìm m để phương trình có nghiệm bằng \( - 2\). Ta thay \(x = - 2\) vào phương trình sau đó tìm m.
Tìm nghiệm còn lại ứng với m vừa tìm được. Sau khi tìm được m ta thay m vào phương trình bậc hai sau đó sử dụng công thức nghiệm để tìm nghiệm của phương trình.
b.Áp dụng hệ thức Viet cho phương trình bậc hai và kết hợp với A để tìm m. Hệ thức Viet: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\)
Cách giải:
Cho phương trình bậc hai \({x^2} - 3x + m = 0\)(1) (m là tham số).
a. Tìm m để phương trình có nghiệm bằng \( - 2\) . Tính nghiệm còn lại ứng với m vừa tìm được.
Phương trình có nghiệm bằng \( - 2\) nên thay \(x = - 2\) vào phương trình ta được:
\({\left( { - 2} \right)^2} - 3.\left( { - 2} \right) + m = 0 \Leftrightarrow m = - 10\)
Với \(m = - 10\) phương trình (1) trở thành:
\({x^2} - 3x - 10 = 0\) (2)
Ta có: \(\Delta = {\left( { - 3} \right)^2} + 4.10 = 49 > 0\) Khi đó phương trình (2) sẽ có hai nghiệm phân biệt:
\(\left[ \begin{array}{l}{x_1} = \dfrac{{3 - 7}}{2} = - 2\\{x_2} = \dfrac{{3 + 7}}{2} = 5\end{array} \right.\)
Vậy nghiệm còn lại của phương trình đã cho khi m = -10 là x = 5.
b.Gọi \({x_1};{x_2}\) là hai nghiệm của phương trình đã cho. Tìm giá trị nhỏ nhất của \(A = x_1^2 + x_2^2 - 3{x_1}{x_2}\)
Phương trình có hai nghiệm khi và chỉ khi: \(\Delta \ge 0 \Leftrightarrow 9 - 4m \ge 0 \Leftrightarrow m \le \dfrac{9}{4}\)
Áp dụng Viet cho phương trình (1) ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 3\\{x_1}{x_2} = m\end{array} \right.\)
Từ A ta có:
\(\begin{array}{l}A = x_1^2 + x_2^2 - 3{x_1}{x_2}\\ = {\left( {{x_1} + {x_2}} \right)^2} - 5{x_1}{x_2}\\ = 9 - 5m\end{array}\)
Ta có:
\(m \le \dfrac{9}{4} \Rightarrow - 5m \ge - 5.\dfrac{9}{4} \Rightarrow 9 - 5m \ge 9 - 5.\dfrac{9}{4} = - \dfrac{9}{4} \Rightarrow A \ge \dfrac{{ - 9}}{4}\)
Vậy giá trị nhỏ nhất của A bằng \(\dfrac{{ - 9}}{4}\) dấu “=” xảy ra khi và chỉ khi: \(m = \dfrac{9}{4}\)
Bài 4.
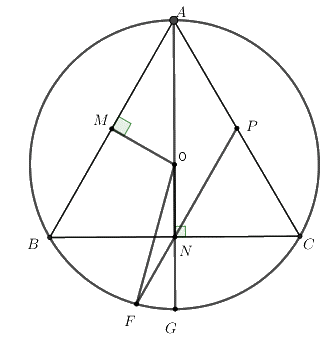
a) Chứng minh tứ giác BMON nội tiếp được đường tròn.
Vì \(\Delta ABC\) là tam giác đều, \(M,\;N\) lần lượt là trung điểm của \(AB,\;BC\) \( \Rightarrow \left\{ \begin{array}{l}OM \bot AB\\ON \bot BC\end{array} \right. \Rightarrow \widehat {OMB} = \widehat {ONB} = {90^0}\) (đường trung tuyến đồng thời là đường cao)
Xét tứ giác \(BMON\) ta có: \(\widehat {OMB} + \widehat {ONB} = {90^0} + {90^0} = {180^0}.\)
\( \Rightarrow BMON\) là tứ giác nội tiếp (tổng hai góc đối diện có tổng bằng \({180^0}\)).
b) Kéo dài AN cắt đường tròn (O) tại G (khác A). Chứng minh ON = NG.
Ta có \(O\) là trọng tâm tâm tam giác \(ABC\) (gt)
\( \Rightarrow ON = \dfrac{1}{2}OA = \dfrac{1}{2}R.\) (tính chất đường trung tuyến trong tam giác)
Lại có:\(OG = ON + NG\)
\(\begin{array}{l} \Rightarrow R = \dfrac{R}{2} + NG \Leftrightarrow NG = \dfrac{R}{2}.\\ \Rightarrow NO = NG = \dfrac{R}{2}.\;\;\left( {dpcm} \right)\end{array}\)
c) PN cắt cung nhỏ của đường tròn (O) tại điểm F. Tính số đo của góc \(\widehat {OFP}\) .
Gọi \(E = OC \cap PN\) ta có \(OC \bot AB\) (do tam giác ABC đều) ;
\(NP//AB\) (do NP là đường trung bình của tam giác ABC.
\( \Rightarrow OC \bot NP\) tại E \( \Rightarrow \Delta OEF\) vuông tại E.
Xét tam giác vuông ONC có : \(O{N^2} = OE.OC \Rightarrow OE = \dfrac{{O{N^2}}}{{OC}} = \dfrac{{{R^2}}}{{4R}} = \dfrac{R}{4}\)
Xét tam giác vuông \(OEF\) có \(\sin \widehat {OFE} = \sin \widehat {OFP} = \dfrac{{OE}}{{ON}} = \dfrac{{\dfrac{R}{4}}}{R} = \dfrac{1}{4} \Rightarrow \widehat {OFP} = \arcsin \dfrac{1}{4} \approx {14^0}28'\)
Câu 5.
Phương pháp:
Sử dụng công thức tính độ dài của cung tròn \({n^0}\) là: \(l = \dfrac{{\pi .R.{n^0}}}{{{{180}^0}}}\)
Cách giải :
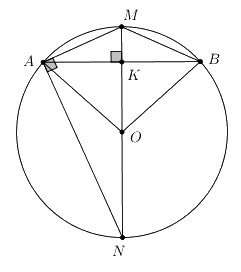
Giả sử AMB là cung tròn của đường tròn tâm O. Vẽ đường kính MN.
M là điểm chính giữa của cung AB \( \Rightarrow OM \bot AB\) và K là trung điểm của AB
\( \Rightarrow AK = \dfrac{1}{2}AB = 15\,\left( m \right)\).
Ta có \(\widehat {MAN} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \Delta AMN\) vuông tại A.
Áp dụng hệ thức lượng trong tam giác vuông AMN có:
\(A{K^2} = KM.KN \Leftrightarrow {15^2} = 5.KN \Leftrightarrow KN = 45\,\,\left( m \right)\)
\( \Rightarrow MN = KM + KN = 5 + 45 = 50\,\,\left( m \right)\)
\( \Rightarrow \) Bán kính đường tròn tâm O là \(R = 25m\).
Xét tam giác vuông ANK có \(\tan \widehat {ANK} = \dfrac{{AK}}{{KN}} = \dfrac{{15}}{{45}} = \dfrac{1}{3} \Rightarrow \widehat {ANK} = \arctan \dfrac{1}{3}\)
\( \Rightarrow \widehat {AOK} = 2\widehat {ANK} = 2\arctan \dfrac{1}{3}\) (góc ở tâm và góc nội tiếp cùng chắn cung AM).
Xét tam giác OAB có \(OA = OB \Rightarrow \Delta OAB\) cân tại O \( \Rightarrow \) Đường cao OK đồng thời là phân giác
\( \Rightarrow \widehat {AOB} = 2\widehat {AOK} = 4\arctan \dfrac{1}{3} \approx 73,{7^0}\).
Vậy độ dài cung AMB là \(l = \dfrac{{\pi .R.{n^0}}}{{{{180}^0}}} = \dfrac{{\pi .25.73,7}}{{180}} \approx 32,18\,\,\left( m \right)\).
Kỳ thi tuyển sinh vào lớp 10 là một bước ngoặt quan trọng trong quá trình học tập của mỗi học sinh. Để đạt kết quả tốt nhất, việc chuẩn bị kỹ lưỡng là vô cùng cần thiết. Đề thi vào 10 môn Toán An Giang năm 2018 là một nguồn tài liệu quý giá để các em học sinh ôn tập và rèn luyện kỹ năng giải toán.
Đề thi vào 10 môn Toán An Giang năm 2018 thường có cấu trúc gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Để giúp các em học sinh hiểu rõ hơn về cấu trúc và nội dung đề thi, chúng ta sẽ cùng phân tích một số câu hỏi điển hình trong đề thi vào 10 môn Toán An Giang năm 2018.
Ví dụ 1: Giải phương trình 2x + 3 = 7
Lời giải:
Ví dụ 2: Tính diện tích hình tròn có bán kính r = 5cm
Lời giải:
Diện tích hình tròn được tính theo công thức: S = πr2
Thay r = 5cm vào công thức, ta được: S = π(52) = 25π cm2
Để đạt kết quả tốt nhất trong kỳ thi vào 10 môn Toán, các em học sinh cần lưu ý những điều sau:
Ngoài đề thi vào 10 môn Toán An Giang năm 2018, các em học sinh có thể tham khảo thêm các tài liệu ôn thi sau:
Đề thi vào 10 môn Toán An Giang năm 2018 là một tài liệu quan trọng giúp các em học sinh chuẩn bị tốt nhất cho kỳ thi sắp tới. Hy vọng rằng với những phân tích và hướng dẫn giải chi tiết trong bài viết này, các em sẽ tự tin hơn và đạt kết quả tốt nhất.