Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Đắk Nông năm 2020 chính thức. Đây là tài liệu vô cùng hữu ích cho các em học sinh đang chuẩn bị cho kỳ thi quan trọng này.
Đề thi bao gồm các dạng bài tập đa dạng, bám sát chương trình học và có độ khó phù hợp, giúp các em làm quen với cấu trúc đề thi thực tế và rèn luyện kỹ năng giải toán.
Bài 1: a) Gọi
Bài 1:
a) Gọi \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình \({x^2} - 3x + 2 = 0.\)
Tính tổng \(S = {x_1} + {x_2}\) và \(P = {x_1}{x_2}.\)
b) Giải phương trình \({x^2} - x + 5 = {x^2} + 2x - 1.\)
c) Giải hệ phương trình: \(\left\{ \begin{array}{l}4x - 3y = - 10\\x + 2y = 3\end{array} \right..\)
Bài 2: Cho biểu thức \(A = \dfrac{x}{{x - 4}} + \dfrac{1}{{\sqrt x - 2}} + \dfrac{1}{{\sqrt x + 2}}\) với \(x \ge 0,\,\,x \ne 4\).
a) Rút gọn biểu thức A.
b) Tìm tất cả các giá trị của x để \(A > 1\).
Bài 3:
a) Vẽ parabol \(\left( P \right):\,\,y = 2{x^2}\).
b) Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 3m - 1 = 0\), (\(m\) là tham số).
Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 10\).
Bài 4: Cho \(\Delta ABC\) có ba góc nhọn. Hai đường cao của \(\Delta ABC\) là \(AD,\,\,BE\) cắt nhau tại \(H\,\,\,\left( {D \in BC,\,\,\,E \in AC} \right).\)
a) Chứng minh \(CDHE\) là tứ giác nội tiếp một đường tròn.
b) Chứng minh \(HA.HD = HB.HE.\)
c) Gọi điểm \(I\)là tâm đường tròn ngoại tiếp tứ giác \(CDHE.\) Chứng minh \(IE\) là tiếp tuyến của đường tròn đường kính \(AB.\)
Bài 5: Cho các số thực dương \(x,\,\,y > 1\). Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{{{x^2}}}{{y - 1}} + \dfrac{{{y^2}}}{{x - 1}}\)
Bài 1:
a) Gọi \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình \({x^2} - 3x + 2 = 0.\)
Tính tổng \(S = {x_1} + {x_2}\) và \(P = {x_1}{x_2}.\)
b) Giải phương trình \({x^2} - x + 5 = {x^2} + 2x - 1.\)
c) Giải hệ phương trình: \(\left\{ \begin{array}{l}4x - 3y = - 10\\x + 2y = 3\end{array} \right..\)
Bài 2: Cho biểu thức \(A = \dfrac{x}{{x - 4}} + \dfrac{1}{{\sqrt x - 2}} + \dfrac{1}{{\sqrt x + 2}}\) với \(x \ge 0,\,\,x \ne 4\).
a) Rút gọn biểu thức A.
b) Tìm tất cả các giá trị của x để \(A > 1\).
Bài 3:
a) Vẽ parabol \(\left( P \right):\,\,y = 2{x^2}\).
b) Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 3m - 1 = 0\), (\(m\) là tham số).
Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 10\).
Bài 4: Cho \(\Delta ABC\) có ba góc nhọn. Hai đường cao của \(\Delta ABC\) là \(AD,\,\,BE\) cắt nhau tại \(H\,\,\,\left( {D \in BC,\,\,\,E \in AC} \right).\)
a) Chứng minh \(CDHE\) là tứ giác nội tiếp một đường tròn.
b) Chứng minh \(HA.HD = HB.HE.\)
c) Gọi điểm \(I\)là tâm đường tròn ngoại tiếp tứ giác \(CDHE.\) Chứng minh \(IE\) là tiếp tuyến của đường tròn đường kính \(AB.\)
Bài 5: Cho các số thực dương \(x,\,\,y > 1\). Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{{{x^2}}}{{y - 1}} + \dfrac{{{y^2}}}{{x - 1}}\)
Bài 1 (2 điểm):
Cách giải:
a) Gọi \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình \({x^2} - 3x + 2 = 0.\)
Tính tổng \(S = {x_1} + {x_2}\) và \(P = {x_1}{x_2}.\)
Phương trình \({x^2} - 3x + 2 = 0\) có: \(a + b + c = 1 - 3 + 2 = 0\)
\( \Rightarrow \) Phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = 1\\{x_2} = \dfrac{c}{a} = 2\end{array} \right..\)
Khi đó ta có: \(\left\{ \begin{array}{l}S = {x_1} + {x_2} = 1 + 2 = 3\\P = {x_1}{x_2} = 1.2 = 2\end{array} \right..\)
Vậy \(S = 3,\,\,P = 2.\)
b) Giải phương trình \({x^2} - x + 5 = {x^2} + 2x - 1.\)
\(\begin{array}{l}\,\,\,\,\,\,\,\,{x^2} - x + 5 = {x^2} + 2x - 1\\ \Leftrightarrow 2x + x = 5 + 1\\ \Leftrightarrow 3x = 6\\ \Leftrightarrow x = 2.\end{array}\)
Vậy tập nghiệm của phương trình là: \(S = \left\{ 2 \right\}.\)
c) Giải hệ phương trình: \(\left\{ \begin{array}{l}4x - 3y = - 10\\x + 2y = 3\end{array} \right..\)
\(\left\{ \begin{array}{l}4x - 3y = - 10\\x + 2y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x - 3y = - 10\\4x + 8y = 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}11y = 22\\x = 3 - 2y\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}y = 2\\x = 3 - 2.\left( { - 2} \right) = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\y = 2\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;\,\,y} \right) = \left( { - 1;\,\,2} \right).\)
Bài 2 (2,0 điểm)
Cách giải:
Cho biểu thức \(A = \dfrac{x}{{x - 4}} + \dfrac{1}{{\sqrt x - 2}} + \dfrac{1}{{\sqrt x + 2}}\) với \(x \ge 0,\,\,x \ne 4\).
a) Rút gọn biểu thức A.
Với \(x \ge 0,\,\,x \ne 4\) ta có:
\(\begin{array}{l}A = \dfrac{x}{{x - 4}} + \dfrac{1}{{\sqrt x - 2}} + \dfrac{1}{{\sqrt x + 2}}\\A = \dfrac{x}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} + \dfrac{1}{{\sqrt x - 2}} + \dfrac{1}{{\sqrt x + 2}}\\A = \dfrac{{x + \sqrt x + 2 + \sqrt x - 2}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\A = \dfrac{{x + 2\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\A = \dfrac{{\sqrt x \left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\A = \dfrac{{\sqrt x }}{{\sqrt x - 2}}\end{array}\)
b) Tìm tất cả các giá trị của x để \(A > 1\).
Ta có:
\(\begin{array}{l}\,\,\,\,\,A > 1\\ \Leftrightarrow \dfrac{{\sqrt x }}{{\sqrt x - 2}} > 1\\ \Leftrightarrow \dfrac{{\sqrt x }}{{\sqrt x - 2}} - 1 > 0\\ \Leftrightarrow \dfrac{{\sqrt x - \sqrt x + 2}}{{\sqrt x - 2}} > 0\\ \Leftrightarrow \dfrac{2}{{\sqrt x - 2}} > 0\\ \Leftrightarrow \sqrt x - 2 > 0\\ \Leftrightarrow \sqrt x > 2\\ \Leftrightarrow x > 4\end{array}\)
Kết hợp điều kiện xác định ta có \(x > 4\) thỏa mãn.
Vậy để \(A > 1\) thì \(x > 4\).
Bài 3 (2,0 điểm)
Cách giải:
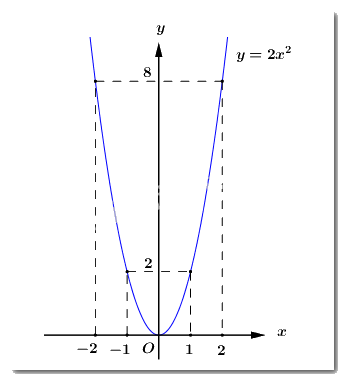
a) Vẽ parabol \(\left( P \right):\,\,y = 2{x^2}\).
Ta có bảng giá trị:
\(x\) | \( - 2\) | \( - 1\) | 0 | 1 | 2 |
\(y = 2{x^2}\) | \(8\) | 2 | 0 | 2 | 8 |
Do đó, parabol \(\left( P \right):\,\,\,y = 2{x^2}\) là đường cong đi qua các điểm \(\left( { - 2;8} \right)\), \(\left( { - 1;2} \right)\), \(\left( {0;0} \right)\), \(\left( {1;2} \right)\), \(\left( {2;8} \right)\) và nhận \(Oy\) làm trục đối xứng.
Đồ thị hàm số:
b) Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 3m - 1 = 0\), (\(m\) là tham số).
Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 10\).
Để phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 3m - 1 = 0\) (*) có 2 nghiệm phân biệt \({x_1},\,\,{x_2}\) thì:
\(\begin{array}{l}\,\,\,\,\,\,\Delta ' > 0\\ \Leftrightarrow {\left( {m + 1} \right)^2} - {m^2} - 3m + 1 > 0\\ \Leftrightarrow {m^2} + 2m + 1 - {m^2} - 3m + 1 > 0\\ \Leftrightarrow - m + 2 > 0\\ \Leftrightarrow m < 2\end{array}\)
Khi đó, áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m + 1} \right) = 2m + 2\\{x_1}{x_2} = {m^2} + 3m - 1\end{array} \right.\).
Theo bài ra ta có:
\(\begin{array}{l}\,\,\,\,\,x_1^2 + x_2^2 = 10\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 10\\ \Leftrightarrow {\left( {2m + 2} \right)^2} - 2\left( {{m^2} + 3m - 1} \right) = 10\\ \Leftrightarrow 4{m^2} + 8m + 4 - 2{m^2} - 6m + 2 = 10\\ \Leftrightarrow 2{m^2} + 2m - 4 = 0\\ \Leftrightarrow {m^2} + m - 2 = 0\\ \Leftrightarrow {m^2} - m + 2m - 2 = 0\\ \Leftrightarrow m\left( {m - 1} \right) + 2\left( {m - 1} \right) = 0\\ \Leftrightarrow \left( {m - 1} \right)\left( {m + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m - 1 = 0\\m + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - 2\end{array} \right.\,\,\,\left( {tm} \right)\end{array}\)
Vậy \(m = 1\) hoặc \(m = - 2\).
Bài 4 (3 điểm):
Cách giải:
Cho \(\Delta ABC\) có ba góc nhọn. Hai đường cao của \(\Delta ABC\) là \(AD,\,\,BE\) cắt nhau tại \(H\,\,\,\left( {D \in BC,\,\,\,E \in AC} \right).\)
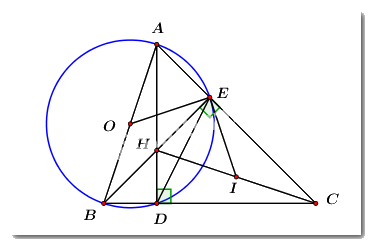
a) Chứng minh \(CDHE\) là tứ giác nội tiếp một đường tròn.
Ta có: \(AD,\,\,BE\) là hai đường cao của \(\Delta ABC\) (gt)
\( \Rightarrow \left\{ \begin{array}{l}AD \bot BC = \left\{ D \right\}\\BE \bot AC = \left\{ E \right\}\end{array} \right.\) \( \Rightarrow \angle ADC = \angle BEC = {90^0}\)
Xét tứ giác \(CDHE\) ta có:
\(\angle HDC + \angle HEC = {90^0} + {90^0} = {180^0}\)
Mà hai góc này là hai góc đối diện
\( \Rightarrow \angle CDHE\) là tứ giác nội tiếp. (dhnb)
b) Chứng minh \(HA.HD = HB.HE.\)
Xét \(\Delta HAE\) và \(\Delta HBD\) ta có:
\(\angle AHE = \angle BHD\) (hai góc đối đỉnh)
\(\begin{array}{l}\angle AEH = \angle BDH = {90^0}\\ \Rightarrow \Delta AHE \sim \Delta BHD\,\,\,\left( {g - g} \right)\\ \Rightarrow \dfrac{{AH}}{{BH}} = \dfrac{{HE}}{{HD}} \Rightarrow AH.DH = BH.EH\,\,\,\left( {dpcm} \right).\end{array}\)
c) Gọi điểm \(I\)là tâm đường tròn ngoại tiếp tứ giác \(CDHE.\) Chứng minh \(IE\) là tiếp tuyến của đường tròn đường kính \(AB.\)
Xét tứ giác \(ABDE\) ta có:
\(\angle ADB = \angle AEB = {90^0}\)
Mà hai đỉnh \(D,\,\,E\) là hai đỉnh liên tiếp của tứ giác
\( \Rightarrow \angle ABDE\) là tứ giác nội tiếp. (dhnb)
Lại có: \(\Delta AEB\) vuông tại \(E.\)
\( \Rightarrow A,\,\,B,\,\,D,\,\,E\) cùng thuộc đường tròn tâm \(O\) đường kính \(AB.\)
Ta có: \(ABDE\) là tứ giác nội tiếp (cmt)
\( \Rightarrow \angle EDC = \angle BAE\) (góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện). (1)
Ta có: \(I\) là tâm đường tròn ngoại tiếp tứ giác \(CDHE\)
\( \Rightarrow I\) là trung điểm của \(HC.\)
\(\Delta ECH\) vuông tại \(E\) có đường trung tuyến \(EI\)
\( \Rightarrow EI = HI = \dfrac{1}{2}HC\) (đường trung tuyến ứng với cạnh huyền của tam giác vuông)
\( \Rightarrow \Delta HEI\) cân tại \(I\) \( \Rightarrow \angle IEH = \angle IHE\) (tính chất tam giác cân)
Hay \(IEH = \angle EHC\) (2)
Tứ giác \(CDHE\) là tứ giác nội tiếp (cmt)
\( \Rightarrow \angle CDE = \angle CHE\) (hai góc nội tiếp cùng chắn cung \(EC\)) (3)
Từ (1), (2) và (3) suy ra: \(\angle EDC = \angle BAE = \angle HEI\)
\(\Delta AOE\) cân tại \(O\,\,\left( {OA = OE} \right)\) \( \Rightarrow \angle OEB = \angle OBE\) (tính chất tam giác cân)
Hay \(\angle BAE = \angle OEA\)
Mà \(\angle OBE + \angle BAE = {90^0}\)
\( \Rightarrow \angle OEB + \angle HEI = {90^0}\)
Hay \(OE \bot EI\)
\( \Rightarrow EI\) là tiếp tuyến của đường tròn đường kính\(AB.\) (đpcm)
Bài 5 (1,0 điểm)
Cách giải:
Cho các số thực dương \(x,\,\,y > 1\). Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{{{x^2}}}{{y - 1}} + \dfrac{{{y^2}}}{{x - 1}}\).
Áp dụng BĐT Cô-si t có:
\(\begin{array}{l}x = x - 1 + 1 \ge 2\sqrt {\left( {x - 1} \right).1} = 2\sqrt {x - 1} \\ \Rightarrow {x^2} \ge 4\left( {x - 1} \right)\\ \Rightarrow \dfrac{{{x^2}}}{{y - 1}} \ge \dfrac{{4\left( {x - 1} \right)}}{{y - 1}}\end{array}\)
Tương tự ta có: \(\dfrac{{{y^2}}}{{x - 1}} \ge \dfrac{{4\left( {y - 1} \right)}}{{x - 1}}\).
Khi đó ta có:
\(\begin{array}{l}P = \dfrac{{{x^2}}}{{y - 1}} + \dfrac{{{y^2}}}{{x - 1}}\\\,\,\,\,\, \ge \dfrac{{4\left( {x - 1} \right)}}{{y - 1}} + \dfrac{{4\left( {y - 1} \right)}}{{x - 1}}\\\,\,\,\, \ge 2\sqrt {\dfrac{{4\left( {x - 1} \right)}}{{y - 1}}.\dfrac{{4\left( {y - 1} \right)}}{{x - 1}}} = 8\end{array}\)
Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}x - 1 = 1\\y - 1 = 1\\\dfrac{{x - 1}}{{y - 1}} = \dfrac{{y - 1}}{{x - 1}}\end{array} \right. \Leftrightarrow x = y = 2\).
Vậy \(\min P = 8 \Leftrightarrow x = y = 2\).
Bài 1 (2 điểm):
Cách giải:
a) Gọi \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình \({x^2} - 3x + 2 = 0.\)
Tính tổng \(S = {x_1} + {x_2}\) và \(P = {x_1}{x_2}.\)
Phương trình \({x^2} - 3x + 2 = 0\) có: \(a + b + c = 1 - 3 + 2 = 0\)
\( \Rightarrow \) Phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = 1\\{x_2} = \dfrac{c}{a} = 2\end{array} \right..\)
Khi đó ta có: \(\left\{ \begin{array}{l}S = {x_1} + {x_2} = 1 + 2 = 3\\P = {x_1}{x_2} = 1.2 = 2\end{array} \right..\)
Vậy \(S = 3,\,\,P = 2.\)
b) Giải phương trình \({x^2} - x + 5 = {x^2} + 2x - 1.\)
\(\begin{array}{l}\,\,\,\,\,\,\,\,{x^2} - x + 5 = {x^2} + 2x - 1\\ \Leftrightarrow 2x + x = 5 + 1\\ \Leftrightarrow 3x = 6\\ \Leftrightarrow x = 2.\end{array}\)
Vậy tập nghiệm của phương trình là: \(S = \left\{ 2 \right\}.\)
c) Giải hệ phương trình: \(\left\{ \begin{array}{l}4x - 3y = - 10\\x + 2y = 3\end{array} \right..\)
\(\left\{ \begin{array}{l}4x - 3y = - 10\\x + 2y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x - 3y = - 10\\4x + 8y = 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}11y = 22\\x = 3 - 2y\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}y = 2\\x = 3 - 2.\left( { - 2} \right) = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\y = 2\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;\,\,y} \right) = \left( { - 1;\,\,2} \right).\)
Bài 2 (2,0 điểm)
Cách giải:
Cho biểu thức \(A = \dfrac{x}{{x - 4}} + \dfrac{1}{{\sqrt x - 2}} + \dfrac{1}{{\sqrt x + 2}}\) với \(x \ge 0,\,\,x \ne 4\).
a) Rút gọn biểu thức A.
Với \(x \ge 0,\,\,x \ne 4\) ta có:
\(\begin{array}{l}A = \dfrac{x}{{x - 4}} + \dfrac{1}{{\sqrt x - 2}} + \dfrac{1}{{\sqrt x + 2}}\\A = \dfrac{x}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} + \dfrac{1}{{\sqrt x - 2}} + \dfrac{1}{{\sqrt x + 2}}\\A = \dfrac{{x + \sqrt x + 2 + \sqrt x - 2}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\A = \dfrac{{x + 2\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\A = \dfrac{{\sqrt x \left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\A = \dfrac{{\sqrt x }}{{\sqrt x - 2}}\end{array}\)
b) Tìm tất cả các giá trị của x để \(A > 1\).
Ta có:
\(\begin{array}{l}\,\,\,\,\,A > 1\\ \Leftrightarrow \dfrac{{\sqrt x }}{{\sqrt x - 2}} > 1\\ \Leftrightarrow \dfrac{{\sqrt x }}{{\sqrt x - 2}} - 1 > 0\\ \Leftrightarrow \dfrac{{\sqrt x - \sqrt x + 2}}{{\sqrt x - 2}} > 0\\ \Leftrightarrow \dfrac{2}{{\sqrt x - 2}} > 0\\ \Leftrightarrow \sqrt x - 2 > 0\\ \Leftrightarrow \sqrt x > 2\\ \Leftrightarrow x > 4\end{array}\)
Kết hợp điều kiện xác định ta có \(x > 4\) thỏa mãn.
Vậy để \(A > 1\) thì \(x > 4\).
Bài 3 (2,0 điểm)
Cách giải:
a) Vẽ parabol \(\left( P \right):\,\,y = 2{x^2}\).
Ta có bảng giá trị:
\(x\) | \( - 2\) | \( - 1\) | 0 | 1 | 2 |
\(y = 2{x^2}\) | \(8\) | 2 | 0 | 2 | 8 |
Do đó, parabol \(\left( P \right):\,\,\,y = 2{x^2}\) là đường cong đi qua các điểm \(\left( { - 2;8} \right)\), \(\left( { - 1;2} \right)\), \(\left( {0;0} \right)\), \(\left( {1;2} \right)\), \(\left( {2;8} \right)\) và nhận \(Oy\) làm trục đối xứng.
Đồ thị hàm số:
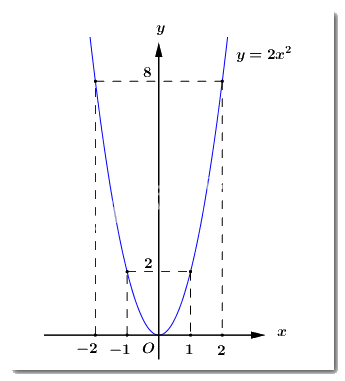
b) Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 3m - 1 = 0\), (\(m\) là tham số).
Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 10\).
Để phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 3m - 1 = 0\) (*) có 2 nghiệm phân biệt \({x_1},\,\,{x_2}\) thì:
\(\begin{array}{l}\,\,\,\,\,\,\Delta ' > 0\\ \Leftrightarrow {\left( {m + 1} \right)^2} - {m^2} - 3m + 1 > 0\\ \Leftrightarrow {m^2} + 2m + 1 - {m^2} - 3m + 1 > 0\\ \Leftrightarrow - m + 2 > 0\\ \Leftrightarrow m < 2\end{array}\)
Khi đó, áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m + 1} \right) = 2m + 2\\{x_1}{x_2} = {m^2} + 3m - 1\end{array} \right.\).
Theo bài ra ta có:
\(\begin{array}{l}\,\,\,\,\,x_1^2 + x_2^2 = 10\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 10\\ \Leftrightarrow {\left( {2m + 2} \right)^2} - 2\left( {{m^2} + 3m - 1} \right) = 10\\ \Leftrightarrow 4{m^2} + 8m + 4 - 2{m^2} - 6m + 2 = 10\\ \Leftrightarrow 2{m^2} + 2m - 4 = 0\\ \Leftrightarrow {m^2} + m - 2 = 0\\ \Leftrightarrow {m^2} - m + 2m - 2 = 0\\ \Leftrightarrow m\left( {m - 1} \right) + 2\left( {m - 1} \right) = 0\\ \Leftrightarrow \left( {m - 1} \right)\left( {m + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m - 1 = 0\\m + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - 2\end{array} \right.\,\,\,\left( {tm} \right)\end{array}\)
Vậy \(m = 1\) hoặc \(m = - 2\).
Bài 4 (3 điểm):
Cách giải:
Cho \(\Delta ABC\) có ba góc nhọn. Hai đường cao của \(\Delta ABC\) là \(AD,\,\,BE\) cắt nhau tại \(H\,\,\,\left( {D \in BC,\,\,\,E \in AC} \right).\)
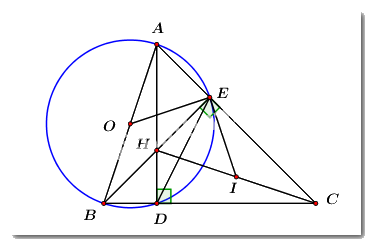
a) Chứng minh \(CDHE\) là tứ giác nội tiếp một đường tròn.
Ta có: \(AD,\,\,BE\) là hai đường cao của \(\Delta ABC\) (gt)
\( \Rightarrow \left\{ \begin{array}{l}AD \bot BC = \left\{ D \right\}\\BE \bot AC = \left\{ E \right\}\end{array} \right.\) \( \Rightarrow \angle ADC = \angle BEC = {90^0}\)
Xét tứ giác \(CDHE\) ta có:
\(\angle HDC + \angle HEC = {90^0} + {90^0} = {180^0}\)
Mà hai góc này là hai góc đối diện
\( \Rightarrow \angle CDHE\) là tứ giác nội tiếp. (dhnb)
b) Chứng minh \(HA.HD = HB.HE.\)
Xét \(\Delta HAE\) và \(\Delta HBD\) ta có:
\(\angle AHE = \angle BHD\) (hai góc đối đỉnh)
\(\begin{array}{l}\angle AEH = \angle BDH = {90^0}\\ \Rightarrow \Delta AHE \sim \Delta BHD\,\,\,\left( {g - g} \right)\\ \Rightarrow \dfrac{{AH}}{{BH}} = \dfrac{{HE}}{{HD}} \Rightarrow AH.DH = BH.EH\,\,\,\left( {dpcm} \right).\end{array}\)
c) Gọi điểm \(I\)là tâm đường tròn ngoại tiếp tứ giác \(CDHE.\) Chứng minh \(IE\) là tiếp tuyến của đường tròn đường kính \(AB.\)
Xét tứ giác \(ABDE\) ta có:
\(\angle ADB = \angle AEB = {90^0}\)
Mà hai đỉnh \(D,\,\,E\) là hai đỉnh liên tiếp của tứ giác
\( \Rightarrow \angle ABDE\) là tứ giác nội tiếp. (dhnb)
Lại có: \(\Delta AEB\) vuông tại \(E.\)
\( \Rightarrow A,\,\,B,\,\,D,\,\,E\) cùng thuộc đường tròn tâm \(O\) đường kính \(AB.\)
Ta có: \(ABDE\) là tứ giác nội tiếp (cmt)
\( \Rightarrow \angle EDC = \angle BAE\) (góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện). (1)
Ta có: \(I\) là tâm đường tròn ngoại tiếp tứ giác \(CDHE\)
\( \Rightarrow I\) là trung điểm của \(HC.\)
\(\Delta ECH\) vuông tại \(E\) có đường trung tuyến \(EI\)
\( \Rightarrow EI = HI = \dfrac{1}{2}HC\) (đường trung tuyến ứng với cạnh huyền của tam giác vuông)
\( \Rightarrow \Delta HEI\) cân tại \(I\) \( \Rightarrow \angle IEH = \angle IHE\) (tính chất tam giác cân)
Hay \(IEH = \angle EHC\) (2)
Tứ giác \(CDHE\) là tứ giác nội tiếp (cmt)
\( \Rightarrow \angle CDE = \angle CHE\) (hai góc nội tiếp cùng chắn cung \(EC\)) (3)
Từ (1), (2) và (3) suy ra: \(\angle EDC = \angle BAE = \angle HEI\)
\(\Delta AOE\) cân tại \(O\,\,\left( {OA = OE} \right)\) \( \Rightarrow \angle OEB = \angle OBE\) (tính chất tam giác cân)
Hay \(\angle BAE = \angle OEA\)
Mà \(\angle OBE + \angle BAE = {90^0}\)
\( \Rightarrow \angle OEB + \angle HEI = {90^0}\)
Hay \(OE \bot EI\)
\( \Rightarrow EI\) là tiếp tuyến của đường tròn đường kính\(AB.\) (đpcm)
Bài 5 (1,0 điểm)
Cách giải:
Cho các số thực dương \(x,\,\,y > 1\). Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{{{x^2}}}{{y - 1}} + \dfrac{{{y^2}}}{{x - 1}}\).
Áp dụng BĐT Cô-si t có:
\(\begin{array}{l}x = x - 1 + 1 \ge 2\sqrt {\left( {x - 1} \right).1} = 2\sqrt {x - 1} \\ \Rightarrow {x^2} \ge 4\left( {x - 1} \right)\\ \Rightarrow \dfrac{{{x^2}}}{{y - 1}} \ge \dfrac{{4\left( {x - 1} \right)}}{{y - 1}}\end{array}\)
Tương tự ta có: \(\dfrac{{{y^2}}}{{x - 1}} \ge \dfrac{{4\left( {y - 1} \right)}}{{x - 1}}\).
Khi đó ta có:
\(\begin{array}{l}P = \dfrac{{{x^2}}}{{y - 1}} + \dfrac{{{y^2}}}{{x - 1}}\\\,\,\,\,\, \ge \dfrac{{4\left( {x - 1} \right)}}{{y - 1}} + \dfrac{{4\left( {y - 1} \right)}}{{x - 1}}\\\,\,\,\, \ge 2\sqrt {\dfrac{{4\left( {x - 1} \right)}}{{y - 1}}.\dfrac{{4\left( {y - 1} \right)}}{{x - 1}}} = 8\end{array}\)
Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}x - 1 = 1\\y - 1 = 1\\\dfrac{{x - 1}}{{y - 1}} = \dfrac{{y - 1}}{{x - 1}}\end{array} \right. \Leftrightarrow x = y = 2\).
Vậy \(\min P = 8 \Leftrightarrow x = y = 2\).
Kỳ thi tuyển sinh vào lớp 10 là một bước ngoặt quan trọng trong quá trình học tập của mỗi học sinh. Để đạt kết quả tốt nhất, việc chuẩn bị kỹ lưỡng và làm quen với các dạng đề thi là vô cùng cần thiết. Bài viết này sẽ cung cấp phân tích chi tiết về Đề thi vào 10 môn Toán Đắk Nông năm 2020, kèm theo hướng dẫn giải chi tiết để giúp các em học sinh tự tin hơn khi bước vào phòng thi.
Đề thi vào 10 môn Toán Đắk Nông năm 2020 thường có cấu trúc gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Chúng ta sẽ cùng phân tích một số câu hỏi điển hình trong Đề thi vào 10 môn Toán Đắk Nông năm 2020 để hiểu rõ hơn về yêu cầu và cách giải:
Để giải phương trình này, chúng ta cần áp dụng các kiến thức về phương trình bậc hai và sử dụng công thức nghiệm. Lưu ý kiểm tra điều kiện của phương trình để đảm bảo nghiệm tìm được là hợp lệ.
Để chứng minh bài toán này, chúng ta cần sử dụng các định lý về tam giác vuông, hệ thức lượng trong tam giác vuông và các tính chất của đường cao. Việc vẽ hình chính xác và trình bày lời giải một cách logic là rất quan trọng.
Để đạt kết quả tốt nhất trong kỳ thi tuyển sinh vào lớp 10 môn Toán, các em học sinh cần có một kế hoạch ôn thi khoa học và hiệu quả. Dưới đây là một số gợi ý:
Ngoài Đề thi vào 10 môn Toán Đắk Nông năm 2020, các em học sinh có thể tham khảo thêm các tài liệu sau:
Hãy luôn giữ tinh thần lạc quan và tự tin trong quá trình ôn thi. Đừng ngại hỏi khi gặp khó khăn và hãy dành thời gian nghỉ ngơi hợp lý để đảm bảo sức khỏe tốt nhất. Chúc các em học sinh đạt kết quả cao trong kỳ thi tuyển sinh vào lớp 10 môn Toán!