Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán của tỉnh Đồng Tháp năm 2021. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi sắp tới.
Chúng tôi cung cấp đầy đủ các đề thi chính thức, kèm theo đáp án chi tiết và lời giải dễ hiểu.
Câu 1 (2 điểm): a) Tính giá trị của biểu thức
Câu 1 (2 điểm):
a) Tính giá trị của biểu thức \(A = \sqrt {16} + \sqrt {25} .\)
b) Cho \(x \ge - 1,\,x \ne 0,\) rút gọn biểu thức \(B = \dfrac{{\left( {\sqrt {x + 1} - 1} \right)\left( {\sqrt {x + 1} + 1} \right)}}{x}.\)
Câu 2 (1 điểm):
Giải hệ phương trình \(\left\{ \begin{array}{l}x - y = 3\\3x + y = 1\end{array} \right..\)
Câu 3 (2 điểm):
a) Vẽ đồ thị của hàm sô \(y = x - 2.\)
b) Xác định hệ số \(a\) để đồ thị hàm số \(y = a{x^2}\) đi qua điểm \(M\left( {2;\,\,1} \right).\)
Câu 4 (1,0 điểm)
Biết rằng phương trình \({x^2} - x - 3 = 0\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\). Tính giá trị của biểu thức\(C = x_1^2 + x_2^2\).
Câu 5 (1,0 điểm)
Theo kế hoạch, một tổ trong xưởng may phải may xong 8400 chiếc khẩu trang trong một thời gian quy định. Do tình hình dịch bệnh Covid-19 diễn biến phức tạp, tổ đã quyết định tăng năng suất nên mỗi ngày tổ đã may được nhiều hơn 102 chiếc khẩu trang so với số khẩu trang phải may trong một ngày theo kế hoạch. Vì vậy, trước thời gian quy định 4 ngày, tổ đã may được 6416 chiếc khẩu trang. Hỏi số khẩu trang mà tổ phải may mỗi ngày theo kế hoạch là bao nhiêu?
Câu 6 (1,0 điểm)
Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\). Biết \(AB = 3cm,\,\,AC = 4cm\). Tính độ dài \(BC\) và đường cao \(AH\).
Câu 7 (2,0 điểm):
Cho đường tròn \(\left( O \right)\). Từ một điểm \(M\) nằm ngoài đường tròn \(\left( O \right)\), kẻ hai tiếp tuyến \(MA,MB\) với đường tròn \(\left( O \right)\) (\(A,B\) là các tiếp điểm).
a) Chứng minh \(MAOB\) nội tiếp.
b) Vẽ đường kính \(BK\) của đường tròn \(\left( O \right)\), \(H\) là điểm trên \(BK\) sao cho \(AH\) vuông góc với \(BK\). Điểm \(I\) là giao điểm của \(AH,\,MK\). Chứng minh \(I\) là trung điểm \(HA\).
Câu 1 (2 điểm):
a) Tính giá trị của biểu thức \(A = \sqrt {16} + \sqrt {25} .\)
b) Cho \(x \ge - 1,\,x \ne 0,\) rút gọn biểu thức \(B = \dfrac{{\left( {\sqrt {x + 1} - 1} \right)\left( {\sqrt {x + 1} + 1} \right)}}{x}.\)
Câu 2 (1 điểm):
Giải hệ phương trình \(\left\{ \begin{array}{l}x - y = 3\\3x + y = 1\end{array} \right..\)
Câu 3 (2 điểm):
a) Vẽ đồ thị của hàm sô \(y = x - 2.\)
b) Xác định hệ số \(a\) để đồ thị hàm số \(y = a{x^2}\) đi qua điểm \(M\left( {2;\,\,1} \right).\)
Câu 4 (1,0 điểm)
Biết rằng phương trình \({x^2} - x - 3 = 0\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\). Tính giá trị của biểu thức\(C = x_1^2 + x_2^2\).
Câu 5 (1,0 điểm)
Theo kế hoạch, một tổ trong xưởng may phải may xong 8400 chiếc khẩu trang trong một thời gian quy định. Do tình hình dịch bệnh Covid-19 diễn biến phức tạp, tổ đã quyết định tăng năng suất nên mỗi ngày tổ đã may được nhiều hơn 102 chiếc khẩu trang so với số khẩu trang phải may trong một ngày theo kế hoạch. Vì vậy, trước thời gian quy định 4 ngày, tổ đã may được 6416 chiếc khẩu trang. Hỏi số khẩu trang mà tổ phải may mỗi ngày theo kế hoạch là bao nhiêu?
Câu 6 (1,0 điểm)
Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\). Biết \(AB = 3cm,\,\,AC = 4cm\). Tính độ dài \(BC\) và đường cao \(AH\).
Câu 7 (2,0 điểm):
Cho đường tròn \(\left( O \right)\). Từ một điểm \(M\) nằm ngoài đường tròn \(\left( O \right)\), kẻ hai tiếp tuyến \(MA,MB\) với đường tròn \(\left( O \right)\) (\(A,B\) là các tiếp điểm).
a) Chứng minh \(MAOB\) nội tiếp.
b) Vẽ đường kính \(BK\) của đường tròn \(\left( O \right)\), \(H\) là điểm trên \(BK\) sao cho \(AH\) vuông góc với \(BK\). Điểm \(I\) là giao điểm của \(AH,\,MK\). Chứng minh \(I\) là trung điểm \(HA\).
Câu 1:
Phương pháp:
a) Sử dụng hằng đẳng thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)
Thực hiện các phép tính với căn bậc hai.
b) Vận dụng hằng đẳng thức \(a - b = \left( {\sqrt a - \sqrt b } \right)\left( {\sqrt a + \sqrt b } \right)\) để rút gọn tử thức
Vận dụng \({\left( {\sqrt A } \right)^2} = A\,\,\,\,\left( {A \ge 0} \right)\)
Cách giải:
a) \(A = \sqrt {16} + \sqrt {25} \)
\(\begin{array}{l}\,\,\,\,\, = \sqrt {{4^2}} + \sqrt {{5^2}} \\\,\,\,\,\, = 4 + 5 = 9.\end{array}\)
Vậy \(A = 9.\)
b) Điều kiện: \(x \ge - 1,\,\,x \ne 0.\)
\(\begin{array}{l}B = \dfrac{{\left( {\sqrt {x + 1} - 1} \right)\left( {\sqrt {x + 1} + 1} \right)}}{x}\\\,\,\,\,\,\, = \dfrac{{{{\left( {\sqrt {x + 1} } \right)}^2} - 1}}{x}\\\,\,\,\,\,\, = \dfrac{{x + 1 - 1}}{x} = 1.\end{array}\)
Vậy với \(x \ge - 1,\,\,x \ne 0\) thì \(B = 1.\)
Câu 2:
Phương pháp:
Sử dụng phương pháp cộng đại số, tìm được nghiệm \(x\)
Sử dụng phương pháp thế, tìm được nghiệm \(y\)
Kết luận nghiệm \(\left( {x;y} \right)\) của hệ phương trình.
Cách giải:
\(\left\{ \begin{array}{l}x - y = 3\\3x + y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x = 4\\y = x - 3\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 1 - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = - 2\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất \(S = \left\{ {\left( {1; - 2} \right)} \right\}.\)
Câu 3:
Phương pháp:
a) Vẽ đồ thị của hàm số \(y = ax + b\)
+ Lập bảng giá trị tương ứng của \(x\) và \(y\)
+ Xác định được các điểm mà đồ thị đi qua, vẽ đồ thị.
b) Thay tọa độ của điểm \(M\left( {2;\,\,1} \right)\) vào hàm số \(y = a{x^2}\), từ đó tìm được \(a\)
Cách giải:
a) Ta có bảng giá trị:
\(x\) | \(0\) | \(2\) |
\(y\) | \( - 2\) | \(0\) |
Vậy đồ thị hàm số \(y = x - 2\) là đường thẳng đi qua các điểm \(\left( {0;\, - 2} \right)\) và \(\left( {2;\,\,0} \right).\)
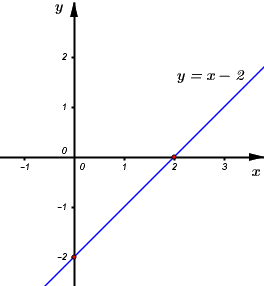
b) Đồ thị hàm số \(y = a{x^2}\) đi qua điểm \(M\left( {2;\,\,1} \right)\) \( \Leftrightarrow 1 = a{.2^2}\)\( \Leftrightarrow a = \dfrac{1}{4}\)
Vậy \(a = \dfrac{1}{4}\) thỏa mãn bài toán.
Câu 4
Phương pháp:
Chứng minh phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}\)
Áp dụng hệ thức Vi – ét, tính được \({x_1} + {x_2};{x_1}.{x_2}\)
Chú ý: \(x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}\)
Cách giải:
Phương trình \({x^2} - x - 3 = 0\) có \(ac = - 3 < 0\) nên phương trình có hai nghiệm phân biệt trái dấu \({x_1},\,\,{x_2}\).
Khi đó áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 1\\{x_1}{x_2} = - 3\end{array} \right.\).
Ta có: \(C = x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = {1^2} - 2.\left( { - 3} \right) = 7\).
Vậy \(C = 7\).
Câu 5
Phương pháp:
Gọi số khẩu trang mà tổ phải may mỗi ngày theo kế hoạch là \(x\) (chiếc) (ĐK: \(x \in {\mathbb{N}^*}\)).
Tính được thời gian theo kế hoạch may xong số khẩu trang
Tính được thời gian theo thực tế may xong số khẩu trang
Lập được phương trình dựa vào thời gian của kế hoạch và thực tế
Giải phương trình, đối chiếu điều kiện và kết luận.
Cách giải:
Gọi số khẩu trang mà tổ phải may mỗi ngày theo kế hoạch là \(x\) (chiếc) (ĐK: \(x \in {\mathbb{N}^*}\)).
Vì xưởng phải may 8400 chiếc khẩu trang nên thời gian để may xong là \(\dfrac{{8400}}{x}\) (ngày).
Vì sau khi tăng năng suất nên mỗi ngày tổ đã may được nhiều hơn 102 chiếc khẩu trang so với số khẩu trang phải may trong một ngày theo kế hoạch nên thực tế mỗi ngày tổ may được \(x + 102\) (chiếc).
Thời gian tổ may được 6416 chiếc khẩu trang theo thực tế là: \(\dfrac{{6416}}{{x + 102}}\) (ngày).
Vì tổ may trước thời gian quy định 4 ngày, tổ đã may được 6416 chiếc khẩu trang nên ta có phương trình:
\(\begin{array}{l}\,\,\,\,\,\,\,\dfrac{{8400}}{x} - \dfrac{{6416}}{{x + 102}} = 4\\ \Leftrightarrow \dfrac{{2100}}{x} - \dfrac{{1604}}{{x + 102}} = 1\\ \Leftrightarrow 2100\left( {x + 102} \right) - 1604x = x\left( {x + 102} \right)\\ \Leftrightarrow 2100x + 214200 - 1604x = {x^2} + 102x\\ \Leftrightarrow {x^2} - 394x - 214200 = 0\\ \Leftrightarrow {x^2} - 700x + 306x - 214200 = 0\\ \Leftrightarrow x\left( {x - 700} \right) + 306\left( {x - 700} \right) = 0\\ \Leftrightarrow \left( {x - 700} \right)\left( {x + 306} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 700\,\,\left( {tm} \right)\\x = - 306\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy số khẩu trang mà tổ phải may mỗi ngày theo kế hoạch là \(700\) chiếc.
Câu 6
Phương pháp:
Áp dụng định lí Pytago trong tam giác vuông \(ABC\), tính được \(BC\)
Áp dụng hệ thức lượng trong tam giác vuông \(ABC\), đường cao \(AH\), tính được \(AH\).
Cách giải:
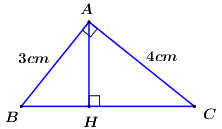
Áp dụng định lí Pytago trong tam giác vuông \(ABC\) ta có:
\(\begin{array}{l}\,\,\,\,\,B{C^2} = A{B^2} + A{C^2}\\ \Rightarrow B{C^2} = {3^2} + {4^2} = 9 + 16 = 25\\ \Rightarrow BC = \sqrt {25} = 5\,\,\left( {cm} \right)\end{array}\)
Áp dụng hệ thức lượng trong tam giác vuông \(ABC\), đường cao \(AH\) ta có:
\(AB.AC = AH.BC \Rightarrow AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{3.4}}{5} = 2,4\,\,\left( {cm} \right)\).
Vậy \(BC = 5\,\,cm,\,\,AH = 2,4\,\,cm\).
Câu 7:
Phương pháp:
a) Vận dụng dấu hiệu nhận biết: Tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp.
b) Gọi \(N\) là giao điểm của \(AB\) với \(MO\).
\(C\) là giao điểm giữa \(MK\) với đường tròn \(\left( O \right)\)
Ta sẽ chứng minh: \(\left\{ \begin{array}{l}NI//BK\\NA = NB = \dfrac{1}{2}AB\end{array} \right.\)
Suy ra \(I\) là trung điểm của \(AH\)
\( \Rightarrow IA = IH\) (định lí đường trung bình của tam giác)
Cách giải:
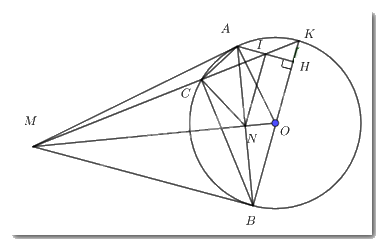
a) Vì \(MA,\,\,MB\) là các tiếp tuyến của \(\left( O \right)\) lần lượt tại \(A,\,\,B\) nên \(\angle MAO = \angle MBO = {90^0}\) (định nghĩa).
Tứ giác \(MAOB\) có \(\angle MAO + \angle MBO = {180^0}\).
Suy ra tứ giác \(MAOB\) nội tiếp (tứ giác có tổng hai góc đối bằng bằng \({180^0}\)).
b) Gọi \(N\) là giao điểm của \(AB\) với \(MO\).
\(C\) là giao điểm giữa \(MK\) với đường tròn \(\left( O \right)\)
Ta có: \(OA = OB \Rightarrow O\) thuộc trung trực của \(AB\).
\(MA = MB\) (tính chất 2 tiếp tuyến cắt nhau) nên \(M\) thuộc trung trực của \(AB\).
\( \Rightarrow OM\) là trung trực của \(AB\) \( \Rightarrow OM \bot AB\) tại \(N\).
Tứ giác \(MCNB\) có \(\angle MCB = \angle MNB = {90^0}\). Suy ra tứ giác \(MCNB\) nội tiếp (tứ giác có hai đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau).
\( \Rightarrow \angle NMB = \angle NCB\) (hai góc cùng chắn một cung \(BN\))
Ta có: \(\angle NMB = \angle NBO\) (cùng phụ với \(\angle MBN\))
\( \Rightarrow \angle NCB = \angle NBO\).
Lại có: \(\angle NCB + \angle NCI = {90^0},\,\,\,\angle NAI + \angle NBO = {90^0}\)
Suy ra \(\angle NCI = \angle NAI\).
Xét tứ giác \(ACNI\) có: \(\angle NCI = \angle NAI\) (cmt), suy ra tứ giác \(ACNI\) nội tiếp (tứ giác có 2 đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau).
\( \Rightarrow \angle ANI = \angle ACI\) (hai góc cùng chắn cung \(AI\)).
Trong \(\left( O \right)\) có: \(\angle ACI = \angle ABK\) (hai góc nội tiếp cùng chắn cung \(AK\))
Suy ra \(\angle ANI = \angle ABK\). Mà hai góc này vị trí đồng vị \( \Rightarrow NI//BK\)
Tam giác \(ABK\) có: \(\left\{ \begin{array}{l}NI//BK\\NA = NB = \dfrac{1}{2}AB\end{array} \right.\)
Suy ra \(I\) là trung điểm của \(AH\)
\( \Rightarrow IA = IH\) (định lí đường trung bình của tam giác) (đpcm).
Câu 1:
Phương pháp:
a) Sử dụng hằng đẳng thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)
Thực hiện các phép tính với căn bậc hai.
b) Vận dụng hằng đẳng thức \(a - b = \left( {\sqrt a - \sqrt b } \right)\left( {\sqrt a + \sqrt b } \right)\) để rút gọn tử thức
Vận dụng \({\left( {\sqrt A } \right)^2} = A\,\,\,\,\left( {A \ge 0} \right)\)
Cách giải:
a) \(A = \sqrt {16} + \sqrt {25} \)
\(\begin{array}{l}\,\,\,\,\, = \sqrt {{4^2}} + \sqrt {{5^2}} \\\,\,\,\,\, = 4 + 5 = 9.\end{array}\)
Vậy \(A = 9.\)
b) Điều kiện: \(x \ge - 1,\,\,x \ne 0.\)
\(\begin{array}{l}B = \dfrac{{\left( {\sqrt {x + 1} - 1} \right)\left( {\sqrt {x + 1} + 1} \right)}}{x}\\\,\,\,\,\,\, = \dfrac{{{{\left( {\sqrt {x + 1} } \right)}^2} - 1}}{x}\\\,\,\,\,\,\, = \dfrac{{x + 1 - 1}}{x} = 1.\end{array}\)
Vậy với \(x \ge - 1,\,\,x \ne 0\) thì \(B = 1.\)
Câu 2:
Phương pháp:
Sử dụng phương pháp cộng đại số, tìm được nghiệm \(x\)
Sử dụng phương pháp thế, tìm được nghiệm \(y\)
Kết luận nghiệm \(\left( {x;y} \right)\) của hệ phương trình.
Cách giải:
\(\left\{ \begin{array}{l}x - y = 3\\3x + y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x = 4\\y = x - 3\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 1 - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = - 2\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất \(S = \left\{ {\left( {1; - 2} \right)} \right\}.\)
Câu 3:
Phương pháp:
a) Vẽ đồ thị của hàm số \(y = ax + b\)
+ Lập bảng giá trị tương ứng của \(x\) và \(y\)
+ Xác định được các điểm mà đồ thị đi qua, vẽ đồ thị.
b) Thay tọa độ của điểm \(M\left( {2;\,\,1} \right)\) vào hàm số \(y = a{x^2}\), từ đó tìm được \(a\)
Cách giải:
a) Ta có bảng giá trị:
\(x\) | \(0\) | \(2\) |
\(y\) | \( - 2\) | \(0\) |
Vậy đồ thị hàm số \(y = x - 2\) là đường thẳng đi qua các điểm \(\left( {0;\, - 2} \right)\) và \(\left( {2;\,\,0} \right).\)
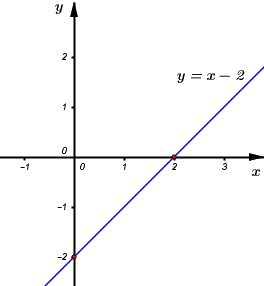
b) Đồ thị hàm số \(y = a{x^2}\) đi qua điểm \(M\left( {2;\,\,1} \right)\) \( \Leftrightarrow 1 = a{.2^2}\)\( \Leftrightarrow a = \dfrac{1}{4}\)
Vậy \(a = \dfrac{1}{4}\) thỏa mãn bài toán.
Câu 4
Phương pháp:
Chứng minh phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}\)
Áp dụng hệ thức Vi – ét, tính được \({x_1} + {x_2};{x_1}.{x_2}\)
Chú ý: \(x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}\)
Cách giải:
Phương trình \({x^2} - x - 3 = 0\) có \(ac = - 3 < 0\) nên phương trình có hai nghiệm phân biệt trái dấu \({x_1},\,\,{x_2}\).
Khi đó áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 1\\{x_1}{x_2} = - 3\end{array} \right.\).
Ta có: \(C = x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = {1^2} - 2.\left( { - 3} \right) = 7\).
Vậy \(C = 7\).
Câu 5
Phương pháp:
Gọi số khẩu trang mà tổ phải may mỗi ngày theo kế hoạch là \(x\) (chiếc) (ĐK: \(x \in {\mathbb{N}^*}\)).
Tính được thời gian theo kế hoạch may xong số khẩu trang
Tính được thời gian theo thực tế may xong số khẩu trang
Lập được phương trình dựa vào thời gian của kế hoạch và thực tế
Giải phương trình, đối chiếu điều kiện và kết luận.
Cách giải:
Gọi số khẩu trang mà tổ phải may mỗi ngày theo kế hoạch là \(x\) (chiếc) (ĐK: \(x \in {\mathbb{N}^*}\)).
Vì xưởng phải may 8400 chiếc khẩu trang nên thời gian để may xong là \(\dfrac{{8400}}{x}\) (ngày).
Vì sau khi tăng năng suất nên mỗi ngày tổ đã may được nhiều hơn 102 chiếc khẩu trang so với số khẩu trang phải may trong một ngày theo kế hoạch nên thực tế mỗi ngày tổ may được \(x + 102\) (chiếc).
Thời gian tổ may được 6416 chiếc khẩu trang theo thực tế là: \(\dfrac{{6416}}{{x + 102}}\) (ngày).
Vì tổ may trước thời gian quy định 4 ngày, tổ đã may được 6416 chiếc khẩu trang nên ta có phương trình:
\(\begin{array}{l}\,\,\,\,\,\,\,\dfrac{{8400}}{x} - \dfrac{{6416}}{{x + 102}} = 4\\ \Leftrightarrow \dfrac{{2100}}{x} - \dfrac{{1604}}{{x + 102}} = 1\\ \Leftrightarrow 2100\left( {x + 102} \right) - 1604x = x\left( {x + 102} \right)\\ \Leftrightarrow 2100x + 214200 - 1604x = {x^2} + 102x\\ \Leftrightarrow {x^2} - 394x - 214200 = 0\\ \Leftrightarrow {x^2} - 700x + 306x - 214200 = 0\\ \Leftrightarrow x\left( {x - 700} \right) + 306\left( {x - 700} \right) = 0\\ \Leftrightarrow \left( {x - 700} \right)\left( {x + 306} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 700\,\,\left( {tm} \right)\\x = - 306\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy số khẩu trang mà tổ phải may mỗi ngày theo kế hoạch là \(700\) chiếc.
Câu 6
Phương pháp:
Áp dụng định lí Pytago trong tam giác vuông \(ABC\), tính được \(BC\)
Áp dụng hệ thức lượng trong tam giác vuông \(ABC\), đường cao \(AH\), tính được \(AH\).
Cách giải:
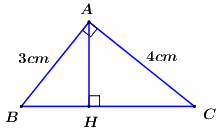
Áp dụng định lí Pytago trong tam giác vuông \(ABC\) ta có:
\(\begin{array}{l}\,\,\,\,\,B{C^2} = A{B^2} + A{C^2}\\ \Rightarrow B{C^2} = {3^2} + {4^2} = 9 + 16 = 25\\ \Rightarrow BC = \sqrt {25} = 5\,\,\left( {cm} \right)\end{array}\)
Áp dụng hệ thức lượng trong tam giác vuông \(ABC\), đường cao \(AH\) ta có:
\(AB.AC = AH.BC \Rightarrow AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{3.4}}{5} = 2,4\,\,\left( {cm} \right)\).
Vậy \(BC = 5\,\,cm,\,\,AH = 2,4\,\,cm\).
Câu 7:
Phương pháp:
a) Vận dụng dấu hiệu nhận biết: Tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp.
b) Gọi \(N\) là giao điểm của \(AB\) với \(MO\).
\(C\) là giao điểm giữa \(MK\) với đường tròn \(\left( O \right)\)
Ta sẽ chứng minh: \(\left\{ \begin{array}{l}NI//BK\\NA = NB = \dfrac{1}{2}AB\end{array} \right.\)
Suy ra \(I\) là trung điểm của \(AH\)
\( \Rightarrow IA = IH\) (định lí đường trung bình của tam giác)
Cách giải:
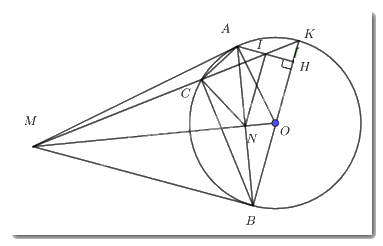
a) Vì \(MA,\,\,MB\) là các tiếp tuyến của \(\left( O \right)\) lần lượt tại \(A,\,\,B\) nên \(\angle MAO = \angle MBO = {90^0}\) (định nghĩa).
Tứ giác \(MAOB\) có \(\angle MAO + \angle MBO = {180^0}\).
Suy ra tứ giác \(MAOB\) nội tiếp (tứ giác có tổng hai góc đối bằng bằng \({180^0}\)).
b) Gọi \(N\) là giao điểm của \(AB\) với \(MO\).
\(C\) là giao điểm giữa \(MK\) với đường tròn \(\left( O \right)\)
Ta có: \(OA = OB \Rightarrow O\) thuộc trung trực của \(AB\).
\(MA = MB\) (tính chất 2 tiếp tuyến cắt nhau) nên \(M\) thuộc trung trực của \(AB\).
\( \Rightarrow OM\) là trung trực của \(AB\) \( \Rightarrow OM \bot AB\) tại \(N\).
Tứ giác \(MCNB\) có \(\angle MCB = \angle MNB = {90^0}\). Suy ra tứ giác \(MCNB\) nội tiếp (tứ giác có hai đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau).
\( \Rightarrow \angle NMB = \angle NCB\) (hai góc cùng chắn một cung \(BN\))
Ta có: \(\angle NMB = \angle NBO\) (cùng phụ với \(\angle MBN\))
\( \Rightarrow \angle NCB = \angle NBO\).
Lại có: \(\angle NCB + \angle NCI = {90^0},\,\,\,\angle NAI + \angle NBO = {90^0}\)
Suy ra \(\angle NCI = \angle NAI\).
Xét tứ giác \(ACNI\) có: \(\angle NCI = \angle NAI\) (cmt), suy ra tứ giác \(ACNI\) nội tiếp (tứ giác có 2 đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau).
\( \Rightarrow \angle ANI = \angle ACI\) (hai góc cùng chắn cung \(AI\)).
Trong \(\left( O \right)\) có: \(\angle ACI = \angle ABK\) (hai góc nội tiếp cùng chắn cung \(AK\))
Suy ra \(\angle ANI = \angle ABK\). Mà hai góc này vị trí đồng vị \( \Rightarrow NI//BK\)
Tam giác \(ABK\) có: \(\left\{ \begin{array}{l}NI//BK\\NA = NB = \dfrac{1}{2}AB\end{array} \right.\)
Suy ra \(I\) là trung điểm của \(AH\)
\( \Rightarrow IA = IH\) (định lí đường trung bình của tam giác) (đpcm).
Kỳ thi tuyển sinh vào lớp 10 là một bước ngoặt quan trọng trong quá trình học tập của mỗi học sinh. Để đạt kết quả tốt nhất, việc chuẩn bị kỹ lưỡng là điều cần thiết. Đề thi vào 10 môn Toán Đồng Tháp năm 2021 là một nguồn tài liệu quý giá để các em học sinh ôn tập và rèn luyện kỹ năng.
Đề thi vào 10 môn Toán Đồng Tháp năm 2021 thường bao gồm các dạng bài tập sau:
Đề thi chính thức năm 2021 có độ khó vừa phải, tập trung vào các kiến thức cơ bản và nâng cao của chương trình Toán lớp 9. Các bài toán đại số chiếm phần lớn trong đề thi, đòi hỏi học sinh phải nắm vững các phương pháp giải phương trình, hệ phương trình, và bất phương trình. Bên cạnh đó, các bài toán hình học cũng yêu cầu học sinh phải có kiến thức vững chắc về các định lý và tính chất hình học.
Ngoài đề thi chính thức, các trường THCS trên địa bàn tỉnh Đồng Tháp cũng tổ chức nhiều đề thi thử để giúp học sinh làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán. Các đề thi thử thường có độ khó cao hơn đề thi chính thức, đòi hỏi học sinh phải có khả năng tư duy logic và sáng tạo.
Dạng 1: Giải phương trình bậc hai
Để giải phương trình bậc hai, ta có thể sử dụng các phương pháp sau:
Dạng 2: Giải hệ phương trình
Để giải hệ phương trình, ta có thể sử dụng các phương pháp sau:
Ngoài đề thi vào 10 môn Toán Đồng Tháp năm 2021, các em học sinh có thể tham khảo thêm các tài liệu sau:
Chúc các em học sinh ôn thi tốt và đạt kết quả cao trong kỳ thi tuyển sinh vào lớp 10 môn Toán Đồng Tháp năm 2021!