Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Bình Thuận năm 2023. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi sắp tới.
Chúng tôi cung cấp đầy đủ các đề thi chính thức, đáp án chi tiết và phương pháp giải bài tập hiệu quả.
Câu 1: Giải phương trình và hệ phương trình sau: a) \({x^2} + 2x - 3 = 0\) b) \(\left\{ {\begin{array}{*{20}{c}}{ - x + 3y = 5}\\{x + y = 3}\end{array}} \right.\)
Câu 1: Giải phương trình và hệ phương trình sau:
a) \({x^2} + 2x - 3 = 0\)
b) \(\left\{ {\begin{array}{*{20}{c}}{ - x + 3y = 5}\\{x + y = 3}\end{array}} \right.\)
Câu 2: Rút gọn các biểu thức sau:
a) \(A = \left( {\sqrt {27} {\rm{ \;}} - \sqrt {12} {\rm{ \;}} + \sqrt {48} } \right)\sqrt 3 \)
b) \(B = \left( {\frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} - 1}} - \frac{1}{{x - \sqrt x }}} \right):\frac{{\sqrt x {\rm{ \;}} + 1}}{{3\sqrt x }}\), với \(x > 0\) và \(x \ne 1\)
Câu 3: Cho hàm số \(y = {x^2}\) có đồ thị \(\left( P \right)\)
a) Vẽ đồ thị \(\left( P \right)\) trên mặt phẳng tọa độ \(Oxy\). b) Tìm giá trị nguyên của tham số \(m\) để đường thẳng \(\left( d \right):y = 2mx - {m^2} + 1\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ lần lượt là \({x_1},{x_2}\) thỏa mãn \({x_1} < 2024 < {x_2}\).
Câu 4: Một công ty dự định thuê một số xe lớn cùng loại để chở vừa hết 210 người đi du lịch Mũi Né. Nhưng thực tế, công ty lại thuê toàn bộ xe nhỏ hơn cùng loại. Biết rằng số xe nhỏ phải thuê nhiều hợ sồ xe lớn là 2 chiếc thì mới chờ vừa hết số người trên và mỗi xe nhỏ chở ít hơn mỗi xe lớn là 12 người. Tính số xe nhỏ đã thuê.
Câu 5: Một cái chai có chứa một lượng nước, phần chứa nước là hình trụ có chiều cao \(10\;{\rm{cm}}\), khi lật ngược chai lại thì phần không chứa nước cũng là một hình trụ có chiều cao \(8\;{\rm{cm}}\) (như hình vẽ bên). Biết thể tích của chai là \(450\pi {\rm{c}}{{\rm{m}}^3}\). Tính bán kính của đáy chai (giả sử độ dày của thành chai và đáy chai không đáng kể).

Câu 6: Cho đường tròn \(\left( O \right)\) và điểm \(A\) nằm bên ngoài đường tròn. Từ \(A\), vẽ hai tiếp tuyến \(AB,AC\) ( \(B,C\) là hai tiếp điểm).
a) Chứng minh tứ giác \(ABOC\) nội tiếp.
b) Vẽ đường kính \(CE\), nối \(AE\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(F\). Chứng minh \(A{B^2} = AE.AF\). c) Cho \(OA\) cắt \(BC\) tại \(H,BF\) cắt \(OA\) tại \(I\). Chứng minh \(I\) là trung điểm của \(AH\).
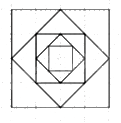
Câu 7: Từ hình vuông đầu tiên, bạn Hùng vẽ hình vuông thứ hai có các đỉnh là trung điểm của các cạnh hình vuông thứ nhất, vẽ tiếp hình vuông thứ ba có các đỉnh là trung điểm của các cạnh hình vuông thứ hai và cứ tiếp tục như vậy (xem hình minh họa bên). Giả sử hình vuông thứ bảy có diện tích bằng \(32(c{m^2})\). Tính diện tích hình vuông thứ năm.
-----HẾT-----
Câu 1 (TH):
Phương pháp:
a) Xét a + b + c từ đó suy ra hai nghiệm của phương trình.
b) Giải hệ phương trình bằng phương pháp thế.
Cách giải:
a) \({x^2} + 2x - 3 = 0\).
Vì \(a + b + c = 1 + 2 - 3 = 0\) nên phương trình có 2 nghiệm phân biệt là \({x_1} = 1\) và \({x_2} = \frac{c}{a} = - 3\)
Vậy phương trình có tập nghiệm là \(S = \left\{ {1; - 3} \right\}\).
b) \(\left\{ {\begin{array}{*{20}{c}}{ - x + 3y = 5}\\{x + y = 3}\end{array} \Leftrightarrow } \right.\left\{ {\begin{array}{*{20}{c}}{x = 3 - y}\\{4y = 8\,\,\,\,}\end{array} \Leftrightarrow } \right.\left\{ {\begin{array}{*{20}{c}}{x = 1}\\{y = 2}\end{array}} \right.\)
Vậy hệ phương trình có nghiệm duy nhất là \(\left( {x,y} \right) = \left( {1;2} \right)\).
Câu 2 (TH):
Phương pháp:
a) Khai căn và thực hiện phép tính.
b) Quy đồng và rút gọn.
Cách giải:
a) \(A = (\sqrt {27} {\rm{ \;}} - \sqrt {12} {\rm{ \;}} + \sqrt {48} )\sqrt 3 \).
\(\begin{array}{*{20}{l}}{A = (\sqrt {{3^2}.3} {\rm{ \;}} - \sqrt {{2^2}.3} {\rm{ \;}} + \sqrt {{4^2}.3} )\sqrt 3 }\\{A = (3\sqrt 3 {\rm{ \;}} - 2\sqrt 3 {\rm{ \;}} + 4\sqrt 3 )\sqrt 3 }\\{A = 5\sqrt 3 .\sqrt 3 }\\{A = 15.}\end{array}\)
Vậy \(A = 15\).
b) \(B = \left( {\frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} - 1}} - \frac{1}{{x - \sqrt x }}} \right):\frac{{\sqrt x {\rm{ \;}} + 1}}{{3\sqrt x }}\), với \(x > 0\) và \(x \ne 1\).
Với \(x > 0\) và \(x \ne 1\) ta có:
\(\begin{array}{l}B = \left( {\frac{{\sqrt x }}{{\sqrt x - 1}} - \frac{1}{{\sqrt x \left( {\sqrt x - 1} \right)}}} \right):\frac{{\sqrt x + 1}}{{3\sqrt x }}\\B = \left( {\frac{x}{{\sqrt x \left( {\sqrt x - 1} \right)}} - \frac{1}{{\sqrt x \left( {\sqrt x - 1} \right)}}} \right):\frac{{\sqrt x + 1}}{{3\sqrt x }}\end{array}\)
\(\begin{array}{l}B = \frac{{x - 1}}{{\sqrt x \left( {\sqrt x - 1} \right)}}:\frac{{\sqrt x + 1}}{{3\sqrt x }}\\B = \frac{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}{{\sqrt x \left( {\sqrt x - 1} \right)}}:\frac{{\sqrt x + 1}}{{3\sqrt x }}\\B = \frac{{\sqrt x + 1}}{{\sqrt x }}.\frac{{3\sqrt x }}{{\sqrt x + 1}} = 3\end{array}\)
Vậy với \(x > 0\) và \(x \ne 1\) thì \(B = 3\).
Câu 3 (VD):
Phương pháp:
a) Cho 5 điểm và vẽ parabol (P).
b) Xét phương trình hoành độ giao điểm, từ đó áp dụng hệ thức vi-et \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = {\rm{ \;}} - \frac{b}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\)
Cách giải:
a) Ta có bảng giá trị sau:

\( \Rightarrow \) Đồ thị hàm số là đường cong parabol đi qua các điểm \(O{\mkern 1mu} \left( {0;0} \right);A\left( { - 2;4} \right);{\mkern 1mu} {\mkern 1mu} B\left( { - 1;1} \right);C\left( {1;1} \right);{\mkern 1mu} {\mkern 1mu} D\left( {2;4} \right)\)
Hệ số \(a = 1 > 0\)nên parabol có bề cong hướng lên. Đồ thị hàm số nhận Oy làm trục đối xứng.
Ta vẽ được đồ thị hàm số \(y = {x^2}\) như sau:
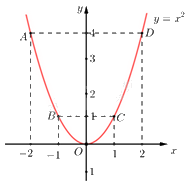
b) Xét phương trình hoành độ giao điểm của (P) và (d) ta được:
\({x^2} = 2mx - {m^2} + 1 \Leftrightarrow {x^2} - 2mx + {m^2} - 1 = 0\) (1)
Ta có: \(\Delta ' = {m^2} - \left( {{m^2} - 1} \right) = 1 > 0\) \(\forall m\)
Suy ra phương trình có hai nghiệm phân biệt với mọi \(m.\)
Khi đó theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}.{x_2} = {m^2} - 1\end{array} \right.\)
Từ giả thiết: \({x_1} < 2024 < {x_2} \Rightarrow \left\{ \begin{array}{l}{x_1} - 2024 < 0\\{x_2} - 2024 > 0\end{array} \right.\)
\(\begin{array}{l} \Rightarrow \left( {{x_1} - 2024} \right)\left( {{x_2} - 2024} \right) < 0\\ \Leftrightarrow {x_1}{x_2} - 2024\left( {{x_1} + {x_2}} \right) + 4096576 < 0\end{array}\)
\(\begin{array}{l} \Rightarrow {m^2} - 1 - 2024.2m + 4096576 < 0\\ \Leftrightarrow {m^2} - 4048m + 4096575 < 0\\ \Leftrightarrow {m^2} - 2025m - 2023m + 4096575 < 0\\ \Leftrightarrow m\left( {m - 2025} \right) - 2023\left( {m - 2025} \right) < 0\\ \Leftrightarrow \left( {m - 2025} \right)\left( {m - 2023} \right) < 0\end{array}\)
TH1: \(\left\{ \begin{array}{l}m - 2025 > 0\\m - 2023 < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 2025\\m < 2023\end{array} \right.\) (vô lí).
TH2: \(\left\{ \begin{array}{l}m - 2025 < 0\\m - 2023 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 2025\\m > 2023\end{array} \right. \Leftrightarrow 2023 < m < 2025\).
Mà m là số nguyên nên \(m = 2024\).
Vậy \(m = 2024\).
Câu 4 (TH):
Phương pháp:

Vì mỗi xe nhỏ chở ít hơn mỗi xe lớn là 12 người nên ta có phương trình: \(\frac{{210}}{{x - 2}} - \frac{{210}}{x} = 12\)
Cách giải:
Gọi x là số xe nhỏ đã thuê \(\left( {x > 2,x \in \mathbb{N}} \right)\).
Khi đó số xe lớn phải thuê là \(x - 2\) (xe)
Số người trên một xe nhỏ là: \(\frac{{210}}{x}\) (người).
Số người trên một xe lớn là: \(\frac{{210}}{{x - 2}}\) (người)
Vì mỗi xe nhỏ chở ít hơn mỗi xe lớn là 12 người nên ta có phương trình:
\(\begin{array}{l}\frac{{210}}{{x - 2}} - \frac{{210}}{x} = 12\\ \Leftrightarrow \frac{{210x}}{{x\left( {x - 2} \right)}} - \frac{{210\left( {x - 2} \right)}}{{x\left( {x - 2} \right)}} = 12\\ \Leftrightarrow \frac{{210x - 210\left( {x - 2} \right)}}{{x\left( {x - 2} \right)}} = 12\\ \Leftrightarrow \frac{{210x - 210x + 420}}{{x\left( {x - 2} \right)}} = 12\\ \Leftrightarrow \frac{{420}}{{x\left( {x - 2} \right)}} = 12\\ \Leftrightarrow 35 = x\left( {x - 2} \right)\\ \Leftrightarrow {x^2} - 2x - 35 = 0\\ \Leftrightarrow {x^2} - 7x + 5x - 35 = 0\\ \Leftrightarrow x\left( {x - 7} \right) + 5\left( {x - 7} \right) = 0\\ \Leftrightarrow \left( {x - 7} \right)\left( {x + 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 7\,\,\,\,\,\left( {tm} \right)\\x = - 5\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy số xe nhỏ đã thuê là 7 xe.
Câu 5 (VD):
Phương pháp:
- Gọi bán kính của đáy chai là x
- Vì khi lật ngược chai lại thì phần không chứa nước cũng là một hình trụ của có chiều cao 8m nên thể tích phần hình trụ không chứa nước đó là: \(8\pi {x^2}\).
- Từ đó tìm được phương trình \(450\pi - 10\pi {x^2} = 8\pi {x^2}\).
Cách giải:
Gọi bán kính của đáy chai là \(x{\mkern 1mu} \left( {cm,x > 0} \right)\)
Lượng nước trong chai là: \(10\pi {x^2}{\mkern 1mu} {\mkern 1mu} \left( {c{m^3}} \right)\).
Thể tích còn lại của chai là: \(450\pi {\rm{ \;}} - 10\pi {x^2}\)
Vì khi lật ngược chai lại thì phần không chứa nước cũng là một hình trụ của có chiều cao 8m nên thể tích phần hình trụ không chứa nước đó là: \(8\pi {x^2}\).
Như vậy ta có phương trình: \(450\pi {\rm{ \;}} - 10\pi {x^2} = 8\pi {x^2}\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow 18\pi {x^2} = 450\pi }\\{ \Leftrightarrow {x^2} = 25}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 5{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} (TM)}\\{x = {\rm{ \;}} - 5{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} (KTM)}\end{array}} \right.}\end{array}\)
Vậy bán kính đáy chai là 5cm.
Câu 6 (VD):
Phương pháp:
a) Tứ giác có tổng hai góc đối bằng \(180^\circ \) là tứ giác nội tiếp.
b) Chứng minh tam giác ABF và tam giác AEB đồng dạng từ đó suy ra \(A{B^2} = AE.AF\).
Cách giải:
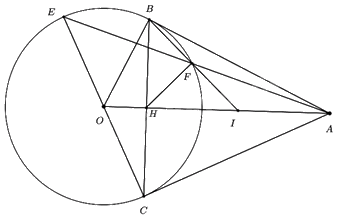
a) Do AB, AC là tiếp tuyến của (O) nên \(OB \bot AB,{\mkern 1mu} {\mkern 1mu} OC \bot AC \Rightarrow \angle ABO = \angle ACO = {90^0}\)
Xét tứ giác ABOC có \(\angle ABO + \angle ACO = {90^0} + {90^0} = {180^0}\)
Mà 2 góc này ở vị trí đối diện nên tứ giác ABOC nội tiếp (dhnb) (đpcm)
b) Xét tam giác ABF và tam giác AEB có:
\(\angle BAE\) chung
\(\angle ABF = \angle AEB\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BF).
$\Rightarrow \Delta ABF\backsim \Delta AEB\left( g.g \right)\Rightarrow \frac{AB}{AF}=\frac{AE}{AB}$ (cặp cạnh tương ứng tỉ lệ).
\( \Rightarrow A{B^2} = AE.AF\) (đpcm)
c) Ta có \(\angle IFA = \angle BFE\) (đối đỉnh),
\(\angle BFE = \angle BCE\) (hai góc nội tiếp cùng chắn cung BE)
\(\angle BCE = \angle OAB\) (hai góc nội tiếp cùng chắn cung OB)
\( \Rightarrow \angle IFA = \angle OAB = \angle IAB\).
Xét \(\Delta IAF\) và \(\Delta IBA\) có \(\angle IFA = \angle IAB{\mkern 1mu} {\mkern 1mu} \left( {cmt} \right)\) và \(\angle BIA\) chung
$\Rightarrow \Delta IAF\backsim \Delta IBA\left( g.g \right)\Rightarrow \frac{IA}{IB}=\frac{IF}{IA}$ (cặp cạnh tương ứng tỉ lệ).
\( \Rightarrow I{A^2} = IB.IF\) (1)
Ta có AB = AC (tính chất 2 tiếp tuyến cắt nhau) => A thuộc trung trực của BC.
OB = OC (cùng bằng bán kính) => O thuộc trung trực của BC.
=> OA là trung trực của BC \( \Rightarrow OA \bot BC\) tại H.
Xét \(\Delta ABO\) vuông tại B, đường cao BH nên \(A{B^2} = AH.AO\) (hệ thức lượng trong tam giác vuông)
Mà \(A{B^2} = AE.AF\) (chứng minh trên) nên suy ra \(AH.AO = AF.AE \Leftrightarrow \frac{{AH}}{{AE}} = \frac{{AF}}{{AO}}\).
Kết hợp với \(\angle EAO\) chung suy ra $\Delta AHF\backsim \Delta AEO\left( c.g.c \right)\Rightarrow \angle AHF=\angle AEO$ (hai góc tương ứng).
Mà \(\angle AEO = \angle FBC\) (cùng chắn cung CF)
\( \Rightarrow \angle AHF = \angle FBC\)\( \Rightarrow \angle IHF = \angle HBI\).
Mà \(\angle BIH\) chung nên suy ra $\Delta IHF\backsim \Delta IBH\left( g.g \right)\Rightarrow \frac{IH}{IB}=\frac{IF}{IH}$ (cặp cạnh tương ứng tỉ lệ).
\( \Rightarrow I{H^2} = IB.IF\) (2)
Từ (1) và (2) ta suy ra \(I{H^2} = I{A^2} \Rightarrow IH = IA\).
Chứng tỏ I là trung điểm của AH (đpcm).
Câu 7 (VDC):
Phương pháp:
Gọi độ dài cạnh của hình vuông đầu tiên là x từ đó tìm lần lượt diện tích của hình vuông đầu tiên, hình vuông thứ hai,…
Cách giải:
Gọi độ dài cạnh của hình vuông đầu tiên là x (x > 0)
Vậy diện tích của hình vuông đầu là \({x^2}\).
Khi đó cạnh của hình vuông thứ 2 có độ dài là: \(\sqrt {{{\left( {\frac{x}{2}} \right)}^2} + {{\left( {\frac{x}{2}} \right)}^2}} {\rm{ \;}} = \sqrt {\frac{{{x^2}}}{4} + \frac{{{x^2}}}{4}} {\rm{ \;}} = \sqrt {\frac{{{x^2}}}{2}} {\rm{ \;}} = \frac{x}{{\sqrt 2 }}\)
Vậy diện tích của hình vuông thứ 2 là \(\frac{{{x^2}}}{2}{\mkern 1mu} \left( {c{m^2}} \right)\).
Tương tự, ta có cạnh của hình vuông thứ 3 là \(\sqrt {{{\left( {\frac{x}{{2\sqrt 2 }}} \right)}^2} + {{\left( {\frac{x}{{2\sqrt 2 }}} \right)}^2}} {\rm{ \;}} = \sqrt {\frac{{{x^2}}}{8} + \frac{{{x^2}}}{8}} {\rm{ \;}} = \sqrt {\frac{{{x^2}}}{4}} {\rm{ \;}} = \frac{x}{2}\)
Vậy diện tích của hình vuông thứ 3 là \(\frac{{{x^2}}}{4}\)\(\left( {c{m^2}} \right)\).
…
Vậy diện tích hình vuông thứ n là \(\frac{{{x^2}}}{{{2^{n - 1}}}}\)\(\left( {c{m^2}} \right)\)
Vậy diện tích hình vuông thứ 7 là \(\frac{{{x^2}}}{{{2^{7 - 1}}}} = 32 \Leftrightarrow {x^2} = 2048\).
Vậy diện tích hình vuông thứ 5 là \(\frac{{{x^2}}}{{{2^{5 - 1}}}} = \frac{{2048}}{{{2^4}}} = 128\)\(\left( {c{m^2}} \right)\).
-----HẾT-----
Câu 1: Giải phương trình và hệ phương trình sau:
a) \({x^2} + 2x - 3 = 0\)
b) \(\left\{ {\begin{array}{*{20}{c}}{ - x + 3y = 5}\\{x + y = 3}\end{array}} \right.\)
Câu 2: Rút gọn các biểu thức sau:
a) \(A = \left( {\sqrt {27} {\rm{ \;}} - \sqrt {12} {\rm{ \;}} + \sqrt {48} } \right)\sqrt 3 \)
b) \(B = \left( {\frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} - 1}} - \frac{1}{{x - \sqrt x }}} \right):\frac{{\sqrt x {\rm{ \;}} + 1}}{{3\sqrt x }}\), với \(x > 0\) và \(x \ne 1\)
Câu 3: Cho hàm số \(y = {x^2}\) có đồ thị \(\left( P \right)\)
a) Vẽ đồ thị \(\left( P \right)\) trên mặt phẳng tọa độ \(Oxy\). b) Tìm giá trị nguyên của tham số \(m\) để đường thẳng \(\left( d \right):y = 2mx - {m^2} + 1\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ lần lượt là \({x_1},{x_2}\) thỏa mãn \({x_1} < 2024 < {x_2}\).
Câu 4: Một công ty dự định thuê một số xe lớn cùng loại để chở vừa hết 210 người đi du lịch Mũi Né. Nhưng thực tế, công ty lại thuê toàn bộ xe nhỏ hơn cùng loại. Biết rằng số xe nhỏ phải thuê nhiều hợ sồ xe lớn là 2 chiếc thì mới chờ vừa hết số người trên và mỗi xe nhỏ chở ít hơn mỗi xe lớn là 12 người. Tính số xe nhỏ đã thuê.
Câu 5: Một cái chai có chứa một lượng nước, phần chứa nước là hình trụ có chiều cao \(10\;{\rm{cm}}\), khi lật ngược chai lại thì phần không chứa nước cũng là một hình trụ có chiều cao \(8\;{\rm{cm}}\) (như hình vẽ bên). Biết thể tích của chai là \(450\pi {\rm{c}}{{\rm{m}}^3}\). Tính bán kính của đáy chai (giả sử độ dày của thành chai và đáy chai không đáng kể).

Câu 6: Cho đường tròn \(\left( O \right)\) và điểm \(A\) nằm bên ngoài đường tròn. Từ \(A\), vẽ hai tiếp tuyến \(AB,AC\) ( \(B,C\) là hai tiếp điểm).
a) Chứng minh tứ giác \(ABOC\) nội tiếp.
b) Vẽ đường kính \(CE\), nối \(AE\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(F\). Chứng minh \(A{B^2} = AE.AF\). c) Cho \(OA\) cắt \(BC\) tại \(H,BF\) cắt \(OA\) tại \(I\). Chứng minh \(I\) là trung điểm của \(AH\).
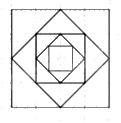
Câu 7: Từ hình vuông đầu tiên, bạn Hùng vẽ hình vuông thứ hai có các đỉnh là trung điểm của các cạnh hình vuông thứ nhất, vẽ tiếp hình vuông thứ ba có các đỉnh là trung điểm của các cạnh hình vuông thứ hai và cứ tiếp tục như vậy (xem hình minh họa bên). Giả sử hình vuông thứ bảy có diện tích bằng \(32(c{m^2})\). Tính diện tích hình vuông thứ năm.
-----HẾT-----
Câu 1 (TH):
Phương pháp:
a) Xét a + b + c từ đó suy ra hai nghiệm của phương trình.
b) Giải hệ phương trình bằng phương pháp thế.
Cách giải:
a) \({x^2} + 2x - 3 = 0\).
Vì \(a + b + c = 1 + 2 - 3 = 0\) nên phương trình có 2 nghiệm phân biệt là \({x_1} = 1\) và \({x_2} = \frac{c}{a} = - 3\)
Vậy phương trình có tập nghiệm là \(S = \left\{ {1; - 3} \right\}\).
b) \(\left\{ {\begin{array}{*{20}{c}}{ - x + 3y = 5}\\{x + y = 3}\end{array} \Leftrightarrow } \right.\left\{ {\begin{array}{*{20}{c}}{x = 3 - y}\\{4y = 8\,\,\,\,}\end{array} \Leftrightarrow } \right.\left\{ {\begin{array}{*{20}{c}}{x = 1}\\{y = 2}\end{array}} \right.\)
Vậy hệ phương trình có nghiệm duy nhất là \(\left( {x,y} \right) = \left( {1;2} \right)\).
Câu 2 (TH):
Phương pháp:
a) Khai căn và thực hiện phép tính.
b) Quy đồng và rút gọn.
Cách giải:
a) \(A = (\sqrt {27} {\rm{ \;}} - \sqrt {12} {\rm{ \;}} + \sqrt {48} )\sqrt 3 \).
\(\begin{array}{*{20}{l}}{A = (\sqrt {{3^2}.3} {\rm{ \;}} - \sqrt {{2^2}.3} {\rm{ \;}} + \sqrt {{4^2}.3} )\sqrt 3 }\\{A = (3\sqrt 3 {\rm{ \;}} - 2\sqrt 3 {\rm{ \;}} + 4\sqrt 3 )\sqrt 3 }\\{A = 5\sqrt 3 .\sqrt 3 }\\{A = 15.}\end{array}\)
Vậy \(A = 15\).
b) \(B = \left( {\frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} - 1}} - \frac{1}{{x - \sqrt x }}} \right):\frac{{\sqrt x {\rm{ \;}} + 1}}{{3\sqrt x }}\), với \(x > 0\) và \(x \ne 1\).
Với \(x > 0\) và \(x \ne 1\) ta có:
\(\begin{array}{l}B = \left( {\frac{{\sqrt x }}{{\sqrt x - 1}} - \frac{1}{{\sqrt x \left( {\sqrt x - 1} \right)}}} \right):\frac{{\sqrt x + 1}}{{3\sqrt x }}\\B = \left( {\frac{x}{{\sqrt x \left( {\sqrt x - 1} \right)}} - \frac{1}{{\sqrt x \left( {\sqrt x - 1} \right)}}} \right):\frac{{\sqrt x + 1}}{{3\sqrt x }}\end{array}\)
\(\begin{array}{l}B = \frac{{x - 1}}{{\sqrt x \left( {\sqrt x - 1} \right)}}:\frac{{\sqrt x + 1}}{{3\sqrt x }}\\B = \frac{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}{{\sqrt x \left( {\sqrt x - 1} \right)}}:\frac{{\sqrt x + 1}}{{3\sqrt x }}\\B = \frac{{\sqrt x + 1}}{{\sqrt x }}.\frac{{3\sqrt x }}{{\sqrt x + 1}} = 3\end{array}\)
Vậy với \(x > 0\) và \(x \ne 1\) thì \(B = 3\).
Câu 3 (VD):
Phương pháp:
a) Cho 5 điểm và vẽ parabol (P).
b) Xét phương trình hoành độ giao điểm, từ đó áp dụng hệ thức vi-et \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = {\rm{ \;}} - \frac{b}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\)
Cách giải:
a) Ta có bảng giá trị sau:

\( \Rightarrow \) Đồ thị hàm số là đường cong parabol đi qua các điểm \(O{\mkern 1mu} \left( {0;0} \right);A\left( { - 2;4} \right);{\mkern 1mu} {\mkern 1mu} B\left( { - 1;1} \right);C\left( {1;1} \right);{\mkern 1mu} {\mkern 1mu} D\left( {2;4} \right)\)
Hệ số \(a = 1 > 0\)nên parabol có bề cong hướng lên. Đồ thị hàm số nhận Oy làm trục đối xứng.
Ta vẽ được đồ thị hàm số \(y = {x^2}\) như sau:
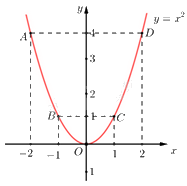
b) Xét phương trình hoành độ giao điểm của (P) và (d) ta được:
\({x^2} = 2mx - {m^2} + 1 \Leftrightarrow {x^2} - 2mx + {m^2} - 1 = 0\) (1)
Ta có: \(\Delta ' = {m^2} - \left( {{m^2} - 1} \right) = 1 > 0\) \(\forall m\)
Suy ra phương trình có hai nghiệm phân biệt với mọi \(m.\)
Khi đó theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}.{x_2} = {m^2} - 1\end{array} \right.\)
Từ giả thiết: \({x_1} < 2024 < {x_2} \Rightarrow \left\{ \begin{array}{l}{x_1} - 2024 < 0\\{x_2} - 2024 > 0\end{array} \right.\)
\(\begin{array}{l} \Rightarrow \left( {{x_1} - 2024} \right)\left( {{x_2} - 2024} \right) < 0\\ \Leftrightarrow {x_1}{x_2} - 2024\left( {{x_1} + {x_2}} \right) + 4096576 < 0\end{array}\)
\(\begin{array}{l} \Rightarrow {m^2} - 1 - 2024.2m + 4096576 < 0\\ \Leftrightarrow {m^2} - 4048m + 4096575 < 0\\ \Leftrightarrow {m^2} - 2025m - 2023m + 4096575 < 0\\ \Leftrightarrow m\left( {m - 2025} \right) - 2023\left( {m - 2025} \right) < 0\\ \Leftrightarrow \left( {m - 2025} \right)\left( {m - 2023} \right) < 0\end{array}\)
TH1: \(\left\{ \begin{array}{l}m - 2025 > 0\\m - 2023 < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 2025\\m < 2023\end{array} \right.\) (vô lí).
TH2: \(\left\{ \begin{array}{l}m - 2025 < 0\\m - 2023 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 2025\\m > 2023\end{array} \right. \Leftrightarrow 2023 < m < 2025\).
Mà m là số nguyên nên \(m = 2024\).
Vậy \(m = 2024\).
Câu 4 (TH):
Phương pháp:

Vì mỗi xe nhỏ chở ít hơn mỗi xe lớn là 12 người nên ta có phương trình: \(\frac{{210}}{{x - 2}} - \frac{{210}}{x} = 12\)
Cách giải:
Gọi x là số xe nhỏ đã thuê \(\left( {x > 2,x \in \mathbb{N}} \right)\).
Khi đó số xe lớn phải thuê là \(x - 2\) (xe)
Số người trên một xe nhỏ là: \(\frac{{210}}{x}\) (người).
Số người trên một xe lớn là: \(\frac{{210}}{{x - 2}}\) (người)
Vì mỗi xe nhỏ chở ít hơn mỗi xe lớn là 12 người nên ta có phương trình:
\(\begin{array}{l}\frac{{210}}{{x - 2}} - \frac{{210}}{x} = 12\\ \Leftrightarrow \frac{{210x}}{{x\left( {x - 2} \right)}} - \frac{{210\left( {x - 2} \right)}}{{x\left( {x - 2} \right)}} = 12\\ \Leftrightarrow \frac{{210x - 210\left( {x - 2} \right)}}{{x\left( {x - 2} \right)}} = 12\\ \Leftrightarrow \frac{{210x - 210x + 420}}{{x\left( {x - 2} \right)}} = 12\\ \Leftrightarrow \frac{{420}}{{x\left( {x - 2} \right)}} = 12\\ \Leftrightarrow 35 = x\left( {x - 2} \right)\\ \Leftrightarrow {x^2} - 2x - 35 = 0\\ \Leftrightarrow {x^2} - 7x + 5x - 35 = 0\\ \Leftrightarrow x\left( {x - 7} \right) + 5\left( {x - 7} \right) = 0\\ \Leftrightarrow \left( {x - 7} \right)\left( {x + 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 7\,\,\,\,\,\left( {tm} \right)\\x = - 5\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy số xe nhỏ đã thuê là 7 xe.
Câu 5 (VD):
Phương pháp:
- Gọi bán kính của đáy chai là x
- Vì khi lật ngược chai lại thì phần không chứa nước cũng là một hình trụ của có chiều cao 8m nên thể tích phần hình trụ không chứa nước đó là: \(8\pi {x^2}\).
- Từ đó tìm được phương trình \(450\pi - 10\pi {x^2} = 8\pi {x^2}\).
Cách giải:
Gọi bán kính của đáy chai là \(x{\mkern 1mu} \left( {cm,x > 0} \right)\)
Lượng nước trong chai là: \(10\pi {x^2}{\mkern 1mu} {\mkern 1mu} \left( {c{m^3}} \right)\).
Thể tích còn lại của chai là: \(450\pi {\rm{ \;}} - 10\pi {x^2}\)
Vì khi lật ngược chai lại thì phần không chứa nước cũng là một hình trụ của có chiều cao 8m nên thể tích phần hình trụ không chứa nước đó là: \(8\pi {x^2}\).
Như vậy ta có phương trình: \(450\pi {\rm{ \;}} - 10\pi {x^2} = 8\pi {x^2}\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow 18\pi {x^2} = 450\pi }\\{ \Leftrightarrow {x^2} = 25}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 5{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} (TM)}\\{x = {\rm{ \;}} - 5{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} (KTM)}\end{array}} \right.}\end{array}\)
Vậy bán kính đáy chai là 5cm.
Câu 6 (VD):
Phương pháp:
a) Tứ giác có tổng hai góc đối bằng \(180^\circ \) là tứ giác nội tiếp.
b) Chứng minh tam giác ABF và tam giác AEB đồng dạng từ đó suy ra \(A{B^2} = AE.AF\).
Cách giải:
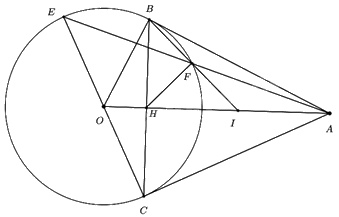
a) Do AB, AC là tiếp tuyến của (O) nên \(OB \bot AB,{\mkern 1mu} {\mkern 1mu} OC \bot AC \Rightarrow \angle ABO = \angle ACO = {90^0}\)
Xét tứ giác ABOC có \(\angle ABO + \angle ACO = {90^0} + {90^0} = {180^0}\)
Mà 2 góc này ở vị trí đối diện nên tứ giác ABOC nội tiếp (dhnb) (đpcm)
b) Xét tam giác ABF và tam giác AEB có:
\(\angle BAE\) chung
\(\angle ABF = \angle AEB\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BF).
$\Rightarrow \Delta ABF\backsim \Delta AEB\left( g.g \right)\Rightarrow \frac{AB}{AF}=\frac{AE}{AB}$ (cặp cạnh tương ứng tỉ lệ).
\( \Rightarrow A{B^2} = AE.AF\) (đpcm)
c) Ta có \(\angle IFA = \angle BFE\) (đối đỉnh),
\(\angle BFE = \angle BCE\) (hai góc nội tiếp cùng chắn cung BE)
\(\angle BCE = \angle OAB\) (hai góc nội tiếp cùng chắn cung OB)
\( \Rightarrow \angle IFA = \angle OAB = \angle IAB\).
Xét \(\Delta IAF\) và \(\Delta IBA\) có \(\angle IFA = \angle IAB{\mkern 1mu} {\mkern 1mu} \left( {cmt} \right)\) và \(\angle BIA\) chung
$\Rightarrow \Delta IAF\backsim \Delta IBA\left( g.g \right)\Rightarrow \frac{IA}{IB}=\frac{IF}{IA}$ (cặp cạnh tương ứng tỉ lệ).
\( \Rightarrow I{A^2} = IB.IF\) (1)
Ta có AB = AC (tính chất 2 tiếp tuyến cắt nhau) => A thuộc trung trực của BC.
OB = OC (cùng bằng bán kính) => O thuộc trung trực của BC.
=> OA là trung trực của BC \( \Rightarrow OA \bot BC\) tại H.
Xét \(\Delta ABO\) vuông tại B, đường cao BH nên \(A{B^2} = AH.AO\) (hệ thức lượng trong tam giác vuông)
Mà \(A{B^2} = AE.AF\) (chứng minh trên) nên suy ra \(AH.AO = AF.AE \Leftrightarrow \frac{{AH}}{{AE}} = \frac{{AF}}{{AO}}\).
Kết hợp với \(\angle EAO\) chung suy ra $\Delta AHF\backsim \Delta AEO\left( c.g.c \right)\Rightarrow \angle AHF=\angle AEO$ (hai góc tương ứng).
Mà \(\angle AEO = \angle FBC\) (cùng chắn cung CF)
\( \Rightarrow \angle AHF = \angle FBC\)\( \Rightarrow \angle IHF = \angle HBI\).
Mà \(\angle BIH\) chung nên suy ra $\Delta IHF\backsim \Delta IBH\left( g.g \right)\Rightarrow \frac{IH}{IB}=\frac{IF}{IH}$ (cặp cạnh tương ứng tỉ lệ).
\( \Rightarrow I{H^2} = IB.IF\) (2)
Từ (1) và (2) ta suy ra \(I{H^2} = I{A^2} \Rightarrow IH = IA\).
Chứng tỏ I là trung điểm của AH (đpcm).
Câu 7 (VDC):
Phương pháp:
Gọi độ dài cạnh của hình vuông đầu tiên là x từ đó tìm lần lượt diện tích của hình vuông đầu tiên, hình vuông thứ hai,…
Cách giải:
Gọi độ dài cạnh của hình vuông đầu tiên là x (x > 0)
Vậy diện tích của hình vuông đầu là \({x^2}\).
Khi đó cạnh của hình vuông thứ 2 có độ dài là: \(\sqrt {{{\left( {\frac{x}{2}} \right)}^2} + {{\left( {\frac{x}{2}} \right)}^2}} {\rm{ \;}} = \sqrt {\frac{{{x^2}}}{4} + \frac{{{x^2}}}{4}} {\rm{ \;}} = \sqrt {\frac{{{x^2}}}{2}} {\rm{ \;}} = \frac{x}{{\sqrt 2 }}\)
Vậy diện tích của hình vuông thứ 2 là \(\frac{{{x^2}}}{2}{\mkern 1mu} \left( {c{m^2}} \right)\).
Tương tự, ta có cạnh của hình vuông thứ 3 là \(\sqrt {{{\left( {\frac{x}{{2\sqrt 2 }}} \right)}^2} + {{\left( {\frac{x}{{2\sqrt 2 }}} \right)}^2}} {\rm{ \;}} = \sqrt {\frac{{{x^2}}}{8} + \frac{{{x^2}}}{8}} {\rm{ \;}} = \sqrt {\frac{{{x^2}}}{4}} {\rm{ \;}} = \frac{x}{2}\)
Vậy diện tích của hình vuông thứ 3 là \(\frac{{{x^2}}}{4}\)\(\left( {c{m^2}} \right)\).
…
Vậy diện tích hình vuông thứ n là \(\frac{{{x^2}}}{{{2^{n - 1}}}}\)\(\left( {c{m^2}} \right)\)
Vậy diện tích hình vuông thứ 7 là \(\frac{{{x^2}}}{{{2^{7 - 1}}}} = 32 \Leftrightarrow {x^2} = 2048\).
Vậy diện tích hình vuông thứ 5 là \(\frac{{{x^2}}}{{{2^{5 - 1}}}} = \frac{{2048}}{{{2^4}}} = 128\)\(\left( {c{m^2}} \right)\).
-----HẾT-----
Kỳ thi tuyển sinh vào lớp 10 môn Toán Bình Thuận năm 2023 là một bước quan trọng trong quá trình học tập của các em học sinh. Đề thi thường bao gồm các dạng bài tập khác nhau, đòi hỏi học sinh phải nắm vững kiến thức cơ bản và kỹ năng giải toán linh hoạt. Năm 2023, đề thi tiếp tục đánh giá khả năng vận dụng kiến thức vào thực tế, khả năng tư duy logic và kỹ năng tính toán của học sinh.
Cấu trúc đề thi thường bao gồm các phần chính sau:
Dưới đây là một số dạng bài tập thường gặp trong đề thi vào 10 môn Toán Bình Thuận năm 2023:
Để ôn thi vào 10 môn Toán Bình Thuận năm 2023 hiệu quả, các em học sinh cần:
Ngoài bộ đề thi vào 10 môn Toán Bình Thuận năm 2023 mà giaitoan.edu.vn cung cấp, các em học sinh có thể tham khảo thêm các tài liệu ôn thi khác như:
Chúc các em học sinh ôn thi tốt và đạt kết quả cao trong kỳ thi tuyển sinh vào lớp 10 môn Toán Bình Thuận năm 2023! Hãy nhớ rằng, sự chuẩn bị kỹ lưỡng và tinh thần tự tin là chìa khóa thành công.
| Năm | Điểm chuẩn |
|---|---|
| 2020 | 8.0 |
| 2021 | 8.5 |
| 2022 | 9.0 |
| Lưu ý: Điểm chuẩn có thể thay đổi theo từng năm. | |