Chào mừng bạn đến với bài kiểm tra năng lực môn Toán - Đề số 3, được thiết kế dành riêng cho các em học sinh đang chuẩn bị bước vào kỳ thi tuyển sinh lớp 10. Đề thi này không chỉ giúp các em làm quen với cấu trúc đề thi mà còn rèn luyện kỹ năng giải quyết các bài toán một cách nhanh chóng và chính xác.
Giaitoan.edu.vn cung cấp đề thi thử đa dạng, bám sát cấu trúc đề thi chính thức, cùng với lời giải chi tiết, giúp các em tự tin đối mặt với kỳ thi quan trọng này.
Đề thi vào lớp 10 môn Toán - Đề số 3 có đáp án và lời giải chi tiết
Đề bài
Câu 1. (2,0 điểm)
1. Tính giá trị của các biểu thức
\(M = \sqrt {36} + \sqrt {25} \)
\(N = \sqrt {{{\left( {\sqrt 5 - 1} \right)}^2}} - \sqrt 5 \)
2. Cho biểu thức \(P = 1 + \dfrac{{x - \sqrt x }}{{\sqrt x - 1}},\) với \(x \ge 0\) và \(x \ne 1\)
a) Rút gọn biểu thức P
b) Tìm giá trị của x, biết P > 3
Câu 2. (2 điểm)
1) Cho parabol \(\left( P \right):\;y = {x^2}\) và đường thẳng \(\left( d \right):\;y = - x + 2.\)
a) Vẽ \(\left( d \right)\) và \(\left( P \right)\) trên cùng một mặt phẳng tọa độ Oxy.
b) Tìm tọa độ giao điểm của parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) bằng phép tính.
2) Không sử dụng máy tính, giải hệ phương trình sau: \(\left\{ \begin{array}{l}3x + y = 5\\2x - y = 10\end{array} \right..\)
Câu 3. (2,5 điểm)
1) Cho phương trình \({x^2} - 2mx + 2m - 1 = 0\) (m là tham số) (1)
a) Giải phương trình (1) với \(m = 2.\)
b) Tìm \(m\) để phương trình (1) có hai nghiệm \({x_1},\;{x_2}\) sao cho: \(\left( {x_1^2 - 2m{x_1} + 3} \right)\left( {x_2^2 - 2m{x_2} - 2} \right) = 50.\)
2) Quãng đường AB dài 50 km. Hai xe máy khởi hành cùng một lúc từ A đến B. Vận tốc xe thứ nhất lớn hơn vận tốc xe thứ hai 10 km/h, nên xe thứ nhất đến B trước xe thứ hai 15 phút. Tính vận tốc của mỗi xe.
Câu 4. (1,0 điểm):
Cho tam giác ABC vuông tại A, đường cao AH \(\left( {H \in BC} \right)\) . Biết AC = 8cm và BC = 10 cm. Tính độ dài AB, BH, CH và AH.
Câu 5. (2,5 điểm)
Cho đường tròn tâm (O), từ điểm M ở bên ngoài đường tròn (O) kẻ các tiếp tuyến MA, MB (A, B là các tiếp điểm), kẻ cát tuyến MCD không đi qua tâm O (C nằm giữa M và D; O và B nằm về hai phía so với cát tuyến MCD).
a) Chứng minh tứ giác MAOB nội tiếp.
b) Chứng minh \(M{B^2} = MC.MD\)
c) Gọi H là giao điểm của AB và OM. Chứng minh AB là phân giác của \(\widehat {CHD}\).
Lời giải chi tiết
Câu 1.
1. Tính giá trị của các biểu thức
\(M = \sqrt {36} + \sqrt {25} \)
\(N = \sqrt {{{\left( {\sqrt 5 - 1} \right)}^2}} - \sqrt 5 \)
Ta có:
\(M = \sqrt {36} + \sqrt {25} \)
\(\;\;\;\;\;= \sqrt {{6^2}} + \sqrt {{5^2}} = 6 + 5 = 11\)
\(N = \sqrt {{{\left( {\sqrt 5 - 1} \right)}^2}} - \sqrt 5 \)
\(\;\;\;\;\;= \left| {\sqrt 5 - 1} \right| - \sqrt 5\)
\(\;\;\;\;\; = \sqrt 5 - 1 - \sqrt 5 \)
\(\;\;\;\;\;= - 1\,\,\left( {Do\,\sqrt 5 - 1 > 0\,\,} \right)\)
2. Cho biểu thức \(P = 1 + \dfrac{{x - \sqrt x }}{{\sqrt x - 1}},\) với \(x \ge 0\) và \(x \ne 1\)
a) Rút gọn biểu thức P
Với \(x \ge 0\) và \(x \ne 1\) ta có:
\(\begin{array}{l}P = 1 + \dfrac{{x - \sqrt x }}{{\sqrt x - 1}}\\\,\,\,\,\, = 1 + \dfrac{{\sqrt x \left( {\sqrt x - 1} \right)}}{{\sqrt x - 1}}\\\,\,\,\,\, = 1 + \sqrt x \end{array}\)
b) Tìm giá trị của x, biết P > 3
\(P > 3 \Leftrightarrow 1 + \sqrt x > 3 \Leftrightarrow \sqrt x > 2 \Leftrightarrow x > 4\)
Kết hợp với điều kiện: \(x \ge 0\) và \(x \ne 1\) ta được \(x > 4\)
Vậy với \(x > 4\) thì \(P > 3\)
Câu 2:
1) Cho parabol \(\left( P \right):\;\;y = {x^2}\) và đường thẳng \(\left( d \right):\;\;y = - x + 2.\)
a) Vẽ \(\left( d \right)\) và \(\left( P \right)\) trên cùng một mặt phẳng tọa độ Oxy.
+) Vẽ đồ thị hàm số: \(\left( d \right):\;\;y = - x + 2.\)
\(x\) | \(0\) | \(2\) |
\(y = - x + 2\) | \(2\) | \(0\) |
+) Vẽ đồ thị hàm số: \(\left( P \right):\;\;y = {x^2}.\)
\(x\) | \( - 2\) | \( - 1\) | \(0\) | \(1\) | \(2\) |
\(y = {x^2}\) | \(4\) | \(1\) | \(0\) | \(1\) | \(4\) |
Đồ thị hàm số:
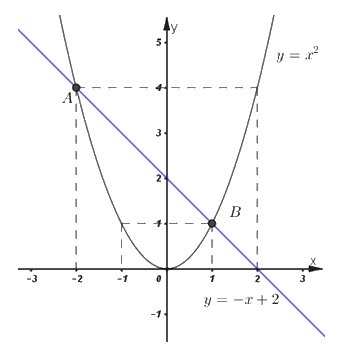
b) Tìm tọa độ giao điểm của parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) bằng phép tính.
Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình hoành độ giao điểm.
Ta có phương trình hoành độ giao điểm của hai đồ thị là:
\(\begin{array}{l}\;\;\; - x + 2 = {x^2}\\ \Leftrightarrow {x^2} + x - 2 = 0\\ \Leftrightarrow {x^2} + 2x - x - 2 = 0\\ \Leftrightarrow x\left( {x + 2} \right) - \left( {x + 2} \right) = 0\\ \Leftrightarrow \left( {x + 2} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 2 = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 2 \Rightarrow y = 4\\x = 1 \Rightarrow y = 1\end{array} \right..\end{array}\)
Vậy hai đồ thị cắt nhau tại hai điểm phân biệt \(A\left( { - 2;\;4} \right)\) và \(B\left( {1;\;1} \right).\)
2) Không sử dụng máy tính, giải hệ phương trình sau: \(\left\{ \begin{array}{l}3x + y = 5\\2x - y = 10\end{array} \right..\)
\(\left\{ \begin{array}{l}3x + y = 5\\2x - y = 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2x - 10\\5x = 15\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 2.3 - 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = - 4\end{array} \right..\)
Vậy hệ phương trình có nghiệm duy nhất: \(\left( {x;\;y} \right) = \left( {3; - 4} \right).\)
Câu 3:
1) Cho phương trình \({x^2} - 2mx + 2m - 1 = 0\) (m là tham số) (1)
a) Giải phương trình (1) với \(m = 2.\)
Thay \(m = 2\) vào phương trình \(\left( 1 \right)\) ta được:
\(\begin{array}{l}\left( 1 \right) \Leftrightarrow {x^2} - 4x + 3 = 0\\ \Leftrightarrow {x^2} - 3x - x + 3 = 0\\ \Leftrightarrow x\left( {x - 3} \right) - \left( {x - 3} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right..\end{array}\)
Vậy với \(m = 2\) thì phương trình có tập nghiệm \(S = \left\{ {1;\;3} \right\}.\)
b) Tìm \(m\) để phương trình (1) có hai nghiệm \({x_1},\;{x_2}\) sao cho: \(\left( {x_1^2 - 2m{x_1} + 3} \right)\left( {x_2^2 - 2m{x_2} - 2} \right) = 50.\)
Phương trình (1) có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0\)
\(\begin{array}{l} \Leftrightarrow {m^2} - 2m + 1 > 0\\ \Leftrightarrow {\left( {m - 1} \right)^2} > 0\\ \Leftrightarrow m - 1 \ne 0\\ \Leftrightarrow m \ne 1.\end{array}\)
Với \(m \ne 1\) thì phương trình (1) có hai nghiệm phân biệt \({x_1},\;\;{x_2}.\)
Khi đó ta có: \(\left\{ \begin{array}{l}x_1^2 - 2m{x_1} + 2m - 1 = 0\\x_1^2 - 2m{x_1} + 2m - 1 = 0\end{array} \right..\)
Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}{x_2} = 2m - 1\end{array} \right..\)
Theo đề bài ta có: \(\left( {x_1^2 - 2m{x_1} + 3} \right)\left( {x_2^2 - 2m{x_2} - 2} \right) = 50\)
\(\begin{array}{l} \Leftrightarrow \left( {x_1^2 - 2m{x_1} + 2m - 1 - 2m + 4} \right)\left( {x_2^2 - 2m{x_2} + 2m - 1 - 2m - 1} \right) = 50\\ \Leftrightarrow \left( {4 - 2m} \right)\left( { - 2m - 1} \right) = 50\\ \Leftrightarrow \left( {2m - 4} \right)\left( {2m + 1} \right) = 50\\ \Leftrightarrow \left( {m - 2} \right)\left( {2m + 1} \right) = 25\\ \Leftrightarrow 2{m^2} + m - 4m - 2 = 25\\ \Leftrightarrow 2{m^2} - 3m - 27 = 0\\ \Leftrightarrow 2{m^2} - 9m + 6m - 27 = 0\\ \Leftrightarrow m\left( {2m - 9} \right) + 3\left( {2m - 9} \right) = 0\\ \Leftrightarrow \left( {2m - 9} \right)\left( {m + 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2m - 9 = 0\\m + 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = \dfrac{9}{2}\;\;\left( {tm} \right)\\m = - 3\;\;\left( {tm} \right)\end{array} \right..\end{array}\)
Vậy \(m = \dfrac{9}{2}\) và \(m = - 3\) thỏa mãn điều kiện bài toán.
2) Quãng đường AB dài 50 km. Hai xe máy khởi hành cùng một lúc từ A đến B. Vận tốc xe thứ nhất lớn hơn vận tốc xe thứ hai 10 km/h, nên xe thứ nhất đến B trước xe thứ hai 15 phút. Tính vận tốc của mỗi xe.
Gọi vận tốc của xe thứ nhất là \(x\;\left( {km/h} \right)\;\;\left( {x > 10} \right).\)
\( \Rightarrow \) Vận tốc của xe thứ hai là: \(x - 10\;\;\left( {km/h} \right).\)
Thời gian xe thứ nhất đi từ A đến B là \(\dfrac{{50}}{x}\,\,\left( h \right)\) ;
Thời gian xe thứ hai đi từ A đến B là: \(\dfrac{{50}}{{x - 10}}\;\;\left( h \right).\)
Vì xe thứ nhất đến B trước xe thứ hai 15 phút = \(\dfrac{1}{4}h\) nên ta có phương trình: \(\dfrac{{50}}{{x - 10}} - \dfrac{{50}}{x} = \dfrac{1}{4}\)
\(\begin{array}{l} \Leftrightarrow 4.50.x - 4.50\left( {x - 10} \right) = x\left( {x - 10} \right)\\ \Leftrightarrow 200x - 200x + 2000 = {x^2} - 10x\\ \Leftrightarrow {x^2} - 10x - 2000 = 0\\ \Leftrightarrow {x^2} - 50x + 40x - 2000 = 0\\ \Leftrightarrow x\left( {x - 50} \right) + 40\left( {x - 50} \right) = 0\\ \Leftrightarrow \left( {x - 50} \right)\left( {x + 40} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 50 = 0\\x + 40 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 50\;\;\left( {tm} \right)\\x = - 40\;\;\left( {ktm} \right)\end{array} \right..\end{array}\)
Vậy vận tốc của xe thứ nhất là \(50\;km/h\) và vận tốc xe thứ hai là \(50 - 10 = 40\;km/h.\)
Câu 4.
Cho tam giác ABC vuông tại A, đường cao AH \(\left( {H \in BC} \right)\) . Biết AC = 8cm và BC = 10 cm. Tính độ dài AB, BH, CH và AH.
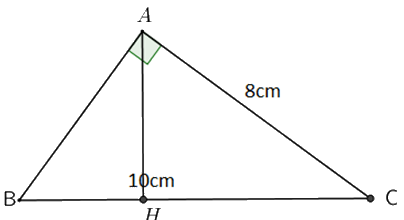
+) Tính AB
Áp dụng định lý Pytago trong tam giác vuông ABC vuông tại A ta có: \(\begin{array}{l}A{B^2} + A{C^2} = B{C^2}\\ \Rightarrow A{B^2} = B{C^2} - A{C^2} = {10^2} - {8^2} = 36\\ \Rightarrow AB = 6\left( {cm} \right)\end{array}\)
+) Tính BH
Áp dụng hệ thức lượng trong tam giác vuông ABC có: \(A{B^2} = BH.BC\)
\(\Rightarrow BH = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{{6^2}}}{{10}} = 3,6\left( {cm} \right)\)
+) Tính CH
Áp dụng hệ thức lượng trong tam giác vuông ABC có: \(A{C^2} = CH.BC \)
\(\Rightarrow CH = \dfrac{{A{C^2}}}{{BC}} = \dfrac{{{8^2}}}{{10}} = 6,4\left( {cm} \right)\)
+) Tính AH
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có: \(A{H^2} = BH.CH = 3,6.6,4 = 23,04\) \( \Rightarrow AH = 4,8\left( {cm} \right)\)
Câu 5.
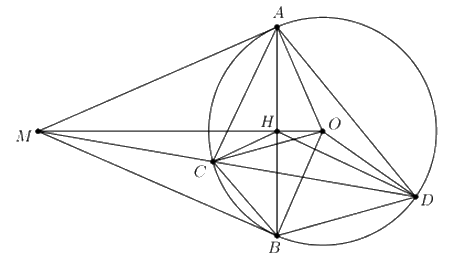
a) Chứng minh tứ giác MAOB nội tiếp.
Ta có \(\widehat {OAM} = \widehat {OBM} = {90^0}\) (Do MA, MB là tiếp tuyến của đường tròn (O))
Xét tứ giác OAMB có: \(\widehat {OAM} + \widehat {OBM} = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác OAMB là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
b) Chứng minh \(M{B^2} = MC.MD\)
Xét tam giác MBC và tam giác MDB có:
\(\widehat {BMD}\) chung;
\(\widehat {MBC} = \widehat {MDB}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung BC)
\( \Rightarrow \Delta MBC \sim \Delta MDB\,\,\left( {g.g} \right) \)
\(\Rightarrow \dfrac{{MB}}{{MD}} = \dfrac{{MC}}{{MB}}\)
\(\Rightarrow M{B^2} = MC.MD\)
c) Gọi H là giao điểm của AB và OM. Chứng minh AB là phân giác của \(\widehat {CHD}\).
Ta có \(MA = MB\) (tính chất hai tiếp tuyến cắt nhau) \( \Rightarrow M\) thuộc trung trực của AB;
\(OA = OB\,\,\left( { = R} \right) \Rightarrow O\) thuộc trung trực của AB;
\( \Rightarrow OM\)là trung trực của AB \( \Rightarrow OM \bot AB\)
Xét tam giác vuông OMB có \(M{B^2} = MH.MO\) (hệ thức lượng trong tam giác vuông).
Mà \(M{B^2} = MC.MD\,\,\left( {cmt} \right) \)
\(\Rightarrow MH.MO = MC.MD\)
\(\Rightarrow \dfrac{{MC}}{{MO}} = \dfrac{{MH}}{{MD}}\)
Xét tam giác MCH và MOD có :
\(\widehat {OMD}\) chung ;
\(\dfrac{{MC}}{{MO}} = \dfrac{{MH}}{{MD}}\,\,\,\left( {cmt} \right)\); \(\Delta MCH \sim \Delta MOD\,\,\left( {c.g.c} \right) \)
\(\Rightarrow \widehat {MHC} = \widehat {MDO}\)
(hai góc tương ứng) (1).
Mà \(\widehat {MHC} + \widehat {OHC} = {180^0}\) \( \Rightarrow \widehat {MDO} + \widehat {OHC} = {180^0} \Rightarrow \) Tứ giác OHCD là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
\( \Rightarrow \widehat {OHD} = \widehat {OCD}\) (2) (hai góc nội tiếp cùng chắn cung OD).
Mà \(\widehat {OCD} = \widehat {ODC} = \widehat {MDO}\) (3) (tam giác OCD cân tại O);
Từ (1), (2) và (3) \( \Rightarrow \widehat {MHC} = \widehat {OHD}\).
\( \Rightarrow {90^0} - \widehat {MHC} = {90^0} - \widehat {OHD} \) \(\Rightarrow \widehat {CHB} = \widehat {BHD}\).
Vậy HB là tia phân giác của góc CHD hay AB là tia phân giác của góc CHD.
Đề thi vào lớp 10 môn Toán đóng vai trò quan trọng trong việc xét tuyển vào các trường THPT chuyên và các trường có yêu cầu cao về môn Toán. Đề số 3 trong bộ đề thi thử của giaitoan.edu.vn được xây dựng dựa trên phân tích cấu trúc đề thi các năm trước, đảm bảo tính sát thực và giúp học sinh làm quen với các dạng bài thường gặp.
Đề số 3 thường bao gồm các dạng bài sau:
Để giúp học sinh hiểu rõ hơn về đề thi, chúng ta sẽ phân tích chi tiết từng câu hỏi trong Đề số 3:
Câu hỏi này yêu cầu học sinh vận dụng kiến thức về phương trình bậc hai, bao gồm việc xác định hệ số, tính delta, và tìm nghiệm của phương trình. Để giải quyết câu hỏi này, học sinh cần nắm vững các công thức và kỹ năng giải phương trình bậc hai.
Câu hỏi này yêu cầu học sinh chứng minh hai tam giác đồng dạng dựa trên các tiêu chí đồng dạng tam giác. Học sinh cần nắm vững các định lý về tam giác đồng dạng và áp dụng chúng một cách linh hoạt.
Câu hỏi này yêu cầu học sinh tìm ước chung lớn nhất (ƯCLN) và bội chung nhỏ nhất (BCNN) của hai hoặc nhiều số. Học sinh cần nắm vững các phương pháp tìm ƯCLN và BCNN, chẳng hạn như phân tích ra thừa số nguyên tố.
Giaitoan.edu.vn cung cấp lời giải chi tiết cho từng câu hỏi trong Đề số 3, giúp học sinh hiểu rõ phương pháp giải và tự tin áp dụng vào các bài toán tương tự. Lời giải mẫu được trình bày một cách rõ ràng, dễ hiểu, kèm theo các chú thích và giải thích cần thiết.
Để đạt kết quả tốt nhất trong kỳ thi vào lớp 10 môn Toán, học sinh cần có những mẹo và kinh nghiệm làm bài thi hiệu quả:
Để nâng cao kỹ năng giải toán và làm quen với các dạng bài khác nhau, học sinh nên luyện tập thường xuyên với các đề thi thử khác tại giaitoan.edu.vn. Việc luyện tập thường xuyên sẽ giúp học sinh tự tin hơn và đạt kết quả tốt nhất trong kỳ thi vào lớp 10 môn Toán.
Trước khi bắt đầu luyện đề, học sinh cần ôn tập kỹ lưỡng kiến thức nền tảng môn Toán lớp 9. Việc nắm vững kiến thức nền tảng sẽ giúp học sinh hiểu rõ hơn về các khái niệm và công thức, từ đó giải quyết các bài toán một cách dễ dàng hơn.
Giaitoan.edu.vn cung cấp nhiều công cụ hỗ trợ học tập online, chẳng hạn như máy tính bỏ túi, công cụ vẽ hình, và các bài giảng video. Học sinh có thể sử dụng các công cụ này để học tập và luyện tập một cách hiệu quả hơn.
Các giáo viên có kinh nghiệm tại giaitoan.edu.vn chia sẻ những lời khuyên hữu ích về cách ôn thi vào lớp 10 môn Toán, giúp học sinh tránh những sai lầm thường gặp và đạt kết quả tốt nhất.
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi vào lớp 10 môn Toán!