Giaitoan.edu.vn xin giới thiệu Đề thi vào 10 môn Toán Quảng Bình năm 2021 (đề số 1) chính thức. Đây là đề thi quan trọng giúp các em học sinh làm quen với cấu trúc và độ khó của kỳ thi tuyển sinh lớp 10 tại Quảng Bình.
Đề thi bao gồm các dạng bài tập khác nhau, từ đại số đến hình học, đòi hỏi học sinh phải có kiến thức vững chắc và kỹ năng giải quyết vấn đề tốt. Chúng tôi cung cấp kèm đáp án chi tiết để các em có thể tự đánh giá và cải thiện kết quả học tập.
Câu 1 (2,0 điểm): Rút gọn các biểu thức sau:
Câu 1 (2,0 điểm):
Rút gọn các biểu thức sau:
a) \(A = \sqrt 8 - \sqrt {32} + \sqrt {50} \)
b) \(B = \left( {3 + \dfrac{{a + \sqrt a }}{{\sqrt a + 1}}} \right).\left( {3 - \dfrac{{a - \sqrt a }}{{\sqrt a - 1}}} \right)\) (với \(a \ge 0,\,\,a \ne 1\)).
Câu 2 (1,5 điểm):
a) Tìm tất cả các giá trị của \(m\) để hàm số \(y = \left( {m - 1} \right)x + 2\) đồng biến trên \(\mathbb{R}\).
b) Giải hệ phương trình \(\left\{ \begin{array}{l}3x + 2y = 8\\3x - 4y = 2\end{array} \right.\)
Câu 3 (2,0 điểm):
Cho phương trình \({x^2} - 6x + m + 4 = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\) (\(m\) là tham số)
a) Giải phương trình \(\left( 1 \right)\) khi \(m = 1\).
b) Tìm tất cả các giá trị của tham số \(m\) để phương trình \(\left( 1 \right)\) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(2020\left( {{x_1} + {x_2}} \right) - 2021{x_1}{x_2} = 2014\).
Câu 4 (1,0 điểm):
Cho \(a,\,\,b\) là các số thực dương. Chứng minh \(\dfrac{{a + b}}{{\sqrt {a\left( {15a + b} \right)} + \sqrt {b\left( {15b + a} \right)} }} \ge \dfrac{1}{4}\).
Câu 5 (3,5 điểm):
Cho đường tròn \(\left( {O;R} \right)\) đường kính \(AB\), dây cung \(MN\) vuông góc với \(AB\) tại \(I\) sao cho \(AI < BI\). Trên đoạn thẳng \(MI\) lấy điểm \(H\) (\(H\) khác \(M\) và \(I\)), tia \(AH\) cắt đường tròn \(\left( {O;R} \right)\) tại điểm thứ hai là \(K\). Chứng minh rằng:
a) Tứ giác \(BIHK\) nội tiếp đường tròn.
b) \(\Delta AHM\) đồng dạng với \(\Delta AMK\).
Câu 1 (TH):
Phương pháp:
a) Sử dụng hằng đẳng thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)
Thực hiện các phép tính với căn bậc hai.
b) Xác định mẫu thức chung của biểu thức
Quy đồng các phân thức, thực hiện các phép toán từ đó rút gọn được biểu thức.
Cách giải:
a) \(A = \sqrt 8 - \sqrt {32} + \sqrt {50} \)
\(\begin{array}{l}A = \sqrt {{2^2}.2} - \sqrt {{4^2}.2} + \sqrt {{5^2}.2} \\A = 2\sqrt 2 - 4\sqrt 2 + 5\sqrt 2 \\A = \left( {2 - 4 + 5} \right)\sqrt 2 \\A = 3\sqrt 2 \end{array}\)
Vậy \(A = 5\sqrt 2 \).
b) Với \(a \ge 0,\,\,a \ne 1\) ta có:
\(\begin{array}{l}B = \left( {3 + \dfrac{{a + \sqrt a }}{{\sqrt a + 1}}} \right).\left( {3 - \dfrac{{a - \sqrt a }}{{\sqrt a - 1}}} \right)\\B = \left( {3 + \dfrac{{\sqrt a \left( {\sqrt a + 1} \right)}}{{\sqrt a + 1}}} \right).\left( {3 - \dfrac{{\sqrt a \left( {\sqrt a - 1} \right)}}{{\sqrt a - 1}}} \right)\\B = \left( {3 + \sqrt a } \right).\left( {3 - \sqrt a } \right)\\B = 9 - a\end{array}\)
Vậy với \(a \ge 0,\,\,a \ne 1\) thì \(B = 9 - a\).
Câu 2 (TH):
Phương pháp:
a) Hàm số \(y = ax + b\) đồng biến trên \(\mathbb{R} \Leftrightarrow a > 0\)
b) Sử dụng phương pháp cộng đại số, tìm được nghiệm \(y\)
Sử dụng phương pháp thế, tìm được nghiệm \(x\)
Kết luận nghiệm \(\left( {x;y} \right)\) của hệ phương trình.
Cách giải:
a) Để hàm số \(y = \left( {m - 1} \right)x + 2\) đồng biến trên \(\mathbb{R}\) thì \(m - 1 > 0 \Leftrightarrow m > 1\).
Vậy hàm số \(y = \left( {m - 1} \right)x + 2\)đồng biến trên \(\mathbb{R}\) khi \(m > 1\).
b) Ta có: \(\left\{ \begin{array}{l}3x + 2y = 8\\3x - 4y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}6y = 6\\3x + 2y = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\3x + 2 = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\x = 2\end{array} \right.\)
Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( {2;1} \right)\).
Câu 3 (VD): \(\)
Phương pháp:
a) Tính nhẩm nghiệm của phương trình bậc hai: Nếu \(a + b + c = 0\) thì phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt: \({x_1} = 1;{x_2} = \dfrac{c}{a}\)
b) Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt \(\Delta > 0\) (hoặc \(\Delta ' > 0\))
Áp dụng hệ thức Vi – ét, tính được \({x_1} + {x_2};{x_1}.{x_2}\) theo \(m\)
Thay vào \(2020\left( {{x_1} + {x_2}} \right) - 2021{x_1}{x_2} = 2014\), ta tìm được \(m\)
Cách giải:
a) Với \(m = 1\) thì \(\left( 1 \right)\) trở thành \({x^2} - 6x + 5 = 0\).
Ta có \(a + b + c = 1 - 6 + 5 = 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ \begin{array}{l}x = 1\\x = \dfrac{c}{a} = 5\end{array} \right.\).
Vậy khi \(m = 1\) thì tập nghiệm của phương trình là \(S = \left\{ {1;5} \right\}\).
b) Phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) \( \Leftrightarrow \Delta ' > 0\) \( \Leftrightarrow 9 - m - 4 > 0 \Leftrightarrow 5 - m > 0 \Leftrightarrow m < 5\).
Khi đó áp dụng hệ thức Vi- ét ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = 6\\{x_1}{x_2} = m + 4\end{array} \right.\)
Khi đó ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,2020\left( {{x_1} + {x_2}} \right) - 2021{x_1}{x_2} = 2014\\ \Leftrightarrow 2020.6 - 2021.\left( {m + 4} \right) = 2014\\ \Leftrightarrow 12120 - 2021m - 8084 = 2014\\ \Leftrightarrow 2021m = 2022\\ \Leftrightarrow m = \dfrac{{2022}}{{2021}}\,\,\,\left( {tm} \right)\end{array}\)
Vậy \(m = \dfrac{{2022}}{{2021}}\).
Câu 4 (VDC):
Phương pháp:
Áp dụng bất đẳng thức Cô – si cho \(\sqrt {16a\left( {15a + b} \right)} \) và \(\sqrt {16b\left( {15b + a} \right)} \)
Từ đó, suy ra \(\sqrt {16a\left( {15a + b} \right)} + \sqrt {16b\left( {15b + a} \right)} \) sau đó, suy ra được \(\dfrac{{a + b}}{{\sqrt {a\left( {15a + b} \right)} + \sqrt {b\left( {15b + a} \right)} }}\)
Cách giải:
Áp dụng BĐT Cô-si ta có:
\(\begin{array}{l}\sqrt {16a\left( {15a + b} \right)} \le \dfrac{{16a + 15a + b}}{2} = \dfrac{{31a + b}}{2}\\\sqrt {16b\left( {15b + a} \right)} \le \dfrac{{16b + 15b + a}}{2} = \dfrac{{31b + a}}{2}\\ \Rightarrow \sqrt {16a\left( {15a + b} \right)} + \sqrt {16b\left( {15b + a} \right)} \le \dfrac{{31a + b + 31b + a}}{2} = 16\left( {a + b} \right)\\ \Rightarrow \sqrt {a\left( {15a + b} \right)} + \sqrt {b\left( {15b + a} \right)} \le 4\left( {a + b} \right)\\ \Rightarrow \dfrac{{a + b}}{{\sqrt {a\left( {15a + b} \right)} + \sqrt {b\left( {15b + a} \right)} }} \ge \dfrac{1}{4}\,\,\,\left( {dpcm} \right)\end{array}\)
Dấu “=” xảy ra khi và chỉ khi \(\left\{ \begin{array}{l}16a = 15a + b\\16b = 15b + a\end{array} \right. \Leftrightarrow a = b\).
Câu 5 (VD):
Phương pháp:
a) Vận dụng dấu hiệu nhận biết: Tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp.
b) Ta sẽ chứng minh
c)
Áp dụng hệ thức lượng trong tam giác vuông \(ABM\), ta có:\(BI.BA = B{M^2}\)
Áp dụng định lý Py – ta – go cho tam giác vuông \(A{M^2} + B{M^2} = A{B^2} = 4{R^2}\)
\( \Rightarrow AH.AK + BI.AB = 4{R^2}\) (đpcm)
Cách giải:
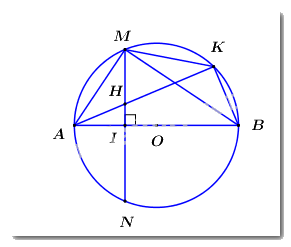
a) Ta có \(\angle AKB = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \angle BKH = {90^0}\).
Xét tứ giác \(BIHK\) có: \(\angle BIH + \angle BKH = {90^0} + {90^0} = {180^0}\) nên \(BIHK\) là tứ giác nội tiếp (dhnb).
b) Ta có: \(\angle AMB = {90^0}\) (góc nội tiếp chắn nửa đường tròn).
\( \Rightarrow \angle AMH + \angle BMH = {90^0} \Rightarrow \angle AMH + \angle ABM = {90^0}\).
Lại có \(\angle ABM = \angle AKM\) (2 góc nội tiếp cùng chắn cung \(AM\)) \( \Rightarrow \angle AMH = \angle AKM\).
Xét \(\Delta AHM\) và \(\Delta AMK\) có: \(\left\{ \begin{array}{l}\angle MAK\,\,chung\\\angle AMH = \angle AKM\,\,\left( {cmt} \right)\end{array} \right. \Rightarrow \Delta AHM \sim \Delta AMK\,\,\left( {g.g} \right)\).
c) Vì \(\Delta AHM \sim \Delta AMK\,\,\left( {cmt} \right) \Rightarrow \dfrac{{AH}}{{AM}} = \dfrac{{AM}}{{AK}}\) (2 cạnh tương ứng) \( \Rightarrow AH.AK = A{M^2}\).
Xét tam giác vuông \(ABM\) có đường cao \(MI\) ta có: \(BI.BA = B{M^2}\) (hệ thức lượng trong tam giác vuông).
\( \Rightarrow AH.AK + BI.AB = A{M^2} + B{M^2}\).
Mà \(\Delta ABM\) vuông tại \(M\,\,\left( {cmt} \right)\) nên áp dụng định lí Pytago ta có \(A{M^2} + B{M^2} = A{B^2} = {\left( {2R} \right)^2} = 4{R^2}\).
Vậy \(AH.AK + BI.AB = 4{R^2}\)(đpcm).
Câu 1 (2,0 điểm):
Rút gọn các biểu thức sau:
a) \(A = \sqrt 8 - \sqrt {32} + \sqrt {50} \)
b) \(B = \left( {3 + \dfrac{{a + \sqrt a }}{{\sqrt a + 1}}} \right).\left( {3 - \dfrac{{a - \sqrt a }}{{\sqrt a - 1}}} \right)\) (với \(a \ge 0,\,\,a \ne 1\)).
Câu 2 (1,5 điểm):
a) Tìm tất cả các giá trị của \(m\) để hàm số \(y = \left( {m - 1} \right)x + 2\) đồng biến trên \(\mathbb{R}\).
b) Giải hệ phương trình \(\left\{ \begin{array}{l}3x + 2y = 8\\3x - 4y = 2\end{array} \right.\)
Câu 3 (2,0 điểm):
Cho phương trình \({x^2} - 6x + m + 4 = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\) (\(m\) là tham số)
a) Giải phương trình \(\left( 1 \right)\) khi \(m = 1\).
b) Tìm tất cả các giá trị của tham số \(m\) để phương trình \(\left( 1 \right)\) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(2020\left( {{x_1} + {x_2}} \right) - 2021{x_1}{x_2} = 2014\).
Câu 4 (1,0 điểm):
Cho \(a,\,\,b\) là các số thực dương. Chứng minh \(\dfrac{{a + b}}{{\sqrt {a\left( {15a + b} \right)} + \sqrt {b\left( {15b + a} \right)} }} \ge \dfrac{1}{4}\).
Câu 5 (3,5 điểm):
Cho đường tròn \(\left( {O;R} \right)\) đường kính \(AB\), dây cung \(MN\) vuông góc với \(AB\) tại \(I\) sao cho \(AI < BI\). Trên đoạn thẳng \(MI\) lấy điểm \(H\) (\(H\) khác \(M\) và \(I\)), tia \(AH\) cắt đường tròn \(\left( {O;R} \right)\) tại điểm thứ hai là \(K\). Chứng minh rằng:
a) Tứ giác \(BIHK\) nội tiếp đường tròn.
b) \(\Delta AHM\) đồng dạng với \(\Delta AMK\).
Câu 1 (TH):
Phương pháp:
a) Sử dụng hằng đẳng thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)
Thực hiện các phép tính với căn bậc hai.
b) Xác định mẫu thức chung của biểu thức
Quy đồng các phân thức, thực hiện các phép toán từ đó rút gọn được biểu thức.
Cách giải:
a) \(A = \sqrt 8 - \sqrt {32} + \sqrt {50} \)
\(\begin{array}{l}A = \sqrt {{2^2}.2} - \sqrt {{4^2}.2} + \sqrt {{5^2}.2} \\A = 2\sqrt 2 - 4\sqrt 2 + 5\sqrt 2 \\A = \left( {2 - 4 + 5} \right)\sqrt 2 \\A = 3\sqrt 2 \end{array}\)
Vậy \(A = 5\sqrt 2 \).
b) Với \(a \ge 0,\,\,a \ne 1\) ta có:
\(\begin{array}{l}B = \left( {3 + \dfrac{{a + \sqrt a }}{{\sqrt a + 1}}} \right).\left( {3 - \dfrac{{a - \sqrt a }}{{\sqrt a - 1}}} \right)\\B = \left( {3 + \dfrac{{\sqrt a \left( {\sqrt a + 1} \right)}}{{\sqrt a + 1}}} \right).\left( {3 - \dfrac{{\sqrt a \left( {\sqrt a - 1} \right)}}{{\sqrt a - 1}}} \right)\\B = \left( {3 + \sqrt a } \right).\left( {3 - \sqrt a } \right)\\B = 9 - a\end{array}\)
Vậy với \(a \ge 0,\,\,a \ne 1\) thì \(B = 9 - a\).
Câu 2 (TH):
Phương pháp:
a) Hàm số \(y = ax + b\) đồng biến trên \(\mathbb{R} \Leftrightarrow a > 0\)
b) Sử dụng phương pháp cộng đại số, tìm được nghiệm \(y\)
Sử dụng phương pháp thế, tìm được nghiệm \(x\)
Kết luận nghiệm \(\left( {x;y} \right)\) của hệ phương trình.
Cách giải:
a) Để hàm số \(y = \left( {m - 1} \right)x + 2\) đồng biến trên \(\mathbb{R}\) thì \(m - 1 > 0 \Leftrightarrow m > 1\).
Vậy hàm số \(y = \left( {m - 1} \right)x + 2\)đồng biến trên \(\mathbb{R}\) khi \(m > 1\).
b) Ta có: \(\left\{ \begin{array}{l}3x + 2y = 8\\3x - 4y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}6y = 6\\3x + 2y = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\3x + 2 = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\x = 2\end{array} \right.\)
Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( {2;1} \right)\).
Câu 3 (VD): \(\)
Phương pháp:
a) Tính nhẩm nghiệm của phương trình bậc hai: Nếu \(a + b + c = 0\) thì phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt: \({x_1} = 1;{x_2} = \dfrac{c}{a}\)
b) Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt \(\Delta > 0\) (hoặc \(\Delta ' > 0\))
Áp dụng hệ thức Vi – ét, tính được \({x_1} + {x_2};{x_1}.{x_2}\) theo \(m\)
Thay vào \(2020\left( {{x_1} + {x_2}} \right) - 2021{x_1}{x_2} = 2014\), ta tìm được \(m\)
Cách giải:
a) Với \(m = 1\) thì \(\left( 1 \right)\) trở thành \({x^2} - 6x + 5 = 0\).
Ta có \(a + b + c = 1 - 6 + 5 = 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ \begin{array}{l}x = 1\\x = \dfrac{c}{a} = 5\end{array} \right.\).
Vậy khi \(m = 1\) thì tập nghiệm của phương trình là \(S = \left\{ {1;5} \right\}\).
b) Phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) \( \Leftrightarrow \Delta ' > 0\) \( \Leftrightarrow 9 - m - 4 > 0 \Leftrightarrow 5 - m > 0 \Leftrightarrow m < 5\).
Khi đó áp dụng hệ thức Vi- ét ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = 6\\{x_1}{x_2} = m + 4\end{array} \right.\)
Khi đó ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,2020\left( {{x_1} + {x_2}} \right) - 2021{x_1}{x_2} = 2014\\ \Leftrightarrow 2020.6 - 2021.\left( {m + 4} \right) = 2014\\ \Leftrightarrow 12120 - 2021m - 8084 = 2014\\ \Leftrightarrow 2021m = 2022\\ \Leftrightarrow m = \dfrac{{2022}}{{2021}}\,\,\,\left( {tm} \right)\end{array}\)
Vậy \(m = \dfrac{{2022}}{{2021}}\).
Câu 4 (VDC):
Phương pháp:
Áp dụng bất đẳng thức Cô – si cho \(\sqrt {16a\left( {15a + b} \right)} \) và \(\sqrt {16b\left( {15b + a} \right)} \)
Từ đó, suy ra \(\sqrt {16a\left( {15a + b} \right)} + \sqrt {16b\left( {15b + a} \right)} \) sau đó, suy ra được \(\dfrac{{a + b}}{{\sqrt {a\left( {15a + b} \right)} + \sqrt {b\left( {15b + a} \right)} }}\)
Cách giải:
Áp dụng BĐT Cô-si ta có:
\(\begin{array}{l}\sqrt {16a\left( {15a + b} \right)} \le \dfrac{{16a + 15a + b}}{2} = \dfrac{{31a + b}}{2}\\\sqrt {16b\left( {15b + a} \right)} \le \dfrac{{16b + 15b + a}}{2} = \dfrac{{31b + a}}{2}\\ \Rightarrow \sqrt {16a\left( {15a + b} \right)} + \sqrt {16b\left( {15b + a} \right)} \le \dfrac{{31a + b + 31b + a}}{2} = 16\left( {a + b} \right)\\ \Rightarrow \sqrt {a\left( {15a + b} \right)} + \sqrt {b\left( {15b + a} \right)} \le 4\left( {a + b} \right)\\ \Rightarrow \dfrac{{a + b}}{{\sqrt {a\left( {15a + b} \right)} + \sqrt {b\left( {15b + a} \right)} }} \ge \dfrac{1}{4}\,\,\,\left( {dpcm} \right)\end{array}\)
Dấu “=” xảy ra khi và chỉ khi \(\left\{ \begin{array}{l}16a = 15a + b\\16b = 15b + a\end{array} \right. \Leftrightarrow a = b\).
Câu 5 (VD):
Phương pháp:
a) Vận dụng dấu hiệu nhận biết: Tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp.
b) Ta sẽ chứng minh
c)
Áp dụng hệ thức lượng trong tam giác vuông \(ABM\), ta có:\(BI.BA = B{M^2}\)
Áp dụng định lý Py – ta – go cho tam giác vuông \(A{M^2} + B{M^2} = A{B^2} = 4{R^2}\)
\( \Rightarrow AH.AK + BI.AB = 4{R^2}\) (đpcm)
Cách giải:
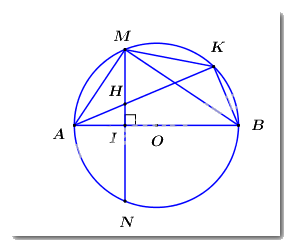
a) Ta có \(\angle AKB = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \angle BKH = {90^0}\).
Xét tứ giác \(BIHK\) có: \(\angle BIH + \angle BKH = {90^0} + {90^0} = {180^0}\) nên \(BIHK\) là tứ giác nội tiếp (dhnb).
b) Ta có: \(\angle AMB = {90^0}\) (góc nội tiếp chắn nửa đường tròn).
\( \Rightarrow \angle AMH + \angle BMH = {90^0} \Rightarrow \angle AMH + \angle ABM = {90^0}\).
Lại có \(\angle ABM = \angle AKM\) (2 góc nội tiếp cùng chắn cung \(AM\)) \( \Rightarrow \angle AMH = \angle AKM\).
Xét \(\Delta AHM\) và \(\Delta AMK\) có: \(\left\{ \begin{array}{l}\angle MAK\,\,chung\\\angle AMH = \angle AKM\,\,\left( {cmt} \right)\end{array} \right. \Rightarrow \Delta AHM \sim \Delta AMK\,\,\left( {g.g} \right)\).
c) Vì \(\Delta AHM \sim \Delta AMK\,\,\left( {cmt} \right) \Rightarrow \dfrac{{AH}}{{AM}} = \dfrac{{AM}}{{AK}}\) (2 cạnh tương ứng) \( \Rightarrow AH.AK = A{M^2}\).
Xét tam giác vuông \(ABM\) có đường cao \(MI\) ta có: \(BI.BA = B{M^2}\) (hệ thức lượng trong tam giác vuông).
\( \Rightarrow AH.AK + BI.AB = A{M^2} + B{M^2}\).
Mà \(\Delta ABM\) vuông tại \(M\,\,\left( {cmt} \right)\) nên áp dụng định lí Pytago ta có \(A{M^2} + B{M^2} = A{B^2} = {\left( {2R} \right)^2} = 4{R^2}\).
Vậy \(AH.AK + BI.AB = 4{R^2}\)(đpcm).
Kỳ thi tuyển sinh vào lớp 10 là một bước ngoặt quan trọng trong quá trình học tập của mỗi học sinh. Việc chuẩn bị kỹ lưỡng, nắm vững kiến thức và làm quen với các dạng đề thi là yếu tố then chốt để đạt kết quả tốt. Đề thi vào 10 môn Toán Quảng Bình năm 2021 (đề số 1) là một tài liệu luyện thi vô cùng hữu ích cho các em học sinh đang chuẩn bị cho kỳ thi này.
Đề thi vào 10 môn Toán Quảng Bình năm 2021 (đề số 1) thường bao gồm các phần sau:
Các dạng bài tập thường xuất hiện trong đề thi bao gồm:
Để giúp các em học sinh hiểu rõ hơn về đề thi, chúng ta sẽ phân tích chi tiết một số câu hỏi tiêu biểu:
Giải phương trình: 2x + 3 = 7
Hướng dẫn giải: Đây là một phương trình bậc nhất một ẩn. Để giải phương trình, ta thực hiện các bước sau:
Cho tam giác ABC vuông tại A, AB = 3cm, AC = 4cm. Tính độ dài cạnh BC.
Hướng dẫn giải: Áp dụng định lý Pitago trong tam giác vuông ABC, ta có:
BC2 = AB2 + AC2 = 32 + 42 = 9 + 16 = 25
Suy ra BC = √25 = 5cm
Ngoài Đề thi vào 10 môn Toán Quảng Bình năm 2021 (đề số 1), các em học sinh có thể tham khảo thêm các tài liệu luyện thi khác như:
Đề thi vào 10 môn Toán Quảng Bình năm 2021 (đề số 1) là một công cụ hữu ích giúp các em học sinh chuẩn bị tốt nhất cho kỳ thi tuyển sinh lớp 10. Chúc các em học sinh đạt kết quả cao trong kỳ thi sắp tới!