Giaitoan.edu.vn xin giới thiệu bộ đề thi vào 10 môn Toán tỉnh Lâm Đồng năm 2021 chính thức, được tổng hợp đầy đủ và cập nhật mới nhất. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi sắp tới.
Chúng tôi cung cấp không chỉ đề thi mà còn cả đáp án chi tiết, giúp các em tự đánh giá năng lực và tìm ra những điểm cần cải thiện.
Câu 1 (0,75 điểm): Tính giá trị biểu thức
Câu 1 (0,75 điểm): Tính giá trị biểu thức: \(A = \sqrt 5 \left( {\sqrt 5 - 3} \right) + \sqrt {45} .\)
Câu 2 (0,75 điểm): Tính diện tích chân đống cát dạng hình tròn có chu vi là \(18,84\,m.\) (Với \(\pi \approx 3,14\))
Câu 3 (0, 75 điểm): Giải phương trình: \({x^4} + 4{x^2} - 5 = 0\)
Câu 4 (0, 75 điểm): Giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{c}}{2x + y = 3}\\{3x - 5y = 11}\end{array}} \right.\)
Câu 5 (0,75 điểm):
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\) \((H \in BC)\). Biết \(BC = 5cm,AB = 3cm\). Tính \(AH\).
Câu 6 (0,75 điểm):
Cho góc nhọn \(\alpha \) biết \(\sin \alpha = 0,6\). Không sử dụng máy tính cầm tay, tính giá trị biểu thức:\(B = 5\cos \alpha - 4\tan \alpha \)
Câu 7 (0,75 điểm):
Cho Parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = 3x + m\). Tìm \(m\) để \(\left( P \right)\) và \(\left( d \right)\) không có điểm chung.
Câu 8 (1,0 điểm):
Hình nón có thể tích là \(96\pi \,\,c{m^3}\)và chiều cao là \(8cm\). Tính diện tích xung quanh của hình nón.
Câu 9 (1,0 điểm):
Chứng minh rằng \(\left( {\sqrt {{{\left( {1 - \sqrt {2022} } \right)}^2}} } \right)\left( {\sqrt {2023 + 2\sqrt {2022} } } \right) = 2021\).
Câu 10 (1,0 điểm):
Một người dự định đi xe gắn máy từ A đến B với vận tốc không đổi. Nhưng thực tế vì có việc gấp, người đó đã tăng vận tốc thêm \(5\,km/h\) so với dự định nên đến \(B\)sớm hơn 15 phút. Tính vận tốc người có dự định đi từ A đến B, biết quãng đường AB dài 70km.
Câu 11 (1 điểm):
Cho phương trình \(2{x^2} - \left( {2m - 1} \right)x + m - 1 = 0\,\)(ẩn \(x,\) tham số \(m\)). Tìm \(m\) để phương trình có hai nghiệm phân biệt cùng dấu. Khi đó hai nghiệm này mang dấu gì?
Câu 12 (0,75 điểm):
Cho C là một điểm nằm trên nửa đường tròn tâm \(\left( O \right)\) đường kính \(AB\,\,\,\left( {C \ne A,\,\,C \ne B} \right).\) Gọi \(H\) là hình chiếu vuông góc của \(C\) trên \(AB,\,\,D\) là điểm đối xứng của \(A\) qua \(C,\,\,I\) là trung điểm của \(CH,\,\,J\) là trung điểm của \(DH\) và \(E\) là giao điểm của \(HD\) và \(BI.\) Chứng minh \(HE.HD = H{C^2}\).
Câu 1 (0,75 điểm): Tính giá trị biểu thức: \(A = \sqrt 5 \left( {\sqrt 5 - 3} \right) + \sqrt {45} .\)
Câu 2 (0,75 điểm): Tính diện tích chân đống cát dạng hình tròn có chu vi là \(18,84\,m.\) (Với \(\pi \approx 3,14\))
Câu 3 (0, 75 điểm): Giải phương trình: \({x^4} + 4{x^2} - 5 = 0\)
Câu 4 (0, 75 điểm): Giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{c}}{2x + y = 3}\\{3x - 5y = 11}\end{array}} \right.\)
Câu 5 (0,75 điểm):
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\) \((H \in BC)\). Biết \(BC = 5cm,AB = 3cm\). Tính \(AH\).
Câu 6 (0,75 điểm):
Cho góc nhọn \(\alpha \) biết \(\sin \alpha = 0,6\). Không sử dụng máy tính cầm tay, tính giá trị biểu thức:\(B = 5\cos \alpha - 4\tan \alpha \)
Câu 7 (0,75 điểm):
Cho Parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = 3x + m\). Tìm \(m\) để \(\left( P \right)\) và \(\left( d \right)\) không có điểm chung.
Câu 8 (1,0 điểm):
Hình nón có thể tích là \(96\pi \,\,c{m^3}\)và chiều cao là \(8cm\). Tính diện tích xung quanh của hình nón.
Câu 9 (1,0 điểm):
Chứng minh rằng \(\left( {\sqrt {{{\left( {1 - \sqrt {2022} } \right)}^2}} } \right)\left( {\sqrt {2023 + 2\sqrt {2022} } } \right) = 2021\).
Câu 10 (1,0 điểm):
Một người dự định đi xe gắn máy từ A đến B với vận tốc không đổi. Nhưng thực tế vì có việc gấp, người đó đã tăng vận tốc thêm \(5\,km/h\) so với dự định nên đến \(B\)sớm hơn 15 phút. Tính vận tốc người có dự định đi từ A đến B, biết quãng đường AB dài 70km.
Câu 11 (1 điểm):
Cho phương trình \(2{x^2} - \left( {2m - 1} \right)x + m - 1 = 0\,\)(ẩn \(x,\) tham số \(m\)). Tìm \(m\) để phương trình có hai nghiệm phân biệt cùng dấu. Khi đó hai nghiệm này mang dấu gì?
Câu 12 (0,75 điểm):
Cho C là một điểm nằm trên nửa đường tròn tâm \(\left( O \right)\) đường kính \(AB\,\,\,\left( {C \ne A,\,\,C \ne B} \right).\) Gọi \(H\) là hình chiếu vuông góc của \(C\) trên \(AB,\,\,D\) là điểm đối xứng của \(A\) qua \(C,\,\,I\) là trung điểm của \(CH,\,\,J\) là trung điểm của \(DH\) và \(E\) là giao điểm của \(HD\) và \(BI.\) Chứng minh \(HE.HD = H{C^2}\).
Câu 1
Phương pháp:
Sử dụng hằng đẳng thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)
Thực hiện các phép tính với căn bậc hai.
Cách giải:
\(\begin{array}{l}A = \sqrt 5 \left( {\sqrt 5 - 3} \right) + \sqrt {45} \\\,\,\,\,\,\, = 5 - 3\sqrt 5 + \sqrt {{3^2}.5} \\\,\,\,\,\,\, = 5 - 3\sqrt 5 + 3\sqrt 5 \\\,\,\,\,\,\, = 5.\end{array}\)
Vậy \(A = 5.\)
Câu 2
Phương pháp:
Bán kính của hình tròn: \(R = \dfrac{C}{{2\pi }}\)
Diện tích của hình tròn: \(S = \pi {R^2}\)
Cách giải:
Bán kính của chân đống cát là: \(R = \dfrac{C}{{2\pi }} = \dfrac{{18,84}}{{2.3,14}} = 3\,\,\left( m \right).\)
Diện tích của chân đống cát đó là: \(S = \pi {R^2} = 3,{14.3^2} = 28,26\,\,{m^2}.\)
Câu 3
Phương pháp:
Đặt \(t = {x^2}\,\,\left( {t \ge 0} \right)\)
Phương trình ban đầu trở thành phương trình bậc hai một ẩn: \(a{t^2} + bt + c = 0\left( {a \ne 0} \right)\)
Tính \(\Delta \), sử dụng công thức nghiệm của phương trình bậc hai một ẩn, tìm được \(t\), lấy \(t\) thỏa mãn điều kiện
Với \(t\) tìm được, ta tìm được \(x\) tương ứng.
Cách giải:
Đặt \({x^2} = t\,\,\,\left( {t \ge 0} \right)\).
Khi đó ta có phương trình: \({t^2} + 4t - 5 = 0\)
Phương trình có: \(\Delta ' = 4 + 5 = 9 > 0\)
\( \Rightarrow \) Phương trình có nghiệm \({t_1} = - 2 + \sqrt 9 = 1\,\,\left( {tm} \right);\,\)\(\,{t_2} = - 2 - \sqrt 9 = - 5\,\,\,\left( {ktm} \right)\)
+) Với \({t_1} = 1 \Rightarrow \) \({x^2} = 1 \Leftrightarrow x = \pm 1\)
Vậy phương trình có tập nghiệm \(S = \left\{ { - 1;\,\,1} \right\}\).
Câu 4
Phương pháp:
Sử dụng phương pháp thế, tìm được \(y\) theo \(x\)
Thay vào phương trình còn lại, tìm được \(x\) và \(y\)
Kết luận nghiệm \(\left( {x;y} \right)\) của hệ phương trình.
Cách giải:
Ta có: \(\left\{ {\begin{array}{*{20}{c}}{2x + y = 3}\\{3x - 5y = 11}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{y = 3 - 2x}\\{3x - 5\left( {3 - 2x} \right) = 11}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{y = 3 - 2x}\\{13x = 26}\end{array}} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3 - 2.2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = - 1\end{array} \right..\)
Vậy hệ phương trình có tập nghiệm \(S = \left\{ {\left( {2;\, - 1} \right)} \right\}\)
Câu 5
Phương pháp:
Áp dụng định lí Pytago cho \(\Delta ABC\) vuông tại \(A\), tính được \(BC\)
Áp dụng hệ thức lượng cho \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\), tính được \(AH\)
Cách giải:
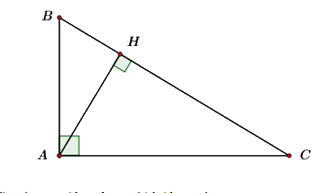
Áp dụng định lí Pytago cho \(\Delta ABC\) vuông tại \(A\) ta có:
\(A{B^2} + A{C^2} = B{C^2}\)\( \Rightarrow A{C^2} = B{C^2} - A{B^2}\)
\(\begin{array}{l} \Leftrightarrow A{C^2} = {5^2} - {3^2} = 16\\ \Rightarrow BC = \,4\,cm.\end{array}\)
Áp dụng hệ thức lượng cho \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(AH.BC = AB.AC\)\( \Rightarrow AH = \dfrac{{AB.AC}}{{BC}}\)
\( \Rightarrow AH = \dfrac{{3.4}}{5} = 2,4\,cm.\)
Vậy \(AH = 2,4\,\,cm.\)
Câu 6
Phương pháp:
Áp dụng hệ thức: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Rightarrow {\cos ^2}\alpha = 1 - {\sin ^2}\alpha \), tính được \(\cos \alpha \), tìm được \(\cos \alpha \) thỏa mãn điều kiện
Tính được \(\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }}\)
Từ đó tính được giá trị biểu thức \(B\)
Cách giải:
Áp dụng hệ thức: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Rightarrow {\cos ^2}\alpha = 1 - {\sin ^2}\alpha \)
\( \Rightarrow {\cos ^2}\alpha = 1 - 0,{6^2} = 1 - 0,36 = 0,64\)
\( \Rightarrow \cos \alpha = \pm 0,8\)
Mà \(\alpha \) là góc nhọn nên \(\cos \alpha > 0\) do đó \(\cos \alpha = 0,8\)
Ta có: \(\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }} = \dfrac{{0,6}}{{0,8}} = \dfrac{3}{4} = 0,75\)
Khi đó: \(B = 5\cos \alpha - 4\tan \alpha \)\( = 5.0,8 - 4.0,75 = 1\)
Vậy \(B = 1.\)
Câu 7
Phương pháp:
Xét phương trình hoành độ giao điểm giữa \(\left( P \right)\) và \(\left( d \right)\) \(\left( 1 \right)\)
\(\left( P \right)\) và \(\left( d \right)\) không có điểm chung khi phương trình \(\left( 1 \right)\) vô nghiệm \( \Leftrightarrow \Delta < 0\) (hoặc \( \Leftrightarrow \Delta ' < 0\))
Cách giải:
Hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là nghiệm của phương trình: \({x^2} = 3x + m \Leftrightarrow {x^2} - 3x - m = 0\,\,\left( 1 \right)\)
Phương trình có: \(\Delta = {\left( { - 3} \right)^2} - 4.\left( { - m} \right) = 9 + 4m\)
\(\left( P \right)\) và \(\left( d \right)\) không có điểm chung khi phương trình \(\left( 1 \right)\)vô nghiệm
\( \Leftrightarrow \Delta < 0 \Leftrightarrow 9 + 4m < 0 \Leftrightarrow m < - \dfrac{9}{4}\)
Vậy \(\left( P \right)\) và \(\left( d \right)\) không có điểm chung khi \(m < - \dfrac{9}{4}.\)
Câu 8
Phương pháp:
Hình nón có chiều cao là \(h\) và bán kính đáy là \(r\) có thể tích là: \(V = \dfrac{1}{3}\pi {r^2}h\), suy ra \(r = \sqrt {\dfrac{{3V}}{{\pi h}}} \)
Đường sinh \(l\) của hình nón được tính theo công thức: \({l^2} = {r^2} + {h^2}\)
Hình nón có đường sinh là \(l\) và bán kính đáy là \(r\) có diện tích xung quanh là: \({S_{xq}} = \pi rl\)
Cách giải:
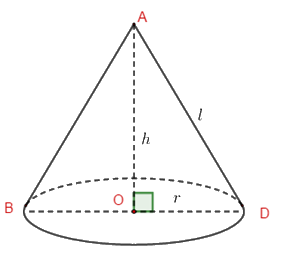
Ta có: \(V = \dfrac{1}{3}\pi {r^2}h\)\( \Rightarrow r = \sqrt {\dfrac{{3V}}{{\pi h}}} \)
\( \Rightarrow \) Bán kính của hình nón là: \(r = \sqrt {\dfrac{{3V}}{{\pi h}}} = \sqrt {\dfrac{{3.96\pi }}{{\pi .8}}} = \sqrt {36} = 6\,cm.\)
Gọi đường sinh của hình nón là \(l.\) Khi đó ta có:
\({l^2} = {h^2} + {r^2} = {8^2} + {6^2} = 100\) \( \Rightarrow l = 10\,\,cm\)
\( \Rightarrow \) Diện tích xung quanh của hình nón là: \({S_{xq}} = \pi rl = \pi .6.10 = 60\pi \,\,c{m^2}.\)
Vậy diện tích xung quanh của hình nón đã cho là \(60\pi \,\,c{m^2}.\)
Câu 9
Phương pháp:
Sử dụng hằng đẳng thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)
Thực hiện các phép tính với căn bậc hai.
Cách giải:
Ta có:
\(\begin{array}{l}VT = \left( {\sqrt {{{\left( {1 - \sqrt {2022} } \right)}^2}} } \right)\left( {\sqrt {2023 + 2\sqrt {2022} } } \right)\\\,\,\,\,\,\,\,\, = \left| {1 - \sqrt {2022} } \right|.\sqrt {{{\left( {\sqrt {2022} + 1} \right)}^2}} \\\,\,\,\,\,\,\,\, = \left( {\sqrt {2022} - 1} \right).\left( {\sqrt {2022} + 1} \right)\,\,\,\,\,\left( {do\,\,\,1 - \sqrt {2022} < 0,\,\,\sqrt {2022} + 1 > 0} \right)\\\,\,\,\,\,\,\,\, = 2022 - 1 = 2021 = VP\,\,\,\,\,\left( {dpcm} \right)\end{array}\)
Vậy \(\left( {\sqrt {{{\left( {1 - \sqrt {2022} } \right)}^2}} } \right)\left( {\sqrt {2023 + 2\sqrt {2022} } } \right) = 2021.\)
Câu 10
Phương pháp:
Gọi vận tốc dự định của người đi xe gắn máy là \(x\,\,\left( {km/h,\,\,x > 0} \right).\)
Tính được thời gian đi hết quãng đường \(AB\) theo dự định theo \(x\)
Tính được vận tốc và thời gian đi hết quãng đường \(AB\) theo thực tế theo \(x\)
Dựa vào giả thiết về thời gian nên ta lập được phương trình.
Giải phương trình, đối chiếu điều kiện và kết luận.
Cách giải:
Đổi \(15\)phút = \(\dfrac{1}{4}\) giờ
Gọi vận tốc dự định của người đi xe gắn máy là \(x\,\,\left( {km/h,\,\,x > 0} \right).\)
\( \Rightarrow \) Thời gian đi hết quãng đường AB dự định là: \(\dfrac{{70}}{x}\left( h \right)\)
Vận tốc khi tăng \(5\,km/h\) so với dự định là: \(x + 5\,\,\left( {km/h} \right)\).
\( \Rightarrow \) Thời gian thực tế xe đi hết quãng đường AB là: \(\dfrac{{70}}{{x + 5}}\,\,\left( h \right).\)
Vì khi tăng vận tốc thêm \(5\,km/h\) so với dự định thì đến \(B\)sớm hơn 15 phútnên ta có phương trình:
\(\begin{array}{l}\,\,\,\,\,\dfrac{{70}}{x} - \dfrac{{70}}{{x + 5}} = \dfrac{1}{4}\\ \Leftrightarrow 280.\left( {x + 5} \right) - 280x = x\left( {x + 5} \right)\\ \Leftrightarrow 280x + 1400 - 280x = {x^2} + 5x\\ \Leftrightarrow {x^2} + 5x - 1400 = 0\end{array}\)
Phương trình có: \(\Delta = {\left( { - 5} \right)^2} + 4.1400 = 5625 > 0\)
\( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \({x_1} = \dfrac{{ - 5 + \sqrt {5625} }}{2} = 35\,\,\,\left( {tm} \right)\) và \({x_2} = \dfrac{{ - 5 - \sqrt {5625} }}{2} = - 40\,\,\,\left( {ktm} \right)\)
Vậy vận tốc dự định của người đi xe gắn máy là \(35\,km/h\).
Câu 11
Phương pháp:
Phương trình có hai nghiệm cùng dấu \( \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\\dfrac{c}{a} > 0\end{array} \right.\)
Áp dụng hệ thức Vi-et tính được \({x_1} + {x_2}\)
Giả sử \({x_1} + {x_2} > 0\), nếu điều giả sử đúng thì phương trình có hai nghiệm phân biệt dương còn nếu điều giả sử sai thì phương trình có hai nghiệm âm phân biệt.
Cách giải:
Phương trình \(2{x^2} - \left( {2m - 1} \right)x + m - 1 = 0\,\,\,\,\left( 1 \right)\) có hai nghiệm phân biệt cùng dấu \( \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\\dfrac{c}{a} > 0\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{\left( {2m - 1} \right)^2} - 4.2\left( {m - 1} \right) > 0\\\dfrac{{m - 1}}{2} > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}4{m^2} - 4m + 1 - 8m + 8 > 0\\m - 1 > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}4{m^2} - 12m + 9 > 0\\m > 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{\left( {2m - 3} \right)^2} > 0\\m > 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2m - 3 \ne 0\\m > 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne \dfrac{3}{2}\\m > 1\end{array} \right.\end{array}\)
Với \(m > 1,\,\,m \ne \dfrac{3}{2}\) thì phương trình đã cho có hai nghiệm cùng dấu.
Áp dụng hệ thức Vi-et ta có: \({x_1} + {x_2} = \dfrac{{2m - 1}}{2}\)
Giả sử \({x_1} + {x_2} > 0\) \( \Leftrightarrow \dfrac{{2m - 1}}{2} > 0\)\( \Leftrightarrow 2m - 1 > 0 \Leftrightarrow m > \dfrac{1}{2}\)
\( \Rightarrow \) Với \(\forall m > 1,\,\,m \ne \dfrac{3}{2}\) thì ta có: \({x_1} + {x_2} > 0\)
\( \Rightarrow \) Phương trình có hai nghiệm cùng dương.
Với \({x_1} + {x_2} < 0\)\( \Leftrightarrow \dfrac{{2m - 1}}{2} < 0\)\( \Leftrightarrow 2m - 1 < 0 \Leftrightarrow m < \dfrac{1}{2}\)
Mâu thuẫn với điều kiện: \(m > 1,\,\,m \ne \dfrac{3}{2}.\)
Vậy với \(m > 1,\,\,m \ne \dfrac{3}{2}\) thì phương trình đã cho có hai nghiệm cùng dương.
Câu 12
Phương pháp:
Ta chỉ ra được: \(\angle CIJ = \angle CBH\); \(\tan CBH = \dfrac{{CH}}{{BH}}\); \(\tan CIJ = \dfrac{{CJ}}{{CI}} = \dfrac{{CJ}}{{HI}}\) từ đó, suy ra \(\dfrac{{CH}}{{BH}} = \dfrac{{CJ}}{{HI}}\)
Ta sẽ chứng minh:
+ \(\angle CHJ = \angle HBI\)
+ \( HE.HJ = HC.HI\)
Mà \(\left\{ \begin{array}{l}HJ = \dfrac{1}{2}HD\,\,\,\left( {gt} \right)\\HI = \dfrac{1}{2}HC\,\,\,\left( {gt} \right)\end{array} \right.\)
Suy ra \(HE.HD = H{C^2}\,\,\,\left( {dpcm} \right).\)
Cách giải:
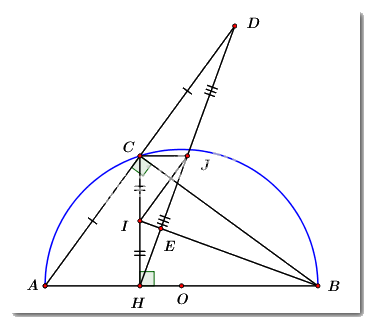
Ta có: \(\angle ACB\) là góc nội tiếp chắn nửa đường tròn \(\angle ACB = {90^0}\) hay \(\angle AC \bot BC\)
Xét \(\Delta AHD\) ta có:
\(C\) là trung điểm của \(AD\) (gt)
\(J\) là trung điểm của \(HD\) (gt)
\( \Rightarrow CJ\) là đường trung bình của \(\Delta AHD\) (định nghĩa đường trung bình của tam giác)
\( \Rightarrow CJ//AB\,\) (tính chất).
Mà \(CH \bot AH\)(do \(H\) là hình chiếu của \(C\) trên \(AB\))
Suy ra \(CJ \bot CH\)tại \(C\) (từ song song đến vuông góc).
\( \Rightarrow \angle HCJ = {90^0}\)
Xét \(\Delta CHD\) ta có:
\(I,\,\,J\) lần lượt là trung điểm của \(CH\) và \(HD\) (gt)
\( \Rightarrow IJ\) là đường trung bình của \(\Delta CHD\) (định nghĩa đường trung bình của tam giác).
\( \Rightarrow IJ//CD\) (tính chất đường trung bình của tam giác).
Lại có: \(BC \bot AC\,\,\left( {cmt} \right)\) hay \(BC \bot CD\)
\( \Rightarrow IJ \bot BC\) (từ song song đến vuông góc).
\( \Rightarrow \angle CIJ = \angle CBH\) (cùng phụ với \(\angle HCB\)) \(\left( 1 \right)\)
Trong \(\Delta CHB\) vuông tại \(H\) ta có: \(\tan CBH = \dfrac{{CH}}{{BH}}\) \(\left( 2 \right)\)
Trong \(\Delta CIJ\) vuông tại \(C\) ta có: \(\tan CIJ = \dfrac{{CJ}}{{CI}} = \dfrac{{CJ}}{{HI}}\) \(\left( 3 \right)\)
Từ \(\left( 1 \right),\,\,\left( 2 \right),\,\,\left( 3 \right)\) suy ra: \(\dfrac{{CH}}{{BH}} = \dfrac{{CJ}}{{HI}}\)
Xét \(\Delta CJH\)và \(\Delta HIB\) ta có:
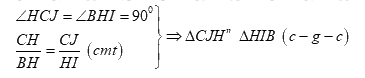
\( \Rightarrow \angle CHJ = \angle HBI\) (2 góc tương ứng)
Mà \(\angle CHJ + \angle CHJ = {90^0}\)
Suy ra \(\angle HBI + \angle EHB = {90^0}\) \( \Rightarrow \Delta EHB\) vuông tại \(E\)
\( \Rightarrow \angle HEB = {90^0}\) hay \(\angle HEI = {90^0}\)
Xét \(\Delta HEI\) và \(\Delta HCJ\) ta có:
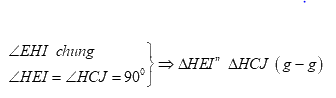
\( \Rightarrow \dfrac{{HE}}{{HC}} = \dfrac{{HI}}{{HJ}}\)\( \Leftrightarrow HE.HJ = HC.HI\)
Mà \(\left\{ \begin{array}{l}HJ = \dfrac{1}{2}HD\,\,\,\left( {gt} \right)\\HI = \dfrac{1}{2}HC\,\,\,\left( {gt} \right)\end{array} \right.\)
Suy ra \(HE.HD = H{C^2}\,\,\,\left( {dpcm} \right).\)
Câu 1
Phương pháp:
Sử dụng hằng đẳng thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)
Thực hiện các phép tính với căn bậc hai.
Cách giải:
\(\begin{array}{l}A = \sqrt 5 \left( {\sqrt 5 - 3} \right) + \sqrt {45} \\\,\,\,\,\,\, = 5 - 3\sqrt 5 + \sqrt {{3^2}.5} \\\,\,\,\,\,\, = 5 - 3\sqrt 5 + 3\sqrt 5 \\\,\,\,\,\,\, = 5.\end{array}\)
Vậy \(A = 5.\)
Câu 2
Phương pháp:
Bán kính của hình tròn: \(R = \dfrac{C}{{2\pi }}\)
Diện tích của hình tròn: \(S = \pi {R^2}\)
Cách giải:
Bán kính của chân đống cát là: \(R = \dfrac{C}{{2\pi }} = \dfrac{{18,84}}{{2.3,14}} = 3\,\,\left( m \right).\)
Diện tích của chân đống cát đó là: \(S = \pi {R^2} = 3,{14.3^2} = 28,26\,\,{m^2}.\)
Câu 3
Phương pháp:
Đặt \(t = {x^2}\,\,\left( {t \ge 0} \right)\)
Phương trình ban đầu trở thành phương trình bậc hai một ẩn: \(a{t^2} + bt + c = 0\left( {a \ne 0} \right)\)
Tính \(\Delta \), sử dụng công thức nghiệm của phương trình bậc hai một ẩn, tìm được \(t\), lấy \(t\) thỏa mãn điều kiện
Với \(t\) tìm được, ta tìm được \(x\) tương ứng.
Cách giải:
Đặt \({x^2} = t\,\,\,\left( {t \ge 0} \right)\).
Khi đó ta có phương trình: \({t^2} + 4t - 5 = 0\)
Phương trình có: \(\Delta ' = 4 + 5 = 9 > 0\)
\( \Rightarrow \) Phương trình có nghiệm \({t_1} = - 2 + \sqrt 9 = 1\,\,\left( {tm} \right);\,\)\(\,{t_2} = - 2 - \sqrt 9 = - 5\,\,\,\left( {ktm} \right)\)
+) Với \({t_1} = 1 \Rightarrow \) \({x^2} = 1 \Leftrightarrow x = \pm 1\)
Vậy phương trình có tập nghiệm \(S = \left\{ { - 1;\,\,1} \right\}\).
Câu 4
Phương pháp:
Sử dụng phương pháp thế, tìm được \(y\) theo \(x\)
Thay vào phương trình còn lại, tìm được \(x\) và \(y\)
Kết luận nghiệm \(\left( {x;y} \right)\) của hệ phương trình.
Cách giải:
Ta có: \(\left\{ {\begin{array}{*{20}{c}}{2x + y = 3}\\{3x - 5y = 11}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{y = 3 - 2x}\\{3x - 5\left( {3 - 2x} \right) = 11}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{y = 3 - 2x}\\{13x = 26}\end{array}} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3 - 2.2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = - 1\end{array} \right..\)
Vậy hệ phương trình có tập nghiệm \(S = \left\{ {\left( {2;\, - 1} \right)} \right\}\)
Câu 5
Phương pháp:
Áp dụng định lí Pytago cho \(\Delta ABC\) vuông tại \(A\), tính được \(BC\)
Áp dụng hệ thức lượng cho \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\), tính được \(AH\)
Cách giải:
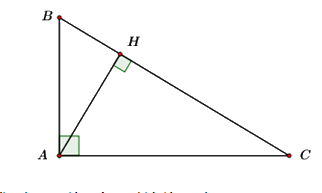
Áp dụng định lí Pytago cho \(\Delta ABC\) vuông tại \(A\) ta có:
\(A{B^2} + A{C^2} = B{C^2}\)\( \Rightarrow A{C^2} = B{C^2} - A{B^2}\)
\(\begin{array}{l} \Leftrightarrow A{C^2} = {5^2} - {3^2} = 16\\ \Rightarrow BC = \,4\,cm.\end{array}\)
Áp dụng hệ thức lượng cho \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(AH.BC = AB.AC\)\( \Rightarrow AH = \dfrac{{AB.AC}}{{BC}}\)
\( \Rightarrow AH = \dfrac{{3.4}}{5} = 2,4\,cm.\)
Vậy \(AH = 2,4\,\,cm.\)
Câu 6
Phương pháp:
Áp dụng hệ thức: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Rightarrow {\cos ^2}\alpha = 1 - {\sin ^2}\alpha \), tính được \(\cos \alpha \), tìm được \(\cos \alpha \) thỏa mãn điều kiện
Tính được \(\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }}\)
Từ đó tính được giá trị biểu thức \(B\)
Cách giải:
Áp dụng hệ thức: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Rightarrow {\cos ^2}\alpha = 1 - {\sin ^2}\alpha \)
\( \Rightarrow {\cos ^2}\alpha = 1 - 0,{6^2} = 1 - 0,36 = 0,64\)
\( \Rightarrow \cos \alpha = \pm 0,8\)
Mà \(\alpha \) là góc nhọn nên \(\cos \alpha > 0\) do đó \(\cos \alpha = 0,8\)
Ta có: \(\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }} = \dfrac{{0,6}}{{0,8}} = \dfrac{3}{4} = 0,75\)
Khi đó: \(B = 5\cos \alpha - 4\tan \alpha \)\( = 5.0,8 - 4.0,75 = 1\)
Vậy \(B = 1.\)
Câu 7
Phương pháp:
Xét phương trình hoành độ giao điểm giữa \(\left( P \right)\) và \(\left( d \right)\) \(\left( 1 \right)\)
\(\left( P \right)\) và \(\left( d \right)\) không có điểm chung khi phương trình \(\left( 1 \right)\) vô nghiệm \( \Leftrightarrow \Delta < 0\) (hoặc \( \Leftrightarrow \Delta ' < 0\))
Cách giải:
Hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là nghiệm của phương trình: \({x^2} = 3x + m \Leftrightarrow {x^2} - 3x - m = 0\,\,\left( 1 \right)\)
Phương trình có: \(\Delta = {\left( { - 3} \right)^2} - 4.\left( { - m} \right) = 9 + 4m\)
\(\left( P \right)\) và \(\left( d \right)\) không có điểm chung khi phương trình \(\left( 1 \right)\)vô nghiệm
\( \Leftrightarrow \Delta < 0 \Leftrightarrow 9 + 4m < 0 \Leftrightarrow m < - \dfrac{9}{4}\)
Vậy \(\left( P \right)\) và \(\left( d \right)\) không có điểm chung khi \(m < - \dfrac{9}{4}.\)
Câu 8
Phương pháp:
Hình nón có chiều cao là \(h\) và bán kính đáy là \(r\) có thể tích là: \(V = \dfrac{1}{3}\pi {r^2}h\), suy ra \(r = \sqrt {\dfrac{{3V}}{{\pi h}}} \)
Đường sinh \(l\) của hình nón được tính theo công thức: \({l^2} = {r^2} + {h^2}\)
Hình nón có đường sinh là \(l\) và bán kính đáy là \(r\) có diện tích xung quanh là: \({S_{xq}} = \pi rl\)
Cách giải:
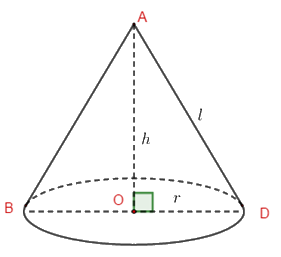
Ta có: \(V = \dfrac{1}{3}\pi {r^2}h\)\( \Rightarrow r = \sqrt {\dfrac{{3V}}{{\pi h}}} \)
\( \Rightarrow \) Bán kính của hình nón là: \(r = \sqrt {\dfrac{{3V}}{{\pi h}}} = \sqrt {\dfrac{{3.96\pi }}{{\pi .8}}} = \sqrt {36} = 6\,cm.\)
Gọi đường sinh của hình nón là \(l.\) Khi đó ta có:
\({l^2} = {h^2} + {r^2} = {8^2} + {6^2} = 100\) \( \Rightarrow l = 10\,\,cm\)
\( \Rightarrow \) Diện tích xung quanh của hình nón là: \({S_{xq}} = \pi rl = \pi .6.10 = 60\pi \,\,c{m^2}.\)
Vậy diện tích xung quanh của hình nón đã cho là \(60\pi \,\,c{m^2}.\)
Câu 9
Phương pháp:
Sử dụng hằng đẳng thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)
Thực hiện các phép tính với căn bậc hai.
Cách giải:
Ta có:
\(\begin{array}{l}VT = \left( {\sqrt {{{\left( {1 - \sqrt {2022} } \right)}^2}} } \right)\left( {\sqrt {2023 + 2\sqrt {2022} } } \right)\\\,\,\,\,\,\,\,\, = \left| {1 - \sqrt {2022} } \right|.\sqrt {{{\left( {\sqrt {2022} + 1} \right)}^2}} \\\,\,\,\,\,\,\,\, = \left( {\sqrt {2022} - 1} \right).\left( {\sqrt {2022} + 1} \right)\,\,\,\,\,\left( {do\,\,\,1 - \sqrt {2022} < 0,\,\,\sqrt {2022} + 1 > 0} \right)\\\,\,\,\,\,\,\,\, = 2022 - 1 = 2021 = VP\,\,\,\,\,\left( {dpcm} \right)\end{array}\)
Vậy \(\left( {\sqrt {{{\left( {1 - \sqrt {2022} } \right)}^2}} } \right)\left( {\sqrt {2023 + 2\sqrt {2022} } } \right) = 2021.\)
Câu 10
Phương pháp:
Gọi vận tốc dự định của người đi xe gắn máy là \(x\,\,\left( {km/h,\,\,x > 0} \right).\)
Tính được thời gian đi hết quãng đường \(AB\) theo dự định theo \(x\)
Tính được vận tốc và thời gian đi hết quãng đường \(AB\) theo thực tế theo \(x\)
Dựa vào giả thiết về thời gian nên ta lập được phương trình.
Giải phương trình, đối chiếu điều kiện và kết luận.
Cách giải:
Đổi \(15\)phút = \(\dfrac{1}{4}\) giờ
Gọi vận tốc dự định của người đi xe gắn máy là \(x\,\,\left( {km/h,\,\,x > 0} \right).\)
\( \Rightarrow \) Thời gian đi hết quãng đường AB dự định là: \(\dfrac{{70}}{x}\left( h \right)\)
Vận tốc khi tăng \(5\,km/h\) so với dự định là: \(x + 5\,\,\left( {km/h} \right)\).
\( \Rightarrow \) Thời gian thực tế xe đi hết quãng đường AB là: \(\dfrac{{70}}{{x + 5}}\,\,\left( h \right).\)
Vì khi tăng vận tốc thêm \(5\,km/h\) so với dự định thì đến \(B\)sớm hơn 15 phútnên ta có phương trình:
\(\begin{array}{l}\,\,\,\,\,\dfrac{{70}}{x} - \dfrac{{70}}{{x + 5}} = \dfrac{1}{4}\\ \Leftrightarrow 280.\left( {x + 5} \right) - 280x = x\left( {x + 5} \right)\\ \Leftrightarrow 280x + 1400 - 280x = {x^2} + 5x\\ \Leftrightarrow {x^2} + 5x - 1400 = 0\end{array}\)
Phương trình có: \(\Delta = {\left( { - 5} \right)^2} + 4.1400 = 5625 > 0\)
\( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \({x_1} = \dfrac{{ - 5 + \sqrt {5625} }}{2} = 35\,\,\,\left( {tm} \right)\) và \({x_2} = \dfrac{{ - 5 - \sqrt {5625} }}{2} = - 40\,\,\,\left( {ktm} \right)\)
Vậy vận tốc dự định của người đi xe gắn máy là \(35\,km/h\).
Câu 11
Phương pháp:
Phương trình có hai nghiệm cùng dấu \( \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\\dfrac{c}{a} > 0\end{array} \right.\)
Áp dụng hệ thức Vi-et tính được \({x_1} + {x_2}\)
Giả sử \({x_1} + {x_2} > 0\), nếu điều giả sử đúng thì phương trình có hai nghiệm phân biệt dương còn nếu điều giả sử sai thì phương trình có hai nghiệm âm phân biệt.
Cách giải:
Phương trình \(2{x^2} - \left( {2m - 1} \right)x + m - 1 = 0\,\,\,\,\left( 1 \right)\) có hai nghiệm phân biệt cùng dấu \( \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\\dfrac{c}{a} > 0\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{\left( {2m - 1} \right)^2} - 4.2\left( {m - 1} \right) > 0\\\dfrac{{m - 1}}{2} > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}4{m^2} - 4m + 1 - 8m + 8 > 0\\m - 1 > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}4{m^2} - 12m + 9 > 0\\m > 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{\left( {2m - 3} \right)^2} > 0\\m > 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2m - 3 \ne 0\\m > 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne \dfrac{3}{2}\\m > 1\end{array} \right.\end{array}\)
Với \(m > 1,\,\,m \ne \dfrac{3}{2}\) thì phương trình đã cho có hai nghiệm cùng dấu.
Áp dụng hệ thức Vi-et ta có: \({x_1} + {x_2} = \dfrac{{2m - 1}}{2}\)
Giả sử \({x_1} + {x_2} > 0\) \( \Leftrightarrow \dfrac{{2m - 1}}{2} > 0\)\( \Leftrightarrow 2m - 1 > 0 \Leftrightarrow m > \dfrac{1}{2}\)
\( \Rightarrow \) Với \(\forall m > 1,\,\,m \ne \dfrac{3}{2}\) thì ta có: \({x_1} + {x_2} > 0\)
\( \Rightarrow \) Phương trình có hai nghiệm cùng dương.
Với \({x_1} + {x_2} < 0\)\( \Leftrightarrow \dfrac{{2m - 1}}{2} < 0\)\( \Leftrightarrow 2m - 1 < 0 \Leftrightarrow m < \dfrac{1}{2}\)
Mâu thuẫn với điều kiện: \(m > 1,\,\,m \ne \dfrac{3}{2}.\)
Vậy với \(m > 1,\,\,m \ne \dfrac{3}{2}\) thì phương trình đã cho có hai nghiệm cùng dương.
Câu 12
Phương pháp:
Ta chỉ ra được: \(\angle CIJ = \angle CBH\); \(\tan CBH = \dfrac{{CH}}{{BH}}\); \(\tan CIJ = \dfrac{{CJ}}{{CI}} = \dfrac{{CJ}}{{HI}}\) từ đó, suy ra \(\dfrac{{CH}}{{BH}} = \dfrac{{CJ}}{{HI}}\)
Ta sẽ chứng minh:
+ \(\angle CHJ = \angle HBI\)
+ \( HE.HJ = HC.HI\)
Mà \(\left\{ \begin{array}{l}HJ = \dfrac{1}{2}HD\,\,\,\left( {gt} \right)\\HI = \dfrac{1}{2}HC\,\,\,\left( {gt} \right)\end{array} \right.\)
Suy ra \(HE.HD = H{C^2}\,\,\,\left( {dpcm} \right).\)
Cách giải:
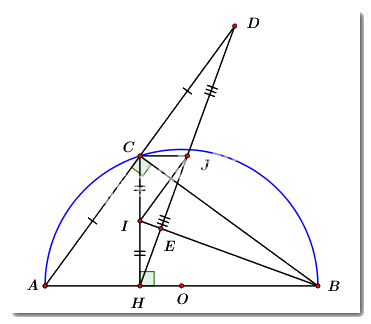
Ta có: \(\angle ACB\) là góc nội tiếp chắn nửa đường tròn \(\angle ACB = {90^0}\) hay \(\angle AC \bot BC\)
Xét \(\Delta AHD\) ta có:
\(C\) là trung điểm của \(AD\) (gt)
\(J\) là trung điểm của \(HD\) (gt)
\( \Rightarrow CJ\) là đường trung bình của \(\Delta AHD\) (định nghĩa đường trung bình của tam giác)
\( \Rightarrow CJ//AB\,\) (tính chất).
Mà \(CH \bot AH\)(do \(H\) là hình chiếu của \(C\) trên \(AB\))
Suy ra \(CJ \bot CH\)tại \(C\) (từ song song đến vuông góc).
\( \Rightarrow \angle HCJ = {90^0}\)
Xét \(\Delta CHD\) ta có:
\(I,\,\,J\) lần lượt là trung điểm của \(CH\) và \(HD\) (gt)
\( \Rightarrow IJ\) là đường trung bình của \(\Delta CHD\) (định nghĩa đường trung bình của tam giác).
\( \Rightarrow IJ//CD\) (tính chất đường trung bình của tam giác).
Lại có: \(BC \bot AC\,\,\left( {cmt} \right)\) hay \(BC \bot CD\)
\( \Rightarrow IJ \bot BC\) (từ song song đến vuông góc).
\( \Rightarrow \angle CIJ = \angle CBH\) (cùng phụ với \(\angle HCB\)) \(\left( 1 \right)\)
Trong \(\Delta CHB\) vuông tại \(H\) ta có: \(\tan CBH = \dfrac{{CH}}{{BH}}\) \(\left( 2 \right)\)
Trong \(\Delta CIJ\) vuông tại \(C\) ta có: \(\tan CIJ = \dfrac{{CJ}}{{CI}} = \dfrac{{CJ}}{{HI}}\) \(\left( 3 \right)\)
Từ \(\left( 1 \right),\,\,\left( 2 \right),\,\,\left( 3 \right)\) suy ra: \(\dfrac{{CH}}{{BH}} = \dfrac{{CJ}}{{HI}}\)
Xét \(\Delta CJH\)và \(\Delta HIB\) ta có:
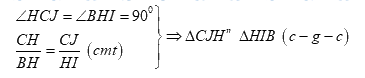
\( \Rightarrow \angle CHJ = \angle HBI\) (2 góc tương ứng)
Mà \(\angle CHJ + \angle CHJ = {90^0}\)
Suy ra \(\angle HBI + \angle EHB = {90^0}\) \( \Rightarrow \Delta EHB\) vuông tại \(E\)
\( \Rightarrow \angle HEB = {90^0}\) hay \(\angle HEI = {90^0}\)
Xét \(\Delta HEI\) và \(\Delta HCJ\) ta có:
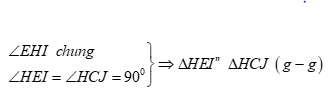
\( \Rightarrow \dfrac{{HE}}{{HC}} = \dfrac{{HI}}{{HJ}}\)\( \Leftrightarrow HE.HJ = HC.HI\)
Mà \(\left\{ \begin{array}{l}HJ = \dfrac{1}{2}HD\,\,\,\left( {gt} \right)\\HI = \dfrac{1}{2}HC\,\,\,\left( {gt} \right)\end{array} \right.\)
Suy ra \(HE.HD = H{C^2}\,\,\,\left( {dpcm} \right).\)
Kỳ thi tuyển sinh vào lớp 10 tại tỉnh Lâm Đồng năm 2021 là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Đề thi môn Toán thường có tính phân loại cao, đòi hỏi học sinh không chỉ nắm vững kiến thức cơ bản mà còn phải có khả năng vận dụng linh hoạt vào giải quyết các bài toán thực tế. Cấu trúc đề thi thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh có cái nhìn sâu sắc hơn về đề thi, chúng tôi sẽ phân tích chi tiết một số đề thi tiêu biểu:
Đề thi số 1 tập trung vào các kiến thức về đại số, đặc biệt là phương trình và hệ phương trình. Các bài toán trong đề thi này đòi hỏi học sinh phải có khả năng biến đổi phương trình một cách linh hoạt và tìm ra nghiệm một cách chính xác. Ngoài ra, đề thi cũng có một số bài toán về hình học phẳng, yêu cầu học sinh phải vận dụng các định lý và tính chất hình học để giải quyết.
Đề thi số 2 có độ khó cao hơn so với đề thi số 1, với nhiều bài toán đòi hỏi học sinh phải có khả năng tư duy logic và sáng tạo. Đề thi này tập trung vào các kiến thức về hình học không gian, yêu cầu học sinh phải có khả năng hình dung và phân tích các hình không gian một cách chính xác. Ngoài ra, đề thi cũng có một số bài toán về tổ hợp - xác suất, đòi hỏi học sinh phải có khả năng tính toán và phân tích các tình huống một cách cẩn thận.
Để đạt kết quả tốt nhất trong kỳ thi tuyển sinh vào lớp 10, các em học sinh cần có một kế hoạch luyện thi khoa học và hiệu quả. Dưới đây là một số lời khuyên:
Ngoài các đề thi vào 10 môn Toán Lâm Đồng năm 2021, các em học sinh có thể tham khảo thêm các tài liệu ôn thi sau:
Chúc các em học sinh ôn thi tốt và đạt kết quả cao trong kỳ thi tuyển sinh vào lớp 10 môn Toán tại tỉnh Lâm Đồng năm 2021! Hãy luôn tự tin vào bản thân và cố gắng hết mình, chắc chắn các em sẽ thành công.