Giaitoan.edu.vn xin giới thiệu Đề thi vào 10 môn Toán Quảng Bình năm 2021 (đề số 2). Đây là đề thi chính thức được sử dụng trong kỳ thi tuyển sinh vào lớp 10 tại tỉnh Quảng Bình năm 2021.
Đề thi này có cấu trúc và độ khó tương tự như các đề thi khác trong kỳ thi tuyển sinh, giúp học sinh làm quen với dạng đề và rèn luyện kỹ năng giải toán.
Câu 1 (2 điểm): Rút gọn các biểu thức:
Câu 1 (2 điểm):
Rút gọn các biểu thức:
a) \(P = \sqrt {12} - \sqrt {27} + \sqrt {48} .\)
b) \(Q = \left( {5 - \dfrac{{x + \sqrt x }}{{\sqrt x + 1}}} \right).\left( {5 + \dfrac{{x - \sqrt x }}{{\sqrt x - 1}}} \right)\) với \(x \ge 0,\,\,x \ne 1.\)
Câu 2 (1,5 điểm):
a) Tìm tất cả các giá trị của \(n\) để hàm số \(y = \left( {n - 1} \right)x + 2\) nghịch biến trên \(\mathbb{R}.\)
b) Giải hệ phương trình \(\left\{ \begin{array}{l}2x + 3y = 8\\ - 4x + 3y = 2\end{array} \right..\)
Câu 3 (2 điểm):
Cho phương trình \({x^2} + 6x + n + 4 = 0\,\,\,\,\left( 1 \right)\) với \(n\) là tham số.
a) Giải phương trình \(\left( 1 \right)\) khi \(n = 1.\)
b) Tìm tất cả các giá trị của \(n\) để phương trình \(\left( 1 \right)\) có hai nghiệm \({x_1},\,\,{x_2}\) thỏa mãn \(2020\left( {{x_1} + {x_2}} \right) + 2021{x_1}{x_2} = - 2014.\)
Câu 4 (1 điểm):
Cho \(a,\,\,b\) là các số thực dương. Chứng minh \(\dfrac{{a + b}}{{\sqrt {a\left( {8a + b} \right)} + \sqrt {b\left( {8b + a} \right)} }} \ge \dfrac{1}{3}.\)
Câu 5 (3,5 điểm):
Cho đường tròn \(\left( {O;\,\,R} \right)\) đường kính \(AB,\) dây cung \(PQ\) vuông góc với \(AB\) tại \(H\) sao cho \(AH > BH.\) Trên đoạn \(PH\) lấy điểm \(E\) (\(E\) khác \(P\) và \(H\)), tia \(BE\) cắt đường tròn \(\left( {O;\,\,R} \right)\) tại điểm thứ hai là \(F.\) Chứng minh rằng:
a) Tứ giác \(AHEF\) nội tiếp đường tròn.
b) \(\Delta BEP\) đồng dạng với \(\Delta BPF.\)
c) \(BE.BF + AH.AB = 4{R^2}.\)
Câu 1 (2 điểm):
Rút gọn các biểu thức:
a) \(P = \sqrt {12} - \sqrt {27} + \sqrt {48} .\)
b) \(Q = \left( {5 - \dfrac{{x + \sqrt x }}{{\sqrt x + 1}}} \right).\left( {5 + \dfrac{{x - \sqrt x }}{{\sqrt x - 1}}} \right)\) với \(x \ge 0,\,\,x \ne 1.\)
Câu 2 (1,5 điểm):
a) Tìm tất cả các giá trị của \(n\) để hàm số \(y = \left( {n - 1} \right)x + 2\) nghịch biến trên \(\mathbb{R}.\)
b) Giải hệ phương trình \(\left\{ \begin{array}{l}2x + 3y = 8\\ - 4x + 3y = 2\end{array} \right..\)
Câu 3 (2 điểm):
Cho phương trình \({x^2} + 6x + n + 4 = 0\,\,\,\,\left( 1 \right)\) với \(n\) là tham số.
a) Giải phương trình \(\left( 1 \right)\) khi \(n = 1.\)
b) Tìm tất cả các giá trị của \(n\) để phương trình \(\left( 1 \right)\) có hai nghiệm \({x_1},\,\,{x_2}\) thỏa mãn \(2020\left( {{x_1} + {x_2}} \right) + 2021{x_1}{x_2} = - 2014.\)
Câu 4 (1 điểm):
Cho \(a,\,\,b\) là các số thực dương. Chứng minh \(\dfrac{{a + b}}{{\sqrt {a\left( {8a + b} \right)} + \sqrt {b\left( {8b + a} \right)} }} \ge \dfrac{1}{3}.\)
Câu 5 (3,5 điểm):
Cho đường tròn \(\left( {O;\,\,R} \right)\) đường kính \(AB,\) dây cung \(PQ\) vuông góc với \(AB\) tại \(H\) sao cho \(AH > BH.\) Trên đoạn \(PH\) lấy điểm \(E\) (\(E\) khác \(P\) và \(H\)), tia \(BE\) cắt đường tròn \(\left( {O;\,\,R} \right)\) tại điểm thứ hai là \(F.\) Chứng minh rằng:
a) Tứ giác \(AHEF\) nội tiếp đường tròn.
b) \(\Delta BEP\) đồng dạng với \(\Delta BPF.\)
c) \(BE.BF + AH.AB = 4{R^2}.\)
Câu 1 (TH):
Phương pháp:
a) Sử dụng hằng đẳng thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)
Thực hiện các phép tính với căn bậc hai.
b) Xác định mẫu thức chung của biểu thức
Quy đồng các phân thức, thực hiện các phép toán từ đó rút gọn được biểu thức.
Cách giải:
a) \(P = \sqrt {12} - \sqrt {27} + \sqrt {48} .\)
\(\begin{array}{l}P = \sqrt {12} - \sqrt {27} + \sqrt {48} .\\\,\,\,\,\, = \sqrt {{2^2}.3} - \sqrt {{3^2}.3} + \sqrt {{4^2}.3} \\\,\,\,\,\, = 2\sqrt 3 - 3\sqrt 3 + 4\sqrt 3 \\\,\,\,\,\, = 3\sqrt 3 .\end{array}\)
Vậy \(P = 3\sqrt 3 .\)
b) \(Q = \left( {5 - \dfrac{{x + \sqrt x }}{{\sqrt x + 1}}} \right).\left( {5 + \dfrac{{x - \sqrt x }}{{\sqrt x - 1}}} \right)\) với \(x \ge 0,\,\,x \ne 1.\)
Điều kiện: \(x \ge 0,\,\,x \ne 1.\)
\(\begin{array}{l}Q = \left( {5 - \dfrac{{x + \sqrt x }}{{\sqrt x + 1}}} \right).\left( {5 + \dfrac{{x - \sqrt x }}{{\sqrt x - 1}}} \right)\\\,\,\,\, = \left( {5 - \dfrac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\sqrt x + 1}}} \right).\left( {5 + \dfrac{{\sqrt x \left( {\sqrt x - 1} \right)}}{{\sqrt x - 1}}} \right)\\\,\,\,\, = \left( {5 - \sqrt x } \right)\left( {5 + \sqrt x } \right)\\\,\,\,\, = 25 - x.\end{array}\)
Vậy \(Q = 25 - x\) khi \(x \ge 0,\,\,x \ne 1.\)
Câu 2 (TH):
Phương pháp:
a) Hàm số \(y = ax + b\) nghịch biến trên \(\mathbb{R} \Leftrightarrow a < 0\)
b) Sử dụng phương pháp cộng đại số, tìm được nghiệm \(x\)
Sử dụng phương pháp thế, tìm được nghiệm \(y\)
Kết luận nghiệm \(\left( {x;y} \right)\) của hệ phương trình.
Cách giải:
a) Hàm số \(y = \left( {n - 1} \right)x + 2\) nghịch biến trên \(\mathbb{R}\) \( \Leftrightarrow n - 1 < 0\) \( \Leftrightarrow n < 1.\)
Vậy \(n < 1\) thì hàm số đã cho nghịch biến trên \(\mathbb{R}.\)
b) \(\left\{ \begin{array}{l}2x + 3y = 8\\ - 4x + 3y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}6x = 6\\y = \dfrac{{8 - 2x}}{3}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = \dfrac{{8 - 2.1}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right.\)
Vậy hệ phương trình có tập nghiệm \(S = \left\{ {\left( {1;\,\,2} \right)} \right\}.\)
Câu 3 (VD):
Phương pháp:
a) Tính nhẩm nghiệm của phương trình bậc hai: Nếu \(a - b + c = 0\) thì phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt: \({x_1} = - 1;{x_2} = - \dfrac{c}{a}\)
b) Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt \(\Delta > 0\) (hoặc \(\Delta ' > 0\))
Áp dụng hệ thức Vi – ét, tính được \({x_1} + {x_2};{x_1}.{x_2}\) theo \(n\)
Thay vào \(2020\left( {{x_1} + {x_2}} \right) + 2021{x_1}{x_2} = - 2014.\), ta tìm được \(n\)
Cách giải:
a) Với \(n = 1\) ta có phương trình \(\left( 1 \right)\) trở thành: \({x^2} + 6x + 5 = 0\)
Phương trình có \(a - b + c = 1 - 6 + 5 = 0\)
\( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \({x_1} = - 1\) và \({x_2} = - \dfrac{c}{a} = - 5.\)
Vậy với \(n = 1\) thì phương trình đã cho có tập nghiệm \(S = \left\{ { - 5; - 1} \right\}.\)
b) Xét phương trình \({x^2} + 6x + n + 4 = 0\,\,\,\,\left( 1 \right)\)
Phương trình có: \(\Delta ' = 9 - n - 4 = 5 - n.\)
Phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) \( \Leftrightarrow \Delta ' > 0\) \( \Leftrightarrow 5 - n > 0\) \( \Leftrightarrow n < 5.\)
Với \(n < 5\) thì phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}.\)
Áp dụng hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 6\\{x_1}{x_2} = n + 4\end{array} \right..\)
Theo đề bài ta có: \(2020\left( {{x_1} + {x_2}} \right) + 2021{x_1}{x_2} = - 2014\)
\(\begin{array}{l} \Leftrightarrow 2020.\left( { - 6} \right) + 2021.\left( {n + 4} \right) = - 2014\\ \Leftrightarrow - 12120 + 2021n + 8084 = - 2014\\ \Leftrightarrow 2021n = 2022\\ \Leftrightarrow n = \dfrac{{2022}}{{2021}}\,\,\,\left( {tm} \right).\end{array}\)
Vậy \(n = \dfrac{{2022}}{{2021}}\) thỏa mãn bài toán.
Câu 4 (VDC):
Phương pháp:
Áp dụng bất đẳng thức Cô – si cho \(\sqrt {9a\left( {8a + b} \right)} \) và \(\sqrt {9b\left( {8b + a} \right)} \)
Từ đó, suy ra \(\sqrt {9a\left( {8a + b} \right)} + \sqrt {9b\left( {8b + a} \right)} \) sau đó, suy ra được \(\dfrac{{a + b}}{{\sqrt {a\left( {8a + b} \right)} + \sqrt {b\left( {8b + a} \right)} }}\)
Cách giải:
Áp dụng BĐT Cô-si ta có:
\(\begin{array}{l}\sqrt {9a\left( {8a + b} \right)} \le \dfrac{{9a + 8a + b}}{2} = \dfrac{{17a + b}}{2}\\\sqrt {9b\left( {8b + a} \right)} \le \dfrac{{9b + 8b + a}}{2} = \dfrac{{17b + a}}{2}\\ \Rightarrow \sqrt {9a\left( {8a + b} \right)} + \sqrt {9b\left( {8b + a} \right)} \le \dfrac{{17a + b}}{2} + \dfrac{{17b + a}}{2} = 9\left( {a + b} \right)\\ \Rightarrow \sqrt {a\left( {8a + b} \right)} + \sqrt {b\left( {8b + a} \right)} \le 3\left( {a + b} \right)\\ \Rightarrow \dfrac{{a + b}}{{\sqrt {a\left( {8a + b} \right)} + \sqrt {b\left( {8b + a} \right)} }} \ge \dfrac{1}{3}\,\,\,\left( {dpcm} \right).\end{array}\)
Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}9a = 8a + b\\9b = 8b + a\end{array} \right. \Leftrightarrow a = b.\)
Vậy \(\dfrac{{a + b}}{{\sqrt {a\left( {8a + b} \right)} + \sqrt {b\left( {8b + a} \right)} }} \ge \dfrac{1}{3}.\)
Câu 5 (VD):
Phương pháp:
a) Vận dụng dấu hiệu nhận biết: Tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp.
b) Ta sẽ chứng minh: \(\angle PEB = {180^0} - \angle FAB\,\,\,\left( 1 \right);\angle FPB = {180^0} - \angle FAB\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) \( \Rightarrow \angle FBB = \angle PEB\,\,\left( { = {{180}^0} - \angle FAB} \right)\)
Chứng minh được:
c)
Áp dụng hệ thức lượng trong \(\Delta APB\)ta có:\(A{P^2} = AH.AB\)
Áp dụng định lý Py – ta – go cho \(\Delta APB\): \(B{P^2} + A{P^2} = A{B^2} = 4{R^2}\)
\( \Rightarrow BE.BF + AH.AB = 4{R^2}\) (đpcm)
Cách giải:
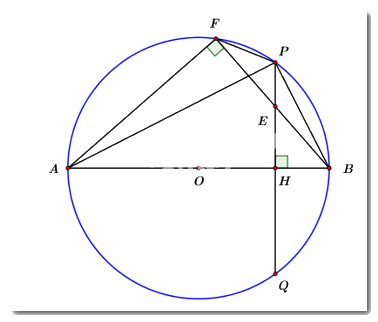
a) Ta có: \(\angle AFB\) là góc nội tiếp chắn nửa đường tròn \(\left( {O;\,\,R} \right).\)
\( \Rightarrow \angle AFB = {90^0}\)
Xét tứ giác \(AHEF\) ta có: \(\angle AFE + \angle AHE = {90^0} + {90^0} = {180^0}\)
\( \Rightarrow AHEF\) là tứ giác nội tiếp. (dhnb)
b) Ta có: \(AHEF\) là tứ giác nội tiếp (cmt)
\( \Rightarrow \angle FAH + \angle FEH = {180^0}\) (tính chất tứ giác nội tiếp)
Lại có: \(\angle PEB = \angle FEH\) (hai góc đối đỉnh).
\( \Rightarrow \angle PEB + \angle FAB = {180^0}\) \( \Rightarrow \angle PEB = {180^0} - \angle FAB\,\,\,\left( 1 \right)\)
Mà \(ABPF\) là tứ giác nội tiếp đường tròn \(\left( {O;\,\,R} \right)\)
\( \Rightarrow \angle FAB + \angle BPF = {180^0}\) \( \Rightarrow \angle FPB = {180^0} - \angle FAB\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) \( \Rightarrow \angle FBB = \angle PEB\,\,\left( { = {{180}^0} - \angle FAB} \right)\)
Xét \(\Delta BEP\) và \(\Delta BPF\) ta có:
\(\begin{array}{l}\angle FBB = \angle PEB\,\,\,\left( {cmt} \right)\\\angle B\,\,chung\\ \Rightarrow \Delta BEP \sim \Delta BPF\,\,\,\left( {g - g} \right).\end{array}\)
c) Ta có: \(\Delta BEP \sim \Delta BPF\,\,\,\left( {cmt} \right)\)
\( \Rightarrow \dfrac{{BE}}{{BP}} = \dfrac{{BP}}{{BF}} \Rightarrow B{P^2} = BE + BF.\)
Vì \(\angle APB\) là góc nội tiếp chắn nửa đường tròn \(\left( {O;\,\,R} \right)\)
\(\angle APB = {90^0}\) hay \(AP \bot PB\)
Áp dụng hệ thức lượng cho \(\Delta APB\) vuông tại \(P\) có đường cao \(PH\) ta có:
\(A{P^2} = AH.AB\)
\( \Rightarrow BE.BF + AH.AB = B{P^2} + A{P^2}\)
Áp dụng định lý Pitago cho \(\Delta APB\) vuông tại \(P\) ta có:
\(\begin{array}{l}B{P^2} + A{P^2} = A{B^2} = {\left( {2R} \right)^2} = 4{R^2}\\ \Rightarrow BE.BF + AH.AB = 4{R^2}\,\,\,\,\left( {dpcm} \right).\end{array}\)
Câu 1 (TH):
Phương pháp:
a) Sử dụng hằng đẳng thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)
Thực hiện các phép tính với căn bậc hai.
b) Xác định mẫu thức chung của biểu thức
Quy đồng các phân thức, thực hiện các phép toán từ đó rút gọn được biểu thức.
Cách giải:
a) \(P = \sqrt {12} - \sqrt {27} + \sqrt {48} .\)
\(\begin{array}{l}P = \sqrt {12} - \sqrt {27} + \sqrt {48} .\\\,\,\,\,\, = \sqrt {{2^2}.3} - \sqrt {{3^2}.3} + \sqrt {{4^2}.3} \\\,\,\,\,\, = 2\sqrt 3 - 3\sqrt 3 + 4\sqrt 3 \\\,\,\,\,\, = 3\sqrt 3 .\end{array}\)
Vậy \(P = 3\sqrt 3 .\)
b) \(Q = \left( {5 - \dfrac{{x + \sqrt x }}{{\sqrt x + 1}}} \right).\left( {5 + \dfrac{{x - \sqrt x }}{{\sqrt x - 1}}} \right)\) với \(x \ge 0,\,\,x \ne 1.\)
Điều kiện: \(x \ge 0,\,\,x \ne 1.\)
\(\begin{array}{l}Q = \left( {5 - \dfrac{{x + \sqrt x }}{{\sqrt x + 1}}} \right).\left( {5 + \dfrac{{x - \sqrt x }}{{\sqrt x - 1}}} \right)\\\,\,\,\, = \left( {5 - \dfrac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\sqrt x + 1}}} \right).\left( {5 + \dfrac{{\sqrt x \left( {\sqrt x - 1} \right)}}{{\sqrt x - 1}}} \right)\\\,\,\,\, = \left( {5 - \sqrt x } \right)\left( {5 + \sqrt x } \right)\\\,\,\,\, = 25 - x.\end{array}\)
Vậy \(Q = 25 - x\) khi \(x \ge 0,\,\,x \ne 1.\)
Câu 2 (TH):
Phương pháp:
a) Hàm số \(y = ax + b\) nghịch biến trên \(\mathbb{R} \Leftrightarrow a < 0\)
b) Sử dụng phương pháp cộng đại số, tìm được nghiệm \(x\)
Sử dụng phương pháp thế, tìm được nghiệm \(y\)
Kết luận nghiệm \(\left( {x;y} \right)\) của hệ phương trình.
Cách giải:
a) Hàm số \(y = \left( {n - 1} \right)x + 2\) nghịch biến trên \(\mathbb{R}\) \( \Leftrightarrow n - 1 < 0\) \( \Leftrightarrow n < 1.\)
Vậy \(n < 1\) thì hàm số đã cho nghịch biến trên \(\mathbb{R}.\)
b) \(\left\{ \begin{array}{l}2x + 3y = 8\\ - 4x + 3y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}6x = 6\\y = \dfrac{{8 - 2x}}{3}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = \dfrac{{8 - 2.1}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right.\)
Vậy hệ phương trình có tập nghiệm \(S = \left\{ {\left( {1;\,\,2} \right)} \right\}.\)
Câu 3 (VD):
Phương pháp:
a) Tính nhẩm nghiệm của phương trình bậc hai: Nếu \(a - b + c = 0\) thì phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt: \({x_1} = - 1;{x_2} = - \dfrac{c}{a}\)
b) Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt \(\Delta > 0\) (hoặc \(\Delta ' > 0\))
Áp dụng hệ thức Vi – ét, tính được \({x_1} + {x_2};{x_1}.{x_2}\) theo \(n\)
Thay vào \(2020\left( {{x_1} + {x_2}} \right) + 2021{x_1}{x_2} = - 2014.\), ta tìm được \(n\)
Cách giải:
a) Với \(n = 1\) ta có phương trình \(\left( 1 \right)\) trở thành: \({x^2} + 6x + 5 = 0\)
Phương trình có \(a - b + c = 1 - 6 + 5 = 0\)
\( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \({x_1} = - 1\) và \({x_2} = - \dfrac{c}{a} = - 5.\)
Vậy với \(n = 1\) thì phương trình đã cho có tập nghiệm \(S = \left\{ { - 5; - 1} \right\}.\)
b) Xét phương trình \({x^2} + 6x + n + 4 = 0\,\,\,\,\left( 1 \right)\)
Phương trình có: \(\Delta ' = 9 - n - 4 = 5 - n.\)
Phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) \( \Leftrightarrow \Delta ' > 0\) \( \Leftrightarrow 5 - n > 0\) \( \Leftrightarrow n < 5.\)
Với \(n < 5\) thì phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}.\)
Áp dụng hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 6\\{x_1}{x_2} = n + 4\end{array} \right..\)
Theo đề bài ta có: \(2020\left( {{x_1} + {x_2}} \right) + 2021{x_1}{x_2} = - 2014\)
\(\begin{array}{l} \Leftrightarrow 2020.\left( { - 6} \right) + 2021.\left( {n + 4} \right) = - 2014\\ \Leftrightarrow - 12120 + 2021n + 8084 = - 2014\\ \Leftrightarrow 2021n = 2022\\ \Leftrightarrow n = \dfrac{{2022}}{{2021}}\,\,\,\left( {tm} \right).\end{array}\)
Vậy \(n = \dfrac{{2022}}{{2021}}\) thỏa mãn bài toán.
Câu 4 (VDC):
Phương pháp:
Áp dụng bất đẳng thức Cô – si cho \(\sqrt {9a\left( {8a + b} \right)} \) và \(\sqrt {9b\left( {8b + a} \right)} \)
Từ đó, suy ra \(\sqrt {9a\left( {8a + b} \right)} + \sqrt {9b\left( {8b + a} \right)} \) sau đó, suy ra được \(\dfrac{{a + b}}{{\sqrt {a\left( {8a + b} \right)} + \sqrt {b\left( {8b + a} \right)} }}\)
Cách giải:
Áp dụng BĐT Cô-si ta có:
\(\begin{array}{l}\sqrt {9a\left( {8a + b} \right)} \le \dfrac{{9a + 8a + b}}{2} = \dfrac{{17a + b}}{2}\\\sqrt {9b\left( {8b + a} \right)} \le \dfrac{{9b + 8b + a}}{2} = \dfrac{{17b + a}}{2}\\ \Rightarrow \sqrt {9a\left( {8a + b} \right)} + \sqrt {9b\left( {8b + a} \right)} \le \dfrac{{17a + b}}{2} + \dfrac{{17b + a}}{2} = 9\left( {a + b} \right)\\ \Rightarrow \sqrt {a\left( {8a + b} \right)} + \sqrt {b\left( {8b + a} \right)} \le 3\left( {a + b} \right)\\ \Rightarrow \dfrac{{a + b}}{{\sqrt {a\left( {8a + b} \right)} + \sqrt {b\left( {8b + a} \right)} }} \ge \dfrac{1}{3}\,\,\,\left( {dpcm} \right).\end{array}\)
Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}9a = 8a + b\\9b = 8b + a\end{array} \right. \Leftrightarrow a = b.\)
Vậy \(\dfrac{{a + b}}{{\sqrt {a\left( {8a + b} \right)} + \sqrt {b\left( {8b + a} \right)} }} \ge \dfrac{1}{3}.\)
Câu 5 (VD):
Phương pháp:
a) Vận dụng dấu hiệu nhận biết: Tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp.
b) Ta sẽ chứng minh: \(\angle PEB = {180^0} - \angle FAB\,\,\,\left( 1 \right);\angle FPB = {180^0} - \angle FAB\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) \( \Rightarrow \angle FBB = \angle PEB\,\,\left( { = {{180}^0} - \angle FAB} \right)\)
Chứng minh được:
c)
Áp dụng hệ thức lượng trong \(\Delta APB\)ta có:\(A{P^2} = AH.AB\)
Áp dụng định lý Py – ta – go cho \(\Delta APB\): \(B{P^2} + A{P^2} = A{B^2} = 4{R^2}\)
\( \Rightarrow BE.BF + AH.AB = 4{R^2}\) (đpcm)
Cách giải:
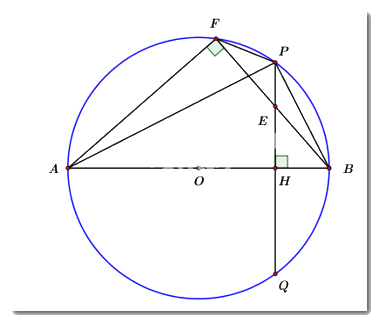
a) Ta có: \(\angle AFB\) là góc nội tiếp chắn nửa đường tròn \(\left( {O;\,\,R} \right).\)
\( \Rightarrow \angle AFB = {90^0}\)
Xét tứ giác \(AHEF\) ta có: \(\angle AFE + \angle AHE = {90^0} + {90^0} = {180^0}\)
\( \Rightarrow AHEF\) là tứ giác nội tiếp. (dhnb)
b) Ta có: \(AHEF\) là tứ giác nội tiếp (cmt)
\( \Rightarrow \angle FAH + \angle FEH = {180^0}\) (tính chất tứ giác nội tiếp)
Lại có: \(\angle PEB = \angle FEH\) (hai góc đối đỉnh).
\( \Rightarrow \angle PEB + \angle FAB = {180^0}\) \( \Rightarrow \angle PEB = {180^0} - \angle FAB\,\,\,\left( 1 \right)\)
Mà \(ABPF\) là tứ giác nội tiếp đường tròn \(\left( {O;\,\,R} \right)\)
\( \Rightarrow \angle FAB + \angle BPF = {180^0}\) \( \Rightarrow \angle FPB = {180^0} - \angle FAB\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) \( \Rightarrow \angle FBB = \angle PEB\,\,\left( { = {{180}^0} - \angle FAB} \right)\)
Xét \(\Delta BEP\) và \(\Delta BPF\) ta có:
\(\begin{array}{l}\angle FBB = \angle PEB\,\,\,\left( {cmt} \right)\\\angle B\,\,chung\\ \Rightarrow \Delta BEP \sim \Delta BPF\,\,\,\left( {g - g} \right).\end{array}\)
c) Ta có: \(\Delta BEP \sim \Delta BPF\,\,\,\left( {cmt} \right)\)
\( \Rightarrow \dfrac{{BE}}{{BP}} = \dfrac{{BP}}{{BF}} \Rightarrow B{P^2} = BE + BF.\)
Vì \(\angle APB\) là góc nội tiếp chắn nửa đường tròn \(\left( {O;\,\,R} \right)\)
\(\angle APB = {90^0}\) hay \(AP \bot PB\)
Áp dụng hệ thức lượng cho \(\Delta APB\) vuông tại \(P\) có đường cao \(PH\) ta có:
\(A{P^2} = AH.AB\)
\( \Rightarrow BE.BF + AH.AB = B{P^2} + A{P^2}\)
Áp dụng định lý Pitago cho \(\Delta APB\) vuông tại \(P\) ta có:
\(\begin{array}{l}B{P^2} + A{P^2} = A{B^2} = {\left( {2R} \right)^2} = 4{R^2}\\ \Rightarrow BE.BF + AH.AB = 4{R^2}\,\,\,\,\left( {dpcm} \right).\end{array}\)
Kỳ thi tuyển sinh vào lớp 10 là một bước ngoặt quan trọng trong quá trình học tập của học sinh. Để chuẩn bị tốt nhất cho kỳ thi này, việc luyện tập với các đề thi thử và đề thi chính thức các năm trước là vô cùng cần thiết. Bài viết này sẽ cung cấp phân tích chi tiết về Đề thi vào 10 môn Toán Quảng Bình năm 2021 (đề số 2), đồng thời hướng dẫn giải các bài toán khó, giúp học sinh tự tin hơn khi bước vào phòng thi.
Đề thi vào 10 môn Toán Quảng Bình năm 2021 (đề số 2) thường bao gồm các phần sau:
Nội dung đề thi thường bao gồm các chủ đề sau:
Một số câu hỏi trong đề thi thường gây khó khăn cho học sinh do yêu cầu vận dụng kiến thức tổng hợp và kỹ năng giải quyết vấn đề. Dưới đây là phân tích chi tiết một số câu hỏi khó thường gặp:
Phương trình bậc hai là một chủ đề quan trọng trong chương trình Toán lớp 9. Để giải quyết các bài toán về phương trình bậc hai, học sinh cần nắm vững các công thức nghiệm, điều kiện có nghiệm, và các phương pháp giải phương trình bậc hai.
Hình học không gian là một chủ đề khó đối với nhiều học sinh. Để giải quyết các bài toán về hình học không gian, học sinh cần có khả năng hình dung không gian, sử dụng các định lý và công thức liên quan đến hình học không gian.
Hệ phương trình là một chủ đề thường xuyên xuất hiện trong các đề thi vào 10. Để giải quyết các bài toán về hệ phương trình, học sinh cần nắm vững các phương pháp giải hệ phương trình, như phương pháp thế, phương pháp cộng đại số, và phương pháp đặt ẩn phụ.
Để giải đề thi vào 10 môn Toán Quảng Bình năm 2021 (đề số 2) hiệu quả, học sinh cần:
Để đạt kết quả tốt nhất trong kỳ thi tuyển sinh vào lớp 10, học sinh nên:
Đề thi vào 10 môn Toán Quảng Bình năm 2021 (đề số 2) là một đề thi quan trọng, giúp học sinh đánh giá năng lực và chuẩn bị tốt nhất cho kỳ thi tuyển sinh. Hy vọng với những phân tích và hướng dẫn giải chi tiết trong bài viết này, học sinh sẽ tự tin hơn và đạt kết quả tốt nhất trong kỳ thi sắp tới.