Chào mừng bạn đến với bài viết phân tích và giải chi tiết Đề số 6 - Đề thi vào lớp 10 môn Toán tại giaitoan.edu.vn. Đây là một trong những đề thi thử quan trọng giúp học sinh làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, cùng với các phương pháp giải nhanh giúp bạn tự tin đối mặt với kỳ thi sắp tới.
Đề thi vào lớp 10 môn Toán - Đề số 6 có đáp án và lời giải chi tiết
Đề bài
Câu 1. (2.5 điểm)
a) Rút gọn các biểu thức
\(A = \sqrt {12} + \sqrt {27} - \sqrt {48} \)
\(B = \left( {\dfrac{1}{{\sqrt x - 1}} - \dfrac{1}{{\sqrt x + 1}}} \right):\dfrac{{x + 1}}{{x - 1}}\) với \(x \ge 0\) và \(x \ne \pm 1\)
b) Giải hệ phương trình \(\left\{ \begin{array}{l}x + 2y = 12\\3x - y = 1\end{array} \right.\)
Câu 2. (2 điểm)
Cho phương trình \({x^2} + 5x + m = 0\left( * \right)\) (m là tham số )
a) Giải phương trình (*) khi \(m = - 3\)
b) Tìm m để phương trình (*) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(9{x_1} + 2{x_2} = 18\)
Câu 3. (2 điểm)
Trong mặt phẳng tọa độ \(\left( {Oxy} \right),\) cho parabol \(\left( P \right):\;\;y = \dfrac{1}{2}{x^2}\) và đường thẳng \(\left( d \right):\;y = \left( {2m - 1} \right)x + 5.\)
a) Vẽ đồ thị của (P).
b) Tìm m để đường thẳng (d) đi qua điểm \(E\left( {7;\;12} \right).\)
c) Đường thẳng \(y = 2\) cắt parabol \(\left( P \right)\) tại hai điểm \(A,\;B.\) Tìm tọa độ của \(A,\;B\) và tính diện tích tam giác \(OAB.\)
Câu 4. (3,5 điểm)
Cho đường tròn tâm \(\left( {O;R} \right)\) có đường kính AB vuông góc với dây cung MN tại H (H nằm giữa O và B). Trên tia MN lấy điểm C nằm ngoài đường tròn \(\left( {O;R} \right)\) sao cho đoạn thẳng AC cắt đường tròn \(\left( {O;R} \right)\) tại điểm K (K khác A), hai dây MN và BK cắt nhau ở E.
a) Chứng minh rằng tứ giác AHEK là tứ giác nội tiếp.
b) Chứng minh CA.CK = CE.CH
c) Qua điểm N kẻ đường thẳng (d) vuông góc với AC, (d) cắt MK tại F. Chứng minh tam giác NFK cân.
d) Khi KE = KC. Chứng minh OK // MN.
Lời giải chi tiết
Câu 1.
a) Rút gọn các biểu thức
\(\begin{array}{l}A = \sqrt {12} + \sqrt {27} - \sqrt {48} \\\,\,\,\,\, = \sqrt {{2^2}.3} + \sqrt {{3^2}.3} - \sqrt {{4^2}.3} \\\,\,\,\,\, = 2\sqrt 3 + 3\sqrt 3 - 4\sqrt 3 \\\,\,\,\,\, = \sqrt 3 .\end{array}\)
\(B = \left( {\dfrac{1}{{\sqrt x - 1}} - \dfrac{1}{{\sqrt x + 1}}} \right):\dfrac{{x + 1}}{{x - 1}}\) với \(x \ge 0\) và \(x \ne \pm 1\)
\(\begin{array}{l}B = \left( {\dfrac{{\sqrt x + 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} - \dfrac{{\sqrt x - 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}} \right):\dfrac{{x + 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\\\;\; = \dfrac{{\sqrt x + 1 - \sqrt x + 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}.\dfrac{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}{{x + 1}}\\\;\; = \dfrac{2}{{x + 1}}.\end{array}\)
b) Giải hệ phương trình \(\left\{ \begin{array}{l}x + 2y = 12\\3x - y = 1\end{array} \right.\)
\(\left\{ \begin{array}{l}x + 2y = 12\\3x - y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + 2y = 12\\y = 3x - 1\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}x + 2\left( {3x - 1} \right) = 12\\y = 3x - 1\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}7x = 14\\y = 3x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 5\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;\;y} \right) = \left( {2;\;5} \right).\)
Câu 2.
Cho phương trình \({x^2} + 5x + m = 0\left( * \right)\) (m là tham số )
a) Giải phương trình (*) khi \(m = - 3\)
Thay \(m = - 3\) vào phương trình (*) ta có: \({x^2} + 5x - 3 = 0\)
Ta có: \(a = 1;b = 5;c = - 3;\)
\(\Delta = {b^2} - 4ac = {5^2} + 12 = 37 > 0\)
Khi đó phương trình có 2 nghiệm phân biệt: \(\left[ \begin{array}{l}{x_1} = \dfrac{{ - 5 - \sqrt {37} }}{2}\\{x_2} = \dfrac{{ - 5 + \sqrt {37} }}{2}\end{array} \right.\)
Vậy khi \(m = - 3\) thì phương trình (*) có tập nghiệm là: \(S = \left\{ {\dfrac{{ - 5 - \sqrt {37} }}{2};\dfrac{{ - 5 + \sqrt {37} }}{2}} \right\}\)
b) Tìm m để phương trình (*) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(9{x_1} + 2{x_2} = 18\,\,\,\left( 3 \right)\)
+) Phương trình (*) có hai nghiệm \({x_1},{x_2}\) khi và chỉ khi \(\Delta \ge 0 \Leftrightarrow 25 - 4m \ge 0 \Leftrightarrow m \le \dfrac{{25}}{4}\)
+) Áp dụng hệ thức Vi-et cho phương trình (*) ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 5\,\,\left( 1 \right)\\{x_1}.{x_2} = m\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Kết hợp (1) và (3) ta được hệ phương trình:
\(\left\{ \begin{array}{l}{x_1} + {x_2} = - 5\\9{x_1} + 2{x_2} = 18\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}2{x_1} + 2{x_2} = - 10\\9{x_1} + 2{x_2} = 18\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l} - 7{x_1} = - 28\\{x_2} = - 5 - {x_1}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_1} = 4\\{x_2} = - 9\end{array} \right.\)
Thay \({x_1} = 4;{x_2} = - 9\) vào (2) ta được: \(4.\left( { - 9} \right) = m \Leftrightarrow m = - 36\left( {tm} \right)\)
Vậy \(m = - 36\) thỏa mãn yêu cầu bài toán.
Câu 3:
Trong mặt phẳng tọa độ \(\left( {Oxy} \right),\) cho parabol \(\left( P \right):\;\;y = \dfrac{1}{2}{x^2}\) và đường thẳng \(\left( d \right):\;y = \left( {2m - 1} \right)x + 5.\)
a) Vẽ đồ thị của (P).
Ta có bảng giá trị:
\(x\) | \( - 4\) | \( - 2\) | \(0\) | \(2\) | \(4\) |
\(y = \dfrac{1}{2}{x^2}\) | \(8\) | \(2\) | \(0\) | \(2\) | \(8\) |
Đồ thị:
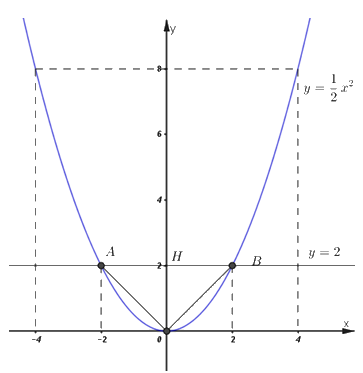
b) Tìm m để đường thẳng (d) đi qua điểm \(E\left( {7;\;12} \right).\)
Đường thẳng \(\left( d \right)\) đi qua điểm \(E\left( {7;\;12} \right) \Rightarrow 12 = \left( {2m - 1} \right).7 + 5\)
\(\begin{array}{l} \Leftrightarrow 12 = 14m - 7 + 5\\ \Leftrightarrow 14m = 14\\ \Leftrightarrow m = 1.\end{array}\)
Vậy \(m = 1\) thỏa mãn điều kiện bài toán.
c) Đường thẳng \(y = 2\) cắt parabol \(\left( P \right)\) tại hai điểm \(A,\;B.\) Tìm tọa độ của \(A,\;B\) và tính diện tích tam giác \(OAB.\)
Phương trình hoành độ giao điểm của đường thẳng \(y = 2\) và parabol \(\left( P \right)\) là:
\(\dfrac{1}{2}{x^2} = 2 \Leftrightarrow {x^2} = 4 \)
\(\Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}A\left( { - 2;\;2} \right)\\B\left( {2;\;2} \right)\end{array} \right..\)
Đường thẳng \(y = 2\) cắt \(\left( P \right)\) tại hai điểm phân biệt \(A\left( { - 2;\;2} \right)\) và \(B\left( {2;\;2} \right).\)
Gọi \(H\) là giao điểm của đường thẳng \(y = 2\) và trục \(Oy \Rightarrow H\left( {0;\;2} \right).\)
Khi đó ta có: \({S_{AOB}} = {S_{AOH}} + {S_{OBH}}.\)
Ta có: \(\left\{ \begin{array}{l}{S_{AOH}} = \dfrac{1}{2}AH.OH = \dfrac{1}{2}.\left| {{x_A}} \right|.\left| {{y_H}} \right| = \dfrac{1}{2}.2.2 = 2\\{S_{BOH}} = \dfrac{1}{2}HB.OH = \dfrac{1}{2}.\left| {{x_B}} \right|.\left| {{y_H}} \right| = \dfrac{1}{2}.2.2 = 2\end{array} \right..\)
\({S_{AOB}} = {S_{AOH}} + {S_{OBH}} = 2 + 2 = 4.\)
Vậy diện tích tam giác \(OAB\) là \(4\;\left( {dvdt} \right).\)
Câu 4.
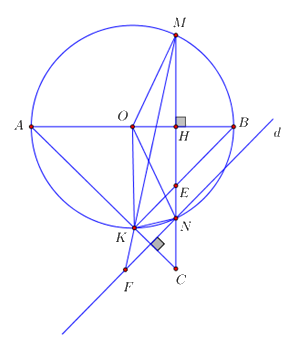
a) Chứng minh rằng tứ giác AHEK là tứ giác nội tiếp.
Ta có \(\widehat {AKB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \widehat {AKE} = {90^0}\).
Xét tứ giác AHEK có \(\widehat {AKE} + \widehat {AHE} = {90^0} + {90^0} = {180^0} \Rightarrow \) tứ giác AHEK là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
b) Chứng minh CA.CK = CE.CH
Xét tam giác CKE và tam giác CHA có:
\(\widehat {CKE} = \widehat {CHA} = {90^0};\)
\(\widehat {ACH}\) chung;
\( \Rightarrow \Delta CKE \sim \Delta CHA\,\,\left( {g.g} \right) \)
\(\Rightarrow \dfrac{{CK}}{{CH}} = \dfrac{{CE}}{{CA}} \)
\(\Rightarrow CA.CK = CE.CH\) (đpcm).
c) Qua điểm N kẻ đường thẳng (d) vuông góc với AC, (d) cắt MK tại F. Chứng minh tam giác NFK cân.
Ta có \(d \bot AC;\,\,\widehat {AKB} = {90^0} \Rightarrow BK \bot AK\)
\(\Rightarrow BK \bot AC \Rightarrow d//BK\). (từ vuông góc đến song song).
Xét tam giác OMN có
\(OM = ON\left( { = R} \right) \Rightarrow \Delta OMN\)cân tại O.
\( \Rightarrow \)Đường cao OH đồng thời là đường phân giác \( \Rightarrow \widehat {MOB} = \widehat {NOB} \Rightarrow \) sđ cung MB = sđ cung NB.
\( \Rightarrow \widehat {MKB} = \widehat {NKB}\) (hai góc nội tiếp chắn hai cung bằng nhau).
Ta có \(\widehat {KFN} = \widehat {MKB}\) (đồng vị);
\(\widehat {KNF} = \widehat {NKB}\) (so le trong);
Mà \(\widehat {MKB} = \widehat {NKB}\,\,\left( {cmt} \right)\)
\(\Rightarrow \widehat {KFN} = \widehat {KNF} \)
\(\Rightarrow \Delta NEK\) cân tại K.
d) Khi KE = KC. Chứng minh OK // MN.
Ta có \(\widehat {AKB} = {90^0} \Rightarrow BK \bot AK \Rightarrow BK \bot AC \Rightarrow \Delta KEC\) vuông tại K.
Lại có KE = KC (gt) \( \Rightarrow \Delta KEC\) vuông cân tại K \( \Rightarrow \widehat {KEC} = {45^0}\) ;
\( \Rightarrow \widehat {HEB} = \widehat {KEC} = {45^0}\) (đối đỉnh) \( \Rightarrow \Delta HEB\) vuông cân tại H \( \Rightarrow \widehat {HBE} = {45^0} \Rightarrow \widehat {OBK} = {45^0}\)
Tam giác OBK có \(OB = OK\;\left( { = R} \right) \Rightarrow \Delta OBK\)cân tại O \( \Rightarrow \widehat {OBK} = \widehat {OKB} = {45^0}\)
\( \Rightarrow \widehat {BOK} = {180^0} - {45^0} - {45^0} = {90^0} \Rightarrow \Delta BOK\)vuông cân tại \(O \Rightarrow OK \bot OB\) ;
Lại có \(MN \bot AB\,\,\left( {gt} \right) \Rightarrow MN \bot OB\).
Vậy MN // OK.
Đề thi vào lớp 10 môn Toán là một bước ngoặt quan trọng trong quá trình học tập của học sinh. Việc làm quen với các dạng bài tập và rèn luyện kỹ năng giải quyết vấn đề là vô cùng cần thiết. Đề số 6 là một đề thi thử điển hình, bao gồm nhiều dạng bài tập khác nhau, từ đại số đến hình học, đòi hỏi học sinh phải có kiến thức vững chắc và khả năng vận dụng linh hoạt.
Đề số 6 thường bao gồm các phần sau:
Dưới đây là lời giải chi tiết cho từng câu hỏi trong Đề số 6. Chúng tôi sẽ trình bày các bước giải một cách rõ ràng, dễ hiểu, kèm theo các chú thích và giải thích cần thiết.
Đề bài: ...
Lời giải: ...
Đề bài: ...
Lời giải: ...
Để giải đề thi hiệu quả, bạn có thể áp dụng một số mẹo sau:
Để nâng cao kỹ năng giải toán, bạn nên luyện tập thêm với các đề thi thử khác. Giaitoan.edu.vn cung cấp một kho đề thi phong phú, đa dạng, đáp ứng nhu cầu ôn tập của học sinh.
Việc luyện đề thường xuyên giúp bạn:
Đề số 6 - Đề thi vào lớp 10 môn Toán là một tài liệu ôn tập hữu ích cho học sinh. Hy vọng rằng, với lời giải chi tiết và các mẹo giải nhanh mà chúng tôi cung cấp, bạn sẽ tự tin hơn khi đối mặt với kỳ thi sắp tới. Chúc bạn thành công!
| Dạng bài | Mức độ khó | Thời gian giải |
|---|---|---|
| Phương trình bậc hai | Trung bình | 5 phút |
| Tam giác đồng dạng | Khó | 10 phút |