Chào mừng các em học sinh đến với Đề số 25 - Đề thi vào lớp 10 môn Toán tại giaitoan.edu.vn. Đây là một trong những đề thi thử quan trọng giúp các em làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Đề thi này được biên soạn dựa trên kiến thức chương trình Toán lớp 9 và các đề thi tuyển sinh vào lớp 10 các năm trước.
Chúng tôi hy vọng đề thi này sẽ là công cụ hữu ích giúp các em đạt kết quả tốt nhất trong kỳ thi sắp tới.
Đề thi vào lớp 10 môn Toán - Đề số 25 có đáp án và lời giải chi tiết
Đề bài
Câu 1 (1,0 điểm). Giải phương trình và hệ phương trình sau:
a) \(2{x^2} - 3x - 2 = 0\)
b) \(\left\{ \begin{array}{l}2x - 3y = 12\\3x + y = 7\end{array} \right.\)
Câu 2 (1,0 điểm).
a) Rút gọn biểu thức \(A = \sqrt {9 - 4\sqrt 5 } + \dfrac{1}{{\sqrt 5 - 2}}\)
b) Vẽ đồ thị của hàm số \(y = \dfrac{3}{4}{x^2}.\)
Câu 3 (1,5 điểm):
a) Khi thực hiện xây dựng trường điển hình đổi mới năm 2017, hai trường trung học cơ sở A và B có tất cả 760 học sinh đăng ký tham gia nội dung hoạt động trải nghiệm. Đến khi tổng kết, số học sinh tham gia đạt tỷ lệ 85% so với số đã đăng ký. Nếu tính riêng thì tỷ lệ học sinh tham gia của trường A và trường B lần lượt là 80% và 89,5%. Tính số học sinh ban đầu đăng ký tham gia của mỗi trường.
b) Tìm tất cả các giá trị của tham số \(m\) sao cho phương trình \(2{x^2} - \left( {m + 5} \right)x - 3{m^2} + 10m - 3 = 0\) có hai nghiệm phân biệt \({x_1},\;\;{x_2}\) thỏa mãn \(x_1^2 + x_2^2 - \left( {{x_1} + {x_2}} \right) + {x_1}{x_2} = 4.\)
Câu 4 (2,5 điểm):
Cho đường tròn tâm O và điểm P nằm ngoài (O). Vẽ tiếp tuyến PC của (O) (C là tiếp điểm) và cát tuyến PAB (PA < PB) sao cho các điểm A, B, C nằm cùng phía so với đường thẳng PO. Gọi M là trung điểm của đoạn AB và CD là đường kính của (O).
a) Chứng minh tứ giác PCMO là tứ giác nội tiếp.
b) Gọi E là giao điểm của đường thẳng PO với đường thẳng BD. Chứng minh AM.DE = AC.DO.
c) Chứng minh đường thẳng CE vuông góc với đường thẳng CA.
Lời giải chi tiết
PHẦN 1. TRẮC NGHIỆM
1.D | 2.C | 3.B | 4.B | 5.D |
11.A | 12.A | 13.C | 14.B | 15.D |
6.C | 7.C | 8.B | 9.C | 10.A |
16.D | 17.D | 18.C | 19.B | 20.A |
PHẦN 2: TỰ LUẬN
Câu 1
a) \(2{x^2} - 3x - 2 = 0\)
Ta có: \(\Delta = {\left( { - 3} \right)^2} - 4.2.\left( { - 2} \right) = 25 > 0\)
Nên phương trình đã cho có hai nghiệm phân biệt: \(\left[ \begin{array}{l}{x_1} = \dfrac{{3 - 5}}{{2.2}} = \dfrac{{ - 1}}{2}\\{x_2} = \dfrac{{3 + 5}}{{2.2}} = 2\end{array} \right.\)
Vậy tập nghiệm của phương trình đã cho là: \(S = \left\{ { - \dfrac{1}{2};2} \right\}\) .
b) \(\left\{ \begin{array}{l}2x - 3y = 12\\3x + y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - 3y = 12\\9x + 3y = 21\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}11x = 33\\y = 7 - 3x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 7 - 3.3\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = - 2\end{array} \right.\)
Vậy hệ phương trình đã cho có 1 nghiệm duy nhất là: \(\left( {x;y} \right) = \left( {3; - 2} \right)\)
Câu 2
a) Rút gọn biểu thức \(A = \sqrt {9 - 4\sqrt 5 } + \dfrac{1}{{\sqrt 5 - 2}}\)
\(\begin{array}{l}A = \sqrt {9 - 4\sqrt 5 } + \dfrac{1}{{\sqrt 5 - 2}}\\ = \sqrt {{2^2} - 2.2.\sqrt 5 + {{\left( {\sqrt 5 } \right)}^2}} + \dfrac{{\sqrt 5 + 2}}{{\left( {\sqrt 5 - 2} \right)\left( {\sqrt 5 + 2} \right)}}\\ = \sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} + \dfrac{{\sqrt 5 + 2}}{{5 - 4}}\\ = \left| {2 - \sqrt 5 } \right| + \sqrt 5 + 2\\ = \sqrt 5 - 2 + \sqrt 5 + 2\left( {\,Do\,\,\,2 - \sqrt 5 < 0} \right)\\ = 2\sqrt 5 \end{array}\)
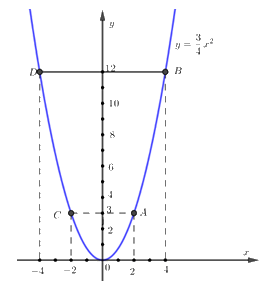
b) Vẽ đồ thị của hàm số \(y = \dfrac{3}{4}{x^2}.\)
Bảng giá trị
x | \( - 4\) | \( - 2\) | 0 | 2 | 4 |
y | 12 | 3 | 0 | 3 | 12 |
Khi đó đồ thị hàm số đã cho là 1 đường cong và đi qua các điểm \(A\left( {2;3} \right);B\left( {4;12} \right);C\left( { - 2;3} \right);D\left( { - 4;12} \right);O\left( {0;0} \right)\)
Câu 3
a) Khi thực hiện xây dựng trường điển hình đổi mới năm 2017, hai trường trung học cơ sở A và B có tất cả 760 học sinh đăng ký tham gia nội dung hoạt động trải nghiệm. Đến khi tổng kết, số học sinh tham gia đạt tỷ lệ 85% so với số đã đăng ký. Nếu tính riêng thì tỷ lệ học sinh tham gia của trường A và trường B lần lượt là 80% và 89,5%. Tính số học sinh ban đầu đăng ký tham gia của mỗi trường.
Gọi số học sinh trường A đăng ký hoạt động là \(x\) (học sinh), \(\left( {x < 760,\;x \in {N^*}} \right).\)
Gọi số học sinh trường B đăng ký hoạt động là \(y\) (học sinh), \(\left( {y < 760,\;y \in {N^*}} \right).\)
Khi đó tổng số học sinh hai trường đăng kí là: \(x + y = 760.\;\;\;\;\;\;\left( 1 \right)\)
Số học sinh hai trường tham gia là: \(760.\dfrac{{85}}{{100}} = 646\) (học sinh).
Số học sinh trường A tham gia là: \(80\% x = \dfrac{4}{5}x\) (học sinh).
Số học sinh trường B tham gia là: \(89,5\% y = \dfrac{{179}}{{200}}y\) (học sinh).
Theo đề bài ta có phương trình: \(\dfrac{4}{5}x + \dfrac{{179}}{{200}}y = 646\;\;\;\left( 2 \right).\)
Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 760\\\dfrac{4}{5}x + \dfrac{{179}}{{200}}y = 646\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x + y = 760\\160x + 179y = 129200\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}160x + 160y = 121600\\160x + 179y = 129200\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}19y = 7600\\x = 760 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 400\;\;\;\left( {tm} \right)\\x = 360\;\;\left( {tm} \right)\end{array} \right..\end{array}\)
Vậy ban đầu trường A có 360 học sinh đăng ký, trường B có 400 học sinh đăng ký.
b) Tìm tất cả các giá trị của tham số \(m\) sao cho phương trình \(2{x^2} - \left( {m + 5} \right)x - 3{m^2} + 10m - 3 = 0\) có hai nghiệm phân biệt \({x_1},\;\;{x_2}\) thỏa mãn \(x_1^2 + x_2^2 - \left( {{x_1} + {x_2}} \right) + {x_1}{x_2} = 4.\)
Phương trình có hai nghiệm phân biệt \({x_1},\;{x_2} \Leftrightarrow \Delta > 0\)
\(\begin{array}{l} \Leftrightarrow {\left( {m + 5} \right)^2} - 4.2\left( { - 3{m^2} + 10m - 3} \right) > 0\\ \Leftrightarrow {m^2} + 10m + 25 + 24{m^2} - 80m + 24 > 0\\ \Leftrightarrow 25{m^2} - 70m + 49 > 0\\ \Leftrightarrow {\left( {5m - 7} \right)^2} > 0\\ \Leftrightarrow m \ne \dfrac{7}{5}\end{array}\)
Với \(m \ne \dfrac{7}{5}\) thì phương trình đã cho có hai nghiệm phân biệt \({x_1},\;{x_2}.\)
Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{m + 5}}{2}\\{x_1}{x_2} = \dfrac{{ - 3{m^2} + 10m - 3}}{2}\end{array} \right..\)
Theo đề bài ta có: \(x_1^2 + x_2^2 - \left( {{x_1} + {x_2}} \right) + {x_1}{x_2} = 4\)
\(\begin{array}{l} \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) + {x_1}{x_2} = 4\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - \left( {{x_1} + {x_2}} \right) - {x_1}{x_2} = 4\\ \Leftrightarrow {\left( {\dfrac{{m + 5}}{2}} \right)^2} - \left( {\dfrac{{m + 5}}{2}} \right) - \dfrac{{ - 3{m^2} + 10m - 3}}{2} = 4\\ \Leftrightarrow {\left( {m + 5} \right)^2} - 2\left( {m + 5} \right) + 2\left( {3{m^2} - 10m + 3} \right) = 16\\ \Leftrightarrow 7{m^2} - 12m + 5 = 0\\ \Leftrightarrow \left( {7m - 5} \right)\left( {m - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}7m - 5 = 0\\m - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = \dfrac{5}{7}\;\;\left( {tm} \right)\\m = 1\;\;\;\;\left( {tm} \right)\end{array} \right..\end{array}\)
Vậy \(m = \dfrac{5}{7}\) hoặc \(m = 1\) thỏa mãn bài toán.
Câu 4
Cho đường tròn tâm O và điểm P nằm ngoài (O). Vẽ tiếp tuyến PC của (O) (C là tiếp điểm) và cát tuyến PAB (PA < PB) sao cho các điểm A, B, C nằm cùng phía so với đường thẳng PO. Gọi M là trung điểm của đoạn AB và CD là đường kính của (O).
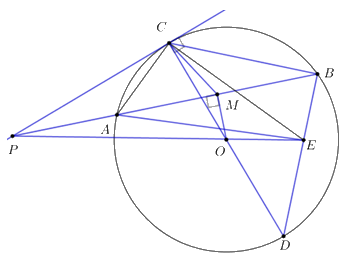
a) Chứng minh tứ giác PCMO là tứ giác nội tiếp.
Ta có \(M\) là trung điểm của \(AB\;\left( {gt} \right) \Rightarrow OM \bot AB\) (tính chất đường kính và dây cung)
\( \Rightarrow \widehat {AMO} = \widehat {PMO} = {90^0}.\)
Có \(PC\) là tiếp tuyến của (O) tại C \( \Rightarrow \widehat {PCO} = {90^0}.\)
Xét tứ giác \(PCMO\) ta có: \(\widehat {PMO} = \widehat {PCO} = {90^0}\;\;\left( {cmt} \right)\)
Mà C và M là 2 đỉnh kề nhau cùng nhìn cạnh PC dưới 1 góc vuông\( \Rightarrow PCMO\) là tứ giác nội tiếp (dấu hiệu nhận biết tứ giác nội tiếp).
b) Gọi E là giao điểm của đường thẳng PO với đường thẳng BD. Chứng minh AM.DE = AC.DO.
Vì tứ giác \(PCMO\) là tứ giác nội tiếp \( \Rightarrow \widehat {POC} = \widehat {PMC}\) (cùng chắn cung \(PC\))
Mà \(\widehat {DOE} = \widehat {POC}\) (hai góc đối đỉnh)
\( \Rightarrow \widehat {DOE} = \widehat {AMC}\;\;\left( { = \widehat {POC}} \right).\)
Xét tam giác: \(\Delta ACM\) và \(\Delta DEO\) ta có:
\(\widehat {DOE} = \widehat {AMC}\;\left( {cmt} \right)\)
\(\widehat {ODE} = \widehat {CAM}\) (hai góc nội tiếp cùng chắn cung \(BC\) của đường tròn (O))
\(\begin{array}{l} \Rightarrow \Delta ACM \sim \Delta DEO\;\left( {g - g} \right)\\ \Rightarrow \dfrac{{AC}}{{DE}} = \dfrac{{AM}}{{DO}}\\ \Rightarrow AC.DO = AM.DE\;\;\left( {dpcm} \right).\end{array}\)
c) Chứng minh đường thẳng CE vuông góc với đường thẳng CA.
Ta có: \(\Delta ACM \sim \Delta DEO\;\left( {cmt} \right)\)
\( \Rightarrow \dfrac{{DE}}{{AC}} = \dfrac{{OD}}{{AM}} = \dfrac{{2OD}}{{2AM}} = \dfrac{{CD}}{{AB}}.\)
Xét \(\Delta DEC\) và ta có:
\(\dfrac{{DE}}{{AC}} = \dfrac{{DC}}{{AB}}\;\;\left( {cmt} \right)\)
\(\widehat {EDC} = \widehat {BAC}\) (hai góc nội tiếp cùng chắn cung \(BC\))
\( \Rightarrow \Delta DEC \sim \Delta ACB\;\left( {c - g - c} \right).\)
\( \Rightarrow \widehat {DCE} = \widehat {CBA}\) (hai góc tương ứng).
Lại có: \(\widehat {CBA} = \widehat {PCA}\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(CA\))
\( \Rightarrow \widehat {DCE} = \widehat {PCA}\;\;\left( { = \widehat {CBA}} \right).\)
Mặt khác: \(\widehat {PCA} + \widehat {ACO} = {90^0}\;\;\left( {gt} \right)\) (PC là tiếp tuyến của đường tròn tại C)
\(\begin{array}{l} \Rightarrow \widehat {DCE} + \widehat {ACO} = {90^0}\\hay\;\;\widehat {ACE} = {90^0}.\\ \Rightarrow AC \bot CE\;\;\left( {dpcm} \right).\end{array}\)
Đề thi vào lớp 10 môn Toán là một kỳ thi quan trọng đánh giá năng lực học tập của học sinh sau nhiều năm học tập ở bậc trung học cơ sở. Việc chuẩn bị kỹ lưỡng và làm quen với các dạng bài tập khác nhau là yếu tố then chốt để đạt kết quả cao. Đề số 25 - Đề thi vào lớp 10 môn Toán tại giaitoan.edu.vn được thiết kế để đáp ứng nhu cầu ôn tập và luyện thi của học sinh.
Đề thi thường bao gồm các phần sau:
Tỷ lệ điểm giữa hai phần có thể khác nhau tùy theo từng tỉnh, thành phố.
Nội dung đề thi thường bao gồm các chủ đề sau:
Ngoài ra, đề thi có thể có các bài toán kết hợp kiến thức của nhiều chủ đề khác nhau.
Giaitoan.edu.vn cung cấp hướng dẫn giải chi tiết cho từng bài toán trong Đề số 25 - Đề thi vào lớp 10 môn Toán. Các lời giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững phương pháp giải và tự tin hơn khi làm bài.
Trong đề thi vào lớp 10 môn Toán, có một số dạng bài tập thường gặp mà học sinh cần nắm vững:
Luyện đề là một bước quan trọng trong quá trình chuẩn bị cho kỳ thi vào lớp 10 môn Toán. Việc luyện đề thường xuyên giúp học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn khi làm bài. Đề số 25 - Đề thi vào lớp 10 môn Toán tại giaitoan.edu.vn là một lựa chọn tuyệt vời để các em luyện tập và nâng cao kiến thức.
Giaitoan.edu.vn là một nền tảng học toán online uy tín, cung cấp các khóa học, bài giảng, đề thi và tài liệu ôn tập chất lượng cao. Chúng tôi cam kết mang đến cho học sinh những trải nghiệm học tập tốt nhất và giúp các em đạt kết quả cao trong kỳ thi vào lớp 10 môn Toán.
| Chủ đề | Mức độ quan trọng |
|---|---|
| Phương trình bậc hai | Rất quan trọng |
| Hệ phương trình | Quan trọng |
| Tam giác đồng dạng | Quan trọng |
| Đường tròn | Trung bình |
| Nguồn: Giaitoan.edu.vn | |
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi vào lớp 10 môn Toán!