Chào mừng các em học sinh đến với Đề số 2 - Đề thi vào lớp 10 môn Toán tại giaitoan.edu.vn. Đây là một trong những đề thi thử quan trọng giúp các em làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Đề thi này được biên soạn dựa trên kiến thức chương trình Toán lớp 9 và các dạng bài thường gặp trong kỳ thi tuyển sinh vào lớp 10. Chúng tôi cung cấp đầy đủ đề thi và đáp án chi tiết để các em có thể tự học và đánh giá năng lực của mình.
Đề thi vào lớp 10 môn Toán - Đề số 2 có đáp án và lời giải chi tiết
Đề bài
Bài 1. (3,0 điểm)
1. Rút gọn biểu thức \(2\sqrt {75} + 3\sqrt {48} - 4\sqrt {27} \)
2. Giải hệ phương trình \(\left\{ \begin{array}{l}2x - y = 8\\3x + 2y = 5\end{array} \right.\)
3. Giải phương trình \(3{x^2} - 7x + 2 = 0\)
Bài 2. (2 điểm)
Cho hai hàm số: \(y = - x + 2\) và \(y = {x^2}\) có đồ thị lần lượt là \(\left( d \right)\) và \(\left( P \right).\)
1) Vẽ \(\left( d \right)\) và \(\left( P \right)\) trên cùng hệ trục tọa độ.
2) Bằng phép toán tìm tọa độ giao điểm của \(\left( d \right)\) và \(\left( P \right).\)
Bài 3. (1 điểm)
Cho phương trình \({x^2} - \left( {m + 1} \right)x + m - 2 = 0\) (với m là tham số).
1) Chứng minh phương trình luôn có hai nghiệm phân biệt với mọi m.
2) Tìm các số nguyên m để phương trình có nghiệm nguyên.
Bài 4. (1,0 điểm)
Cho tam giác ABC vuông tại A, đường cao AH \(\left( {H \in BC} \right)\) . Biết BH = 3,6cm và HC = 6,4 cm. Tính độ dài BC, AH, AB, AC.
Bài 5. (3 điểm).
Cho tam giác ABC vuông tại A \(\left( {AB < AC} \right)\), M là trung điểm của cạnh AC. Đường tròn đường kính MC cắt BC tại N. Đường thẳng BM cắt đường tròn đường kính MC tại D.
1. Chứng minh tứ giác BADC nội tiếp.
2. Chứng minh DB là phân giác của góc ADN.
3. BA và CD kéo dài cắt nhau tại P. Chứng minh ba điểm P, M, N thẳng hàng.
Lời giải chi tiết
Bài 1.
1. Rút gọn biểu thức \(2\sqrt {75} + 3\sqrt {48} - 4\sqrt {27} \)
Ta có:
\(\begin{array}{l}\;\;\;2\sqrt {75} + 3\sqrt {48} - 4\sqrt {27} \\ = 2\sqrt {{5^2}.3} + 3\sqrt {{4^2}.3} - 4\sqrt {{3^2}.3} \\ = 10\sqrt 3 + 12\sqrt 3 - 12\sqrt 3 \\ = 10\sqrt 3 .\end{array}\)
2. Giải hệ phương trình \(\left\{ \begin{array}{l}2x - y = 8\\3x + 2y = 5\end{array} \right.\)
\(\left\{ \begin{array}{l}2x - y = 8\\3x + 2y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2x - 8\\3x + 2y = 5\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}y = 2x - 8\\3x + 2\left( {2x - 8} \right) = 5\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}y = 2x - 8\\7x = 21\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 2x - 8\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = - 2\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất là: \(\left( {x;y} \right) = \left( {3; - 2} \right)\)
3. Giải phương trình \(3{x^2} - 7x + 2 = 0\)
Ta có: \(a = 3;\;\;b = - 7;\;\;c = 2\)
\(\Delta = {b^2} - 4ac = {\left( { - 7} \right)^2} - 4.3.2 = 25 > 0 \)
\(\Rightarrow \sqrt \Delta = 5\)
Khi đó phương trình đã cho có hai nghiệm phân biệt là: \(\left[ \begin{array}{l}{x_1} = \dfrac{{7 - 5}}{6} = \dfrac{1}{3}\\{x_2} = \dfrac{{7 + 5}}{6} = 2\end{array} \right.\)
Vậy tập nghiệm của phương trình đã cho là: \(S = \left\{ {\dfrac{1}{3};2} \right\}\)
Bài 2: Cho hai hàm số: \(y = - x + 2\) và \(y = {x^2}\) có đồ thị lần lượt là \(\left( d \right)\) và \(\left( P \right).\)
1) Vẽ \(\left( d \right)\) và \(\left( P \right)\) trên cùng hệ trục tọa độ.
+) Vẽ đồ thị hàm số: \(\left( d \right):\;\;y = - x + 2.\)
\(x\) | \(0\) | \(2\) |
\(y = - x + 2\) | \(2\) | \(0\) |
+) Vẽ đồ thị hàm số: \(\left( P \right):\;\;y = {x^2}.\)
\(x\) | \( - 2\) | \( - 1\) | \(0\) | \(1\) | \(2\) |
\(y = {x^2}\) | \(4\) | \(1\) | \(0\) | \(1\) | \(4\) |
Đồ thị hàm số:
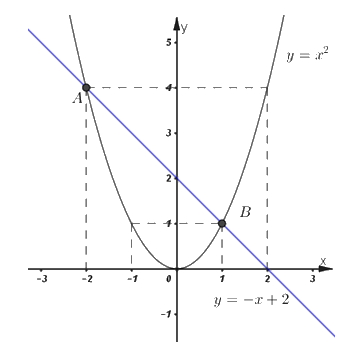
2) Bằng phép toán tìm tọa độ giao điểm của \(\left( d \right)\) và \(\left( P \right).\)
Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình hoành độ giao điểm.
Ta có phương trình hoành độ giao điểm của hai đồ thị là:
\(\begin{array}{l} - x + 2 = {x^2}\\ \Leftrightarrow {x^2} + x - 2 = 0\\ \Leftrightarrow {x^2} + 2x - x - 2 = 0\\ \Leftrightarrow x\left( {x + 2} \right) - \left( {x + 2} \right) = 0\\ \Leftrightarrow \left( {x + 2} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 2 = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 2 \Rightarrow y = 4\\x = 1 \Rightarrow y = 1\end{array} \right..\end{array}\)
Vậy hai đồ thị cắt nhau tại hai điểm phân biệt \(A\left( { - 2;\;4} \right)\) và \(B\left( {1;\;1} \right).\)
Bài 3:
1) Chứng minh phương trình luôn có hai nghiệm phân biệt với mọi m.
Ta có: \(\Delta = {\left( {m + 1} \right)^2} - 4\left( {m - 2} \right)\)\(\, = {m^2} + 2m + 1 - 4m + 8 \)\(\,= {m^2} - 2m + 1 + 8 \)\(\,= {\left( {m - 1} \right)^2} + 8.\)
Vì \({\left( {m - 1} \right)^2} \ge 0\;\;\forall m \)\(\,\Rightarrow {\left( {m - 1} \right)^2} + 8 > 0\;\forall m.\)
Hay \(\Delta > 0\;\forall m \Rightarrow \) phương trình luôn có hai nghiệm phân biệt với mọi \(m.\)
2) Tìm các số nguyên m để phương trình có nghiệm nguyên.
Phương trình đã cho luôn có hai nghiệm phân biệt với mọi \(m.\)
Đề bài yêu cầu tìm \(m \in Z\) để \(x \in Z.\) Ta đưa bài toán về dạng tìm x nguyên để m nguyên.
Ta có: \({x^2} - \left( {m + 1} \right)x + m - 2 = 0\)
\(\Leftrightarrow {x^2} - mx - x + m - 2 = 0\)
\(\begin{array}{l} \Leftrightarrow {x^2} - x - 2 = m\left( {x - 1} \right)\\ \Leftrightarrow m = \dfrac{{{x^2} - x - 2}}{{x - 1}} = \dfrac{{x\left( {x - 1} \right) - 2}}{{x - 1}}\;\;\left( {x \ne 1} \right)\\ \Leftrightarrow m = x - \dfrac{2}{{x - 1}}.\\ \Rightarrow m \in Z \Leftrightarrow \left( {x - \dfrac{2}{{x - 1}}} \right) \in Z \\\Leftrightarrow \dfrac{2}{{x - 1}} \in Z\,\,\left( {Do\,\,x \in Z} \right)\\ \Leftrightarrow \left( {x - 1} \right) \in U\left( 2 \right).\end{array}\)
Mà \(U\left( 2 \right) = \left\{ { - 2;\; - 1;\;1;\;2} \right\}.\)
\( \Rightarrow \left[ \begin{array}{l}x - 1 = - 2\\x - 1 = - 1\\x - 1 = 1\\x - 1 = 2\end{array} \right. \)
\(\Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 0\\x = 2\\x = 3\end{array} \right.\,\,\left( {tm} \right) \)
\(\Rightarrow \left[ \begin{array}{l}m = 0\\m = 2\\m = 0\\m = 2\end{array} \right.\)
\(\Leftrightarrow \left[ \begin{array}{l}m = 0\;\;\left( {tm} \right)\\m = 2\;\;\;\left( {tm} \right)\end{array} \right..\)
Vậy với \(m = 0\) và \(m = 2\) thỏa mãn yêu cầu bài toán.
Bài 4.
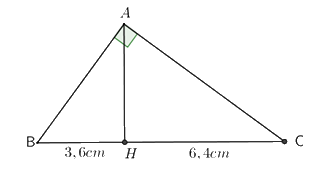
Ta có: \(\left( {H \in BC} \right)\) nên : \(BC = BH + HC = 3,6 + 6,4 = 10\left( {cm} \right)\)
Áp dụng hệ thức lượng trong tam giác ABC vuông tại A với đường cao AH ta có:
\(A{H^2} = BH.HC\)
\(\Rightarrow A{H^2} = 3,6.6,4 = 23,04\)
\(\Rightarrow AH = 4,8\left( {cm} \right)\)
Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H ta có:
\(A{B^2} = A{H^2} + B{H^2} \)\(\,= 4,{8^2} + 3,{6^2} = 36 \)
\(\Rightarrow AB = 6\left( {cm} \right)\)
Áp dụng định lý Pytago trong tam giác vuông ABC vuông tại A ta có:
\(A{C^2} = B{C^2} - A{B^2}\)\(\, = {10^2} - {6^2} = 64\)
\(\Rightarrow AC = 8\left( {cm} \right)\)
Vậy: BC = 10 cm; AH = 4,8 cm; AB = 6 cm; AC = 8 cm.
Bài 5.
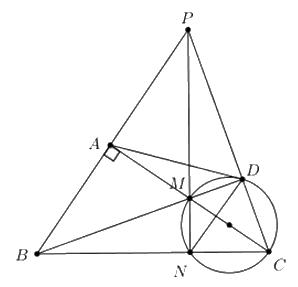
1. Chứng minh tứ giác BADC nội tiếp.
Ta có \(\widehat {MDC} = {90^0}\) (góc nội tiếp chắn nửa đường tròn đường kính MC) \( \Rightarrow \widehat {BDC} = {90^0}\).(Do B, M, D thẳng hàng)
Có \(\widehat {BAC} = {90^0}\) (do giả thiết tam giác ABC vuông tại A)
Xét tứ giác BADC có \(\widehat {BAC} = \widehat {BDC} = {90^0} \Rightarrow \) Hai điểm A và D cùng nhìn BC dưới góc 900 \( \Rightarrow \) Tứ giác BADC là tứ giác nội tiếp (Tứ giác có hai đỉnh cùng nhìn 1 cạnh dưới các góc bằng nhau).
2. Chứng minh DB là phân giác của góc ADN.
Do BADC là tứ giác nội tiếp (cmt) \( \Rightarrow \widehat {ADB} = \widehat {ACB}\) (hai góc nội tiếp cùng chắn cung AB).
Lại có \(\widehat {ACB} = \widehat {MCN} = \widehat {MDN}\) (hai góc nội tiếp cùng chắn cung MN của đường tròn đường kính MC).
\( \Rightarrow \widehat {ADB} = \widehat {MDN} = \widehat {BDN} \Rightarrow BD\) là tia phân giác của góc ADN.
3. BA và CD kéo dài cắt nhau tại P. Chứng minh ba điểm P, M, N thẳng hàng.
Ta có \(\widehat {BDC} = {90^0}\,\,\left( {cmt} \right) \Rightarrow BD \bot DC \Rightarrow BD \bot PC\)
Tam giác ABC vuông tại A \( \Rightarrow AC \bot AB \Rightarrow AC \bot PB\)
Xét tam giác PBC có \(BD \bot PC;\,\,AC \bot PB;\,\,AC \cap BD = M \Rightarrow M\) là trực tâm tam giác PBC.
\( \Rightarrow PM \bot BC\).
Lại có \(\widehat {MNC} = {90^0}\) (góc nội tiếp chắn nửa đường tròn đường kính MC) \( \Rightarrow MN \bot NC \Rightarrow MN \bot BC\)
Qua điểm M nằm ngoài đường thẳng BC ta kẻ được \(PM \bot BC\) và \(MN \bot BC\)
\( \Rightarrow PM \equiv MN\) hay ba điểm P, M, N thẳng hàng.
Kỳ thi tuyển sinh vào lớp 10 là một bước ngoặt quan trọng trong quá trình học tập của mỗi học sinh. Để đạt kết quả tốt nhất, việc luyện tập thường xuyên với các đề thi thử là vô cùng cần thiết. Đề số 2 - Đề thi vào lớp 10 môn Toán tại giaitoan.edu.vn được thiết kế để giúp các em học sinh làm quen với áp lực phòng thi, rèn luyện tốc độ giải đề và củng cố kiến thức đã học.
Đề thi thường bao gồm các dạng bài sau:
Sau khi hoàn thành bài thi, các em có thể tham khảo đáp án chi tiết và lời giải của từng bài toán. Chúng tôi cung cấp các lời giải ngắn gọn, dễ hiểu, giúp các em nắm vững phương pháp giải và tránh những sai lầm thường gặp.
Dưới đây là một số dạng bài tập thường gặp trong đề thi vào lớp 10 môn Toán:
Đây là một trong những dạng bài tập cơ bản nhất, đòi hỏi các em phải nắm vững các phương pháp giải phương trình và hệ phương trình như phương pháp thế, phương pháp cộng đại số, phương pháp đặt ẩn phụ.
Các em cần nắm vững các quy tắc giải bất phương trình và các bất đẳng thức cơ bản.
Các em cần hiểu rõ định nghĩa hàm số, cách xác định tập xác định, tập giá trị và đồ thị hàm số.
Các em cần nắm vững các định lý, tính chất cơ bản của hình học và biết cách áp dụng chúng để giải quyết các bài toán.
Việc luyện tập thường xuyên với các đề thi thử là yếu tố then chốt để đạt kết quả tốt trong kỳ thi tuyển sinh vào lớp 10. Thông qua việc luyện tập, các em sẽ làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và củng cố kiến thức đã học. Đừng ngần ngại tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè nếu gặp khó khăn.
| Chương | Kiến thức trọng tâm |
|---|---|
| Đại số | Phương trình, hệ phương trình, bất phương trình, hàm số |
| Hình học | Tam giác, tứ giác, đường tròn, hệ thức lượng |
| Số học | Số nguyên tố, ước số, bội số, phân số |
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi tuyển sinh vào lớp 10!