Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Hưng Yên năm 2019 chính thức. Đây là tài liệu vô cùng hữu ích cho các em học sinh đang chuẩn bị cho kỳ thi quan trọng này.
Đề thi được biên soạn theo cấu trúc đề thi chính thức, giúp các em làm quen với dạng bài và rèn luyện kỹ năng giải quyết vấn đề. Cùng với đáp án chi tiết, các em có thể tự đánh giá năng lực và tìm ra những điểm cần cải thiện.
PHẦN TRẮC NGHIỆM (3 điểm) Câu 1: Xác định tham số
PHẦN TRẮC NGHIỆM (3 điểm)
Câu 1: Xác định tham số \(a\) để hệ phương trình \(\left\{ \begin{array}{l}\left( {a - 1} \right)x - y = a + 2\\2x - y = 3\end{array} \right.\) có nghiệm duy nhất.
A. \(a \ne 3\) B. \(a \ne 0\) C. \(a \ne - 2\) D. \(a \ne 1\)
Câu 2 : Tìm \(m\) để đường thẳng \(\left( d \right):\,\,y = {m^2}x + m\,\,\left( {m \ne 0} \right)\) song song với đường thẳng \(\left( {d'} \right):\,\,y = 4x - 2.\)
A. \(m = - 4\) B. \(m = - 2\) C. \(m = 4\) D. \(m = 2\)
Câu 3: Tính chiều cao của đài kiểm soát không lưu Nội Bài. Biết bóng của đài kiểm soát được chiếu bởi ánh sáng mặt trời xuống đất dài \(200\,m\) và góc tạo bởi tia sáng với mặt đất là \({25^0}24'\) (kết quả làm tròn đến hàng đơn vị).
A. \(221\,m\) B. \(181\,m\) C. \(86\,m\)D. \(95\,m\) |
Câu 4: Cho đường tròn \(\left( {O;\,\,10cm} \right)\) và dây \(AB\) cách tâm \(O\) một khoảng bằng \(6cm.\) Tính độ dài dây \(AB.\)
A. \(16\,cm\) B. \(12\,cm\) C. \(8\,cm\) D. \(10\,cm\)
Câu 5: Cho \(\Delta ABC\) vuông tại\(A,\) đường cao \(AH.\) Khẳng định bào sau đây đúng?
A. \(A{H^2} = HB.BC\)B. \(A{H^2} = HB.AB\)C. \(A{H^2} = HB.HC\) D. \(A{H^2} = HB.AC\)
Câu 6: Cổng vào một ngôi biệt thự có hình dạng là một parabol được biểu diễn bởi đồ thị hàm số \(y = - {x^2}.\) Biết khoảng cách giữa hai chân cổng là \(4\,m.\) Một chiếc ô tô tải có thùng xe là một hình hộp chữ nhật có chiều rộng là \(2,4\,m.\) Hỏi chiều cao lớn nhất có thể của ô tô là bao nhiêu để ô tô có thể đi qua cổng?
A. \(2,\,4\,m\) B. \(1,44\,m\) C. \(4\,m\) D. \(2,56\,m\) |
Câu 7: Trên hình vẽ là ba nửa đường tròn đường kính \(AB,\,\,AC,\,\,CB.\) Biết \(DC \bot AB = \left\{ C \right\},\) khi đó tỉ số diện tích hình giới hạn bởi ba nửa đường tròn nói trên và diện tích hình tròn bán kính \(DC\) là:
A. \(\dfrac{{\sqrt 7 }}{3}\) B. \(\dfrac{1}{3}\) C. \(\dfrac{1}{2}\) D. \(\dfrac{1}{4}\) |
Câu 8 : Căn bậc hai số học của \(36\) là:
A. \( - 6\) B. \(6\) C. \(72\) D. \(18\)
Câu 9: Gọi \(S\) là tập hợp các giá trị nguyên của \(m\) để đường thẳng\(y = 6x + m - 5\) và parabol \(y = {x^2}\) cắt nhau tại hai điểm phân biệt bằm bên phải trục tung. Tính tổng các phần tử của tập \(S.\)
A. 3 B. -3 C. 6 D. -6
Câu 10: Trong các hàm số sau, hàm số nào là đồng biến trên \(\mathbb{R}?\)
A. \(y = - x + 5\) B. \(y = 2x + 1\) C. \(y = 2019 - 2x\) D. \(y = 2020\)
Câu 11: Tìm tất cả các giá trị của \(m\) để hàm số bậc nhất \(y = \left( {2019 - m} \right)x + 2020\) nghịch biến trên \(\mathbb{R}.\)
A. \(m > - 2019\) B. \(m > 2019\) C. \(m < 2019\) D. \(m < - 2019\)
Câu 12: Cho \(\Delta ABC\) vuông tại\(A.\) Khẳng định nào sau đây là đúng?
A. \(\sin B = \dfrac{{AC}}{{AB}}\) B. \(\sin B = \dfrac{{AB}}{{BC}}\) C. \(\sin B = \dfrac{{AB}}{{AC}}\) D. \(\sin B = \dfrac{{AC}}{{BC}}\)
Câu 13: Biểu thức \(\sqrt {2x - 8} \) có nghĩa khi và chỉ khi:
A. \(x \le - 4\)B. \(x \le 4\)C. \(x \ge - 4\) D. \(x \ge 4\)
Câu 14: Cho hình vẽ, biết \(AB\) là đường kính của đường tròn tâm \(O,\,\,\angle ABC = {40^0}.\) Tính số đo \(\angle BMC.\)
A. \({40^0}\) B. \({60^0}\) C. \({80^0}\)D. \({50^0}\)
Câu 15: Tìm \(m\) để đồ thị hàm số \(y = \left( {m + 5} \right){x^2}\) đi qua điểm \(A\left( { - 1;\,\,2} \right).\)
A. \(m = - 3\) B. \(m = 6\) C. \(m = 3\) D. \(m = - 7\)
Câu 16: Tâm \(O\) của đường tròn \(\left( {O;\,\,5cm} \right)\) cách đường thẳng \(d\) một khoảng bằng \(6\,cm.\) Tìm số điểm chung của đường thẳng \(d\) và đường tròn \(\left( {O;\,\,5cm} \right).\)
A. Có ít nhất một điểm chung. B. Có hai điểm chung phân biệt. C. Có một điểm chung duy nhất. D. Không có điểm chung.
Câu 17: Một quả bóng nhựa mềm dành cho trẻ em có dạng hình cầu, đường kính \(7\,cm.\) Tính diện tích bề mặt quả bóng (lấy \(\pi \approx 3,14\) và kết quả làm tròn đến chữ số thập phân thứ hai).
A. \(381,\,51\,c{m^2}\)B. \(153,\,86\,c{m^2}\) C. \(615,44\,c{m^2}\)D. \(179,50\,c{m^2}\)
Câu 18: Phương trình nào sau đây là phương trình bậc hai một ẩn?
A. \( - {x^2} + x - 2 = 0\) B. \( - 2x + 5 = 0\)C. \(3xy + 4x - 6 = 0\)D. \({x^3} + 2{x^2} = 0\)
Câu 19: Lúc \(8\) giờ, kim giờ và kim phút của đồng hồ tạo thành một góc ở tâm có số đo là:
A. \({80^0}\) B. \({240^0}\) C. \({120^0}\) D. \({40^0}\)
Câu 20: Giá trị của biểu thức: \(E = \dfrac{1}{{\sqrt 2 - 1}} - \dfrac{1}{{\sqrt 2 + 1}}\) bằng:
A. \( - 2\) B. \( - 2\sqrt 2 \) C. \(2\) D. \(2\sqrt 2 \)
Câu 21: Hệ số góc của đường thẳng \(\left( d \right):\,\,y = - 2x + 3\) là:
A. \( - 2\) B. \( - \dfrac{3}{2}\) C. \(\dfrac{3}{2}\) D. \(3\)
Câu 22: Trong các hệ phương trình sau, hệ phương trình nào là hệ phương trình bậc nhất hai ẩn?
A. \(\left\{ \begin{array}{l}xy + 3x = 1\\y - 2x = 1\end{array} \right.\) B. \(\left\{ \begin{array}{l}x + y = 3\\2x + y = 1\end{array} \right.\) C. \(\left\{ \begin{array}{l}{x^2} + 3y = 1\\ - x + 2y = - 2\end{array} \right.\) D. \(\left\{ \begin{array}{l}x - 2y = 1\\x + 2{y^2} = - 1\end{array} \right.\)
Câu 23: Cho hàm số \(y = 9{x^2}.\) Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến khi \(x > 0.\) B. Hàm số đồng biến trên \(\mathbb{R}.\)
C. Hàm số đồng biến khi \(x > 0.\) D. Hàm số đồng biến khi \(x < 0.\)
Câu 24: Từ một tâm tôn hình chữ nhật có kích thước \(0,5\,m \times 2,4\,m\) người ta gò tấm tôn đó thành mặt xung quanh của thùng đựng nước hình trụ có chiều cao bằng \(0,5\,m\) (phần mép hàn không đáng kể).
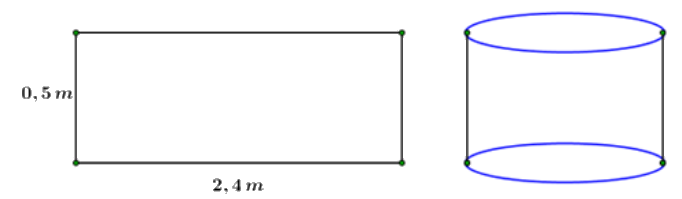
Thể tích \(V\) của thùng.
A. \(V = \dfrac{{12}}{{25\pi }}\,{m^3}\) B. \(V = \dfrac{{36}}{{25\pi }}\,{m^3}\) C. \(V = \dfrac{6}{{5\pi }}\,{m^3}\) D. \(V = \dfrac{{18}}{{25\pi }}\,{m^3}\)
Câu 25: Nghiệm tổng quát của phương trình \(2x - y = 1\) là:
A. \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = 1 - 2x\end{array} \right.\) B. \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = 2x - 1\end{array} \right.\) C. \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = 2x + 1\end{array} \right.\) D. \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = - 2x - 1\end{array} \right.\)
PHẦN TỰ LUẬN (7 điểm)
Câu 1 (1,5 điểm):
a) Rút gọn biểu thức \(P = \sqrt 5 \left( {\sqrt 5 + 2} \right) - \sqrt {20} \)
b) Tìm giá trị của \(m\) để đường thẳng \(\left( d \right):\,y = mx + 3\) đi qua điểm \(A\left( {1;5} \right)\)
c) Giải hệ phương trình \(\left\{ \begin{array}{l}3x - y = 7\\x + y = 5\end{array} \right.\)
Câu 2 (1,5 điểm):
Cho phương trình \({x^2} - 4mx + m - 1 = 0\) (\(m\) là tham số)
a) Giải phương trình với \(m = 4\)
b) Tìm \(m\) để phương trình có hai nghiệm phân biệt thỏa mãn điều kiện:
\({x_1}\left( {{x_1} + 2} \right) + {x_2}\left( {{x_2} + 2} \right) = 20\)
Câu 3 (1,5 điểm):
Cho tam giác \(ABC\) nhọn \(\left( {AB < AC} \right)\) nội tiếp đường tròn \(\left( O \right).\) Vẽ các đường cao \(BD,CE\) của tam giác \(ABC\) \(\left( {D \in AC;E \in AB} \right)\)
a) Chứng minh tứ giác \(BCDE\) nội tiếp một đường tròn
b) Gọi giao điểm của \(AO\) với \(BD\) và \(ED\) lần lượt là \(K,M.\) Chứng minh \(\dfrac{1}{{M{D^2}}} = \dfrac{1}{{K{D^2}}} + \dfrac{1}{{A{D^2}}}\)
Câu 4 (0,5 điểm):
Cho các số thực dương \(x,\,\,y,\,\,z\) thỏa mãn \({x^2} + {y^2} + {z^2} = 3xyz.\)
Tìm giá trị lớn nhất của biểu thức: \(P = \dfrac{{{x^2}}}{{{x^4} + yz}} + \dfrac{{{y^2}}}{{{y^4} + xz}} + \dfrac{{{z^2}}}{{{z^4} + xy}}.\)
PHẦN TRẮC NGHIỆM (3 điểm)
1. A | 2. D | 3. D | 4. A | 5.C |
6. B | 7. D | 8. B | 9. B | 10. B |
11. B | 12. D | 13. D | 14. D | 15. A |
16. D | 17. B | 18. A | 19. C | 20. C |
21. A | 22. B | 23. C | 24. D | 25. B |
Câu 1:
Phương pháp:
Hệ phương trình \(\left\{ \begin{array}{l}{a_1}x + {b_1}y = {c_1}\\{a_2}c + {b_2}y = {c_2}\end{array} \right.\) có nghiệm duy nhất \( \Leftrightarrow \dfrac{{{a_1}}}{{{a_2}}} \ne \dfrac{{{b_1}}}{{{b_2}}}.\)
Cách giải:
Hệ phương trình có nghiệm duy nhất \( \Leftrightarrow \dfrac{{a - 1}}{2} \ne \dfrac{{ - 1}}{{ - 1}} \Leftrightarrow a - 1 \ne 2 \Leftrightarrow a \ne 3.\)
Chọn A.
Câu 2:
Phương pháp:
Cho hai đường thẳng \(d:\,\,y = ax + b\) và \(d':\,\,y = a'x + b'.\)
Khi đó: \(d//d' \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right..\)
Cách giải:
\(\left( d \right):\,\,y = {m^2}x + m\,\,\left( {m \ne 0} \right)\) song song với đường thẳng \(\left( {d'} \right):\,\,y = 4x - 2.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{m^2} = 4\\m \ne - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 2\\m = - 2\end{array} \right.\\m \ne - 2\end{array} \right. \Leftrightarrow m = 2.\)
Chọn D.
Câu 3:
Phương pháp:
Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để làm bài.
Cách giải:
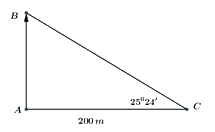
Gọi các điểm như hình vẽ.
Khi đó chiều cao của đài kiểm soát là: \(AB = AC.\tan \angle C = 200.\tan {25^0}24' \approx 95\,m.\)
Chọn D.
Câu 4:
Phương pháp:
Sử dụng mối liên hệ giữa đường kính và dây cung để làm bài toán.
Cách giải:
Gọi \(H\) là hình chiếu của \(O\) trên \(AB \Rightarrow OH \bot AB,\,\,\,H\) là trung điểm của\(AB\) (mối liên hệ giữa đường kính và dây cung). Theo đề bài ta có: \(OA = R = 10\,cm,\,\,OH = d\left( {O;\,\,AB} \right) = 6cm.\) Áp dụng định lý Pi-ta-go ta có: \(\begin{array}{l}AH = \sqrt {O{A^2} - O{H^2}} = \sqrt {{{10}^2} - {6^2}} = 8cm.\\ \Rightarrow AB = 2AH = 16\,\,cm.\end{array}\) Chọn A. |
Câu 5:
Phương pháp:
Áp dụng các công thức hệ thức lượng trong tam giác vuông để làm bài.
Cách giải:
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có: \(A{H^2} = HB.HC.\) Chọn C. |
Câu 6:
Phương pháp:
Sử dụng phương pháp tọa độ hóa.
Cách giải:
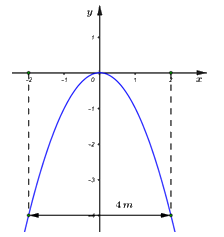
Ta có đồ thị hàm số của cổng biệt thự như hình vẽ.
Khi đó cổng biệt thự có chiều cao \(h = 4\,m.\)
Chiều rộng của thùng xe ô tô tải là \(2,4\,m \Rightarrow {x_0} = \dfrac{1}{2}.2,4 = 1,2m.\)
\( \Rightarrow \) Chiều cao lớn nhất của ô tô tải là: \({h_0} = 1,{2^2} = 1,44m.\)
Chọn B.
Câu 7:
Phương pháp:
Công thức tính diện tích hình tròn bán kính \(R:\,\,\,S = \pi {R^2}.\)
Cách giải:
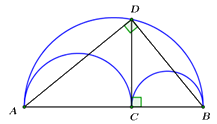
Xét đường tròn đường kính \(AB\) ta có: \(\angle ADB\) là góc nội tiếp chắn nửa đường tròn
\( \Rightarrow \angle ADB = {90^0}.\)
Áp dụng hệ thức lượng trong tam giác vuông ta có: \(C{D^2} = AC.CB.\)
Diện tích hình tròn bán kính \(CD\) là: \({S_0} = \pi C{D^2} = \pi .AC.CB.\)
Diện tích nửa đường tròn đường kính \(AB\) là: \({S_1} = \dfrac{1}{2}.\pi .{\left( {\dfrac{{AB}}{2}} \right)^2} = \dfrac{{\pi A{B^2}}}{8}.\)
Diện tích nửa đường tròn đường kính \(AC\) là: \({S_2} = \dfrac{1}{2}.\pi .{\left( {\dfrac{{AC}}{2}} \right)^2} = \dfrac{{\pi A{C^2}}}{8}.\)
Diện tích nửa đường tròn đường kính \(BC\) là: \({S_3} = \dfrac{1}{2}.\pi .{\left( {\dfrac{{BC}}{2}} \right)^2} = \dfrac{{\pi B{C^2}}}{8}.\)
\( \Rightarrow \) Diện tích hình được giới hạn bởi ba đường tròn là:
\(S = {S_1} - {S_2} - {S_3} = \dfrac{{\pi A{B^2}}}{8} - \dfrac{{\pi A{C^2}}}{8} - \dfrac{{\pi B{C^2}}}{8} = \dfrac{\pi }{8}\left( {A{B^2} - A{C^2} - B{C^2}} \right).\)
Lại có: \(AB = AC + BC \Rightarrow A{B^2} = A{C^2} + 2AC.BC + B{C^2}\)
\(\begin{array}{l} \Rightarrow S = \dfrac{\pi }{8}\left( {A{B^2} - A{C^2} - B{C^2}} \right) = \dfrac{\pi }{8}\left( {A{C^2} + B{C^2} + 2AC.BC - A{C^2} - B{C^2}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{\pi }{8}.2AC.BC = \dfrac{{\pi .AB.BC}}{4}.\\ \Rightarrow \dfrac{S}{{{S_0}}} = \dfrac{{\dfrac{{\pi .AB.BC}}{4}}}{{\pi .AC.BC}} = \dfrac{1}{4}.\end{array}\)
Chọn D.
Câu 8:
Phương pháp:
Số dương \(a\) có căn bậc hai số học là \(\sqrt a .\)
Cách giải:
Ta có \(36\) có căn bậc hai số học là \(\sqrt {36} = 6.\)
Chọn B.
Câu 9:
Phương pháp:
Lập phương trình hoành độ giao điểm \(\left( * \right)\) của hai đồ thị hàm số.
Đường thẳng \(d\) cắt \(\left( P \right)\) tại hai điểm phân biệt nằm phía bên phải trục tung \( \Leftrightarrow \left( * \right)\) có hai nghiệm dương phân biệt \( \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\ - \dfrac{b}{a} > 0\\\dfrac{c}{a} > 0\end{array} \right..\)
Cách giải:
Phương trình hoành độ giao điểm của \(d:\,\,y = 6x + m - 5\) và parabol \(\left( P \right):\,\,y = {x^2}\) là:
\({x^2} = 6x + m - 5 \Leftrightarrow {x^2} - 6x - m + 5 = 0\,\,\,\,\left( * \right)\)
Đường thẳng \(d\) cắt \(\left( P \right)\) tại hai điểm phân biệt nằm phía bên phải trục tung \( \Leftrightarrow \left( * \right)\) có hai nghiệm dương phân biệt \( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\ - \dfrac{b}{a} > 0\\\dfrac{c}{a} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}9 + m - 5 > 0\\3 > 0\\ - m + 5 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > - 4\\m < 5\end{array} \right. \Leftrightarrow - 4 < m < 5\)
Lại có: \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 3; - 2; - 1;\,\,0;\,\,1;\,\,2;\,\,3;\,\,4} \right\}.\)
\( \Rightarrow S = - 3 - 2 - 1 + 0 + 1 + 2 + 3 + 4 = 4.\)
Chọn B.
Câu 10:
Phương pháp:
Hàm số \(y = ax + b\,\,\,\left( {a \ne 0} \right)\) đồng biến trên \(\mathbb{R} \Leftrightarrow a > 0.\)
Cách giải:
Trong các hàm số ở các đáp án chỉ có đáp án B là hàm số có hệ số góc \(a = 2 > 0 \Rightarrow y = 2x + 1\) là hàm số đồng biến trên \(\mathbb{R}.\)
Chọn B.
Câu 11:
Phương pháp:
Hàm số \(y = ax + b\,\,\,\left( {a \ne 0} \right)\) nghịch biến trên \(\mathbb{R} \Leftrightarrow a < 0.\)
Cách giải:
Hàm số bậc nhất \(y = \left( {2019 - m} \right)x + 2020\) nghịch biến trên \(\mathbb{R}\)
\( \Leftrightarrow 2019 - m < 0 \Leftrightarrow m > 2019.\)
Chọn B.
Câu 12:
Phương pháp:
Sử dụng công thức tỉ số lượng giác của góc nhọn trong tam giác vuông.
Cách giải:
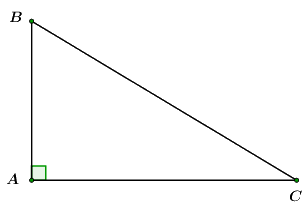
Ta có: \(\sin B = \frac{{AC}}{{BC}}.\)
Chọn D.
Câu 13:
Phương pháp:
Hàm số \(y = \sqrt {f\left( x \right)} \) xác định \( \Leftrightarrow f\left( x \right) \ge 0.\)
Cách giải:
Biểu thức \(\sqrt {2x - 8} \) xác định \( \Leftrightarrow 2x - 8 \ge 0 \Leftrightarrow 2x \ge 8 \Leftrightarrow x \ge 4.\)
Chọn D.
Câu 14:
Phương pháp:
Sử dụng tính chất của góc nội tiếp có số đo bằng nửa số đo cung bị chắn.
Cách giải:
Ta có: \(\angle ABC\) là góc nội tiếp chắn cung \(AC \Rightarrow cung\,\,AC\,\,\,nho = 2.\angle ABC = {2.40^0} = {80^0}.\)
Ta có: \(cung\,\,AB = cung\,\,AC\,\,nho\,\, + \,\,cung\,\,\,BC\,\,\,nho = {180^0}\)
\( \Rightarrow cung\,\,BC\,\,nho = {180^0} - cung\,\,AC\,\,nho = {180^0} - {80^0} = {100^0}.\)
Mà \(\angle BMC\) là góc nội tiếp chắn cung \(BC\) nhỏ
\( \Rightarrow \angle BMC = \frac{1}{2}\,\,cung\,\,BC\,\,nho = \frac{1}{2}{.100^0} = {50^0}.\)
Chọn D.
Câu 15:
Phương pháp:
Thay tọa độ điểm \(A\) vào công thức hàm số để tìm \(m.\)
Cách giải:
\(A\left( { - 1;\,\,2} \right)\) thuộc đồ thị hàm số \(y = \left( {m + 5} \right){x^2} \Rightarrow 2 = \left( {m + 5} \right).{\left( { - 1} \right)^2} \Leftrightarrow m + 5 = 2 \Leftrightarrow m = - 3.\)
Chọn A.
Câu 16:
Phương pháp:
Cho đường tròn \(\left( {O;\,\,R} \right)\) và đường thẳng \(d.\) Khi đó:
+) Nếu \(d = \left( {O;\,\,d} \right) = R \Rightarrow d\) và \(\left( {O;\,\,R} \right)\) có một điểm chung.
+) Nếu \(d = \left( {O;\,\,d} \right) > R \Rightarrow d\) và \(\left( {O;\,\,R} \right)\) có không có điểm chung.
+) Nếu \(d = \left( {O;\,\,d} \right) < R \Rightarrow d\) và \(\left( {O;\,\,R} \right)\) có hai điểm chung phân biệt.
Cách giải:
Ta có: \(d\left( {O;\,\,d} \right) = 6 > R = 5 \Rightarrow d\) và \(\left( {O;\,\,R} \right)\) có hai điểm chung phân biệt.
Chọn B.
Câu 17:
Phương pháp:
Diện tích mặt cầu bán kính \(R:\,\,\,S = 4\pi {R^2}.\)
Cách giải:
Diện tích bề mặt quả bóng là: \(S = 4\pi {R^2} = 4.3,{14.7^2} = 615,44\,\,c{m^2}.\)
Chọn C.
Câu 18:
Phương pháp:
Phương trình bậc hai một ẩn có dạng: \(a{x^2} + bx + c = 0\,\,\,\left( {a \ne 0} \right).\)
Cách giải:
Trong các đáp án, chỉ có đáp án A có phương trình là phương trình bậc hia một ẩn.
Chọn A.
Câu 19:
Phương pháp:
Góc ở tâm có số đo bằng cung bị chắn.
Cách giải:
Lúc \(8\) giờ, kim giờ và kim phút của đồng hồ tạo thành góc ở tâm có số đo là \({120^0}.\)
Chọn C.
Câu 20:
Phương pháp:
Trục căn thức ở mẫu hoặc quy đồng mẫu các phân thức để tính giá trị của biểu thức.
Cách giải:
\(E = \frac{1}{{\sqrt 2 - 1}} - \frac{1}{{\sqrt 2 + 1}} = \frac{{\sqrt 2 + 1 - \sqrt 2 + 1}}{{\left( {\sqrt 2 - 1} \right)\left( {\sqrt 2 + 1} \right)}} = \frac{2}{{2 - 1}} = 2.\)
Chọn C.
Câu 21:
Phương pháp:
Đường thẳng \(y = ax + b\) có hệ số góc là \(a.\)
Cách giải:
Ta có: đường thẳng \(y = - 2x + 3\) có hệ số góc là \(a = - 2.\)
Chọn A.
Câu 22:
Phương pháp:
Hệ phương trình bậc nhất hai ẩn có dạng: \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right..\)
Cách giải:
Trong các đáp án trên chỉ có hệ phương trình ở đáp án B có dạng là hệ phương trình bậc nhất hai ẩn.
Chọn B.
Câu 23:
Phương pháp:
Hàm số \(y = a{x^2}\,\,\,\left( {a > 0} \right):\)
+) Đồng biến khi \(x > 0\) và nghịch biến khi \(x < 0.\)
Cách giải:
Xét hàm số \(y = 9{x^2}\) có \(a = 9 > 0\)
\( \Rightarrow \) Hàm số đồng biến khi \(x > 0\) và nghịch biến khi \(x < 0.\)
Chọn C.
Câu 24:
Phương pháp:
Thể tích hình trụ có chiều cao \(h\) và bán kính đáy \(R\) là: \(V = \pi {R^2}h.\)
Cách giải:
Theo đề bài ta có chu vi đáy của thùng nước là: \(2,4\,m.\)
\( \Rightarrow \) Thùng đựng nước có bán kính đáy là: \(R = \frac{{2,4}}{{2\pi }} = \frac{{1,2}}{\pi }\,\,m\) và chiều cao là: \(h = 0,5\,m.\)
Thể tích của thùng đựng nước là: \(V = \pi .0,5.{\left( {\frac{{1,2}}{\pi }} \right)^2} = \frac{{18}}{{25\pi }}\,\,{m^3}.\)
Chọn D.
Câu 25:
Phương pháp:
Tìm nghiệm \(y\) theo \(x.\)
Cách giải:
Ta có: \(2x - y = 1 \Leftrightarrow y = 2x - 1\)
\( \Rightarrow \) Nghiệm của phương trình là: \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = 2x - 1\end{array} \right..\)
Chọn B.
PHẦN TỰ LUẬN (7 điểm)
Câu 1 (VD)
Phương pháp:
a) Sử dụng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,\,A < 0\end{array} \right..\)
b) Thay tọa độ điểm \(A\left( {1;5} \right)\) vào phương trình đường thẳng \(\left( d \right)\) để tìm \(m\)
c) Giải hệ phương trình bằng phương pháp thế.
Cách giải:
a) Rút gọn biểu thức \(P = \sqrt 5 \left( {\sqrt 5 + 2} \right) - \sqrt {20} \)
\(P = \sqrt 5 \left( {\sqrt 5 + 2} \right) - \sqrt {20} = \sqrt 5 .\sqrt 5 + 2\sqrt 5 - 2\sqrt 5 = 5\)
Vậy \(P = 5\).
b) Tìm giá trị của \(m\) để đường thẳng \(\left( d \right):\,y = mx + 3\) đi qua điểm \(A\left( {1;5} \right)\)
Đường thẳng \(\left( d \right):\,y = mx + 3\)đi qua điểm \(A\left( {1;5} \right)\) nên ta có:
\(5 = m.1 + 3 \Leftrightarrow m = 2\)
Vậy với \(m = 2\) thì đường thẳng \(\left( d \right):\,y = mx + 3\)đi qua điểm \(A\left( {1;5} \right)\).
c) Giải hệ phương trình \(\left\{ \begin{array}{l}3x - y = 7\\x + y = 5\end{array} \right.\)
Ta có :
\(\left\{ \begin{array}{l}3x - y = 7\\x + y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 5 - x\\3x - \left( {5 - x} \right) = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 5 - x\\4x = 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 5 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 2\end{array} \right.\)
Vậy nghiệm của hệ phương trình là: \(\left( {x;y} \right) = \left( {3;2} \right)\)
Câu 2 (VD)
Phương pháp:
a) Thay \(m = 4\) vào phương trình rồi giải.
b) Tìm biệt thức \(\Delta '\) , rồi sử dụng định lý Vi-et, biến đổi biểu thức đã cho về dạng tổng và tích của hai nghiệm.
Cách giải:
a) Giải phương trình với \(m = 4\)
Với \(m = 4\) ta có phương trình: \({x^2} - 4x + 4 - 1 = 0 \Leftrightarrow {x^2} - 4x + 3 = 0\,\,\,\left( 1 \right)\)
Phương trình (1) có hệ số \(a = 1;\,b = - 4;\,c = 3 \Rightarrow a + b + c = 0\)
Nên phương trình (1) có hai nghiệm là \({x_1} = 1;\,{x_2} = \frac{c}{a} = 3\)
Vậy với \(m = 4\) thì tập nghiệm của phương trình là: \(S = \left\{ {1;3} \right\}\)
b) Tìm \(m\) để phương trình có hai nghiệm phân biệt thỏa mãn điều kiện:
\({x_1}\left( {{x_1} + 2} \right) + {x_2}\left( {{x_2} + 2} \right) = 20\)
Phương trình \({x^2} - 4x + m - 1 = 0\,\,\,\left( * \right)\)
Có \(\Delta ' = {\left( { - 2} \right)^2} - 1.\left( {m - 1} \right) = 5 - m\)
Để phương trình (*) có hai nghiệm phân biệt \({x_1};\,{x_2}\) thì \(\Delta ' > 0 \Leftrightarrow 5 - m > 0 \Leftrightarrow m < 5\)
Theo hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a} = 4\\{x_1}.{x_2} = \frac{c}{a} = m - 1\end{array} \right.\)
Ta có:
\(\begin{array}{l}{x_1}\left( {{x_1} + 2} \right) + {x_2}\left( {{x_2} + 2} \right) = 20\\ \Leftrightarrow {x_1}^2 + 2{x_1} + x_2^2 + 2{x_2} = 20\\ \Leftrightarrow x_1^2 + x_2^2 + 2\left( {{x_1} + {x_2}} \right) = 20\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}.{x_2} + 2\left( {x{ & _1} + {x_2}} \right) = 20\\ \Leftrightarrow \,\,\,{4^2} - 2\left( {m - 1} \right) + 2.4\, = 20\\ \Leftrightarrow 16\,\, - 2\left( {m - 1} \right) + 8 = 20\\ \Leftrightarrow 2\left( {m - 1} \right) = 4\\ \Leftrightarrow m - 1 = 2 \Leftrightarrow m = 3\,\left( {tm} \right)\end{array}\)
Vậy \(m = 3\) là giá trị cần tìm.
Câu 3 (VD):
Phương pháp:
a) Chỉ ra tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới các góc bằng nhau là tứ giác nội tiếp
b) Chứng minh \(DM \bot AO\) rồi sử dụng hệ thức lượng trong tam giác vuông
Cách giải:
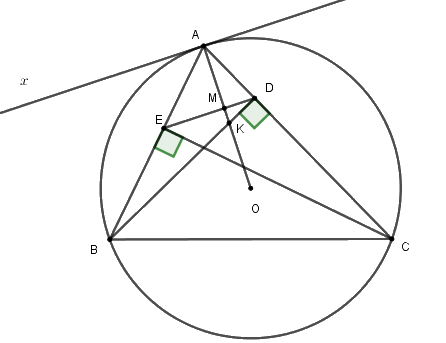
a) Vì \(BD,CE\) là hai đường cao của tam giác \(ABC\) nên \(\angle BEC = \angle BDC = 90^\circ \)
Xét tứ giác \(BCDE\) có \(\angle BEC = \angle BDC = 90^\circ \) (cmt) nên hai đỉnh \(E,D\) kề nhau cùng nhìn cạnh \(BC\) dưới các góc \(90^\circ \) , suy ra tứ giác \(BCDE\) là tứ giác nội tiếp. (dhnb)
b) Kẻ tiếp tuyến \(Ax\) với đường tròn \(\left( O \right)\)
Suy ra \(OA \bot Ax\)
+ Vì tứ giác \(BCDE\) là tứ giác nội tiếp (theo câu a) nên \(\angle BCD = \angle AED\) (1) (cùng bù với \(\angle BED\) )
+ Xét đường tròn \(\left( O \right)\) có \(\angle BAx = \angle BCA\) (2) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(AB\))
Từ (1) và (2) suy ra \(\angle BAx = \angle AED\) mà hai góc ở vị trí so le trong nên \(Ax//ED\)
Mà \(Ax \bot AO\left( {cmt} \right) \Rightarrow ED \bot AO = \left\{ M \right\}.\)
Xét tam giác \(ADK\) vuông tại \(D\) có \(DM\) là đường cao.
Theo hệ thức lượng trong tam giác vuông ta có: \(\frac{1}{{D{M^2}}} = \frac{1}{{D{K^2}}} + \frac{1}{{D{A^2}}}\) (đpcm)
Câu 4 (VDC)
Phương pháp:
Sử dụng liên tiếp bất đẳng thức Cô – si cho hai số dương \(a + b \ge 2\sqrt {ab} \) để đánh giá \(P\).
Cách giải:
\({x^2} + {y^2} + {z^2} = 3xyz \Rightarrow \frac{x}{{yz}} + \frac{y}{{xz}} + \frac{z}{{xy}} = 3\)
Áp dụng bất đẳng thức Cô – si cho hai số dương \(\frac{x}{{yz}};\frac{y}{{zx}}\) ta có: \(\frac{x}{{yz}} + \frac{y}{{zx}} \ge 2\sqrt {\frac{x}{{yz}}.\frac{y}{{zx}}} = \frac{2}{z}\)
Tương tự ta cũng có \(\frac{y}{{zx}} + \frac{z}{{xy}} \ge \frac{2}{x};\frac{z}{{xy}} + \frac{x}{{yz}} \ge \frac{2}{y}\)
\( \Rightarrow \left( {\frac{x}{{yz}} + \frac{y}{{zx}}} \right) + \left( {\frac{y}{{zx}} + \frac{z}{{xy}}} \right) + \left( {\frac{z}{{xy}} + \frac{x}{{yz}}} \right) \ge \frac{2}{z} + \frac{2}{x} + \frac{2}{y}\)
\( \Rightarrow \frac{x}{{yz}} + \frac{y}{{zx}} + \frac{z}{{xy}} \ge \frac{1}{x} + \frac{1}{y} + \frac{1}{z} \Rightarrow \frac{1}{x} + \frac{1}{y} + \frac{1}{z} \le 3\)
Lại có: \({x^4} + yz \ge 2\sqrt {{x^4}yz} = 2{x^2}\sqrt {yz} \Rightarrow \frac{{{x^2}}}{{{x^4} + yz}} \le \frac{1}{{2\sqrt {yz} }} = \frac{1}{4}.2.\frac{1}{{\sqrt y }}.\frac{1}{{\sqrt z }} \le \frac{1}{4}\left( {\frac{1}{y} + \frac{1}{z}} \right)\)
Tương tự \(\frac{{{y^2}}}{{{y^4} + xz}} \le \frac{1}{4}\left( {\frac{1}{x} + \frac{1}{z}} \right);\frac{{{z^2}}}{{{z^4} + xy}} \le \frac{1}{4}\left( {\frac{1}{x} + \frac{1}{y}} \right)\)
Suy ra \(P = \frac{{{x^2}}}{{{x^4} + yz}} + \frac{{{y^2}}}{{{y^4} + xz}} + \frac{{{z^2}}}{{{z^4} + xy}} \le \frac{1}{4}\left( {\frac{2}{x} + \frac{2}{y} + \frac{2}{z}} \right) = \frac{1}{2}\left( {\frac{1}{x} + \frac{1}{y} + \frac{1}{z}} \right) \le \frac{3}{2}\)
\( \Rightarrow P \le \frac{3}{2}\).
Dấu “=” xảy ra khi \(x = y = z = 1\).
Vậy \({P_{\max }} = \frac{3}{2}\) khi \(x = y = z = 1\).
PHẦN TRẮC NGHIỆM (3 điểm)
Câu 1: Xác định tham số \(a\) để hệ phương trình \(\left\{ \begin{array}{l}\left( {a - 1} \right)x - y = a + 2\\2x - y = 3\end{array} \right.\) có nghiệm duy nhất.
A. \(a \ne 3\) B. \(a \ne 0\) C. \(a \ne - 2\) D. \(a \ne 1\)
Câu 2 : Tìm \(m\) để đường thẳng \(\left( d \right):\,\,y = {m^2}x + m\,\,\left( {m \ne 0} \right)\) song song với đường thẳng \(\left( {d'} \right):\,\,y = 4x - 2.\)
A. \(m = - 4\) B. \(m = - 2\) C. \(m = 4\) D. \(m = 2\)
Câu 3: Tính chiều cao của đài kiểm soát không lưu Nội Bài. Biết bóng của đài kiểm soát được chiếu bởi ánh sáng mặt trời xuống đất dài \(200\,m\) và góc tạo bởi tia sáng với mặt đất là \({25^0}24'\) (kết quả làm tròn đến hàng đơn vị).
A. \(221\,m\) B. \(181\,m\) C. \(86\,m\)D. \(95\,m\) |
Câu 4: Cho đường tròn \(\left( {O;\,\,10cm} \right)\) và dây \(AB\) cách tâm \(O\) một khoảng bằng \(6cm.\) Tính độ dài dây \(AB.\)
A. \(16\,cm\) B. \(12\,cm\) C. \(8\,cm\) D. \(10\,cm\)
Câu 5: Cho \(\Delta ABC\) vuông tại\(A,\) đường cao \(AH.\) Khẳng định bào sau đây đúng?
A. \(A{H^2} = HB.BC\)B. \(A{H^2} = HB.AB\)C. \(A{H^2} = HB.HC\) D. \(A{H^2} = HB.AC\)
Câu 6: Cổng vào một ngôi biệt thự có hình dạng là một parabol được biểu diễn bởi đồ thị hàm số \(y = - {x^2}.\) Biết khoảng cách giữa hai chân cổng là \(4\,m.\) Một chiếc ô tô tải có thùng xe là một hình hộp chữ nhật có chiều rộng là \(2,4\,m.\) Hỏi chiều cao lớn nhất có thể của ô tô là bao nhiêu để ô tô có thể đi qua cổng?
A. \(2,\,4\,m\) B. \(1,44\,m\) C. \(4\,m\) D. \(2,56\,m\) |
Câu 7: Trên hình vẽ là ba nửa đường tròn đường kính \(AB,\,\,AC,\,\,CB.\) Biết \(DC \bot AB = \left\{ C \right\},\) khi đó tỉ số diện tích hình giới hạn bởi ba nửa đường tròn nói trên và diện tích hình tròn bán kính \(DC\) là:
A. \(\dfrac{{\sqrt 7 }}{3}\) B. \(\dfrac{1}{3}\) C. \(\dfrac{1}{2}\) D. \(\dfrac{1}{4}\) |
Câu 8 : Căn bậc hai số học của \(36\) là:
A. \( - 6\) B. \(6\) C. \(72\) D. \(18\)
Câu 9: Gọi \(S\) là tập hợp các giá trị nguyên của \(m\) để đường thẳng\(y = 6x + m - 5\) và parabol \(y = {x^2}\) cắt nhau tại hai điểm phân biệt bằm bên phải trục tung. Tính tổng các phần tử của tập \(S.\)
A. 3 B. -3 C. 6 D. -6
Câu 10: Trong các hàm số sau, hàm số nào là đồng biến trên \(\mathbb{R}?\)
A. \(y = - x + 5\) B. \(y = 2x + 1\) C. \(y = 2019 - 2x\) D. \(y = 2020\)
Câu 11: Tìm tất cả các giá trị của \(m\) để hàm số bậc nhất \(y = \left( {2019 - m} \right)x + 2020\) nghịch biến trên \(\mathbb{R}.\)
A. \(m > - 2019\) B. \(m > 2019\) C. \(m < 2019\) D. \(m < - 2019\)
Câu 12: Cho \(\Delta ABC\) vuông tại\(A.\) Khẳng định nào sau đây là đúng?
A. \(\sin B = \dfrac{{AC}}{{AB}}\) B. \(\sin B = \dfrac{{AB}}{{BC}}\) C. \(\sin B = \dfrac{{AB}}{{AC}}\) D. \(\sin B = \dfrac{{AC}}{{BC}}\)
Câu 13: Biểu thức \(\sqrt {2x - 8} \) có nghĩa khi và chỉ khi:
A. \(x \le - 4\)B. \(x \le 4\)C. \(x \ge - 4\) D. \(x \ge 4\)
Câu 14: Cho hình vẽ, biết \(AB\) là đường kính của đường tròn tâm \(O,\,\,\angle ABC = {40^0}.\) Tính số đo \(\angle BMC.\)
A. \({40^0}\) B. \({60^0}\) C. \({80^0}\)D. \({50^0}\)
Câu 15: Tìm \(m\) để đồ thị hàm số \(y = \left( {m + 5} \right){x^2}\) đi qua điểm \(A\left( { - 1;\,\,2} \right).\)
A. \(m = - 3\) B. \(m = 6\) C. \(m = 3\) D. \(m = - 7\)
Câu 16: Tâm \(O\) của đường tròn \(\left( {O;\,\,5cm} \right)\) cách đường thẳng \(d\) một khoảng bằng \(6\,cm.\) Tìm số điểm chung của đường thẳng \(d\) và đường tròn \(\left( {O;\,\,5cm} \right).\)
A. Có ít nhất một điểm chung. B. Có hai điểm chung phân biệt. C. Có một điểm chung duy nhất. D. Không có điểm chung.
Câu 17: Một quả bóng nhựa mềm dành cho trẻ em có dạng hình cầu, đường kính \(7\,cm.\) Tính diện tích bề mặt quả bóng (lấy \(\pi \approx 3,14\) và kết quả làm tròn đến chữ số thập phân thứ hai).
A. \(381,\,51\,c{m^2}\)B. \(153,\,86\,c{m^2}\) C. \(615,44\,c{m^2}\)D. \(179,50\,c{m^2}\)
Câu 18: Phương trình nào sau đây là phương trình bậc hai một ẩn?
A. \( - {x^2} + x - 2 = 0\) B. \( - 2x + 5 = 0\)C. \(3xy + 4x - 6 = 0\)D. \({x^3} + 2{x^2} = 0\)
Câu 19: Lúc \(8\) giờ, kim giờ và kim phút của đồng hồ tạo thành một góc ở tâm có số đo là:
A. \({80^0}\) B. \({240^0}\) C. \({120^0}\) D. \({40^0}\)
Câu 20: Giá trị của biểu thức: \(E = \dfrac{1}{{\sqrt 2 - 1}} - \dfrac{1}{{\sqrt 2 + 1}}\) bằng:
A. \( - 2\) B. \( - 2\sqrt 2 \) C. \(2\) D. \(2\sqrt 2 \)
Câu 21: Hệ số góc của đường thẳng \(\left( d \right):\,\,y = - 2x + 3\) là:
A. \( - 2\) B. \( - \dfrac{3}{2}\) C. \(\dfrac{3}{2}\) D. \(3\)
Câu 22: Trong các hệ phương trình sau, hệ phương trình nào là hệ phương trình bậc nhất hai ẩn?
A. \(\left\{ \begin{array}{l}xy + 3x = 1\\y - 2x = 1\end{array} \right.\) B. \(\left\{ \begin{array}{l}x + y = 3\\2x + y = 1\end{array} \right.\) C. \(\left\{ \begin{array}{l}{x^2} + 3y = 1\\ - x + 2y = - 2\end{array} \right.\) D. \(\left\{ \begin{array}{l}x - 2y = 1\\x + 2{y^2} = - 1\end{array} \right.\)
Câu 23: Cho hàm số \(y = 9{x^2}.\) Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến khi \(x > 0.\) B. Hàm số đồng biến trên \(\mathbb{R}.\)
C. Hàm số đồng biến khi \(x > 0.\) D. Hàm số đồng biến khi \(x < 0.\)
Câu 24: Từ một tâm tôn hình chữ nhật có kích thước \(0,5\,m \times 2,4\,m\) người ta gò tấm tôn đó thành mặt xung quanh của thùng đựng nước hình trụ có chiều cao bằng \(0,5\,m\) (phần mép hàn không đáng kể).
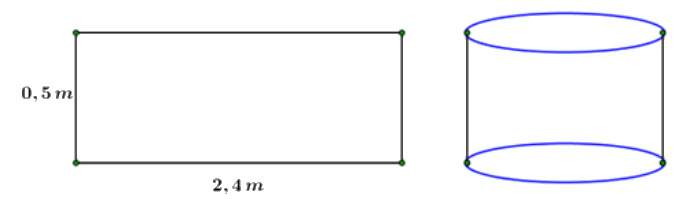
Thể tích \(V\) của thùng.
A. \(V = \dfrac{{12}}{{25\pi }}\,{m^3}\) B. \(V = \dfrac{{36}}{{25\pi }}\,{m^3}\) C. \(V = \dfrac{6}{{5\pi }}\,{m^3}\) D. \(V = \dfrac{{18}}{{25\pi }}\,{m^3}\)
Câu 25: Nghiệm tổng quát của phương trình \(2x - y = 1\) là:
A. \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = 1 - 2x\end{array} \right.\) B. \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = 2x - 1\end{array} \right.\) C. \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = 2x + 1\end{array} \right.\) D. \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = - 2x - 1\end{array} \right.\)
PHẦN TỰ LUẬN (7 điểm)
Câu 1 (1,5 điểm):
a) Rút gọn biểu thức \(P = \sqrt 5 \left( {\sqrt 5 + 2} \right) - \sqrt {20} \)
b) Tìm giá trị của \(m\) để đường thẳng \(\left( d \right):\,y = mx + 3\) đi qua điểm \(A\left( {1;5} \right)\)
c) Giải hệ phương trình \(\left\{ \begin{array}{l}3x - y = 7\\x + y = 5\end{array} \right.\)
Câu 2 (1,5 điểm):
Cho phương trình \({x^2} - 4mx + m - 1 = 0\) (\(m\) là tham số)
a) Giải phương trình với \(m = 4\)
b) Tìm \(m\) để phương trình có hai nghiệm phân biệt thỏa mãn điều kiện:
\({x_1}\left( {{x_1} + 2} \right) + {x_2}\left( {{x_2} + 2} \right) = 20\)
Câu 3 (1,5 điểm):
Cho tam giác \(ABC\) nhọn \(\left( {AB < AC} \right)\) nội tiếp đường tròn \(\left( O \right).\) Vẽ các đường cao \(BD,CE\) của tam giác \(ABC\) \(\left( {D \in AC;E \in AB} \right)\)
a) Chứng minh tứ giác \(BCDE\) nội tiếp một đường tròn
b) Gọi giao điểm của \(AO\) với \(BD\) và \(ED\) lần lượt là \(K,M.\) Chứng minh \(\dfrac{1}{{M{D^2}}} = \dfrac{1}{{K{D^2}}} + \dfrac{1}{{A{D^2}}}\)
Câu 4 (0,5 điểm):
Cho các số thực dương \(x,\,\,y,\,\,z\) thỏa mãn \({x^2} + {y^2} + {z^2} = 3xyz.\)
Tìm giá trị lớn nhất của biểu thức: \(P = \dfrac{{{x^2}}}{{{x^4} + yz}} + \dfrac{{{y^2}}}{{{y^4} + xz}} + \dfrac{{{z^2}}}{{{z^4} + xy}}.\)
PHẦN TRẮC NGHIỆM (3 điểm)
1. A | 2. D | 3. D | 4. A | 5.C |
6. B | 7. D | 8. B | 9. B | 10. B |
11. B | 12. D | 13. D | 14. D | 15. A |
16. D | 17. B | 18. A | 19. C | 20. C |
21. A | 22. B | 23. C | 24. D | 25. B |
Câu 1:
Phương pháp:
Hệ phương trình \(\left\{ \begin{array}{l}{a_1}x + {b_1}y = {c_1}\\{a_2}c + {b_2}y = {c_2}\end{array} \right.\) có nghiệm duy nhất \( \Leftrightarrow \dfrac{{{a_1}}}{{{a_2}}} \ne \dfrac{{{b_1}}}{{{b_2}}}.\)
Cách giải:
Hệ phương trình có nghiệm duy nhất \( \Leftrightarrow \dfrac{{a - 1}}{2} \ne \dfrac{{ - 1}}{{ - 1}} \Leftrightarrow a - 1 \ne 2 \Leftrightarrow a \ne 3.\)
Chọn A.
Câu 2:
Phương pháp:
Cho hai đường thẳng \(d:\,\,y = ax + b\) và \(d':\,\,y = a'x + b'.\)
Khi đó: \(d//d' \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right..\)
Cách giải:
\(\left( d \right):\,\,y = {m^2}x + m\,\,\left( {m \ne 0} \right)\) song song với đường thẳng \(\left( {d'} \right):\,\,y = 4x - 2.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{m^2} = 4\\m \ne - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 2\\m = - 2\end{array} \right.\\m \ne - 2\end{array} \right. \Leftrightarrow m = 2.\)
Chọn D.
Câu 3:
Phương pháp:
Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để làm bài.
Cách giải:
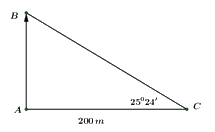
Gọi các điểm như hình vẽ.
Khi đó chiều cao của đài kiểm soát là: \(AB = AC.\tan \angle C = 200.\tan {25^0}24' \approx 95\,m.\)
Chọn D.
Câu 4:
Phương pháp:
Sử dụng mối liên hệ giữa đường kính và dây cung để làm bài toán.
Cách giải:
Gọi \(H\) là hình chiếu của \(O\) trên \(AB \Rightarrow OH \bot AB,\,\,\,H\) là trung điểm của\(AB\) (mối liên hệ giữa đường kính và dây cung). Theo đề bài ta có: \(OA = R = 10\,cm,\,\,OH = d\left( {O;\,\,AB} \right) = 6cm.\) Áp dụng định lý Pi-ta-go ta có: \(\begin{array}{l}AH = \sqrt {O{A^2} - O{H^2}} = \sqrt {{{10}^2} - {6^2}} = 8cm.\\ \Rightarrow AB = 2AH = 16\,\,cm.\end{array}\) Chọn A. |
Câu 5:
Phương pháp:
Áp dụng các công thức hệ thức lượng trong tam giác vuông để làm bài.
Cách giải:
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có: \(A{H^2} = HB.HC.\) Chọn C. |
Câu 6:
Phương pháp:
Sử dụng phương pháp tọa độ hóa.
Cách giải:
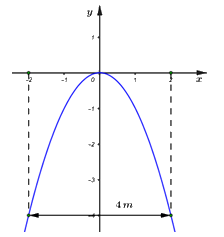
Ta có đồ thị hàm số của cổng biệt thự như hình vẽ.
Khi đó cổng biệt thự có chiều cao \(h = 4\,m.\)
Chiều rộng của thùng xe ô tô tải là \(2,4\,m \Rightarrow {x_0} = \dfrac{1}{2}.2,4 = 1,2m.\)
\( \Rightarrow \) Chiều cao lớn nhất của ô tô tải là: \({h_0} = 1,{2^2} = 1,44m.\)
Chọn B.
Câu 7:
Phương pháp:
Công thức tính diện tích hình tròn bán kính \(R:\,\,\,S = \pi {R^2}.\)
Cách giải:
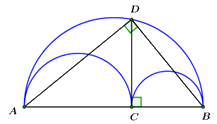
Xét đường tròn đường kính \(AB\) ta có: \(\angle ADB\) là góc nội tiếp chắn nửa đường tròn
\( \Rightarrow \angle ADB = {90^0}.\)
Áp dụng hệ thức lượng trong tam giác vuông ta có: \(C{D^2} = AC.CB.\)
Diện tích hình tròn bán kính \(CD\) là: \({S_0} = \pi C{D^2} = \pi .AC.CB.\)
Diện tích nửa đường tròn đường kính \(AB\) là: \({S_1} = \dfrac{1}{2}.\pi .{\left( {\dfrac{{AB}}{2}} \right)^2} = \dfrac{{\pi A{B^2}}}{8}.\)
Diện tích nửa đường tròn đường kính \(AC\) là: \({S_2} = \dfrac{1}{2}.\pi .{\left( {\dfrac{{AC}}{2}} \right)^2} = \dfrac{{\pi A{C^2}}}{8}.\)
Diện tích nửa đường tròn đường kính \(BC\) là: \({S_3} = \dfrac{1}{2}.\pi .{\left( {\dfrac{{BC}}{2}} \right)^2} = \dfrac{{\pi B{C^2}}}{8}.\)
\( \Rightarrow \) Diện tích hình được giới hạn bởi ba đường tròn là:
\(S = {S_1} - {S_2} - {S_3} = \dfrac{{\pi A{B^2}}}{8} - \dfrac{{\pi A{C^2}}}{8} - \dfrac{{\pi B{C^2}}}{8} = \dfrac{\pi }{8}\left( {A{B^2} - A{C^2} - B{C^2}} \right).\)
Lại có: \(AB = AC + BC \Rightarrow A{B^2} = A{C^2} + 2AC.BC + B{C^2}\)
\(\begin{array}{l} \Rightarrow S = \dfrac{\pi }{8}\left( {A{B^2} - A{C^2} - B{C^2}} \right) = \dfrac{\pi }{8}\left( {A{C^2} + B{C^2} + 2AC.BC - A{C^2} - B{C^2}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{\pi }{8}.2AC.BC = \dfrac{{\pi .AB.BC}}{4}.\\ \Rightarrow \dfrac{S}{{{S_0}}} = \dfrac{{\dfrac{{\pi .AB.BC}}{4}}}{{\pi .AC.BC}} = \dfrac{1}{4}.\end{array}\)
Chọn D.
Câu 8:
Phương pháp:
Số dương \(a\) có căn bậc hai số học là \(\sqrt a .\)
Cách giải:
Ta có \(36\) có căn bậc hai số học là \(\sqrt {36} = 6.\)
Chọn B.
Câu 9:
Phương pháp:
Lập phương trình hoành độ giao điểm \(\left( * \right)\) của hai đồ thị hàm số.
Đường thẳng \(d\) cắt \(\left( P \right)\) tại hai điểm phân biệt nằm phía bên phải trục tung \( \Leftrightarrow \left( * \right)\) có hai nghiệm dương phân biệt \( \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\ - \dfrac{b}{a} > 0\\\dfrac{c}{a} > 0\end{array} \right..\)
Cách giải:
Phương trình hoành độ giao điểm của \(d:\,\,y = 6x + m - 5\) và parabol \(\left( P \right):\,\,y = {x^2}\) là:
\({x^2} = 6x + m - 5 \Leftrightarrow {x^2} - 6x - m + 5 = 0\,\,\,\,\left( * \right)\)
Đường thẳng \(d\) cắt \(\left( P \right)\) tại hai điểm phân biệt nằm phía bên phải trục tung \( \Leftrightarrow \left( * \right)\) có hai nghiệm dương phân biệt \( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\ - \dfrac{b}{a} > 0\\\dfrac{c}{a} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}9 + m - 5 > 0\\3 > 0\\ - m + 5 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > - 4\\m < 5\end{array} \right. \Leftrightarrow - 4 < m < 5\)
Lại có: \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 3; - 2; - 1;\,\,0;\,\,1;\,\,2;\,\,3;\,\,4} \right\}.\)
\( \Rightarrow S = - 3 - 2 - 1 + 0 + 1 + 2 + 3 + 4 = 4.\)
Chọn B.
Câu 10:
Phương pháp:
Hàm số \(y = ax + b\,\,\,\left( {a \ne 0} \right)\) đồng biến trên \(\mathbb{R} \Leftrightarrow a > 0.\)
Cách giải:
Trong các hàm số ở các đáp án chỉ có đáp án B là hàm số có hệ số góc \(a = 2 > 0 \Rightarrow y = 2x + 1\) là hàm số đồng biến trên \(\mathbb{R}.\)
Chọn B.
Câu 11:
Phương pháp:
Hàm số \(y = ax + b\,\,\,\left( {a \ne 0} \right)\) nghịch biến trên \(\mathbb{R} \Leftrightarrow a < 0.\)
Cách giải:
Hàm số bậc nhất \(y = \left( {2019 - m} \right)x + 2020\) nghịch biến trên \(\mathbb{R}\)
\( \Leftrightarrow 2019 - m < 0 \Leftrightarrow m > 2019.\)
Chọn B.
Câu 12:
Phương pháp:
Sử dụng công thức tỉ số lượng giác của góc nhọn trong tam giác vuông.
Cách giải:
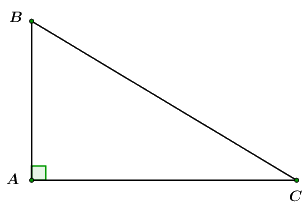
Ta có: \(\sin B = \frac{{AC}}{{BC}}.\)
Chọn D.
Câu 13:
Phương pháp:
Hàm số \(y = \sqrt {f\left( x \right)} \) xác định \( \Leftrightarrow f\left( x \right) \ge 0.\)
Cách giải:
Biểu thức \(\sqrt {2x - 8} \) xác định \( \Leftrightarrow 2x - 8 \ge 0 \Leftrightarrow 2x \ge 8 \Leftrightarrow x \ge 4.\)
Chọn D.
Câu 14:
Phương pháp:
Sử dụng tính chất của góc nội tiếp có số đo bằng nửa số đo cung bị chắn.
Cách giải:
Ta có: \(\angle ABC\) là góc nội tiếp chắn cung \(AC \Rightarrow cung\,\,AC\,\,\,nho = 2.\angle ABC = {2.40^0} = {80^0}.\)
Ta có: \(cung\,\,AB = cung\,\,AC\,\,nho\,\, + \,\,cung\,\,\,BC\,\,\,nho = {180^0}\)
\( \Rightarrow cung\,\,BC\,\,nho = {180^0} - cung\,\,AC\,\,nho = {180^0} - {80^0} = {100^0}.\)
Mà \(\angle BMC\) là góc nội tiếp chắn cung \(BC\) nhỏ
\( \Rightarrow \angle BMC = \frac{1}{2}\,\,cung\,\,BC\,\,nho = \frac{1}{2}{.100^0} = {50^0}.\)
Chọn D.
Câu 15:
Phương pháp:
Thay tọa độ điểm \(A\) vào công thức hàm số để tìm \(m.\)
Cách giải:
\(A\left( { - 1;\,\,2} \right)\) thuộc đồ thị hàm số \(y = \left( {m + 5} \right){x^2} \Rightarrow 2 = \left( {m + 5} \right).{\left( { - 1} \right)^2} \Leftrightarrow m + 5 = 2 \Leftrightarrow m = - 3.\)
Chọn A.
Câu 16:
Phương pháp:
Cho đường tròn \(\left( {O;\,\,R} \right)\) và đường thẳng \(d.\) Khi đó:
+) Nếu \(d = \left( {O;\,\,d} \right) = R \Rightarrow d\) và \(\left( {O;\,\,R} \right)\) có một điểm chung.
+) Nếu \(d = \left( {O;\,\,d} \right) > R \Rightarrow d\) và \(\left( {O;\,\,R} \right)\) có không có điểm chung.
+) Nếu \(d = \left( {O;\,\,d} \right) < R \Rightarrow d\) và \(\left( {O;\,\,R} \right)\) có hai điểm chung phân biệt.
Cách giải:
Ta có: \(d\left( {O;\,\,d} \right) = 6 > R = 5 \Rightarrow d\) và \(\left( {O;\,\,R} \right)\) có hai điểm chung phân biệt.
Chọn B.
Câu 17:
Phương pháp:
Diện tích mặt cầu bán kính \(R:\,\,\,S = 4\pi {R^2}.\)
Cách giải:
Diện tích bề mặt quả bóng là: \(S = 4\pi {R^2} = 4.3,{14.7^2} = 615,44\,\,c{m^2}.\)
Chọn C.
Câu 18:
Phương pháp:
Phương trình bậc hai một ẩn có dạng: \(a{x^2} + bx + c = 0\,\,\,\left( {a \ne 0} \right).\)
Cách giải:
Trong các đáp án, chỉ có đáp án A có phương trình là phương trình bậc hia một ẩn.
Chọn A.
Câu 19:
Phương pháp:
Góc ở tâm có số đo bằng cung bị chắn.
Cách giải:
Lúc \(8\) giờ, kim giờ và kim phút của đồng hồ tạo thành góc ở tâm có số đo là \({120^0}.\)
Chọn C.
Câu 20:
Phương pháp:
Trục căn thức ở mẫu hoặc quy đồng mẫu các phân thức để tính giá trị của biểu thức.
Cách giải:
\(E = \frac{1}{{\sqrt 2 - 1}} - \frac{1}{{\sqrt 2 + 1}} = \frac{{\sqrt 2 + 1 - \sqrt 2 + 1}}{{\left( {\sqrt 2 - 1} \right)\left( {\sqrt 2 + 1} \right)}} = \frac{2}{{2 - 1}} = 2.\)
Chọn C.
Câu 21:
Phương pháp:
Đường thẳng \(y = ax + b\) có hệ số góc là \(a.\)
Cách giải:
Ta có: đường thẳng \(y = - 2x + 3\) có hệ số góc là \(a = - 2.\)
Chọn A.
Câu 22:
Phương pháp:
Hệ phương trình bậc nhất hai ẩn có dạng: \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right..\)
Cách giải:
Trong các đáp án trên chỉ có hệ phương trình ở đáp án B có dạng là hệ phương trình bậc nhất hai ẩn.
Chọn B.
Câu 23:
Phương pháp:
Hàm số \(y = a{x^2}\,\,\,\left( {a > 0} \right):\)
+) Đồng biến khi \(x > 0\) và nghịch biến khi \(x < 0.\)
Cách giải:
Xét hàm số \(y = 9{x^2}\) có \(a = 9 > 0\)
\( \Rightarrow \) Hàm số đồng biến khi \(x > 0\) và nghịch biến khi \(x < 0.\)
Chọn C.
Câu 24:
Phương pháp:
Thể tích hình trụ có chiều cao \(h\) và bán kính đáy \(R\) là: \(V = \pi {R^2}h.\)
Cách giải:
Theo đề bài ta có chu vi đáy của thùng nước là: \(2,4\,m.\)
\( \Rightarrow \) Thùng đựng nước có bán kính đáy là: \(R = \frac{{2,4}}{{2\pi }} = \frac{{1,2}}{\pi }\,\,m\) và chiều cao là: \(h = 0,5\,m.\)
Thể tích của thùng đựng nước là: \(V = \pi .0,5.{\left( {\frac{{1,2}}{\pi }} \right)^2} = \frac{{18}}{{25\pi }}\,\,{m^3}.\)
Chọn D.
Câu 25:
Phương pháp:
Tìm nghiệm \(y\) theo \(x.\)
Cách giải:
Ta có: \(2x - y = 1 \Leftrightarrow y = 2x - 1\)
\( \Rightarrow \) Nghiệm của phương trình là: \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = 2x - 1\end{array} \right..\)
Chọn B.
PHẦN TỰ LUẬN (7 điểm)
Câu 1 (VD)
Phương pháp:
a) Sử dụng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,\,A < 0\end{array} \right..\)
b) Thay tọa độ điểm \(A\left( {1;5} \right)\) vào phương trình đường thẳng \(\left( d \right)\) để tìm \(m\)
c) Giải hệ phương trình bằng phương pháp thế.
Cách giải:
a) Rút gọn biểu thức \(P = \sqrt 5 \left( {\sqrt 5 + 2} \right) - \sqrt {20} \)
\(P = \sqrt 5 \left( {\sqrt 5 + 2} \right) - \sqrt {20} = \sqrt 5 .\sqrt 5 + 2\sqrt 5 - 2\sqrt 5 = 5\)
Vậy \(P = 5\).
b) Tìm giá trị của \(m\) để đường thẳng \(\left( d \right):\,y = mx + 3\) đi qua điểm \(A\left( {1;5} \right)\)
Đường thẳng \(\left( d \right):\,y = mx + 3\)đi qua điểm \(A\left( {1;5} \right)\) nên ta có:
\(5 = m.1 + 3 \Leftrightarrow m = 2\)
Vậy với \(m = 2\) thì đường thẳng \(\left( d \right):\,y = mx + 3\)đi qua điểm \(A\left( {1;5} \right)\).
c) Giải hệ phương trình \(\left\{ \begin{array}{l}3x - y = 7\\x + y = 5\end{array} \right.\)
Ta có :
\(\left\{ \begin{array}{l}3x - y = 7\\x + y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 5 - x\\3x - \left( {5 - x} \right) = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 5 - x\\4x = 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 5 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 2\end{array} \right.\)
Vậy nghiệm của hệ phương trình là: \(\left( {x;y} \right) = \left( {3;2} \right)\)
Câu 2 (VD)
Phương pháp:
a) Thay \(m = 4\) vào phương trình rồi giải.
b) Tìm biệt thức \(\Delta '\) , rồi sử dụng định lý Vi-et, biến đổi biểu thức đã cho về dạng tổng và tích của hai nghiệm.
Cách giải:
a) Giải phương trình với \(m = 4\)
Với \(m = 4\) ta có phương trình: \({x^2} - 4x + 4 - 1 = 0 \Leftrightarrow {x^2} - 4x + 3 = 0\,\,\,\left( 1 \right)\)
Phương trình (1) có hệ số \(a = 1;\,b = - 4;\,c = 3 \Rightarrow a + b + c = 0\)
Nên phương trình (1) có hai nghiệm là \({x_1} = 1;\,{x_2} = \frac{c}{a} = 3\)
Vậy với \(m = 4\) thì tập nghiệm của phương trình là: \(S = \left\{ {1;3} \right\}\)
b) Tìm \(m\) để phương trình có hai nghiệm phân biệt thỏa mãn điều kiện:
\({x_1}\left( {{x_1} + 2} \right) + {x_2}\left( {{x_2} + 2} \right) = 20\)
Phương trình \({x^2} - 4x + m - 1 = 0\,\,\,\left( * \right)\)
Có \(\Delta ' = {\left( { - 2} \right)^2} - 1.\left( {m - 1} \right) = 5 - m\)
Để phương trình (*) có hai nghiệm phân biệt \({x_1};\,{x_2}\) thì \(\Delta ' > 0 \Leftrightarrow 5 - m > 0 \Leftrightarrow m < 5\)
Theo hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a} = 4\\{x_1}.{x_2} = \frac{c}{a} = m - 1\end{array} \right.\)
Ta có:
\(\begin{array}{l}{x_1}\left( {{x_1} + 2} \right) + {x_2}\left( {{x_2} + 2} \right) = 20\\ \Leftrightarrow {x_1}^2 + 2{x_1} + x_2^2 + 2{x_2} = 20\\ \Leftrightarrow x_1^2 + x_2^2 + 2\left( {{x_1} + {x_2}} \right) = 20\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}.{x_2} + 2\left( {x{ & _1} + {x_2}} \right) = 20\\ \Leftrightarrow \,\,\,{4^2} - 2\left( {m - 1} \right) + 2.4\, = 20\\ \Leftrightarrow 16\,\, - 2\left( {m - 1} \right) + 8 = 20\\ \Leftrightarrow 2\left( {m - 1} \right) = 4\\ \Leftrightarrow m - 1 = 2 \Leftrightarrow m = 3\,\left( {tm} \right)\end{array}\)
Vậy \(m = 3\) là giá trị cần tìm.
Câu 3 (VD):
Phương pháp:
a) Chỉ ra tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới các góc bằng nhau là tứ giác nội tiếp
b) Chứng minh \(DM \bot AO\) rồi sử dụng hệ thức lượng trong tam giác vuông
Cách giải:
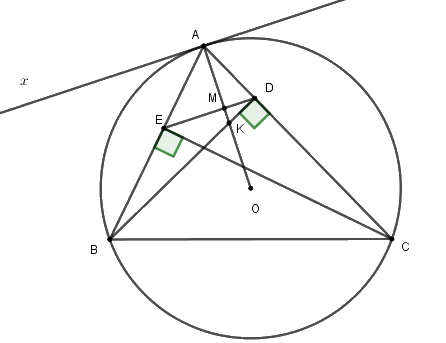
a) Vì \(BD,CE\) là hai đường cao của tam giác \(ABC\) nên \(\angle BEC = \angle BDC = 90^\circ \)
Xét tứ giác \(BCDE\) có \(\angle BEC = \angle BDC = 90^\circ \) (cmt) nên hai đỉnh \(E,D\) kề nhau cùng nhìn cạnh \(BC\) dưới các góc \(90^\circ \) , suy ra tứ giác \(BCDE\) là tứ giác nội tiếp. (dhnb)
b) Kẻ tiếp tuyến \(Ax\) với đường tròn \(\left( O \right)\)
Suy ra \(OA \bot Ax\)
+ Vì tứ giác \(BCDE\) là tứ giác nội tiếp (theo câu a) nên \(\angle BCD = \angle AED\) (1) (cùng bù với \(\angle BED\) )
+ Xét đường tròn \(\left( O \right)\) có \(\angle BAx = \angle BCA\) (2) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(AB\))
Từ (1) và (2) suy ra \(\angle BAx = \angle AED\) mà hai góc ở vị trí so le trong nên \(Ax//ED\)
Mà \(Ax \bot AO\left( {cmt} \right) \Rightarrow ED \bot AO = \left\{ M \right\}.\)
Xét tam giác \(ADK\) vuông tại \(D\) có \(DM\) là đường cao.
Theo hệ thức lượng trong tam giác vuông ta có: \(\frac{1}{{D{M^2}}} = \frac{1}{{D{K^2}}} + \frac{1}{{D{A^2}}}\) (đpcm)
Câu 4 (VDC)
Phương pháp:
Sử dụng liên tiếp bất đẳng thức Cô – si cho hai số dương \(a + b \ge 2\sqrt {ab} \) để đánh giá \(P\).
Cách giải:
\({x^2} + {y^2} + {z^2} = 3xyz \Rightarrow \frac{x}{{yz}} + \frac{y}{{xz}} + \frac{z}{{xy}} = 3\)
Áp dụng bất đẳng thức Cô – si cho hai số dương \(\frac{x}{{yz}};\frac{y}{{zx}}\) ta có: \(\frac{x}{{yz}} + \frac{y}{{zx}} \ge 2\sqrt {\frac{x}{{yz}}.\frac{y}{{zx}}} = \frac{2}{z}\)
Tương tự ta cũng có \(\frac{y}{{zx}} + \frac{z}{{xy}} \ge \frac{2}{x};\frac{z}{{xy}} + \frac{x}{{yz}} \ge \frac{2}{y}\)
\( \Rightarrow \left( {\frac{x}{{yz}} + \frac{y}{{zx}}} \right) + \left( {\frac{y}{{zx}} + \frac{z}{{xy}}} \right) + \left( {\frac{z}{{xy}} + \frac{x}{{yz}}} \right) \ge \frac{2}{z} + \frac{2}{x} + \frac{2}{y}\)
\( \Rightarrow \frac{x}{{yz}} + \frac{y}{{zx}} + \frac{z}{{xy}} \ge \frac{1}{x} + \frac{1}{y} + \frac{1}{z} \Rightarrow \frac{1}{x} + \frac{1}{y} + \frac{1}{z} \le 3\)
Lại có: \({x^4} + yz \ge 2\sqrt {{x^4}yz} = 2{x^2}\sqrt {yz} \Rightarrow \frac{{{x^2}}}{{{x^4} + yz}} \le \frac{1}{{2\sqrt {yz} }} = \frac{1}{4}.2.\frac{1}{{\sqrt y }}.\frac{1}{{\sqrt z }} \le \frac{1}{4}\left( {\frac{1}{y} + \frac{1}{z}} \right)\)
Tương tự \(\frac{{{y^2}}}{{{y^4} + xz}} \le \frac{1}{4}\left( {\frac{1}{x} + \frac{1}{z}} \right);\frac{{{z^2}}}{{{z^4} + xy}} \le \frac{1}{4}\left( {\frac{1}{x} + \frac{1}{y}} \right)\)
Suy ra \(P = \frac{{{x^2}}}{{{x^4} + yz}} + \frac{{{y^2}}}{{{y^4} + xz}} + \frac{{{z^2}}}{{{z^4} + xy}} \le \frac{1}{4}\left( {\frac{2}{x} + \frac{2}{y} + \frac{2}{z}} \right) = \frac{1}{2}\left( {\frac{1}{x} + \frac{1}{y} + \frac{1}{z}} \right) \le \frac{3}{2}\)
\( \Rightarrow P \le \frac{3}{2}\).
Dấu “=” xảy ra khi \(x = y = z = 1\).
Vậy \({P_{\max }} = \frac{3}{2}\) khi \(x = y = z = 1\).
Kỳ thi tuyển sinh vào lớp 10 là một bước ngoặt quan trọng trong sự nghiệp học tập của mỗi học sinh. Để đạt kết quả tốt nhất, việc chuẩn bị kỹ lưỡng là vô cùng cần thiết. Trong đó, việc làm quen với các đề thi thử và đề thi chính thức của các năm trước đóng vai trò then chốt. Bài viết này sẽ cung cấp phân tích chi tiết về Đề thi vào 10 môn Toán Hưng Yên năm 2019, cùng với hướng dẫn giải các bài toán khó, giúp các em học sinh tự tin bước vào kỳ thi.
Đề thi vào 10 môn Toán Hưng Yên năm 2019 thường có cấu trúc gồm các phần sau:
Để chuẩn bị tốt nhất cho kỳ thi, các em học sinh cần nắm vững các kiến thức trọng tâm sau:
Dưới đây là phân tích một số câu hỏi khó thường gặp trong Đề thi vào 10 môn Toán Hưng Yên năm 2019:
Một bài toán thường gặp là tìm nghiệm của phương trình bậc hai. Để giải quyết bài toán này, các em cần nắm vững công thức nghiệm của phương trình bậc hai và biết cách áp dụng vào từng trường hợp cụ thể.
Các bài toán về hình học không gian thường đòi hỏi học sinh phải có khả năng hình dung không gian và vận dụng các định lý, hệ thức liên quan. Để giải quyết bài toán này, các em cần vẽ hình minh họa và phân tích các mối quan hệ giữa các yếu tố trong hình.
Các bài toán về ứng dụng thực tế thường đòi hỏi học sinh phải có khả năng chuyển đổi bài toán từ ngôn ngữ toán học sang ngôn ngữ thực tế và ngược lại. Để giải quyết bài toán này, các em cần đọc kỹ đề bài, xác định các yếu tố quan trọng và xây dựng mô hình toán học phù hợp.
Để đạt kết quả tốt nhất trong kỳ thi, các em học sinh cần:
Ngoài Đề thi vào 10 môn Toán Hưng Yên năm 2019, các em học sinh có thể tham khảo thêm các tài liệu ôn thi sau:
Hãy dành thời gian ôn tập kiến thức một cách hệ thống và luyện tập thường xuyên với các đề thi thử. Đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè khi gặp khó khăn. Chúc các em học sinh đạt kết quả tốt nhất trong kỳ thi tuyển sinh vào lớp 10!
| Dạng bài | Mức độ khó | Lời khuyên |
|---|---|---|
| Phương trình bậc hai | Trung bình | Nắm vững công thức nghiệm |
| Hình học không gian | Khó | Vẽ hình minh họa |
| Ứng dụng thực tế | Trung bình - Khó | Chuyển đổi ngôn ngữ |