Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Thái Bình năm 2021 chính thức. Đây là tài liệu ôn tập vô cùng quan trọng dành cho các em học sinh đang chuẩn bị cho kỳ thi sắp tới.
Chúng tôi cung cấp đầy đủ các đề thi, đáp án chi tiết và phương pháp giải bài tập giúp các em nắm vững kiến thức và tự tin làm bài.
Câu 1 (2 điểm): Cho biểu thức
Câu 1 (2 điểm):
Cho biểu thức \(P = \dfrac{1}{{\sqrt x - 2}} - \dfrac{2}{{\sqrt x + 1}} + \dfrac{{2\sqrt x - 7}}{{x - \sqrt x - 2}}\) với \(x \ge 0,\,\,x \ne 4.\)
a) Chứng minh: \(P = \dfrac{1}{{\sqrt x + 1}}.\)
b) Tính giá trị của biểu thức \(P\) khi \(x = 3 - 2\sqrt 2 .\)
c) Tìm giá trị lớn nhất của biểu thức \(P.\)
Câu 2 (2 điểm):
a) Giải phương trình: \({x^2} + 3x - 1 = 0.\)
b) Một mảnh vườn hình chữ nhật có chu vi bằng \(60\,m.\) Nếu giảm chiều dài đi \(1m\) và tăng chiều rộng lên \(1m\) thì mảnh vườn trở thành hình vuông. Tính chiều dài và chiều rộng của mảnh vườn đó.
Câu 3 (2 điểm):
Cho parabol \(\left( P \right):\,\,y = {x^2}\) và đường thẳng \(\left( d \right):\,\,y = mx + 1,\) với \(m\) là tham số.
a) Tìm \(m\) để đường thẳng \(\left( d \right)\) và parabol \(\left( P \right)\) cùng đi qua điểm có hoành độ \(x = 2.\)
b) Chứng minh đường thẳng \(\left( d \right)\) luôn cắt parabol \(\left( P \right)\) tại hai điểm phân biệt với mọi \(m.\)
Gọi \({x_1},\,\,{x_2}\) là các hoành độ giao điểm, tìm \(m\) để \({x_2}\left( {x_1^2 - 1} \right) = 3.\)
Câu 4 (3,5 điểm):
Cho \(\Delta ABC\,\,\,\left( {AB < AC} \right)\) nội tiếp đường tròn tâm \(O\) đường kính \(BC\) cố định, điểm \(D\) bất kì thuộc cung nhỏ \(AC\)\(\left( {D \ne A,\,\,D \ne C} \right).\) Tia \(BA\) cắt tia \(CD\) tại điểm \(G.\) Điểm \(I\) là giao điểm của \(BD\) và \(AC.\) Kẻ \(AE\) vuông góc với \(BC\) tại điểm \(E,\) đường thẳng \(AE\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(F.\) Gọi \(H\) là hình chiếu vuông góc của điểm \(A\) trên \(BD,\,\,K\) là giao điểm của \(BC\) và \(DF.\) Chứng minh:
a) Tứ giác \(AIDG\) nội tiếp đường tròn.
b) \(BE.BC = BH.BI.\)
c) Ba điểm \(G,\,\,I,\,\,K\) thẳng hàng.
d) Đường tròn ngoại tiếp \(\Delta AKD\) luôn đi qua một điểm cố định khác \(A\) khi điểm \(D\) di động trên cung nhỏ \(AC.\)
Câu 5 (0,5 điểm):
Giải phương trình \({x^2} + 6x + 1 - \left( {2x + 1} \right)\sqrt {{x^2} + 2x + 3} = 0\).
Câu 1
Phương pháp:
a) Xác định mẫu thức chung, thực hiện quy đồng sau rút gọn được biểu thức \(P\)
b) Vận dụng hẳng đẳng thức \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,khi\,\,A \ge 0\\ - A\,\,khi\,\, - A < 0\end{array} \right.\), xác định được \(\sqrt x \)
Thay giá trị của \(\sqrt x \) vào biểu thức \(P\), tính được giá trị của biểu thức \(P\).
c) Từ điều kiện \(x \ge 0,\,\,x \ne 4\), nhận xét được mẫu thức của \(P\) từ đó suy ra giá trị lớn nhất của \(P\)
Cách giải:
a) Điều kiện: \(x \ge 0,\,\,x \ne 4.\)
\(\begin{array}{l}P = \dfrac{1}{{\sqrt x - 2}} - \dfrac{2}{{\sqrt x + 1}} + \dfrac{{2\sqrt x - 7}}{{x - \sqrt x - 2}}\\\,\,\,\,\, = \dfrac{1}{{\sqrt x - 2}} - \dfrac{2}{{\sqrt x + 1}} + \dfrac{{2\sqrt x - 7}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 2} \right)}}\\\,\,\,\, = \dfrac{{\sqrt x + 1 - 2\left( {\sqrt x - 2} \right) + 2\sqrt x - 7}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 2} \right)}}\\\,\,\,\, = \dfrac{{\sqrt x + 1 - 2\sqrt x + 4 + 2\sqrt x - 7}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 2} \right)}}\\\,\,\, = \dfrac{{\sqrt x - 2}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 2} \right)}}\\\,\,\, = \dfrac{1}{{\sqrt x + 1}}.\end{array}\)
Vậy với \(x \ge 0,\,\,x \ne 4\) thì \(P = \dfrac{1}{{\sqrt x + 1}}.\)
b) Điều kiện: \(x \ge 0,\,\,x \ne 4.\)
Ta có: \(x = 3 - 2\sqrt 2 = {\left( {\sqrt 2 - 1} \right)^2}\) thỏa mãn điều kiện.
\( \Rightarrow \sqrt x = \sqrt {3 - 2\sqrt 2 } = \sqrt {{{\left( {\sqrt 2 - 1} \right)}^2}} \) \( = \left| {\sqrt 2 - 1} \right| = \sqrt 2 - 1\) \(\left( {do\,\,\,\sqrt 2 - 1 > 0} \right)\)
Thay \(\sqrt x = \sqrt 2 - 1\) vào biểu thức \(P\) ta được: \(P = \dfrac{1}{{\sqrt x + 1}} = \dfrac{1}{{\sqrt 2 - 1 + 1}} = \dfrac{1}{{\sqrt 2 }} = \dfrac{{\sqrt 2 }}{2}.\)
Vậy với \(x = 3 - 2\sqrt 2 \) thì \(P = \dfrac{{\sqrt 2 }}{2}.\)
c) Điều kiện: \(x \ge 0,\,\,x \ne 4.\)
Ta có: \(P = \dfrac{1}{{\sqrt x + 1}}.\)
Với \(\forall x \ge 0,\,\,x \ne 4\) ta có: \(\sqrt x \ge 0 \Rightarrow \sqrt x + 1 \ge 1\)
\( \Rightarrow \dfrac{1}{{\sqrt x + 1}} \le 1\)\( \Rightarrow P \le 1\)
Dấu “=” xảy ra \( \Leftrightarrow \sqrt x + 1 = 1 \Leftrightarrow \sqrt x = 0 \Leftrightarrow x = 0\,\,\,\left( {tm} \right)\)
Vậy với \(x = 0\) thì giá trị lớn nhất của \(P\) là \(1.\)
Câu 2
Phương pháp:
a) Vận dụng công thức nghiệm của phương trình bậc hai một ẩn, tìm nghiệm của phương trình.
b) Gọi chiều dài và chiều rộng của mảnh vườn lần lượt là \(x,\,\,y\,\,\left( m \right),\,\,\,\left( {0 < y < 15 < x} \right).\)
+ Chu vi của mảnh vườn là \(60m\)\( \Rightarrow \) Nửa chu vi của mảnh vườn, từ đó lập được phương trình (1)
+ Nếu giảm chiều dài đi \(1m\) và tăng chiều rộng lên \(1m\) thì mảnh vườn trở thành hình vuông nên ta lập phương trình (2)
+ Từ (1) và (2), ta có hệ phương trình. Giải hệ phương trình, tìm nghiệm và kết luận.
Cách giải:
a) Phương trình \({x^2} + 3x - 1 - 0\) có: \(\Delta = {\left( { - 3} \right)^2} - 4.\left( { - 1} \right) = 13 > 0\)
\( \Rightarrow \) Phương trình có hai nghiệm phân biệt \({x_1} = \dfrac{{ - 3 + \sqrt {13} }}{2}\) và \({x_2} = \dfrac{{ - 3 - \sqrt {13} }}{2}.\)
Vậy phương trình có tập nghiệm: \(S = \left\{ {\dfrac{{ - 3 - \sqrt {13} }}{2};\,\,\dfrac{{ - 3 + \sqrt {13} }}{2}} \right\}.\)
b) Nửa chu vi của mảnh vườn đã cho là: \(60:2 = 30\,\,\left( m \right).\)
Gọi chiều dài và chiều rộng của mảnh vườn lần lượt là \(x,\,\,y\,\,\left( m \right),\,\,\,\left( {0 < y < 15 < x} \right).\)
\( \Rightarrow x + y = 30\,\,\,\,\left( 1 \right).\)
Nếu giảm chiều dài đi \(1m\) và tăng chiều rộng lên \(1m\) thì mảnh vườn trở thành hình vuông nên ta có phương trình: \(x - 1 = y + 1\)\( \Leftrightarrow x - y = 2\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 30\\x - y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x = 32\\y = x - 2\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 16\,\,\,\,\left( {tm} \right)\\y = 16 - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 16\\y = 14\,\,\,\left( {tm} \right)\end{array} \right.\)
Vậy chiều dài mảnh vườn là \(16\,\,m\) và chiều rộng mảnh vườn là \(14\,m.\)
Câu 3:
Phương pháp:
a) + Gọi \(A\left( {2;\,\,{y_A}} \right)\) là điểm mà đường thẳng \(\left( d \right)\) và parabol \(\left( P \right)\) đều đi qua.
+ \(A\left( {2;\,{y_A}} \right) \in \left( P \right)\)\( \Rightarrow {y_A}\)
+ Thay \(x = 2\) và tung độ \({y_A}\) vừa tìm được vào đường thẳng \(d\)\( \Rightarrow \) tìm được \(m\) và kết luận.
b) + Xét phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\): phương trình (*) (là một phương trình bậc hai một ẩn \(x\))
+ Đường thẳng \(\left( d \right)\) luôn cắt parabol \(\left( P \right)\) tại hai điểm phân biệt với mọi \(m \Leftrightarrow \left( * \right)\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta > 0,\forall m\)
+ Gọi \({x_1},\,\,{x_2}\) là các hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) \( \Rightarrow \) \({x_1},\,\,{x_2}\) là các nghiệm của phương trình \(\left( * \right)\)
\( \Rightarrow x_1^2 = m{x_1} + 1\) (1)
+ Áp dụng hệ thức Vi – ét, tính được \({x_1} + {x_2};{x_1}{x_2}\) theo tham số \(m\) (2)
+ Thay (1) và (2) vào hệ thức của đề bài, tìm được tham số \(m\).
Cách giải:
a) Gọi \(A\left( {2;\,\,{y_A}} \right)\) là điểm mà đường thẳng \(\left( d \right)\) và parabol \(\left( P \right)\) đều đi qua.
Khi đó ta có: \(A\left( {2;\,{y_A}} \right) \in \left( P \right)\) \( \Rightarrow {y_A} = {2^2} = 4\)\( \Rightarrow A\left( {2;\,\,4} \right).\)
Lại có: \(A\left( {2;\,\,4} \right) \in \left( d \right)\) \( \Rightarrow 4 = m.2 + 1 \Leftrightarrow m = \dfrac{3}{2}\)
Vậy \(m = \dfrac{3}{2}\) thỏa mãn bài toán.
b) Phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) là: \({x^2} = mx + 1 \Leftrightarrow {x^2} - mx - 1 = 0\,\,\,\left( * \right)\)
Phương trình \(\left( * \right)\) có: \(\Delta = {m^2} + 4 > 0\,\,\forall m\)
\( \Rightarrow \left( * \right)\) luôn có hai nghiệm phân biệt với mọi \(m.\)
\( \Rightarrow \left( d \right)\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt với mọi \(m.\)
Gọi \({x_1},\,\,{x_2}\) là các hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) \( \Rightarrow \) \({x_1},\,\,{x_2}\) là các nghiệm của phương trình \(\left( * \right)\)
\( \Rightarrow x_1^2 = m{x_1} + 1\)
Áp dụng hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m\\{x_1}{x_2} = - 1\end{array} \right..\)
Theo đề bài ta có: \({x_2}\left( {x_1^2 - 1} \right) = 3\)
\(\begin{array}{l} \Leftrightarrow {x_2}\left( {m{x_1} + 1 - 1} \right) = 3\\ \Leftrightarrow m{x_1}{x_2} = 3\\ \Leftrightarrow - m = 3\\ \Leftrightarrow m = - 3.\end{array}\)
Vậy \(m = - 3\) thỏa mãn bài toán.
Câu 4:
Phương pháp:
a) Tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp: chứng minh \(\angle GAI + \angle GDI = {180^0}\)\(\angle ABC\) là tứ giác nội tiếp
b) Chứng minh: \(\angle BHE = \angle BCI\); \( \Rightarrow BE.BC = BH.BI\,\,\)
c) Chứng minh: \(IK \bot BC\) và \(GI \bot BC\)\( \Rightarrow G,\,\,I,\,\,K\) thằng hàng.
d) Chứng minh: \(\angle OAB = \angle CKD = \dfrac{1}{2}\,\,sd\,\,cung\,\,AC\)
\( \Rightarrow OKDA\) là tứ giác nội tiếp. (tứ giác có góc ngoài bằng góc trong tại đỉnh đối diện)
\( \Rightarrow \) Đường tròn ngoại tiếp \(\Delta AKD\) đi qua điểm \(O\) cố định.
Cách giải:
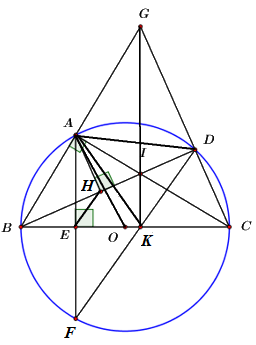
a) Ta có: \(\angle BAC,\)\(\angle BDC\) là góc nội tiếp chắn nửa đường tròn \(\left( O \right)\)\( \Rightarrow \angle BAC = \angle BDC = {90^0}.\)
\( \Rightarrow \angle GAI = \angle GDI = {90^0}\)
Xét tứ giác \(AIDG\) ta có: \(\angle GAI + \angle GDI = {90^0} + {90^0} = {180^0}\)
\(\angle ABC\) là tứ giác nội tiếp. (dhnb)
b) Xét tứ giác \(ABEH\) ta có: \(\angle AEB = \angle AHB = {90^0}\,\,\,\left( {gt} \right)\)
\( \Rightarrow ABEH\) là tứ giác nội tiếp. (tứ giác có hai đỉnh kề nhau cùng nhìn cạnh đối diện dưới các góc bằng nhau)
\( \Rightarrow \angle BHE = \angle BAE\) (hai góc nội tiếp cùng chắn cung \(BE\))
Mà \(\angle BAE = \angle BCA\) (hai góc cùng phụ \(\angle ABC\))
\( \Rightarrow \angle BHE = \angle BCA = \angle BCI\)
Xét \(\Delta BHE\) và \(\Delta BCI\) có:
c) Ta có: \(BC \bot AF \Rightarrow \,\,cung\,\,AB = cung\,\,FB\) (đường kính vuông góc với một dây thì đi qua điểm ở chính giữa của cung căng dây đó).
\( \Rightarrow \angle BDF = \angle BCA\) (hai góc nội tiếp chắn 2 cung bằng nhau).
Hay \(\angle IDK = \angle ICK\)
\( \Rightarrow CDJK\) là tức giác nội tiếp. (tứ giác có 2 đỉnh kề nhau cùng nhìn 1 cạnh dưới các góc bằng nhau)
\( \Rightarrow \angle IKC + \angle IDC = {180^0}\). Mà \(\angle IDC = \angle BDC = {90^0}\,\,\,\left( {cmt} \right)\)
\( \Rightarrow \angle IKC = {90^0} \Rightarrow IK \bot BC\,\,\,\left( 1 \right)\)
Xét \(\Delta GBC\) có \(\left\{ \begin{array}{l}AC \bot BG\\BD \bot CG\\AC \cap BD = \left\{ I \right\}\end{array} \right.\)
\( \Rightarrow I\) là trực tâm \(\Delta GBC\) \( \Rightarrow GI \bot BC\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) \( \Rightarrow G,\,\,I,\,\,K\) thằng hàng. (đpcm)
d) Ta có: \(OA = \dfrac{1}{2}BC = OB\) (đường trung tuyến ứng với cạnh huyền trong tam giác vuông)
\( \Rightarrow \Delta OAB\) cân tại \(O\) \( \Rightarrow \angle OAB = \angle OBA = \angle ABC = \dfrac{1}{2}\,\,sd\,\,cung\,\,AC\) \(\left( 3 \right)\)
Lại có: \(\angle CKD = \dfrac{1}{2}\left( {sd\,\,cung\,\,CD + sd\,\,cng\,\,BF} \right)\)\( = \dfrac{1}{2}\left( {sd\,\,cung\,\,CD + sd\,\,cung\,\,AB} \right)\)
Vì \(OH \bot BD\,\,\left( {gt} \right)\)\( \Rightarrow cung\,\,AB = cung\,\,AD\)
\( \Rightarrow \angle CKD = \dfrac{1}{2}\left( {sd\,\,cung\,\,CD + \,sd\,\,cung\,\,AD} \right)\)\( = \dfrac{1}{2}sd\,\,cung\,\,AC\,\,\,\left( 4 \right)\)
Từ \(\left( 3 \right)\) và \(\left( 4 \right)\) \( \Rightarrow \angle OAB = \angle CKD\)
\( \Rightarrow OKDA\) là tứ giác nội tiếp. (tứ giác có góc ngoài bằng góc trong tại đỉnh đối diện)
\( \Rightarrow \) Đường tròn ngoại tiếp \(\Delta AKD\) đi qua điểm \(O\) cố định. (đpcm)
Câu 5:
Phương pháp:
+ Xác định điều kiện của phương trình, \(\sqrt {f\left( x \right)} \) có nghĩa \( \Leftrightarrow f\left( x \right) \ge 0\)
+ Đặt \(\left\{ \begin{array}{l}a = 2x + 1\\b = \sqrt {{x^2} + 2x + 3} \,\,\left( {b \ge 0} \right)\end{array} \right.\), biến đổi phương trình ban đầu theo \(a,b\)
+ Giải phương trình bậc hai ẩn \(b\) với tham số \(a\), tìm được mối liên hệ của \(a,b\)
+ Với \(a,b\) ta tìm được nghiệm \(x\), đối chiếu và kết luận.
Cách giải:
ĐKXĐ: \({x^2} + 2x + 3 \ge 0 \Leftrightarrow {\left( {x + 1} \right)^2} + 2 \ge 0\) (luôn đúng).
Đặt \(\left\{ \begin{array}{l}a = 2x + 1\\b = \sqrt {{x^2} + 2x + 3} \,\,\left( {b \ge 0} \right)\end{array} \right.\) ta có \(2a + {b^2} = 4x + 2 + {x^2} + 2x + 3 = {x^2} + 6x + 5\)
\( \Rightarrow {x^2} + 6x + 1 = 2a + {b^2} - 4\).
Khi đó phương trình trở thành:
\(2a + {b^2} - 4 - ab = 0 \Leftrightarrow {b^2} - ab + 2a - 4 = 0\,\,\left( * \right)\)
Coi (*) là phương trình bậc hai ẩn \(b\) với tham số \(a\) ta có
\(\Delta = {a^2} - 4\left( {2a - 4} \right) = {a^2} - 8a + 16 = {\left( {a - 4} \right)^2} \ge 0\,\,\forall a\)
Khi đó phương trình (*) có 2 nghiệm \(\left[ \begin{array}{l}b = \dfrac{{a + a - 4}}{2} = a - 2\\b = \dfrac{{a - a + 4}}{2} = 2\,\,\left( {tm} \right)\end{array} \right.\)
+) TH1: \(b = 2 \Rightarrow \sqrt {{x^2} + 2x + 3} = 2\) \( \Leftrightarrow {x^2} + 2x + 3 = 4 \Leftrightarrow {x^2} + 2x - 1 = 0\)
Ta có \(\Delta ' = 1 + 1 = 2 > 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ \begin{array}{l}x = - 1 + \sqrt 2 \\x = - 1 - \sqrt 2 \end{array} \right.\).
+) TH2: \(b = a - 2 \ge 0 \Leftrightarrow a \ge 2\).
Khi đó ta có \(\sqrt {{x^2} + 2x + 3} = 2x - 1\) \( \Leftrightarrow \left\{ \begin{array}{l}2x - 1 \ge 0\\{x^2} + 2x + 3 = 4{x^2} - 4x + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge \dfrac{1}{2}\\3{x^2} - 6x - 2 = 0\,\,\,\left( 1 \right)\end{array} \right.\)
Ta có \(\Delta ' = {3^2} - 3.\left( { - 2} \right) = 15 > 0\) nên phương trình (1) có 2 nghiệm phân biệt \(\left[ \begin{array}{l}x = \dfrac{{3 + \sqrt {15} }}{3}\,\,\left( {tm} \right)\\x = \dfrac{{3 - \sqrt {15} }}{3}\,\,\left( {ktm} \right)\end{array} \right.\).
Vậy tập nghiệm của phương trình đã cho là \(S = \left\{ { - 1 + \sqrt 2 ; - 1 - \sqrt 2 ;\dfrac{{3 + \sqrt {15} }}{3}} \right\}\).
Câu 1 (2 điểm):
Cho biểu thức \(P = \dfrac{1}{{\sqrt x - 2}} - \dfrac{2}{{\sqrt x + 1}} + \dfrac{{2\sqrt x - 7}}{{x - \sqrt x - 2}}\) với \(x \ge 0,\,\,x \ne 4.\)
a) Chứng minh: \(P = \dfrac{1}{{\sqrt x + 1}}.\)
b) Tính giá trị của biểu thức \(P\) khi \(x = 3 - 2\sqrt 2 .\)
c) Tìm giá trị lớn nhất của biểu thức \(P.\)
Câu 2 (2 điểm):
a) Giải phương trình: \({x^2} + 3x - 1 = 0.\)
b) Một mảnh vườn hình chữ nhật có chu vi bằng \(60\,m.\) Nếu giảm chiều dài đi \(1m\) và tăng chiều rộng lên \(1m\) thì mảnh vườn trở thành hình vuông. Tính chiều dài và chiều rộng của mảnh vườn đó.
Câu 3 (2 điểm):
Cho parabol \(\left( P \right):\,\,y = {x^2}\) và đường thẳng \(\left( d \right):\,\,y = mx + 1,\) với \(m\) là tham số.
a) Tìm \(m\) để đường thẳng \(\left( d \right)\) và parabol \(\left( P \right)\) cùng đi qua điểm có hoành độ \(x = 2.\)
b) Chứng minh đường thẳng \(\left( d \right)\) luôn cắt parabol \(\left( P \right)\) tại hai điểm phân biệt với mọi \(m.\)
Gọi \({x_1},\,\,{x_2}\) là các hoành độ giao điểm, tìm \(m\) để \({x_2}\left( {x_1^2 - 1} \right) = 3.\)
Câu 4 (3,5 điểm):
Cho \(\Delta ABC\,\,\,\left( {AB < AC} \right)\) nội tiếp đường tròn tâm \(O\) đường kính \(BC\) cố định, điểm \(D\) bất kì thuộc cung nhỏ \(AC\)\(\left( {D \ne A,\,\,D \ne C} \right).\) Tia \(BA\) cắt tia \(CD\) tại điểm \(G.\) Điểm \(I\) là giao điểm của \(BD\) và \(AC.\) Kẻ \(AE\) vuông góc với \(BC\) tại điểm \(E,\) đường thẳng \(AE\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(F.\) Gọi \(H\) là hình chiếu vuông góc của điểm \(A\) trên \(BD,\,\,K\) là giao điểm của \(BC\) và \(DF.\) Chứng minh:
a) Tứ giác \(AIDG\) nội tiếp đường tròn.
b) \(BE.BC = BH.BI.\)
c) Ba điểm \(G,\,\,I,\,\,K\) thẳng hàng.
d) Đường tròn ngoại tiếp \(\Delta AKD\) luôn đi qua một điểm cố định khác \(A\) khi điểm \(D\) di động trên cung nhỏ \(AC.\)
Câu 5 (0,5 điểm):
Giải phương trình \({x^2} + 6x + 1 - \left( {2x + 1} \right)\sqrt {{x^2} + 2x + 3} = 0\).
Câu 1
Phương pháp:
a) Xác định mẫu thức chung, thực hiện quy đồng sau rút gọn được biểu thức \(P\)
b) Vận dụng hẳng đẳng thức \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,khi\,\,A \ge 0\\ - A\,\,khi\,\, - A < 0\end{array} \right.\), xác định được \(\sqrt x \)
Thay giá trị của \(\sqrt x \) vào biểu thức \(P\), tính được giá trị của biểu thức \(P\).
c) Từ điều kiện \(x \ge 0,\,\,x \ne 4\), nhận xét được mẫu thức của \(P\) từ đó suy ra giá trị lớn nhất của \(P\)
Cách giải:
a) Điều kiện: \(x \ge 0,\,\,x \ne 4.\)
\(\begin{array}{l}P = \dfrac{1}{{\sqrt x - 2}} - \dfrac{2}{{\sqrt x + 1}} + \dfrac{{2\sqrt x - 7}}{{x - \sqrt x - 2}}\\\,\,\,\,\, = \dfrac{1}{{\sqrt x - 2}} - \dfrac{2}{{\sqrt x + 1}} + \dfrac{{2\sqrt x - 7}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 2} \right)}}\\\,\,\,\, = \dfrac{{\sqrt x + 1 - 2\left( {\sqrt x - 2} \right) + 2\sqrt x - 7}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 2} \right)}}\\\,\,\,\, = \dfrac{{\sqrt x + 1 - 2\sqrt x + 4 + 2\sqrt x - 7}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 2} \right)}}\\\,\,\, = \dfrac{{\sqrt x - 2}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 2} \right)}}\\\,\,\, = \dfrac{1}{{\sqrt x + 1}}.\end{array}\)
Vậy với \(x \ge 0,\,\,x \ne 4\) thì \(P = \dfrac{1}{{\sqrt x + 1}}.\)
b) Điều kiện: \(x \ge 0,\,\,x \ne 4.\)
Ta có: \(x = 3 - 2\sqrt 2 = {\left( {\sqrt 2 - 1} \right)^2}\) thỏa mãn điều kiện.
\( \Rightarrow \sqrt x = \sqrt {3 - 2\sqrt 2 } = \sqrt {{{\left( {\sqrt 2 - 1} \right)}^2}} \) \( = \left| {\sqrt 2 - 1} \right| = \sqrt 2 - 1\) \(\left( {do\,\,\,\sqrt 2 - 1 > 0} \right)\)
Thay \(\sqrt x = \sqrt 2 - 1\) vào biểu thức \(P\) ta được: \(P = \dfrac{1}{{\sqrt x + 1}} = \dfrac{1}{{\sqrt 2 - 1 + 1}} = \dfrac{1}{{\sqrt 2 }} = \dfrac{{\sqrt 2 }}{2}.\)
Vậy với \(x = 3 - 2\sqrt 2 \) thì \(P = \dfrac{{\sqrt 2 }}{2}.\)
c) Điều kiện: \(x \ge 0,\,\,x \ne 4.\)
Ta có: \(P = \dfrac{1}{{\sqrt x + 1}}.\)
Với \(\forall x \ge 0,\,\,x \ne 4\) ta có: \(\sqrt x \ge 0 \Rightarrow \sqrt x + 1 \ge 1\)
\( \Rightarrow \dfrac{1}{{\sqrt x + 1}} \le 1\)\( \Rightarrow P \le 1\)
Dấu “=” xảy ra \( \Leftrightarrow \sqrt x + 1 = 1 \Leftrightarrow \sqrt x = 0 \Leftrightarrow x = 0\,\,\,\left( {tm} \right)\)
Vậy với \(x = 0\) thì giá trị lớn nhất của \(P\) là \(1.\)
Câu 2
Phương pháp:
a) Vận dụng công thức nghiệm của phương trình bậc hai một ẩn, tìm nghiệm của phương trình.
b) Gọi chiều dài và chiều rộng của mảnh vườn lần lượt là \(x,\,\,y\,\,\left( m \right),\,\,\,\left( {0 < y < 15 < x} \right).\)
+ Chu vi của mảnh vườn là \(60m\)\( \Rightarrow \) Nửa chu vi của mảnh vườn, từ đó lập được phương trình (1)
+ Nếu giảm chiều dài đi \(1m\) và tăng chiều rộng lên \(1m\) thì mảnh vườn trở thành hình vuông nên ta lập phương trình (2)
+ Từ (1) và (2), ta có hệ phương trình. Giải hệ phương trình, tìm nghiệm và kết luận.
Cách giải:
a) Phương trình \({x^2} + 3x - 1 - 0\) có: \(\Delta = {\left( { - 3} \right)^2} - 4.\left( { - 1} \right) = 13 > 0\)
\( \Rightarrow \) Phương trình có hai nghiệm phân biệt \({x_1} = \dfrac{{ - 3 + \sqrt {13} }}{2}\) và \({x_2} = \dfrac{{ - 3 - \sqrt {13} }}{2}.\)
Vậy phương trình có tập nghiệm: \(S = \left\{ {\dfrac{{ - 3 - \sqrt {13} }}{2};\,\,\dfrac{{ - 3 + \sqrt {13} }}{2}} \right\}.\)
b) Nửa chu vi của mảnh vườn đã cho là: \(60:2 = 30\,\,\left( m \right).\)
Gọi chiều dài và chiều rộng của mảnh vườn lần lượt là \(x,\,\,y\,\,\left( m \right),\,\,\,\left( {0 < y < 15 < x} \right).\)
\( \Rightarrow x + y = 30\,\,\,\,\left( 1 \right).\)
Nếu giảm chiều dài đi \(1m\) và tăng chiều rộng lên \(1m\) thì mảnh vườn trở thành hình vuông nên ta có phương trình: \(x - 1 = y + 1\)\( \Leftrightarrow x - y = 2\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 30\\x - y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x = 32\\y = x - 2\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 16\,\,\,\,\left( {tm} \right)\\y = 16 - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 16\\y = 14\,\,\,\left( {tm} \right)\end{array} \right.\)
Vậy chiều dài mảnh vườn là \(16\,\,m\) và chiều rộng mảnh vườn là \(14\,m.\)
Câu 3:
Phương pháp:
a) + Gọi \(A\left( {2;\,\,{y_A}} \right)\) là điểm mà đường thẳng \(\left( d \right)\) và parabol \(\left( P \right)\) đều đi qua.
+ \(A\left( {2;\,{y_A}} \right) \in \left( P \right)\)\( \Rightarrow {y_A}\)
+ Thay \(x = 2\) và tung độ \({y_A}\) vừa tìm được vào đường thẳng \(d\)\( \Rightarrow \) tìm được \(m\) và kết luận.
b) + Xét phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\): phương trình (*) (là một phương trình bậc hai một ẩn \(x\))
+ Đường thẳng \(\left( d \right)\) luôn cắt parabol \(\left( P \right)\) tại hai điểm phân biệt với mọi \(m \Leftrightarrow \left( * \right)\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta > 0,\forall m\)
+ Gọi \({x_1},\,\,{x_2}\) là các hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) \( \Rightarrow \) \({x_1},\,\,{x_2}\) là các nghiệm của phương trình \(\left( * \right)\)
\( \Rightarrow x_1^2 = m{x_1} + 1\) (1)
+ Áp dụng hệ thức Vi – ét, tính được \({x_1} + {x_2};{x_1}{x_2}\) theo tham số \(m\) (2)
+ Thay (1) và (2) vào hệ thức của đề bài, tìm được tham số \(m\).
Cách giải:
a) Gọi \(A\left( {2;\,\,{y_A}} \right)\) là điểm mà đường thẳng \(\left( d \right)\) và parabol \(\left( P \right)\) đều đi qua.
Khi đó ta có: \(A\left( {2;\,{y_A}} \right) \in \left( P \right)\) \( \Rightarrow {y_A} = {2^2} = 4\)\( \Rightarrow A\left( {2;\,\,4} \right).\)
Lại có: \(A\left( {2;\,\,4} \right) \in \left( d \right)\) \( \Rightarrow 4 = m.2 + 1 \Leftrightarrow m = \dfrac{3}{2}\)
Vậy \(m = \dfrac{3}{2}\) thỏa mãn bài toán.
b) Phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) là: \({x^2} = mx + 1 \Leftrightarrow {x^2} - mx - 1 = 0\,\,\,\left( * \right)\)
Phương trình \(\left( * \right)\) có: \(\Delta = {m^2} + 4 > 0\,\,\forall m\)
\( \Rightarrow \left( * \right)\) luôn có hai nghiệm phân biệt với mọi \(m.\)
\( \Rightarrow \left( d \right)\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt với mọi \(m.\)
Gọi \({x_1},\,\,{x_2}\) là các hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) \( \Rightarrow \) \({x_1},\,\,{x_2}\) là các nghiệm của phương trình \(\left( * \right)\)
\( \Rightarrow x_1^2 = m{x_1} + 1\)
Áp dụng hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m\\{x_1}{x_2} = - 1\end{array} \right..\)
Theo đề bài ta có: \({x_2}\left( {x_1^2 - 1} \right) = 3\)
\(\begin{array}{l} \Leftrightarrow {x_2}\left( {m{x_1} + 1 - 1} \right) = 3\\ \Leftrightarrow m{x_1}{x_2} = 3\\ \Leftrightarrow - m = 3\\ \Leftrightarrow m = - 3.\end{array}\)
Vậy \(m = - 3\) thỏa mãn bài toán.
Câu 4:
Phương pháp:
a) Tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp: chứng minh \(\angle GAI + \angle GDI = {180^0}\)\(\angle ABC\) là tứ giác nội tiếp
b) Chứng minh: \(\angle BHE = \angle BCI\); \( \Rightarrow BE.BC = BH.BI\,\,\)
c) Chứng minh: \(IK \bot BC\) và \(GI \bot BC\)\( \Rightarrow G,\,\,I,\,\,K\) thằng hàng.
d) Chứng minh: \(\angle OAB = \angle CKD = \dfrac{1}{2}\,\,sd\,\,cung\,\,AC\)
\( \Rightarrow OKDA\) là tứ giác nội tiếp. (tứ giác có góc ngoài bằng góc trong tại đỉnh đối diện)
\( \Rightarrow \) Đường tròn ngoại tiếp \(\Delta AKD\) đi qua điểm \(O\) cố định.
Cách giải:
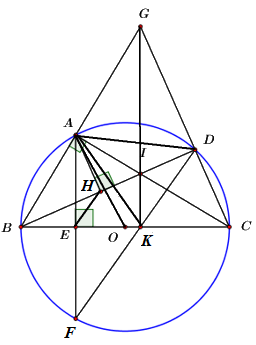
a) Ta có: \(\angle BAC,\)\(\angle BDC\) là góc nội tiếp chắn nửa đường tròn \(\left( O \right)\)\( \Rightarrow \angle BAC = \angle BDC = {90^0}.\)
\( \Rightarrow \angle GAI = \angle GDI = {90^0}\)
Xét tứ giác \(AIDG\) ta có: \(\angle GAI + \angle GDI = {90^0} + {90^0} = {180^0}\)
\(\angle ABC\) là tứ giác nội tiếp. (dhnb)
b) Xét tứ giác \(ABEH\) ta có: \(\angle AEB = \angle AHB = {90^0}\,\,\,\left( {gt} \right)\)
\( \Rightarrow ABEH\) là tứ giác nội tiếp. (tứ giác có hai đỉnh kề nhau cùng nhìn cạnh đối diện dưới các góc bằng nhau)
\( \Rightarrow \angle BHE = \angle BAE\) (hai góc nội tiếp cùng chắn cung \(BE\))
Mà \(\angle BAE = \angle BCA\) (hai góc cùng phụ \(\angle ABC\))
\( \Rightarrow \angle BHE = \angle BCA = \angle BCI\)
Xét \(\Delta BHE\) và \(\Delta BCI\) có:
c) Ta có: \(BC \bot AF \Rightarrow \,\,cung\,\,AB = cung\,\,FB\) (đường kính vuông góc với một dây thì đi qua điểm ở chính giữa của cung căng dây đó).
\( \Rightarrow \angle BDF = \angle BCA\) (hai góc nội tiếp chắn 2 cung bằng nhau).
Hay \(\angle IDK = \angle ICK\)
\( \Rightarrow CDJK\) là tức giác nội tiếp. (tứ giác có 2 đỉnh kề nhau cùng nhìn 1 cạnh dưới các góc bằng nhau)
\( \Rightarrow \angle IKC + \angle IDC = {180^0}\). Mà \(\angle IDC = \angle BDC = {90^0}\,\,\,\left( {cmt} \right)\)
\( \Rightarrow \angle IKC = {90^0} \Rightarrow IK \bot BC\,\,\,\left( 1 \right)\)
Xét \(\Delta GBC\) có \(\left\{ \begin{array}{l}AC \bot BG\\BD \bot CG\\AC \cap BD = \left\{ I \right\}\end{array} \right.\)
\( \Rightarrow I\) là trực tâm \(\Delta GBC\) \( \Rightarrow GI \bot BC\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) \( \Rightarrow G,\,\,I,\,\,K\) thằng hàng. (đpcm)
d) Ta có: \(OA = \dfrac{1}{2}BC = OB\) (đường trung tuyến ứng với cạnh huyền trong tam giác vuông)
\( \Rightarrow \Delta OAB\) cân tại \(O\) \( \Rightarrow \angle OAB = \angle OBA = \angle ABC = \dfrac{1}{2}\,\,sd\,\,cung\,\,AC\) \(\left( 3 \right)\)
Lại có: \(\angle CKD = \dfrac{1}{2}\left( {sd\,\,cung\,\,CD + sd\,\,cng\,\,BF} \right)\)\( = \dfrac{1}{2}\left( {sd\,\,cung\,\,CD + sd\,\,cung\,\,AB} \right)\)
Vì \(OH \bot BD\,\,\left( {gt} \right)\)\( \Rightarrow cung\,\,AB = cung\,\,AD\)
\( \Rightarrow \angle CKD = \dfrac{1}{2}\left( {sd\,\,cung\,\,CD + \,sd\,\,cung\,\,AD} \right)\)\( = \dfrac{1}{2}sd\,\,cung\,\,AC\,\,\,\left( 4 \right)\)
Từ \(\left( 3 \right)\) và \(\left( 4 \right)\) \( \Rightarrow \angle OAB = \angle CKD\)
\( \Rightarrow OKDA\) là tứ giác nội tiếp. (tứ giác có góc ngoài bằng góc trong tại đỉnh đối diện)
\( \Rightarrow \) Đường tròn ngoại tiếp \(\Delta AKD\) đi qua điểm \(O\) cố định. (đpcm)
Câu 5:
Phương pháp:
+ Xác định điều kiện của phương trình, \(\sqrt {f\left( x \right)} \) có nghĩa \( \Leftrightarrow f\left( x \right) \ge 0\)
+ Đặt \(\left\{ \begin{array}{l}a = 2x + 1\\b = \sqrt {{x^2} + 2x + 3} \,\,\left( {b \ge 0} \right)\end{array} \right.\), biến đổi phương trình ban đầu theo \(a,b\)
+ Giải phương trình bậc hai ẩn \(b\) với tham số \(a\), tìm được mối liên hệ của \(a,b\)
+ Với \(a,b\) ta tìm được nghiệm \(x\), đối chiếu và kết luận.
Cách giải:
ĐKXĐ: \({x^2} + 2x + 3 \ge 0 \Leftrightarrow {\left( {x + 1} \right)^2} + 2 \ge 0\) (luôn đúng).
Đặt \(\left\{ \begin{array}{l}a = 2x + 1\\b = \sqrt {{x^2} + 2x + 3} \,\,\left( {b \ge 0} \right)\end{array} \right.\) ta có \(2a + {b^2} = 4x + 2 + {x^2} + 2x + 3 = {x^2} + 6x + 5\)
\( \Rightarrow {x^2} + 6x + 1 = 2a + {b^2} - 4\).
Khi đó phương trình trở thành:
\(2a + {b^2} - 4 - ab = 0 \Leftrightarrow {b^2} - ab + 2a - 4 = 0\,\,\left( * \right)\)
Coi (*) là phương trình bậc hai ẩn \(b\) với tham số \(a\) ta có
\(\Delta = {a^2} - 4\left( {2a - 4} \right) = {a^2} - 8a + 16 = {\left( {a - 4} \right)^2} \ge 0\,\,\forall a\)
Khi đó phương trình (*) có 2 nghiệm \(\left[ \begin{array}{l}b = \dfrac{{a + a - 4}}{2} = a - 2\\b = \dfrac{{a - a + 4}}{2} = 2\,\,\left( {tm} \right)\end{array} \right.\)
+) TH1: \(b = 2 \Rightarrow \sqrt {{x^2} + 2x + 3} = 2\) \( \Leftrightarrow {x^2} + 2x + 3 = 4 \Leftrightarrow {x^2} + 2x - 1 = 0\)
Ta có \(\Delta ' = 1 + 1 = 2 > 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ \begin{array}{l}x = - 1 + \sqrt 2 \\x = - 1 - \sqrt 2 \end{array} \right.\).
+) TH2: \(b = a - 2 \ge 0 \Leftrightarrow a \ge 2\).
Khi đó ta có \(\sqrt {{x^2} + 2x + 3} = 2x - 1\) \( \Leftrightarrow \left\{ \begin{array}{l}2x - 1 \ge 0\\{x^2} + 2x + 3 = 4{x^2} - 4x + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge \dfrac{1}{2}\\3{x^2} - 6x - 2 = 0\,\,\,\left( 1 \right)\end{array} \right.\)
Ta có \(\Delta ' = {3^2} - 3.\left( { - 2} \right) = 15 > 0\) nên phương trình (1) có 2 nghiệm phân biệt \(\left[ \begin{array}{l}x = \dfrac{{3 + \sqrt {15} }}{3}\,\,\left( {tm} \right)\\x = \dfrac{{3 - \sqrt {15} }}{3}\,\,\left( {ktm} \right)\end{array} \right.\).
Vậy tập nghiệm của phương trình đã cho là \(S = \left\{ { - 1 + \sqrt 2 ; - 1 - \sqrt 2 ;\dfrac{{3 + \sqrt {15} }}{3}} \right\}\).
Kỳ thi tuyển sinh vào lớp 10 môn Toán Thái Bình năm 2021 là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Đề thi thường bao gồm các dạng bài tập thuộc chương trình Toán lớp 9, tập trung vào các chủ đề chính như Đại số, Hình học và số học. Việc nắm vững kiến thức cơ bản và luyện tập thường xuyên là chìa khóa để đạt kết quả tốt trong kỳ thi này.
Thông thường, đề thi vào 10 môn Toán Thái Bình năm 2021 có cấu trúc như sau:
Đề thi số 1 tập trung vào các kiến thức về phương trình bậc hai và hệ phương trình. Các câu hỏi yêu cầu học sinh giải phương trình, tìm điều kiện để phương trình có nghiệm, và ứng dụng phương trình vào giải quyết các bài toán thực tế.
Đề thi số 2 chú trọng vào các kiến thức về hình học, đặc biệt là tam giác đồng dạng và đường tròn. Các câu hỏi yêu cầu học sinh chứng minh các tính chất hình học, tính độ dài các đoạn thẳng, và tính diện tích hình học.
Để giải đề thi vào 10 môn Toán Thái Bình năm 2021 hiệu quả, các em học sinh cần:
Ngoài các đề thi, các em học sinh có thể tham khảo thêm các tài liệu ôn thi sau:
Trước kỳ thi, hãy giữ tâm lý thoải mái, tự tin và có chế độ ăn uống, nghỉ ngơi hợp lý. Trong khi làm bài, hãy đọc kỹ đề bài, phân bổ thời gian hợp lý và kiểm tra lại kết quả trước khi nộp bài. Chúc các em thành công!
| Năm | Điểm chuẩn |
|---|---|
| 2019 | 8.0 |
| 2020 | 8.5 |
| 2021 | 9.0 |