Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp các đề thi thử vào lớp 10 môn Toán chất lượng cao. Đề số 20 là một trong những đề thi được thiết kế để giúp học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin bước vào kỳ thi quan trọng.
Đề thi này bao gồm các dạng bài tập đa dạng, từ trắc nghiệm đến tự luận, bao phủ đầy đủ các kiến thức trọng tâm của chương trình Toán lớp 9.
Đề thi vào lớp 10 môn Toán - Đề số 20 có đáp án và lời giải chi tiết
Đề bài
Câu 1. (2,0 điểm)
a) Giải phương trình: \({x^2} + x - 12 = 0.\)
b) Giải hệ phương trình: \(\left\{ \begin{array}{l}x - 2y = 6\\2x + y = 2\end{array} \right.\)
Câu 2 (2,0 điểm) Cho parabol: \(y = 3{x^2}\) và đường thẳng \(d:\,\,y = x + m - 1\) (với m là tham số).
a) Vẽ parabol (P).
b) Tìm tất cả các giá trị của m để (P) cắt (d) tại đúng một điểm.
Câu 3 (1,5 điểm). Một mảnh vườn hình chữ nhật có chiều dài hơn chiều rộng 5m. Nếu tăng chiều dài thêm 10m và chiều rộng thêm 5m thì diện tích mảnh vườn đó tăng gấp đôi. Tính chiều dài và chiều rộng mảnh vườn đó.
Câu 4 (3,5 điểm). Cho tam giác ABC vuông tại A, M là trung điểm của cạnh AC. Vẽ đường tròn đường kính MC cắt cạnh BC tại N \(\left( {N \ne C} \right).\) Đường thẳng BM cắt đường tròn đường kính MC tại D \(\left( {D \ne M} \right).\) Chứng minh:
a) Tứ giác BADC nội tiếp được trong một đường tròn. Xác định tâm O của đường tròn đó.
b) \(CM.CA = CN.CB.\)
c) \(O{M^2} = ON.OC.\)
Câu 5 (1,0 điểm). Cho hai số dương x, y thỏa mãn \(xy = 2018.\) Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{2}{x} + \dfrac{{1009}}{y} - \dfrac{{2018}}{{2018x + 4y}}.\)
Lời giải chi tiết
Câu 1. (2,0 điểm)
a) Giải phương trình: \({x^2} + x - 12 = 0.\)
Ta có: \(\Delta = 1 + 48 = 49 > 0 \Rightarrow \sqrt \Delta = 7\)
Khi đó phương trình đã cho có hai nghiệm phân biệt: \({x_1} = \dfrac{{ - 1 - 7}}{2} = - 4;{x_1} = \dfrac{{ - 1 + 7}}{2} = 3\)
Vậy tập nghiệm của phương trình là: \(S = \left\{ { - 4;3} \right\}\)
b) Giải hệ phương trình: \(\left\{ \begin{array}{l}x - 2y = 6\\2x + y = 2\end{array} \right.\)
\(\left\{ \begin{array}{l}x - 2y = 6\\2x + y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - 4y = 12\\2x + y = 2\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l} - 5y = 10\\x = 6 + 2y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = - 2\\x = 6 + 2.\left( { - 2} \right)\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}y = - 2\\x = 2\end{array} \right.\)
Vậy hệ phương trình có nghiệm là: \(\left( {x;y} \right) = \left( {2; - 2} \right)\)
Câu 2 (2,0 điểm)
Cho parabol: \(y = 3{x^2}\) và đường thẳng \(d:\,\,y = x + m - 1\) ( với m là tham số).
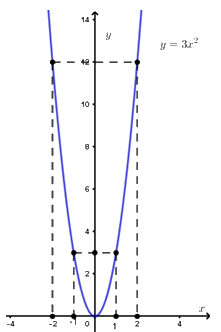
a) Vẽ parabol (P).
Bảng giá trị
\(x\) | \( - 2\) | \( - 1\) | 0 | 1 | 2 |
\(y = 3{x^2}\) | \(12\) | 3 | 0 | 3 | 12 |
Vậy parabol (P) đi qua các điểm có tọa độ tương ứng là: \(\left( { - 2;12} \right);\left( { - 1;3} \right);\left( {0;0} \right);\left( {1;3} \right);\left( {2;12} \right)\)
b) Tìm tất cả các giá trị của m để (P) cắt (d) tại đúng một điểm.
Phương trình hoành độ giao điểm của (P) và (d) là: \(3{x^2} - x - m + 1 = 0\,\,\left( 1 \right)\)
Số giao điểm của (P) và (d) cũng chính là số nghiệm của phương trình (1).
(P) cắt (d) tại đúng một điểm khi và chỉ khi phương trình (1) có nghiệm kép \( \Leftrightarrow \Delta = 0 \)
\(\Leftrightarrow 1 - 12\left( { - m + 1} \right) = 0 \Leftrightarrow m = \dfrac{{11}}{{12}}\)
Vậy với \(m = \dfrac{{11}}{{12}}\) thì (P) cắt (d) tại đúng một điểm.
Câu 3 (1,5 điểm).
Gọi chiều rộng của hình chữ nhật là x (m) (x > 0)
Chiều dài của hình chữ nhật là: x + 5 (m)
Diện tích ban đầu của hình chữ nhật là: \(x\left( {x + 5} \right)\,\,\left( {{m^2}} \right)\)
Tăng chiều dài thêm 10m, chiều rộng thêm 5m thì ta có chiều dài và chiều rộng sau khi thay đổi lần lượt là: \(x + 5 + 10\left( m \right);x + 5\left( m \right)\) .
Diện tích của hình chữ nhật sau khi thay đổi là: \(\left( {x + 15} \right)\left( {x + 5} \right)\left( {{m^2}} \right)\)
Theo bài ra ta có phương trình:
\(\begin{array}{l}\left( {x + 15} \right)\left( {x + 5} \right) = 2x\left( {x + 5} \right)\\ \Leftrightarrow {x^2} + 20x + 75 = 2{x^2} + 10x\\ \Leftrightarrow {x^2} - 10x - 75 = 0\\ \Leftrightarrow {x^2} + 5x - 15x - 75 = 0\\ \Leftrightarrow \left( {x + 5} \right)\left( {x - 15} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = - 5\left( {ktm} \right)\\x = 15\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy chiều rộng của hình chữ nhật là 15m; chiều dài của hình chữ nhật là: 20m.
Câu 4 (3,5 điểm).Cho tam giác ABC vuông tại A, M là trung điểm của cạnh AC. Vẽ đường tròn đường kính MC cắt cạnh BC tại N \(\left( {N \ne C} \right).\) Đường thẳng BM cắt đường tròn đường kính MC tại D \(\left( {D \ne M} \right).\) Chứng minh:
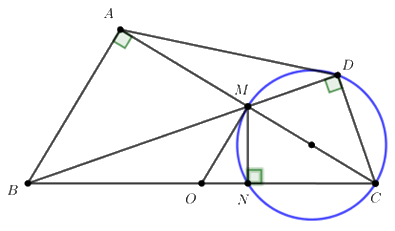
a) Tứ giác BADC nội tiếp được trong một đường tròn. Xác định tâm O của đường tròn đó.
Ta có: D thuộc đường tròn đường kính MC nên \(\angle MDC = {90^0}\,\,hay\,\,\angle BDC = {90^0}\)
Nên D thuộc đường tròn đường kính BC (1)
Có: \(\angle BAC = {90^0}\) (gt tam giác ABC vuông tại A) nên A thuộc đường tròn đường kính BC. (2)
Từ (1) và (2) suy ra 4 điểm B, A,D, C cùng thuộc đường tròn đường kính BC.
Hay tứ giác BADC nội tiếp đường tròn đường kính BC.
Gọi O là trung điểm của BC, Khi đó ta có tâm O của đường tròn chính là trung điểm của BC và bán kính chính bằng nửa độ dài BC.
b) \(CM.CA = CN.CB.\)
Xét tam giác CMN và tam giác CBA có:
\(\angle CNM = \angle CAB = {90^0}\)
\(\angle NCM\) chung
Nên \(\Delta CMN \sim \Delta CBA\left( {g - g} \right)\)
\( \Rightarrow \dfrac{{CM}}{{CB}} = \dfrac{{CN}}{{CA}}\)
\(\Rightarrow CM.CA = CB.CN\) (điều phải chứng minh)
c) \(O{M^2} = ON.OC.\)
Ta có: O là trung điểm của BC (cm câu a)
M là trung điểm của AC (gt)
Nên OM là đường trung bình của tam giác ABC
Khi đó ta có: \(OM\parallel AB\) . Mà \(AB \bot AC\left( {gt} \right)\)
\(\Rightarrow OM \bot AC\,\,hay\,\,\,OM\,\,\, \bot MC\)
Xét tam giác vuông OMC có MN là đường cao.
\( \Rightarrow O{M^2} = ON.OC\) (điều phải chứng minh)
Câu 5 (1,0 điểm).Cho hai số dương x, y thỏa mãn \(xy = 2018.\) Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{2}{x} + \dfrac{{1009}}{y} - \dfrac{{2018}}{{2018x + 4y}}.\)
Cách giải:
Áp dung bất đẳng thức Cauchy cho hai số dương: \(\dfrac{2}{x};\dfrac{{1009}}{y}\) ta có:
\(\dfrac{2}{x} + \dfrac{{1009}}{y} \ge 2\sqrt {\dfrac{2}{x}.\dfrac{{1009}}{y}} = 2\sqrt {\dfrac{{2018}}{{2018}}} = 2\) (1)
Áp dụng bất đẳng thức Cauchy cho hai số dương: \(2018x;4y\) ta có:
Khi đó ta có: \(\dfrac{{2018}}{{2018x + 4y}} \le \dfrac{{2018}}{{8072}} = \dfrac{1}{4}\)
\(\Rightarrow \dfrac{{2018}}{{2018x + 4y}} \ge - \dfrac{1}{4}\)
\(P = \dfrac{2}{x} + \dfrac{{1009}}{y} - \dfrac{{2018}}{{2018x + 4y}} \ge 2 - \dfrac{1}{4} = \dfrac{7}{4}\)
Vậy \({P_{\min }} = \dfrac{7}{4}\) . Dấu “=” xảy ra khi và chỉ khi: \(\left\{ \begin{array}{l}x = 2\\y = 1009\end{array} \right.\)
Kỳ thi vào lớp 10 là một bước ngoặt quan trọng trong quá trình học tập của mỗi học sinh. Để đạt kết quả tốt nhất, việc luyện tập thường xuyên với các đề thi thử là vô cùng cần thiết. Đề số 20 - Đề thi vào lớp 10 môn Toán tại giaitoan.edu.vn được xây dựng với mục tiêu cung cấp một công cụ ôn tập hiệu quả, giúp học sinh tự đánh giá năng lực và tìm ra những điểm cần cải thiện.
Đề thi số 20 bao gồm các phần chính sau:
Các dạng bài tập thường xuất hiện trong đề thi bao gồm:
Để giúp học sinh hiểu rõ hơn về đề thi và cách giải các bài tập, giaitoan.edu.vn cung cấp hướng dẫn giải chi tiết cho từng câu hỏi. Hướng dẫn giải bao gồm:
Luyện tập với Đề số 20 - Đề thi vào lớp 10 môn Toán tại giaitoan.edu.vn mang lại nhiều lợi ích cho học sinh:
Để đạt kết quả tốt nhất trong kỳ thi vào lớp 10 môn Toán, học sinh cần có một kế hoạch ôn tập khoa học và hiệu quả. Dưới đây là một số mẹo hữu ích:
Đề số 20 - Đề thi vào lớp 10 môn Toán tại giaitoan.edu.vn là một công cụ ôn tập hữu ích, giúp học sinh chuẩn bị tốt nhất cho kỳ thi quan trọng. Hãy luyện tập thường xuyên và áp dụng các mẹo ôn thi hiệu quả để đạt kết quả cao nhất!
| Dạng bài tập | Mức độ khó | Lời khuyên |
|---|---|---|
| Giải phương trình bậc hai | Trung bình | Nắm vững công thức nghiệm và điều kiện xác định. |
| Chứng minh các tính chất hình học | Khó | Vẽ hình chính xác và sử dụng các định lý, tính chất đã học. |
| Giải bài toán thực tế | Trung bình - Khó | Đọc kỹ đề bài và xác định các yếu tố liên quan. |