Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Trà Vinh năm 2018 chính thức. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi sắp tới.
Bộ đề thi này bao gồm các đề thi chính thức của kỳ thi tuyển sinh vào lớp 10 chuyên và không chuyên của tỉnh Trà Vinh năm 2018, kèm theo đáp án chi tiết và lời giải bài tập.
Bài 1 (VD). (3,0 điểm) Rút gọn biểu thức
Bài 1 (VD). (3,0 điểm)
Bài 2 (VD) (2 điểm)
Cho hai hàm số: \(y = - x + 2\) và \(y = {x^2}\) có đồ thị lần lượt là \(\left( d \right)\) và \(\left( P \right).\)
1) Vẽ \(\left( d \right)\) và \(\left( P \right)\) trên cùng hệ trục tọa độ.
2) Bằng phép toán tìm tọa độ giao điểm của \(\left( d \right)\) và \(\left( P \right).\)
Bài 3 (VD) (1 điểm)
Cho phương trình \({x^2} - \left( {m + 1} \right)x + m - 2 = 0\) (với m là tham số).
1) Chứng minh phương trình luôn có hai nghiệm phân biệt với mọi m.
2) Tìm các số nguyên m để phương trình có nghiệm nguyên.
Bài 4 (VD). (1,0 điểm)
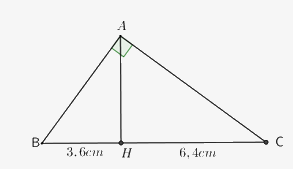
Cho tam giác ABC vuông tại A, đường cao AH \(\left( {H \in BC} \right)\) . Biết BH = 3,6cm và HC = 6,4 cm. Tính độ dài BC, AH, AB, AC.
Bài 5 (VD). (3 điểm).
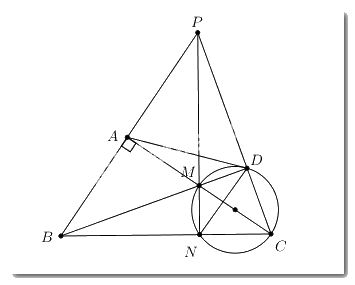
Cho tam giác ABC vuông tại A \(\left( {AB < AC} \right)\), M là trung điểm của cạnh AC. Đường tròn đường kính MC cắt BC tại N. Đường thẳng BM cắt đường tròn đường kính MC tại D.
1. Chứng minh tứ giác BADC nội tiếp.
2. Chứng minh DB là phân giác của góc ADN.
3. BA và CD kéo dài cắt nhau tại P. Chứng minh ba điểm P, M, N thẳng hàng.
Bài 1 (VD). (3,0 điểm)
Bài 2 (VD) (2 điểm)
Cho hai hàm số: \(y = - x + 2\) và \(y = {x^2}\) có đồ thị lần lượt là \(\left( d \right)\) và \(\left( P \right).\)
1) Vẽ \(\left( d \right)\) và \(\left( P \right)\) trên cùng hệ trục tọa độ.
2) Bằng phép toán tìm tọa độ giao điểm của \(\left( d \right)\) và \(\left( P \right).\)
Bài 3 (VD) (1 điểm)
Cho phương trình \({x^2} - \left( {m + 1} \right)x + m - 2 = 0\) (với m là tham số).
1) Chứng minh phương trình luôn có hai nghiệm phân biệt với mọi m.
2) Tìm các số nguyên m để phương trình có nghiệm nguyên.
Bài 4 (VD). (1,0 điểm)
Cho tam giác ABC vuông tại A, đường cao AH \(\left( {H \in BC} \right)\) . Biết BH = 3,6cm và HC = 6,4 cm. Tính độ dài BC, AH, AB, AC.
Bài 5 (VD). (3 điểm).
Cho tam giác ABC vuông tại A \(\left( {AB < AC} \right)\), M là trung điểm của cạnh AC. Đường tròn đường kính MC cắt BC tại N. Đường thẳng BM cắt đường tròn đường kính MC tại D.
1. Chứng minh tứ giác BADC nội tiếp.
2. Chứng minh DB là phân giác của góc ADN.
3. BA và CD kéo dài cắt nhau tại P. Chứng minh ba điểm P, M, N thẳng hàng.
Bài 1.
Phương pháp:
Cách giải:
1. Rút gọn biểu thức \(2\sqrt {75} + 3\sqrt {48} - 4\sqrt {27} \)
Ta có:
\(\begin{array}{l}\;\;\;2\sqrt {75} + 3\sqrt {48} - 4\sqrt {27} \\ = 2\sqrt {{5^2}.3} + 3\sqrt {{4^2}.3} - 4\sqrt {{3^2}.3} \\ = 10\sqrt 3 + 12\sqrt 3 - 12\sqrt 3 \\ = 10\sqrt 3 .\end{array}\)
2. Giải hệ phương trình \(\left\{ \begin{array}{l}2x - y = 8\\3x + 2y = 5\end{array} \right.\)
\(\left\{ \begin{array}{l}2x - y = 8\\3x + 2y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2x - 8\\3x + 2y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2x - 8\\3x + 2\left( {2x - 8} \right) = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2x - 8\\7x = 21\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 2x - 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = - 2\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất là: \(\left( {x;y} \right) = \left( {3; - 2} \right)\)
3. Giải phương trình \(3{x^2} - 7x + 2 = 0\)
Ta có: \(a = 3;\;\;b = - 7;\;\;c = 2\)
\(\Delta = {b^2} - 4ac = {\left( { - 7} \right)^2} - 4.3.2 = 25 > 0 \Rightarrow \sqrt \Delta = 5\)
Khi đó phương trình đã cho có hai nghiệm phân biệt là: \(\left[ \begin{array}{l}{x_1} = \dfrac{{7 - 5}}{6} = \dfrac{1}{3}\\{x_2} = \dfrac{{7 + 5}}{6} = 2\end{array} \right.\)
Vậy tập nghiệm của phương trình đã cho là: \(S = \left\{ {\dfrac{1}{3};2} \right\}\)
Bài 2: Cho hai hàm số: \(y = - x + 2\) và \(y = {x^2}\) có đồ thị lần lượt là \(\left( d \right)\) và \(\left( P \right).\)
Phương pháp:
1) Lập bảng giá trị các điểm mà từng đồ thị đi qua sau đó vẽ cả 2 đồ thị đã cho trên cùng hệ trục tọa độ.
2) Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình hoành độ giao điểm.
+) Giải phương trình hoành độ tìm hoành độ giao điểm sau đó thể vào một trong hai phương trình của hai đồ thị để tìm tung độ.
Cách giải:
1) Vẽ \(\left( d \right)\) và \(\left( P \right)\) trên cùng hệ trục tọa độ.
+) Vẽ đồ thị hàm số: \(\left( d \right):\;\;y = - x + 2.\)
\(x\) | \(0\) | \(2\) |
\(y = - x + 2\) | \(2\) | \(0\) |
+) Vẽ đồ thị hàm số: \(\left( P \right):\;\;y = {x^2}.\)
\(x\) | \( - 2\) | \( - 1\) | \(0\) | \(1\) | \(2\) |
\(y = {x^2}\) | \(4\) | \(1\) | \(0\) | \(1\) | \(4\) |
Đồ thị hàm số:
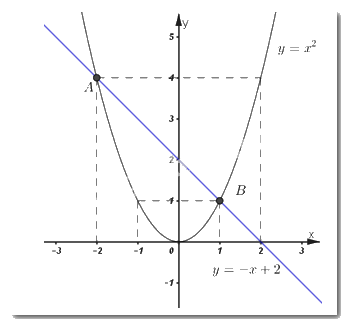
2) Bằng phép toán tìm tọa độ giao điểm của \(\left( d \right)\) và \(\left( P \right).\)
Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình hoành độ giao điểm.
Ta có phương trình hoành độ giao điểm của hai đồ thị là:
\(\begin{array}{l} - x + 2 = {x^2}\\ \Leftrightarrow {x^2} + x - 2 = 0\\ \Leftrightarrow {x^2} + 2x - x - 2 = 0\\ \Leftrightarrow x\left( {x + 2} \right) - \left( {x + 2} \right) = 0\\ \Leftrightarrow \left( {x + 2} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 2 = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 2 \Rightarrow y = 4\\x = 1 \Rightarrow y = 1\end{array} \right..\end{array}\)
Vậy hai đồ thị cắt nhau tại hai điểm phân biệt \(A\left( { - 2;\;4} \right)\) và \(B\left( {1;\;1} \right).\)
Bài 3:
Phương pháp:
+) Phương trình có hai nghiệm phân biệt với mọi \(m \Leftrightarrow \Delta > 0\;\;\forall m.\)
+) Từ phương trình đã cho, cô lập m, đưa phương trình về dạng \(m = A\left( x \right) + \dfrac{C}{{B\left( x \right)}}\) , với C là hằng số, tìm điều kiện để C chia hết cho B(x), tức là B(x) là ước của C.
Cách giải:
1) Chứng minh phương trình luôn có hai nghiệm phân biệt với mọi m.
Ta có: \(\Delta = {\left( {m + 1} \right)^2} - 4\left( {m - 2} \right) = {m^2} + 2m + 1 - 4m + 8 = {m^2} - 2m + 1 + 8 = {\left( {m - 1} \right)^2} + 8.\)
Vì \({\left( {m - 1} \right)^2} \ge 0\;\;\forall m \Rightarrow {\left( {m - 1} \right)^2} + 8 > 0\;\forall m.\)
Hay \(\Delta > 0\;\forall m \Rightarrow \) phương trình luôn có hai nghiệm phân biệt với mọi \(m.\)
2) Tìm các số nguyên m để phương trình có nghiệm nguyên.
Phương trình đã cho luôn có hai nghiệm phân biệt với mọi \(m.\)
Đề bài yêu cầu tìm \(m \in Z\) để \(x \in Z.\) Ta đưa bài toán về dạng tìm x nguyên để m nguyên.
Ta có: \({x^2} - \left( {m + 1} \right)x + m - 2 = 0 \Leftrightarrow {x^2} - mx - x + m - 2 = 0\)
\(\begin{array}{l} \Leftrightarrow {x^2} - x - 2 = m\left( {x - 1} \right)\\ \Leftrightarrow m = \dfrac{{{x^2} - x - 2}}{{x - 1}} = \dfrac{{x\left( {x - 1} \right) - 2}}{{x - 1}}\;\;\left( {x \ne 1} \right)\\ \Leftrightarrow m = x - \dfrac{2}{{x - 1}}.\\ \Rightarrow m \in Z \Leftrightarrow \left( {x - \dfrac{2}{{x - 1}}} \right) \in Z \Leftrightarrow \dfrac{2}{{x - 1}} \in Z\,\,\left( {Do\,\,x \in Z} \right) \Leftrightarrow \left( {x - 1} \right) \in U\left( 2 \right).\end{array}\)
Mà \(U\left( 2 \right) = \left\{ { - 2;\; - 1;\;1;\;2} \right\}.\)
\( \Rightarrow \left[ \begin{array}{l}x - 1 = - 2\\x - 1 = - 1\\x - 1 = 1\\x - 1 = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 0\\x = 2\\x = 3\end{array} \right.\,\,\left( {tm} \right) \Rightarrow \left[ \begin{array}{l}m = 0\\m = 2\\m = 0\\m = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\;\;\left( {tm} \right)\\m = 2\;\;\;\left( {tm} \right)\end{array} \right..\)
Vậy với \(m = 0\) và \(m = 2\) thỏa mãn yêu cầu bài toán.
Bài 4.
Phương pháp:
Áp dụng hệ thức lượng trong tam giác vuông ABC với chiều cao AH để tính AH: \(A{H^2} = BH.CH\)
Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H để tính AB: \(A{H^2} + B{H^2} = A{B^2}\)
Áp dụng định lý Pytago trong tam giác vuông ABC vuông tại A để tính AC: \(A{C^2} = B{C^2} - A{B^2}.\)
Cách giải:
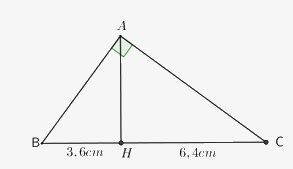
Ta có: \(\left( {H \in BC} \right)\) nên : \(BC = BH + HC = 3,6 + 6,4 = 10\left( {cm} \right)\)
Áp dụng hệ thức lượng trong tam giác ABC vuông tại A với đường cao AH ta có:
\(A{H^2} = BH.HC \Rightarrow A{H^2} = 3,6.6,4 = 23,04 \Rightarrow AH = 4,8\left( {cm} \right)\)
Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H ta có:
\(A{B^2} = A{H^2} + B{H^2} = 4,{8^2} + 3,{6^2} = 36 \Rightarrow AB = 6\left( {cm} \right)\)
Áp dụng định lý Pytago trong tam giác vuông ABC vuông tại A ta có:
\(A{C^2} = B{C^2} - A{B^2} = {10^2} - {6^2} = 64 \Rightarrow AC = 8\left( {cm} \right)\)
Vậy: BC = 10 cm; AH = 4,8 cm; AB = 6 cm; AC = 8 cm.
Bài 5.
Phương pháp:
1. Chứng minh tứ giác BADC có hai đỉnh A và D cùng nhìn BC dưới các góc bằng nhau.
2. Chứng minh hai góc ADB và BDN cùng bằng góc ACB.
3. Chứng minh M là trực tâm của tam giác PBC \( \Rightarrow PM \bot BC\)
Chứng minh \(MN \bot BC\), từ đó suy ra P, M, N thẳng hàng.
Cách giải:
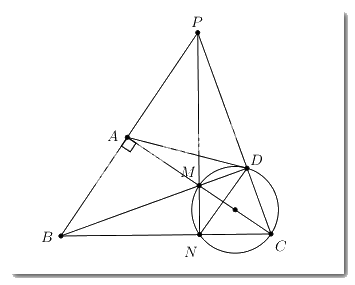
1. Chứng minh tứ giác BADC nội tiếp.
Ta có \(\widehat {MDC} = {90^0}\) (góc nội tiếp chắn nửa đường tròn đường kính MC) \( \Rightarrow \widehat {BDC} = {90^0}\).(Do B, M, D thẳng hàng)
Có \(\widehat {BAC} = {90^0}\) (do giả thiết tam giác ABC vuông tại A)
Xét tứ giác BADC có \(\widehat {BAC} = \widehat {BDC} = {90^0} \Rightarrow \) Hai điểm A và D cùng nhìn BC dưới góc 900 \( \Rightarrow \) Tứ giác BADC là tứ giác nội tiếp (Tứ giác có hai đỉnh cùng nhìn 1 cạnh dưới các góc bằng nhau).
2. Chứng minh DB là phân giác của góc ADN.
Do BADC là tứ giác nội tiếp (cmt) \( \Rightarrow \widehat {ADB} = \widehat {ACB}\) (hai góc nội tiếp cùng chắn cung AB).
Lại có \(\widehat {ACB} = \widehat {MCN} = \widehat {MDN}\) (hai góc nội tiếp cùng chắn cung MN của đường tròn đường kính MC).
\( \Rightarrow \widehat {ADB} = \widehat {MDN} = \widehat {BDN} \Rightarrow BD\) là tia phân giác của góc ADN.
3. BA và CD kéo dài cắt nhau tại P. Chứng minh ba điểm P, M, N thẳng hàng.
Ta có \(\widehat {BDC} = {90^0}\,\,\left( {cmt} \right) \Rightarrow BD \bot DC \Rightarrow BD \bot PC\)
Tam giác ABC vuông tại A \( \Rightarrow AC \bot AB \Rightarrow AC \bot PB\)
Xét tam giác PBC có \(BD \bot PC;\,\,AC \bot PB;\,\,AC \cap BD = M \Rightarrow M\) là trực tâm tam giác PBC.
\( \Rightarrow PM \bot BC\).
Lại có \(\widehat {MNC} = {90^0}\) (góc nội tiếp chắn nửa đường tròn đường kính MC) \( \Rightarrow MN \bot NC \Rightarrow MN \bot BC\)
Qua điểm M nằm ngoài đường thẳng BC ta kẻ được \(PM \bot BC\) và \(MN \bot BC\)
\( \Rightarrow PM \equiv MN\) hay ba điểm P, M, N thẳng hàng.
Bài 1.
Phương pháp:
Cách giải:
1. Rút gọn biểu thức \(2\sqrt {75} + 3\sqrt {48} - 4\sqrt {27} \)
Ta có:
\(\begin{array}{l}\;\;\;2\sqrt {75} + 3\sqrt {48} - 4\sqrt {27} \\ = 2\sqrt {{5^2}.3} + 3\sqrt {{4^2}.3} - 4\sqrt {{3^2}.3} \\ = 10\sqrt 3 + 12\sqrt 3 - 12\sqrt 3 \\ = 10\sqrt 3 .\end{array}\)
2. Giải hệ phương trình \(\left\{ \begin{array}{l}2x - y = 8\\3x + 2y = 5\end{array} \right.\)
\(\left\{ \begin{array}{l}2x - y = 8\\3x + 2y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2x - 8\\3x + 2y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2x - 8\\3x + 2\left( {2x - 8} \right) = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2x - 8\\7x = 21\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 2x - 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = - 2\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất là: \(\left( {x;y} \right) = \left( {3; - 2} \right)\)
3. Giải phương trình \(3{x^2} - 7x + 2 = 0\)
Ta có: \(a = 3;\;\;b = - 7;\;\;c = 2\)
\(\Delta = {b^2} - 4ac = {\left( { - 7} \right)^2} - 4.3.2 = 25 > 0 \Rightarrow \sqrt \Delta = 5\)
Khi đó phương trình đã cho có hai nghiệm phân biệt là: \(\left[ \begin{array}{l}{x_1} = \dfrac{{7 - 5}}{6} = \dfrac{1}{3}\\{x_2} = \dfrac{{7 + 5}}{6} = 2\end{array} \right.\)
Vậy tập nghiệm của phương trình đã cho là: \(S = \left\{ {\dfrac{1}{3};2} \right\}\)
Bài 2: Cho hai hàm số: \(y = - x + 2\) và \(y = {x^2}\) có đồ thị lần lượt là \(\left( d \right)\) và \(\left( P \right).\)
Phương pháp:
1) Lập bảng giá trị các điểm mà từng đồ thị đi qua sau đó vẽ cả 2 đồ thị đã cho trên cùng hệ trục tọa độ.
2) Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình hoành độ giao điểm.
+) Giải phương trình hoành độ tìm hoành độ giao điểm sau đó thể vào một trong hai phương trình của hai đồ thị để tìm tung độ.
Cách giải:
1) Vẽ \(\left( d \right)\) và \(\left( P \right)\) trên cùng hệ trục tọa độ.
+) Vẽ đồ thị hàm số: \(\left( d \right):\;\;y = - x + 2.\)
\(x\) | \(0\) | \(2\) |
\(y = - x + 2\) | \(2\) | \(0\) |
+) Vẽ đồ thị hàm số: \(\left( P \right):\;\;y = {x^2}.\)
\(x\) | \( - 2\) | \( - 1\) | \(0\) | \(1\) | \(2\) |
\(y = {x^2}\) | \(4\) | \(1\) | \(0\) | \(1\) | \(4\) |
Đồ thị hàm số:
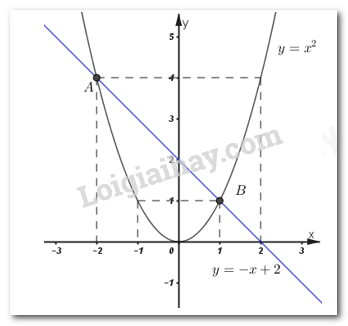
2) Bằng phép toán tìm tọa độ giao điểm của \(\left( d \right)\) và \(\left( P \right).\)
Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình hoành độ giao điểm.
Ta có phương trình hoành độ giao điểm của hai đồ thị là:
\(\begin{array}{l} - x + 2 = {x^2}\\ \Leftrightarrow {x^2} + x - 2 = 0\\ \Leftrightarrow {x^2} + 2x - x - 2 = 0\\ \Leftrightarrow x\left( {x + 2} \right) - \left( {x + 2} \right) = 0\\ \Leftrightarrow \left( {x + 2} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 2 = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 2 \Rightarrow y = 4\\x = 1 \Rightarrow y = 1\end{array} \right..\end{array}\)
Vậy hai đồ thị cắt nhau tại hai điểm phân biệt \(A\left( { - 2;\;4} \right)\) và \(B\left( {1;\;1} \right).\)
Bài 3:
Phương pháp:
+) Phương trình có hai nghiệm phân biệt với mọi \(m \Leftrightarrow \Delta > 0\;\;\forall m.\)
+) Từ phương trình đã cho, cô lập m, đưa phương trình về dạng \(m = A\left( x \right) + \dfrac{C}{{B\left( x \right)}}\) , với C là hằng số, tìm điều kiện để C chia hết cho B(x), tức là B(x) là ước của C.
Cách giải:
1) Chứng minh phương trình luôn có hai nghiệm phân biệt với mọi m.
Ta có: \(\Delta = {\left( {m + 1} \right)^2} - 4\left( {m - 2} \right) = {m^2} + 2m + 1 - 4m + 8 = {m^2} - 2m + 1 + 8 = {\left( {m - 1} \right)^2} + 8.\)
Vì \({\left( {m - 1} \right)^2} \ge 0\;\;\forall m \Rightarrow {\left( {m - 1} \right)^2} + 8 > 0\;\forall m.\)
Hay \(\Delta > 0\;\forall m \Rightarrow \) phương trình luôn có hai nghiệm phân biệt với mọi \(m.\)
2) Tìm các số nguyên m để phương trình có nghiệm nguyên.
Phương trình đã cho luôn có hai nghiệm phân biệt với mọi \(m.\)
Đề bài yêu cầu tìm \(m \in Z\) để \(x \in Z.\) Ta đưa bài toán về dạng tìm x nguyên để m nguyên.
Ta có: \({x^2} - \left( {m + 1} \right)x + m - 2 = 0 \Leftrightarrow {x^2} - mx - x + m - 2 = 0\)
\(\begin{array}{l} \Leftrightarrow {x^2} - x - 2 = m\left( {x - 1} \right)\\ \Leftrightarrow m = \dfrac{{{x^2} - x - 2}}{{x - 1}} = \dfrac{{x\left( {x - 1} \right) - 2}}{{x - 1}}\;\;\left( {x \ne 1} \right)\\ \Leftrightarrow m = x - \dfrac{2}{{x - 1}}.\\ \Rightarrow m \in Z \Leftrightarrow \left( {x - \dfrac{2}{{x - 1}}} \right) \in Z \Leftrightarrow \dfrac{2}{{x - 1}} \in Z\,\,\left( {Do\,\,x \in Z} \right) \Leftrightarrow \left( {x - 1} \right) \in U\left( 2 \right).\end{array}\)
Mà \(U\left( 2 \right) = \left\{ { - 2;\; - 1;\;1;\;2} \right\}.\)
\( \Rightarrow \left[ \begin{array}{l}x - 1 = - 2\\x - 1 = - 1\\x - 1 = 1\\x - 1 = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 0\\x = 2\\x = 3\end{array} \right.\,\,\left( {tm} \right) \Rightarrow \left[ \begin{array}{l}m = 0\\m = 2\\m = 0\\m = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\;\;\left( {tm} \right)\\m = 2\;\;\;\left( {tm} \right)\end{array} \right..\)
Vậy với \(m = 0\) và \(m = 2\) thỏa mãn yêu cầu bài toán.
Bài 4.
Phương pháp:
Áp dụng hệ thức lượng trong tam giác vuông ABC với chiều cao AH để tính AH: \(A{H^2} = BH.CH\)
Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H để tính AB: \(A{H^2} + B{H^2} = A{B^2}\)
Áp dụng định lý Pytago trong tam giác vuông ABC vuông tại A để tính AC: \(A{C^2} = B{C^2} - A{B^2}.\)
Cách giải:
Ta có: \(\left( {H \in BC} \right)\) nên : \(BC = BH + HC = 3,6 + 6,4 = 10\left( {cm} \right)\)
Áp dụng hệ thức lượng trong tam giác ABC vuông tại A với đường cao AH ta có:
\(A{H^2} = BH.HC \Rightarrow A{H^2} = 3,6.6,4 = 23,04 \Rightarrow AH = 4,8\left( {cm} \right)\)
Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H ta có:
\(A{B^2} = A{H^2} + B{H^2} = 4,{8^2} + 3,{6^2} = 36 \Rightarrow AB = 6\left( {cm} \right)\)
Áp dụng định lý Pytago trong tam giác vuông ABC vuông tại A ta có:
\(A{C^2} = B{C^2} - A{B^2} = {10^2} - {6^2} = 64 \Rightarrow AC = 8\left( {cm} \right)\)
Vậy: BC = 10 cm; AH = 4,8 cm; AB = 6 cm; AC = 8 cm.
Bài 5.
Phương pháp:
1. Chứng minh tứ giác BADC có hai đỉnh A và D cùng nhìn BC dưới các góc bằng nhau.
2. Chứng minh hai góc ADB và BDN cùng bằng góc ACB.
3. Chứng minh M là trực tâm của tam giác PBC \( \Rightarrow PM \bot BC\)
Chứng minh \(MN \bot BC\), từ đó suy ra P, M, N thẳng hàng.
Cách giải:
1. Chứng minh tứ giác BADC nội tiếp.
Ta có \(\widehat {MDC} = {90^0}\) (góc nội tiếp chắn nửa đường tròn đường kính MC) \( \Rightarrow \widehat {BDC} = {90^0}\).(Do B, M, D thẳng hàng)
Có \(\widehat {BAC} = {90^0}\) (do giả thiết tam giác ABC vuông tại A)
Xét tứ giác BADC có \(\widehat {BAC} = \widehat {BDC} = {90^0} \Rightarrow \) Hai điểm A và D cùng nhìn BC dưới góc 900 \( \Rightarrow \) Tứ giác BADC là tứ giác nội tiếp (Tứ giác có hai đỉnh cùng nhìn 1 cạnh dưới các góc bằng nhau).
2. Chứng minh DB là phân giác của góc ADN.
Do BADC là tứ giác nội tiếp (cmt) \( \Rightarrow \widehat {ADB} = \widehat {ACB}\) (hai góc nội tiếp cùng chắn cung AB).
Lại có \(\widehat {ACB} = \widehat {MCN} = \widehat {MDN}\) (hai góc nội tiếp cùng chắn cung MN của đường tròn đường kính MC).
\( \Rightarrow \widehat {ADB} = \widehat {MDN} = \widehat {BDN} \Rightarrow BD\) là tia phân giác của góc ADN.
3. BA và CD kéo dài cắt nhau tại P. Chứng minh ba điểm P, M, N thẳng hàng.
Ta có \(\widehat {BDC} = {90^0}\,\,\left( {cmt} \right) \Rightarrow BD \bot DC \Rightarrow BD \bot PC\)
Tam giác ABC vuông tại A \( \Rightarrow AC \bot AB \Rightarrow AC \bot PB\)
Xét tam giác PBC có \(BD \bot PC;\,\,AC \bot PB;\,\,AC \cap BD = M \Rightarrow M\) là trực tâm tam giác PBC.
\( \Rightarrow PM \bot BC\).
Lại có \(\widehat {MNC} = {90^0}\) (góc nội tiếp chắn nửa đường tròn đường kính MC) \( \Rightarrow MN \bot NC \Rightarrow MN \bot BC\)
Qua điểm M nằm ngoài đường thẳng BC ta kẻ được \(PM \bot BC\) và \(MN \bot BC\)
\( \Rightarrow PM \equiv MN\) hay ba điểm P, M, N thẳng hàng.
Kỳ thi tuyển sinh vào lớp 10 môn Toán Trà Vinh năm 2018 là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Để chuẩn bị tốt nhất cho kỳ thi này, việc nắm vững cấu trúc đề thi, các dạng bài tập thường gặp và phương pháp giải quyết là vô cùng cần thiết. Bài viết này sẽ cung cấp cho các em một cái nhìn tổng quan về đề thi vào 10 môn Toán Trà Vinh năm 2018, phân tích chi tiết các dạng bài tập và hướng dẫn giải một số bài tập điển hình.
Đề thi vào 10 môn Toán Trà Vinh năm 2018 thường bao gồm các phần sau:
Các dạng bài tập thường gặp trong đề thi vào 10 môn Toán Trà Vinh năm 2018 bao gồm:
Đây là một trong những dạng bài tập thường gặp nhất trong đề thi vào 10 môn Toán. Các em cần nắm vững các phương pháp giải phương trình và hệ phương trình như phương pháp thế, phương pháp cộng đại số, phương pháp đặt ẩn phụ. Ngoài ra, các em cũng cần chú ý đến điều kiện xác định của phương trình và hệ phương trình.
Các em cần nắm vững các bất đẳng thức cơ bản như bất đẳng thức Cauchy-Schwarz, bất đẳng thức AM-GM, bất đẳng thức Bunyakovsky. Ngoài ra, các em cũng cần biết cách chứng minh bất đẳng thức và giải bất đẳng thức.
Các em cần nắm vững các khái niệm về hàm số như tập xác định, tập giá trị, tính đơn điệu, tính chẵn lẻ. Ngoài ra, các em cũng cần biết cách vẽ đồ thị hàm số và giải các bài toán liên quan đến hàm số.
Các em cần nắm vững các định lý và tính chất cơ bản của hình học phẳng như định lý Pitago, định lý Thales, định lý đường phân giác. Ngoài ra, các em cũng cần biết cách chứng minh các tính chất hình học và giải các bài toán liên quan đến hình học phẳng.
Các em cần nắm vững các khái niệm về hình học không gian như đường thẳng và mặt phẳng, góc giữa đường thẳng và mặt phẳng, khoảng cách giữa hai đường thẳng. Ngoài ra, các em cũng cần biết cách giải các bài toán liên quan đến hình học không gian.
Các em cần nắm vững các khái niệm về số học như số nguyên tố, ước chung lớn nhất, bội chung nhỏ nhất. Ngoài ra, các em cũng cần biết cách giải các bài toán liên quan đến số học.
Các bài toán thực tế thường yêu cầu các em vận dụng kiến thức toán học vào giải quyết các vấn đề trong cuộc sống. Các em cần đọc kỹ đề bài, xác định các yếu tố toán học liên quan và xây dựng mô hình toán học để giải quyết bài toán.
Bài 1: Giải phương trình 2x + 3 = 7
Giải:
2x + 3 = 7
2x = 7 - 3
2x = 4
x = 2
Bài 2: Chứng minh bất đẳng thức a2 + b2 ≥ 2ab
Giải:
(a - b)2 ≥ 0
a2 - 2ab + b2 ≥ 0
a2 + b2 ≥ 2ab
Đề thi vào 10 môn Toán Trà Vinh năm 2018 là một kỳ thi quan trọng, đòi hỏi các em học sinh phải có sự chuẩn bị kỹ lưỡng. Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để tự tin bước vào kỳ thi và đạt kết quả tốt nhất. Chúc các em thành công!