Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh An Giang năm 2019 chính thức. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi sắp tới.
Đề thi vào 10 môn Toán An Giang năm 2019 được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm, đảm bảo độ chính xác và tính cập nhật cao. Các em có thể tải đề thi miễn phí và tham khảo lời giải chi tiết tại website của chúng tôi.
Bài 1 (3 điểm): Giải các phương trình và hệ phương trình sau đây:
Bài 1 (3 điểm): Giải các phương trình và hệ phương trình sau đây:
a) \(\dfrac{x}{{\sqrt 3 }} + \sqrt 3 x = \sqrt 3 \) b) \({x^2} + 6x - 5 = 0\)
c) \(\left\{ \begin{array}{l}\sqrt 2 x + y = \sqrt 2 + 2\\2\sqrt 2 x - y = 2\sqrt 2 - 2\end{array} \right.\)
Bài 2 (1,5 điểm):
Cho hàm số có đồ thị là Parabol \(\left( P \right):y = 0,25{x^2}\).
a) Vẽ đồ thị \(\left( P \right)\) của hàm số đã cho.
b) Qua điểm \(A\left( {0;1} \right)\) vẽ đường thẳng song song với trục hoành \(Ox\) cắt \(\left( P \right)\) tại hai điểm \(E\) và \(F\). Viết tọa độ của \(E\) và \(F\).
Bài 3 (2 điểm): Cho phương trình bậc hai \({x^2} - \left( {m + 2} \right)x + 2m = 0\,\,\,\left( * \right)\) (\(m\) là tham số)
a) Chứng minh rằng phương trình (*) luôn có nghiệm với mọi \(m.\)
b) Tìm các giá trị của \(m\) để phương trình (*) có hai nghiệm \({x_1},\,\,{x_2}\) thỏa mãn: \( - 1 \le \dfrac{{2\left( {{x_1} + {x_2}} \right)}}{{{x_1}{x_2}}} \le 1.\)
Bài 4 (2,5 điểm)
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 4cm,\,\,AC = 3cm\). Lấy điểm \(D\) thuộc cạnh \(AB\,\,\left( {AD < DB} \right)\). Đường tròn \(\left( O \right)\) đường kính \(BD\) cắt \(CB\) tại \(E\), kéo dài \(CD\) cắt đường tròn \(\left( O \right)\) tại \(F\).
a) Chứng minh rằng \(ACED\) là tứ giác nội tiếp.
b) Biết \(BF = 3cm\). Tính \(BC\) và diện tích tam giác \(BFC\).
c) Kéo dài \(AF\) cắt đường tròn \(\left( O \right)\) tại \(G\). Chứng minh rằng \(BA\) là tia phân giác của góc \(CBG\).
Bài 5 (1 điểm):
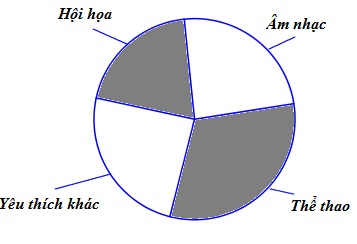
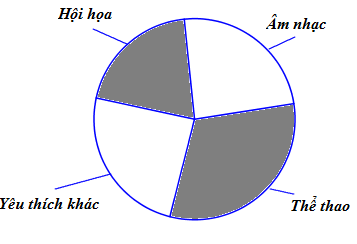
Trường A tiến hành khảo sát 1500 học sinh về sự yêu thích hội họa, thể thao, âm nhạc và các yêu thích khác. Mỗi học sinh chỉ chọn một yêu thích. Biết số học sinh yêu thích hội họa chiếm tỉ lệ 20% so với số học sinh toàn trường.
Số học sinh yêu thích thể thao hơn số học sinh yêu thích âm nhạc là 30 học sinh; số học sinh yêu thích thể thao và hội họa bằng với số học sinh yêu thích âm nhạc và các yêu thích khác.
a) Tính số học sinh yêu thích hội họa.
b) Hỏi tổng số học sinh yêu thích thể thao và âm nhạc là bao nhiêu?
Bài 1
Phương pháp:
a) Quy đồng mẫu số rồi đưa về phương trình bậc nhất \(ax + b = 0\,\,\left( {a \ne 0} \right) \Leftrightarrow x = - \dfrac{b}{a}\)
b) Sử dụng công thức nghiệm thu gọn của phương trình bậc hai \(a{x^2} + bx + c = 0\,\)
có \(\Delta ' = {\left( {b'} \right)^2} - ac\). Với \(\Delta ' > 0\) thì phương trình có hai nghiệm phân biệt \({x_1} = \dfrac{{ - b' + \sqrt {\Delta '} }}{a};{x_2} = \dfrac{{ - b' - \sqrt {\Delta '} }}{a}\)
c) Giải hệ phương trình bằng phương pháp cộng đại số
Cách giải:
\(a)\,\,\,\dfrac{x}{{\sqrt 3 }} + \sqrt 3 x = \sqrt 3 \Leftrightarrow \dfrac{{x + 3x}}{{\sqrt 3 }} = \sqrt 3 \Leftrightarrow x + 3x = 3 \Leftrightarrow 4x = 3 \Leftrightarrow x = \dfrac{3}{4}\)
Vậy tập nghiệm của phương trình \(S = \left\{ {\dfrac{3}{4}} \right\}.\)
b) Phương trình \({x^2} + 6x - 5 = 0\) có \(\Delta ' = {3^2} - 1.\left( { - 5} \right) = 14 > 0\) nên phương trình có hai nghiệm phân biệt \({x_1} = - 3 + \sqrt {14} ;{x_2} = - 3 - \sqrt {14} \)
Vậy tập nghiệm của phương trình là:\(S = \left\{ { - 3 + \sqrt {14} ; - 3 - \sqrt {14} } \right\}.\)
c) \(\left\{ \begin{array}{l}\sqrt 2 x + y = \sqrt 2 + 2\\2\sqrt 2 x - y = 2\sqrt 2 - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\sqrt 2 x + y = \sqrt 2 + 2\\3\sqrt 2 x = 3\sqrt 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\\sqrt 2 .1 + y = \sqrt 2 + 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right.\)
Hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {1;2} \right).\)
Bài 2
Phương pháp:
a) +) Tìm các điểm đi qua của đồ thị hàm số.
+) Vẽ đồ thị.
b) Cho \(y = 1\) giải phương trình tìm \(x\) và kết luận.
Cách giải:
a) Vẽ đồ thị \(\left( P \right)\) của hàm số đã cho.
Cho \(x\) nhận các giá trị \( - 4; - 2;0;2;4\) ta có bảng sau:
\(x\) | \( - 4\) | \( - 2\) | \(0\) | \(2\) | \(4\) |
\(y\) | \(4\) | \(1\) | \(0\) | \(1\) | \(4\) |
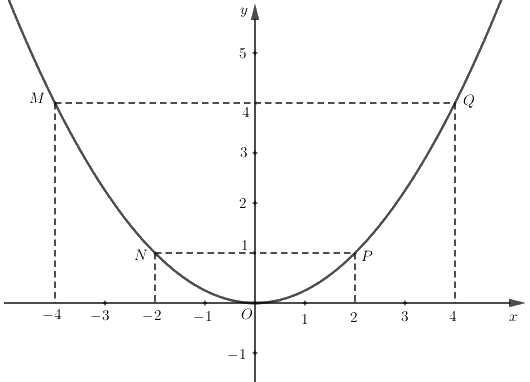
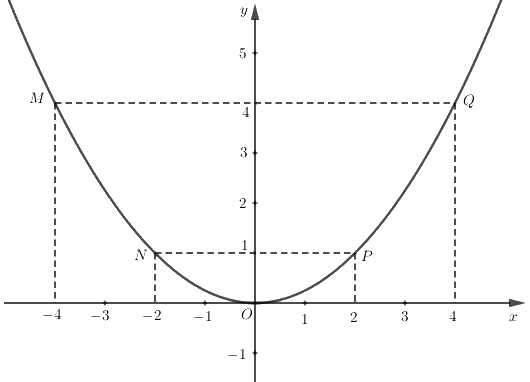
Do đó đồ thị hàm số \(y = 0,25{x^2}\) là parabol đi qua các điểm \(M\left( { - 4;4} \right),N\left( { - 2;1} \right),O\left( {0;0} \right),P\left( {2;1} \right),Q\left( {4;4} \right)\)
Vẽ đồ thị:
b) Qua điểm \(A\left( {0;1} \right)\) vẽ đường thẳng song song với trục hoành \(Ox\) cắt \(\left( P \right)\) tại hai điểm \(E\) và \(F\). Viết tọa độ của \(E\) và \(F\).
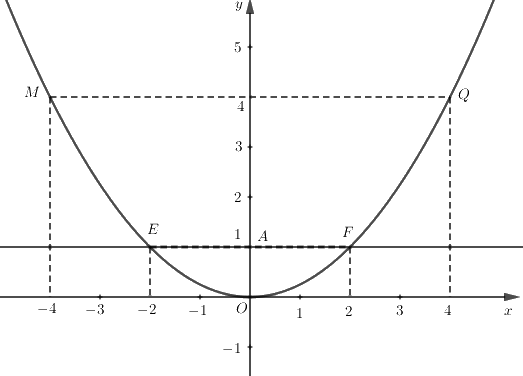
Đường thẳng đi qua \(A\left( {0;1} \right)\) và song song với trục hoành có phương trình \(y = 1\).
Xét phương trình hoành độ giao điểm của đường thẳng \(y = 1\) và parabol \(y = 0,25{x^2}\) ta có
\(0,25{x^2} = 1 \Leftrightarrow {x^2} = 4 \Leftrightarrow x = \pm 2\).
Với \(x = 2 \Rightarrow y = 1\)
Với \(x = - 2 \Rightarrow y = 1\)
Vậy hai điểm \(E\) và \(F\) có tọa độ lần lượt là \(\left( { - 2;1} \right)\)và \(\left( {2;1} \right)\).
Bài 3
Phương pháp:
a) Phương trình có hai nghiệm \( \Leftrightarrow \Delta \ge 0.\)
b) Áp dụng hệ thức Vi-ét và biểu thức bài cho để tìm \(m\), đối chiếu với điều kiện rồi kết luận.
Cách giải:
a) Chứng minh rằng phương trình (*) luôn có nghiệm với mọi \(m.\)
\({x^2} - \left( {m + 2} \right)x + 2m = 0\,\,\,\left( * \right)\)
Có: \(\Delta = {\left( {m + 2} \right)^2} - 4.2m = {m^2} + 4m + 4 - 8m = {m^2} - 4m + 4 = {\left( {m - 2} \right)^2} \ge 0\,\,\forall m\)
\( \Rightarrow \) Phương trình (*) luôn có nghiệm với mọi \(m.\)
b) Tìm các giá trị của \(m\) để phương trình (*) có hai nghiệm \({x_1},\,\,{x_2}\) thỏa mãn: \( - 1 \le \dfrac{{2\left( {{x_1} + {x_2}} \right)}}{{{x_1}{x_2}}} \le 1.\)
Theo câu a) ta có phương trình (*) luôn có nghiệm với mọi \(m.\)
Gọi \({x_1};{x_2}\) là hai nghiệm của phương trình (*)
Áp dụng hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m + 2\\{x_1}{x_2} = 2m\end{array} \right..\)
Theo đề bài ta có: \( - 1 \le \dfrac{{2\left( {{x_1} + {x_2}} \right)}}{{{x_1}{x_2}}} \le 1\)
\(\begin{array}{l} \Leftrightarrow - 1 \le \dfrac{{2\left( {m + 2} \right)}}{{2m}} \le 1 \Leftrightarrow \left\{ \begin{array}{l}2m \ne 0\\\dfrac{{m + 2}}{m} \ge - 1\\\dfrac{{m + 2}}{m} \le 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\\dfrac{{m + 2 + m}}{m} \ge 0\\\dfrac{{m + 2 - m}}{m} \le 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\\dfrac{{2m + 2}}{m} \ge 0\\\dfrac{2}{m} \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\\left[ \begin{array}{l}m > 0\\m \le - 1\end{array} \right.\\m < 0\end{array} \right. \Leftrightarrow m \le - 1.\end{array}\)
Vậy \(m \le - 1\) thỏa mãn bài toán.
Bài 4
Phương pháp:
a) Chứng minh tứ giác \(ACED\) có tổng hai góc đối bằng 1800.
b) Áp dụng định lí Pytago trong tam giác vuông \(ABC\) tính \(BC\).
Chứng minh tam giác \(BFC\) vuông. Áp dụng định lí Pytago trong tam giác vuông tính \(FC\), từ đó tính diện tích tam giác \(BFC\).
c) Chứng minh \(\angle GBD = \angle ABC = \angle AFC\), từ đó suy ra điều phải chứng minh.
Cách giải:
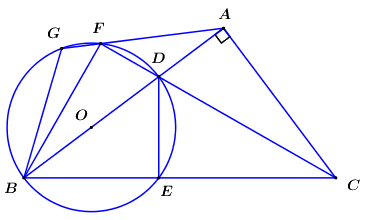
a) Chứng minh rằng \(ACED\) là tứ giác nội tiếp.
Ta có \(\angle BED = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow DE \bot BC \Rightarrow \angle CED = {90^0}\).
Xét tứ giác \(ACED\) có \(\angle CAD + \angle CED = {90^0} + {90^0} = {180^0}\) \( \Rightarrow \)Tứ giác \(ACED\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
b) Biết \(BF = 3cm\). Tính \(BC\) và diện tích tam giác \(BFC\).
Áp dụng định lí Pytago trong tam giác vuông \(ABC\) ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} = {4^2} + {3^2} = 16 + 9 = 25\\ \Rightarrow BC = \sqrt {25} = 5\,\,\left( {cm} \right)\end{array}\)
Ta có \(\angle BFD = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow BF \bot FD\) hay \(BF \bot FC \Rightarrow \Delta BFC\) vuông tại \(F\).
Áp dụng định lí Pytago trong tam giác vuông \(BFC\) ta có:
\(F{C^2} = B{C^2} - B{F^2} = {5^2} - {3^2} = 25 - 9 = 16\)
\( \Rightarrow FC = \sqrt {16} = 4\,\,\left( {cm} \right)\).
Vậy \({S_{BFC}} = \dfrac{1}{2}FB.FC = \dfrac{1}{2}.3.4 = 6\,\,\left( {c{m^2}} \right)\).
c) Kéo dài \(AF\) cắt đường tròn \(\left( O \right)\) tại \(G\). Chứng minh rằng \(BA\) là tia phân giác của góc \(\angle CBG\).
Nhận thấy bốn điểm \(B,\,\,D,\,\,F,\,\,G\) cùng thuộc \(\left( O \right) \Rightarrow \) Tứ giác \(BDFG\) là tứ giác nội tiếp.
\( \Rightarrow \angle GBD = \angle AFD = \angle AFC\) (1) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp).
Xét tứ giác \(AFBC\) có: \(\angle BAC = \angle BFC = {90^0} \Rightarrow \) Tứ giác \(AFBC\) là tứ giác nội tiếp (Tứ giác có 2 đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau).
Do đó \(\angle ABC = \angle AFC\,\,\left( 2 \right)\) (hai góc nội tiếp cùng chắn cung \(AC\)).
Từ (1) và (2) \( \Rightarrow \angle GBD = \angle ABC \Rightarrow BA\) là tia phân giác của góc \(\angle CBG\) (đpcm).
Bài 5
Phương pháp:
a) Số học sinh yêu thích hội họa chiếm tỉ lệ 20% so với số học sinh toàn trường nên ta có thể tính được số học sinh yêu thích hội họa.
b) Giải bài toán bằng cách lập phương trình.
Cách giải:
a) Tính số học sinh yêu thích hội họa.
Vì số học sinh yêu thích hội họa chiếm tỉ lệ 20% so với số học sinh toàn trường nên số học sinh yêu thích hội họa là: \(1500.20:100 = 300\) (học sinh).
b) Hỏi tổng số học sinh yêu thích thể thao và âm nhạc là bao nhiêu?
Gọi số học sinh yêu thích thể thao là \(x\) (học sinh) \(\left( {30\, < \,x < 1200,\,\,x \in \mathbb{N}*} \right).\)
Số học sinh chọn yêu thích khác là \(y\) (học sinh) \(\left( {y < 1200,\,\,y \in \mathbb{N}*} \right).\)
Số học sinh yêu thích thể thao hơn số học sinh yêu thích âm nhạc là \(30\) học sinh
\( \Rightarrow \) Số học sinh yêu thích âm nhạc là \(x - 30\) (học sinh).
Tổng số học sinh của trường là \(1500\) học sinh, số học sinh yêu thích hội họa là \(300\) học sinh nên số học sinh yêu thích thể thao, âm nhạc và các yêu thích khác là:
\(1500 - 300 = 1200\) (học sinh)
Khi đó ta có phương trình: \(x + x - 30 + y = 1200 \Leftrightarrow 2x + y = 1230\,\,\,\left( 1 \right)\)
Số học sinh yêu thích thể thao và hội họa bằng với số học sinh yêu thích âm nhạc và các yêu thích khác nên ta có phương trình: \(x + 300 = x - 30 + y \Leftrightarrow y = 330\,\,\,\left( {tm} \right)\,\,\,\,\)
Thay \(y = 330\) vào phương trình \(\left( 1 \right)\) ta được:\(2x = 1230 - y = 1230 - 330 = 900 \Leftrightarrow x = 450\,\,\,\left( {tm} \right)\)
\( \Rightarrow \) Số học sinh yêu thích âm nhạc là: \(450 - 30 = 420\) (học sinh).
Vậy tổng số học sinh yêu thích thể thao và âm nhạc là: \(450 + 420 = 870\) học sinh.
Bài 1 (3 điểm): Giải các phương trình và hệ phương trình sau đây:
a) \(\dfrac{x}{{\sqrt 3 }} + \sqrt 3 x = \sqrt 3 \) b) \({x^2} + 6x - 5 = 0\)
c) \(\left\{ \begin{array}{l}\sqrt 2 x + y = \sqrt 2 + 2\\2\sqrt 2 x - y = 2\sqrt 2 - 2\end{array} \right.\)
Bài 2 (1,5 điểm):
Cho hàm số có đồ thị là Parabol \(\left( P \right):y = 0,25{x^2}\).
a) Vẽ đồ thị \(\left( P \right)\) của hàm số đã cho.
b) Qua điểm \(A\left( {0;1} \right)\) vẽ đường thẳng song song với trục hoành \(Ox\) cắt \(\left( P \right)\) tại hai điểm \(E\) và \(F\). Viết tọa độ của \(E\) và \(F\).
Bài 3 (2 điểm): Cho phương trình bậc hai \({x^2} - \left( {m + 2} \right)x + 2m = 0\,\,\,\left( * \right)\) (\(m\) là tham số)
a) Chứng minh rằng phương trình (*) luôn có nghiệm với mọi \(m.\)
b) Tìm các giá trị của \(m\) để phương trình (*) có hai nghiệm \({x_1},\,\,{x_2}\) thỏa mãn: \( - 1 \le \dfrac{{2\left( {{x_1} + {x_2}} \right)}}{{{x_1}{x_2}}} \le 1.\)
Bài 4 (2,5 điểm)
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 4cm,\,\,AC = 3cm\). Lấy điểm \(D\) thuộc cạnh \(AB\,\,\left( {AD < DB} \right)\). Đường tròn \(\left( O \right)\) đường kính \(BD\) cắt \(CB\) tại \(E\), kéo dài \(CD\) cắt đường tròn \(\left( O \right)\) tại \(F\).
a) Chứng minh rằng \(ACED\) là tứ giác nội tiếp.
b) Biết \(BF = 3cm\). Tính \(BC\) và diện tích tam giác \(BFC\).
c) Kéo dài \(AF\) cắt đường tròn \(\left( O \right)\) tại \(G\). Chứng minh rằng \(BA\) là tia phân giác của góc \(CBG\).
Bài 5 (1 điểm):
Trường A tiến hành khảo sát 1500 học sinh về sự yêu thích hội họa, thể thao, âm nhạc và các yêu thích khác. Mỗi học sinh chỉ chọn một yêu thích. Biết số học sinh yêu thích hội họa chiếm tỉ lệ 20% so với số học sinh toàn trường.
Số học sinh yêu thích thể thao hơn số học sinh yêu thích âm nhạc là 30 học sinh; số học sinh yêu thích thể thao và hội họa bằng với số học sinh yêu thích âm nhạc và các yêu thích khác.
a) Tính số học sinh yêu thích hội họa.
b) Hỏi tổng số học sinh yêu thích thể thao và âm nhạc là bao nhiêu?
Bài 1
Phương pháp:
a) Quy đồng mẫu số rồi đưa về phương trình bậc nhất \(ax + b = 0\,\,\left( {a \ne 0} \right) \Leftrightarrow x = - \dfrac{b}{a}\)
b) Sử dụng công thức nghiệm thu gọn của phương trình bậc hai \(a{x^2} + bx + c = 0\,\)
có \(\Delta ' = {\left( {b'} \right)^2} - ac\). Với \(\Delta ' > 0\) thì phương trình có hai nghiệm phân biệt \({x_1} = \dfrac{{ - b' + \sqrt {\Delta '} }}{a};{x_2} = \dfrac{{ - b' - \sqrt {\Delta '} }}{a}\)
c) Giải hệ phương trình bằng phương pháp cộng đại số
Cách giải:
\(a)\,\,\,\dfrac{x}{{\sqrt 3 }} + \sqrt 3 x = \sqrt 3 \Leftrightarrow \dfrac{{x + 3x}}{{\sqrt 3 }} = \sqrt 3 \Leftrightarrow x + 3x = 3 \Leftrightarrow 4x = 3 \Leftrightarrow x = \dfrac{3}{4}\)
Vậy tập nghiệm của phương trình \(S = \left\{ {\dfrac{3}{4}} \right\}.\)
b) Phương trình \({x^2} + 6x - 5 = 0\) có \(\Delta ' = {3^2} - 1.\left( { - 5} \right) = 14 > 0\) nên phương trình có hai nghiệm phân biệt \({x_1} = - 3 + \sqrt {14} ;{x_2} = - 3 - \sqrt {14} \)
Vậy tập nghiệm của phương trình là:\(S = \left\{ { - 3 + \sqrt {14} ; - 3 - \sqrt {14} } \right\}.\)
c) \(\left\{ \begin{array}{l}\sqrt 2 x + y = \sqrt 2 + 2\\2\sqrt 2 x - y = 2\sqrt 2 - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\sqrt 2 x + y = \sqrt 2 + 2\\3\sqrt 2 x = 3\sqrt 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\\sqrt 2 .1 + y = \sqrt 2 + 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right.\)
Hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {1;2} \right).\)
Bài 2
Phương pháp:
a) +) Tìm các điểm đi qua của đồ thị hàm số.
+) Vẽ đồ thị.
b) Cho \(y = 1\) giải phương trình tìm \(x\) và kết luận.
Cách giải:
a) Vẽ đồ thị \(\left( P \right)\) của hàm số đã cho.
Cho \(x\) nhận các giá trị \( - 4; - 2;0;2;4\) ta có bảng sau:
\(x\) | \( - 4\) | \( - 2\) | \(0\) | \(2\) | \(4\) |
\(y\) | \(4\) | \(1\) | \(0\) | \(1\) | \(4\) |
Do đó đồ thị hàm số \(y = 0,25{x^2}\) là parabol đi qua các điểm \(M\left( { - 4;4} \right),N\left( { - 2;1} \right),O\left( {0;0} \right),P\left( {2;1} \right),Q\left( {4;4} \right)\)
Vẽ đồ thị:
b) Qua điểm \(A\left( {0;1} \right)\) vẽ đường thẳng song song với trục hoành \(Ox\) cắt \(\left( P \right)\) tại hai điểm \(E\) và \(F\). Viết tọa độ của \(E\) và \(F\).
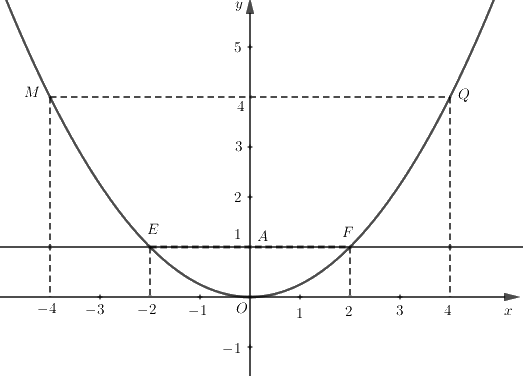
Đường thẳng đi qua \(A\left( {0;1} \right)\) và song song với trục hoành có phương trình \(y = 1\).
Xét phương trình hoành độ giao điểm của đường thẳng \(y = 1\) và parabol \(y = 0,25{x^2}\) ta có
\(0,25{x^2} = 1 \Leftrightarrow {x^2} = 4 \Leftrightarrow x = \pm 2\).
Với \(x = 2 \Rightarrow y = 1\)
Với \(x = - 2 \Rightarrow y = 1\)
Vậy hai điểm \(E\) và \(F\) có tọa độ lần lượt là \(\left( { - 2;1} \right)\)và \(\left( {2;1} \right)\).
Bài 3
Phương pháp:
a) Phương trình có hai nghiệm \( \Leftrightarrow \Delta \ge 0.\)
b) Áp dụng hệ thức Vi-ét và biểu thức bài cho để tìm \(m\), đối chiếu với điều kiện rồi kết luận.
Cách giải:
a) Chứng minh rằng phương trình (*) luôn có nghiệm với mọi \(m.\)
\({x^2} - \left( {m + 2} \right)x + 2m = 0\,\,\,\left( * \right)\)
Có: \(\Delta = {\left( {m + 2} \right)^2} - 4.2m = {m^2} + 4m + 4 - 8m = {m^2} - 4m + 4 = {\left( {m - 2} \right)^2} \ge 0\,\,\forall m\)
\( \Rightarrow \) Phương trình (*) luôn có nghiệm với mọi \(m.\)
b) Tìm các giá trị của \(m\) để phương trình (*) có hai nghiệm \({x_1},\,\,{x_2}\) thỏa mãn: \( - 1 \le \dfrac{{2\left( {{x_1} + {x_2}} \right)}}{{{x_1}{x_2}}} \le 1.\)
Theo câu a) ta có phương trình (*) luôn có nghiệm với mọi \(m.\)
Gọi \({x_1};{x_2}\) là hai nghiệm của phương trình (*)
Áp dụng hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m + 2\\{x_1}{x_2} = 2m\end{array} \right..\)
Theo đề bài ta có: \( - 1 \le \dfrac{{2\left( {{x_1} + {x_2}} \right)}}{{{x_1}{x_2}}} \le 1\)
\(\begin{array}{l} \Leftrightarrow - 1 \le \dfrac{{2\left( {m + 2} \right)}}{{2m}} \le 1 \Leftrightarrow \left\{ \begin{array}{l}2m \ne 0\\\dfrac{{m + 2}}{m} \ge - 1\\\dfrac{{m + 2}}{m} \le 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\\dfrac{{m + 2 + m}}{m} \ge 0\\\dfrac{{m + 2 - m}}{m} \le 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\\dfrac{{2m + 2}}{m} \ge 0\\\dfrac{2}{m} \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\\left[ \begin{array}{l}m > 0\\m \le - 1\end{array} \right.\\m < 0\end{array} \right. \Leftrightarrow m \le - 1.\end{array}\)
Vậy \(m \le - 1\) thỏa mãn bài toán.
Bài 4
Phương pháp:
a) Chứng minh tứ giác \(ACED\) có tổng hai góc đối bằng 1800.
b) Áp dụng định lí Pytago trong tam giác vuông \(ABC\) tính \(BC\).
Chứng minh tam giác \(BFC\) vuông. Áp dụng định lí Pytago trong tam giác vuông tính \(FC\), từ đó tính diện tích tam giác \(BFC\).
c) Chứng minh \(\angle GBD = \angle ABC = \angle AFC\), từ đó suy ra điều phải chứng minh.
Cách giải:
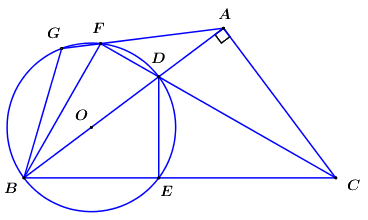
a) Chứng minh rằng \(ACED\) là tứ giác nội tiếp.
Ta có \(\angle BED = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow DE \bot BC \Rightarrow \angle CED = {90^0}\).
Xét tứ giác \(ACED\) có \(\angle CAD + \angle CED = {90^0} + {90^0} = {180^0}\) \( \Rightarrow \)Tứ giác \(ACED\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
b) Biết \(BF = 3cm\). Tính \(BC\) và diện tích tam giác \(BFC\).
Áp dụng định lí Pytago trong tam giác vuông \(ABC\) ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} = {4^2} + {3^2} = 16 + 9 = 25\\ \Rightarrow BC = \sqrt {25} = 5\,\,\left( {cm} \right)\end{array}\)
Ta có \(\angle BFD = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow BF \bot FD\) hay \(BF \bot FC \Rightarrow \Delta BFC\) vuông tại \(F\).
Áp dụng định lí Pytago trong tam giác vuông \(BFC\) ta có:
\(F{C^2} = B{C^2} - B{F^2} = {5^2} - {3^2} = 25 - 9 = 16\)
\( \Rightarrow FC = \sqrt {16} = 4\,\,\left( {cm} \right)\).
Vậy \({S_{BFC}} = \dfrac{1}{2}FB.FC = \dfrac{1}{2}.3.4 = 6\,\,\left( {c{m^2}} \right)\).
c) Kéo dài \(AF\) cắt đường tròn \(\left( O \right)\) tại \(G\). Chứng minh rằng \(BA\) là tia phân giác của góc \(\angle CBG\).
Nhận thấy bốn điểm \(B,\,\,D,\,\,F,\,\,G\) cùng thuộc \(\left( O \right) \Rightarrow \) Tứ giác \(BDFG\) là tứ giác nội tiếp.
\( \Rightarrow \angle GBD = \angle AFD = \angle AFC\) (1) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp).
Xét tứ giác \(AFBC\) có: \(\angle BAC = \angle BFC = {90^0} \Rightarrow \) Tứ giác \(AFBC\) là tứ giác nội tiếp (Tứ giác có 2 đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau).
Do đó \(\angle ABC = \angle AFC\,\,\left( 2 \right)\) (hai góc nội tiếp cùng chắn cung \(AC\)).
Từ (1) và (2) \( \Rightarrow \angle GBD = \angle ABC \Rightarrow BA\) là tia phân giác của góc \(\angle CBG\) (đpcm).
Bài 5
Phương pháp:
a) Số học sinh yêu thích hội họa chiếm tỉ lệ 20% so với số học sinh toàn trường nên ta có thể tính được số học sinh yêu thích hội họa.
b) Giải bài toán bằng cách lập phương trình.
Cách giải:
a) Tính số học sinh yêu thích hội họa.
Vì số học sinh yêu thích hội họa chiếm tỉ lệ 20% so với số học sinh toàn trường nên số học sinh yêu thích hội họa là: \(1500.20:100 = 300\) (học sinh).
b) Hỏi tổng số học sinh yêu thích thể thao và âm nhạc là bao nhiêu?
Gọi số học sinh yêu thích thể thao là \(x\) (học sinh) \(\left( {30\, < \,x < 1200,\,\,x \in \mathbb{N}*} \right).\)
Số học sinh chọn yêu thích khác là \(y\) (học sinh) \(\left( {y < 1200,\,\,y \in \mathbb{N}*} \right).\)
Số học sinh yêu thích thể thao hơn số học sinh yêu thích âm nhạc là \(30\) học sinh
\( \Rightarrow \) Số học sinh yêu thích âm nhạc là \(x - 30\) (học sinh).
Tổng số học sinh của trường là \(1500\) học sinh, số học sinh yêu thích hội họa là \(300\) học sinh nên số học sinh yêu thích thể thao, âm nhạc và các yêu thích khác là:
\(1500 - 300 = 1200\) (học sinh)
Khi đó ta có phương trình: \(x + x - 30 + y = 1200 \Leftrightarrow 2x + y = 1230\,\,\,\left( 1 \right)\)
Số học sinh yêu thích thể thao và hội họa bằng với số học sinh yêu thích âm nhạc và các yêu thích khác nên ta có phương trình: \(x + 300 = x - 30 + y \Leftrightarrow y = 330\,\,\,\left( {tm} \right)\,\,\,\,\)
Thay \(y = 330\) vào phương trình \(\left( 1 \right)\) ta được:\(2x = 1230 - y = 1230 - 330 = 900 \Leftrightarrow x = 450\,\,\,\left( {tm} \right)\)
\( \Rightarrow \) Số học sinh yêu thích âm nhạc là: \(450 - 30 = 420\) (học sinh).
Vậy tổng số học sinh yêu thích thể thao và âm nhạc là: \(450 + 420 = 870\) học sinh.
Kỳ thi tuyển sinh vào lớp 10 là một bước ngoặt quan trọng trong quá trình học tập của mỗi học sinh. Để đạt kết quả tốt nhất, việc chuẩn bị kỹ lưỡng là vô cùng cần thiết. Đề thi vào 10 môn Toán An Giang năm 2019 là một nguồn tài liệu quý giá, giúp học sinh nắm vững kiến thức và kỹ năng cần thiết.
Đề thi vào 10 môn Toán An Giang năm 2019 thường bao gồm các dạng bài tập sau:
Chúng ta sẽ cùng phân tích một số câu hỏi điển hình trong đề thi vào 10 môn Toán An Giang năm 2019 để hiểu rõ hơn về yêu cầu của đề thi.
Để giải quyết câu hỏi này, học sinh cần nắm vững các kiến thức về phương trình bậc hai, phương trình bậc ba, và các phương pháp giải phương trình khác.
Để chứng minh một bài toán hình học, học sinh cần nắm vững các định lý, tính chất, và các phương pháp chứng minh hình học.
Để đạt kết quả tốt nhất trong kỳ thi vào 10 môn Toán, học sinh cần lưu ý những điều sau:
Ngoài đề thi vào 10 môn Toán An Giang năm 2019, học sinh có thể tham khảo thêm các tài liệu ôn thi sau:
Giaitoan.edu.vn là một website học toán online uy tín, cung cấp các khóa học chất lượng cao, các bài giảng chi tiết, và các đề thi thử đa dạng. Chúng tôi cam kết đồng hành cùng học sinh trên con đường chinh phục kiến thức và đạt được thành công trong kỳ thi vào 10.
Hy vọng rằng, với những thông tin và phân tích trên, các em học sinh sẽ có thêm kiến thức và tự tin hơn trong kỳ thi tuyển sinh vào lớp 10 môn Toán tỉnh An Giang năm 2019.