Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Quảng Bình năm 2019 chính thức. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi sắp tới.
Bộ đề thi này bao gồm các đề thi chính thức của các trường THPT chuyên và không chuyên trên địa bàn tỉnh Quảng Bình, được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm của Giaitoan.edu.vn.
Câu 1 (2 điểm): Cho biểu thức
Câu 1 (2 điểm): Cho biểu thức \(A = \dfrac{1}{y} + \dfrac{2}{{y + 1}} - \dfrac{1}{{{y^2} + y}}.\)
a) Tìm điều kiện xác định và rút họn biểu thức \(A.\)
b) Tìm giá trị nguyên của \(y\) để \(A\) nhận giá trị nguyên.
Câu 2 (1,5 điểm): Cho hàm số \(y = \left( {a - 2} \right)x + 5\) có đồ thị là đường thẳng \(d.\)
a) Với giá trị nào của \(a\) thì hàm số trên đồng biến trên \(\mathbb{R}.\)
b) Tìm \(a\) để đường thẳng \(d\) đi qua điểm \(M\left( {2;3} \right)\).
Câu 3 (2 điểm): Cho phương trình \({x^2} - \left( {m + 1} \right)x + 2m - 2 = 0\,\,\,\,\left( 1 \right)\) (với \(m\) là tham số).
a) Giải phương trình \(\left( 1 \right)\) khi \(m = 2.\)
b) Tìm giá trị của \(m\) để phương trình \(\left( 1 \right)\) có hai nghiệm \({x_1},\,\,{x_2}\) thỏa mãn \(3\left( {{x_1} + {x_2}} \right) - {x_1}{x_2} = 10.\)
Câu 4 (1,0 điểm):
Cho \(x,y\) là hai số thực dương thỏa mãn \(x + y = \dfrac{{2020}}{{2019}}\). Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{{2019}}{x} + \dfrac{1}{{2019y}}\)
Câu 5 (3,5 điểm): Từ một điểm \(A\) nằm ngoài đường tròn tâm \(O,\) ta kẻ hai tiếp tuyến \(AB,\,\,AC\) với đường tròn (\(B,\,\,C\) là các tiếp điểm). Trên cung nhỏ \(BC\) lấy một điểm \(M\left( {M \ne B,\,\,M \ne C} \right),\) kẻ \(MI \bot AB,\,\,MK \bot AC\,\,\left( {I \in AB,\,\,K \in AC} \right).\)
a) Chứng minh \(AIMK\) là tứ giác nội tiếp đường tròn.
b) Kẻ \(MP \bot BC\,\,\left( {P \in BC} \right).\) Chứng minh rằng \(\angle MPK = \angle MBC.\)
c) Xác định vị trí của \(M\) trên cung nhỏ \(BC\) để tích \(MI.MK.MP\) đạt giá trị lớn nhất.
Câu 1 (2 điểm): Cho biểu thức \(A = \dfrac{1}{y} + \dfrac{2}{{y + 1}} - \dfrac{1}{{{y^2} + y}}.\)
a) Tìm điều kiện xác định và rút họn biểu thức \(A.\)
b) Tìm giá trị nguyên của \(y\) để \(A\) nhận giá trị nguyên.
Câu 2 (1,5 điểm): Cho hàm số \(y = \left( {a - 2} \right)x + 5\) có đồ thị là đường thẳng \(d.\)
a) Với giá trị nào của \(a\) thì hàm số trên đồng biến trên \(\mathbb{R}.\)
b) Tìm \(a\) để đường thẳng \(d\) đi qua điểm \(M\left( {2;3} \right)\).
Câu 3 (2 điểm): Cho phương trình \({x^2} - \left( {m + 1} \right)x + 2m - 2 = 0\,\,\,\,\left( 1 \right)\) (với \(m\) là tham số).
a) Giải phương trình \(\left( 1 \right)\) khi \(m = 2.\)
b) Tìm giá trị của \(m\) để phương trình \(\left( 1 \right)\) có hai nghiệm \({x_1},\,\,{x_2}\) thỏa mãn \(3\left( {{x_1} + {x_2}} \right) - {x_1}{x_2} = 10.\)
Câu 4 (1,0 điểm):
Cho \(x,y\) là hai số thực dương thỏa mãn \(x + y = \dfrac{{2020}}{{2019}}\). Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{{2019}}{x} + \dfrac{1}{{2019y}}\)
Câu 5 (3,5 điểm): Từ một điểm \(A\) nằm ngoài đường tròn tâm \(O,\) ta kẻ hai tiếp tuyến \(AB,\,\,AC\) với đường tròn (\(B,\,\,C\) là các tiếp điểm). Trên cung nhỏ \(BC\) lấy một điểm \(M\left( {M \ne B,\,\,M \ne C} \right),\) kẻ \(MI \bot AB,\,\,MK \bot AC\,\,\left( {I \in AB,\,\,K \in AC} \right).\)
a) Chứng minh \(AIMK\) là tứ giác nội tiếp đường tròn.
b) Kẻ \(MP \bot BC\,\,\left( {P \in BC} \right).\) Chứng minh rằng \(\angle MPK = \angle MBC.\)
c) Xác định vị trí của \(M\) trên cung nhỏ \(BC\) để tích \(MI.MK.MP\) đạt giá trị lớn nhất.
Câu 1 (TH):
Phương pháp:
a) Sử dụng hằng đẳng thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)
Thực hiện các phép tính với căn bậc hai.
b) Xác định mẫu thức chung của biểu thức
Quy đồng các phân thức, thực hiện các phép toán từ đó rút gọn được biểu thức.
Cách giải:
a) \(P = \sqrt {12} - \sqrt {27} + \sqrt {48} .\)
\(\begin{array}{l}P = \sqrt {12} - \sqrt {27} + \sqrt {48} .\\\,\,\,\,\, = \sqrt {{2^2}.3} - \sqrt {{3^2}.3} + \sqrt {{4^2}.3} \\\,\,\,\,\, = 2\sqrt 3 - 3\sqrt 3 + 4\sqrt 3 \\\,\,\,\,\, = 3\sqrt 3 .\end{array}\)
Vậy \(P = 3\sqrt 3 .\)
b) \(Q = \left( {5 - \dfrac{{x + \sqrt x }}{{\sqrt x + 1}}} \right).\left( {5 + \dfrac{{x - \sqrt x }}{{\sqrt x - 1}}} \right)\) với \(x \ge 0,\,\,x \ne 1.\)
Điều kiện: \(x \ge 0,\,\,x \ne 1.\)
\(\begin{array}{l}Q = \left( {5 - \dfrac{{x + \sqrt x }}{{\sqrt x + 1}}} \right).\left( {5 + \dfrac{{x - \sqrt x }}{{\sqrt x - 1}}} \right)\\\,\,\,\, = \left( {5 - \dfrac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\sqrt x + 1}}} \right).\left( {5 + \dfrac{{\sqrt x \left( {\sqrt x - 1} \right)}}{{\sqrt x - 1}}} \right)\\\,\,\,\, = \left( {5 - \sqrt x } \right)\left( {5 + \sqrt x } \right)\\\,\,\,\, = 25 - x.\end{array}\)
Vậy \(Q = 25 - x\) khi \(x \ge 0,\,\,x \ne 1.\)
Câu 2 (TH):
Phương pháp:
a) Hàm số \(y = ax + b\) nghịch biến trên \(\mathbb{R} \Leftrightarrow a < 0\)
b) Sử dụng phương pháp cộng đại số, tìm được nghiệm \(x\)
Sử dụng phương pháp thế, tìm được nghiệm \(y\)
Kết luận nghiệm \(\left( {x;y} \right)\) của hệ phương trình.
Cách giải:
a) Hàm số \(y = \left( {n - 1} \right)x + 2\) nghịch biến trên \(\mathbb{R}\) \( \Leftrightarrow n - 1 < 0\) \( \Leftrightarrow n < 1.\)
Vậy \(n < 1\) thì hàm số đã cho nghịch biến trên \(\mathbb{R}.\)
b) \(\left\{ \begin{array}{l}2x + 3y = 8\\ - 4x + 3y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}6x = 6\\y = \dfrac{{8 - 2x}}{3}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = \dfrac{{8 - 2.1}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right.\)
Vậy hệ phương trình có tập nghiệm \(S = \left\{ {\left( {1;\,\,2} \right)} \right\}.\)
Câu 3 (VD):
Phương pháp:
a) Tính nhẩm nghiệm của phương trình bậc hai: Nếu \(a - b + c = 0\) thì phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt: \({x_1} = - 1;{x_2} = - \dfrac{c}{a}\)
b) Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt \(\Delta > 0\) (hoặc \(\Delta ' > 0\))
Áp dụng hệ thức Vi – ét, tính được \({x_1} + {x_2};{x_1}.{x_2}\) theo \(n\)
Thay vào \(2020\left( {{x_1} + {x_2}} \right) + 2021{x_1}{x_2} = - 2014.\), ta tìm được \(n\)
Cách giải:
a) Với \(n = 1\) ta có phương trình \(\left( 1 \right)\) trở thành: \({x^2} + 6x + 5 = 0\)
Phương trình có \(a - b + c = 1 - 6 + 5 = 0\)
\( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \({x_1} = - 1\) và \({x_2} = - \dfrac{c}{a} = - 5.\)
Vậy với \(n = 1\) thì phương trình đã cho có tập nghiệm \(S = \left\{ { - 5; - 1} \right\}.\)
b) Xét phương trình \({x^2} + 6x + n + 4 = 0\,\,\,\,\left( 1 \right)\)
Phương trình có: \(\Delta ' = 9 - n - 4 = 5 - n.\)
Phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) \( \Leftrightarrow \Delta ' > 0\) \( \Leftrightarrow 5 - n > 0\) \( \Leftrightarrow n < 5.\)
Với \(n < 5\) thì phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}.\)
Áp dụng hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 6\\{x_1}{x_2} = n + 4\end{array} \right..\)
Theo đề bài ta có: \(2020\left( {{x_1} + {x_2}} \right) + 2021{x_1}{x_2} = - 2014\)
\(\begin{array}{l} \Leftrightarrow 2020.\left( { - 6} \right) + 2021.\left( {n + 4} \right) = - 2014\\ \Leftrightarrow - 12120 + 2021n + 8084 = - 2014\\ \Leftrightarrow 2021n = 2022\\ \Leftrightarrow n = \dfrac{{2022}}{{2021}}\,\,\,\left( {tm} \right).\end{array}\)
Vậy \(n = \dfrac{{2022}}{{2021}}\) thỏa mãn bài toán.
Câu 4 (VDC):
Phương pháp:
Áp dụng bất đẳng thức Cô – si cho \(\sqrt {9a\left( {8a + b} \right)} \) và \(\sqrt {9b\left( {8b + a} \right)} \)
Từ đó, suy ra \(\sqrt {9a\left( {8a + b} \right)} + \sqrt {9b\left( {8b + a} \right)} \) sau đó, suy ra được \(\dfrac{{a + b}}{{\sqrt {a\left( {8a + b} \right)} + \sqrt {b\left( {8b + a} \right)} }}\)
Cách giải:
Áp dụng BĐT Cô-si ta có:
\(\begin{array}{l}\sqrt {9a\left( {8a + b} \right)} \le \dfrac{{9a + 8a + b}}{2} = \dfrac{{17a + b}}{2}\\\sqrt {9b\left( {8b + a} \right)} \le \dfrac{{9b + 8b + a}}{2} = \dfrac{{17b + a}}{2}\\ \Rightarrow \sqrt {9a\left( {8a + b} \right)} + \sqrt {9b\left( {8b + a} \right)} \le \dfrac{{17a + b}}{2} + \dfrac{{17b + a}}{2} = 9\left( {a + b} \right)\\ \Rightarrow \sqrt {a\left( {8a + b} \right)} + \sqrt {b\left( {8b + a} \right)} \le 3\left( {a + b} \right)\\ \Rightarrow \dfrac{{a + b}}{{\sqrt {a\left( {8a + b} \right)} + \sqrt {b\left( {8b + a} \right)} }} \ge \dfrac{1}{3}\,\,\,\left( {dpcm} \right).\end{array}\)
Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}9a = 8a + b\\9b = 8b + a\end{array} \right. \Leftrightarrow a = b.\)
Vậy \(\dfrac{{a + b}}{{\sqrt {a\left( {8a + b} \right)} + \sqrt {b\left( {8b + a} \right)} }} \ge \dfrac{1}{3}.\)
Câu 5 (VD):
Phương pháp:
a) Vận dụng dấu hiệu nhận biết: Tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp.
b) Ta sẽ chứng minh: \(\angle PEB = {180^0} - \angle FAB\,\,\,\left( 1 \right);\angle FPB = {180^0} - \angle FAB\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) \( \Rightarrow \angle FBB = \angle PEB\,\,\left( { = {{180}^0} - \angle FAB} \right)\)
Chứng minh được:
c)
Áp dụng hệ thức lượng trong \(\Delta APB\)ta có:\(A{P^2} = AH.AB\)
Áp dụng định lý Py – ta – go cho \(\Delta APB\): \(B{P^2} + A{P^2} = A{B^2} = 4{R^2}\)
\( \Rightarrow BE.BF + AH.AB = 4{R^2}\) (đpcm)
Cách giải:
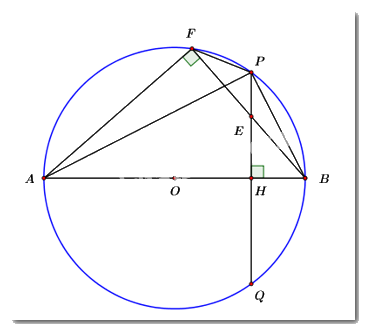
a) Ta có: \(\angle AFB\) là góc nội tiếp chắn nửa đường tròn \(\left( {O;\,\,R} \right).\)
\( \Rightarrow \angle AFB = {90^0}\)
Xét tứ giác \(AHEF\) ta có: \(\angle AFE + \angle AHE = {90^0} + {90^0} = {180^0}\)
\( \Rightarrow AHEF\) là tứ giác nội tiếp. (dhnb)
b) Ta có: \(AHEF\) là tứ giác nội tiếp (cmt)
\( \Rightarrow \angle FAH + \angle FEH = {180^0}\) (tính chất tứ giác nội tiếp)
Lại có: \(\angle PEB = \angle FEH\) (hai góc đối đỉnh).
\( \Rightarrow \angle PEB + \angle FAB = {180^0}\) \( \Rightarrow \angle PEB = {180^0} - \angle FAB\,\,\,\left( 1 \right)\)
Mà \(ABPF\) là tứ giác nội tiếp đường tròn \(\left( {O;\,\,R} \right)\)
\( \Rightarrow \angle FAB + \angle BPF = {180^0}\) \( \Rightarrow \angle FPB = {180^0} - \angle FAB\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) \( \Rightarrow \angle FBB = \angle PEB\,\,\left( { = {{180}^0} - \angle FAB} \right)\)
Xét \(\Delta BEP\) và \(\Delta BPF\) ta có:
\(\begin{array}{l}\angle FBB = \angle PEB\,\,\,\left( {cmt} \right)\\\angle B\,\,chung\\ \Rightarrow \Delta BEP \backsim \Delta BPF\,\,\,\left( {g - g} \right).\end{array}\)
c) Ta có: \(\Delta BEP \backsim \Delta BPF\,\,\,\left( {cmt} \right)\)
\( \Rightarrow \dfrac{{BE}}{{BP}} = \dfrac{{BP}}{{BF}} \Rightarrow B{P^2} = BE + BF.\)
Vì \(\angle APB\) là góc nội tiếp chắn nửa đường tròn \(\left( {O;\,\,R} \right)\)
\(\angle APB = {90^0}\) hay \(AP \bot PB\)
Áp dụng hệ thức lượng cho \(\Delta APB\) vuông tại \(P\) có đường cao \(PH\) ta có:
\(A{P^2} = AH.AB\)
\( \Rightarrow BE.BF + AH.AB = B{P^2} + A{P^2}\)
Áp dụng định lý Pitago cho \(\Delta APB\) vuông tại \(P\) ta có:
\(\begin{array}{l}B{P^2} + A{P^2} = A{B^2} = {\left( {2R} \right)^2} = 4{R^2}\\ \Rightarrow BE.BF + AH.AB = 4{R^2}\,\,\,\,\left( {dpcm} \right).\end{array}\)
Câu 1 (TH):
Phương pháp:
a) Sử dụng hằng đẳng thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)
Thực hiện các phép tính với căn bậc hai.
b) Xác định mẫu thức chung của biểu thức
Quy đồng các phân thức, thực hiện các phép toán từ đó rút gọn được biểu thức.
Cách giải:
a) \(P = \sqrt {12} - \sqrt {27} + \sqrt {48} .\)
\(\begin{array}{l}P = \sqrt {12} - \sqrt {27} + \sqrt {48} .\\\,\,\,\,\, = \sqrt {{2^2}.3} - \sqrt {{3^2}.3} + \sqrt {{4^2}.3} \\\,\,\,\,\, = 2\sqrt 3 - 3\sqrt 3 + 4\sqrt 3 \\\,\,\,\,\, = 3\sqrt 3 .\end{array}\)
Vậy \(P = 3\sqrt 3 .\)
b) \(Q = \left( {5 - \dfrac{{x + \sqrt x }}{{\sqrt x + 1}}} \right).\left( {5 + \dfrac{{x - \sqrt x }}{{\sqrt x - 1}}} \right)\) với \(x \ge 0,\,\,x \ne 1.\)
Điều kiện: \(x \ge 0,\,\,x \ne 1.\)
\(\begin{array}{l}Q = \left( {5 - \dfrac{{x + \sqrt x }}{{\sqrt x + 1}}} \right).\left( {5 + \dfrac{{x - \sqrt x }}{{\sqrt x - 1}}} \right)\\\,\,\,\, = \left( {5 - \dfrac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\sqrt x + 1}}} \right).\left( {5 + \dfrac{{\sqrt x \left( {\sqrt x - 1} \right)}}{{\sqrt x - 1}}} \right)\\\,\,\,\, = \left( {5 - \sqrt x } \right)\left( {5 + \sqrt x } \right)\\\,\,\,\, = 25 - x.\end{array}\)
Vậy \(Q = 25 - x\) khi \(x \ge 0,\,\,x \ne 1.\)
Câu 2 (TH):
Phương pháp:
a) Hàm số \(y = ax + b\) nghịch biến trên \(\mathbb{R} \Leftrightarrow a < 0\)
b) Sử dụng phương pháp cộng đại số, tìm được nghiệm \(x\)
Sử dụng phương pháp thế, tìm được nghiệm \(y\)
Kết luận nghiệm \(\left( {x;y} \right)\) của hệ phương trình.
Cách giải:
a) Hàm số \(y = \left( {n - 1} \right)x + 2\) nghịch biến trên \(\mathbb{R}\) \( \Leftrightarrow n - 1 < 0\) \( \Leftrightarrow n < 1.\)
Vậy \(n < 1\) thì hàm số đã cho nghịch biến trên \(\mathbb{R}.\)
b) \(\left\{ \begin{array}{l}2x + 3y = 8\\ - 4x + 3y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}6x = 6\\y = \dfrac{{8 - 2x}}{3}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = \dfrac{{8 - 2.1}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right.\)
Vậy hệ phương trình có tập nghiệm \(S = \left\{ {\left( {1;\,\,2} \right)} \right\}.\)
Câu 3 (VD):
Phương pháp:
a) Tính nhẩm nghiệm của phương trình bậc hai: Nếu \(a - b + c = 0\) thì phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt: \({x_1} = - 1;{x_2} = - \dfrac{c}{a}\)
b) Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt \(\Delta > 0\) (hoặc \(\Delta ' > 0\))
Áp dụng hệ thức Vi – ét, tính được \({x_1} + {x_2};{x_1}.{x_2}\) theo \(n\)
Thay vào \(2020\left( {{x_1} + {x_2}} \right) + 2021{x_1}{x_2} = - 2014.\), ta tìm được \(n\)
Cách giải:
a) Với \(n = 1\) ta có phương trình \(\left( 1 \right)\) trở thành: \({x^2} + 6x + 5 = 0\)
Phương trình có \(a - b + c = 1 - 6 + 5 = 0\)
\( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \({x_1} = - 1\) và \({x_2} = - \dfrac{c}{a} = - 5.\)
Vậy với \(n = 1\) thì phương trình đã cho có tập nghiệm \(S = \left\{ { - 5; - 1} \right\}.\)
b) Xét phương trình \({x^2} + 6x + n + 4 = 0\,\,\,\,\left( 1 \right)\)
Phương trình có: \(\Delta ' = 9 - n - 4 = 5 - n.\)
Phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) \( \Leftrightarrow \Delta ' > 0\) \( \Leftrightarrow 5 - n > 0\) \( \Leftrightarrow n < 5.\)
Với \(n < 5\) thì phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}.\)
Áp dụng hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 6\\{x_1}{x_2} = n + 4\end{array} \right..\)
Theo đề bài ta có: \(2020\left( {{x_1} + {x_2}} \right) + 2021{x_1}{x_2} = - 2014\)
\(\begin{array}{l} \Leftrightarrow 2020.\left( { - 6} \right) + 2021.\left( {n + 4} \right) = - 2014\\ \Leftrightarrow - 12120 + 2021n + 8084 = - 2014\\ \Leftrightarrow 2021n = 2022\\ \Leftrightarrow n = \dfrac{{2022}}{{2021}}\,\,\,\left( {tm} \right).\end{array}\)
Vậy \(n = \dfrac{{2022}}{{2021}}\) thỏa mãn bài toán.
Câu 4 (VDC):
Phương pháp:
Áp dụng bất đẳng thức Cô – si cho \(\sqrt {9a\left( {8a + b} \right)} \) và \(\sqrt {9b\left( {8b + a} \right)} \)
Từ đó, suy ra \(\sqrt {9a\left( {8a + b} \right)} + \sqrt {9b\left( {8b + a} \right)} \) sau đó, suy ra được \(\dfrac{{a + b}}{{\sqrt {a\left( {8a + b} \right)} + \sqrt {b\left( {8b + a} \right)} }}\)
Cách giải:
Áp dụng BĐT Cô-si ta có:
\(\begin{array}{l}\sqrt {9a\left( {8a + b} \right)} \le \dfrac{{9a + 8a + b}}{2} = \dfrac{{17a + b}}{2}\\\sqrt {9b\left( {8b + a} \right)} \le \dfrac{{9b + 8b + a}}{2} = \dfrac{{17b + a}}{2}\\ \Rightarrow \sqrt {9a\left( {8a + b} \right)} + \sqrt {9b\left( {8b + a} \right)} \le \dfrac{{17a + b}}{2} + \dfrac{{17b + a}}{2} = 9\left( {a + b} \right)\\ \Rightarrow \sqrt {a\left( {8a + b} \right)} + \sqrt {b\left( {8b + a} \right)} \le 3\left( {a + b} \right)\\ \Rightarrow \dfrac{{a + b}}{{\sqrt {a\left( {8a + b} \right)} + \sqrt {b\left( {8b + a} \right)} }} \ge \dfrac{1}{3}\,\,\,\left( {dpcm} \right).\end{array}\)
Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}9a = 8a + b\\9b = 8b + a\end{array} \right. \Leftrightarrow a = b.\)
Vậy \(\dfrac{{a + b}}{{\sqrt {a\left( {8a + b} \right)} + \sqrt {b\left( {8b + a} \right)} }} \ge \dfrac{1}{3}.\)
Câu 5 (VD):
Phương pháp:
a) Vận dụng dấu hiệu nhận biết: Tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp.
b) Ta sẽ chứng minh: \(\angle PEB = {180^0} - \angle FAB\,\,\,\left( 1 \right);\angle FPB = {180^0} - \angle FAB\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) \( \Rightarrow \angle FBB = \angle PEB\,\,\left( { = {{180}^0} - \angle FAB} \right)\)
Chứng minh được:
c)
Áp dụng hệ thức lượng trong \(\Delta APB\)ta có:\(A{P^2} = AH.AB\)
Áp dụng định lý Py – ta – go cho \(\Delta APB\): \(B{P^2} + A{P^2} = A{B^2} = 4{R^2}\)
\( \Rightarrow BE.BF + AH.AB = 4{R^2}\) (đpcm)
Cách giải:
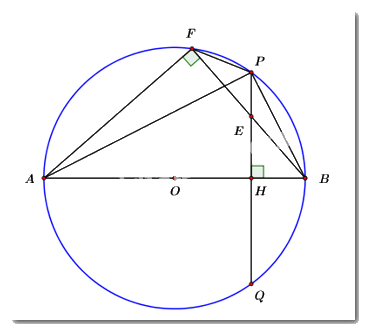
a) Ta có: \(\angle AFB\) là góc nội tiếp chắn nửa đường tròn \(\left( {O;\,\,R} \right).\)
\( \Rightarrow \angle AFB = {90^0}\)
Xét tứ giác \(AHEF\) ta có: \(\angle AFE + \angle AHE = {90^0} + {90^0} = {180^0}\)
\( \Rightarrow AHEF\) là tứ giác nội tiếp. (dhnb)
b) Ta có: \(AHEF\) là tứ giác nội tiếp (cmt)
\( \Rightarrow \angle FAH + \angle FEH = {180^0}\) (tính chất tứ giác nội tiếp)
Lại có: \(\angle PEB = \angle FEH\) (hai góc đối đỉnh).
\( \Rightarrow \angle PEB + \angle FAB = {180^0}\) \( \Rightarrow \angle PEB = {180^0} - \angle FAB\,\,\,\left( 1 \right)\)
Mà \(ABPF\) là tứ giác nội tiếp đường tròn \(\left( {O;\,\,R} \right)\)
\( \Rightarrow \angle FAB + \angle BPF = {180^0}\) \( \Rightarrow \angle FPB = {180^0} - \angle FAB\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) \( \Rightarrow \angle FBB = \angle PEB\,\,\left( { = {{180}^0} - \angle FAB} \right)\)
Xét \(\Delta BEP\) và \(\Delta BPF\) ta có:
\(\begin{array}{l}\angle FBB = \angle PEB\,\,\,\left( {cmt} \right)\\\angle B\,\,chung\\ \Rightarrow \Delta BEP \backsim \Delta BPF\,\,\,\left( {g - g} \right).\end{array}\)
c) Ta có: \(\Delta BEP \backsim \Delta BPF\,\,\,\left( {cmt} \right)\)
\( \Rightarrow \dfrac{{BE}}{{BP}} = \dfrac{{BP}}{{BF}} \Rightarrow B{P^2} = BE + BF.\)
Vì \(\angle APB\) là góc nội tiếp chắn nửa đường tròn \(\left( {O;\,\,R} \right)\)
\(\angle APB = {90^0}\) hay \(AP \bot PB\)
Áp dụng hệ thức lượng cho \(\Delta APB\) vuông tại \(P\) có đường cao \(PH\) ta có:
\(A{P^2} = AH.AB\)
\( \Rightarrow BE.BF + AH.AB = B{P^2} + A{P^2}\)
Áp dụng định lý Pitago cho \(\Delta APB\) vuông tại \(P\) ta có:
\(\begin{array}{l}B{P^2} + A{P^2} = A{B^2} = {\left( {2R} \right)^2} = 4{R^2}\\ \Rightarrow BE.BF + AH.AB = 4{R^2}\,\,\,\,\left( {dpcm} \right).\end{array}\)
Kỳ thi tuyển sinh vào lớp 10 là một bước ngoặt quan trọng trong quá trình học tập của mỗi học sinh. Để đạt kết quả tốt nhất, việc chuẩn bị kỹ lưỡng là vô cùng cần thiết. Đề thi vào 10 môn Toán Quảng Bình năm 2019 là một nguồn tài liệu quý giá để các em học sinh ôn tập và rèn luyện kỹ năng giải toán.
Đề thi vào 10 môn Toán Quảng Bình năm 2019 thường có cấu trúc gồm các phần sau:
Các chủ đề toán học thường xuyên xuất hiện trong đề thi vào 10 môn Toán Quảng Bình năm 2019 bao gồm:
Để giải đề thi vào 10 môn Toán Quảng Bình năm 2019 hiệu quả, các em học sinh cần:
Việc luyện tập với đề thi vào 10 môn Toán Quảng Bình năm 2019 mang lại nhiều lợi ích cho các em học sinh:
Giaitoan.edu.vn là một nền tảng học toán online uy tín, cung cấp các khóa học toán chất lượng cao, đội ngũ giáo viên giàu kinh nghiệm và các tài liệu ôn thi hữu ích. Chúng tôi cam kết giúp các em học sinh đạt kết quả tốt nhất trong kỳ thi tuyển sinh vào lớp 10.
Ngoài việc luyện tập với đề thi vào 10 môn Toán Quảng Bình năm 2019, các em học sinh cũng nên:
Đề thi vào 10 môn Toán Quảng Bình năm 2019 là một tài liệu quan trọng giúp các em học sinh ôn tập và rèn luyện kỹ năng giải toán. Hy vọng rằng với những thông tin và hướng dẫn trên, các em học sinh sẽ đạt kết quả tốt nhất trong kỳ thi sắp tới. Chúc các em thành công!